Metal–ligand bonding in tricarbonyliron(0) complexes bearing thiochalcone ligands

Abstract

This quantum chemical study aims to address metal–ligand bonding interactions between iron and thiochalcones in a series of recently synthesized tricarbonyliron(0) complexes with hetaryl- and/or ferrocenyl-functionalized thiochalcone ligands. A wide variety of theoretical methods, including both topological and orbital approaches, were used to shed light on the bonding situation of the thiochalcones η⁴-coordinated through their 1-thia-1,3-diene fragment to the Fe(CO)₃ moiety. In general, the interaction of Fe(CO)₃ with thiochalcones is considerably weaker than in comparison to the interaction with butadiene as well as with 1-thia-1,3-diene (substituted with two methyl groups). The decomposition of the Fe(CO)₃–thiochalcone binding energy reveals the dominant covalent nature of the interaction between the Fe(CO)₃ and thiochalcone fragments. This is confirmed by a more detailed examination of diatomic interactions between the Fe center and the 1-thia-1,3-diene fragment of thiochalcones. Further analysis of the Fe(CO)₃–thiochalcone bonding indicates extensive π-back-donation from the occupied d-orbitals of Fe to the LUMO of thiochalcone (π*). This explains (i) changes in the bond lengths of the η⁴-coordinated fragment of thiochalcones and (ii) charge distribution among the Fe center and the ligands in the complexes. Despite its formal zero oxidation state, the Fe center bears a positive atomic charge, while the thiochalcone and carbonyl ligands acquire ancillary electron charge. π-Delocalization is observed within the 1-thia-1,3-diene fragment of the η⁴-coordinated thiochalcones, yet the central C–C bond of the fragment exhibits somewhat stronger π-character.

---

Introduction

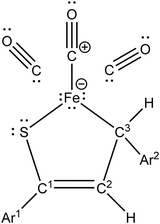
Iron(0) carbonyl complexes with π-ligands have been known for a long time in organometallic chemistry.¹ Among such complexes, those containing dienes with conjugated double bonds are of particular interest in organic synthesis because their stability makes them very useful intermediates.^2,3 To this date, the synthesis and characterization of many tricarbonyliron(0) complexes bearing a 1,3-diene, 1-aza-1,3-diene or 1-oxa-1,3-diene π-ligand have been reported.^3–5 These complexes proved to be valuable synthetic building blocks^6,7 and their several promising biological applications were also noticed.^8,9 The Fe(CO)₃ moiety in these complexes serves as (i) a protecting group preventing the π-ligands from undesirable reactions¹⁰ or (ii) a group ensuring a high level of regio- and stereocontrol in reactions.^11,12

In contrast to the aforementioned heterodiene π-ligands, thiochalcones (that is, α,β-unsaturated aromatic thioketones) have hardly ever been coordinated to the Fe(CO)₃ moiety. The synthesis and experimental characterization of Fe(CO)₃ complexes with α,β-unsaturated thioamides and several thioesters containing phenyl substituents were described by Alper and Brandes.¹³ In our recent joint synthetic-theoretical study,¹⁴ a series of Fe(CO)₃ complexes with 1-thia-1,3-dienes was obtained as the main product from the reaction of thiochalcones with triiron dodecacarbonyl and characterized by means of X-ray crystallography (Scheme 1). It should be noted that the reaction of thiochalcones with Fe₃(CO)₁₂ also led to other products whose formation was elucidated by the plausible reaction mechanism derived from quantum chemical calculations.¹⁴

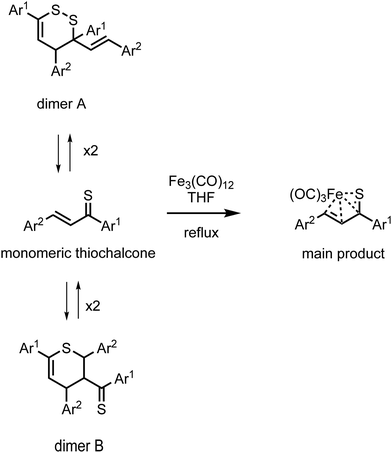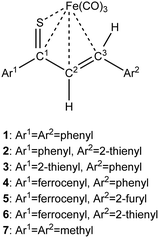
Scheme 1 Synthesis of Fe(CO)₃ complexes with 1-thia-1,3-dienes bearing aromatic groups Ar¹ and Ar² (thiochalcones).

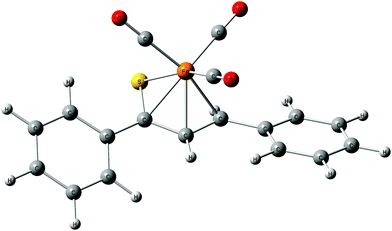
As a follow-up to this contribution, we provide here a detailed and comprehensive theoretical picture of metal–ligand bonding in a series of six 18-electron tricarbonyl(η⁴-1-thia-1,3-diene)iron(0) complexes 1–6 (Chart 1). Complexes 1, 3, 4 and 6 were previously investigated by X-ray diffraction (XRD)¹⁴ while the crystal structures of 2 and 5 are currently reported for the first time (Fig. 1 and Section S1, ESI†). The thiochalcone ligands in these complexes are functionalized with hetaryl and ferrocenyl groups, which originates from our ongoing interest in aromatic and cycloaliphatic thioketones.^15–22 For comparison, the present study additionally includes model complex 7 (Chart 1) in order to assess the effect of aromatic groups Ar¹ and Ar² for 1–6. In the series of complexes 1–7, the metal–ligand bonds cover both the iron-thiadiene interaction and three iron–carbonyl bonds. Here, we focus on the former because the Fe–CO bond in various complexes has already been the subject of a great number of computational studies.^23–27 By contrast, the metal–ligand bonding between Fe and thiochalcones has not been elucidated from a computational quantum chemical perspective so far. Thus, the interactions between the Fe center and the 1,3-thiadiene ligands in 1–7 will be examined here using a wide variety of modern quantum chemical methods. The theoretical picture of these interactions is relevant to the understanding of bonding patterns in related complexes and their reactivity.

Chart 1 Schematic representation of complexes 1–7.

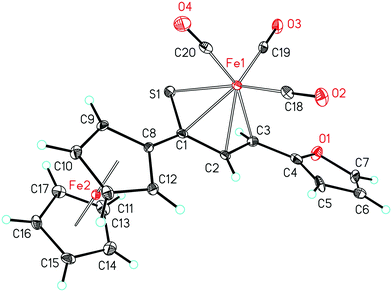Fig. 1 Molecular structure of complex 5. Displacement ellipsoids are drawn at the 30% probability level. Hydrogen atoms are shown with arbitrary radii.

Computational details

Complexes 1–6 in their initial geometries extracted from the corresponding XRD crystal structures were subjected to the procedure of geometry optimization without any geometrical restraints imposed. The initial structure of model complex 7 was adapted from complex 1, while the two phenyl rings were replaced by methyl groups. The geometry relaxations were carried out at the ωB97X-D/def2-SVP level of theory,^28,29 considering a closed-shell singlet state, a triplet and a quintet state, respectively. Harmonic vibrational frequency calculations were performed at the same level of theory to verify that the optimized structures corresponded to true local minima on the 3N-6 dimensional potential energy surface. As shown in previous studies,^30,31 the ωB97X-D density functional is capable of describing the geometrical as well as the electronic structure of iron complexes accurately. The choice of this functional was further validated within the scope of the present contribution (Section S2, ESI†). For the optimized structures of 1–7, additional single-point calculations were performed at several levels of theory: CASSCF/def2-SVP^29,32 with an active space of 4 electrons in 6 orbitals (Fig. S4–S9, ESI†), MP2/def2-TZVPD^29,33,34 and B3LYP/def2-TZVPD.^29,34,35 The wave functions generated by the B3LYP density functional were used by the quantum theory of atoms in molecules (QTAIM),³⁶ the source function (SF)³⁷ and the interacting quantum atoms (IQA) method,³⁸ while the analysis of the transition state coupled with natural orbitals for chemical valence (ETS-NOCV)³⁹ and the natural bond orbital (NBO) method⁴⁰ operated on ωB97X-D/def2-SVP wave functions.

Geometry optimizations and single-point energy calculations were carried out using the Gaussian 16 C.01 program.⁴¹ The QTAIM, SF and IQA implementations available in AIMAll 19.10.12 were used.⁴² Multiwfn 3.8⁴³ was employed to establish the composition of frontier molecular orbitals in terms of natural atomic orbitals⁴⁴ and to perform the ETS-NOCV analysis. The NBO analysis was done with the NBO 6.0 program.⁴⁵ Further computational details can be found in Section S2 (ESI†).

Results and discussion

Electronic structure

First, the fully relaxed equilibrium structures of complexes 1–6 were obtained at the DFT level while various electron configurations were taken into account to establish a robust computational protocol to evaluate the ground state of this class of Fe(0) complexes. The optimized geometries in the closed-shell singlet configuration turn out to be closest to the corresponding geometries extracted from the XRD crystal structures measured here and in our previous study.¹⁴ Moreover, the energy of each complex optimized for the singlet spin state lies substantially lower than the energies of the complex optimized for high-spin configurations (i.e. triplet and quintet states; Table S3, ESI†). The geometrical structures of 1–6 in high-spin configurations show the thiochalcone ligands coordinated in a different fashion from that found for the singlet ground state. For example, the complexes in quintet configurations demonstrate the dominant Fe–S interaction rather than the η⁴-coordination of 1-thia-1,3-diene. A reduction in ligand hapticity was previously observed for tricarbonyl(pentadiene)iron complexes in their excited triplet states.⁴⁶

The DFT-predicted singlet ground state configuration of 1–6 was confirmed by CASSCF calculations. The leading configuration state function corresponds in all cases to the DFT configuration. Thus, the single-reference DFT wave functions seem adequate for representing complexes 1–6 in the present study.

Geometrical structure

Complexes 1–6 in their optimized geometries in the ground state show no significant deviations from the corresponding geometries extracted from the XRD crystal structures.¹⁴ The calculated bond lengths of their 1-thia-1,3-diene fragment differ marginally from the experimental values. Slightly more pronounced differences of up to 4.5 pm are observed for the calculated distances between the Fe center and the thiadiene ligand. More specifically, the calculated Fe–S distance tends to be overestimated, while the calculated distances between Fe and the C¹–C²–C³ atoms are systematically shortened (Table 1).

Table 1 Calculated and experimental interatomic distances (in ppm) and angle (in °) for complexes 1–7. Experimental values are shown in parentheses

Complex	Fe–S	Fe–C^1	Fe–C^2	Fe–C^3	S–C^1–C^2–C^3
1	233.2 (232.3)	208.7 (211.0)	206.6 (208.5)	212.9 (217.9)	3.6 (1.7)
2	233.8 (231.0)	207.1 (210.4)	207.0 (208.3)	212.6 (217.3)	5.9 (0.6)
3	233.7 (232.4)	207.9 (212.4)	206.8 (208.6)	212.7 (216.6)	4.7 (1.3)
4	233.7 (233.4)	208.3 (210.6)	206.7 (207.9)	212.4 (215.9)	4.3 (2.0)
5	233.8 (232.4)	208.3 (211.6)	206.5 (207.3)	212.0 (216.5)	4.4 (0.5)
6	233.7 (232.5)	208.0 (212.1)	206.8 (207.0)	213.0 (216.8)	4.6 (1.3)
7	234.0	207.2	206.3	211.5	6.0

---

The relaxed structures of 1–7 demonstrate that the S–C¹–C²–C³ atoms of thiadiene ligands are almost planar and adopt a cisoid conformation (Fig. 2). This is reflected in the very small values of the angle defined by the S–C¹–C²–C³ atoms (Table 1). The Fe(CO)₃ moiety is positioned on the one side of the plane formed by the S–C¹–C²–C³ atoms and these atoms are in the immediate proximity of the Fe center. The resulting η⁴ coordination mode of the S–C¹–C²–C³ atoms to Fe is in agreement with experimental observations. It is known that, in the crystals of 1–6, the coordination sphere of their Fe center consists of three carbonyl ligands and the η⁴-1-thia-1,3-diene ligand sitting on the opposite side of the Fe(CO)₃ tripod (Fig. 1).¹⁴ The η⁴ coordination mode was also found in the crystal structures of tricarbonyliron(0) complexes of α,β-unsaturated thioamides.¹³ These structures however revealed a significant distortion of the thiocarbonyl sulfur from the plane formed by the adjacent C¹–C²–C³ atoms. The planarity of the η⁴-coordinated S–C¹–C²–C³ atoms for 1–6 resembles that reported for the structure of (η⁴-s-cis-1,3-butadiene)tricarbonyliron(0).⁴⁷ The Fe center of 1–7 in their optimized geometries is almost equidistant from the C¹ and C² atoms and both these distances are shorter than Fe–S and Fe–C³ (Table 1). The calculated Fe–S distances of 1–7 are longer than the Fe–S distance measured for the Fe(CO)₃ complex of η⁴-coordinated N,N-diethyl-2,3-diphenylpropenethioamide (213.6 pm).¹³

Fig. 2 Optimized equilibrium structure of complex 1.

It is instructive to inspect structural alternations of the free thiochalcone ligands upon coordination to Fe(CO)₃ (Table 2). The S–C¹ bond of 1–6 is significantly elongated compared to a typical C=S bond length of 162 pm.⁴⁸ For free thiochalcone ligands, their C¹–C² bond is much longer than the C²–C³ one. As a result of complexation, the C¹–C² and C²–C³ bonds try to equalize their lengths, yet the former is usually slightly shorter. These bond lengths in 1–6 are between a typical single (154 pm) and a typical double C–C bond length (134 pm).⁴⁸

Table 2 Calculated bond lengths (in pm) in the S–C¹–C²–C³ fragment of complexes 1–7. The corresponding bond lengths of the free thiadiene ligands are shown in parentheses

Complex	S–C^1	C^1–C^2	C^2–C^3
1	174.9 (164.5)	141.9 (146.9)	141.9 (134.8)
2	174.8 (164.6)	141.8 (146.5)	142.1 (135.0)
3	174.8 (165.0)	141.9 (147.0)	141.9 (134.7)
4	174.8 (164.9)	141.7 (147.0)	142.0 (134.6)
5	174.9 (165.0)	141.5 (146.6)	142.2 (134.8)
6	174.9 (164.9)	141.6 (146.6)	142.0 (134.8)
7	174.6 (163.7)	141.7 (147.2)	142.0 (134.3)

---

As evident from the simulations, introduction of the aromatic moieties, Ar¹ and Ar² in 1–6, does not affect the predicted distances between the Fe center and the S–C¹–C²–C³ atoms significantly, as well as the bond lengths between the S–C¹–C²–C³ atoms. Furthermore, the calculated geometry of the η⁴-coordinated ligand fragment in 1–6 is comparable to that obtained for 7.

The calculated geometrical structures of 1–7 may provide a clue about the nature of metal–ligand bonding between the Fe center and the thiadiene ligands. The planarity of the S–C¹–C²–C³ fragment of 1–7, the lengthening of their S–C¹ bond and the equilibrating C¹–C² and C²–C³ bond lengths suggest the coordination of the delocalized π-system of S–C¹–C²–C³ to the Fe center. These geometrical features seem to rule out the coordination to iron via the lone pair donation from the thiocarbonyl sulfur atoms.

Charge distribution

The distribution of electron charge among the metal center and ligands of 1–7 was probed using the QTAIM partial atomic charges of the Fe center and the atoms constituting the carbonyl and thiadiene ligands (Table 3). Although the metal center in 1–6 has a zero formal oxidation state, its atomic charge is predicted to be approximately 0.83 e, which is not far from the Fe atomic charge of 0.76 e calculated for Fe(CO)₅.²⁷ Both the thiochalcone and three carbonyl ligands of 1–6 acquire an ancillary electron charge. The significant amount of electron charge is transferred to the thiochalcone ligands and much of it is distributed among the S–C¹–C²–C³–C⁴ atoms (Table S4, ESI†). This is in line with the computational results reported for the (η⁴-butadiene)Fe(CO)₃ complex in which the dominant Fe → butadiene electron back-donation was observed.⁴⁹ The presence of the aromatic Ar¹ and Ar² groups in 1–6 marginally affects the electron charge localized at the metal center and the ligands. The thiadiene ligand of complex 7 gains a somewhat smaller extra electron charge because the C¹–C²–C³ atoms of the free ligand are already more negatively charged by the donating inductive effect of methyl groups (Table S4, ESI†). The CO ligands of 7 are most negatively charged among all the studied complexes.

Table 3 Electron charge (in e) acquired by the metal center and ligands of complexes 1–7

Complex	Fe	CO	Thiadiene
1	0.831	−0.131; −0.134; −0.148	−0.417
2	0.831	−0.118; −0.136; −0.154	−0.423
3	0.833	−0.122; −0.135; −0.148	−0.427
4	0.831	−0.129; −0.138; −0.152	−0.412
5	0.831	−0.129; −0.139; −0.140	−0.422
6	0.830	−0.127; −0.140; −0.150	−0.413
7	0.823	−0.138; −0.143; −0.164	−0.377

---

Binding energy

Let us now estimate the strength of the interaction between the Fe(CO)₃ and thiadiene fragments of 1–7. To this end, the Fe(CO)₃–thiadiene binding energy (E_bind) was calculated for the complexes (Table 4). The E_bind values of 1–6 fall in a narrow range from −343.4 to −356.9 kJ mol⁻¹ (at the MP2/def2-TZVPD level). From the comparison of these values with the E_bind value of 7, it can be inferred that the aromatic Ar¹ and Ar² groups of 1–6 lead to a weakening of the interaction between the Fe(CO)₃ and thiochalcone fragments. In general, the Fe(CO)₃ moiety binds with the thiadiene fragment of 1–7 more weakly than with butadiene in the well-known prototype complex (η⁴-butadiene)Fe(CO)₃, with its E_bind energy being ca. −510 kJ mol⁻¹.⁴⁹

Table 4 Decomposition of the IQA binding energy (E_bind) between the Fe(CO)₃ and thiadiene fragments of complexes 1–7. For comparison, the E_bind values calculated using the supermolecular MP2/def2-TZVPD method are shown in parentheses. All energies are given in kJ mol⁻¹

Complex	E bind	E def	E cl	E xc
1	−373.2 (−355.7)	856.5	−450.2	−779.5
2	−368.7 (−351.5)	832.6	−418.8	−782.5
3	−367.8 (−345.8)	846.6	−437.6	−776.8
4	−371.3 (−356.9)	851.8	−440.2	−782.9
5	−368.9 (−343.4)	856.0	−440.3	−784.6
6	−364.6 (−346.5)	835.4	−415.0	−785.1
7	−400.5 (−387.1)	806.4	−433.3	−773.6

---

The E_bind energy was also obtained from the IQA method and the resulting values illustrate a similar strength of the Fe(CO)₃–thiochalcone interaction for 1–6 while complex 7 is characterized by a stronger interaction (Table 4). Within the IQA method, E_bind of 1–7 is retrieved from three contributions: the destabilizing electronic deformation (E_def) suffered by two fragments upon their complexation, the stabilizing classical coulombic interaction (E_cl) between the fragments and their stabilizing exchange–correlation interaction (E_xc). Both stabilizing contributions are essential to compensate for the E_def destabilization. Of the E_cl and E_xc contributions, the latter predominates in the stabilizing Fe(CO)₃–thiadiene interaction. The importance of E_xc suggests the dominant covalent character of the interaction between the Fe(CO)₃ and thiadiene fragments of 1–7. This finding seems to be in line with the significant role of orbital interaction effects reported previously for the (η⁴-butadiene)Fe(CO)₃ complex.⁴⁹ The IQA results for 1–7 allow us to find the source of less stabilizing E_bind values for 1–6 in comparison to 7. Complex 7 experiences smaller E_def destabilization, and therefore its E_bind value becomes more negative. The more destabilizing E_def energy of 1–6 is associated with the growing kinetic electron energy of the thiochalcones due to their enhanced charge transfer (Table 3). This is also accompanied by the increased charge separation at the carbonyl ligands, thus the more positive atomic charges of their carbons (Table S4, ESI†). The relatively large ionization potential of carbon induces a relevant E_def destabilization in the carbonyl carbon atoms which lose electron charge.

Quantum chemical topology perspective

The QTAIM topological analysis of the electron density (ρ) for 1–7 was carried out to obtain the local description of the η⁴-coordination of thiadiene ligands to the Fe center. The analysis gives essentially identical topologies for the coordinated S–C¹–C²–C³ fragment in all seven complexes. Their molecular graphs show the presence of four bond paths between the Fe center and the S–C¹–C²–C³ atoms (Fig. 3 and Fig. S10–S15, ESI†). Thus, the number of the bond paths reflects the formal hapticity of thiadiene ligands. It is not so common for complexes with ligands demonstrating higher hapticity.⁵⁰ The Fe–S, Fe–C¹, Fe–C² and Fe–C³ bond paths are curved near the S–C¹–C²–C³ atoms. Each of the bond paths is associated with its bond critical point (BCP) and these BCPs intersperse with three ring critical points (RCPs). The four BCPs are characterized by relatively low values of ρ and its Laplacian (∇²ρ) (Table 5 and Tables S5–S10, ESI†). The magnitudes of ρ and ∇²ρ for these BCPs do not differ much from those observed in other iron(0) complexes with organic ligands.^51–53 These BCPs exhibit positive ∇²ρ values yet a negative sign of the total energy density (H) is observed. Therefore, such BCP characteristics are indicative of an intermediate type of atomic interactions, that is, between pure closed-shell and shared interactions.⁵⁴ The intermediate type of Fe–S, Fe–C¹, Fe–C² and Fe–C³ interactions is also supported by the ratio of the potential energy density to the kinetic energy density (1 < |V|/G < 2).⁵⁵ In general, the main features of the four BCPs are quite typical of the coordination of organic π-ligands to transition metals.⁵⁰ Three RCPs located in the close proximity of the four BCPs show almost identical ρ values to those at the four BCPs (Table S10, ESI†). This is due to the fact that both the BCPs and the RCPs occur in the region of very flat ρ between the Fe center and the S–C¹–C²–C³ atoms. The SF analysis carried out at the four BCPs and the three RCPs indicates that the S–C¹–C²–C³ atoms in 1–7 provide a total contribution of 34–46% to the ρ at these critical points, while the Fe(CO)₃ moiety yields a less variable share of 35–40%. All the aforementioned QTAIM parameters of critical points suggest a considerable delocalization of ρ between the interacting fragments of 1–7.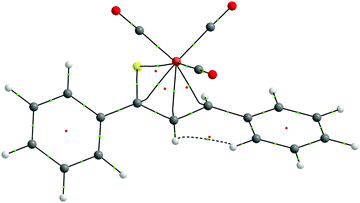

Fig. 3 QTAIM molecular graph of complex 1. Bond paths are drawn with black lines. Bond critical points are shown as small green spheres, and ring critical points as small red spheres. The viewpoint is the same as in Fig. 2.

Table 5 QTAIM, SF and IQA parameters for the interaction between the Fe center and the thiadiene ligand for complexes 1 and 7 (in parentheses)

Parameter^a	Fe–S	Fe–C^1	Fe–C^2	Fe–C^3
a ρ, ∇^2ρ and H are expressed in atomic units; SF in percentage points; Vcl, Vxc and Einter are given in kJ mol^−1.
ρ	0.070 (0.069)	0.084 (0.087)	0.084 (0.085)	0.080 (0.083)
∇^2ρ	0.161 (0.169)	0.219 (0.215)	0.242 (0.249)	0.206 (0.188)
H	−0.021 (−0.019)	−0.026 (−0.028)	−0.026 (−0.026)	−0.022 (−0.025)
|V|/G	1.34 (1.32)	1.32 (1.34)	1.30 (1.29)	1.30 (1.35)
SF(S–C^1–C^2–C^3)	46.1 (47.0)	41.8 (42.6)	38.9 (39.8)	34.6 (35.4)
SF(Fe(CO)3)	37.1 (36.1)	37.5 (38.2)	37.6 (37.6)	39.1 (40.1)
δ	0.649 (0.641)	0.456 (0.477)	0.394 (0.398)	0.520 (0.555)
V cl	−38.7 (−38.7)	−146.6 (−148.4)	−40.9 (−38.6)	−86.3 (−85.8)
V xc	−308.8 (−302.2)	−256.0 (−269.9)	−222.3 (−222.8)	−281.3 (−302.1)
E inter	−347.5 (−340.9)	−402.7 (−418.3)	−263.1 (−261.4)	−367.6 (−387.9)

---

In addition to the QTAIM parameters at critical points, the delocalization index (δ), the IQA interaction energy (E_inter) and its classical coulombic (V_cl) and exchange–correlation (V_xc) components were calculated between the pairs of atoms involved in the iron-thiadiene interaction (Table 5 and Tables S5–S9, ESI†). The δ values of the Fe–S, Fe–C¹, Fe–C² and Fe–C³ pairs add up to ca. 2 for each of the studied complexes. It means that approximately four electrons participate in the iron-thiadiene interaction, as expected for complexes obeying the 18-electron rule. The interaction in the pairs is always dominated by the V_xc component, which signals a partial covalent character of the diatomic interaction. The strongest E_inter interaction is observed for Fe–C¹, while the weakest occurs for Fe–C². This results from the V_cl component which covers the electrostatic interaction between the oppositely-charged Fe and C atoms. The C¹ atom possesses a more negative charge than the C² atom (Table S4, ESI†), and therefore the Fe–C¹ pair is stabilized to a greater extent by the V_cl component.

It is interesting to check on whether the IQA diatomic energies of the four pairs involved in the iron-thiadiene interaction can handle the effect of the aromatic groups in 1–6 (Ar¹ and Ar²). Compared to 7, the complexes with thiochalcone ligands show less stabilizing E_inter energies of Fe–C¹ and Fe–C³ pairs. Their V_xc component is mainly responsible for the lesser stabilization. This may be explained in terms of electron charge that is shared with atoms to which a given atom is not bonded. The QTAIM analysis reveals that the C¹ and C³ atoms of 1–6 possess greater electron charge due to resonance effects with the adjacent Ar¹ and Ar² groups. The C¹ and C³ electron charge shared with Fe is simultaneously slightly smaller in 1–6 than in complex 7. This is reflected in the δ values and consequently in the V_xc values. The effect is more pronounced for the C³ atom.

The coordination of thiochalcones to Fe(CO)₃ gives rise to significant changes in the characteristics of BCPs corresponding to three covalent bonds of S–C¹–C²–C³ (Table 6 and Tables S11–S16, ESI†). Obviously, these characteristics provide evidence for the shared interactions between the S–C¹–C²–C³ atoms (∇²ρ < 0, H < 0, |V|/G > 2). There is a clear localization of double bonds for S–C¹ and C²–C³ in the free thiochalcone ligands (δ > 1.6). However, the three bonds of S–C¹–C²–C³ look quite similar upon coordination to Fe(CO)₃. The δ values of S–C¹ and C¹–C² become practically identical and the third bond shows only a slightly smaller δ value. All three δ values signal that more than a single electron pair is shared in each of the bonds. The IQA E_inter energies indicate that the weakening of S–C¹ and C²–C³ is accompanied by an increase in the strength of the C¹–C² bond. The weakening of S–C¹ is particularly significant and its strength decreases almost by half. It is mainly affected by the diminished V_cl stabilization due to the negative charge acquired by the S atom as the result of coordination (Table S4, ESI†). The SF analysis of ρ reveals a source contribution from the Fe(CO)₃ moiety at the BCPs of S–C¹, C¹–C² and C²–C³ in 1–7, which may be indicative of back-donation from Fe(CO)₃ to the thiadiene ligands.

Table 6 QTAIM, SF and IQA parameters for three bonds of the S–C¹–C²–C³ fragment of complex 1. The corresponding bond lengths of the free thiochalcone are shown in parentheses

Parameter^a	S–C^1	C^1–C^2	C^2–C^3
a ρ, ∇^2ρ and H are expressed in atomic units; SF in percentage points; Vcl, Vxc and Einter are given in kJ mol^−1.
ρ	0.200 (0.236)	0.302 (0.278)	0.301 (0.347)
∇^2ρ	−0.362 (−0.264)	−0.825 (−0.759)	−0.832 (−1.071)
H	−0.171 (−0.288)	−0.308 (−0.265)	−0.308 (−0.399)
|V|/G	3.13 (2.30)	4.03 (4.54)	4.08 (4.04)
SF(S–C^1–C^2–C^3)	88.5 (94.3)	88.3 (90.4)	86.4 (90.4)
SF(Fe(CO)3)	4.0	3.0	3.0
δ	1.256 (1.755)	1.249 (1.132)	1.223 (1.624)
V cl	−17.4 (−530.8)	94.0 (69.2)	90.7 (145.7)
V xc	−857.8 (−1122.9)	−1009.4 (−903.2)	−994.0 (−1240.9)
E inter	−875.2 (−1653.7)	−915.4 (−833.9)	−903.3 (−1095.2)

---

Macchi et al.⁵⁶ postulated that QTAIM topological properties, such as curvature of bond paths, location of critical points and estimated bond orders between atoms involved in the metal–ligand interaction, can serve as criteria pointing to the proper bonding model for transition metal complexes. According to these criteria, the curvature of Fe–S, Fe–C¹, Fe–C² and Fe–C³ bond paths forming rings with the S–C¹–C²–C³ bond paths in 1–7, together with the δ values of S–C¹–C²–C³ being much greater than those of Fe–S, Fe–C¹, Fe–C² and Fe–C³, point towards a Fe(CO)₃–thiadiene bonding picture that is in agreement with the classical donor–acceptor orbital model. This orbital model assumes metal ← ligand σ-donation and synergistic metal → ligand π-back-donation as the dominant factors determining bonding.⁵⁷

Orbital perspective

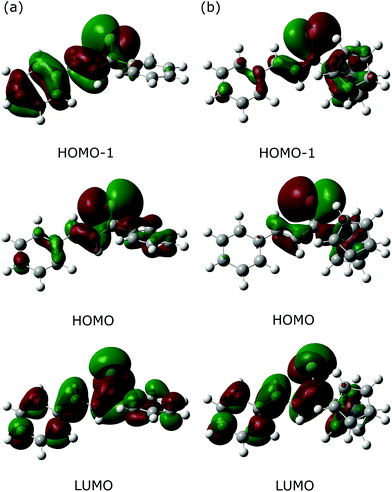
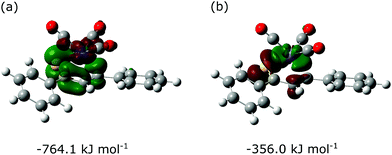
As an alternative approach, the Fe(CO)₃–thiadiene bonding in 1–7 was interpreted in terms of orbital-based descriptors. Such an approach commenced with an inspection of the ground-state frontier molecular orbitals for the free thiadiene ligands. Although their HOMO−1, HOMO and LUMO are delocalized over the entire molecules (Fig. 4), the composition analysis of these molecular orbitals reveals a few dominant contributions from individual atomic orbitals. The HOMO−1 and HOMO show major contributions from the valence p-orbitals of thiocarbonyl sulfur and the p-orbitals of C² (Table S17, ESI†). The HOMO involves the sulfur lone pair p-orbital lying in the molecular plane, while the HOMO−1 contains the sulfur out-of-plane p-orbital forming the π-bond of thiocarbonyl group. The functionalization of thiochalcone with a ferrocenyl group leads to a relevant share of iron d-orbitals in the HOMO. The main share to the LUMO originates from the valence p-orbitals of the S, C¹ and C³ atoms; they provide a contribution of more than 60% in total. By contrast, the atomic orbitals of C² yield a minor contribution to the LUMO. The introduction of aromatic Ar¹ and Ar² groups into thiadienes produces a significant lowering in the energy of the LUMO (Table S18, ESI†). The energy of HOMO−1 raises in 1–6, while their HOMO energy is marginally affected. Such changes in orbital energies are essentially typical of conjugative substituent effect.⁵⁸

Fig. 4 Contours of three frontier molecular orbitals for the free thiochalcone ligands forming complexes (a) 1 and (b) 4. For these orbitals, their parts possessing either positive or negative sign are colored green and red, respectively. The contours are plotted with an isovalue of 0.02 a.u.

Next, the ETS-NOCV analysis was carried out to explore the interactions between the NOCVs defining the channels for electron charge transfer between the Fe(CO)₃ and thiadiene fragments of 1–7. The energies (ΔE_orb) associated with two leading pairwise NOCV interactions in each complex cover over 80% of the total stabilization (Σ) from all NOCV pairs (Table 7). The most stabilizing pairwise NOCV interaction corresponds to the electron density rearrangement operating from the region around the Fe center to the region of S–C¹–C²–C³ (Fig. 5a). One of the involved NOCVs possesses significant contributions of the p-type orbitals of S–C¹–C²–C³ and the other NOCV is dominated by the p- and d-orbitals of the Fe center (Table S19, ESI†). It is clearly evident that the deformation density contour between C¹ and C² takes shape of a π-type orbital, which illustrates an extended π-delocalization within S–C¹–C²–C³ upon complexation. The reverse direction of charge transfer relates to the second most stabilizing pairwise NOCV interaction. The electron density is increased at the Fe center and is depleted mostly in the p-orbitals of the S and C² atoms (Fig. 5b). The most stabilizing pairwise NOCV interaction can be interpreted as metal → ligand π-back-donation in which electrons are shifted from the occupied orbitals of Fe into the virtual orbitals of the ligand. The ΔE_orb of the back-donation for 7 is less stabilizing than for 1–6 due to the higher LUMO energy of the former. The back-donation in 1–7 is favored over the second most stabilizing interaction representing metal ← ligand σ-donation from the filled orbitals of the ligand to the d-orbitals of Fe. The same situation also pertained to the (η⁴-butadiene)Fe(CO)₃ complex.⁵⁹

Table 7 Leading and total ETS-NOCV orbital interaction energies (ΔE_orb, in kJ mol⁻¹) for complexes 1–7

Complex	ΔEorb
	Metal → ligand	Metal ← ligand	Σ
1	−764.1	−356.0	−1379.0
2	−780.4	−344.1	−1387.7
3	−776.8	−346.3	−1385.4
4	−768.5	−349.7	−1379.2
5	−763.2	−355.1	−1380.8
6	−764.8	−347.6	−1374.4
7	−753.0	−359.5	−1363.1

---

Fig. 5 Deformation densities of two leading pairwise NOCV orbital interactions between the Fe(CO)₃ and thiochalcone fragments of complex 1. Stabilization energies associated with these interactions are also shown. Green- and red-colored isosurfaces identify regions where charge density buildup and depletion occur, respectively. The contours are plotted with an isovalue of 0.0035 a.u.

It is essential to relate the orbital description of both the free thiadiene ligands and 1–7 to the changes of bond lengths in the coordinated S–C¹–C²–C³ fragment. The σ-donation from the thiadiene ligands involves their HOMO and HOMO−1 that are bonding between S and C¹ and between C² and C³ (Fig. 4). This transfer leads to the elongation of S–C¹ and C²–C³. The charge distribution in 1–7 mainly comes from the π-back-donation to the thiadiene LUMO (Fig. 5a) that is bonding between C¹ and C² and antibonding between S and C¹ and between C² and C³. The effect of the back-donation is the compression of C¹–C² bond length, together with further elongation of S–C¹ and C²–C³.

To further explore the orbital perspective on bonding in complexes 1–7, an NBO analysis was carried out (Section S3, ESI†). The NBO search of the optimal Lewis structure yielded a common pattern of NBOs around the Fe center of all seven complexes (Chart 2). This pattern reveals that there are two NBOs between the Fe center and the coordinated thiadiene ligand. These two NBOs correspond to σ-type Fe–S and Fe–C³ bonds although their constituent natural hybrids show noticeable bond bending (Fig. S16, ESI†). The Fe center also forms an NBO with one of the carbonyl ligands. The metal possesses its own three lone electron pairs and, in consequence, the Fe center is saturated according to the duodectet rule of Landis and Weinhold.⁴⁰ As for the coordinated thiadiene ligands, the pattern indicates that the thiocarbonyl sulfur retains its two lone pairs, the S–C¹ and C²–C³ bonds are described by single σ-type NBOs while an additional π-type NBO appears between the C¹ and C² atoms.

Chart 2 NBO optimal Lewis structure for 1–7.

The optimal Lewis structure described above implies that all seven complexes feature a metallacyclic form of their Fe(CO)₃–thiadiene bonding.⁵⁷ This conclusion should however be treated with great caution. First, it is in apparent contradiction with the previous findings assigning the donor–acceptor bonding model to 1–7. Second, the optimal Lewis structures found for 1–7 cover from 96.5 to 97.3% of the total electron density of the complexes. It means that the localized bonding picture provided by the optimal Lewis structures (1–7) is incomplete because these complexes represent strongly delocalized systems. Some part of the delocalization obviously results from the presence of aromatic Ar¹ and Ar² groups but the optimal Lewis structure of complex 7 still describes only 97.3% of its total electron density. For that reason, the metallacyclic model seems improper to elucidate the Fe(CO)₃–thiadiene bonding in 1–7. The metallacyclic form of Fe(CO)₃–thiadiene interaction results in the occurrence of C¹–C² double bond. The typical double-bond nature of C¹–C² is questionable because the C¹–C² and C²–C³ bond lengths are practically equalized. Nevertheless, the C¹–C² bond should possess a somewhat stronger π-character than C²–C³. The stronger π-character is correlated with the NMR deshielding of C². From the ¹³C NMR spectra measured for 1, 3 and 6,¹⁴ it is known that their C² atom presents a more positive chemical shift than C³.

Significant π-delocalization extended over the S–C¹–C²–C³ atoms is reflected in the values of Wiberg bond index (WBI)⁶⁰ included in the NBO analysis. The WBI values of S–C¹, C²–C² and C²–C³ range from 1.15 to 1.33, with the upper extreme characterizing the central C¹–C² bond (Table S20, ESI†). The higher WBI of C¹–C² is in line with the stronger π-character of this bond. The WBI values between the Fe center and each of the S–C¹–C²–C³ atoms do not exceed 0.45. For Fe–S and Fe–C³, a larger amount of their covalent bond character is indicated by their higher WBI values, as compared to those of Fe–C¹ and Fe–C².

Conclusions

This study of the metal–ligand bonding between Fe(CO)₃ and thiochalcones was performed for a series of isolated complexes 1–6 in their optimized geometrical structures that turned out to be quite close to the reference geometries extracted from the XRD crystal structures. Thus, the main conclusions on the bonding situation in the isolated complexes may also elucidate the Fe(CO)₃–thiochalcone bonding in the crystals of 1–6. According to the calculated E_bind values, the Fe(CO)₃ moiety binds with thiochalcones more weakly than with the alkyl analog of thiochalcone (7) and butadiene. The tetrahapticity of thiochalcones in 1–6 is reflected in four QTAIM bond paths between the Fe center and the S–C¹–C²–C³ atoms of the coordinated thiochalcone ligands. The corresponding four IQA diatomic interactions show the prevalent covalent character, yet they differ in their strength. The Fe–C¹ interaction is the strongest due to significant electrostatic stabilization. In general, both the topological- and orbital-based methods indicate that the Fe(CO)₃–thiochalcone bonding may appropriately be described in terms of metal–ligand σ-donation and π-back-donation defined by the donor–acceptor model. The π-back-donation from the occupied d-orbitals of Fe to the LUMO of thiochalcone dominates the Fe(CO)₃–thiochalcone bonding in 1–6. This ETS-NOCV result is in agreement with the charge distribution among the Fe center and the ligands. Moreover, the dominant π-back-donation explains changes in the bond lengths of S–C¹–C²–C³. The values of δ and WBI provide evidence for π-delocalization within the η⁴-coordinated S–C¹–C²–C³ fragment of thiochalcones. Although the C¹–C² and C²–C³ bond lengths are practically equalized, the former presents somewhat stronger π-character.

Results presented in this study contribute to better understanding of iron-thiochalcone bonding and they should contribute to the burgeoning interest in the complexes of iron carbonyls with the relatively little known class of 1,3-thiadienes.

Funding

This research was funded by the Alexander von Humboldt Foundation (Bonn, Germany) within its Research Group Linkage Programme (‘Institutspartnerschaft’ grant for research cooperation between University of Jena (Germany) and University of Lodz (Poland), 2018–2022).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partially supported by PL-Grid Infrastructure.

References

1. H. Reihlen, A. Gruhl, G. V. Heßling and O. Pfrengle, Justus Liebigs Ann. Chem., 1930, 482, 161–182.
2. A. J. Pearson, Iron Compounds in Organic Synthesis, Academic Press, London, 1994.
3. H.-J. Knölker, Chem. Soc. Rev., 1999, 28, 151–157.
4. W. Imhof, A. Göbel, D. Braga, P. De Leonardis and E. Tedesco, Organometallics, 1999, 18, 736–747.
5. H.-J. Knölker, Chem. Rev., 2000, 100, 2941–2962.
6. R. Grée, Synthesis, 1989, 341–355.
7. H.-J. Knölker, A. Braier, D. J. Bröcher, S. Cämmerer, W. Fröhner, P. Gonser, H. Hermann, D. Herzberg, K. R. Reddy and G. Rohde, Pure Appl. Chem., 2001, 73, 1075–1086.
8. C. Hirschhäuser, J. Velcicky, D. Schlawe, E. Hessler, A. Majdalani, J.-M. Neudörfl, A. Prokop, T. Wieder and H.-G. Schmalz, Chem. – Eur. J., 2013, 19, 13017–13029.
9. S. Botov, E. Stamellou, S. Romanski, M. Guttentag, R. Alberto, J.-M. Neudörfl, B. Yard and H.-G. Schmalz, Organometallics, 2013, 32, 3587–3594.
10. W. A. Donaldson and S. Chaudhury, Eur. J. Org. Chem., 2009, 3831–3843.
11. J. T. Wasicak, R. A. Craig, R. Henry, B. Dasgupta, H. Li and W. A. Donaldson, Tetrahedron, 1997, 53, 4185–4198.
12. C. Iwata and Y. Takemoto, Chem. Commun., 1996, 2497–2504.
13. H. Alper and D. A. Brandes, Organometallics, 1991, 10, 2457–2467.
14. P. Buday, P. Seeber, C. Zens, H. Abul-Futouh, H. Görls, S. Gräfe, P. Matczak, S. Kupfer, W. Weigand and G. Mlostoń, Chem. – Eur. J., 2020, 26, 11412–11416.
15. G. Mlostoń, K. Urbaniak, K. Gębicki, P. Grzelak and H. Heimgartner, Heteroat. Chem., 2014, 25, 548–555.
16. G. Mlostoń, P. Grzelak, R. Hamera-Fałdyga, M. Jasiński, P. Pipiak, K. Urbaniak, Ł. Albrecht, J. Hejmanowska and H. Heimgartner, Phosphorus, Sulfur Silicon Relat. Elem., 2017, 192, 204–211.
17. S. Gröber, P. Matczak, S. Domagała, T. Weisheit, H. Görls, A. Düver, G. Mlostoń and W. Weigand, Materials, 2019, 12, 2832.
18. P. Matczak, G. Mlostoń, R. Hamera-Fałdyga, H. Görls and W. Weigand, Molecules, 2019, 24, 3950.
19. G. Mlostoń, M. Kowalczyk, A. U. Augustin, P. G. Jones and D. B. Werz, Beilstein J. Org. Chem., 2020, 16, 1288–1295.
20. G. Mlostoń, K. Urbaniak, M. Jasiński, E.-U. Würthwein, H. Heimgartner, R. Zimmer and H.-U. Reissig, Chem. – Eur. J., 2020, 26, 237–248.
21. G. Mlostoń, K. Urbaniak, M. Sobiecka, H. Heimgartner, E.-U. Würthwein, R. Zimmer, D. Lentz and H.-U. Reissig, Molecules, 2021, 26, 2544.
22. H. Beer, A. Linke, J. Bresien, G. Mlostoń, M. Celeda, A. Villinger and A. Schulz, Inorg. Chem., 2022, 61, 2031–2038.
23. M. J. Calhorda and E. J. S. Vichi, Organometallics, 1990, 9, 1060–1067.
24. D. Tiana, E. Francisco, M. A. Blanco, P. Macchi, A. Sironi and A. M. Pendas, J. Chem. Theory Comput., 2010, 6, 1064–1074.
25. Y. Zeng, S. Wang, H. Feng, Y. Xie, R. B. King and H. F. Schaefer III, New J. Chem., 2011, 35, 920–929.
26. M. Gruden and M. Zlatar, Theor. Chem. Acc., 2020, 139, 126.
27. G. Frenking, I. Fernández, N. Holzmann, S. Pan, I. Krossing and M. Zhou, JACS Au, 2021, 1, 623–645.
28. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
29. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
30. G. W. Roffe and H. Cox, J. Phys. Chem. A, 2013, 117, 3017–3024.
31. M. M. Flores-Leonar, R. Moreno-Esparza, V. M. Ugalde-Saldivar and C. Amador-Bedolla, ChemistrySelect, 2017, 2, 4717–4724.
32. B. O. Roos, P. R. Taylor and P. E. M. Sigbahn, Chem. Phys., 1980, 48, 157–173.
33. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
34. D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105.
35. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
36. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon, Oxford, 1990.
37. C. Gatti, F. Cargnoni and L. Bertini, J. Comput. Chem., 2003, 24, 422–436.
38. M. A. Blanco, A. Martín Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109.
39. M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
40. F. Weinhold and C. R. Landis, Valency and Bonding: A Natural Bond Orbital Donor–Acceptor Perspective, Cambridge University Press, New York, 2005.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 C.01, Gaussian, Inc., Wallingford CT, 2016.
42. T. A. Keith, AIMAll 19.10.12, TK Gristmill Software, Overland Park KS, 2019.
43. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
44. T. Lu and F. Chen, Acta Chim. Sin., 2011, 69, 2393–2406.
45. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison WI, 2013.
46. S. J. Gravelle, L. J. van de Burgt and E. Weitz, J. Phys. Chem., 1993, 97, 5272.
47. G. J. Reiss, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2010, 66, m1369.
48. CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton FL, 2002.
49. O. Gonzalez-Blanco and V. Branchadell, Organometallics, 1997, 16, 475–481.
50. L. J. Farrugia, C. Evans, D. Lentz and M. Roemer, J. Am. Chem. Soc., 2009, 131, 1251–1268.
51. L. J. Farrugia, C. Evans and M. Tegel, J. Phys. Chem. A, 2006, 110, 7952–7961.
52. T. N. Danks and G. Wagner, J. Organomet. Chem., 2011, 696, 622–631.
53. A. Sirohiwal, V. R. Hathwar, D. Dey and D. Chopra, ChemPhysChem, 2017, 18, 2859–2863.
54. R. F. W. Bader and H. Essén, J. Chem. Phys., 1984, 80, 1943–1960.
55. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
56. P. Macchi, D. M. Proserpio and A. Sironi, J. Am. Chem. Soc., 1998, 120, 1447–1455.
57. G. Frenking and N. Fröhlich, Chem. Rev., 2000, 100, 717–774.
58. I. Fleming, Molecular Orbitals and Organic Chemical Reactions, Wiley, Chichester, UK, 2010.
59. O. Gonzaalez-Blanco, V. Branchadell and R. Gree, Chem. – Eur. J., 1999, 5, 1722–1727.
60. K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096.

---

Footnote

† Electronic supplementary information (ESI) available: Crystallographic data (excluding structure factors) has been deposited with the Cambridge Crystallographic Data Centre as supplementary publication CCDC 2169541 for 2, 2169542 for 5. CCDC 2169541 and 2169542. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2nj01315k

---