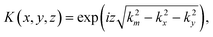Open Access Article
Open Access ArticleWidefield phototransient imaging for visualizing 3D motion of resonant particles in scattering environments†
Matz
Liebel
 *a,
Franco V. A.
Camargo
*a,
Franco V. A.
Camargo
 b,
Giulio
Cerullo
b,
Giulio
Cerullo
 bc and
Niek F.
van Hulst
bc and
Niek F.
van Hulst
 *ad
*ad
aICFO – Institut de Ciencies Fotoniques, The Barcelona Institute of Science and Technology, 08860 Castelldefels, Barcelona, Spain. E-mail: matz.liebel@icfo.eu
bIstituto di Fotonica e Nanotecnologie-CNR, Piazza L. da Vinci 32, 20133 Milano, Italy
cDipartimento di Fisica, Politecnico di Milano, Piazza L. da Vinci 32, 20133 Milano, Italy
dICREA – Institució Catalana de Recerca i Estudis Avançats, Passeig Lluís Companys 23, 08010 Barcelona, Spain. E-mail: niek.vanhulst@icfo.eu
First published on 7th January 2022
Abstract
Identifying, visualising and ultimately tracking dynamically moving non-fluorescent nanoparticles in the presence of non-specific scattering is a long-standing challenge across the nano- and life-sciences. In this work we demonstrate that our recently developed ultrafast holographic transient (UHT) microscope is ideally suited for meeting this challenge. We show that UHT microscopy allows reliably distinguishing off-resonant, dielectric, from resonant, metallic, nanoparticles, based on the phototransient signal: a pre-requisite for single-particle tracking in scattering environments. We then demonstrate the capability of UHT microscopy to holographically localize in 3D single particles over large volumes of view. Ultimately, we combine the two concepts to simultaneously track several tens of freely diffusing gold nanoparticles, within a 110 × 110 × 110 μm volume of view at an integration time of 10 ms per frame, while simultaneously recording their phototransient signals. The combined experimental concepts outlined and validated in this work lay the foundation for background-free 3D single-particle tracking applications or spectroscopy in scattering environments and are immediately applicable to systems as diverse as live cells and tissues or supported heterogeneous catalysts.
Photothermal imaging and spectroscopy are key methodologies for visualising, quantifying and ultimately studying non-fluorescent nano-objects down to the single molecule level.1–7 Its unrivalled combination of sensitivity and specificity makes photothermal microscopy, in principle, an ideal candidate for single-particle tracking applications. Unfortunately, the traditional lock-in amplifier-based signal detection schemes that are often necessary to ensure sufficient signal-to-noise ratios are difficult to combine with high-speed imaging over large fields of view, even in relatively simple 2D scenarios.8,9 Recently, we introduced a nonlinear holographic imaging methodology that enables high-speed, lock-in amplifier-like, signal demodulation using comparatively slow cameras operated in a widefield imaging configuration.10 When combined with femtosecond pulses, this so-called ultrafast holographic transient (UHT) microscope allowed us to widefield-record pump–probe time-delay dependent transient dynamics of a variety of gold nanoparticles (NPs) with diameters ranging from 20 to 200 nm. Further, the holographic aspect of our approach allowed computational image propagation and refocussing.
In this article we show that UHT microscopy is ideally suited for 3D single-particle tracking, even in its most challenging form: the simultaneous observation of many freely diffusing NPs in large 3D volumes of observation.11 We first demonstrate that it is possible to discriminate resonant, metallic, from off-resonant, dielectric, NPs with comparable scattering signals, using 2D samples with immobilised particles. Next, we demonstrate that UHT signals are independent of the nominal sample-defocus by using static, pseudo-3D samples, in the form of 2D immobilised NPs that we place at precisely defined z-positions with respect to the image plane. Finally, we address dynamically moving systems by performing UHT-based tracking and time-dependent transient spectroscopy of freely diffusing Au NPs in large, 110 × 110 × 110 μm, volumes of observation.
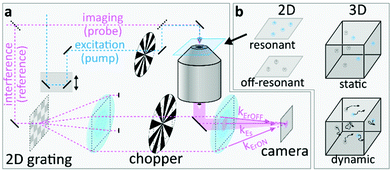
Fig. 1 introduces the basic concept of UHT, which we only briefly describe here, referring the interested reader to our proof-of-concept work10 for a detailed discussion of the more technical and spectroscopy-related aspects. Fig. 1a shows a schematic of an UHT microscope,10 a multiplexed off-axis holographic imaging system12 which is modified to allow generating, demodulating and, ultimately, detecting photoinduced signals with ultrafast pulses (Methods). Briefly, a probe beam illuminates the sample which is imaged onto a conventional CMOS camera in either a dark-field or a bright-field configuration. A 2D 0-π phase grating, conjugate with the camera plane, generates two reference waves which interfere at different angles with the signal scattered/transmitted by the sample. The system outlined above is similar to a conventional multiplexed off-axis holographic microscope13 which allows using arbitrarily broadband pulses, as the grating ensures interference across the entire camera chip.12,14–17 To record photoinduced signals, an additional pump pulse illuminates the sample at a variable, but precisely controlled, pump–probe time-delay. Rather than recording separate sample images in the presence (pumpON) or absence (pumpOFF) of the pump pulse, the UHT microscope simultaneously records the pumpON and pumpOFF images in a single camera exposure via a multiplexed holographic demodulation scheme.10
The recorded image, IUHT (x,y), can be described as:
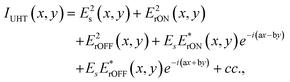 | (1) |
Fig. 2a shows a typical UHT image, acquired for 80 nm Au NPs in dark-field configuration, alongside its Fourier transformation. Interference between the probe and the reference fields directly manifests itself as oscillatory modulation of the NPs’ point-spread-functions (PSFs). As mentioned above, a spatial Fourier transformation allows selectively isolating the interference terms 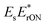 and
and 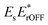 in the Fourier plane followed by removal of the linear phase ramp and an inverse Fourier transformation.10,18,19
in the Fourier plane followed by removal of the linear phase ramp and an inverse Fourier transformation.10,18,19
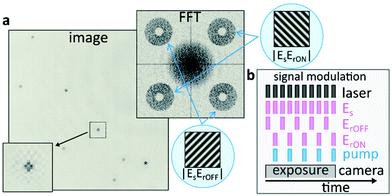 | ||
| Fig. 2 Image processing and signal demodulation in UHT microscopy. (a) Typical UHT image of multiple 80 nm Au NPs alongside its Fourier transformation and a magnification of a point-spread-function to highlight the interference pattern. The central part of the Fourier transformation (DC) contains the amplitude square terms shown in eqn (1). The four terms along the diagonals are the respective interference terms which are displaced as a result of the linear phase terms. The cartoon insets visualise how linear phase terms would manifest themselves in the most intuitive case of interference between two plane waves. (b) UHT modulation scheme that allows encoding and retrieving the desired information from a single camera exposure. Each “bar” represents a laser pulse but the modulation scheme is equally applicable to CW-illumination. | ||
To selectively encode the image-information recorded in the presence (absence) of the pump pulse into ESE*rON(ESE*rOFF), we modulate both the pump beam and the reference waves with optical choppers (Fig. 2b). The camera detects multiple probe pulses, within a single exposure, which interrogate the sample both with and without pump excitation. The synchronised pump and reference modulation ensures that the ErON (ErOFF) reference wave only interferes with probe pulses that interrogate the sample in the presence (absence) of the pump pulse. This all-optical lock-in camera can, in principle, operate at arbitrarily fast demodulation frequencies which are independent of the CMOS camera frame rate, as the demodulation purely relies on computational hologram post-processing and not on fast electronics. As such, the all-optical widefield lock-in modality of the UHT microscope conveniently eliminates the need for point scanning, which is necessary when operating with single-pixel-detector-based lock-in amplifiers, thus making UHT microscopy an ideal candidate for widefield observations of dynamic scenes.
A key asset of UHT microscopy in the context of biological or biomedical imaging is its capability to discriminate resonant particles from the off-resonant scattering background which might arise from cells or tissue.20 To explore the applicability of UHT microscopy to such scenarios, we compare UHT signals obtained for 60 nm Au and 100 nm latex spheres that we deposit on bare coverglass (Fig. 3a). The holographically recorded scattering amplitude of both sets of particles is similar (Fig. 3b), thus making them essentially indistinguishable when measured in a linear colour-blind fashion.12 Their pump–probe time-delay dependent UHT response, however, differs considerably as can be seen by evaluating the scattering signal change computed as the difference between images acquired in the presence and absence of the pump pulse (Fig. 3c). The latex NPs show no transient signal, as expected for off-resonantly excited particles probed far off-resonance (Fig. 3d). Contrary, the Au NPs exhibit an instrument-response limited decrease in differential scattering signal, ΔS/S, due to the generation of hot electrons21 followed by thermalisation on the picosecond time-scale. We note that the ΔS/S signal-differences between individual NPs are due to the Gaussian spatial profile of the pump beam, which only weakly photoexcites NPs positioned at its wings.
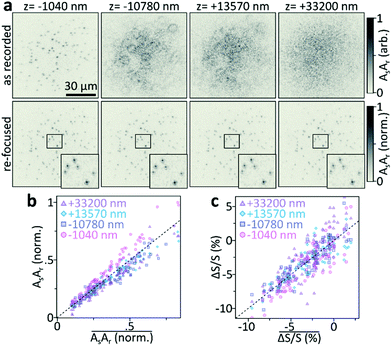
Beyond being able to simultaneously observe, and identify, many individual nano-objects within a large observation plane, the holographic nature of our method furthermore allows computational image propagation, post-acquisition, to 3D-localise many individual particles from a single camera exposure. Fig. 4a demonstrates these capabilities by imaging an out of focus 2D sample composed of many individual 60 nm diameter Au NPs, immobilised on a flat coverglass, at different defocus distances with respect to the image plane. For small defocus distances, similar to those employed in our proof-of-principle work (z = −1040 nm), we still observe many individual particles, which however blur into a speckle-like pattern as we move the sample further away from the image plane (z = 10.7–33.2 μm, Fig. 4a, top). Despite this apparent loss of information, computational re-focussing (Methods) of all four recordings results in nearly identical in-focus images (Fig. 4a, bottom).
To further quantify these observations, we compare the signals retrieved from the four z-positions. Fig. 4b correlates the signal of each particle in all four images with the mean signal of the respective particle. Within our z-range, the scattering signal is essentially independent of the sample's position with respect to the focal plane of the imaging system. Even though this observation might seem surprising at first, the near-identical signal levels are expected if we consider the image-collection and re-focusing operation. Signal loss occurs if the detector fails to record the sample information and it is hence sufficient to employ a detector that is large enough to fully capture the defocused point-spread-functions of the individual particles. Even though defocusing lowers the detected photons per camera pixel, the interferometric detection methodology, with a reference wave that covers the entire detector, ensures camera operation at the shot-noise limit, thus preventing problems associated with entering the dark-noise regime of a camera.22 Computational re-focussing, a deconvolution operation, will hence always recover the in-focus NP-signal as long as their density is sufficiently low in the field of view and the signal-to-noise ratio is sufficiently high to observe the NP when physically in focus.
Thus far, we discussed imaging considerations as applied to 3D single-particle-localisation experiments with linear holography. However, the UHT microscope relies on signals recorded in a pump–probe fashion where an ultrafast pump pulse induces a time-dependent transient signal, or differential scattering (ΔS/S(t)) change. Maximum UHT signals are generally obtained when probing the sample immediately after photoexcitation,10 maximising the magnitude of the photoinduced signal before the onset of relaxation processes. To demonstrate that UHT-based 3D single-particle-localisation experiments are indeed possible, we repeat the re-focusing experiments (Fig. 4a and b) but for differential scattering signals measured with the UHT microscope. A 400 nm pump pulse photoexcites the same set of 60 nm Au NPs and a 550 nm probe pulse captures the UHT-response as the average signal in the 0–3.6 ps time-window (computed from 31 individually acquired pump–probe delays). Fig. 4c, once again, shows that near-identical signals are obtained for in- and out-of-focus recordings, following digital refocusing. In other words, UHT microscopy should be well suited for 3D nonlinear localisation experiments over large volumes of view.
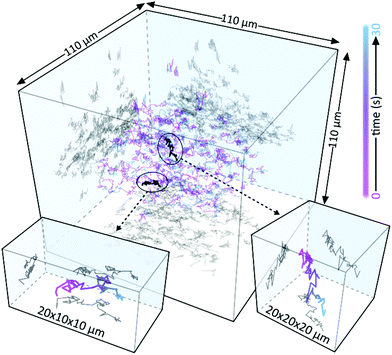
Following these static proof-of-concept experiments, we now concentrate on freely diffusing particles within a large 3D volume of 110 × 110 × 110 μm. Fig. 5a shows a 3D representation of typically acquired linear holographic datasets where we combined results of three consecutively performed 3D tracking experiments on a total of 140 freely diffusing Au NPs. To obtain the trajectories shown we first acquire 60 holograms over a total observation time of 30 s, using a camera exposure of 10 ms per image followed by a 500 ms waiting time. We then computationally propagate each hologram over a total of 150 μm, following the same procedure as previously described for the static samples (Fig. 4), and then localise all NPs in 3D (Methods), with localisation precisions typically being better than 15 nm. The 3D coordinates of all particles in all 60 frames are then linked to obtain 3D trajectories using the procedure outlined in detail by Jaqaman et al.15,16,23
To demonstrate that the particles observed are, indeed, resonant Au NPs with their corresponding transient dynamics, and hence that 3D tracking can be applied to the transient signals, we follow a different approach. Rather than acquiring the entire video at a fixed pump–probe time-delay, with maximum NP-UHT response, we acquire consecutive images at either negative or positive pump–probe time-delays following the procedure described in Fig. 6a. In our approach, we first acquire a single UHT image at a positive pump–probe delay, using a 10 ms camera integration time. We then move to a negative delay and record a second image. The two acquisitions are separated by a waiting time of 500 ms to allow sufficient time for physically moving the translation stage (Fig. 1a) that controls the pump–probe delay. In this experimental configuration we expect UHT signals at positive time delays and no signal at negative delays, which should allow us to demonstrate that the signal is photoinduced and not a potential artefact due to other experimental factors. Even though smaller particles are readily detectable10 we opted for rather large 100 nm Au NPs, with relatively slow diffusion coefficients, to ensure confident trajectory-linking even with the 500 ms waiting-time between frames. The differential scattering histograms reported in Fig. 6b show the absence of UHT signals for negative time delays and a marked signal increase at positive delays, thus verifying that UHT microscopy is capable of identifying resonant particles while, simultaneously, following their rapid 3D motion within a large volume of observation. As in the data reported in Fig. 4 we, once again, observe a large spread of UHT signals as the pump-beam's fluence is not constant across our large field of illumination. Fig. 6c shows examples of time-delay switching on the single-particle level where the individual NPs are centred and re-focused for representation purposes only. One particle is contained in the central area of the pump beam, corresponding to the peak of pump fluence, and the other in its spatial wing, in a region of negligible pump fluence. Even though both particles are visible in the pumpOFF and pumpON images, only the NP in the high pump fluence area exhibits a UHT signal and only for positive time-delays.
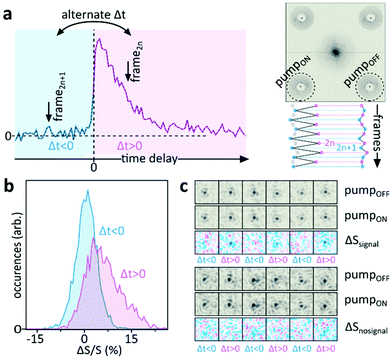 | ||
| Fig. 6 In situ modulation of UHT signals for freely diffusing particles. (a) Alternating the pump–probe time-delay between image acquisitions switches the UHT signal on and off (left) which allows identifying resonant NPs as long as the same particle can be followed over several frames (right). (b) Comparison between the differential scattering signal histograms of all freely diffusing NPs acquired before (blue) and after (pink) photoexcitation. We note that the ΔS/S signal inversion, as compared to Fig. 4c, is due to the different size of the NPs, a different probe wavelength and the fact that the NPs are immersed in water (n = 1.334) rather than immobilized on a glass surface in air. (c) Comparison of pumpOFF and pumpON images and difference between the two (ΔS) for a particle located in a high-fluence region (top) or a region of negligible pump-fluence (bottom). The freely diffusing particles are computationally re-focused and centred for representation purposes only, their physical position changes due to Brownian motion. Imaging is performed using a camera exposure of 10 ms followed by a 500 ms waiting-time to allow physical movement of the translation stage; pump: 400 nm, probe: 566 nm wavelength. | ||
We finally perform pump–probe time-dependent transient scattering spectroscopy on a freely diffusing 100 nm Au NP. Fig. 7a shows the as-recorded holographic image acquired with the focus placed in the vicinity of the glass-water interface. The two visible particles are stuck to the glass surface. We computationally propagate by approximately 10 μm above the recording plane where we identify a freely diffusing NP (Fig. 7b, top). By continuously maximizing its amplitude via computational propagation, we are able to follow the xyz-motion of said particle for holographic images acquired at different times, as shown in ESI Video 1.† Simultaneously, we record UHT images where the particle is only visible for positive time delays (Fig. 7b, bottom), in agreement with the observations made previously (Fig. 6). Finally, we use UHT microscopy to follow the 3D trajectory of the NP while changing the pump–probe time delay, which allows recording the 3D trajectory as well as the transient dynamics of a rapidly diffusing object (Fig. 7c and ESI video 1†). As expected, the ΔS/S signal of the gold NP decays on the picosecond timescale due to hot electron cooling via coupling with phonons.
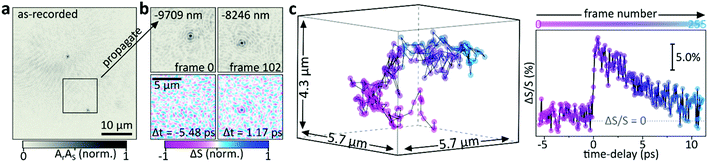 | ||
| Fig. 7 Transient spectroscopy of freely moving objects. (a) As acquired image recorded at the glass-water interface highlighting the region of interest where a freely diffusing 100 nm Au NP is identified by (b) computationally propagating approximately −9709 nm (frame 0) or −8246 nm (frame 102). Transient UHT images obtained at the same frames but for two different pump–probe delays are shown below (see ESI Video 1†). (c) 3D trajectory of the freely diffusing NP shown in (a) alongside the simultaneously recorded transient scattering time-trace. 500 ms waiting-time between frames, 10 ms integration; pump: 400 nm, probe: 566 nm wavelength. | ||
To summarise, we showed that UHT microscopy10 is ideally suited for single-particle tracking applications over large volumes of view. Analogous to photothermal microscopy, UHT microscopy allows identifying and isolating resonant particles, such as the gold NPs employed in this work, from off-resonant particles, which is the key requirement for imaging applications in scattering environments such as live cells or tissue.9 The holographic all-optical lock-in modality exploited in UHT microscopy further eliminates all limitations of traditional photothermal imaging, where lock-in amplifier based point-scanning severely limits the technique's applicability to observing dynamic systems, even in a simple 2D context.9 The relatively slow frame-rates of 2 frames-per-second employed here were solely chosen to allow changing the pump–probe time-delay between image acquisitions, which was necessary to conclusively demonstrate that the UHT signals observed are indeed pump-induced and not an artefact of our imaging system. For high-speed tracking applications the camera exposures of 10 ms, used here, correspond to a nominal frame rate of 100 frames-per-second and it should easily be possible to further increase the frame rate to up to half the laser's repetition rate by employing a faster camera and further boost the sensitivity by using a laser with higher repetition rate. These capabilities make UHT microscopy an ideal candidate for both high-speed and long-term tracking of resonant particles in 3D scattering environments. As such, we envision immediate applications in the context of cellular particle-internalisation dynamics of theranostic or nanomedical agents as well as their transport through cells and tissue.
Methods
Microscope
The UHT microscope employed in this work is analogous to our previous implementation10 based on a 1 kHz, 100 fs amplified Ti:sapphire laser24 delivering both the 400 nm pump pulse as the second harmonic and the probe pulse via a home-built non-collinear optical parametric amplifier (NOPA). A 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 beam-splitter generates the probe and the reference from the NOPA output. A F = 200 mm achromatic lens focuses the collinear pump and probe pulses onto the sample. Residual pump light is removed with a 488 nm long-pass filter (488 nm EdgeBasic™, Semrock) and the probe scattering is collected with a home-built transmission dark-field microscope (NA = 0.5, Olympus RMS20X-PF) and imaged onto a CMOS camera (acA2040-90um Basler ace, Basler AG) at a magnification of 37×. Off-axis holography is implemented by interfering the sample scattering with two of the first diffraction orders of a 2D 0-π phase grating (25.6 grooves per mm) which we relay-image (nominal magnification 0.5×) onto the same CMOS camera. Two synchronized mechanical choppers are used to modulate both the reference waves as well as the pump pulse as described in detail previously10 and in the main text. The signal to reference time-delay is adjusted with a mechanical delay line. Pump–probe time-delay dependent images are recorded in an automatized fashion with a computer-controlled translation stage (M-531.PD1, Physik Instrumente).
10 beam-splitter generates the probe and the reference from the NOPA output. A F = 200 mm achromatic lens focuses the collinear pump and probe pulses onto the sample. Residual pump light is removed with a 488 nm long-pass filter (488 nm EdgeBasic™, Semrock) and the probe scattering is collected with a home-built transmission dark-field microscope (NA = 0.5, Olympus RMS20X-PF) and imaged onto a CMOS camera (acA2040-90um Basler ace, Basler AG) at a magnification of 37×. Off-axis holography is implemented by interfering the sample scattering with two of the first diffraction orders of a 2D 0-π phase grating (25.6 grooves per mm) which we relay-image (nominal magnification 0.5×) onto the same CMOS camera. Two synchronized mechanical choppers are used to modulate both the reference waves as well as the pump pulse as described in detail previously10 and in the main text. The signal to reference time-delay is adjusted with a mechanical delay line. Pump–probe time-delay dependent images are recorded in an automatized fashion with a computer-controlled translation stage (M-531.PD1, Physik Instrumente).
Sample preparation
#1.5 coverglass is cleaned by 10 min sonication in acetone, 10 min sonication in MilliQ, drying under a stream of N2 followed by 5 min oxygen plasma treatment (Femto, Diener electronic GmbH). The cleaned glass is then incubated with PLL-g-PEG (SuSoS AG), for approximately 10 min, followed by a dilute 60 nm Au NP-solution (BBI Solutions). The latex NP-sample is fabricated by drying 5 μl of 100 nm polystyrene particles (Sigma Aldrich) on glass. For experiments on freely diffusing particles we dilute the NP stock solution using MiliQ water containing 0.5% polyacrylic acid to reduce the NPs’ mobility. The solutions are imaged using a coverglass sandwich with separation between the two glasses of ≈200 μm.Experimental parameters
Due to the Gaussian beam-shapes the fluences vary widely across the field of observation and we solely quote 1/e values for Fig. 4 and 5 with nominal fluences being: 1.00 mJ cm−2 pump, 0.75 mJ cm−2 probe, 10 ms integration time.Angular spectrum method
We perform image-propagation via the angular spectrum method.25 Briefly the processed NxN holograms are convolved with a propagation kernel of the form:where km = 2nπ/λ, with n = 1 being the refractive index of air. The discretized spatial frequencies are (kx, ky) = 2π/nΔx(x,y) for (−N/2 ≤ x,y < N/2), with Δx representing the magnified pixel size of the imaging system.
3D localization, large volume
For 3D localization, each hologram is propagated from −75 μm to +75 μm with a spacing between different z-planes (dz) of 500 nm. The resulting image cube is then used to identify candidate particles by applying multiple convolutions in combination with noise and particle-size based thresholding.26 To achieve sub-pixel localization in the x,y-coordinates, particles that are in focus at a specific z-plane are fitted by a 2D Gaussian. For the z-coordinate, sub-dz localization is achieved by first calculating the Tamura values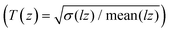 for a region of interest of (≈3 × 3 μm), centred about the intensity maxima for each z-plane, and then fitting a parabola using the two most adjacent pixel values along the maximum.15
for a region of interest of (≈3 × 3 μm), centred about the intensity maxima for each z-plane, and then fitting a parabola using the two most adjacent pixel values along the maximum.15
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support through the RTI2018-099957-J-I00 and PGC2018-096875-B-I00 projects funded by MCIN/ AEI /10.13039/501100011033/ FEDER “A way to make Europe”, by the Ministry of Science and Innovations (MICINN “Severo Ochoa” program for Centers of Excellence in R&D CEX2019-000910-S), the Catalan AGAUR (2017SGR1369), Fundació Privada Cellex, Fundació Privada Mir-Puig, and the Generalitat de Catalunya through the CERCA program. N.F.v.H. acknowledges the financial support by the European Commission (ERC Advanced Grant 670949-LightNet). G.C. acknowledges support by the European Union Horizon 2020 Programme under Grant Agreement 881603 Graphene Core 3.References
- A. Gaiduk, M. Yorulmaz, P. V. Ruijgrok and M. Orrit, Room-Temperature Detection of a Single Molecule's Absorption by Photothermal Contrast, Science, 2010, 330(6002), 353–356 CrossRef CAS PubMed.
- K. Mawatari, T. Kitamori and T. Sawada, Individual Detection of Single-Nanometer-Sized Particles in Liquid by Photothermal Microscope, Anal. Chem., 1998, 70(23), 5037–5041, DOI:10.1021/ac980250m.
- D. Boyer, P. Tamarat, A. Maali, B. Lounis and M. Orrit, Photothermal Imaging of Nanometer-Sized Metal Particles among Scatterers, Science, 2002, 297(5584), 1160–1163, DOI:10.1126/science.1073765.
- Y. C. Huang, T. H. Chen, J. Y. Juo, S. W. Chu and C. L. Hsieh, Quantitative Imaging of Single Light-Absorbing Nanoparticles by Widefield Interferometric Photothermal Microscopy, ACS Photonics, 2021, 8(2), 592–602, DOI:10.1021/acsphotonics.0c01648.
- M. Tamamitsu, K. Toda, H. Shimada, T. Honda, M. Takarada, K. Okabe, Y. Nagashima, R. Horisaki and T. Ideguchi, Label-Free Biochemical Quantitative Phase Imaging with Mid-Infrared Photothermal Effect, Optica, 2020, 7(4), 359, DOI:10.1364/optica.390186.
- D. Zhang, C. Li, M. Slipchenko, C. Zhang and J. X. Cheng, Depth-Resolved Mid-Infrared Photothermal Imaging of Living Cells and Organisms at Sub-Micron Resolution, Sci. Adv., 2016, 2, e1600521, DOI:10.1364/NTM.2017.NM4C.1.
- S. Adhikari, P. Spaeth, A. Kar, M. D. Baaske, S. Khatua and M. Orrit, Photothermal Microscopy: Imaging the Optical Absorption of Single Nanoparticles and Single Molecules, ACS Nano, 2020, 14(12), 16414–16445, DOI:10.1021/acsnano.0c07638.
- P. Vermeulen, L. Cognet and B. Lounis, Photothermal Microscopy: Optical Detection of Small Absorbers in Scattering Environments, J. Microsc., 2014, 254(3), 115–121, DOI:10.1111/jmi.12130.
- D. Lasne, G. A. Blab, S. Berciaud, M. Heine, L. Groc, D. Choquet, L. Cognet and B. Lounis, Single Nanoparticle Photothermal Tracking (SNaPT) of 5-Nm Gold Beads in Live Cells, Biophys. J., 2006, 91(12), 4598–4604, DOI:10.1529/biophysj.106.089771.
- M. Liebel, F. V. A. Camargo, G. Cerullo and N. F. van Hulst, Ultrafast Transient Holographic Microscopy, Nano Lett., 2021, 21, 1666–1671, DOI:10.1021/acs.nanolett.0c04416.
- P. Memmolo, L. Miccio, M. Paturzo, G. Di Caprio, G. Coppola, P. A. Netti and P. Ferraro, Recent Advances in Holographic 3D Particle Tracking, Adv. Opt. Photonics, 2015, 7(4), 713–755, DOI:10.1364/AOP.7.000713.
- L. Saemisch, N. F. Van Hulst and M. Liebel, One-Shot Phase Image Distinction of Plasmonic and Dielectric Nanoparticles, Nano Lett., 2021, 21, 4021–4028, DOI:10.1021/acs.nanolett.1c00866.
- M. Rubin, G. Dardikman, S. K. Mirsky, N. A. Turko and N. T. Shaked, Six-Pack off-Axis Holography, Opt. Lett., 2017, 42(22), 4611–4614 CrossRef PubMed.
- P. Bon, G. Maucort, B. Wattellier and S. Monneret, Quadriwave Lateral Shearing Interferometry for Quantitative Phase Microscopy of Living Cells, Opt. Express, 2009, 17(15), 13080–13094, DOI:10.1364/OE.17.013080.
- M. Liebel, J. O. Arroyo, V. S. Beltrán, J. Osmond, A. Jo, H. Lee, R. Quidant and N. F. van Hulst, 3D Tracking of Extracellular Vesicles by Holographic Fluorescence Imaging, Sci. Adv., 2020, 6(45), eabc2508, DOI:10.1126/SCIADV.ABC2508.
- M. Liebel, N. Pazos-Perez, N. F. van Hulst and R. A. Alvarez-Puebla, Surface-Enhanced Raman Scattering Holography, Nat. Nanotechnol., 2020, 15, 1005–1011, DOI:10.1038/s41565-020-0771-9.
- A. A. Maznev, T. F. Crimmins and K. A. Nelson, How to Make Femtosecond Pulses Overlap, Opt. Lett., 1998, 23(17), 1378–1380, DOI:10.1364/OL.23.001378.
- M. Takeda, H. Ina and S. Kobayashi, Fourier-Transform Method of Fringe-Pattern Analysis for Computer-Based Topography and Interferometry, J. Opt. Soc. Am., 1982, 72(1), 156, DOI:10.1364/JOSA.72.000156.
- E. Cuche, P. Marquet and C. Depeursinge, Spatial Filtering for Zero-Order and Twin-Image Elimination in Digital off-Axis Holography, Appl. Opt., 2000, 39(23), 4070–4075, DOI:10.1364/AO.39.004070.
- C. Pache, N. L. Bocchio, A. Bouwens, M. Villiger, C. Berclaz, J. Goulley, M. I. Gibson, C. Santschi and T. Lasser, Fast Three-Dimensional Imaging of Gold Nanoparticles in Living Cells with Photothermal Optical Lock-in Optical Coherence Microscopy, Opt. Express, 2012, 20(19), 21385, DOI:10.1364/oe.20.021385.
- A. Block, M. Liebel, R. Yu, M. Spector, Y. Sivan, F. J. García De Abajo and N. F. Van Hulst, Tracking Ultrafast Hot-Electron Diffusion in Space and Time by Ultrafast Thermomodulation Microscopy, Sci. Adv., 2019, 5(5), eaav8965, DOI:10.1126/sciadv.aav8965.
- U. Ortiz-Orruño, A. Jo, H. Lee, N. F. Van Hulst and M. Liebel, Precise Nanosizing with High Dynamic Range Holography, Nano Lett., 2021, 21(1), 317–322, DOI:10.1021/acs.nanolett.0c03699.
- K. Jaqaman, D. Loerke, M. Mettlen, H. Kuwata, S. Grinstein, S. L. Schmid and G. Danuser, Robust Single-Particle Tracking in Live-Cell Time-Lapse Sequences, Nat. Methods, 2008, 5(8), 695–702, DOI:10.1038/nmeth.1237.
- C. Manzoni, D. Polli and G. Cerullo, Two-Color Pump-Probe System Broadly Tunable over the Visible and the near Infrared with Sub-30 Fs Temporal Resolution, Rev. Sci. Instrum., 2006, 77(2), 023103, DOI:10.1063/1.2167128.
- J. W. Goodman, Introduction to Fourier Optics, ed. W. H. Freeman, 3rd edn, 2005 Search PubMed.
- P. Viola and M. Jones, Rapid Object Detection Using a Boosted Cascade of Simple Features. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001, Kauai, HI, USA, 2001; 2005; pp I-511–I-518. DOI:10.1109/cvpr.2001.990517.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr06837g |
| This journal is © The Royal Society of Chemistry 2022 |