Open Access Article
Open Access ArticleTheory-augmented informatics of ionic liquid electrolytes for co-design with nanoporous electrode materials†
Stephen E.
Weitzner
 *,
Tuan Anh
Pham
*,
Tuan Anh
Pham
 and
Eric R.
Meshot
and
Eric R.
Meshot
 *
*
Lawrence Livermore National Laboratory, 7000 East Avenue, Livermore, CA, USA. E-mail: weitzner1@llnl.gov; meshot1@llnl.gov
First published on 12th March 2022
Abstract
Ionic liquids possess compelling properties and vast chemical diversity, promising unprecedented performance and tunability for advanced electrochemical applications in catalysis, sensing, and energy storage. However, with broad tunability comes intractable, multidimensional parameter spaces not easily traversed by empirical approaches, limiting both scientific understanding and technological breakthroughs with these novel materials. In this Communication, we propose an extensible figure of merit that co-optimizes key ionic liquid properties, including electrochemical stability window, viscosity, and molecular ion size with respect to pore sizes of nanoporous electrodes typically utilized in electrochemical technologies. We coupled density functional theory (DFT) with informatics to augment physiochemical property databases to screen for high-performance room-temperature ionic liquid (RTIL) candidate compounds. This co-design framework revealed a number of promising RTILs that are underrepresented in the literature and thus warrant future follow-up investigations.
Room-temperature ionic liquids (RTILs) are promising for future electrochemical applications as safe and high-performance alternatives to conventional electrolytes due to their low volatility, large conductivity, broad chemical tunability, high thermal stability, and wide electrochemical stability window (ESW).1,2 This ensemble of exciting properties in addition to their dual function as both solvents and electrolytes makes this class of material important to technological roadmaps in catalysis, sensing, gas capture, and electrochemical energy storage (EES) devices, such as lithium ion batteries and electrical double layer capacitors (EDLCs).2–11 However, harnessing the promise of RTILs to maximize EES device performance beyond current benchmarks remains an outstanding challenge due to the combinatorial nature of leveraging numerous RTIL properties to couple with the high surface-area, nanoporous electrodes typically employed in EES devices.3,12,13
The importance of RTIL ion-pore coupling was recently highlighted as a key factor in the rational design of future EES devices.14 A primary example of this coupling emerged in earlier studies that showed the capacitance of RTIL-based EDLCs varied by a factor of 1.5–2 depending on the electrode pore size, with maximal capacitance achieved when the ion and pore sizes matched.15 At the same time, capacitance may be limited in electrodes when spatial confinement created by small pores hinders the formation of a compact electrical double layer of ions. This can be the case even if the ESW is large, such as with ammonium-based RTILs that have values up to ∼6 V (exceeding aqueous and commercial polymer electrolytes).16,17 Pore size has also been shown to affect ionic transport18,19 and the melting point20 of an ionic liquid. In addition, engineering hierarchical pore size distributions underscores the importance of other phenomena across multiple length scales, such as transport through macropores and ion desolvation in intermediately sized mesopores.21–23 Detailed experimental13,24–26 and theoretical24,27–31 investigations revealed elucidating descriptions of the RTIL properties under nanoconfinement, yet it is challenging to extrapolate from these fundamental results based on a narrow parameter space to successfully identify RTILs with fully optimized performance.
Experimental and theoretical tools for co-optimizing performance across multidimensional parameter spaces have been slow to develop, which critically limits the ability to capitalize on the technological potential of RTILs. Recent work has made progress in this area, screening RTILs for EES applications with informatics-based approaches, which rely on compiled RTIL physiochemical property databases comprised of experimental and theoretical data sets.32–34 This way large parameter spaces can be searched to identify candidate RTILs with desirable properties for EES such as low viscosity (high ionic conductivity) or high ESW (large operational voltage window). However, major challenges arise due to gaps in property spaces, key properties may be entirely missing, or critical physics omitted that inform on true device performance (such as ion-pore coupling).
In this Communication, we couple density functional theory (DFT) with informatics to augment physicochemical property databases and screen for high-performance room-temperature ionic liquid (RTIL) candidates based on an extensible figure of merit (FOM). Instead of relying on a single descriptor as with prior studies, our figure of merit incorporates three principal factors of electrolytes that dictate performance in EES applications, including the ESW, viscosity, and ion size. The first determines the maximal energy density; the second is a proxy for ionic conductivity and thus power density; and the third is related to the ease with which electrolyte ions can enter and fill nanopores within the electrodes. Incorporating multiple RTIL properties (i.e., ESW, viscosity, ion size) and structural characteristics of the electrode (i.e., pore size) into the design criteria could provide practical guidance for enhancing performance in EES devices and other electrochemical systems.
To quantitatively benchmark the EES performance of RTIL candidates in nanoporous electrodes, we derived a new figure of merit that encompasses both electrolyte and electrode characteristics, expressed as:
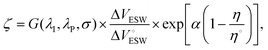 | (1) |
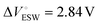 and η° = 0.0344 Pa s, respectively.35,36 We additionally include a model parameter α to control the degree to which viscosity is emphasized. The selected value for this study (α = 0.1) weights the FOM such that high performance is predicted in the range of 0.05 to 0.2 Pa s in the case of [EMIM][TFSI], for example. Viscosity values in this range are sufficiently low to enable good capacitive performance.37 The extent of the ion-pore size mismatch is accounted for by introducing a scaling factor
and η° = 0.0344 Pa s, respectively.35,36 We additionally include a model parameter α to control the degree to which viscosity is emphasized. The selected value for this study (α = 0.1) weights the FOM such that high performance is predicted in the range of 0.05 to 0.2 Pa s in the case of [EMIM][TFSI], for example. Viscosity values in this range are sufficiently low to enable good capacitive performance.37 The extent of the ion-pore size mismatch is accounted for by introducing a scaling factor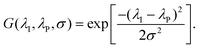 | (2) |
Here, λI = max(λC,λA) is the maximum ion size associated with the RTIL, λP is the average electrode pore size, and σ is an empirical parameter that controls the width of the Gaussian function. We use a a value of 0.33 Å, which was obtained by fitting eqn (2) to the normalized capacitance vs. pore size distribution of [EMIM][TFSI] reported in ref. 15, but this function may be readily re-parameterized depending on the pore size distribution of the electrode material of interest. The FOM depends linearly on the ESW of the RTIL, and in the limit of low viscosity, it is determined solely by the ESW and the degree of ion-pore size mismatch. On the other hand, the FOM is reduced to zero for RTILs that have a high viscosity or a large mismatch with the pore size.
Experimental determination of multiple properties for a large set of RTILs is cumbersome and presents roadblocks to progress. Instead, we combine existing experimental data with those computed from first principles to efficiently construct a multidimensional property map to screen RTILs candidates using the FOM. The ESW and ion sizes were obtained from DFT calculations, while viscosity data at standard temperature and pressure (T = 298 K and P = 1 bar) were retrieved from the from the NIST ILThermo database.35,36 While properties derived from bulk experiments and DFT calculations under vaccuum may differ when under nanoconfinement in real devices,14 we expect the comparisons and trends among sets of RTILs outlined in this study still hold as good predictors of high-performing RTILs. Our DFT calculations were carried out for a select set of 33 cations and 77 anions to generate 2171 stable ion pairs (14.6 of the ion pairs are predicted to be unstable based on a frontier orbital energy analysis). Incorporating viscosity as a key EES parameter reduces the sample size of RTIL candidates to 61 due to the limited experimental viscosity data currently available.
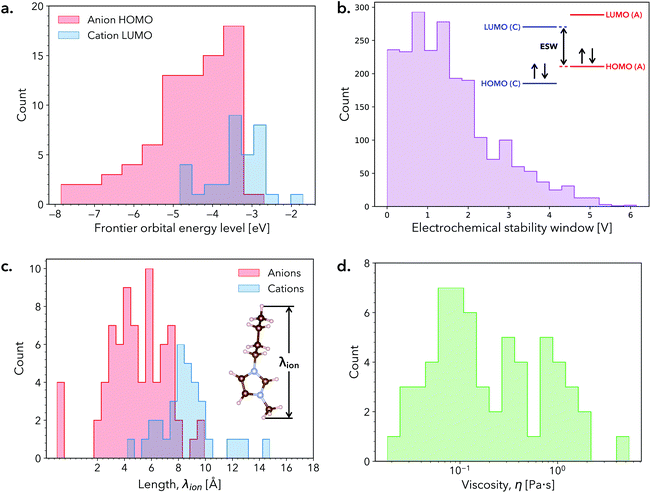
In this work, we estimate the ESW of RTILs by employing the approach described in ref. 38. Briefly, the ESW is estimated as the difference between the cation LUMO level and anion HOMO level in vacuum, which correspond to the cathodic and anodic stability limits of the RTIL, respectively (section S1 of the ESI†). Histograms of the cation LUMO and anion HOMO levels are shown in Fig. 1a. While both histograms are skewed towards lower energy levels, the anion HOMO levels exhibit a relatively broader spread. The resultant distribution of ESW values is shown in Fig. 1b, which is skewed towards higher voltages, with a majority of the predicted RTILs having ESWs of <3 V. Interestingly, many of the RTILs in the tail of the ESW histogram are composed of PF6−, B(CN)4−, and BF4− (see ESI†), which have previously been identified as components of promising candidate RTILs for EES applications.16,33,39–41
To compute the RTIL ion size, we extracted the largest interatomic distance (i.e., length) from DFT-optimized molecular geometries as a proxy for size to capture trends (Fig. 1c). Although, some ions are anisotropic in their geometry and thus have narrower dimensions in certain orientations, this metric provides an upper bound with respect to a given pore size. The histograms of cation and anion sizes overlap in a fairly narrow range, indicating that for many RTILs a large size discrepancy between cation and anion size exist. Further, our analysis assumes that the largest ion dictates the performance to conserve parity under positive and negative voltages biases, which consequently means that the size of cations is often the determining factor. The bulky nature of these molecular salts is immediately apparent, with all RTIL ions exhibiting sizes larger than common aqueous salts (some nearly 10× larger). This size difference is worth noting because ion-pore coupling may play a meaningful role in EES performance in larger pores and/or a larger range of pore sizes than for aqueous salts.
Fig. 1d presents a histogram of RTIL viscosity values for the subset of 61 stable compositions identified with DFT calculations. In contrast to the relatively small composition-dependent shifts observed in RTIL ESWs, RTIL viscosity values may span 2–3 orders of magnitude, underscoring the fact that RTILs with similar ESWs may exhibit vastly different transport properties. Large variations in viscosity translate to large variations in ionic conductivity and hence may have an important impact on the power density of EES devices.42 Moreover, RTILs with lower viscosity exhibit higher degrees of fluidity, indicating that they may be more apt to infiltrate into porous electrodes. Although surface tension of the electrolyte and chemical functionalization of the electrode surface also likely influence infiltration, they are neither widely tabulated quantities nor straight forward to incorporate in our figure of merit. However, the physics governed by these factors may be implemented in future developments.
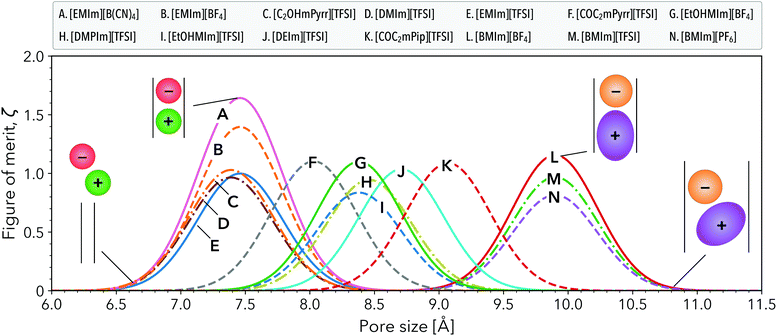
To illustrate the effect of ion size in our FOM, ζ, we consider the extreme cases at a microscopically flat interface that can be fully wet by RTILs versus nanoporous electrodes wherein confinement may hinder wetting and infiltration/intercalation. In Fig. 2a, we plot RTIL ESW scaled by G against viscosity in the limit of a flat interface.33,41 In this context, we can set G = 1 universally since there are no nanoconfinement effects, hence ζ depends solely on the ESW and viscosity of the RTIL. We additionally show ζ as a contour map, with the highest performing candidates appearing near the top-left corner of the plot (large ΔVESW, small η). [EMIM][TFSI], which sets the relative scale of the FOM, has ζ = 1 and is highlighted with a red marker. Interestingly, we find that the data is clustered in two regions, with ζ ∼ 0.75 appearing as a natural boundary. Of the 61 RTILs considered in this work, we identify 14 candidates with ζ > 0.75. We consider these to be high-performing candidates as they are clustered near [EMIM][TFSI] within the property map, suggesting that they exhibit a similar anomalously high capacitive performance.15 Properties of these 61 RTILs are summarized in the ESI.†
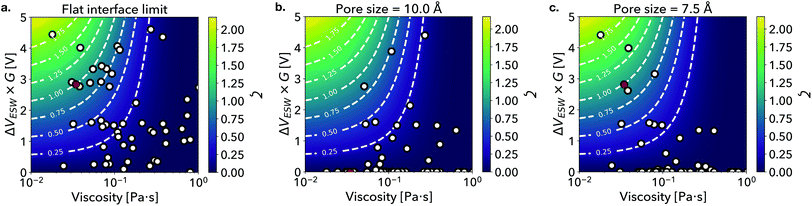 | ||
| Fig. 2 Property maps depicting the scaled ESW vs. viscosity of the set of ionic liquids considered in this work in the (a) flat interface limit and under nanoconfinement with (b) 10.0 Å and (c) 7.5 Å pore sizes. The marker associated with [EMIM][TFSI] is highlighted in red and a contour plot of the figure of merit is included in each figure as a visual guide. The full progression of figure of merit values as pore size evolves from 3.0 to 13.5 Å can be view in the supplementary movie in the ESI.† | ||
As we approach the other extreme of nanoconfinement where ion size effects become prominent, we find that that our candidate list becomes more nuanced. In Fig. 2b and c, we consider pore sizes of λP = 10 and λP = 7.5, which are typically pore sizes found in nanoporous carbon electrode materials.25 For both pore sizes, we observe that a number of scatter points are suppressed to ζ = 0 due to extensive ion-pore size mismatch, effectively filtering the candidate list for pore-size compatible RTILs. The suppression of ζ is reflective of the decrease in capacitive performance reported by Largeot et al. when electrode pore size deviated from the effective ion size of [EMIM][TFSI], as shown in Fig. 2b. Physically, the decrease in capacitive performance with larger pore sizes was attributed to a larger average distance between the molecular ion center and the charged pore wall.15 Conversely, when the pore size is made smaller than the ion size, the performance is similarly predicted to decrease as the ion cannot physically be accommodated within the pore volume. In comparison to Fig. 2a, we find that in the case of 10 Å pores our methodology identifies a small subset of 2 candidates with ζ > 0.75 out of the original 14 candidates, while for 7.5 Å pores we identify another subset containing 5 candidates.
Rational selection of RTILs to complement varying degrees of electrode porosity is a foundational requirement for co-design. In the case of multimodal pore size distributions,43 a co-design framework is especially important to select specific RTIL mixtures to target multiple pore sizes within a single electrode material.44Fig. 3 illustrates how our framework guides this selection process, with ζ vs. pore size plotted for the 14 high-performance candidates from Fig. 2a. This subset of RTILs already possesses desirable viscosity and ESW values, however our FOM predicts each compound to be maximally effective over a specific range of pore sizes. The inset schematics in Fig. 3 depict multiple scenarios of generic cation and anion infiltration into nanoscale slit pores spanning the pore size axis. For example, the FOM is maximized when the optimal pore-ion size matching criterion is met. In contrast, the FOM is low when the pore size is smaller than that optimal criterion as ions do not fit inside the pore, or when the ions can fit but are highly disordered inside the largest pores due to excessive free volume.
The first set of peaks in Fig. 3 centered near 7.4 Å identifies popular RTILs, including [EMIM][B(CN)4], [EMIM][BF4], and [EMIM][TFSI]. Two other less commonly studied RTILs, [C2OHmPyrr][TFSI] and [DMIm][TFSI], also appear in this pore size regime. Interestingly, our FOM predicts these RTILs to have similar capacitive performance as [EMIm][TFSI] for pore sizes between 7–8 Å, while [EMIm][B(CN)4] and [EMIM][BF4] outperform [EMIM][TFSI]. This trend is consistent with experimental measurements of capacitive performance for the same set of [EMIm]+–based RTILs using porous carbon electrodes.45 Also consistent with our predictions, prior experiments using carbon electrodes with a mean pore size of 7.6 Å revealed [EMIm][BF4] to exhibit a greater capacitive performance over [DMPIm][TFSI] for low current densities.46
At slightly larger pore sizes (8.0–9.3 Å), several alternative RTILs are predicted to have comparable performance to the optimized [EMIm][TFSI] case, including [COC2mPyrr][TFSI], [EtOHMIm][BF4], [DMPIm][TFSI], [EtOHMIm][TFSI], [DEIm][TFSI], and[COC2mPip][TFSI]. These are not heavily represented in experimental EES literature, yet they have been cited as promising candidates for electrochemical applications due to their large ESWs and high(low) ionic conductivities(viscosities).47–49 Based on our FOM, this set of alternative RTILs can provide good performance in these intermediate pore sizes, whereas the more common [EMIm]+– and [BMIm]+–based RTILs may be less effective.
For even larger pore sizes 9.5–10.5 Å, [BMIm]+–containing RTILs emerged as the most compelling candidates, with maximized performance predicted at 9.9 Å and on par with optimized [EMIm][TFSI]. Both experiments50 and simulations51,52 indicate that increasing the alkyl chain length on the imidazolium cation decreases capacitance. Our FOM predictions reveal a similar trend comparing [EMIm]+ to [BMIm]+ (e.g., the [BF4]− and [TFSI]− cases), even when evaluated at their optimized pore sizes of 7.4 Å to 9.9 Å, respectively. Our down-selected candidates do not contain ions with sizes larger than ∼10 Å, even though our initial screening considered several larger ions. For example, we analyzed RTILs containing quaternary phosphonium cations (see ESI Table S1†), but these were predicted to have low FOM values due to their high viscosities (>0.5 Pa s).53,54 Promising RTIL electrolytes that meet the size-matching criterion in pores larger than 11 Å may be detected using our framework by considering an expanded set of RTILs in the future.
In summary, we developed a quantitative figure of merit based on a combination of tabulated experimental physicochemical data and first-principles electrochemical calculations to evaluate the performance of RTILs for EES devices. Our figure of merit is predicated on the ESW and viscosity of the RTIL electrolyte, as well as the degree of size mismatch between RTIL ions and electrode pores. Our analysis identified several known high performance RTIL electrolytes, while simultaneously identifying several candidate RTIL electrolytes that are underrepresented in the literature. Importantly, our figure of merit provides approximate bounds for the electrode pore size that would yield optimal EDLC device performance when paired with a specific RTIL electrolyte, providing a useful guide for the co-design of electrode and electrolyte materials for EES applications.
While future experimental work is needed to further validate our figure of merit, we envision several potential ways to refine our analysis. Specifically, the chemical hardness and static polarizabilties of RTILs may be proxies for the propensity for charge transfer and the dielectric properties, respectively. Future refinements may also include kinetic descriptors for ion transfer between the bulk electrolyte and pore interior. Our framework assumes that cations and anions are equally available for nanopore filling. In real carbon electrode materials, there may be hierarchical pore size distributions that influence ion transport rates to the nanopore entrance, and thus additional parameterization may be needed. Nevertheless, data scarcity challenges require the adoption of additional predictive methods to help augment physicochemical property data sets of useful parameters (e.g., dielectric permittivity). Finally, the present co-design framework relies on known RTILs and established pore structures, yet it is important to work toward more predictive methods that could guide synthesis of new RTIL chemistry and porous electrode materials to outperform state-of-the-art EES devices.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory (LLNL) under Contract DE-AC52-07NA27344. Funding was provided by LLNL Laboratory Directed Research and Development (LDRD) Program Tracking No. 21-ERD-024. This study was part of a user project at the Molecular Foundry, supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.References
- B. Pal, S. Yang, S. Ramesh, V. Thangadurai and R. Jose, Nanoscale Adv., 2019, 1, 3807–3835 RSC.
- C. Xu, G. Yang, D. Wu, M. Yao, C. Xing, J. Zhang, H. Zhang, F. Li, Y. Feng and S. Qi, et al. , Chem. – Asian J., 2021, 16, 549–562 CrossRef CAS PubMed.
- M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036 CrossRef CAS PubMed.
- M. Salanne, B. Rotenberg, K. Naoi, K. Kaneko, P.-L. Taberna, C. P. Grey, B. Dunn and P. Simon, Nat. Energy, 2016, 1, 1–10 Search PubMed.
- R. Sheldon, Chem. Commun., 2001, 2399–2407 RSC.
- A. Eftekhari, Energy Storage Mater., 2017, 9, 47–69 CrossRef.
- J. B. Goodenough, H. D. Abruna and M. V. Buchanan, Basic Research Needs for Electrical Energy Storage, Report of the Basic Energy Sciences Workshop on Electrical Energy Storage, April 2–4, 2007.
- P. Simon and Y. Gogotsi, Nanoscience and Technology: A Collection of Reviews from Nature Journals, 2010, pp. 320–329 Search PubMed.
- J. R. Miller and P. Simon, Science, 2008, 321, 651–652 CrossRef CAS PubMed.
- S. Zeng, X. Zhang, L. Bai, X. Zhang, H. Wang, J. Wang, D. Bao, M. Li, X. Liu and S. Zhang, Chem. Rev., 2017, 117, 9625–9673 CrossRef CAS PubMed.
- S. Zhang, J. Zhang, Y. Zhang and Y. Deng, Chem. Rev., 2017, 117, 6755–6833 CrossRef CAS PubMed.
- S. Kondrat, C. Perez, V. Presser, Y. Gogotsi and A. Kornyshev, Energy Environ. Sci., 2012, 5, 6474–6479 RSC.
- A. C. Forse, C. Merlet, J. M. Griffin and C. P. Grey, J. Am. Chem. Soc., 2016, 138, 5731–5744 CrossRef CAS PubMed.
- X. Wang, M. Salari, D.-E. Jiang, J. C. Varela, B. Anasori, D. J. Wesolowski, S. Dai, M. W. Grinstaff and Y. Gogotsi, Nat. Rev. Mater., 2020, 5, 787–808 CrossRef CAS.
- C. Largeot, C. Portet, J. Chmiola, P.-L. Taberna, Y. Gogotsi and P. Simon, J. Am. Chem. Soc., 2008, 130, 2730–2731 CrossRef CAS PubMed.
- M. P. Mousavi, B. E. Wilson, S. Kashefolgheta, E. L. Anderson, S. He, P. Bühlmann and A. Stein, ACS Appl. Mater. Interfaces, 2016, 8, 3396–3406 CrossRef CAS PubMed.
- L. Chen, S. Venkatram, C. Kim, R. Batra, A. Chandrasekaran and R. Ramprasad, Chem. Mater., 2019, 31, 4598–4604 CrossRef CAS.
- Y. He, R. Qiao, J. Vatamanu, O. Borodin, D. Bedrov, J. Huang and B. G. Sumpter, J. Phys. Chem. Lett., 2016, 7, 36–42 CrossRef CAS PubMed.
- A. Ghoufi, A. Szymczyk and P. Malfreyt, Sci. Rep., 2016, 6, 1–9 CrossRef PubMed.
- M. Kanakubo, Y. Hiejima, K. Minami, T. Aizawa and H. Nanjo, Chem. Commun., 2006, 1828–1830 RSC.
- C. Young, J. Lin, J. Wang, B. Ding, X. Zhang, S. M. Alshehri, T. Ahamad, R. R. Salunkhe, S. A. Hossain and J. H. Khan, et al. , Chem. – Eur. J., 2018, 24, 6127–6132 CrossRef CAS PubMed.
- M. Kim, T. Park, C. Wang, J. Tang, H. Lim, M. S. A. Hossain, M. Konarova, J. W. Yi, J. Na and J. Kim, et al. , ACS Appl. Mater. Interfaces, 2020, 12, 34065–34073 CrossRef CAS PubMed.
- M. Kim, X. Xu, R. Xin, J. Earnshaw, A. Ashok, J. Kim, T. Park, A. K. Nanjundan, W. A. El-Said and J. W. Yi, et al. , ACS Appl. Mater. Interfaces, 2021, 13, 52034–52043 CrossRef CAS PubMed.
- T. A. Pham, R. M. Coulthard, M. Zobel, A. Maiti, S. F. Buchsbaum, C. Loeb, P. G. Campbell, D. L. Plata, B. C. Wood and F. Fornasiero, et al. , J. Phys. Chem. Lett., 2020, 11, 6150–6155 CrossRef CAS PubMed.
- R. Futamura, T. Iiyama, Y. Takasaki, Y. Gogotsi, M. J. Biggs, M. Salanne, J. Ségalini, P. Simon and K. Kaneko, Nat. Mater., 2017, 16, 1225–1232 CrossRef CAS PubMed.
- M. Busch, T. Hofmann, B. Frick, J. P. Embs, B. Dyatkin and P. Huber, Phys. Rev. Mater., 2020, 4, 055401 CrossRef CAS.
- C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, Nat. Mater., 2012, 11, 306–310 CrossRef CAS PubMed.
- C. Merlet, C. Péan, B. Rotenberg, P. A. Madden, B. Daffos, P.-L. Taberna, P. Simon and M. Salanne, Nat. Commun., 2013, 4, 1–6 Search PubMed.
- G. Feng and P. T. Cummings, J. Phys. Chem. Lett., 2011, 2, 2859–2864 CrossRef CAS.
- P. Wu, J. Huang, V. Meunier, B. G. Sumpter and R. Qiao, ACS Nano, 2011, 5, 9044–9051 CrossRef CAS PubMed.
- D.-E. Jiang, Z. Jin and J. Wu, Nano Lett., 2011, 11, 5373–5377 CrossRef CAS PubMed.
- S. Pandian, S. Raju, K. S. Hariharan, S. M. Kolake, D.-H. Park and M.-J. Lee, J. Power Sources, 2015, 286, 204–209 CrossRef CAS.
- C. Lian, H. Liu, C. Li and J. Wu, AIChE J., 2019, 65, 804–810 CrossRef CAS.
- C. Schütter, M. Husch, T. Korth and A. Balducci, J. Phys. Chem. C, 2015, 119, 13413–13424 CrossRef.
- Q. Dong, C. D. Muzny, A. Kazakov, V. Diky, J. W. Magee, J. A. Widegren, R. D. Chirico, K. N. Marsh and M. Frenkel, J. Chem. Eng. Data, 2007, 52, 1151–1159 CrossRef CAS.
- A. Kazakov, J. Magee, R. Chirico, V. Diky, K. Kroenlein, C. Muzny and M. Frenkel, Ionic Liquids Database - ILThermo (v2.0), Accessed on October 24th, 2021, 2013 Search PubMed.
- S. Fletcher, F. Sillars, R. Carter, A. Cruden, M. Mirzaeian, N. Hudson, J. Parkinson and P. Hall, J. Power Sources, 2010, 195, 7484–7488 CrossRef CAS.
- S. P. Ong, O. Andreussi, Y. Wu, N. Marzari and G. Ceder, Chem. Mater., 2011, 23, 2979–2986 CrossRef CAS.
- S. Kazemiabnavi, Z. Zhang, K. Thornton and S. Banerjee, J. Phys. Chem. B, 2016, 120, 5691–5702 CrossRef CAS PubMed.
- N. V. Ilawe, J. Fu, S. Ramanathan, B. M. Wong and J. Wu, J. Phys. Chem. C, 2016, 120, 27757–27767 CrossRef CAS.
- K. Karu, A. Ruzanov, H. Ers, V. Ivaništšev, I. Lage-Estebanez and J. García de la Vega, Computation, 2016, 4, 25 CrossRef.
- K. Tochigi and H. Yamamoto, J. Phys. Chem. C, 2007, 111, 15989–15994 CrossRef CAS.
- C.-P. Elverfeldt, Y. J. Lee and M. Fröba, ACS Appl. Mater. Interfaces, 2019, 11, 24423–24434 CrossRef CAS PubMed.
- N. C. Osti, A. Gallegos, B. Dyatkin, J. Wu, Y. Gogotsi and E. Mamontov, J. Phys. Chem. C, 2018, 122, 10476–10481 CrossRef CAS.
- H. Kurig, M. Vestli, K. Tonurist, A. Jänes and E. Lust, J. Electrochem. Soc., 2012, 159, A944 CrossRef CAS.
- F. B. Sillars, S. I. Fletcher, M. Mirzaeian and P. J. Hall, Phys. Chem. Chem. Phys., 2012, 14, 6094–6100 RSC.
- S.-H. Yeon, K.-S. Kim, S. Choi, H. Lee, H. S. Kim and H. Kim, Electrochim. Acta, 2005, 50, 5399–5407 CrossRef CAS.
- T. Belhocine, S. A. Forsyth, H. N. Gunaratne, M. Nieuwenhuyzen, P. Nockemann, A. V. Puga, K. R. Seddon, G. Srinivasan and K. Whiston, Phys. Chem. Chem. Phys., 2015, 17, 10398–10416 RSC.
- M. Vraneš, N. Cvjetićanin, S. Papović, M. Pavlović, I. Szilágyi and S. Gadžurić, Ionics, 2019, 25, 5501–5513 CrossRef.
- V. Lockett, M. Horne, R. Sedev, T. Rodopoulos and J. Ralston, Phys. Chem. Chem. Phys., 2010, 12, 12499–12512 RSC.
- S. Jo, S.-W. Park, Y. Shim and Y. Jung, Electrochim. Acta, 2017, 247, 634–645 CrossRef CAS.
- J. Yang, C. Lian and H. Liu, Chem. Eng. Sci., 2020, 227, 115927 CrossRef CAS.
- T. Makino, M. Kanakubo, T. Matsuki, E. Kamio, H. Takaba and H. Matsuyama, Fluid Phase Equilib., 2016, 420, 89–96 CrossRef CAS.
- P. Nancarrow, A. Al-Othman, D. K. Mital and S. Döpking, Energy, 2021, 220, 119761 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr07515b |
| This journal is © The Royal Society of Chemistry 2022 |