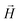Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nanopolymers for magnetic applications: how to choose the architecture?
Deniz
Mostarac
 *ab,
Yan
Xiong
c,
Oleg
Gang
cd and
Sofia
Kantorovich
*ab,
Yan
Xiong
c,
Oleg
Gang
cd and
Sofia
Kantorovich
 a
a
aFaculty of Physics, University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria. E-mail: deniz.mostarac@univie.ac.at
bResearch Platform MMM Mathematics-Magnetism-Materials, Vienna, Austria
cColumbia University, New York, USA
dBrookhaven National Laboratories, New York, USA
First published on 16th June 2022
Abstract
Directional assembly of nanoscale objects results in morphologies that can broadly be classified as supra-molecular nanopolymers. Such morphologies, given a functional choice of the monomers used as building blocks, can be of ubiquitous utility in optical, magnetic, rheological, and medical applications. These applications, however, require a profound understanding of the interplay between monomer shape and bonding on one side, and polymeric properties – on the other. Recently, we fabricated nanopolymers using cuboid DNA nanochambers, as they not only allow fine-tuning of the resulting morphologies but can also carry magnetic nanoparticles. However, it is not known if the cuboid shape and inter-cuboid connectivity restrict the equilibrium confirmations of the resulting nanopolymers, making them less responsive to external stimuli. In this work, using Molecular Dynamics simulations, we perform an extensive comparison between various nanopolymer architectures to explore their polymeric properties, and their response to an applied magnetic field if magnetic nanoparticles are embedded. We explain the impact of monomer shape and bonding on the mechanical and magnetic properties and show that DNA nanochambers can build highly responsive and magnetically controllable nanopolymers.
1. Introduction
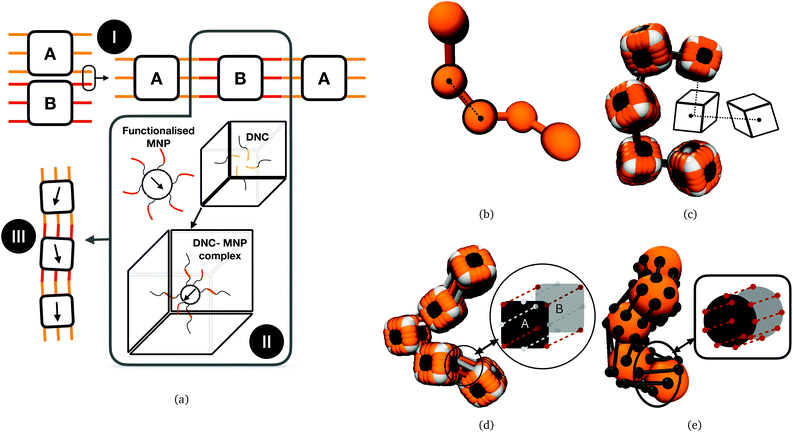
Stimuli-responsive materials are one of the most alluring systems in modern science and one of the central research topics in soft mater physics.1,2 Responsiveness to magnetic fields is of particular interest among the plethora of stimuli one can use to modify material properties,3–6 in case it is advantageous to have dynamic intensity control and/or great spatial resolution. Furthermore, magnetic fields typically do not interfere with biological tissues and processes, which makes them useful for in vivo stimulation of engineered materials.7 Polymer-like structures with magnetic nanoparticles (MNPs), commonly referred to as magnetic filaments (MFs) are one of the soft matter systems that emerged in attempts to capitalize on this potential. The elegant simplicity of merging polymer-like systems and MNPs as a solution to the problem of magneto-responsive material design has naturally sparked a great deal of theoretical research. Nanoscopic, polymer-like structures have been shown to exhibit extraordinary plasmonic,8–13 magnetic,14–17 electronic18–20 and mechanical21,22 properties. Theoretically, the properties of MFs exposed to external magnetic fields have been mostly explored in bulk.23–30 MFs with super-paramagnetic MNPs have been theoretically investigated in artificial swimmer designs.31–33 In-field behaviour (i.e. buckling, coiling and bending) of MFs with super-paramagnetic MNPs has been investigated under multiple conditions,34,35 such as having the MFs grafted to a surface,36 or exposed to a rotating or fast precessing magnetic field.37–39 MFs in general are promising as a basis for bio-medical application designs.40–42 MFs with paramagnetic monomers have been investigated and characterized as potential micro-mixers,43 as well as for cargo capture and transport purposes.44It is important to underline that while there is a breadth of designs of magnetoresponsive micro- and nanoscopic systems that can be nominally considered as magnetic filaments,45–74 many of them are fundamentally incompatible with the idea of a polymer-like entity controllable with magnetic fields. A MF as a representative member of highly magneto-responsive, smart nanomaterials, is a compelling system only as far as it has a flexible backbone and a highly tuneable nanostructure. Despite exciting strategies such as exploiting entropy to tailor spatially organized structures of nanoparticles in polymeric systems,75 and the amount or research summarized in the paragraph above might suggest, it remains a matter of fact that flexible, nanoscale MFs, with a finely tuneable nanostructure, have not been synthesized yet. The key difficulty in such an endeavour is instilling selective, anisotropic interactions between nano-objects that are otherwise entirely isotropic, with colloids that are chemically stable and when crosslinked, remain so permanently. Thus, even though a lot of variously shaped magnetic nanoparticles are currently available,76 how to efficiently crosslink them remains a challenge. To this end, DNA nano-objects have emerged as one of the most prominent candidates, due to their structural programmability and selectivity of sequence-specific interactions.77–93 Assembly of such DNA nano-objects offers an attractive route for forming 1D array, polymer-like morphologies – nanopolymers, composed of nano-sized monomers.91,92,94–105 Recently, we explored the phase diagram of divalent cuboid DNA nanochambers (DNCs) as a function of bond design, length and number of DNA linkages involved in the inter-cuboid connectivity. DNC nano-objects are created by DNA origami technology. They consist of four double-layer DNA helix walls (outer layer: 12 × 12 double helices, inner layer: 10 × 10 double helices) that enclose a cavity (25 nm × 25 nm × 28 nm). Furthermore, ssDNA linkers with sequence-based specificity placed at a pair of opposite faces of the cubic DNC surface (meaning front and back face) form bonding sites, facilitating directional (lateral) inter-object interactions. We have shown that DNCs can form nanopolymers and can be used as templates for targeted assembly of nanoparticles.92,106 A schematic depiction of DNCs with complimentary bonding sites on their surface, forming nanopolymers, as well using DNCs to incorporate MNPs to form DNC–MNP complexes, resulting in nanoscopic MFs, are shown in Fig. 1(a). Resulting filaments are not conventional polymer-like structures, distinct in both crosslinking and monomer shape. MNPs are encapsulated in cubic DNCs that are connected to each other via multiple bonds holding their adjacent faces together. There is a complex interplay between bonding and monomer shape that affects the mechanical and magnetic properties of MFs. Moreover, on the length-scales characteristic to DNCs, depending on the magnetic material, the MNPs used to form DNC–MNP complexes could be ferro- or super-paramagnetic. The type of magnetic relaxation will have a profound impact on magnetic and mechanical properties of the MFs, particularly in conjunction with the interplay between monomer shape and inter-monomer connectivity. Recently published strategy of crosslinking nanostructures under the influence of an applied magnetic field presented in Kapuscinski et al.107 and references therein, suggest that DNC–MNP complexes with ferromagnetic MNPs could form MFs where the remnant magnetisation is coaligned with the polymer backbone. Below, step-by-step, we reveal the impact of monomer shape, bonding, and magnetic characteristics of MNPs on the equilibrium properties of nanopolymers, using Molecular Dynamics (MD) simulations. Even though the solvent is not modelled explicitly here, θ-solvent conditions are assumed. Comparing nanopolymers with different architectures and/or magnetic nature of monomers, we reveal that DNC-based nanopolymers represent a compelling, finely tuneable platform for creating magneto-responsive materials. In effect, this work establishes guidelines how to efficiently use DNCs to synthesize MFs with desired properties.
2. Results
Computational models we use in this study are depicted in Fig. 1(b)–(e). These models are designed to encompass a range of polymeric systems with different monomer shape and crosslinking. Fig. 1(b) and (c) show representations of polymer-like systems, with spherical and cubic monomer shape, respectively, crosslinked centre-to-centre (CTC), meaning that only the translational degrees of freedom of monomers are restricted. Combination of CTC crosslinking and spherical monomer shape corresponds to a self-avoiding walk.108 The DNC nanopolymer model shown in Fig. 1(d) captures the distinctive cuboid monomer shape together with the specific inter-monomer connections, we refer to as face-to-face crosslinking (FTF), where for the adjacent faces, A and B, of two cubes, all the corners and side midpoints are bonded. Model depicted in Fig. 1(e), is designed to reproduce the characteristics of FTF crosslinking, in conjunction with spherical monomers. Important to note is that FTF crosslinking leads to a stiffer polymer backbone as it couples not only the translational but also rotational degrees of freedom of monomers. In other words, monomers can still rotate, but cannot do so freely with respect to their neighbours along the backbone.By varying the equilibrium bond length r0, we vary the equilibrium inter-monomer distance. This corresponds to varying the length design parameter of the self-assembly phase, as discussed in Xiong et al.106 Details of the implementation of all the above-mentioned realizations are provided in Simulation methods part in Section 4.4.
2.1. Polymeric properties of DNC nanopolymers
We start the discussion by considering the polymeric properties of designs shown in Fig. 1, where monomers are not magnetic. We calculate the normalized end-to-end distance,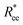 , as the distance between the centres of mass of the first and the L-th monomer:
, as the distance between the centres of mass of the first and the L-th monomer: 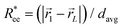 , with davg denoting the average inter-monomer distance between neighbouring monomers along the backbone. The value of davg is calculated separately for each crosslinking approach, monomer shape, L and r0, as the mean value of all nearest-neighbour distances inside a nanopolymer. Our aim here is to underline DNC features, that is, cuboid monomer shape and specific inter-monomer connectivity, and how they lead to unique properties. The results of how monomer shape, crosslinking and r0, manifest themselves in
, with davg denoting the average inter-monomer distance between neighbouring monomers along the backbone. The value of davg is calculated separately for each crosslinking approach, monomer shape, L and r0, as the mean value of all nearest-neighbour distances inside a nanopolymer. Our aim here is to underline DNC features, that is, cuboid monomer shape and specific inter-monomer connectivity, and how they lead to unique properties. The results of how monomer shape, crosslinking and r0, manifest themselves in 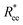 are shown in Fig. 2.
are shown in Fig. 2.
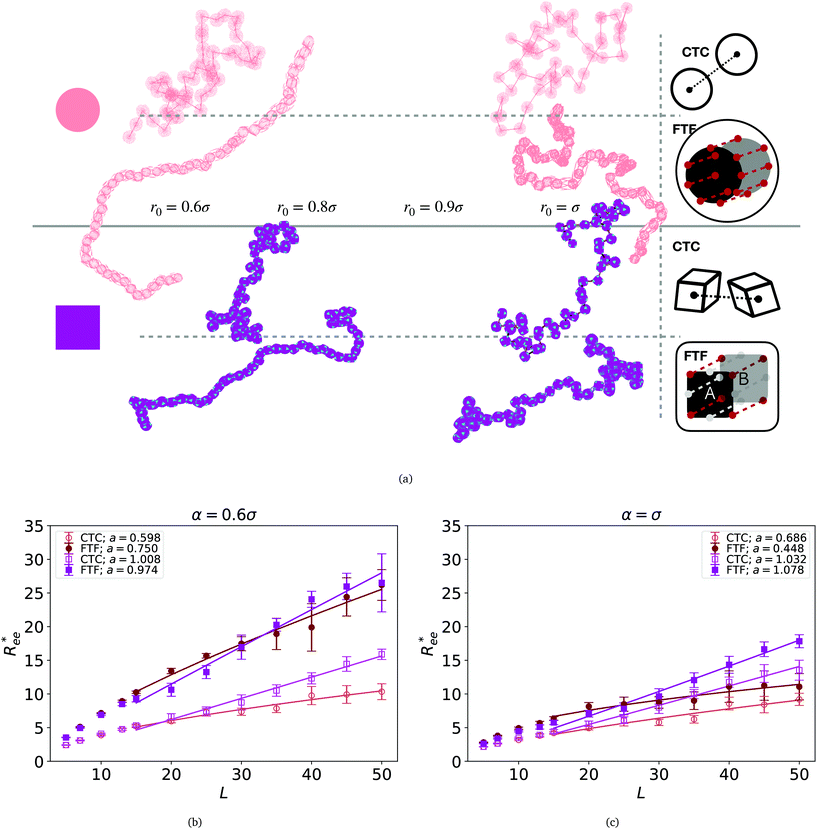 | ||
Fig. 2 (a) Representative simulation snapshots of nanopolymer conformations, across the combinations of monomer shape, crosslinking approach and r0 we explored. (b) and (c) show normalized end-to-end distance, 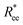 as a function of monomer number L, for different r0 = ασ, where α ∈ {0.6, 1}, and σ is particle size. Datapoints for nanopolymers with spherical monomers are represented with spherical symbols (red); datapoints for nanopolymers with cubic monomers are represented with square symbols (purple). Filled symbols, shown in a darker color shade, represent nanopolymer models with FTF crosslinking; non-filed symbols, shown in a lighter color shade, are for CTC crosslinking. Error bars are calculated as the standard deviation of as a function of monomer number L, for different r0 = ασ, where α ∈ {0.6, 1}, and σ is particle size. Datapoints for nanopolymers with spherical monomers are represented with spherical symbols (red); datapoints for nanopolymers with cubic monomers are represented with square symbols (purple). Filled symbols, shown in a darker color shade, represent nanopolymer models with FTF crosslinking; non-filed symbols, shown in a lighter color shade, are for CTC crosslinking. Error bars are calculated as the standard deviation of 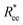 across 40 independent simulations. Solid lines represent the power-law fits, explained in the text. Values of the fit exponents are shown in the legend. All fit parameters are shown in Table 1. across 40 independent simulations. Solid lines represent the power-law fits, explained in the text. Values of the fit exponents are shown in the legend. All fit parameters are shown in Table 1. | ||
To help visualize key points in the results presented below, in Fig. 2(a), we show representative simulation snapshots of the conformations our models take, across the combinations of monomer shape, crosslinking approach and r0 we explored. Independently from value of r0, presented as increasing from Fig. 2(b)–(c), the most rigid nanoscopic polymer model is the one with FTF crosslinking with cubic monomers, whereas conformations with most coiling are assumed by the nanopolymers with spherical monomers and CTC crosslinking, as is to be expected from a self-avoiding walk. Differences between models are exacerbated for smaller r0. It is interesting to underline that the shape of the monomers manifests itself only for relatively large values of L. Thus, below L = 15 the behaviour of the end-to-end distance is defined exclusively by the type of crosslinking. The way 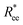 grows with L depends predominantly on the monomer shape. The
grows with L depends predominantly on the monomer shape. The 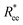 gradient decreases, with increasing L, especially for nanopolymers with spherical monomers. To quantify the differences between the growth rates, for each of the models, we fit the simulation data with bLa power-law, starting from L ≥ 15. These fits are shown in Fig. 2 with solid lines. The fit parameters are collected in Table 1. Nanopolymers with spherical monomers and CTC crosslinking exhibit the scaling of a self-avoiding walk (a ∼ 0.5). The situation changes drastically for FTF crosslinking of spherical monomers: the exponent a decreases with α and never corresponds to a self-avoiding walk. For cubic monomers,
gradient decreases, with increasing L, especially for nanopolymers with spherical monomers. To quantify the differences between the growth rates, for each of the models, we fit the simulation data with bLa power-law, starting from L ≥ 15. These fits are shown in Fig. 2 with solid lines. The fit parameters are collected in Table 1. Nanopolymers with spherical monomers and CTC crosslinking exhibit the scaling of a self-avoiding walk (a ∼ 0.5). The situation changes drastically for FTF crosslinking of spherical monomers: the exponent a decreases with α and never corresponds to a self-avoiding walk. For cubic monomers, 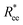 grows almost linearly with L independently from the type of crosslinking. The latter affects the prefactor b. Nanopolymers with FTF crosslinking are in general straighter than their CTC counterparts. The closest to unity exponent a can be found for a nanopolymer with cubic monomers and CTC crosslinking, with r0 corresponding to monomer close contact. For nanopolymers with CTC crosslinking, increase in α leads to an expected increase of the scaling exponent a, regardless of monomer shape. The growth of the equilibrium inter-particle distance can be regarded as an increase of an effective monomer diameter or swelling of the nanopolymer. However, the shape of monomers manifests itself in a nontrivial way when their rotational degrees of freedom are coupled to the backbone. Nanopolymers with FTF crosslinking have difficulties to coil for short bonds (α = 0.6). An increase in α leads to coiling, where for filaments with spherical monomers, conformations become more compact, and we see a decrease in a. However, there is an additional, purely steric coupling between the relative orientation of cubic monomers. In fact, relative orientation coupling between cubic monomers is mostly steric, which is why a is so similar for nanopolymers with cubic monomers, regardless of crosslinking. These points are also depicted by the typical conformations presented in Fig. 2(a).
grows almost linearly with L independently from the type of crosslinking. The latter affects the prefactor b. Nanopolymers with FTF crosslinking are in general straighter than their CTC counterparts. The closest to unity exponent a can be found for a nanopolymer with cubic monomers and CTC crosslinking, with r0 corresponding to monomer close contact. For nanopolymers with CTC crosslinking, increase in α leads to an expected increase of the scaling exponent a, regardless of monomer shape. The growth of the equilibrium inter-particle distance can be regarded as an increase of an effective monomer diameter or swelling of the nanopolymer. However, the shape of monomers manifests itself in a nontrivial way when their rotational degrees of freedom are coupled to the backbone. Nanopolymers with FTF crosslinking have difficulties to coil for short bonds (α = 0.6). An increase in α leads to coiling, where for filaments with spherical monomers, conformations become more compact, and we see a decrease in a. However, there is an additional, purely steric coupling between the relative orientation of cubic monomers. In fact, relative orientation coupling between cubic monomers is mostly steric, which is why a is so similar for nanopolymers with cubic monomers, regardless of crosslinking. These points are also depicted by the typical conformations presented in Fig. 2(a).
| Bond length | Shape | Fit, CTC | Fit, FTF |
|---|---|---|---|
| r 0 = 0.6σ | ○ | a = 0.598, b = 1.008 | a = 0.750, b = 1.361 |
| □ | a = 1.008, b = 0.303 | a = 0.974, b = 0.620 | |
| r 0 = 0.8σ | ○ | a = 0.665, b = 0.740 | a = 0.523, b = 2.228 |
| □ | a = 1.071, b = 0.230 | a = 1.018, b = 0.412 | |
| r 0 = 0.9σ | ○ | a = 0.676, b = 0.676 | a = 0.485, b = 2.051 |
| □ | a = 1.052, b = 0.237 | a = 1.076, b = 0.295 | |
| r 0 = σ | ○ | a = 0.686, b = 0.622 | a = 0.448, b = 1.981 |
| □ | a = 1.032, b = 0.248 | a = 1.078, b = 0.265 |
One can conclude that shape effects, albeit less pronounced compared to crosslinking effects, are still present. We attribute this to the fact that at r0 = 0.6σ, where σ is monomer size, crosslinking ensures that monomers are essentially touching. Most intuitive way to imagine monomer shape effecting 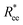 , is the way it restricts monomers sliding past one another or rolling over each other's surface. Spherical monomers can easily do both of those things. Cubic monomers instead are limited in either of the motions when crosslinked. If, however, crosslinking is restrictive enough to minimize such behaviour regardless the monomer shape,
, is the way it restricts monomers sliding past one another or rolling over each other's surface. Spherical monomers can easily do both of those things. Cubic monomers instead are limited in either of the motions when crosslinked. If, however, crosslinking is restrictive enough to minimize such behaviour regardless the monomer shape, 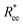 profiles are grouping, like we see in Fig. 2(b). This explanation is corroborated by persistence length Lp values, shown in Table 2. We extract Lp from the decay of the autocorrelation function
profiles are grouping, like we see in Fig. 2(b). This explanation is corroborated by persistence length Lp values, shown in Table 2. We extract Lp from the decay of the autocorrelation function
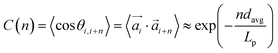 | (1) |
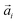 connecting each pair i of neighbouring monomers along the backbone, separated by n monomers. Here, we see that models with FTF crosslinking can have several times higher Lp than their counterparts with CTC crosslinking, where we achieve the highest difference between CTC crosslinked nanopolymers with spherical monomers, and FTF crosslinked nanopolymers with cubic monomers (DNC nanopolymer). Previously, it has been shown that the intricate relationship between the magnetic nature of monomers and crosslinking can result in notably different structural properties and responsiveness of MFs to external magnetic fields, underlining that the crosslinking mechanism strongly affects both magnetic and structural properties.15 Considering the peculiarities of DNC nanopolymer crosslinking and the fact that monomer shape affects magnetic properties even in non-crosslinked systems,109,110 we expect an interesting shape-crosslinking interplay once MNPs are incorporated in DNCs.
connecting each pair i of neighbouring monomers along the backbone, separated by n monomers. Here, we see that models with FTF crosslinking can have several times higher Lp than their counterparts with CTC crosslinking, where we achieve the highest difference between CTC crosslinked nanopolymers with spherical monomers, and FTF crosslinked nanopolymers with cubic monomers (DNC nanopolymer). Previously, it has been shown that the intricate relationship between the magnetic nature of monomers and crosslinking can result in notably different structural properties and responsiveness of MFs to external magnetic fields, underlining that the crosslinking mechanism strongly affects both magnetic and structural properties.15 Considering the peculiarities of DNC nanopolymer crosslinking and the fact that monomer shape affects magnetic properties even in non-crosslinked systems,109,110 we expect an interesting shape-crosslinking interplay once MNPs are incorporated in DNCs.
| Bond length | Shape | L p, CTC | L p, FTF |
|---|---|---|---|
| r 0 = 0.6σ | ○ | 1.08 | 8.41 |
| □ | 1.37 | 8.73 | |
| r 0 = σ | ○ | 1.06 | 2.09 |
| □ | 1.31 | 2.24 |
2.2.2. Polymeric and magnetic properties of DNC nanopolymer based MFs
In this section, we present how the magnetic nature and shape of FTF crosslinked monomers, relate to the response to external magnetic fields of MFs with 20 monomers. We compare these results to the magnetic response of a reference filament design with ferromagnetic MNPs, crosslinked with a single bond (see eqn (14)) between each monomer pair, that couples both the translational and rotational degrees of freedom of monomers. We refer to this as constrained crosslinking, in line with ref. 15.Note that, keeping the analogy to the prospective experimental system, independently from the monomer shape, which is realized in terms of steric interactions (see Section 4.2), the magnetic core is assumed to be spherical in all models. However, considering the actual size of the DNCs, we allow for the possibility of a spherical MNP to be ferro- or super-paramagnetic, abbreviated below to SPM and FM correspondingly. This way, we allow for the possibilities that without a magnetic field applied, MFs can be non-magnetic or have a remnant magnetization.
In Fig. 3(a), we plot the square of the normalized gyration radius 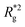 , defined as:
, defined as:
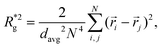 | (2) |
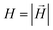 . Here,
. Here, 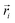 is the position vector of the i-th filament monomer in the lab coordinate frame and davg is an average inter-monomer distance as discussed above. Comparing qualitatively across Fig. 3(a), the difference between overall
is the position vector of the i-th filament monomer in the lab coordinate frame and davg is an average inter-monomer distance as discussed above. Comparing qualitatively across Fig. 3(a), the difference between overall 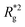 profiles for different r0 is stark. For r0 = 0.6σ the profiles are basically flat, regardless of monomers shape and the values of
profiles for different r0 is stark. For r0 = 0.6σ the profiles are basically flat, regardless of monomers shape and the values of 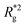 are higher than for the reference system. Results for r0 = σ, reveal a rapid, field induced increase. Longer bonds make the shape effects visible. MFs with cubic monomers, due to lower inter-monomer correlations inherent to monomer shape anisotropy, have lower
are higher than for the reference system. Results for r0 = σ, reveal a rapid, field induced increase. Longer bonds make the shape effects visible. MFs with cubic monomers, due to lower inter-monomer correlations inherent to monomer shape anisotropy, have lower 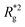 profiles overall, compared to their counterparts with spherical monomers. Interestingly, having super-paramagnetic monomers further diminishes inter-monomer correlations, compared to their ferromagnetic counterparts.
profiles overall, compared to their counterparts with spherical monomers. Interestingly, having super-paramagnetic monomers further diminishes inter-monomer correlations, compared to their ferromagnetic counterparts.
 | ||
Fig. 3 Comparison between models with FTF crosslinking: (a) 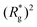 versus H. Black dashed line corresponds to the versus H. Black dashed line corresponds to the 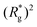 of a fully elongated filament conformation. (b) of a fully elongated filament conformation. (b) 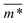 versus H. Data for MFs with spherical monomers are represented with spherical symbols (can); data for MFs with cubic monomers are represented with square symbols (orange). Filled symbols, shown in a darker color shade, represent MFs with ferromagnetic monomers; non-filed symbols, shown in a lighter color shade, represent MFs with super-paramagnetic monomers. Reference system of filament with ferromagnetic monomers and constrained crosslinking15 is shown with a grey, full line. Errorbars are comparable to symbol size and are as such not shown. (c) Showing typical conformations occurring during the runtime of two separate simulations (orange and purple are meant to distinguish conformations found in independent simulation runs performed for the same system), revealing bend backbone conformations of DNC MFs with super-paramagnetic monomers and r0 = σ. versus H. Data for MFs with spherical monomers are represented with spherical symbols (can); data for MFs with cubic monomers are represented with square symbols (orange). Filled symbols, shown in a darker color shade, represent MFs with ferromagnetic monomers; non-filed symbols, shown in a lighter color shade, represent MFs with super-paramagnetic monomers. Reference system of filament with ferromagnetic monomers and constrained crosslinking15 is shown with a grey, full line. Errorbars are comparable to symbol size and are as such not shown. (c) Showing typical conformations occurring during the runtime of two separate simulations (orange and purple are meant to distinguish conformations found in independent simulation runs performed for the same system), revealing bend backbone conformations of DNC MFs with super-paramagnetic monomers and r0 = σ. | ||
We continue our investigations of filament response to external magnetic fields, by analysing the average value of the normalized projection of filament magnetic moment, ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , on to the direction of
, on to the direction of 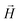 ,
, 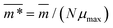 , with μmax denoting the maximum dipole moment of a monomer. In accordance with Fig. 3(a) and (b) reveals that larger values of r0 result in a lower magnetization. Still, as apparent in the magnetization profiles, relatively low to moderate external magnetic fields are sufficient for MFs to be magnetized to saturation. For lower r0 = 0.6σ, FTF crosslinking is restrictive enough to keep the monomers and dipole moments well oriented along
, with μmax denoting the maximum dipole moment of a monomer. In accordance with Fig. 3(a) and (b) reveals that larger values of r0 result in a lower magnetization. Still, as apparent in the magnetization profiles, relatively low to moderate external magnetic fields are sufficient for MFs to be magnetized to saturation. For lower r0 = 0.6σ, FTF crosslinking is restrictive enough to keep the monomers and dipole moments well oriented along 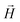 , regardless of monomer shape, or magnetic nature of MNPs. MFs with super-paramagnetic monomers have an overall lower magnetization, because of the effect of local dipole fields between neighbouring monomers, that introduce fluctuations of the direction of the individual dipole moments within the filament. Instead, MFs with ferromagnetic monomers as can be seen from Fig. 3(b) are basically rod-like compared to the rest of the models presented. As r0 increases, monomers can move more freely and dipole moment orientations can fluctuate more, compared to the MFs with lower r0, which leads to an overall decrease in magnetization profiles. The shape anisotropy of cubes, on average, further inhibits the ability of dipole moments to predominately align with
, regardless of monomer shape, or magnetic nature of MNPs. MFs with super-paramagnetic monomers have an overall lower magnetization, because of the effect of local dipole fields between neighbouring monomers, that introduce fluctuations of the direction of the individual dipole moments within the filament. Instead, MFs with ferromagnetic monomers as can be seen from Fig. 3(b) are basically rod-like compared to the rest of the models presented. As r0 increases, monomers can move more freely and dipole moment orientations can fluctuate more, compared to the MFs with lower r0, which leads to an overall decrease in magnetization profiles. The shape anisotropy of cubes, on average, further inhibits the ability of dipole moments to predominately align with 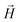 . This in turn means that cubic monomers crosslinked with FTF crosslinking, that is DNC MFs, while generally more elongated, have monomer dipole moments that fluctuate more than their counterparts with spherical monomers. Therefore, an increase in r0, leads to a more pronounced magnetization decrease in MFs with cubic monomers than for those made of spherical monomers. In fact, magnetization profiles for MFs with spherical, super-paramagnetic monomers and MFs with cubic, ferromagnetic monomers are basically indistinguishable.
. This in turn means that cubic monomers crosslinked with FTF crosslinking, that is DNC MFs, while generally more elongated, have monomer dipole moments that fluctuate more than their counterparts with spherical monomers. Therefore, an increase in r0, leads to a more pronounced magnetization decrease in MFs with cubic monomers than for those made of spherical monomers. In fact, magnetization profiles for MFs with spherical, super-paramagnetic monomers and MFs with cubic, ferromagnetic monomers are basically indistinguishable.
In summary, Fig. 3 underlines an effect that permeates the results presented in this work, namely the decorrelation of dipole monomer orientation in MFs with cubic monomers. DNC MFs have monomer dipole moments that locally fluctuate more. Zeeman coupling can compensate for this effect for all models, but DNC MFs with super-paramagnetic NPs that do not fully stretch for high H. Instead, as it is shown in Fig. 3(c), we captured several instances of persisting conformations of DNC MFs with a bent backbone. This bending is a signature of MFs with super-paramagnetic spherical monomers15 that is clearly intensified by the cubic shape. In the next subsection we analyse whether the relative drawbacks we underlined – less magnetically correlated monomers and more persistent bent backbone conformations – affect the mechanical response of DNC nanopolymer based MFs.
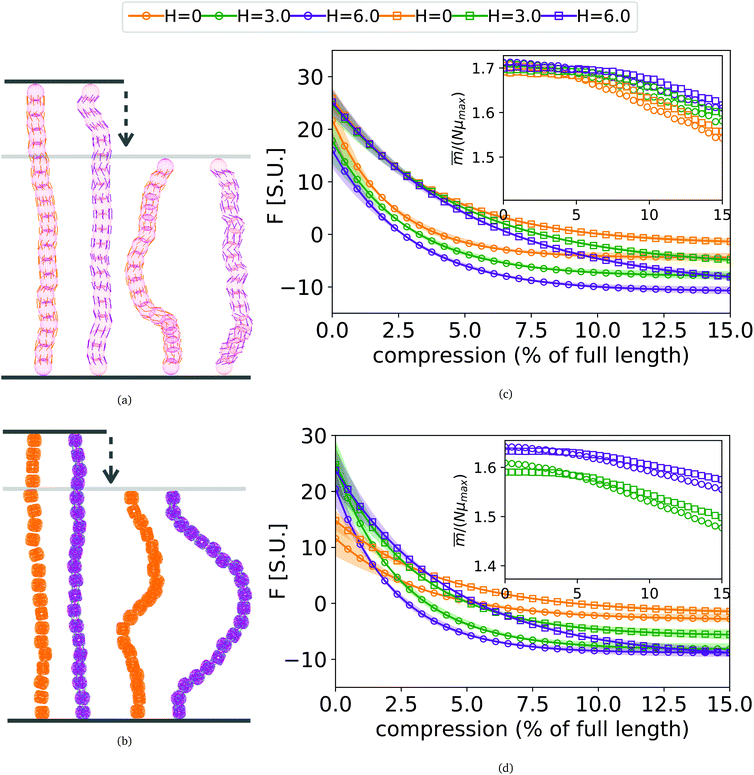
3. In-field compression of DNC nanopolymer based MFs in a slit geometry
As depicted in Fig. 4(a) and (b), we fix the ends of fully stretched FTF crosslinked MFs with 20 monomers (length of all bonds is their equilibrium length r0), with different monomer shape and/or magnetic nature of colloids, on the surface of two semi-infinite slit walls. By moving one of the slit walls vertically towards the other, in steps Δd, we elucidate the effects of confinement on MFs and their response to compression, with and without an external magnetic field pointing antiparallelly to the direction of compression. A detailed explanation of the simulation protocol can be found in Section 4.4. The initial, fully stretched conformation (no compression) of a filament is entropically disadvantageous. Indeed, this is confirmed by Fig. 3(a), where one can notice that the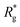 never approaches that of a rod,
never approaches that of a rod, 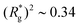 As a result of this, looking at Fig. 4(c) and (d), the projection on the axis of compression of the force a filament exerts the bottom wall is positive. This shows that the filament is pulling on the bottom wall. With further compression, entropy grows as the filament is given more freedom to fluctuate. At a certain compression, dC, the filament can reach conformations corresponding to its equilibrium
As a result of this, looking at Fig. 4(c) and (d), the projection on the axis of compression of the force a filament exerts the bottom wall is positive. This shows that the filament is pulling on the bottom wall. With further compression, entropy grows as the filament is given more freedom to fluctuate. At a certain compression, dC, the filament can reach conformations corresponding to its equilibrium 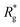 , shown in Fig. 3(a). For such conformations, no net force is exerted on to the walls, and the force-displacement curves cross zero. Looking at orange curves in Fig. 4(c) we compare MFs with ferromagnetic spherical monomers (circles) to their counterparts with cubic ones (squares), without an external magnetic field applied. We see that they stop pulling on the wall at different dC. MFs with spherical monomers have a slightly higher
, shown in Fig. 3(a). For such conformations, no net force is exerted on to the walls, and the force-displacement curves cross zero. Looking at orange curves in Fig. 4(c) we compare MFs with ferromagnetic spherical monomers (circles) to their counterparts with cubic ones (squares), without an external magnetic field applied. We see that they stop pulling on the wall at different dC. MFs with spherical monomers have a slightly higher 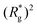 (see Fig. 3(a)) than their counterparts with cubic monomers. Therefore, they do not need to be given as much leeway to be able to reach equilibrium (R*r)2 corresponding a freely moving filament. For further displacement of the top wall in the range we explored, MFs with ferromagnetic monomers, regardless of monomer shape, oscillate around the zero position.
(see Fig. 3(a)) than their counterparts with cubic monomers. Therefore, they do not need to be given as much leeway to be able to reach equilibrium (R*r)2 corresponding a freely moving filament. For further displacement of the top wall in the range we explored, MFs with ferromagnetic monomers, regardless of monomer shape, oscillate around the zero position.
Switching on the external magnetic field, depicted by green (H = 3) and violet (H = 6) curves, we see the ramifications of correlations induced by Zeeman coupling. Stretched out configurations with head-to-tail dipole arrangements are facilitated by Zeeman coupling leading to smaller values of dC. However, given that the 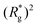 profiles of freely moving MFs with spherical monomers and r0 = 0.6σ are basically flat, only a small difference between dC at any strength of magnetic field applied is observed. For their counterparts with cubic monomers, a difference can be noticed if the field is switched on. This is in line with the small
profiles of freely moving MFs with spherical monomers and r0 = 0.6σ are basically flat, only a small difference between dC at any strength of magnetic field applied is observed. For their counterparts with cubic monomers, a difference can be noticed if the field is switched on. This is in line with the small 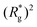 increase observed in Fig. 3(a). On further compression past dC, the force becomes repulsive, corresponding to MFs pushing on to the bottom wall. Notice that for MFs with cubic monomers, the repulsive regime is reached for larger compression, than for their counterparts with spherical monomers. This is entirely in line with the dipole de-correlation effect we referred to earlier.
increase observed in Fig. 3(a). On further compression past dC, the force becomes repulsive, corresponding to MFs pushing on to the bottom wall. Notice that for MFs with cubic monomers, the repulsive regime is reached for larger compression, than for their counterparts with spherical monomers. This is entirely in line with the dipole de-correlation effect we referred to earlier.
Force-compression curves for MFs with super-paramagnetic monomers, shown in Fig. 4(d), exhibit qualitatively the same trends seen in Fig. 4(c). The most apparent difference, however, is a strong dependence of dC on H for MFs with the same monomer shape. This can be understood from the magnetization curves in Fig. 3(b), where for MFs with ferromagnetic monomers, H = 3 is already sufficiently strong to reach magnetization saturation, while for MFs with super-paramagnetic monomers it is not.
Looking at insets of Fig. 4(c) and (d), showing the projection of the magnetization on the vertical axis, of the non-immobilized part of the filament, at equilibrium for MFs with ferromagnetic and super-paramagnetic monomers respectively, we see a crossover between two linear magnetization regimes. The change of the regimes happens at corresponding values of dC. The differences between ferro- and super-paramagnetic monomers is manifested in the absolute scale of the magnetization before dC. Past dC, the growing separation between the magnetization curves reflects the competition between entropy on one side and dipole–dipole interactions with Zeeman coupling, on the other.
3. Conclusion
In this work, using computational models, we compare nanopolymers with different architectures and/or magnetic nature of monomers. It turns out that cubic monomer shape makes nanopolymers more rigid only if the inter-monomer bonds are short enough and the number of monomers is rather high. For moderately long nanopolymers (15 < L < 30) with comparable crosslinking, end-to-end distance largely similar regardless of monomer shape.Apart from varying monomer shape, we also consider different types of crosslinking: we investigate the differences between nanopolymer designs with centre-to-centre and face-to-face crosslinking. The latter is of particular interest as it represents well recently synthesized nanopolymers based on cubic DNA nano-chambers (DNCs). As expected, face-to-face crosslinking results in more linear conformations and for short bond length can double the equilibrium end-to-end distance, if number of monomers in the nanopolymer is large enough.
Next, using the aforementioned model, we demonstrate that DNC nanopolymers represent a compelling, finely tuneable platform for creating magneto-responsive materials. We are encouraged by the fact that, even the lowest magnetization we observed for filaments based on DNCs at a given applied field is still significantly higher than that of conventional magnetic nanoparticle suspensions (ferrofluids). Furthermore, the magnetic fields needed for a DNC-based magnetic filament to reach magnetic saturation are relatively low, as the thermal fluctuations are hindered by both monomer shape and multiple inter-monomer bonds. We show that the steric penalty brought by cubic monomer shape to initial susceptibility can be compensated with bond length: if the bonds are short enough, the initial slope of magnetization curves for nanopolymers made of spheres and cubes basically coincide. In general, cubic monomer shape slightly diminishes magneto-responsiveness, as quantified by magnetization, most pronounced for DNC MFs with super-paramagnetic monomers. While notable, the difference to their counterparts with spherical monomers is not high enough to discourage the use of DNC nanopolymers for filament designs with super-paramagnetic MNPs. Quite on the contrary, it opens the door to interesting phenomenology related to backbone bending noted for MFs with super-paramagnetic monomers.
Finally, we investigate the mechanical resistance to compression that MFs with different architecture and/or magnetic nature of monomers exhibit, by grafting two filament ends on slit walls, one of which is then moved towards the other. Compared with filament designs with spherical monomers, cubic monomer shape of DNC MFs proves to be advantageous, with a smoother and more controllable resistance to compression.
Currently, we are investigating rheology and dynamics of the systems introduced here, as one would expect the shape of the monomers to affect hydrodynamic behaviour of the nanopolymers.
4. Simulation methods
In this section we explain in detail the general computational scheme, interactions and computational models used in this work.4.1. General scheme
We performed Molecular Dynamics (MD) simulations in the ESPResSo software package.111 The effects of the background fluid were handled implicitly, via the Langevin thermostat112 at fixed temperature T. In practice it means that the Langevin equations of motion are integrated over time t numerically: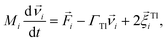 | (3) |
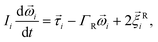 | (4) |
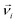 denotes the translational velocity,
denotes the translational velocity, 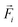 is the force acting on it, ΓTl denotes the translational friction coefficient,
is the force acting on it, ΓTl denotes the translational friction coefficient, 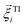 is a stochastic force modelling the random forces of the implicit solvent. In eqn (4), Ii denotes i-th particle inertia tensor,
is a stochastic force modelling the random forces of the implicit solvent. In eqn (4), Ii denotes i-th particle inertia tensor, 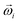 is its rotational velocity, τi is torque acting on it, ΓR denotes the rotational friction coefficient, and the
is its rotational velocity, τi is torque acting on it, ΓR denotes the rotational friction coefficient, and the 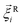 is a stochastic torque serving for the same purpose as
is a stochastic torque serving for the same purpose as 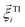 . Both stochastic terms satisfy the conditions on their time averages:113
. Both stochastic terms satisfy the conditions on their time averages:113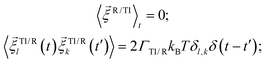 | (5) |
Forces and torques in eqn (3) and (4) are calculated from inter-particle interaction potentials. In all our simulations here, we used no periodic boundary conditions, as the focus is always on a single polymer-like chain per simulation box. For the integration, velocity Verlet algorithm was used.114
4.2. Raspberry model and steric interactions
If particles are spherical and we are not interested in their surface properties, but rather in their effective excluded volume, the typical approach to model their steric repulsion in MD is to use Weeks–Chandler–Andersen pair potential (WCA):115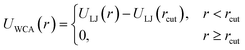 | (6) |
| ULJ(r) = 4{(σ/r)12 − (σ/r)6} | (7) |
For non-spherical particles, or spherical particles whose surface properties matter, there are two ways of modelling steric interactions: the first one is on each MD integration step to solve an algebraic system of equations to check for the overlap of complex shapes; the second one is to build the particle complex shape out of spherical beads – WCA centres of required size σ. The second method is less accurate but is much faster. The particle resulting from the second method is usually addressed as a raspberry particle.116 This is how we construct the cubes. Positions, radii, and parameters for the steric interactions between the WCA-spheres that make out cubic-shaped monomers are calculated using the superball model for q = 2, developed by Donaldson et al.,110 where q is the shape parameter in the superball equation given by:
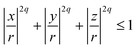 | (8) |
If q → ∞, eqn (8) is describing a cube with perfectly sharp edges with its centre in (0,0,0). With q = 1, eqn (8) describes a sphere with radius r centred at the origin.
ESPResSo makes use of the concept of virtual sites.111 The virtual particle or site is fixed with respect to the reference frame of the real particle to which it is attributed. It is possible to define any number of virtual sites at any position with respect to the reference frame of a given real particle. The interactions between virtual–virtual and virtual–real particles can be specified using any suitable potential. All forces exerted on the virtual particles as a consequence of such interactions are instantaneously propagated to the reference real particle in each time step. These features allow to define rigid bodies with any shape by defining proper arrangements of virtual sites. In Fig. 1(c) and (d) one can see a raspberry representation of cubes employed in this study, that we used successfully for investigating magnetic and charged cubes in previous works.110,117
4.3. Magnetic interactions
Monomers in this work can be either ferromagnetic or super-paramagnetic. Dipole moments of ferromagnetic monomers or monomers with ferromagnetic MNPs embedded within them, are modelled as central, point-particle dipole moments,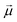 , of a fixed length
, of a fixed length 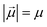 . Long-range magnetic inter-particle interactions are accounted for via the standard dipole–dipole pair potential:
. Long-range magnetic inter-particle interactions are accounted for via the standard dipole–dipole pair potential: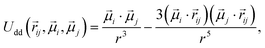 | (9) |
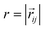 , and
, and 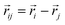 is the displacement vector connecting i and j monomer centres with dipole moments
is the displacement vector connecting i and j monomer centres with dipole moments 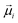 and
and 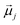 , respectively. Zeeman interactions coming from the presence of an external magnetic field
, respectively. Zeeman interactions coming from the presence of an external magnetic field 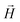 , are realized via Zeeman coupling potential:
, are realized via Zeeman coupling potential: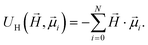 | (10) |
To model the phenomenology of super-paramagnetic MNPs accurately, one needs to calculate the total field 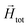 in each point of the system. The total magnetic field is the sum of
in each point of the system. The total magnetic field is the sum of 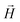 and the dipole field
and the dipole field 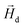 . The latter field, created by particle j, at position
. The latter field, created by particle j, at position 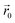 is given by:
is given by:
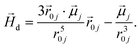 | (11) |
To study of the response of MFs to fields of arbitrary strength, we define the dipole moment 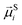 , of an i-th super-paramagnetic particle at a given temperature T, as:
, of an i-th super-paramagnetic particle at a given temperature T, as:
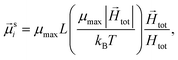 | (12) |
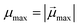 is the modulus of the maximal magnetic moment,
is the modulus of the maximal magnetic moment, 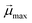 . Here, kB is the Boltzmann constant and L(α) is the Langevin function:
. Here, kB is the Boltzmann constant and L(α) is the Langevin function: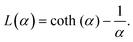 | (13) |
Not only does this approach lend itself to account for nonlinear effects but, the expression (12) is a generalisation of mean-field approaches, such as the modified mean field approach.118 The difference here is that we do not need to make any assumption to calculate 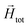 . This approach is also verified by the analytical calculations for super-paramagnetic particle magnetization.119
. This approach is also verified by the analytical calculations for super-paramagnetic particle magnetization.119
4.4. Simulation protocol
As schematically depicted in Fig. 1, we want to highlight the impact of crosslinking together with monomer shape, on the equilibrium properties of resulting polymer-like chains. We model the bonds in our models as finitely extendable springs, described by FENE potential:120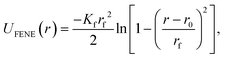 | (14) |
By CTC crosslinking, it is to be understood that the centres of mass of neighbouring monomers are bonded centre-to-centre via FENE bonds as shown in Fig. 1(b) and (c). In this way, we ensure a close contact between the monomers, without restricting their rotations. By FTF crosslinking, we aim to establish a notion of relative orientation of monomers with respect to their nearest neighbours, as well as to couple their rotational degrees of freedom with the backbone.
For chains of spherical monomers, we achieve this by creating two crowns of virtual sites on opposite sides of spherical monomers, that serve as anchoring points for FENE bonds, see, Fig. 1(e). Positions of virtual sites that make the crowns are determined by finding the cross-section of a sphere with diameter σ and a plane, whose normal vector is pointing in the direction in along which the backbone is initially spanning. We are looking for circles of points that solve this problem, whose centres are located at ri + σ/4 and ri − σ/4, respectively, where ri is the position of the centre of the i-th monomer. We create 8 equidistant virtual sites on each of the resulting circles on the surface of the spherical monomer. For each pair of monomers, adjacent virtual sites are linked by FENE bonds. In this way we introduce the notion of relative orientation for spherical monomers, and fully couple their rotational degrees of freedom.
For chains of cubic monomers, FTF crosslinking captures the relevant characteristics of the crosslinking that ensues due to the divalent, “polychromatic” nature of Mkl; k = 16 and/or k = 64 DNC from Xiong et al.106 We attach FENE bonds between adjacent corner particles on neighbouring monomers, and between adjacent central edge virtual sites on the faces of neighbouring monomers, schematically depicted in Fig. 1(d).
Timestep by which the equations of motion (3) and (4) propagate the system in all our simulations is 10−2. For investigations of end-to-end distance scaling as a function of monomer number, we create chains of L monomers, L∈[2,50] and place each of them in a separate simulation box initially fully straight and stretched, with the backbone orientated randomly. We run forty parallel, model/length specific simulations, for different values of r0 at constant T = 1. We firstly make sure that system relaxes into an equilibrium configuration, by running an integration cycle for 2.1 × 106 integration steps. After the relaxation cycle, we start recording simulation snapshots every 7000 integrations, to minimise correlations between observed polymer-like chain conformations. The total length of the measurement cycle is 1.05 × 107 integrations.
For models with magnetic monomers, we use the same simulation protocol as above, except for that we ran 15 parallel, model specific simulations, for different values of r0 and external magnetic field H, at constant T = 1.
For response of confined DNC MFs to compression, we placed two parallel steric planes and graft on them to opposite ends of a given chain model. Each chain is in a separate simulation box and initially fully straight and stretched. External field direction is perpendicular to steric planes, along the z axis. We run ten parallel, model specific simulations, for different values of external magnetic field H at constant T = 1. Compression was realized by moving the steric planes in increments of 0.1 every 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 integrations, until we reached maximum desired compression of five length-scales. With this we ensure that chains reach equilibrium before each compression step.
000 integrations, until we reached maximum desired compression of five length-scales. With this we ensure that chains reach equilibrium before each compression step.
4.5. Reduced units
Interaction potential between a pair of monomers in chains is determined by the interplay between the steric interaction and FENE bonds between them. We match the parameters so, that the magnitude of the interactions between nearest neighbours in different crosslinking scenarios is nearly the same for a given value of r0. This is achieved by tuning dimensionless simulation parameters. Thus, the diameter of spherical monomers was set to σ = 0.91 while, for cubic monomers, diameter of the central particle is set to σ = 1. With the choice of σ for central particle in the cube, according to the superball model developed by Donaldson et al.110 for shape parameter q = 2, corner virtual sites have σ = 0.41 while vertex virtual sites have σ = 0.49. Based on interaction potential matching we determined that the energy scale of the steric repulsion between spherical monomers should be 100 times higher than that of cubic monomers. Therefore, for central particles in the cubes and all virtual sites on the shell, constituting cubic monomers, ε = 1, while for spherical monomers ε = 100. The overall energy scale in our simulations is determined by the choice of the reduced temperature kBT = 1. The reduced characteristic mass of all massive particles in our simulations is taken to be m = 1. Given that we are only interested in equilibrium properties, this value does not affect the results, rather the speed of the convergence. However, the tensor of inertia of cube central particle must be set to represent the fact that they carry a shell of virtual sites that reproduce a cuboid shape. Finally, for simulations of polymer-like chains, following results from interaction potential matching we determined that FENE bonds in centre-to-centre crosslinking should be 9 times as rigid as the ones in face-to-face crosslinking. Therefore, for FTF crosslinking, Kf = 10, while for CTC crosslinking Kf = 90. Equilibrium length of FENE bonds r0 = αrmin, was set to be a α multiple (α∈0.6, 0.8, 0.9, 1.0) of the particle size (rmin = σ). Maximal extension of each FENE bond, rf, was set to be 3 times the equilibrium bond length r0.We consider reduced saturated magnetic moment of μmax2 = 3, for a range of reduced external magnetic fields H ≤ 6. Given a choice of a particular magnetic nanoparticle, such as using magnetite nanoparticles coated with a thin layer of stabilising agent (i.e., oleic acid coating, 2 nm thick), σ corresponds (not uniquely) to a colloid with a magnetic core of 15 nm with a dipole moment of 8.5 × 10−19 A m2. This also means that the maximum of the applied magnetic field range we explored represents moderate fields of only 0.072 T.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. S. K. and D. M. were supported by FWF Project SAM P 33748, we also aknowledge a partial support of RSF 19-12-00209.References
- A. C. Balazs, T. Emrick and T. P. Russell, Science, 2006, 314, 1107–1110 CrossRef CAS PubMed.
- J. Hu and S. Liu, Macromolecules, 2010, 43, 8315–8330 CrossRef CAS.
- F. D. Jochum and P. Theato, Chem. Soc. Rev., 2013, 42, 7468–7483 RSC.
- S. Dai, P. Ravi and K. C. Tam, Soft Matter, 2008, 4, 435–449 RSC.
- J. P. Magnusson, A. Khan, G. Pasparakis, A. O. Saeed, W. Wang and C. Alexander, J. Am. Chem. Soc., 2008, 130, 10852–10853 CrossRef CAS PubMed.
- R. V. Ulijn, J. Mater. Chem., 2006, 16, 2217–2225 RSC.
- R. Tietze, J. Zaloga, H. Unterweger, S. Lyer, R. P. Friedrich, C. Janko, M. Pöttler, S. Dürr and C. Alexiou, Biochem. Biophys. Res. Commun., 2015, 468, 463–470 CrossRef CAS PubMed.
- B. Gao, G. Arya and A. R. Tao, Nat. Nanotechnol., 2012, 7, 433–437 CrossRef CAS PubMed.
- A. Klinkova, H. Thérien-Aubin, A. Ahmed, D. Nykypanchuk, R. M. Choueiri, B. Gagnon, A. Muntyanu, O. Gang, G. C. Walker and E. Kumacheva, Nano Lett., 2014, 14, 6314–6321 CrossRef CAS PubMed.
- Z. Nie, D. Fava, M. Rubinstein and E. Kumacheva, J. Am. Chem. Soc., 2008, 130, 3683–3689 CrossRef CAS PubMed.
- A. Lukach, K. Liu, H. Therien-Aubin and E. Kumacheva, J. Am. Chem. Soc., 2012, 134, 18853–18859 CrossRef CAS PubMed.
- S. Vial, D. Nykypanchuk, K. G. Yager, A. V. Tkachenko and O. Gang, ACS Nano, 2013, 7, 5437–5445 CrossRef CAS PubMed.
- F. N. Gür, C. P. McPolin, S. Raza, M. Mayer, D. J. Roth, A. M. Steiner, M. Löffler, A. Fery, M. L. Brongersma and A. V. Zayats, Nano Lett., 2018, 18, 7323–7329 CrossRef PubMed.
- P. A. Sánchez, J. J. Cerda, T. M. Sintes, A. O. Ivanov and S. S. Kantorovich, Soft Matter, 2015, 11, 2963–2972 RSC.
- D. Mostarac, P. A. Sánchez and S. Kantorovich, Nanoscale, 2020, 12, 13933–13947 RSC.
- S. S. Park, Z. J. Urbach, C. A. Brisbois, K. A. Parker, B. E. Partridge, T. Oh, V. P. Dravid, M. Olvera de la Cruz and C. A. Mirkin, Adv. Mater., 2020, 32, 1906626 CrossRef CAS PubMed.
- S. A. Maier, P. G. Kik, H. A. Atwater, S. Meltzer, E. Harel, B. E. Koel and A. A. Requicha, Nat. Mater., 2003, 2, 229–232 CrossRef CAS PubMed.
- J. Zhang, H. Zou, Q. Qing, Y. Yang, Q. Li, Z. Liu, X. Guo and Z. Du, J. Phys. Chem. B, 2003, 107, 3712–3718 CrossRef CAS.
- C. Tian, M. A. L. Cordeiro, J. Lhermitte, H. L. Xin, L. Shani, M. Liu, C. Ma, Y. Yeshurun, D. DiMarzio and O. Gang, ACS Nano, 2017, 11, 7036–7048 CrossRef CAS PubMed.
- H. Hu, S. Wang, X. Feng, M. Pauly, G. Decher and Y. Long, Chem. Soc. Rev., 2020, 49, 509–553 RSC.
- L. Zhou, A. E. Marras, H.-J. Su and C. E. Castro, ACS Nano, 2014, 8, 27–34 CrossRef CAS PubMed.
- W. Pfeifer, P. Lill, C. Gatsogiannis and B. Saccà, ACS Nano, 2018, 12, 44–55 CrossRef CAS PubMed.
- A. Cēbers, J. Phys.: Condens. Matter, 2003, 15, S1335 CrossRef.
- V. P. Shcherbakov and M. Winklhofer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 061803 CrossRef PubMed.
- A. Cēbers and I. Javaitis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 021404 CrossRef PubMed.
- A. Cēbers, Curr. Opin. Colloid Interface Sci., 2005, 10, 167–175 CrossRef.
- M. Belovs and A. Cēbers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 051503 CrossRef CAS PubMed.
- A. Cēbers and T. Cīrulis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 031504 CrossRef PubMed.
- K. Ērglis, D. Zhulenkovs, A. Sharipo and A. Cēbers, J. Phys.: Condens. Matter, 2008, 20, 204107 CrossRef PubMed.
- A. A. Kuznetsov, J. Magn. Magn. Mater., 2019, 470, 28–32 CrossRef CAS.
- E. Gauger and H. Stark, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021907 CrossRef PubMed.
- M. Roper, R. Dreyfus, J. Baudry, M. Fermigier, J. Bibette and H. A. Stone, J. Fluid Mech., 2006, 554, 167–190 CrossRef.
- M. Roper, R. Dreyfus, J. Baudry, M. Fermigier, J. Bibette and H. A. Stone, Proc. R. Soc. A, 2008, 464, 877–904 CrossRef.
- S. Huang, G. Pessot, P. Cremer, R. Weeber, C. Holm, J. Nowak, S. Odenbach, A. M. Menzel and G. K. Auernhammer, Soft Matter, 2016, 12, 228–237 RSC.
- J. Zhao, D. Du and S. L. Biswal, Phys. Rev. E, 2018, 98, 012602 CrossRef CAS PubMed.
- J. Wei, F. Song and J. Dobnikar, Langmuir, 2016, 32, 9321–9328 CrossRef CAS PubMed.
- S. Kuei, B. Garza and S. L. Biswal, Phys. Rev. Fluids, 2017, 2, 104102 CrossRef.
- J. M. Dempster, P. Vázquez-Montejo and M. O. de la Cruz, Phys. Rev. E, 2017, 95, 052606 CrossRef PubMed.
- P. Vázquez-Montejo, J. M. Dempster and M. O. de la Cruz, Phys. Rev. Mater., 2017, 1, 064402 CrossRef.
- O. Philippova, A. Barabanova, V. Molchanov and A. Khokhlov, Eur. Polym. J., 2011, 47, 542–559 CrossRef CAS.
- O. S. Pak, W. Gao, J. Wang and E. Lauga, Soft Matter, 2011, 7, 8169–8181 RSC.
- P. A. Sánchez, E. S. Pyanzina, E. V. Novak, J. J. Cerdà, T. Sintes and S. S. Kantorovich, Macromolecules, 2015, 48, 7658–7669 CrossRef PubMed.
- S. L. Biswal and A. P. Gast, Anal. Chem., 2004, 76, 6448–6455 CrossRef CAS PubMed.
- T. Yang, T. O. Tasci, K. B. Neeves, N. Wu and D. W. Marr, Langmuir, 2017, 33, 5932–5937 CrossRef CAS PubMed.
- E. M. Furst, C. Suzuki, M. Fermigier and A. P. Gast, Langmuir, 1998, 14, 7334–7336 CrossRef CAS.
- E. M. Furst and A. P. Gast, Phys. Rev. Lett., 1999, 82, 4130–4133 CrossRef CAS.
- C. Goubault, P. Jop, M. Fermigier, J. Baudry, E. Bertrand and J. Bibette, Phys. Rev. Lett., 2003, 91, 260802 CrossRef CAS PubMed.
- L. Cohen-Tannoudji, E. Bertrand, L. Bressy, C. Goubault, J. Baudry, J. Klein, J. F. Joanny and J. Bibette, Phys. Rev. Lett., 2005, 94, 038301 CrossRef PubMed.
- H. Singh, P. E. Laibinis and T. A. Hatton, Langmuir, 2005, 21, 11500–11509 CrossRef CAS PubMed.
- H. Singh, P. E. Laibinis and T. A. Hatton, Nano Lett., 2005, 5, 2149–2154 CrossRef CAS PubMed.
- F. Martínez-Pedrero, M. Tirado-Miranda, A. Schmitt and J. Callejas-Fernández, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011405 CrossRef PubMed.
- B. A. Evans, A. R. Shields, R. L. Carroll, S. Washburn, M. R. Falvo and R. Superfine, Nano Lett., 2007, 7, 1428–1434 CrossRef CAS PubMed.
- J. J. Benkoski, S. E. Bowles, R. L. Jones, J. F. Douglas, J. Pyun and A. Karim, J. Polym. Sci., Part B: Polym. Phys., 2008, 46, 2267–2277 CrossRef CAS.
- Z. Zhou, G. Liu and D. Han, ACS Nano, 2009, 3, 165–172 CrossRef CAS PubMed.
- J. J. Benkoski, J. L. Breidenich, O. M. Uy, A. T. Hayes, R. M. Deacon, H. B. Land, J. M. Spicer, P. Y. Keng and J. Pyun, J. Mater. Chem., 2011, 21, 7314–7325 RSC.
- H. Wang, Y. Yu, Y. Sun and Q. Chen, Nano, 2011, 06, 1–17 CrossRef.
- D. Sarkar and M. Mandal, J. Phys. Chem. C, 2012, 116, 3227–3234 CrossRef CAS.
- J. L. Breidenich, M. C. Wei, G. V. Clatterbaugh, J. J. Benkoski, P. Y. Keng and J. Pyun, Soft Matter, 2012, 8, 5334–5341 RSC.
- E. Busseron, Y. Ruff, E. Moulin and N. Giuseppone, Nanoscale, 2013, 5, 7098–7140 RSC.
- J. Byrom, P. Han, M. Savory and S. L. Biswal, Langmuir, 2014, 30, 9045–9052 CrossRef CAS PubMed.
- M. B. Bannwarth, S. Utech, S. Ebert, D. A. Weitz, D. Crespy and K. Landfester, ACS Nano, 2015, 9, 2720–2728 CrossRef CAS PubMed.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 862–865 CrossRef CAS PubMed.
- A. Hosseinifar, M. Shariaty-Niassar, S. Seyyed Ebrahimi and M. Moshref-Javadi, Langmuir, 2017, 33, 14728–14737 CrossRef CAS PubMed.
- Y. Xiong, Q. Chen, N. Tao, J. Ye, Y. Tang, J. Feng and X. Gu, Nanotechnology, 2007, 18, 345301 CrossRef.
- Z. Zhou, G. Liu and D. Han, ACS Nano, 2008, 3, 165–172 CrossRef PubMed.
- F. Zhang and C.-C. Wang, J. Phys. Chem. C, 2008, 112, 15151–15156 CrossRef CAS.
- M. Ma, Q. Zhang, J. Dou, H. Zhang, D. Yin, W. Geng and Y. Zhou, J. Colloid Interface Sci., 2012, 374, 339–344 CrossRef CAS PubMed.
- L. J. Hill and J. Pyun, ACS Appl. Mater. Interfaces, 2014, 6, 6022–6032 CrossRef CAS PubMed.
- S. H. Xu, G. T. Fei, H. M. Ouyang, Y. Zhang, P. C. Huo and L. De Zhang, J. Mater. Chem. C, 2015, 3, 2072–2079 RSC.
- X. Wen, L. Gu and A. M. Bittner, Z. Phys. Chem., 2018, 232, 1631–1646 CrossRef CAS.
- B. Bharti, A.-L. Fameau, M. Rubinstein and O. D. Velev, Nat. Mater., 2015, 14, 1104–1109 CrossRef CAS PubMed.
- M. Bennet, L. Bertinetti, R. K. Neely, A. Schertel, A. Körnig, C. Flors, F. D. Müller, D. Schüler, S. Klumpp and D. Faivre, Faraday Discuss., 2015, 181, 71–83 RSC.
- É. Bereczk-Tompa, F. Vonderviszt, B. Horváth, I. Szalai and M. Pósfai, Nanoscale, 2017, 9, 15062–15069 RSC.
- S. Kralj and D. Makovec, ACS Nano, 2015, 9, 9700–9707 CrossRef CAS PubMed.
- G. Zhu, Z. Huang, Z. Xu and L.-T. Yan, Acc. Chem. Res., 2018, 51, 900–909 CrossRef CAS PubMed.
- P. Tierno, Phys. Chem. Chem. Phys., 2014, 16, 23515–23528 RSC.
- R. J. Macfarlane, M. N. O'Brien, S. H. Petrosko and C. A. Mirkin, Angew. Chem., Int. Ed., 2013, 52, 5688–5698 CrossRef CAS PubMed.
- Y. Tian, J. R. Lhermitte, L. Bai, T. Vo, H. L. Xin, H. Li, R. Li, M. Fukuto, K. G. Yager and J. S. Kahn, et al. , Nat. Mater., 2020, 19, 789–796 CrossRef CAS PubMed.
- M. R. Jones, N. C. Seeman and C. A. Mirkin, Spherical Nucleic Acids, 2020, pp. 167–197 Search PubMed.
- T. Vo, V. Venkatasubramanian, S. Kumar, B. Srinivasan, S. Pal, Y. Zhang and O. Gang, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4982–4987 CrossRef CAS PubMed.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55 CrossRef CAS PubMed.
- L. Feng, R. Dreyfus, R. Sha, N. C. Seeman and P. M. Chaikin, Adv. Mater., 2013, 25, 2779–2783 CrossRef CAS PubMed.
- G. Yao, J. Li, Q. Li, X. Chen, X. Liu, F. Wang, Z. Qu, Z. Ge, R. P. Narayanan and D. Williams, et al. , Nat. Mater., 2020, 19, 781–788 CrossRef CAS PubMed.
- A. Travesset, ACS Nano, 2017, 11, 5375–5382 CrossRef CAS PubMed.
- S. Sun, S. Yang, H. L. Xin, D. Nykypanchuk, M. Liu, H. Zhang and O. Gang, Nat. Commun., 2020, 11, 1–10 CrossRef PubMed.
- F. Romano and F. Sciortino, Nat. Mater., 2011, 10, 171–173 CrossRef CAS PubMed.
- D. Nykypanchuk, M. M. Maye, D. Van Der Lelie and O. Gang, Nature, 2008, 451, 549–552 CrossRef CAS PubMed.
- S. Y. Park, A. K. Lytton-Jean, B. Lee, S. Weigand, G. C. Schatz and C. A. Mirkin, Nature, 2008, 451, 553–556 CrossRef CAS PubMed.
- P. W. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS PubMed.
- J. Zheng, J. J. Birktoft, Y. Chen, T. Wang, R. Sha, P. E. Constantinou, S. L. Ginell, C. Mao and N. C. Seeman, Nature, 2009, 461, 74–77 CrossRef CAS PubMed.
- W. Liu, J. Halverson, Y. Tian, A. V. Tkachenko and O. Gang, Nat. Chem., 2016, 8, 867–873 CrossRef CAS PubMed.
- Z. Lin, H. Emamy, B. Minevich, Y. Xiong, S. Xiang, S. Kumar, Y. Ke and O. Gang, J. Am. Chem. Soc., 2020, 142, 17531–17542 CrossRef CAS PubMed.
- Y. Xiong, S. Yang, Y. Tian, A. Michelson, S. Xiang, H. Xin and O. Gang, ACS Nano, 2020, 14, 6823–6833 CrossRef CAS PubMed.
- Z. Lin, Y. Xiong, S. Xiang and O. Gang, J. Am. Chem. Soc., 2019, 141, 6797–6801 CrossRef CAS PubMed.
- W.-B. Zhang, X. Yu, C.-L. Wang, H.-J. Sun, I.-F. Hsieh, Y. Li, X.-H. Dong, K. Yue, R. Van Horn and S. Z. Cheng, Macromolecules, 2014, 47, 1221–1239 CrossRef CAS.
- C. Yi, H. Liu, S. Zhang, Y. Yang, Y. Zhang, Z. Lu, E. Kumacheva and Z. Nie, Science, 2020, 369, 1369–1374 CrossRef CAS PubMed.
- Z. Su, R. Zhang, X.-Y. Yan, Q.-Y. Guo, J. Huang, W. Shan, Y. Liu, T. Liu, M. Huang and S. Z. Cheng, Prog. Polym. Sci., 2020, 103, 101230 CrossRef CAS.
- T. Aida, E. Meijer and S. Stupp, Science, 2012, 335, 813–817 CrossRef CAS PubMed.
- M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, ACS Nano, 2010, 4, 3591–3605 CrossRef CAS PubMed.
- E. Benson, A. Mohammed, D. Rayneau-Kirkhope, A. Gådin, P. Orponen and B. Högberg, ACS Nano, 2018, 12, 9291–9299 CrossRef CAS PubMed.
- P. Wang, J.-H. Huh, H. Park, D. Yang, Y. Zhang, Y. Zhang, J. Lee, S. Lee and Y. Ke, Nano Lett., 2020, 20, 8926–8932 CrossRef CAS PubMed.
- N. P. Agarwal, M. Matthies, B. Joffroy and T. L. Schmidt, ACS Nano, 2018, 12, 2546–2553 CrossRef CAS PubMed.
- A. Buchberger, C. R. Simmons, N. E. Fahmi, R. Freeman and N. Stephanopoulos, J. Am. Chem. Soc., 2019, 142, 1406–1416 CrossRef PubMed.
- Y. Suzuki, I. Kawamata, K. Mizuno and S. Murata, Angew. Chem., Int. Ed., 2020, 59, 6230–6234 CrossRef CAS PubMed.
- C. Lee, J. Y. Lee and D.-N. Kim, Nat. Commun., 2017, 8, 1–8 CrossRef CAS PubMed.
- Y. Xiong, Z. Lin, D. Mostarac, B. Minevich, Q. Peng, G. Zhu, P. A. Sánchez, S. Kantorovich, Y. Ke and O. Gang, Nano Lett., 2021, 21, 10547–10554 CrossRef CAS PubMed.
- M. Kapuscinski, P. Munier, M. Segad and L. Bergström, Nano Lett., 2020, 20, 7359–7366 CrossRef CAS PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- S. Kantorovich, E. Pyanzina and F. Sciortino, Soft Matter, 2013, 9, 6594–6603 RSC.
- J. G. Donaldson, P. Linse and S. S. Kantorovich, Nanoscale, 2017, 9, 6448–6462 RSC.
- A. Arnold, O. Lenz, S. Kesselheim, R. Weeber, F. Fahrenberger, D. Roehm, P. Košovan and C. Holm, Meshfree Methods for Partial Differential Equations VI, Springer Berlin Heidelberg, 2013, vol. 89, pp. 1–23 Search PubMed.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford university press, 2017 Search PubMed.
- G. E. Uhlenbeck and L. S. Ornstein, Phys. Rev., 1930, 36, 823 CrossRef CAS.
- D. C. Rapaport, The art of molecular dynamics simulation, Cambridge university press, 2004 Search PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- V. Lobaskin and B. Dünweg, New J. Phys., 2004, 6, 54 CrossRef.
- M. Rosenberg, F. Dekker, J. G. Donaldson, A. P. Philipse and S. S. Kantorovich, Soft Matter, 2020, 16, 4451–4461 RSC.
- A. O. Ivanov and O. B. Kuznetsova, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 041405 CrossRef CAS PubMed.
- E. A. Elfimova, A. O. Ivanov and P. J. Camp, Nanoscale, 2019, 11, 21834–21846 RSC.
- K. Kremer and G. S. Grest, J. Phys.: Condens. Matter, 1990, 2, SA295 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |