Monovalent ion-mediated charge–charge interactions drive aggregation of surface-functionalized gold nanoparticles

Abstract

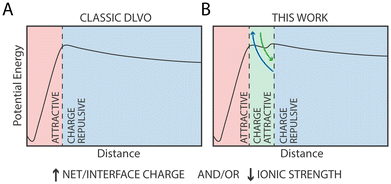
Monolayer-protected metal nanoparticles (NPs) are not only promising materials with a wide range of potential industrial and biological applications, but they are also a powerful tool to investigate the behaviour of matter at nanoscopic scales, including the stability of dispersions and colloidal systems. This stability is dependent on a delicate balance between attractive and repulsive interactions that occur in the solution, and it is described in quantitative terms by the classic Derjaguin–Landau–Vewey–Overbeek (DLVO) theory, that posits that aggregation between NPs is driven by van der Waals interactions and opposed by electrostatic interactions. To investigate the limits of this theory at the nanoscale, where the continuum assumptions required by the DLVO theory break down, here we investigate NP dimerization by computing the Potential of Mean Force (PMF) of this process using fully atomistic MD simulations. Serendipitously, we find that electrostatic interactions can lead to the formation of metastable NP dimers at physiological ion concentrations. These dimers are stabilized by complexes formed by negatively charged ligands belonging to distinct NPs that are bridged by positively charged monovalent ions present in solution. We validate our findings by collecting tomographic EM images of NPs in solution and by quantifying their radial distribution function, that shows a marked peak at interparticle distance comparable with that of MD simulations. Taken together, our results suggest that not only van der Waals interactions, but also electrostatic interactions mediated by monovalent ions at physiological concentrations, contribute to attraction between nano-sized charged objects at very short length scales.

---

Introduction

The stability of dispersions and colloidal systems is an important requirement in biological environments as well as in the formulation of industrial products, including in manufacturing, food, and pharma. This stability is dependent on a delicate balance between attractive van der Waals forces and repulsive electrostatic interactions that occur in the solution, and it is described in quantitative terms by the classic Derjaguin–Landau–Vewey–Overbeek (DLVO) theory.¹

The DLVO theory is generally adequate for large particles or in the long-range regime, but at smaller (“nano”) length scales or at high (>100 mM) ionic strengths, such as those found in biological systems, the continuum assumptions required by the DLVO theory break down. Consequently, several discrepancies arise between the DLVO predictions and experimental results, due to deficiencies in the appropriate description of solvent polarization,² finite size of ions³ or hydration forces.^4,5 These discrepancies, generally defined as non-DLVO forces, can lead to unreliable predictions when the interparticle distance is less than 2 nm.¹

Self-assembled monolayer-protected nanoparticles (SAM-NPs) have emerged in the last few years as a powerful tool to investigate non-DLVO forces.^6–8 In addition to their extremely promising application potential in a variety of fields, including biology,⁹ biomedicine,¹⁰ sensing,¹¹ and catalysis,¹² the chemistry of SAM-NPs makes them particularly well-suited to investigate aggregation propensity and dispersion stability of NPs in solution.

SAM-NPs are nanomaterials consisting of a metal core coated with a ligand shell. This shell, composed by thiolate ligands^9,13–15 such as alkanethiols,¹⁶ oligonucleotides,¹⁷ or polyethylene glycols,¹⁸ defines the boundaries between the NPs and the surrounding environment, and it provides the NP with both colloidal stability and specific functionality. Consequently, the physicochemical properties of NPs can be tailored by changing the functional groups, allowing to design advanced materials able to exert specific functions.¹⁹ However, even though this class of material is technologically highly meaningful, we still lack a consensus quantitative understanding of how surface chemistry, and namely hydrophobicity and charge localization, might influence the aggregation energy.

In fact, because of their nanometer scales, NPs are characterized by an extremely high surface-to-volume ratio and, therefore, NPs in solution tend to aggregate to minimize the surface energy, resulting in the rapid settling of the suspension.¹ Numerous previous studies have focused on the role of charges,²⁰ solvent ion concentration,²¹ solubility, and wettability,²² and it has been demonstrated that the charge and morphology of the ligand shell play a fundamental role on determining NPs’ properties.²³

In particular, the role of ions in promoting NP aggregation has been thoroughly investigated^24,25 in large part due to the well-known ability of multivalent cations to bridge charged ligands and to promote NP aggregation.^26–28 Monovalent ions, on the other hand, are generally treated as electrolytes, and any effect they might have on particle aggregation is usually attributed to their ability to screen electrostatic repulsion,²⁹ to promote depletion-type interactions,³⁰ or to change the local structure of water (the so-called “ion effect”³¹).

An alternative mechanism, whereby monovalent ions could directly promote NP aggregation via direct interactions with charged ligands, has been proposed based on dynamic light scattering (DLS) experiments and a semi-empirical theory combining DLVO and density functional theory (DFT) calculations.³² This mechanism is supported by theoretical considerations based on classical models such as Poisson–Boltzmann³³ or using computational methods, such as Monte Carlo (MC) or Molecular Dynamics (MD) simulations, that suggest that ion-mediated like-charge interactions might drive the stability of colloids,^34–37 polymers,^36,38 and biopolymers,³⁹ and mediate the interaction between AuNPs homogeneously functionalized with negatively charged short thiolate ligands.^40–42

On the other hand, analogous theoretical approaches provide a competing mechanism, suggesting that van der Waals interactions are the driving force behind NP aggregation, in agreement with DLVO theory.^43–45 Amongst those, both MC and MD simulations suggest that ligand-mediated short-range attractive interactions between monolayer-protected AuNPs can lead to aggregation despite long-range electrostatic energy barriers,^43,44 including specifically for thiol coated AuNPs.⁴⁵

To clarify this controversy, and to gain atomistic-level insights into the mechanism of NP aggregation, here we investigate NP aggregation with two high-resolution methodologies: by explicitly computing the Potential of Mean Force (PMF) of this process using fully atomistic MD simulations, a computational method with kcal accuracy,^43–48 and by directly collecting cryogenic electron tomography images of NPs in solution.⁴⁹ Both approaches suggest that already at physiological ion concentrations, NP dimers are stabilized by complexes formed by negatively charged ligands of the two NPs and positively charged monovalent ions. Taken together, our results suggest that not only van der Waals forces, but also electrostatic interactions mediated by monovalent ions at physiological concentrations, contribute to attraction between nano-sized charged particles at very short length scales.

Experimental

Molecular dynamics simulations

The systems investigated in this study consist of dimers of identical NPs in aqueous salt solution. For the NPs structures, we prepared models of mercapto undecane carboxylic acid (MUA) and octanethiol (OT) functionalized Au-NPs compatible with the OPLS forcefield⁵⁰ as derived by Salassi et al.⁵¹ The TIP3P model was employed for the water molecules. The core of the NPs (diameter of ∼2 nm) is composed of 144 Au atoms and 60 S atoms representing the grafting point of each ligand.⁵² The icosahedral symmetry of the core was kept using an elastic network. The NP surface is protected by 60 ligands that are bound to the NP core via Au–S bonds. We generated various ligand shells with different OT-MUA ratio, which led to NPs with different total charge. In particular, we built NPs with three different coating ratios: 100%OT, 50%OT : 50%MUA (“50%OT”) and 33%OT : 67%MUA (“33%OT”). The disposition of the grafted molecules is random for each OT-MUA ratio, unless described otherwise. Fig. 1 shows the chemical structures of the OT and MUA ligands and a representative disposition of the grafted molecules. Of note, all MUA ligands were considered as deprotonated. In the case of charged NPs, the system charge was neutralized by simply adding sodium counterions; a final concentration of 0.1M was mimicked by including the appropriate number of water molecules in the simulations. The total number of particles in our simulations was of about up to ∼133 000 (including ∼43 000 water molecules). Every system (NPs solvated in water and neutralized with Na⁺ counterions) was enclosed in an orthogonal box and treated under periodic boundary conditions. NP type dictated the total charge of every system and consequently the number of Na⁺ in solution. Box sizes of about 16 × 8 × 8 nm³ were employed for 50%OT and 100%OT, while a cell with a dimension of 24 × 8 × 8 nm³ was used for 33%OT. To neutralize the systems containing NPs with negatively charged ligands (50%OT and 33%OT), 60 and 80 Na⁺ were added, respectively. All the MD simulation were performed using the GROMACS 2018.3 package.⁵³ The van der Waals interactions were truncated using a cutoff value of 1.4 nm and a switching function was applied to the tail region (1.2–1.4 nm) to smoothly bring the van der Waals potential to zero at the cutoff distance. Electrostatic interactions were taken into account by means of the Particle Mesh Ewald (PME) algorithm⁵⁴ using a Fourier grid space of 0.12 nm and a 1.4 nm real-space cutoff. The bonds involving hydrogen atoms were constrained using the LINCS⁵⁵ and SETTLE algorithms.⁵⁶ The integration time step was set to 2 fs.

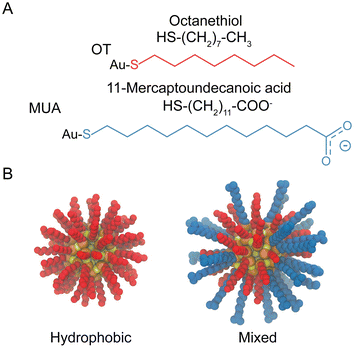Fig. 1 Structural and geometrical characteristics of NPs. (A) The surfactants forming the ligands shell; (B) NPs models for 100%OT and 50%OT.

For every system, we used umbrella sampling⁵⁷ (US) to estimate the free energy profile (or potential of mean force, PMF) along the chosen reaction coordinate: the interparticle distance (ζ), which was defined as the distance between the center of mass of both NP cores. To generate starting configurations for every umbrella window, we pulled two NPs away from an initial dimer state (ζ = 2 nm) to the complete separation (until ζ was typically 6–7 nm). Dimer states were built by putting the NPs at distances short enough to spontaneously observe dimerization during the initial equilibration runs (20 ns), which were performed using a Berendsen thermostat and a Berendsen barostat,⁵⁸ with coupling time constants of 2 ps, to control the temperature (298 K) and pressure (1 atm). Then, NPs were pulled with a force of 1300 kJ mol⁻¹ nm⁻² and at constant velocity (0.001 nm ps⁻¹) while using a Nosé–Hoover chain thermostat⁵⁹ and a Parrinello–Rahman barostat,⁶⁰ respectively, with coupling time constants of 1 ps to control the temperature (298 K) and pressure (1 atm). From this trajectory, we extracted configurations at equispaced values (every 0.2 nm) along the reaction coordinate ζ. Consequently, about 20–25 initial configurations for the independent umbrella simulations were built. Each configuration was equilibrated for 5 ns, using the same algorithms and parameters described above for the equilibration of the dimer states, while constraining its interparticle distance at the original value. Subsequently, a 60 ns production run (using the same algorithms and parameters employed for the pulling simulation) was carried out for every window. A harmonic biasing potential with a force constant of 1250 kJ mol⁻¹ nm⁻² was applied to restrain the system at the initial value of ζ during these simulations and, therefore, only a local region of the complete PMF was sampled in each of them. Then, we used the weighted histogram analysis method (WHAM) to reconstruct the free energy profile along the selected reaction coordinate, through the combination of the umbrella histograms obtained for each of the windows, and to quantify the statistical errors on the estimated PMF.⁶¹ Statistical errors were estimated with bootstrap analysis using WHAM analysis tool implemented in GROMACS (100 bootstraps). The convergence of the PMF profiles, estimated from the US simulations, with the sampling time per window can be found in ESI, Fig. S1.†

Complexes

To investigate the formation of R-COO⁻ : Na⁺ : ⁻COO-R complexes as a function of the ionic strength and NP type, we calculated the total number of these interactions. We characterized the formation of these complexes by the presence of a sodium ion within a cutoff distance of 0.35 nm of two or more carboxylate groups simultaneously. To do so, we first computed the distances between all R-COO⁻ : Na⁺ pairs and subsequently defined an event (complex formation) for every sodium ion that was able to bridge (showing distances below the mentioned 0.35 nm threshold⁶²) two or more carboxylates from different NPs. For each complex, we also computed the number of ligands involved in every event.

Ligand density maps

To investigate the interaction between NPs as a function of the interparticle distance, we calculated, as a 2-D density map, the spatial distribution of the beads forming both the hydrophobic and hydrophilic ligands. Considering the cylindrical geometry of the dimers, these 2-D density maps were computed as a function of the distance along the axis passing through the center of mass of both NP cores and the radial distance from this axis. The density was normalized by the number of bins for a given radius. Moreover, in order to analyze the ligand distribution on the NP surface and how this influences the aggregation energy profile, we also generated maps of the ligand densities in the ligand shell. To do so, we projected the cartesian coordinates of selected beads (see below) onto the plane that contains the center of mass of one of the NP cores and is perpendicular to the line that joins the center of mass of both NP cores. This allowed us to describe the position of the selected beads (the terminal carbon bead of every ligand) in a 2-D map using longitude and latitude coordinates. Following this approach, the projections of the center of mass of both NP cores coincide and define the origin of the map (i.e., they have both coordinates [0, 0]), and the ligand density distribution can be easily described using the above-mentioned selected beads for both MUA and OT ligands as reference. These quantities were computed by averaging over the MD trajectories.

Charge density

To evaluate the distribution of charges around NPs, we computed the charge density. To do so, we binned the simulation box in sub-volumes and assigned the number of positive and negative charges per sub-volume (q_e nm⁻³). Subsequently, we projected the charges per bin onto the xy plane of the simulation box (q_e nm⁻²). The analysis run is 5 ns.

Synthesis and characterization of gold nanoparticles

Synthesis of gold nanoparticles functionalized with a binary mixture of thiolated molecules was done in two major step: synthesis of oleylamine coated gold nanoparticles and then ligand exchange of oleylamine by a desired mixture of thiols.

Synthesis of oleylamine-coated gold nanoparticles (OAm-AuNPs). All chemicals were purchased from Sigma-Aldrich and used without further purification. 392 mg of hydrogen tetrachloroaurate trihydrate (HAuCl₄·3H₂O) were dissolved in 32 mL of oleylamine and 40 mL of n-octane, in a three-necks round bottom flask and stirred at room temperature under argon atmosphere. The solution of reducing agent was prepared by dissolving 170 mg of tert-butylamine-borane complex (tBAB) in 8 mL of oleylamine and injected to the flask containing the gold solution. The reaction was stirred from one to two hours before quenching it with 120 mL of ethanol. The so-obtained nanoparticles were purified by cycles of centrifugation, with washing in ethanol and redispersion in dichloromethane. The final purified particles were dried under vacuum.

Ligand exchange of OAm-AuNPs. To make MUA : OT gold nanoparticles, the solution containing the two thiolate ligands was prepared by dissolving 30 mg of mercaptoundecanoic acid (MUA) and 24 μL of n-octanethiol (OT) (feed ratio of 1 to 1) in 30 mL of dichloromethane. 60 mg of nanoparticles were dissolved in 4 mL of dichloromethane and the solutions were mixed and stirred for two days. The nanoparticles were then washed 5 times with a mixture of acetone and dichloromethane by centrifugation and purified with DI–water using 30 kDa Amicon Ultra-15 centrifugal filter devices. Finally, the concentrated nanoparticles were lyophilized. MUS : OT was prepared by the same protocol as was reported previously.⁶³ Conventional transmission electron microscopy (TEM) was used to obtained particle size distribution on a carbon film coated grid containing dry powder. Image segmentation and size analysis were carried out in ImageJ (NIH, ver. 1.53c). Feret's diameters were used as the NP diameter.

Nuclear magnetic resonance (NMR) spectroscopy was utilized for characterizing particle purity and for obtaining ligand ratios. To do cryogenic electron tomography, a dispersion at concentration of 40 mg ml⁻¹ was prepared for MUS : OT gold nanoparticles, and for MUA : OT nanoparticles at 20 mg ml⁻¹. The freshly prepared dispersions were used for this method.

Cryogenic electron tomography of nanoparticle dispersions

A 4ul aliquot of dispersion of gold nanoparticles was placed on a quantifoil grid (1.2/1.3, EMS) and then a filter paper was applied to remove excess dispersion. For MUS-OT, no salt was added to the sample. For MUA-OT, a salt concentration of 20 mM NaOH was added to the sample. The thin film of dispersion was vitrified by liquid ethane in a homemade plunge freeze device. Vitrification rate was of the order of 10⁷ K s⁻¹ (ref. 64) so that the population of aggregates does not vary during the freezing process. The vitrified grid was loaded to a cryogenic holder Gatan 626 (Gatan, USA) and transferred to a transmission electron microscope F20 (Thermofisher, USA). Images were recorded in low dose mode at magnification of 50 000× at 4096 × 4096 pixels. Tilt series were acquired from −60° to 60° at an incremental angle of 2° by Tomography 4.0 (Thermofisher, USA). The tilt series images were binned by 2 and then aligned by Inspect3D (Thermofisher, USA). The reconstruction was carried out in Inspect3D (Thermofisher, USA) using SIRT algorithm, at the final pixel size of 0.41 nm. The identification of locations of nanoparticles in the tomograms was carried out in Imaris (Oxford Instruments, UK) and the 3D centroid positions were exported to calculate radial distribution functions.

Results and discussion

Potential of mean force between highly charged NPs reveals the presence of a non-DLVO metastable minimum

To understand the role of the ligand shell composition on the free energy of aggregation, we performed atomistic MD simulations where we estimated the potential of mean force (PMF) between identical NPs using umbrella sampling (see Materials and methods for details) at physiological (0.1 M) ion concentration. This approach allows us to compute the separation energy between two identical NPs without any a priori assumption other than the initial NP–NP interface, that we selected randomly. The NPs used in the simulations have a metal core diameter of 2 nm, and three different coatings: 100%OT, random 50%OT : 50%MUA (“50%OT”) and random 33%OT : 67%MUA (“33%OT”). The typical length of extended OT ligands is of ∼0.8 nm, while that of extended MUA ligands is ∼1.2 nm.

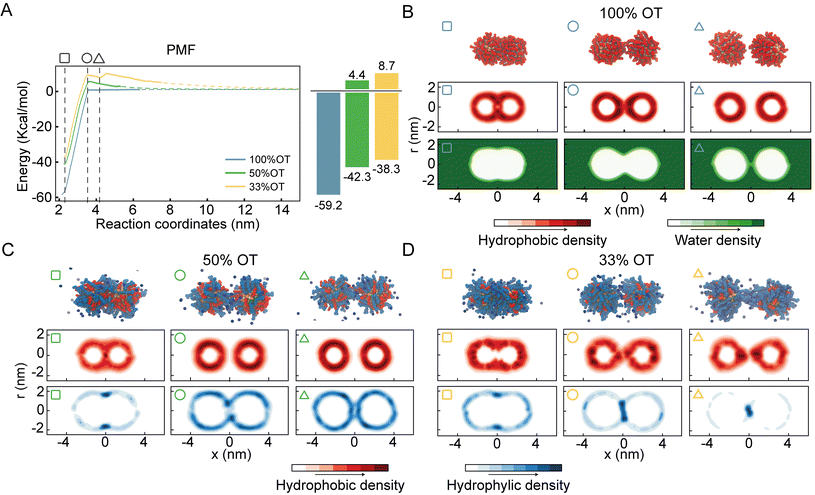
For purely hydrophobic NPs (100%OT), the PMF shows that there is no interaction between the two NPs until the distance between their center of mass (interparticle distance) is ∼3.5 nm; at shorter distances, they start attracting each other (Fig. 2A).

Fig. 2 Aggregation behaviour of surface-functionalized (MUA-OT) gold nanoparticles (NPs). (A) Dimerization potentials of mean force (PMFs) and corresponding error bars (shaded) between identical NPs. Light blue: 100%OT; Green 50%OT; yellow: 33%OT. Error bars are estimated from bootstrap analysis (n = 100). (B) Density maps for 100%OT NPs at different interparticle distances (square: 2.2 nm, circle: 3.5 nm, triangle: 4.2 nm). Top: Snapshot of the interacting dimer; middle: hydrophobic density; bottom: water density. (C) 50%OT and (D) 33%OT ligand density maps as function of interparticle distance. Top: Snapshot of the interacting dimer; middle: hydrophobic ligand density; bottom: hydrophilic ligand density.

Here, and in all the PMF, the dashed line represents an exponential fit, computed with data from barrier to infinity.

Interestingly, this distance is about twice the length, measured from the NP surface, of an OT ligand in its most extended state (ESI, Fig. S2†). Moreover, according to the computed PMF, the aggregation of 100%OT NPs is a barrierless process leading to a primary minimum that is 59.2 kcal mol⁻¹ more stable than the fully separated state. This indicates that this primary minimum corresponds to a highly stable aggregated state, in agreement with experimental observations²² and classical DLVO theory based on Hamaker constants.¹

For mixed NPs (50%OT and 33%OT), we observed two major differences with respect to the purely hydrophobic 100%OT NPs. First, the stability of the primary minimum with respect to the fully separated state is smaller in the presence of charged ligands, being of 42.3 and 38.3 kcal mol⁻¹, respectively, for the 50%OT and the 33%OT (Fig. 2A). Second, NP aggregation is not spontaneous anymore, and there is an energy barrier, due to the presence of negative charges on the NP surface, that must be overcome to reach the aggregated state. This “electrostatic” energy barrier for aggregation appears at an interparticle distance ζ ∼3.5 nm and amounts to 4.4 and 8.7 kcal mol⁻¹ for the 50%OT and 33%OT NPs, respectively (Fig. 2A). Taken together, our results quantify to what extent the ligand shell composition plays a role in determining the aggregation energy, and they are consistent with predictions based on DLVO theory, namely that aggregation between NPs is driven by van der Waals interactions and opposed by electrostatic interactions.^65,66

Quite unexpectedly, however, we observed the presence of a secondary minimum in the energy profile for the 33%OT NP located quite close to the primary minimum (Fig. 2A, yellow curve). This secondary metastable minimum presents a barrier of ∼3 kcal mol⁻¹. Interestingly, this minimum is located at a much shorter NP–NP distance than the classical secondary minimum predicted by DLVO theory¹ and it is rather localized at a distance where electrostatic repulsion is already dominant (Fig. 2A).

Of note, increasing ionic strength (180 mM) or switching to divalent ions such as Ca²⁺ leads to the disappearance of this secondary minimum (ESI, Fig. S3†). In these conditions, the additional electrostatic screening provided by the excess counter charges leads to a behaviour that is qualitatively similar to that of 100%OT NPs (Fig. 2A, blue curve). This observation suggests that the secondary minimum we have identified (Fig. 2A, yellow curve) is likely to be present only in a specific range of NP ligand charge and ionic strength.

To further investigate this observation, we first analysed the dimers’ geometrical properties. To this end, we first generated ligand density maps at minimum core–core distance (∼2.2 nm) (ESI, Fig. S4†). In these maps OT and MUA local densities are represented in red and blue, respectively, while light colour means an equiprobability to find both ligands. The dashed lines identify the interface between NPs. From these maps, we quantified the effective ligands’ coverage percentage of the interface via a simple sum of the various (OT, red; MUA, blue) contributions. Consistent with the nature of the NPs, the amount of charged ligands at the interface is proportional to the amount of charged ligands in the NP (i.e. 33%OT > 50%OT > 100%OT).

Next, we calculated separately the density of both the hydrophobic and hydrophilic beads as a function of the interparticle distance. Fig. 2B shows the density maps for the hydrophobic atoms (middle panel) and water (bottom panel) in the case of the 100%OT NPs at different interparticle distances. In all the plots, the interparticle distance increases from left to right. At short core–core distances (ζ ∼2.2 nm), the contact site is completely determined by hydrophobic interactions between the OT ligands, and water molecules are not able to come close to the geometrical center of the dimer (Fig. 2B, left). For intermediate distances (ζ ∼3.5 nm), the hydrophobic ligands in the 100%OT appear elongated, binding together the dimer (Fig. 2B, center). For larger interparticle distances (ζ ∼4.2 nm), water molecules can penetrate and approach the dimer interface and physically separate the aliphatic ligands (Fig. 2B, right).

Fig. 2C and D show the average density for both the aliphatic chains and the charged beads for 50%OT and 33%OT, respectively. For both systems, at the minimum separation distance (ζ ∼2.2 nm), the contact site is completely hydrophobic (Fig. 2C and D, left) and the density profile for the hydrophilic ligands shows an accumulation in the boundaries of the interfacial region in a ring-shaped fashion. At larger distances (ζ ∼3.5 nm), however, important differences between the 50%OT and the 33%OT NPs can be observed, as the hydrophilic beads in the 50%OT NP do not populate the interfacial region, while for the 33%OT NPs a higher hydrophilic density and a general deformation, from ring shaped to disk shaped, can be observed in the contact region. This difference in behaviour becomes even more pronounced at larger distances (ζ ∼4.2 nm).

Overall, this analysis suggests a correspondence between the ligands’ organization at the interface, in particular referring to the hydrophilic beads, and the observed presence of a metastable minimum in the aggregation PMF.

The metastable dimer of highly charged NPs originates from the complexation between like-charged ligands

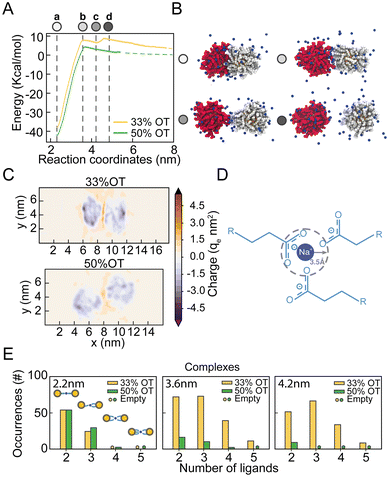
From the analysis of the distribution of hydrophilic and hydrophobic ligands among the NPs, it appears that the unexpected presence of a distinct minimum in the PMF of the 33%OT system at 4.2 nm might originate from the interaction between like-charged ligands. To test this hypothesis, we further investigated the behaviour of hydrophilic ligands and counterions along the reaction pathway.

To obtain a better picture on the aggregation pathway for the 33%OT, we explored NP–NP behaviour for distinctive core–core distances where we observed sudden changes in the energy profile: (a) at 2.2 nm, the minimum distance of interaction (Fig. 3A, point a, white); (b) at 3.6 nm, the aggregation barrier (Fig. 3A, point b, light gray); (c) at 4.2 nm, the newly found minimum (Fig. 3A, point c, grey); (d) at 4.6 nm, where the NPs are fully separated (Fig. 3A, point d, dark grey). As it can be appreciated in Fig. 3B, as the two NPs separate from each other, ligands extend at the interface between the two NPs and interact not only amongst them, but also with multiple positively charged sodium ions. To further characterize the role of electrostatic interactions in the aggregation of charged NPs, we first computed the electrostatic density maps for two NPs, 33%OT and 50%OT, at 4.2 nm interparticle distance, i.e., where the newly found minimum was observed for 33%OT but not for 50%OT (Fig. 3C). Quite interestingly, the heat maps show that despite the high negative charge given by the presence of the NPs, the systems have a net positive charge at the interface, and that this charge is higher in the case of 33%OT, further indicating the presence of multiple positive sodium ions at the interface between the two identical NPs. Of note, such an elevated net positive charge at the interface (1.6 M) is achieved despite the relatively low Na⁺ concentration (0.1 M) in our system.

Fig. 3 The secondary minimum in the NP–NP PMFs is characterized by ion-mediated interparticle complexes. (A) Potential of mean force of dimerization and corresponding error bars (shaded) for 33%OT and 50%OT NPs. Error bars are estimated from bootstrap analysis (n = 100). Selected remarkable points characterizing the energy profile are highlighted: (a) first minimum; (b) first barrier, (c) second local minimum, (d) completely separated NPs. (B) Snapshots of the highlighted distances in the PMF. Colors are used to visually separate the NPs in the dimer, sodium ions are shown in blue. (C) Electrostatic density maps for 33%OT and 50%OT at 4.2 nm interparticle distance. (D) Pictorial representation of charged ligand-ion-charged ligand interparticle complexes. (E) Occurrences of charged ligand–ion-charged ligand interparticle complexes at different interparticle distances.

To better discriminate this behaviour at the atomistic level, we next computed the occurrences of R-COO⁻ : Na⁺ : ⁻COO-R complexes for both the inter-NPs interactions. We defined the formation of a complex when a sodium ion lies within 0.35 nm of two or more carboxylates simultaneously (Fig. 3D). Remarkably, we observed that moving away from the primary minimum, the two 33%OT NPs engage in multiple 3-mer and 4-mer inter-NP complexes involving multiple charged ligands, while this is instead not the case for the 50%OT NPs (Fig. 3E and ESI, Fig. S5†). Interestingly, a similar stabilizing role for monovalent cations has been suggested for AuNPs homogeneously functionalized with short negatively charged thiolate ligands based on theoretical studies.^40–42

Patterning of ligands on the NP surface modulates the appearance of a metastable minimum

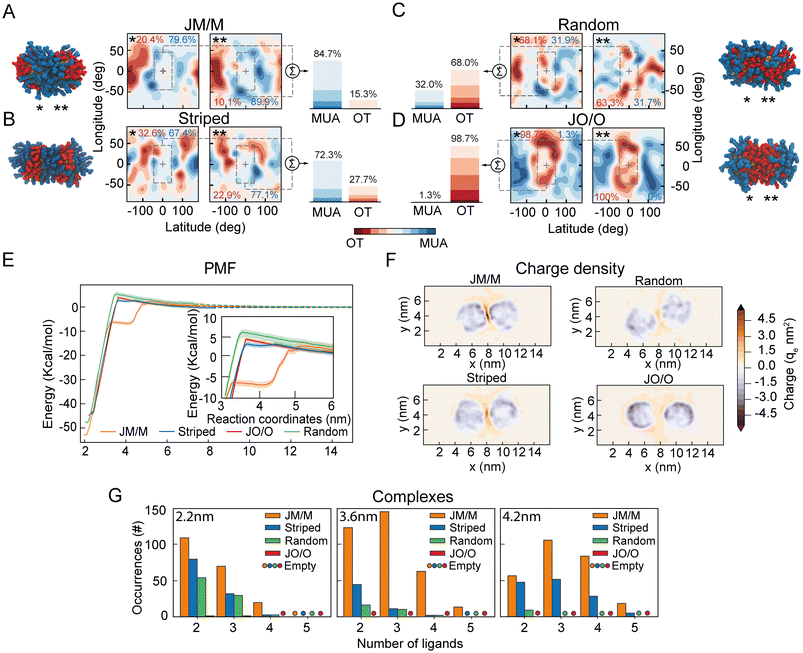
Our data suggest that ion-mediated charge–charge interactions between surface ligands promote the appearance of a metastable secondary minimum between highly charged NPs (33%OT), and that this minimum is absent in NPs with lower charge (50%OT). As this phenomenon appears to be driven by the organization of the surface ligands at the interface between NPs, we next wondered whether a reorganization of the ligand shell topography could lead to a similar behaviour even in NPs with overall lower total charge.

To test this hypothesis, we designed two new distinct surface patterns for the 50%OT NPs: (1) Completely asymmetrical “Janus-like” NPs, with all OT ligands in one half of the NPs and all MUA ligands on the other side; (2) striped NPs with MUA patches at the poles and an OT ligands strip located at the equator. We next compared these two new patterns with the fully random 50%OT we previously investigated (Fig. 2 and 3), where OT and MUA ligands are randomly distributed throughout the NP surface (ESI, Fig. S6†). Despite the difference in shell topography, all NPs have the same OT/MUA ratio (50%OT, 50%MUA) and charge (−30q_e).

Afterward, we prepared dimers of identical NPs, choosing the relative orientation between the NPs to define the number of MUA ligands at the interface. Thus, we arranged the NPs in four different ways: (1) a pair of Janus NPs with the MUA side at the interface (JM/M) (Fig. 4A); (2) a pair of striped NPs with the MUA patches at the interface (Fig. 4B); (3) a pair of random NPs randomly oriented (Fig. 4C); and (4) a pair of Janus NPs with the OT side at the interface (JO/O) (Fig. 4D). To quantify the number of charged ligands at the interface for these orientations, we generated ligand density maps at minimum core–core distance (∼2.2 nm) (Fig. 4A–D). In these maps OT and MUA local densities are represented in red and blue, respectively, while light color means an equiprobability to find both ligands. The dashed lines identify the interface between NPs. From these maps, we quantified the effective ligands’ coverage percentage of the interface via a simple sum of the various (OT, red; MUA, blue) contributions (Fig. 4A–D). These data confirm that there is a trend in the number of charged ligands at the interface with JM/M (85 ± 1%) > Striped (72 ± 5%) > Random (32 ± 0.1%) > JO/O (1 ± 0.7%).

Fig. 4 Patterning of ligands on the surface of low-charge NP modulates the appearance of a metastable minimum. (A–D) NP–NP dimers for JM/M, Striped, Random, and JO/O conformation. Left: Representative snapshots. OT: red, MUA: blue. Middle: Ligand density maps at the NP–NP interface. Right: Effective ligands’ coverage percentage. (E) Corresponding PMFs and corresponding error bars (shaded). Error bars are estimated from bootstrap analysis (n = 100). (F) Charge density at the NP–NP interface at 4.2 nm interparticle distance. The analysis run is 5 ns. (G) Occurrences of charged ligand-ion-charged ligand interparticle complexes at different interparticle distances.

Next, to properly quantify the role of the interfacial ligand topography on the free energy of aggregation, we computed the separation PMFs for the aforementioned orientations (Fig. 4E). The PMFs show that the primary minimum is located at ζ ∼2.2 nm for all systems (Fig. 4E). As expected, the electrostatic aggregation barrier is similar for all topographies (Fig. 4E), as this barrier is modulated by the total charge on the NP according to the classical DLVO theory.

However, both JM/M and Striped arrangements exhibit a secondary metastable minimum in the energy profile, like the one previously observed for the 33%OT NP (Fig. 3). For the JM/M NPs, the metastable state is located at values of ζ between 3.5 nm and 4.2 nm, and the energy required to overcome this barrier and fully separate the NPs is ∼6 kcal. On the other hand, the Striped secondary barrier is shallower (∼1 kcal) and within the PMF statistical error. Overall, these data suggest that, for a given ratio of hydrophobic vs. charged ligands on the NP shell, the organization of charged ligands on the NP surface modulates the appearance of this metastable state. Increasing the number of charged ligands at the interface, like in JM/M and Striped (Fig. 4A–D), correlates with the presence of the metastable state.

To further investigate the molecular properties of this minimum, we next explored the distribution of ions and charged ligands at the interface and around the NPs at an interparticle distance compatible with the secondary minimum (ζ ∼4.2 nm). Fig. 4F and ESI, Fig. S7† depict the charge density for the four systems. Consistently with the maps previously computed for the random 33%OT and 50%OT NPs (Fig. 3), the heat maps for these four systems show that, as the number of charged ligands at the interface increase, the charge density also increases. Overall, these data further confirm that highly negatively charged patches at the interface might be able to accumulate ions and promote dimer stabilization.

Finally, to further correlate the presence of a secondary minimum with the formation of interparticle charge-ion-charge complexes, we quantified the formation of these complexes as a function of the core–core distance for the various surface patterns (Fig. 4G). As expected, their number increases with the number of charged ligands at the interface (Fig. 4G). Remarkably, for interparticle distances of 4.2 nm, no or negligible complex formation is observed for the random and JO/O homodimers, while substantial formation of interparticle complexes can be observed at the interface for the JM/M and Striped ones. Of note, these complexes are solely promoted by a rearrangement of the ions towards the NP–NP interface, as the total charge of the two NPs plus their surrounding ions remains constant at all interparticle distances (ESI, Fig. S8†).

NPs in solution form dimers at interparticle distances comparable with those predicted by MD simulations

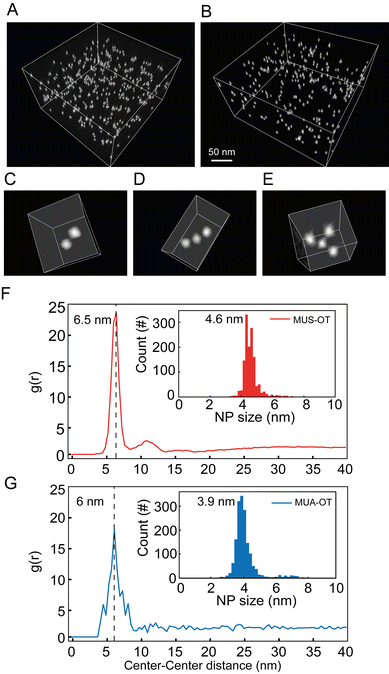
In order to validate the main observation extracted from the MD simulations (i.e. that charged NPs form dimers in solution at interparticle distances of approximately 2 times the radius of the metal core plus the ligand shell) and to assess whether this is a general rule for NP functionalized with a binary self-assembled monolayer of hydrophobic and hydrophilic surfactants, we next prepared two sets of gold nanoparticles that were functionalized with a binary self-assembled monolayer (SAM) of thiols and investigated their dispersion states by cryogenic electron tomography (cryo-ET).⁴⁶ The first sample (namely, MUS : OT) was composed of a gold NP core (average diameter of 4.6 nm, Fig. S9†) functionalized with 11-mercaptoundercane sulfonate (MUS, 70%) and OT (30%). The other sample was MUA : OT that was made of gold NP core with an average diameter of 3.9 nm (Fig. S9†) and functionalized with 11-mercaptoundecanoic acid (MUA, 84%) and OT (16%). Here, OT was chosen to mimic the hydrophobic component of the two thiols in the MD simulations, while MUS and MUA function as salt bridging thiolated ligands. The quantification of the interparticle distance between NPs can be achieved by cryogenic electron tomography (cryo-ET) via the radial distribution function (RDF) calculated from the spatial positions of the NPs.⁴⁶ In the cryo-ET approach, an aqueous dispersion of the NPs was vitrified quickly so that the frozen sample maintained the state of the dispersion prior to vitrification. The vitrified sample was subsequently imaged by transmission electron microscopy at cryogenic temperature (−176 °C) and at a series of tilt angles. The obtained tilt series was then aligned and further used to reconstruct a tomogram (i.e. 3D image) of the sample. From the tomogram, NPs were identified, and their centroid positions were used to calculate the corresponding RDFs.

Fig. 5A and B show a representative tomogram of a sample of MUS : OT and of MUA : OT, respectively. From the tomograms, various aggregate states of NPs can be directly visualized. A few of such oligomeric states are represented in Fig. 5C–E as a dimer, trimer, and tetramer. RDFs calculated from centroid positions of NPs identified in the tomogram are plotted in Fig. 5F for MUS : OT and Fig. 5G for MUA : OT sample. The first nearest neighbour distances were clearly determined by the maximum peaks observed in the RDF for both samples. Those can be observed at 6.5 nm and 6.0 nm for MUS : OT and MUA : OT, respectively (Fig. 5F and G). These distances are higher than the sum of particle core diameters, that are of 4.6 nm and 3.9 nm, respectively (Fig. 5F, G and ESI, Fig. S9†), and the average interparticle distance is about 1.9–2.1 nm larger than the sum of particle core diameters. This value is more than twice the length of the hydrophobic ligand (OT) in its most extended state, suggesting that the NP oligomeric states are mediated by the longer ligands, MUA and MUS, for MUA : OT and MUS : OT NPs respectively. Also, the observed experimental values of 1.9–2.1 nm are in perfect agreement with the MD simulations, where the ion-mediated minimum between the NPs is found at a distance that is 2.0 nm larger than the core–core minimum distance (ζ ∼4.2 nm vs. ζ ∼2.2 nm, Fig. 3A). Notably, however, no peak corresponding to the primary minimum was observed for the MUS : OT NPs (Fig. 5F) while only a minor peak corresponding to the primary minimum was observed for the MUA : OT NPs (Fig. 5G). These observations suggest that the free energy barrier to transition from the ion-mediated metastable state and the primary minimum is likely underestimated in our MD simulations, as only a minor fraction of the NPs in our experimental setting overcomes it at room temperature. However, the good geometrical agreement in terms of interparticle distances strongly suggests that the most populated state in the cyro-ET samples corresponds to the ion-mediated metastable minimum we identified in our free energy profiles.

Fig. 5 Cryo-ET of vitrified aqueous dispersion of NPs. (A) Tomogram of gold NP functionalized with a mixture of MUS (70%) : OT (30%) dispersed in water. (B) Tomogram of gold NP functionalized with a mixture of MUA (84%) : OT (16%) dispersed in NaOH 30 mm. (C–E) Representative oligomer states found in these sets of samples; (C): dimer, (D): trimer, (E): tetramer. (F) Radial distribution function plotted as function of NP–NP centroid distance for MUS : OT sample. The size-distribution of the corresponding NPs is shown in the inset. (G) Radial distribution function plotted as function of NP–NP centroid distance for MUA : OT sample. The size-distribution of the corresponding NPs is shown in the inset.

Conclusions

In this work, we have extensively characterized the dimerization PMFs between identical NPs containing different ratios of hydrophobic/charged ligands and with different ligand patterns on the NP surface. In agreement with the DLVO theory, we found that the primary minimum describing irreversible NP aggregation is driven by van der Waals interactions, while the barrier that prevents such aggregation is modulated by the electrostatic repulsion between two NPs of identical charge. We foresee that the extensive quantitative characterization of the dimerization profile of identical NPs we provide here will be useful for the validation and the development of extensively used CG models to describe the behaviour of NPs in biological-like contexts.^10,67,68

Serendipitously, we found that, in the presence of monovalent cations at physiological-like concentration (0.1 M), as the charge on the NP surface increases, a metastable minimum along the dimerization PMF appears. Notably, this minimum is found at an interparticle distance that is much shorter than what classical DLVO theory would predict for a secondary minimum, but it is rather found at a distance compatible with fully extended surface ligands barely touching each other. Our analyses suggest that this minimum correlates with the presence of like-charged ligands bridged by a counterion, and it is thus of electrostatic origin.

The current model for NP aggregation posits that in the absence of charged ligands, i.e. for purely hydrophobic particles such as 100% OT, NPs in water would inevitably attract each other and aggregate in the primary (core-to-core) minimum following a barrierless pathway. Substituting hydrophobic OT ligands with charged ones, such as MUS or MUA, leads to the appearance of an electrostatic repulsion that is proportional to the density of charged ligands on the NP (Fig. 6A). In the extreme case, i.e., for NPs constituted by 100% charged ligands, this results in entirely soluble NPs’ solutions that do not form aggregates.⁴⁹

Fig. 6 Conceptual model of the nanoscale contribution of distinct physico-chemical forces on NP aggregation: A) classic DLVO potential energy profile; B) potential energy profile identified in this work. In this profile, short-range interactions between charged ligands and monovalent ions introduce charge-mediated attractive forces that stabilize NPs’ complexes.

However, at specific intermediate hydrophobic/hydrophilic ratios, we could observe aggregates in our cryo-TEM images (Fig. 5). According to our data and previous work,³² this aggregation, in the presence of monovalent ions, is reversible, indicating that it is unlikely a consequence of the system falling in the primary (core-to-core) minimum. This interpretation is further supported by the observation that the geometrical distance between NPs in the cryo-ET images is not compatible with that of the primary minimum, where the two NPs would be at a distance corresponding to the diameter of their Au core.

Rather, our MD simulations suggest that the most likely explanation of this phenomenon is that at short range, specific and directional interactions between charged ligands and monovalent ions introduce charge-mediated attractive forces that stabilize NPs’ complexes (Fig. 6B). While quantitative comparison between experiments and simulations has limitations due to intrinsic differences between the experimental system and the computational one, most notably the ratio of charged vs. protonated MUA/MUS ligands or the lack of electronic polarization in our atomistic force field, our simulations provide a qualitative explanation of the phenomenon observed experimentally.

The observation that the presence of a metastable state can be modulated by both ion concentration and by the patterning of ligands on the NP surface suggests that this phenomenon is inherently local, leading to important conceptual and practical consequences. First, this behaviour can't be described within the framework of the standard DLVO theory, and specific extension (as in other extended-DLVO theories^3–5) must be implemented if one wants to take this specific behaviour into account. Second, this behaviour can be exquisitely sensitive to kinetic processes such as NP surface ligand exchange, that could thus dynamically alter the propensity for NP aggregation over time.⁶⁹ Third, our data could explain why selective aggregation and precipitation of like-charged nanoparticles (NPs) can be induced by monovalent cations at relatively low ion concentrations³² unlike, for example, much larger lipidic vesicles, where only very high concentrations of monovalent ions, unlike divalent ions, are required for aggregation.⁷⁰ As the size of gold NPs in these experiments (as in our simulations) is much smaller than those of lipid vesicles, our data suggest that local nanoscopic interactions might be at the origin of such behaviour.

Finally, we want to further point out some limitations of our approach. First, the PMFs we computed are obtained from the separation of two NPs from an initial dimeric state. While this approach is helpful to discriminate between different NP–NP interfaces, there is no guarantee that our profiles represent the minimum free energy path for the opposite, and more frequent, process: nanoparticle aggregation. Rather, our profiles could be considered as upper limits for the aggregation process, that could instead have lower barriers and different minima. Also, computational approaches such as atomistic simulations inherently carry some systematic error, generally in the order of 1 kcal mol⁻¹.⁷¹

Second, it must be pointed out that a direct comparison of our data with experimental results can only be qualitatively for four main reasons. First, in our simulations we assume a single protonation state for all MUA ligands. This is not the case in experiments, and hence our total charge is much higher than that of a corresponding name-sake (e.g., 33%OT) NP. Second, our simulations only consist of two NPs. As such, we are completely neglecting contributions arising from interactions between the NP dimer and other NPs, typically resulting, in experimental contexts, in larger NP assemblies. Third, inherent differences in ionic strength between experimental conditions and molecular simulations induce different electrostatic screening for NP dimerization. Fourth, since concomitant binding of ions to multiple charged surfactants inherently induces polarization effects, it is likely that the use of a non-polarizable classical force fields might result in quantitative inaccuracies. In our specific case, our data suggests that the barrier between the metastable state and the global free energy minimum is underestimated in the MD simulations with respect to the cryo-EM experiments.

Taken together, our results suggest that electrostatic interactions taking place at the nanometer scale, in the form of charged ligand-monovalent ion-charged ligand complexes, promote attractive interactions between charged NPs. We anticipate that our results will remain valid not only for diverse NPs (e.g., those carrying different charged ligands such as citrate), but that they will also be instrumental to explain phenomena taking place in biological systems, especially since monovalent ions are found at much larger concentrations than divalent ones.⁷²These could include interactions between NPs and proteins, between NPs and lipid membranes⁷³ as well as direct protein–protein interactions such as those driving reversible protein aggregation or protein phase separation.

Author contributions

E. P., S. V. and F. S. conceptualized and designed the research; E. P. performed the MD simulations and data analyses with the help of P. C.; Q. K. O. performed the cryo-ET experiment; F. O. and M. T. synthesized and characterized the NPs used for the cryo-ET experiments; S. V. supervised the project; the manuscript was written through contributions of all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Swiss National Science Foundation through the National Center of Competence in Research Bio-Inspired Materials. P. C. acknowledges support from the Novartis Foundation for Biomedical Research grant #17C139. F. S., F. O., T. M., and Q. O. thank the Swiss National Science Foundation for financial support (grant number 200020_185062). This work was supported by grants from the Swiss National Supercomputing Centre (CSCS) under project ID s1011 and s1030. All authors thank Giulia Rossi, Enrico Lavagna, and Davide Bochicchio for many fruitful discussions, for sharing their results and for a critical reading of the manuscript.

References

1. P. C. Hiemenz, R. Rajagopalan and R. Rajagopalan, Principles of Colloid and Surface Chemistry, Revised and Expanded, CRC Press, 2016.
2. R. P. Misra, S. Das and S. K. Mitra, J. Chem. Phys., 2013, 138, 114703.
3. J. S. Sin, J. Chem. Phys., 2017, 147, 214702.
4. R. M. Pashley, P. M. Mcguiggan, B. W. Ninham, J. Brady and D. F. Evans, Direct Measurements of Surface Forces between Bilayers of Double-Chained Quaternary Ammonium Acetate and Bromide Surfactants, 1986, vol. 90.
5. H. J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152.
6. V. Merk, C. Rehbock, F. Becker, U. Hagemann, H. Nienhaus and S. Barcikowski, Langmuir, 2014, 30, 4213–4222.
7. B. J. Thio, J. H. Lee, J. C. Meredith and A. A. Keller, Langmuir, 2010, 26, 13995–14003.
8. D. Grasso, K. Subramaniam, M. Butkus, K. Strevett and J. Bergendahl, Rev. Environ. Sci. Biotechnol., 2002, 1, 17–38.
9. C. Vericat, M. E. Vela, G. Benitez, P. Carro and R. C. Salvarezza, Chem. Soc. Rev., 2010, 39, 1805–1834.
10. P. Pengo, M. Şologan, L. Pasquato, F. Guida, S. Pacor, A. Tossi, F. Stellacci, D. Marson, S. Boccardo, S. Pricl and P. Posocco, Eur. Biophys. J., 2017, 46, 749–771.
11. C. Pezzato, S. Maiti, J. L. Y. Chen, A. Cazzolaro, C. Gobbo and L. J. Prins, Chem. Commun., 2015, 51, 9922–9931.
12. G. Pieters and L. J. Prins, New J. Chem., 2012, 36, 1931–1939.
13. L. H. Dubois and R. G. Nuzzo, Synthesis, structure, and properties of model organic surfaces, 1992, vol. 43.
14. D. P. Woodruff, Phys. Chem. Chem. Phys., 2008, 10, 7211–7221.
15. H. Häkkinen, Nat. Chem., 2012, 4, 443–455.
16. X. Liu, M. Yu, H. Kim, M. Mameli and F. Stellacci, Nat. Commun., 2012, 3, 1–9.
17. X. Xu, N. L. Rosi, Y. Wang, F. Huo and C. A. Mirkin, J. Am. Chem. Soc., 2006, 128, 9286–9287.
18. J. Manson, D. Kumar, B. J. Meenan and D. Dixon, Gold Bull., 2011, 44, 99–105.
19. M.-C. Daniel and D. Astruc,  DOI:10.1021/cr030698.
20. M. Moglianetti, E. Ponomarev, M. Szybowski, F. Stellacci and J. Reguera, J. Phys. D: Appl. Phys., 2015, 48, 434001.
21. H. Jonassen, A. L. Kjøniksen and M. Hiorth, Colloid Polym. Sci., 2012, 290, 919–929.
22. A. Centrone, E. Penzo, M. Sharma, J. W. Myerson, A. M. Jackson, N. Marzari and F. Stellacci, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9886–9891.
23. Q. Ong, Z. Luo and F. Stellacci, Acc. Chem. Res., 2017, 50, 1911–1919.
24. E. Katz and I. Willner, Angew. Chem., Int. Ed., 2004, 43, 6042–6108.
25. Y. Li, M. Girard, M. Shen, J. A. Millan and M. O. de La Cruz, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11838–11843.
26. F. P. Zamborini, J. F. Hicks and R. W. Murray, J. Am. Chem. Soc., 2000, 122, 4514–4515.
27. D. Aili, K. Enander, J. Rydberg, I. Nesterenko, F. Björefors, L. Baltzer and B. Liedberg, J. Am. Chem. Soc., 2008, 130, 5780–5788.
28. T. Bian, A. Gardin, J. Gemen, L. Houben, C. Perego, B. Lee, N. Elad, Z. Chu, G. M. Pavan and R. Klajn, Nat. Chem., 2021, 13, 940–949.
29. T. Laaksonen, P. Ahonen, C. Johans and K. Kontturi, ChemPhysChem, 2006, 7, 2143–2149.
30. M. Olvera De La Cruz, L. Belloni, M. Delsanti, J. P. Dalbiez, O. Spalla and M. Drifford, J. Chem. Phys., 1995, 103, 5781–5791.
31. T. López-León, A. B. Jódar-Reyes, D. Bastos-González and J. L. Ortega-Vinuesa, J. Phys. Chem. B, 2003, 107, 5696–5708.
32. D. Wang, B. Tejerina, I. Lagzi, B. Kowalczyk and B. A. Grzybowski, ACS Nano, 2011, 5, 530–536.
33. F. Fogolari, A. Brigo and H. Molinari, J. Mol. Recognit., 2002, 15, 377–392.
34. E. W. Gomez, N. G. Clack, H. J. Wu and J. T. Groves, Soft Matter, 2009, 5, 1931–1936.
35. P. Hopkins, A. J. Archer and R. Evans, J. Chem. Phys., 2009, 131, 124704.
36. Y. Zheng, C. Lin, J. S. Zhang and Z. J. Tan, Sci. Rep., 2020, 10, 21586.
37. X. Zhang, J. S. Zhang, Y. Z. Shi, X. L. Zhu and Z. J. Tan, Sci. Rep., 2016, 6, 23434.
38. M. E. A. Bassalah, J. J. Cerdà, T. Sintes, A. Aschi and T. Othman, Eur. Polym. J., 2017, 96, 55–68.
39. A. G. Cherstvy, Phys. Chem. Chem. Phys., 2011, 13, 9942–9968.
40. S. A. Alsharif, L. Y. Chen, A. Tlahuice-Flores, R. L. Whetten and M. J. Yacaman, Phys. Chem. Chem. Phys., 2014, 16, 3909–3913.
41. O. D. Villarreal, L. Y. Chen, R. L. Whetten and M. J. Yacaman, Phys. Chem. Chem. Phys., 2015, 17, 3680–3688.
42. O. D. Villarreal, L. Y. Chen, R. L. Whetten and B. Demeler, J. Phys. Chem. B, 2015, 119(50), 15502–15508.
43. R. C. van Lehn and A. Alexander-Katz, Langmuir, 2013, 29, 8788–8798.
44. G. Munaò, A. Correa, A. Pizzirusso and G. Milano, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 38.
45. D. B. Sridhar, R. Gupta and B. Rai, Phys. Chem. Chem. Phys., 2018, 20, 25883–25891.
46. J. S. Zhang, X. Zhang, Z. L. Zhang and Z. J. Tan, Sci. Rep., 2017, 7, 14145.
47. A. Cardellini, M. Alberghini, A. G. Rajan, R. P. Misra, D. Blankschtein and P. Asinari, Nanoscale, 2019, 11, 3925–3932.
48. C. Waltmann, N. Horst and A. Travesset, J. Chem. Phys., 2018, 149, 034109.
49. Q. Ong, T. Mao, N. I. Anaraki, Ł. Richter, C. Malinverni, X. Xu, F. Olgiati, P. H. J. Silva, A. Murello, A. Neels, D. Demurtas, S. Shimizu and F. Stellacci, Mater. Horiz., 2022, 9, 303–311.
50. W. L. Jorgensen, J. D. Madura and C. J. Swenson, J. Am. Chem. Soc., 1984, 106, 6638–6646.
51. S. Salassi, F. Simonelli, D. Bochicchio, R. Ferrando and G. Rossi, J. Phys. Chem. C, 2017, 121, 10927–10935.
52. O. Lopez-Acevedo, J. Akola and R. Whetten, J. Phys. Chem. C, 2009, 113, 5035–5038.
53. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindah, SoftwareX, 2015, 1–2, 19–25.
54. U. Essmann, L. Perera and M. L. Berkowitz, J. Chem. Phys., 1995, 103, 8577–8593.
55. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
56. S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962.
57. G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199.
58. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
59. D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074.
60. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
61. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021.
62. E. Heikkilä, H. Martinez-Seara, A. A. Gurtovenko, I. Vattulainen and J. Akola, Biochim. Biophys. Acta, Biomembr., 2014, 11(1838), 2852–2860.
63. Y. Yang, L. A. Serrano and S. Guldin, Langmuir, 2018, 34(23), 6820–6826.
64. T. Engstrom, J. A. Clinger, K. A. Spoth, O. B. Clarke, D. S. Closs, R. Jayne, B. A. Apker and R. E. Thorne, IUCrJ, 2021, 8, 867–877.
65. A. Sánchez-Iglesias, M. Grzelczak, T. Altantzis, B. Goris, J. Pérez-Juste, S. Bals, G. van Tendeloo, S. H. Donaldson, B. F. Chmelka, J. N. Israelachvili and L. M. Liz-Marzán, ACS Nano, 2012, 6, 11059–11065.
66. H. Nakanishi, A. Deák, G. Hólló and I. Lagzi, Angew. Chem., Int. Ed., 2018, 57, 16062–16066.
67. V. Francia, D. Montizaan and A. Salvati, Beilstein J. Nanotechnol., 2020, 11, 338–353.
68. A. Verma and F. Stellacci, Small, 2010, 6, 12–21.
69. M. R. Dewi, G. Laufersky and T. Nann, RSC Adv., 2014, 4, 34217–34220.
70. S. Ohki, N. Düzgüneş and K. Leonards, Biochemistry, 1982, 21, 2127–2133.
71. S. Wan, R. C. Sinclair and P. v. Coveney, Philos. Trans. R. Soc., A, 2021, 379, 20200082.
72. Cellular electrolyte metabolism – Mammals – BNID 110745, https://bionumbers.hms.harvard.edu/bionumber.aspx?id=110745, (accessed January 15, 2022).
73. E. Lavagna, D. Bochicchio, A. L. de Marco, Z. P. Güven, F. Stellacci and G. Rossi, Nanoscale, 2022, 14, 6912–6921.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr02824g

---