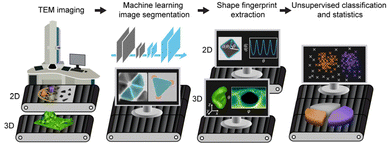
Seeking regularity from irregularity: unveiling the synthesis–nanomorphology relationships of heterogeneous nanomaterials using unsupervised machine learning†
Lehan
Yao
 a,
Hyosung
An
a,
Hyosung
An
 ab,
Shan
Zhou
ab,
Shan
Zhou
 a,
Ahyoung
Kim
a,
Ahyoung
Kim
 a,
Erik
Luijten
a,
Erik
Luijten
 cdef and
Qian
Chen
cdef and
Qian
Chen
 *aghi
*aghi
aDepartment of Materials Science and Engineering, University of Illinois, Urbana, IL 61801, USA. E-mail: qchen20@illinois.edu
bDepartment of Petrochemical Materials Engineering, Chonnam National University, Yeosu, 59631, Korea
cDepartment of Materials Science and Engineering, Northwestern University, Evanston, IL 60208, USA
dDepartment of Engineering Sciences and Applied Mathematics, Northwestern University, Evanston, IL 60208, USA
eDepartment of Chemistry, Northwestern University, Evanston, IL 60208, USA
fDepartment of Physics and Astronomy, Northwestern University, Evanston, IL 60208, USA
gDepartment of Chemistry, University of Illinois, Urbana, IL 61801, USA
hMaterials Research Laboratory, University of Illinois, Urbana, IL 61801, USA
iBeckman Institute for Advanced Science and Technology, University of Illinois, Urbana, IL 61801, USA
First published on 24th October 2022
Abstract
Nanoscale morphology of functional materials determines their chemical and physical properties. However, despite increasing use of transmission electron microscopy (TEM) to directly image nanomorphology, it remains challenging to quantify the information embedded in TEM data sets, and to use nanomorphology to link synthesis and processing conditions to properties. We develop an automated, descriptor-free analysis workflow for TEM data that utilizes convolutional neural networks and unsupervised learning to quantify and classify nanomorphology, and thereby reveal synthesis–nanomorphology relationships in three different systems. While TEM records nanomorphology readily in two-dimensional (2D) images or three-dimensional (3D) tomograms, we advance the analysis of these images by identifying and applying a universal shape fingerprint function to characterize nanomorphology. After dimensionality reduction through principal component analysis, this function then serves as the input for morphology grouping through unsupervised learning. We demonstrate the wide applicability of our workflow to both 2D and 3D TEM data sets, and to both inorganic and organic nanomaterials, including tetrahedral gold nanoparticles mixed with irregularly shaped impurities, hybrid polymer-patched gold nanoprisms, and polyamide membranes with irregular and heterogeneous 3D crumple structures. In each of these systems, unsupervised nanomorphology grouping identifies both the diversity and the similarity of the nanomaterial across different synthesis conditions, revealing how synthetic parameters guide nanomorphology development. Our work opens possibilities for enhancing synthesis of nanomaterials through artificial intelligence and for understanding and controlling complex nanomorphology, both for 2D systems and in the far less explored case of 3D structures, such as those with embedded voids or hidden interfaces.
Introduction
The advent of high-resolution direct imaging techniques such as transmission electron microscopy (TEM) has revealed the ubiquitous presence of complex nanomorphology in systems as diverse as proteins,1,2 polymer thin films,3–6 colloidal nanoparticles (NPs),7–10 and their assemblies.11–14 This morphological complexity can originate from factors like local gradients (e.g., concentration, temperature, stress), mass fluctuation, shape-templating, self-organization, and liquid–liquid phase separation.5,15,16–20 The complex morphologies in turn can determine the chemical and physical properties of materials. For example, morphological details of NPs as fine as corner truncation and surface curvature can dictate their local chemical environment and their optical, electronic, and catalytic properties.21–26 For spatially extended materials, e.g., polymeric thin film separation membranes, the inner voids and interconnected network topology determine the permeation pathways of solvents and separation performance.5,15,16,27–30For these reasons, it is important to synthetically control the nanomorphology of materials, and to do so in a predictable manner; a goal that has been hindered by challenges in characterizing and analyzing them in an automated, standardized, and high-throughput manner. Ensemble methods, including light/X-ray/neutron scattering, can resolve averaged characteristic dimensions of nanomaterials,31–35 but not their nanomorphology and heterogeneities. TEM, on the other hand, can capture nanomorphology either as projected images in two dimensions (2D) or as tilt-series and reconstructed three-dimensional (3D) volumes with nanometer resolution. Several analysis methods have been developed to extract nanomorphology from TEM data sets, including the recent application of machine learning (ML)-based convolutional neural networks (CNNs) to identify and segment NP features.36,37 Unsupervised ML algorithms, e.g., k-means,38 the Gaussian mixture model (GMM),39 and density-based spatial clustering of applications with noise (DBSCAN),40 have also been used to categorize materials according to their morphology. However, these efforts concern 2D TEM images of simple nanomorphologies, which can be described by a small set of shape descriptors chosen by humans (e.g., size and aspect ratio), and of simple samples containing one chemical component, often only inorganic materials. What remains greatly underexplored is the regime of complex nanomorphologies of real-world materials. These can be heterogeneous, containing multiple types of shapes in one sample; they can be irregularly shaped, not sufficiently captured by conventional shape descriptors and making it difficult for humans to objectively choose the appropriate descriptors; they can be hybrid with multiple components, including organic ones that have low contrast under TEM; and they can have 3D features, with multiple features overlaying or agglomerated in 2D projections and requiring a larger parameter space to describe the shape comprehensively. Here we develop and implement a unified ML-based nanomorphology analysis and classification workflow that is robustly applicable to three systems representing real-world materials containing all the above-mentioned complexity aspects. Using this workflow, we are able to elucidate the synthesis–nanomorphology relationship in these systems at a highly quantitative level. As illustrated in Scheme 1, our workflow starts from the segmentation of samples—i.e., recognizing the shape contours of the features—from TEM images using CNNs. Recent work by us and others has used CNNs with a single output channel to recognize NPs in TEM images by solving a pixel-wise binary classification problem.36,37 To account for complex materials systems, in this work we incorporate multiple channels in the output layer of the CNN, with each channel associated with a different physical meaning during training. Such a multi-channeled CNN has been shown to distinguish different atoms in scanning transmission electron microscopy images.41 Here we demonstrate that it accurately separates overlaying NPs and differentiates between inorganic and organic components in a single particle. Next, the workflow utilizes a universal fingerprint function42 to characterize the nanomaterial morphology based on the segmented contours, which applies to arbitrary, irregular, and even 3D shapes not studied before. This fingerprint function provides a comprehensive description of the nanomaterial morphology based on the spatial coordinates of the segmented shape contours. No empirical decisions are needed on which specific shape descriptor is relevant. Lastly, using this fingerprint function as input, followed by dimensional reduction via principal component analysis (PCA), we perform GMM clustering to classify the corresponding nanomorphology instances into groups with similar features to quantitatively elucidate the synthesis–nanomorphology relationships. We apply this workflow to three complex nanomaterials systems, namely (i) gold tetrahedral NPs that are traditionally considered difficult to synthesize and that are typically accompanied by irregularly shaped impurity NPs; (ii) gold nanoprisms decorated with amorphous polymer patches; and (iii) polyamide membranes with 3D void structures used for water purification and molecular separation. Each system represents a morphological complication that previous methods have been unable to solve, and collectively the three systems cover a spectrum of sample features: high-contrast inorganic and low-contrast organic components; 2D and 3D nanomorphologies; separated as well as overlaying features. This approach allows us to relate nanomorphologies to synthesis conditions in a high-throughput and high-fidelity manner.
Results and discussion
Overview of the nanomorphology segmentation–fingerprinting–classification workflow
For segmentation of the TEM images of the NP systems (i) and (ii), we use a U-Net neural network36,37 with symmetric encoder–decoder architecture (Fig. S1†). The output layer is modified to have three channels to predict different species and resolve overlaying NPs. We use image augmentation of a few manually labeled images to readily generate thousands of images that serve as the training data set and greatly improve the efficiency of the image segmentation process (Fig. S2†). Although all the training images derive from a small initial set, we find that with carefully selecting and labeling representative images the trained U-Net delivers consistently good predictions (Fig. S3 and S4†). The trained U-Net is then used to segment experimental TEM images, followed by extraction of the feature contours, which serve as the input for the fingerprint analysis.Our choice of the fingerprint function applies to diverse nanomorphologies and utilizes all the coordinates of the shape contours. Inspired by previous work,42 we describe a shape contour by the length d(θ) of the distance vector with orientation θ connecting a point along the shape contour and the centroid of the contour as a function of θ (Scheme 1). Subsequently, the discrete points along the shape contour are converted to a continuous one-dimensional function with range θ∈(−180°,180°). This definition applies directly to convex shapes but can result in complications for concave shapes (Fig. S5†). We overcome this by redefining d(θ) as the sum of the segment lengths of the distance vector that reside within the shape contours, thus extending this concept to arbitrary 2D contours, including concave ones (Fig. S5†). We show that using this definition, the diverse nanomorphologies present in the three systems studied here are sufficiently described for quantitative comparison and classification. Moreover, we extend this fingerprint for the analysis of 3D nanomorphologies obtained from TEM tomographs, where a 2D function d(θ,φ) in the spherical coordinate system is used to describe a 3D surface contour consisting of variable numbers of meshes5 within a well-defined domain of θ∈(0°,180°) and φ∈(0°,360°).
Classification, the last step in our workflow, relates nanomorphology to synthesis conditions. Previous classification methods used specific shape descriptors such as particle area and aspect ratio as inputs.38–40 Such descriptors only selectively retain partial information embedded in shape contours, and can vary across shapes. For example, edge length is typically used to describe triangular nanoprisms and nanocubes, whereas the major axis length is more suitable for nanorods. In contrast, the contour fingerprint function used here captures most of the shape information, unselectively, for all shapes. Choosing an interval of 1° for θ to achieve sufficiently high spatial resolution, we obtain a fingerprint of a 2D shape that is effectively a feature vector of 360 elements. To make this vector usable in our classification approach, we perform a dimensional reduction through PCA, which projects high-dimensional data onto a low-dimensional space while maximizing their variance, thus retaining the most important (combination of) features in an unsupervised manner. We find that usually the first few principal components (PCs) of the shape fingerprint contain a large fraction of the total variance (Fig. S6–S8†), i.e., faithfully represent the original data. GMM is then applied to the dimension-reduced feature vectors for nanomorphology classification. In our systems, the nanomorphologies are classified into more than two groups. To determine the optimal number of groups, we use the Bayesian information criterion (BIC) and the Akaike information criterion (AIC),43 which quantitatively evaluate the separation of data points into groups while preventing the model from becoming too complicated due to the assignment of too many groups (ESI and Fig. S6–S8†). We now discuss the insights obtained from this workflow for three representative systems.
System (i): high-throughput individualization and shape characterization quantify yield and structural details in gold tetrahedra synthesis
Nanoparticles with attractive interactions, a frequent occurrence in aggregation and self-assembly studies, tend to partially or completely stack on top of each other, resulting in overlaying features in 2D projected TEM images, which can make automated image segmentation challenging. Here, we use the synthesis of gold tetrahedral NPs to demonstrate how our workflow addresses this problem. After segmentation, the NPs are classified into impurities and desirable tetrahedral products of different shapes and sizes, to quantify the relationships between yield, nanomorphology, and seed concentration in the synthesis. We choose gold tetrahedral NPs because their synthesis has been traditionally difficult with extensive, irregularly shaped impurities44,45 that are hard to quantify using conventional shape descriptors. They are also of interest because of their theoretically predicted symmetry-breaking optical properties and their unusual self-assembled structures (e.g., quasi-crystals and Boerdijk–Coxeter helices),46–48 which can depend on the control of fine shape details such as corner truncation22,49 that we quantify below. The facets of these NPs, typically polygonal in shape, favor assembly driven by van der Waals attractions even during TEM sample preparation, leading to overlapping shape contours under TEM imaging.Indeed, as shown in Fig. 1a, gold tetrahedral NPs that are synthesized following a seeded growth method45 pack densely on a TEM grid (Fig. 1b). Conventional threshold-based segmentation recognizes such overlaying projections as a single connected structure. Post-processing algorithms such as watershed transformation can further segment them into individual NPs by drawing lines to cut through the “neck” region between two touching NPs,36,39 but this method is more suitable for rounded shapes than for NPs with polygonal projections (Fig. S9†). Moreover, the watershed algorithm separates NPs without recovering the overlaying parts of the contours, so that for two overlaying NPs neither of the segmented contours reflect the true particle shape (Fig. S9†). For this reason, some recent work opted to simply filter out the overlaying contours,38 which can potentially lead to a bias in yield analysis. For example (Fig. 1c), well-facetted tetrahedral NPs tend to overlay more frequently than irregularly shaped impurities, so that discarding overlaying features would underestimate the yield.
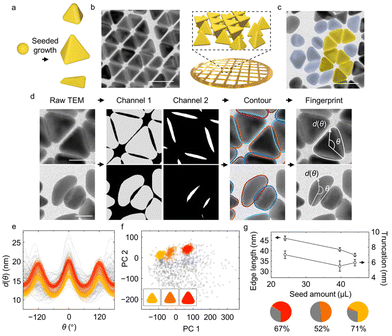 | ||
| Fig. 1 Identification of overlaying gold tetrahedral NPs and yield analysis. (a) Schematic of gold tetrahedral NPs synthesis through the seeded growth method. Different reaction conditions give rise to different product shapes, accompanied by impurities. (b) TEM image and schematic of as-synthesized tetrahedral NPs assembled into overlaying structures after deposition on the TEM grid. (c) TEM image containing tetrahedral NPs (shaded in yellow) and impurities (shaded in blue gray). (d) Workflow of shape fingerprint extraction from raw TEM images. Two output channels from U-Net identify the non-overlaying parts of NPs (gray, Channel 1) and the overlaying of NPs (white, Channel 2) from the input TEM images. Combining closed regions in each channel yields the reconstructed individual NP contours. The shape fingerprints d(θ) of both tetrahedra and impurities are then extracted from the reconstructed contours. (e) Full set of shape fingerprints collected, including tetrahedral NPs (colored) and impurities (gray). Different colors indicate classes identified by the GMM (cf. panel (f)). (f) Full set of shape fingerprints projected onto their first two principal components (PCs). Insets show the average NP shape of the classes identified by the GMM. (g) Average edge length (triangular symbols) and truncation (circular symbols) as a function of seed amount. Circular charts show the fraction of each GMM class at the three different seed amounts (24.0 μL, 39.7 μL, 44.0 μL; see ESI† for more details). Percentages indicates the yield of non-impurity (colored) classes. Scale bars: 50 nm in panels (b) and (c); 25 nm in panel (d). | ||
We address this issue using the trained U-Net with three output channels. In this approach, a pixel in the TEM image is classified to belong to (i) a non-overlaying part of a NP (Channel 1); (ii) an overlaying part of NPs (Channel 2); or (iii) the background (Channel 3) (Fig. 1d). Combining the segmented contour in Channels 1 and 2 makes it then possible to restore the full contours of overlaying tetrahedral NPs and impurities without bias (Fig. 1d, see ESI and Fig. S9 and S10† for details and evaluations). Shape fingerprint functions (Fig. 1e) are calculated from the contours.
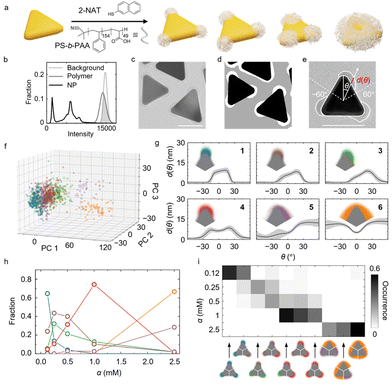
Classification of the shape fingerprints from ∼2700 NPs synthesized at three different conditions separates impurities from tetrahedral NPs and identifies subgroups of tetrahedral NPs with distinctive edge lengths and truncations (Fig. S6e and f†). We use this approach to assess the effect of the amount of spherical gold seed NPs in the synthesis. Most shape fingerprints exhibit three peaks (Fig. 1e), corresponding to the triangular projection of tetrahedral NPs. The remaining fingerprints, which exhibit randomly distributed features, are classified as impurities. PCA-based dimensionality reduction of the shape fingerprints (Fig. 1f) shows that the first two PCs recover 85% of the total variance, indicating successful dimensionality reduction (Fig. S6a†). Lastly, an unsupervised GMM with six centers (suggested by BIC, Fig. S6d†) is used for shape classification. Three major clusters in the PC space are identified, corresponding to three different fingerprints (Fig. 1e, colored curves). Relating each of the three groups to the corresponding averaged NP shape in real space (Fig. 1f inset), we find that they correspond to tetrahedral NPs of different sizes and extents of truncation. Moreover, we find (Fig. S6e and f†) that PC 1 correlates with the particle edge length and PC 2 with the extent of truncation, suggesting that, without a priori judgement or selection, these two shape descriptors identify the principal differences between the products across seed amounts. These observations are consistent with previous studies, where truncation of tetrahedral NPs was shown to be synthetically determined by the competition of gold deposition and oxidative etching, which can be changed by the concentration of added precursor, surfactant, and seed.50,51
In addition to the three major groups of tetrahedral NPs, the GMM also recognizes impurities among the products. The yield of desired tetrahedral NPs displays a non-monotonic trend with the seed amount (Fig. 1g). In addition, the edge length of the tetrahedral NPs (with impurities eliminated) decreases from 46 nm to 38 nm (Fig. 1g) as the seed amount increases given the same growth condition, consistent with earlier hypotheses in the synthesis literature;45,52,53 in the presence of more seeds, the amount of growth species per seed is reduced, resulting in smaller NPs. Lastly, the extent of truncation, defined as the distance between the corner and triangle vertices extended from three edges (cf. ESI and Fig. S11†), also changes with the seed amount (Fig. 1g).
System (ii): multi-component segmentation and patch pattern recognition reveal morphology–formation mechanism in patchy nanoprisms
In the second system, we demonstrate the ability of our analysis workflow to delineate the shape and location of multiple components in a hybrid nanomaterial, which is crucial for engineering their applications as heterojunction for optoelectronics,54 tandem catalysts,55 composite membranes,56 and patchy NPs.57 We use a representative patchy NP—gold nanoprisms coated with polymer patches—as the system of focus. The shape and spatial pattern of the patches controls the anisotropic interaction potential and can determine symmetry-breaking properties important in directed self-assembly, drug delivery, catalysis, and photonic crystals,57–60 calling for automated morphology analysis workflow. The polymeric patch also poses a general analysis challenge due to its low TEM contrast.Using our trained three-channeled U-Net, we can robustly segment the inorganic core and polymer patches without having to adjust the intensity threshold. The subsequent classification of the segmented contours allows us to discern asymmetric versus symmetric polymer patch expansion as a function of the ligand concentration used in the synthesis. The occurrence of different patches is analyzed both for the global ensemble of prisms and in terms of their distribution on the prisms.
The patchy gold prisms are synthesized following our previous method by incubating as-synthesized gold prisms in a solution of thiol ligand (2-naphthalenethiol, 2-NAT) and block copolymer (polystyrene-b-poly(acrylic acid), PS-b-PAA) (Fig. 2a).21 The 2-NAT ligands adsorb onto the highly curved prism tips via thiol–gold bonds to render the tip area hydrophobic, and PS-b-PAA polymers then adsorb onto ligand-coated area via hydrophobic attraction. By controlling the ligand concentration (denoted as the ratio of 2-NAT concentration to the optical density of the prism suspension at its maximum extinction wavelength, α), we control the accessible tip area that polymers can adsorb onto, resulting into various patch patterns on the prism surface.21 As shown in Fig. 2b and c, whereas the gold cores have a distinct contrast against the background, polymer patches and background have a large overlapping range of intensity. Therefore, simply applying a threshold to single out polymer patches results in incorrect segmentation. While pretreatments such as Gaussian filtering can improve the segmentation, such methods sacrifice image spatial resolution and nanoscale morphology details.36 In contrast, our modified U-Net with three output channels predicts both the gold core and polymer patches in a threshold-free manner at pixel-wise accuracy as high as 99. 5% (Fig. 2d and ESI†). Furthermore, the U-Net is also proven to work with varying material contrast (cf. ESI and Fig. S12†). About 1000 contours of segmented polymer patches (∼300 contours for gold cores) are collected from the TEM images of the patchy prisms synthesized at different α conditions.
Choosing the centroid of the gold prisms as the coordinate center, we obtain shape fingerprints of both the polymer patches and gold cores. Given the threefold symmetry of the triangular prism core, we focus on the fingerprints of the patches on each tip with θ∈(−60°,60°). The position θ = 0° in the patch fingerprints is found from the local maximum of d(θ) in the fingerprints of gold cores, which is the orientation of the tip (Fig. 2e). The fingerprints of the cores also serve as reference for determining the patch patterns, i.e., the orientation and position of the patches relative to the core.
Combined with BIC, GMM classifies the patches into six groups based on their shape fingerprints after PCA (Fig. 2f and g and Fig. S7†). The average patch shapes (Fig. 2g, insets) illustrate that important parameters determining the patch shape grouping are the patch coverage and the symmetry of individual patches relative to the prism tip. The patch coverage is defined as the angular range θ of the gold core covered by a polymer patch, which determines, for example, the effective valency of the patchy NPs during assembly.57,61–66 As shown in Fig. 2g and S7g,† patch coverage increases from groups 1 to 6. Regarding the symmetry of patches, the fingerprints of groups 1, 4, and 6 show patch distributions symmetric around θ = 0°, whereas the fingerprints of groups 2, 3 and 5 suggest asymmetric patch growth. This symmetry breaking in patch growth was not captured in our earlier work using specific patch shape descriptors.21
Ligand concentration alters the fractions of the six patch groups. As α increases, the fractions of groups with higher patch coverage increase (Fig. 2h), consistent with the ligand island expansion mechanism proposed in our earlier work. The 2-NAT ligands expand their coverage on the prism tip with increasing α due to strong ligand–ligand attraction, thereby recruiting more polymers to the tip.21 Regarding the patch symmetry along the tip, the groups representing symmetric (groups 1, 4, and 6) and asymmetric (groups 2, 3 and 5) patches dominate alternatingly as α increases. At the lowest ligand concentration, α = 0.12 mM, the dominant patch shape (group 1) is symmetric. As α increases to 0.25 mM and 0.5 mM, the asymmetric groups 2 and 3 become the dominant patch shapes. Comparison of the fingerprints of groups 1, and 2, 3 (Fig. 2g) suggests that the ligands tend to extend along one side of the prism at this ligand concentration. At even higher α (α = 1.0 and 2.5 mM), the symmetric patch shapes (groups 4 and 6) take over. We speculate that starting from a small symmetric patch on the tip, the initial random polymer chain adsorption on one side of the tip promotes more polymer adsorption on the same side to maximize polymer–polymer contacts, which gives rise to asymmetric patch growth. On the other hand, asymmetric patches have a higher surface area exposed to the solvent than the symmetric ones, which yields less favorable polymer–solvent interaction. The two effects compete as α increases, leading to a switch between symmetric and asymmetric patch coverages before the three patches fully merge into a single domain.
Lastly, we examine the occurrence of different patch combinations on prisms. Fig. 2i shows the ten most frequently observed combinations, illustrating a tendency toward higher patch coverage with increasing α. Thus, utilizing our ML-assisted TEM image segmentation and analysis workflow allows us to uncover and quantify the complexity in the morphology of hybrid NPs. These insights into the synthesis mechanism of the hybrid NPs can guide the design of other hybrid nanomaterials, such as core–shell NPs, Janus particles, and heterostructures in optoelectronic devices.54,67,68
System (iii): 3D tomograph quantification and classification guide synthetic control of irregular crumple structures on polyamide membranes
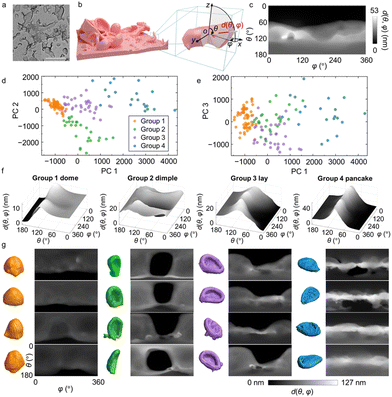
In the third system, we extend the use of our workflow to characterize and understand 3D nanomorphology. While 3D structures of proteins and crystals are well studied by imaging techniques such as cryo-electron microscopy69,70 and synchrotron X-ray tomography,71 characterization of synthetic nanomaterials of irregular 3D shapes remains limited. We focus on polyamide membranes exhibiting heterogeneously distributed crumples, involving inner voids and concave surfaces (Fig. 3a). The crumples can be seen as individual and non-interconnecting folds of membranes of 10–20 nm thickness.5 Polyamide membranes are the active layer of thin-film composites for water purification and molecular separation, whose morphologies closely relate to membrane separation metrics.5TEM-based electron tomography is used to image polyamide membranes in 3D at sub-nm voxel resolution. Experimentally, tilt series of 2D projections of the membranes are collected under TEM and reconstructed into 3D volumes (Fig. 3b). We isolate the crumples in each membrane to serve as input of our analysis and classification workflow. For the fingerprint function, we consider the polar angle θ and azimuthal angle φ in the spherical coordinate system to determine a distance vector in 3D (Fig. 3b). To capture the structural features of the membrane, we measure the distance d(θ,φ) as the segment length of the distance vector of orientation (θ,φ) that resides within the membrane volume, excluding void spaces (Fig. 3b, red line). Higher values of d(θ,φ) suggest that more membrane mass is distributed along the vector direction. This conversion “collapses” the 3D crumples into 2D shape fingerprints maps. For example, the shape fingerprint (Fig. 3c) of the crumpled membrane in Fig. 3b describes a morphology with most of its mass distributed below its centroid, suggesting a bowl-like crumple with concavity facing upwards.
Using PCA of the fingerprints, we choose the first three PCs with a cumulative variance of 73% (Fig. S8†) and utilize GMM to classify the crumples into four groups: “dome”, “dimple”, “lay”, and “pancake”, each named after their apparent shapes (Fig. 3d and e). Previous studies have shown that the crumples exhibit different effective moduli depending on the morphology groups they belong to.72 Despite the variety of crumples observed in the membrane (Fig. 3a), they consistently fall into these four groups; crumples within each group show high quantitative similarity in their fingerprints (Fig. 3f and g; Fig. S13†) and 3D tomographs (Fig. 3g), confirming the robustness of this classification for recognizing similar shapes in a diverse collection of nanomorphologies. Specifically, group 1 has high d(θ,φ) regions spanning the top part of the fingerprint maps and vanishing d(θ,φ) regions at the bottom, which corresponds to dome-shaped crumples with an opening at the bottom. Group 2 has low d(θ,φ) regions as a basin in the center of the map (θ ≈ 90° and φ ≈ 180°), indicating the existence of a concave surface on the vertical side of the crumples, which we refer to as standing dimples. Group 3 shows a similarly concave surface as well. But unlike group 2, the center position of the concave region in group 3 is off the horizontal center of the crumple, resulting in a V-shaped region of vanishing d(θ,φ) values in the map. The corresponding 3D crumple shape resembles a sofa, which we denote as “lay”. Group 4 shows high d(θ,φ) regions clustered in a belt at θ = 90°, while the d(θ,φ) values near the vertical Poles (θ = 0°, 180°) are low. This type of fingerprint corresponds to a “pancake” with most of its mass positioned at the middle plane, θ = 90°.
The four groups of crumples identified by the GMM show distinct curvature-related features. Considering different combinations of local Gaussian curvature G and mean curvature H, we can distinguish the mesh vertices on the crumple surface as four surface curvature structures: tip (G > 0,H > 0), tube (G ≈ 0,H > 0), saddle (G < 0,H ≈ 0), and valley (G > 0,H < 0) (cf. ESI and Fig. S8a†).5,73 As illustrated in Fig. 4a, for group 4 (“pancake”), the long perimeter results in the highest fraction belonging to “tube”, unlike for other groups. Due to the mostly convex shape of domes, the tip dominates in this group while dimple and lay have more balanced fractions between tip and tube. Dimples and lays are very similar in terms of all G and H curvatures, and as a result we regarded them as the same group in our previous report.5 Nevertheless, our 3D shape fingerprint method successfully differentiates dimples and lays in terms of the orientation of the concavity of their surface relative to the substrate, an aspect not recognized by the conventional average curvature descriptors.
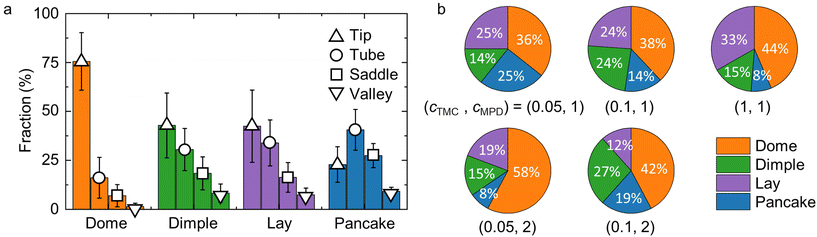 | ||
| Fig. 4 Morphological features of polyamide membrane crumple groups and their fractions under different reaction conditions. (a) Fractions of different surface elements in each crumple group. The surface elements are defined in the Supporting information and Fig. S8a.† (b) Fractions of each crumple group in membranes synthesized at different monomer concentrations. Colors denote the crumple group and match those used in panel (a). The units of MPD and TMC concentrations are in w/v%. | ||
Finally, we examine the fractions of crumple groups under synthesis at different concentrations of two monomers, m-phenylenediamine (MPD) and trimesoyl chloride (TMC). Fig. 4b illustrates that the four crumple groups are observed under all five reaction conditions, suggesting that the morphologies identified by GMM are common across synthesis conditions. However, the fractions of each crumple group vary for different reaction conditions. At a fixed MPD concentration of 1 w/v%, increasing the TMC concentration yields more domes and fewer pancakes. Given that the average size of dome crumples is smaller than that of pancakes, we infer that a high TMC concentration generally leads to smaller crumples. This classification of the crumples of a polyamide membrane demonstrates the applicability of our workflow to the characterization of 3D, irregular, and heterogeneous nanomaterials.
Conclusions
We have developed a high-throughput analysis workflow to connect synthesis conditions and nanomorphologies by integrating automated TEM image segmentation enabled by CNN and a descriptor-free, quantitative morphological fingerprint-based unsupervised classification. This characterization method applies to a variety of materials, including metal NPs, soft nanomaterials with irregular shapes and heterogeneity in 3D, and hybrid nanomaterials. Other than NP shape characterization, the ability to separate overlaying NPs also has potential applications in analyzing complicated self-assembled NP structures from single TEM projections, for example double layered Moiré patterns with overlaying projections, and even 3D self-assemblies containing multiple layers.74,75 Our approach can potentially guide the synthesis of nanomaterials with targeted morphology and also the processing and understanding of naturally occurring materials with unknown and heterogeneous nanomorphologies, such as geocolloids76 and nanoplastics.77–79 Going beyond TEM data, we anticipate that our image-based analysis workflow can also be applicable to other real-space morphology characterization techniques such as scanning electron microscopy, atomic force microscopy, and synchrotron X-ray tomography describing 2D or 3D morphologies.Data availability
Python codes of training data augmentation, manually labeled images, and the augmented training datasets of tetrahedral NPs and patchy nanoprisms are available at: https://github.com/chenlabUIUC/trainingDataAugmentation.MATLAB code examples of shape fingerprint extraction for tetrahedral NPs, patchy nanoprisms, and polyamide membrane crumples are available at: https://github.com/chenlabUIUC/ShapeFingerprintExtraction.
Author contributions
Lehan Yao and Qian Chen: conceptualized the project. Hyosung An, Ahyoung Kim, and Shan Zhou performed the sample synthesis and TEM imaging. Lehan Yao, Erik Luijten, and Qian Chen performed the machine learning and the analysis of experimental data. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering, under Award Numbers DE-SC0020723 and DE-SC0020885. Experiments were carried out in part at the Materials Research Laboratory (MRL) Central Research Facilities, University of Illinois.References
- X. Jiang, A. J. Halmes, G. Licari, J. W. Smith, Y. Song, E. G. Moore, Q. Chen, E. Tajkhorshid, C. M. Rienstra and J. S. Moore, Multivalent polymer–peptide conjugates—a general platform for inhibiting amyloid beta peptide aggregation, ACS Macro Lett., 2019, 8, 1365–1371 CrossRef CAS.
- J. W. Smith, X. Jiang, H. An, A. M. Barclay, G. Licari, E. Tajkhorshid, E. G. Moore, C. M. Rienstra, J. S. Moore and Q. Chen, Polymer–peptide conjugates convert amyloid into protein Nanobundles through Fragmentation and Lateral Association, ACS Appl. Nano Mater., 2020, 3, 937–945 CrossRef CAS PubMed.
- F. Pacheco, R. Sougrat, M. Reinhard, J. O. Leckie and I. Pinnau, 3D visualization of the internal nanostructure of polyamide thin films in RO membranes, J. Membr. Sci., 2016, 501, 33–44 CrossRef CAS.
- T. E. Culp, Y. Shen, M. Geitner, M. Paul, A. Roy, M. J. Behr, S. Rosenberg, J. Gu, M. Kumar and E. D. Gomez, Electron tomography reveals details of the internal microstructure of desalination membranes, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8694–8699 CrossRef CAS PubMed.
- X. Song, J. W. Smith, J. Kim, N. J. Zaluzec, W. Chen, H. An, J. M. Dennison, D. G. Cahill, M. A. Kulzick and Q. Chen, Unraveling the morphology–function relationships of polyamide membranes using quantitative electron tomography, ACS Appl. Mater. Interfaces, 2019, 11, 8517–8526 CrossRef CAS PubMed.
- H. An, J. W. Smith, W. Chen, Z. Ou and Q. Chen, Charting the quantitative relationship between two-dimensional morphology parameters of polyamide membranes and synthesis conditions, Mol. Syst. Des. Eng., 2020, 5, 102–109 RSC.
- Z. L. Wang, Transmission electron microscopy of shape-controlled nanocrystals and their assemblies, J. Phys. Chem. B, 2000, 104, 1153–1175 CrossRef CAS.
- C. Lofton and W. Sigmund, Mechanisms controlling crystal habits of gold and silver colloids, Adv. Funct. Mater., 2005, 15, 1197–1208 CrossRef CAS.
- M. N. O'Brien, M. R. Jones, K. A. Brown and C. A. Mirkin, Universal noble metal nanoparticle seeds realized through iterative reductive growth and oxidative dissolution reactions, J. Am. Chem. Soc., 2014, 136, 7603–7606 CrossRef.
- Y. Yin and A. P. Alivisatos, Colloidal nanocrystal synthesis and the organic–inorganic interface, Nature, 2005, 437, 664–670 CrossRef CAS PubMed.
- J. Park, H. Zheng, W. C. Lee, P. L. Geissler, E. Rabani and A. P. Alivisatos, Direct observation of nanoparticle superlattice formation by using liquid cell transmission electron microscopy, ACS Nano, 2012, 6, 2078–2085 CrossRef CAS PubMed.
- J. Kim, Z. Ou, M. R. Jones, X. Song and Q. Chen, Imaging the polymerization of multivalent nanoparticles in solution, Nat. Commun., 2017, 8, 761 CrossRef PubMed.
- Z. Ou, Z. Wang, B. Luo, E. Luijten and Q. Chen, Kinetic pathways of crystallization at the nanoscale, Nat. Mater., 2020, 19, 450–455 CrossRef CAS.
- C. Liu, Z. Ou, F. Guo, B. Luo, W. Chen, L. Qi and Q. Chen, “Colloid–atom duality” in the assembly dynamics of concave gold nanoarrows, J. Am. Chem. Soc., 2020, 142, 11669–11673 CrossRef CAS PubMed.
- S. Karan, Z. Jiang and A. G. Livingston, Sub–10 nm polyamide nanofilms with ultrafast solvent transport for molecular separation, Science, 2015, 348, 1347–1351 CrossRef CAS PubMed.
- H. Yan, X. Miao, J. Xu, G. Pan, Y. Zhang, Y. Shi, M. Guo and Y. Liu, The porous structure of the fully-aromatic polyamide film in reverse osmosis membranes, J. Membr. Sci., 2015, 475, 504–510 CrossRef CAS.
- H. Wang, H. Y. Jeong, M. Imura, L. Wang, L. Radhakrishnan, N. Fujita, T. Castle, O. Terasaki and Y. Yamauchi, Shape- and size-controlled synthesis in hard templates: sophisticated chemical reduction for mesoporous monocrystalline platinum nanoparticles, J. Am. Chem. Soc., 2011, 133, 14526–14529 CrossRef CAS PubMed.
- Z. Ou, A. Kim, W. Huang, P. V. Braun, X. Li and Q. Chen, Reconfigurable nanoscale soft materials, Curr. Opin. Solid State Mater. Sci., 2019, 23, 41–49 CrossRef CAS.
- J. J. Teo, Y. Chang and H. C. Zeng, Fabrications of hollow nanocubes of Cu2O and Cu via reductive self-assembly of CuO nanocrystals, Langmuir, 2006, 22, 7369–7377 CrossRef CAS PubMed.
- K. W. Gotrik, A. F. Hannon, J. G. Son, B. Keller, A. Alexander-Katz and C. A. Ross, Morphology control in block copolymer films using mixed solvent vapors, ACS Nano, 2012, 6, 8052–8059 CrossRef CAS.
- A. Kim, S. Zhou, L. Yao, S. Ni, B. Luo, C. E. Sing and Q. Chen, Tip-patched nanoprisms from formation of ligand islands, J. Am. Chem. Soc., 2019, 141, 11796–11800 CrossRef CAS PubMed.
- P. Zheng, D. Paria, H. Wang, M. Li and I. Barman, Optical properties of symmetry-breaking tetrahedral nanoparticles, Nanoscale, 2020, 12, 832–842 RSC.
- A. L. Koh, K. Bao, I. Khan, W. E. Smith, G. Kothleitner, P. Nordlander, S. A. Maier and D. W. McComb, Electron energy-loss spectroscopy (EELS) of surface plasmons in single silver nanoparticles and dimers: influence of beam damage and mapping of dark modes, ACS Nano, 2009, 3, 3015–3022 CrossRef CAS PubMed.
- R. Narayanan and M. A. El-Sayed, Catalysis with transition metal nanoparticles in colloidal solution: nanoparticle shape dependence and stability, J. Phys. Chem. B, 2005, 109, 12663–12676 CrossRef CAS PubMed.
- H. Lee, Utilization of shape-controlled nanoparticles as catalysts with enhanced activity and selectivity, RSC Adv., 2014, 4, 41017–41027 RSC.
- S. Kim, J. Kwag, C. Machello, S. Kang, J. Heo, C. F. Reboul, D. Kang, S. Kang, S. Shim, S.-J. Park, B. H. Kim, T. Hyeon, P. Ercius, H. Elmlund and J. Park, Correlating 3D surface atomic structure and catalytic activities of Pt nanocrystals, Nano Lett., 2021, 21, 1175–1183 CrossRef CAS PubMed.
- J. G. Wijmans and R. W. Baker, The solution-diffusion model: a review, J. Membr. Sci., 1995, 107, 1–21 CrossRef CAS.
- G. M. Geise, H. B. Park, A. C. Sagle, B. D. Freeman and J. E. McGrath, Water permeability and water/salt selectivity tradeoff in polymers for desalination, J. Membr. Sci., 2011, 369, 130–138 CrossRef CAS.
- J. Xu, H. Yan, Y. Zhang, G. Pan and Y. Liu, The morphology of fully-aromatic polyamide separation layer and its relationship with separation performance of TFC membranes, J. Membr. Sci., 2017, 541, 174–188 CrossRef CAS.
- M. Hirose, H. Ito and Y. Kamiyama, Effect of skin layer surface structures on the flux behaviour of RO membranes, J. Membr. Sci., 1996, 121, 209–215 CrossRef CAS.
- P. S. Singh, S. V. Joshi, J. J. Trivedi, C. V. Devmurari, A. P. Rao and P. K. Ghosh, Probing the structural variations of thin film composite RO membranes obtained by coating polyamide over polysulfone membranes of different pore dimensions, J. Membr. Sci., 2006, 278, 19–25 CrossRef CAS.
- Y. Zhang, S. Pal, B. Srinivasan, T. Vo, S. Kumar and O. Gang, Selective transformations between nanoparticle superlattices via the reprogramming of DNA-mediated interactions, Nat. Mater., 2015, 14, 840–847 CrossRef CAS PubMed.
- Y. Kim, R. J. Macfarlane, M. R. Jones and C. A. Mirkin, Transmutable nanoparticles with reconfigurable surface ligands, Science, 2016, 351, 579–582 CrossRef CAS PubMed.
- T. Li, A. J. Senesi and B. Lee, Small angle X-ray scattering for nanoparticle research, Chem. Rev., 2016, 116, 11128–11180 CrossRef CAS PubMed.
- W. Wu, W. E. Wallace, E. K. Lin, G. W. Lynn, C. J. Glinka, E. T. Ryan and H.-M. Ho, Properties of nanoporous silica thin films determined by high-resolution X-ray reflectivity and small-angle neutron scattering, J. Appl. Phys., 2000, 87, 1193–1200 CrossRef CAS.
- L. Yao, Z. Ou, B. Luo, C. Xu and Q. Chen, Machine learning to reveal nanoparticle dynamics from liquid-phase TEM videos, ACS Cent. Sci., 2020, 6, 1421–1430 CrossRef CAS PubMed.
- L. Mill, D. Wolff, N. Gerrits, P. Philipp, L. Kling, F. Vollnhals, A. Ignatenko, C. Jaremenko, Y. Huang, O. D. Castro, J.-N. Audinot, I. Nelissen, T. Wirtz, A. Maier and S. Christiansen, Synthetic image rendering solves annotation problem in deep learning nanoparticle segmentation, Small Methods, 2021, 5, 2100223 CrossRef CAS PubMed.
- X. Wang, J. Li, H. D. Ha, J. C. Dahl, J. C. Ondry, I. Moreno-Hernandez, T. Head-Gordon and A. P. Alivisatos, AutoDetect-mNP: an unsupervised machine learning algorithm for automated analysis of transmission electron microscope images of metal nanoparticles, JACS Au, 2021, 1, 316–327 CrossRef CAS PubMed.
- B. Lee, S. Yoon, J. W. Lee, Y. Kim, J. Chang, J. Yun, J. C. Ro, J.-S. Lee and J. H. Lee, Statistical characterization of the morphologies of nanoparticles through machine learning based electron microscopy image analysis, ACS Nano, 2020, 14, 17125–17133 CrossRef CAS PubMed.
- T. J. A. Slater, Y.-C. Wang, G. M. Leteba, J. Quiroz, P. H. C. Camargo, S. J. Haigh and C. S. Allen, Automated single-particle reconstruction of heterogeneous inorganic nanoparticles, Microsc. Microanal., 2020, 26, 1168–1175 CrossRef CAS PubMed.
- M. Ziatdinov, O. Dyck, X. Li, B. G. Sumpter, S. Jesse, R. K. Vasudevan and S. V. Kalinin, Building and exploring libraries of atomic defects in graphene: scanning transmission electron and scanning tunneling microscopy study, Sci. Adv., 2019, 5, eaaw8989 CrossRef CAS.
- C. R. Laramy, K. A. Brown, M. N. O'Brien and C. A. Mirkin, High-throughput, algorithmic determination of nanoparticle structure from electron microscopy images, ACS Nano, 2015, 9, 12488–12495 CrossRef CAS PubMed.
- G. Schwarz, Estimating the dimension of a model, Ann. Stat., 1978, 6, 461–464 Search PubMed.
- F. Kim, S. Connor, H. Song, T. Kuykendall and P. Yang, Platonic gold nanocrystals, Angew. Chem., Int. Ed., 2004, 43, 3673–3677 CrossRef CAS PubMed.
- Y. Zheng, W. Liu, T. Lv, M. Luo, H. Hu, P. Lu, S.-I. Choi, C. Zhang, J. Tao, Y. Zhu, Z.-Y. Li and Y. Xia, Seed-mediated synthesis of gold tetrahedra in high purity and with tunable, well-controlled sizes, Chem. – Asian J., 2014, 9, 2635–2640 CrossRef CAS PubMed.
- Y. Nagaoka, H. Zhu, D. Eggert and O. Chen, Single-component quasicrystalline nanocrystal superlattices through flexible polygon tiling rule, Science, 2018, 362, 1396–1400 CrossRef CAS PubMed.
- Y. Nagaoka, R. Tan, R. Li, H. Zhu, D. Eggert, Y. A. Wu, Y. Liu, Z. Wang and O. Chen, Superstructures generated from truncated tetrahedral quantum dots, Nature, 2018, 561, 378–382 CrossRef CAS PubMed.
- Y. Zhu, J. He, C. Shang, X. Miao, J. Huang, Z. Liu, H. Chen and Y. Han, Chiral gold nanowires with Boerdijk–Coxeter–Bernal structure, J. Am. Chem. Soc., 2014, 136, 12746–12752 CrossRef CAS PubMed.
- P. F. Damasceno, M. Engel and S. C. Glotzer, Crystalline assemblies and densest packings of a family of truncated tetrahedra and the role of directional entropic forces, ACS Nano, 2012, 6, 609–614 CrossRef CAS PubMed.
- R. Long, S. Zhou, B. J. Wiley and Y. Xiong, Oxidative etching for controlled synthesis of metal nanocrystals: atomic addition and subtraction, Chem. Soc. Rev., 2014, 43, 6288–6310 RSC.
- Y. Zheng, J. Zeng, A. Ruditskiy, M. Liu and Y. Xia, Oxidative etching and its role in manipulating the nucleation and growth of noble-metal nanocrystals, Chem. Mater., 2014, 26, 22–33 CrossRef CAS.
- Y. Zheng, Y. Ma, J. Zeng, X. Zhong, M. Jin, Z.-Y. Li and Y. Xia, Seed-mediated synthesis of single-crystal gold nanospheres with controlled diameters in the range 5–30 nm and their self-assembly upon dilution, Chem. – Asian J., 2013, 8, 792–799 CrossRef CAS PubMed.
- S. Jeong, Y. Liu, Y. Zhong, X. Zhan, Y. Li, Y. Wang, P. M. Cha, J. Chen and X. Ye, Heterometallic seed-mediated growth of monodisperse colloidal copper nanorods with widely tunable plasmonic resonances, Nano Lett., 2020, 20, 7263–7271 CrossRef CAS PubMed.
- S. Akers, E. Kautz, A. Trevino-Gavito, M. Olszta, B. E. Matthews, L. Wang, Y. Du and S. R. Spurgeon, Rapid and flexible segmentation of electron microscopy data using few-shot machine learning, npj Comput. Mater., 2021, 7, 1–9 CrossRef.
- H. J. Cho, D. Kim, J. Li, D. Su and B. Xu, Zeolite-encapsulated Pt nanoparticles for tandem catalysis, J. Am. Chem. Soc., 2018, 140, 13514–13520 CrossRef CAS PubMed.
- H. Zhang, X. Li, C. Zhao, T. Fu, Y. Shi and H. Na, Composite membranes based on highly sulfonated PEEK and PBI: Morphology characteristics and performance, J. Membr. Sci., 2008, 308, 66–74 CrossRef CAS.
- Z. Zhang and S. C. Glotzer, Self-assembly of patchy particles, Nano Lett., 2004, 4, 1407–1413 CrossRef CAS PubMed.
- I. Coluzza, P. D. J. van Oostrum, B. Capone, E. Reimhult and C. Dellago, Sequence controlled self-knotting colloidal patchy polymers, Phys. Rev. Lett., 2013, 110, 075501 CrossRef PubMed.
- D. Rodríguez-Fernández and L. M. Liz-Marzán, Metallic Janus and patchy particles, Part. Part. Syst. Charact., 2013, 30, 46–60 CrossRef.
- C. M. Liddell, C. J. Summers and A. M. Gokhale, Stereological estimation of the morphology distribution of ZnS clusters for photonic crystal applications, Mater. Charact., 2003, 50, 69–79 CrossRef CAS.
- M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, Directed self-assembly of nanoparticles, ACS Nano, 2010, 4, 3591–3605 CrossRef CAS PubMed.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Colloids with valence and specific directional bonding, Nature, 2012, 491, 51–55 CrossRef CAS PubMed.
- E. Słyk, W. Rżysko and P. Bryk, Two-dimensional binary mixtures of patchy particles and spherical colloids, Soft Matter, 2016, 12, 9538–9548 RSC.
- E. Bianchi, B. Capone, I. Coluzza, L. Rovigatti and P. D. J. van Oostrum, Limiting the valence: advancements and new perspectives on patchy colloids, soft functionalized nanoparticles and biomolecules, Phys. Chem. Chem. Phys., 2017, 19, 19847–19868 RSC.
- A. Travesset, Soft skyrmions, spontaneous valence and selection rules in nanoparticle superlattices, ACS Nano, 2017, 11, 5375–5382 CrossRef CAS PubMed.
- S. Sun, S. Yang, H. L. Xin, D. Nykypanchuk, M. Liu, H. Zhang and O. Gang, Valence-programmable nanoparticle architectures, Nat. Commun., 2020, 11, 2279 CrossRef CAS PubMed.
- C. Bae, J. Lee, L. Yao, S. Park, Y. Lee, J. Lee, Q. Chen and J. Kim, Mechanistic insight into gold nanorod transformation in nanoscale confinement of ZIF-8, Nano Res., 2021, 14, 66–73 CrossRef CAS.
- H. Hu, F. Ji, Y. Xu, J. Yu, Q. Liu, L. Chen, Q. Chen, P. Wen, Y. Lifshitz, Y. Wang, Q. Zhang and S.-T. Lee, Reversible and precise self-assembly of Janus metal-organosilica nanoparticles through a linker-free approach, ACS Nano, 2016, 10, 7323–7330 CrossRef CAS PubMed.
- M. Adrian, J. Dubochet, J. Lepault and A. W. McDowall, Cryo-electron microscopy of viruses, Nature, 1984, 308, 32–36 CrossRef CAS PubMed.
- R. Henderson, J. M. Baldwin, T. A. Ceska, F. Zemlin, E. Beckmann and K. H. Downing, Model for the structure of bacteriorhodopsin based on high-resolution electron cryo-microscopy, J. Mol. Biol., 1990, 213, 899–929 CrossRef CAS PubMed.
- U. Bonse and F. Busch, X-ray computed microtomography (μCT) using synchrotron radiation (SR), Prog. Biophys. Mol. Biol., 1996, 65, 133–169 CrossRef CAS.
- H. An, J. W. Smith, B. Ji, S. Cotty, S. Zhou, L. Yao, F. C. Kalutantirige, W. Chen, Z. Ou, X. Su, J. Feng and Q. Chen, Mechanism and performance relevance of nanomorphogenesis in polyamide films revealed by quantitative 3D imaging and machine learning, Sci. Adv., 2022, 8, abk1888 CrossRef PubMed.
- H. Elliott, R. S. Fischer, K. A. Myers, R. A. Desai, L. Gao, C. S. Chen, R. S. Adelstein, C. M. Waterman and G. Danuser, Myosin II controls cellular branching morphogenesis and migration in three dimensions by minimizing cell-surface curvature, Nat. Cell Biol., 2015, 17, 137–147 CrossRef CAS.
- A. Singh, C. Dickinson and K. M. Ryan, Insight into the 3D architecture and quasicrystal symmetry of multilayer nanorod assemblies from Moiré interference patterns, ACS Nano, 2012, 6, 3339–3345 CrossRef CAS PubMed.
- E. Cepeda-Perez, D. Doblas, T. Kraus and N. de Jonge, Electron microscopy of nanoparticle superlattice formation at a solid-liquid interface in nonpolar liquids, Sci. Adv., 2020, 6, eaba1404 CrossRef CAS PubMed.
- A. Wolthoorn, E. J. M. Temminghoff and W. H. van Riemsdijk, Colloid formation in groundwater by subsurface aeration: characterisation of the geo-colloids and their counterparts, Appl. Geochem., 2004, 19, 1391–1402 CrossRef CAS.
- R. Lehner, C. Weder, A. Petri-Fink and B. Rothen-Rutishauser, Emergence of nanoplastic in the environment and possible impact on human health, Environ. Sci. Technol., 2019, 53, 1748–1765 CrossRef CAS PubMed.
- D. M. Mitrano, P. Wick and B. Nowack, Placing nanoplastics in the context of global plastic pollution, Nat. Nanotechnol., 2021, 16, 491–500 CrossRef CAS PubMed.
- L. M. Hernandez, E. G. Xu, H. C. E. Larsson, R. Tahara, V. B. Maisuria and N. Tufenkji, Plastic teabags release billions of microparticles and nanoparticles into tea, Environ. Sci. Technol., 2019, 53, 12300–12310 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of synthesis, sample preparation, and electron tomography imaging methods; full workflow of the machine-learning-based image segmentation, fingerprint extraction, and unsupervised classification with figures; additional figure of neural network architecture. (PDF). See DOI: https://doi.org/10.1039/d2nr03712b |
| This journal is © The Royal Society of Chemistry 2022 |