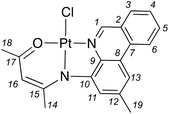
Platinum(II) complexes of benzannulated N∧N−∧O-amido ligands: bright orange phosphors with long-lived excited states†
Issiah B.
Lozada
 a,
J. A. Gareth
Williams
a,
J. A. Gareth
Williams
 *b and
David E.
Herbert
*b and
David E.
Herbert
 *a
*a
aDepartment of Chemistry and the Manitoba Institute for Materials, University of Manitoba, 144 Dysart Road, Winnipeg, Manitoba R3T 2N2, Canada. E-mail: david.herbert@umanitoba.ca
bDepartment of Chemistry, Durham University, Durham, DH1 3LE, UK. E-mail: j.a.g.williams@durham.ac.uk
First published on 27th October 2021
Abstract
The synthesis, structural characterization and photophysical properties of a series of platinum(II) complexes of benzannulated pincer-type diarylamido ligands are described. The ligands all contain tricyclic phenanthridine (3,4-benzoquinoline) rings as donor arms, which were elaborated into N∧N−∧O-coordinating β-enaminoketonato chelates via partial condensation with acetylacetone. The proligands are easily deprotonated, and metallation can be achieved under mild conditions using simple Pt(II) salts and Ag2O as a base. The resulting Pt(II) complexes exhibit strong metal-to-ligand charge-transfer absorptions in the region of ∼450–575 nm and are phosphorescent in solution at room temperature, emitting bright orange light (λmax ∼ 600 nm) with quantum yields of up to 16% and excited-state lifetimes on the order of ∼20 μs, representing significant improvements to these photophysical properties compared with many previously reported N∧N∧O or N∧N∧N-ligated systems. Computational modelling reveals that the lowest-lying triplet state is populated efficiently thanks to strong coupling between singlet and triplet excited state manifolds, as in cyclometallated compounds of Pt(II). Substituents (CH3, tBu, or CF3) in the 2-position of the phenanthridinyl unit are found to have little influence on the optical properties, but the emission is severely quenched when a methyl substituent is introduced ortho to the coordinating nitrogen. Molecular distortions in the excited state are shown to be primarily responsible for the quenching in this complex.
Introduction
Emissive platinum(II) complexes have long been the subject of intensive investigation, thanks to the myriad potential applications of their phosphorescence including in light-emitting diodes,1–4 imaging,5–7 and sensing.5,8,9 This ubiquity is owed both to the high spin–orbit coupling (SOC) constant of the 5d transition metal, which leads to efficient population of the lowest-lying triplet excited state (T1) through intersystem crossing and its subsequent radiative decay, and to a mature coordination chemistry in which ligand design can be used to control emission colour and intensity.10,11 Amongst the brightest Pt(II) emitters, multidentate cyclometallating ligands are common,12 mostly derived from C–H activation of phenylpyridine derivatives and related molecules. With respect to tridentate analogs, C∧N∧N,13–15 N∧C∧N16,17 and C∧N∧C18 architectures predominate. In these ligands, the synergy of strong σ-donation from Pt–C bonds and the π-accepting character of the heterocycle leads to the stabilization of charge-transfer (CT) excited states relative to metal-centered (MC) ones. The chelating ligand arrangement also increases molecular rigidity, which helps to suppress excited-state distortions that promote non-radiative decay processes detrimental to emission.19Installation of aryl ligands via intramolecular cyclometalation of aryl C–H bonds by Pt(II), however, can require harsh reaction conditions.20 In comparison, deprotonation of N–H or O–H units and binding to Pt(II) is typically much more facile. Pt(II) complexes of monoanionic, all-heteroatom coordinating tridentate ligands have accordingly been reported, including N∧N∧N scaffolds derived from deprotonated isoindolates21 or diarylamido units,22,23 and N∧N∧O architectures based on 6-(ortho-phenoxy)bipyridines24,25 and related Schiff-base pyridine-imine and pyridine-hydrazone phenolates.26 The photophysical properties of these exemplars, however, often pale compared to those of their cyclometallated cousins, with smaller phosphorescence quantum yields and shorter phosphorescence lifetimes.
We have been interested in incorporating benzannulated N-heterocycles into multidentate scaffolds in order to delineate design principles for tuning photophysical properties of transition metal complexes.27,28 Our work to date has focused on phenanthridines (3,4-benzoquinolines). 2,4-Functionalized phenanthridines amenable for elaboration into multidentate scaffolds can be readily prepared via one-pot Pd-catalyzed cross-coupling/condensation reactions of 2-formylphenylboronic acids and a substituted aniline.29 Here, we targeted (N∧N∧O)Pt(II) complexes of simple β-enaminoketonato architectures30 bearing phenanthridinyl donor arms. Using ligands that are simple to prepare, complexation to Pt(II) can be achieved under similarly mild conditions. The complexes display quite bright orange emission at room temperature, with significantly improved quantum yields compared to those of related N∧N∧O-ligated systems24–26 and longer lifetimes compared to leading N∧N∧N-stabilized congeners.21 Structure–property correlations indicate that substituents in the phenanthridinyl ligand impact molecular rigidity rather than ligand electronics, confirmed by density functional theory (DFT) modelling of the lowest lying triplet excited states.
Results and discussion
Proligands L1–L4 were prepared via acid-catalyzed condensation of the appropriately functionalized (4-amino)phenanthridine (P1–P4) with acetylacetone (Scheme 1a) as previously described.31 Platinum complexes 1–4 were obtained by refluxing a mixture of PtCl2 and the respective proligands in THF in the presence of a Brønsted base (Scheme 1b). As for 3 and 4,31 we found the use of Ag2O allowed for the highest yields compared with alkoxide bases (e.g., NaOtBu). Work-up enabled isolation of bright orange solids in moderate (1, 34%; 2, 49%) to high (3, 87%; 4, 86%) yields. The Pt(II) complexes are stable to both air and ambient moisture in solution and as solids. Coordination of the ligands to Pt(II) induces a shift to higher frequency of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH resonance of the phenanthridinyl ligand arm observed by 1H NMR [δ(N
CH resonance of the phenanthridinyl ligand arm observed by 1H NMR [δ(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH): L1, 9.29 ppm; 1, 10.04 ppm]. Similarly, the 1H resonance of the methyl substituent at this same carbon in 2 also shifts to a higher frequency [δ(N
CH): L1, 9.29 ppm; 1, 10.04 ppm]. Similarly, the 1H resonance of the methyl substituent at this same carbon in 2 also shifts to a higher frequency [δ(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)): L2, 3.05 ppm; 2, 3.53 ppm]. This characteristic shift of the N
C(CH3)): L2, 3.05 ppm; 2, 3.53 ppm]. This characteristic shift of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH1H resonance, and in the case of 2 the N
CH1H resonance, and in the case of 2 the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3), upon coordination to a Lewis acidic metal ion is also diagnostic in other square-planar Pt(II) complexes supported by phenanthridine-based ligand frameworks.22,23,31,32 Observation of coupling between the N
C(CH3), upon coordination to a Lewis acidic metal ion is also diagnostic in other square-planar Pt(II) complexes supported by phenanthridine-based ligand frameworks.22,23,31,32 Observation of coupling between the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH and spin-active 195Pt (3JPtH = 40 Hz in 1) further supports the binding of the phenanthridinyl donor to the metal centre. High resolution mass spectra (HRMS) of 1 and 2 are consistent with the proposed molecular formulae.
CH and spin-active 195Pt (3JPtH = 40 Hz in 1) further supports the binding of the phenanthridinyl donor to the metal centre. High resolution mass spectra (HRMS) of 1 and 2 are consistent with the proposed molecular formulae.
 | ||
| Scheme 1 Synthesis of (a) proligands L1–L4 and (b) Pt complexes 1–4 with yields in parentheses. The IUPAC numbering system for phenanthridines is illustrated in italics for the proligands. | ||
The solid-state structures of three of the Pt(II) complexes were established using single-crystal X-ray diffraction (Fig. 1; the structure of 3 has been previously reported31). In each complex, the Pt(II) ion is arranged in a pseudo-square planar coordination environment with the chloride ligand trans to the amido nitrogen donor, and the fused tricyclic phenanthridinyl unit more or less coplanar with the square coordination plane of Pt(II). Of the series, 2 exhibits a significant distortion as revealed by the angles of 19.5° (θ: Cl2–Pt2–N3–C21) and 30.6° (θ: Cl1–Pt1–N1–C1; two molecules are present in the asymmetric unit) between the phenanthridinyl and metal coordination planes due to the increased steric congestion arising from the methyl substituent at the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C carbon of the heterocyclic donor arm. Accordingly, the calculated τδ value33 for 2 is more distorted from an ideal square-planar coordination environment compared with 1, 3 and 4 (τδ for 2: 0.16; 1: 0.03; 3: 0.03; 4: 0.02). Moreover, the N2–Pt1–Cl1/N4–Pt2–Cl2 angles are smaller in 2 [168.24(10)° and 172.48(9)°, respectively, for the two molecules in the asymmetric unit] compared with 1 [177.45(17)°], 3 [176.70(11)°]31 or 4 [177.97(18)°]. These distortions in the ground state of 2 have implications for its photophysics (vide infra). The four proligands present NMR and IR spectra consistent with the keto-enamine tautomer predominating in solution.31 In the Pt(II) complexes, the C–O distance is still quite short but does elongate slightly compared to in the proligand (C17–O1 1.278–1.297 Å, cf. 1.244(3) in tBuLH31), while the C15–N2 distance contracts (1.322–1.334 Å, cf. 1.363(3) in tBuLH31). This implies at least some C–O–Pt/C
C carbon of the heterocyclic donor arm. Accordingly, the calculated τδ value33 for 2 is more distorted from an ideal square-planar coordination environment compared with 1, 3 and 4 (τδ for 2: 0.16; 1: 0.03; 3: 0.03; 4: 0.02). Moreover, the N2–Pt1–Cl1/N4–Pt2–Cl2 angles are smaller in 2 [168.24(10)° and 172.48(9)°, respectively, for the two molecules in the asymmetric unit] compared with 1 [177.45(17)°], 3 [176.70(11)°]31 or 4 [177.97(18)°]. These distortions in the ground state of 2 have implications for its photophysics (vide infra). The four proligands present NMR and IR spectra consistent with the keto-enamine tautomer predominating in solution.31 In the Pt(II) complexes, the C–O distance is still quite short but does elongate slightly compared to in the proligand (C17–O1 1.278–1.297 Å, cf. 1.244(3) in tBuLH31), while the C15–N2 distance contracts (1.322–1.334 Å, cf. 1.363(3) in tBuLH31). This implies at least some C–O–Pt/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–Pt character. Indeed, the Pt1–N2 distances (1.998–1.987 Å) are not significantly different from unambiguous Pt–Nimine distances trans to chloro ligands reported for square-planar Pt(II) complexes with closely related coordination environments.26
N–Pt character. Indeed, the Pt1–N2 distances (1.998–1.987 Å) are not significantly different from unambiguous Pt–Nimine distances trans to chloro ligands reported for square-planar Pt(II) complexes with closely related coordination environments.26
Electrochemistry
Deprotonation of L1–L4 and installation on Pt(II) introduces at least partial amido character, which, in the context of pincer-type tridentate ligand scaffolds, should be accessible for electrochemical oxidation.34 Similarly, low-lying, vacant π* orbitals in the benzannulated ligand framework are anticipated to be accessible for electrochemical reduction.35 Electrochemical analysis of L1–L4 (Fig. S1†) and 1–4 (Fig. 2) was therefore undertaken using cyclic voltammetry and differential pulse voltammetry. Largely irreversible anodic and cathodic events are observed, which become more reversible at increased scan rates for 1 and 3, and to a lesser extent for 2 (Fig. S2†). Related bis(quinolinyl)amido, bis(phenanthridinyl)amido and (phenanthridinyl/quinolinyl)amido Pt(II) chloro complexes show closely related redox behavior.32 Here, however, the oxidation events are shifted to more positive potentials due to the stabilization proffered by the imine/enolato character evident in the solid-state structures. The cathodic events are similarly accessible at less negative potentials and are much more reversible, with the exception of 2, which presents an electron-donating substituent at the (Me)C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N sub-unit hosting the majority of the orbital density for its LUMO. The results, summarized in Table 1, have been used to estimate experimental HOMO–LUMO gaps.
N sub-unit hosting the majority of the orbital density for its LUMO. The results, summarized in Table 1, have been used to estimate experimental HOMO–LUMO gaps.
 | ||
| Fig. 2 Cyclic voltammograms (solid lines; 100 mV s−1) and differential pulse voltammograms (dashed lines) of 1–4 in CH2Cl2 containing 0.1 M [nBu4N][PF6] at 295 K. | ||
| Compound |
E
1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/V a/V |
E
HOMO/LUMO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b/eV b/eV |
ΔEHOMO–LUMO/eV |
E
g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
|---|---|---|---|---|
| a vs. FcH0/+ in CH2Cl2 at scan rates of 100 mV s−1. b Estimated using eqn (1) and (2) (see ESI†). c Estimated using eqn (3) for L1–4, and eqn (4) for 1–4 (see ESI†). | ||||
| L1 | −2.50, 0.64 | −5.44/−2.30 | 3.14 | 3.22 |
| L2 | −2.63, 0.53 | −5.33/−2.17 | 3.16 | 3.22 |
| L3 | −2.53, 0.66 | −5.46/−2.27 | 3.19 | 3.24 |
| L4 | −2.30, 0.82 | −5.62/−2.50 | 3.12 | 3.20 |
| 1 | −1.95, 0.72 | −5.52/−2.85 | 2.67 | 2.68 |
| 2 | −2.05, 0.71 | −5.51/−2.75 | 2.76 | 2.74 |
| 3 | −1.96, 0.71 | −5.51/−2.84 | 2.67 | 2.70 |
| 4 | −1.74, 0.85 | −5.65/−3.06 | 2.59 | 2.61 |
A general destabilization of the HOMO energies of the ligands is expected on going from electron-withdrawing (CF3) to electron-releasing (CH3, tBu) substitution in the 2-position of the phenanthridinyl unit. A further destabilization results from introducing an electron-releasing CH3 substituent into the 6-position as in L2 (EHOMO/eV: L2 > L3 ≈ L1 > L4). Consequently, oxidation events occur at lower potentials for L1–L3, with the most negative oxidation potential for L2 and most positive oxidation potential observed for L4. A similar trend can be discerned in the irreversible cathodic events associated with reduction of the ligands, with L2 reduced at the most negative potential. This implies that the LUMO energies of the proligands are in the order ELUMO/eV: L2 > L3 ≈ L1 > L4. Overall, however, the HOMO–LUMO gaps estimated from electrochemistry (ΔEHOMO–LUMO) are quite similar for L1–L4, indicating that substitution induces similar perturbations to the two frontier molecular orbitals of the ligands. Consistent with this, the UV-Vis spectra of the four proligands are quite similar, except for L3 which presents a broader and slightly blue-shifted λmax (Fig. S3†).
Upon deprotonation and coordination to Lewis acidic Pt(II), a shift to more positive potentials is observed for both the oxidation and reduction potentials. While it might be expected that the bigger change to the character of the HOMOs of 1–4 through introduction of metal/chloride character would more significantly impact oxidation than reduction involving the largely phenanthridine-localized LUMO, the observed shifts suggest a larger stabilization of the LUMO energies (ΔELUMO/meV: L1vs. 1, −550; L2vs. 2, −580; L3vs. 3, −570; L4vs. 4, −560; ΔEHOMO/meV: L1vs. 1, −180; L2vs. 2, −190; L3vs. 3, −50; L4vs. 4, −30). For the series, the electrochemically estimated HOMO energies of 1–3 are comparable, while the HOMO of 4 is further stabilized (ΔEstab ∼ 140 meV vs. 1). In sharp contrast, the LUMO energies mirror the trend observed for the proligands: ELUMO/eV: 2 > 3 ≈ 1 > 4, with a larger stabilization energy of 210 meV in 4 relative to 1. Electronic perturbations by the substituent in the frontier molecular orbital energies are evidently larger for the LUMO than the HOMO in the complexes. We return to these points later.
UV-Vis absorption and emission spectroscopy
As noted above, all four complexes are bright orange solids and give rise to similarly coloured solutions. UV-Vis absorption spectra (Fig. 3a) accordingly exhibit broad and strong bands in the visible region of the electromagnetic spectrum (λmax ∼ 460 nm, ε > 5000 M−1 cm−1) consistent with transitions of charge-transfer character. In addition, two strong transitions are evident in the UV (λ ∼ 260 nm, ε > 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1; λ ∼ 350 nm, ε > 11
000 M−1 cm−1; λ ∼ 350 nm, ε > 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1), ascribable to ligand-based excitations. Comparison with analogous Pt(II) chloride complexes of monoanionic, pincer-type N-8-quinolinyl-4-aminophenanthridines22,23,32 favours a mixed [M+L]LCT assignment for the lowest energy manifold. Such Namido–Pt–Cl systems can be compartmentalized in terms of the character of the donor (nCl + dPt + nNamido) and acceptor (largely phenanthridine-based π* orbitals, with significant contribution from the HC
000 M−1 cm−1), ascribable to ligand-based excitations. Comparison with analogous Pt(II) chloride complexes of monoanionic, pincer-type N-8-quinolinyl-4-aminophenanthridines22,23,32 favours a mixed [M+L]LCT assignment for the lowest energy manifold. Such Namido–Pt–Cl systems can be compartmentalized in terms of the character of the donor (nCl + dPt + nNamido) and acceptor (largely phenanthridine-based π* orbitals, with significant contribution from the HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N sub-unit) molecular fragments.
N sub-unit) molecular fragments.
 | ||
| Fig. 3 (a) UV-Vis absorption spectra of 1–4 in CH2Cl2 at 295 K. (b) UV-Vis absorption spectra of 4 in a variety of solvents illustrating the solvatochromism of the lowest energy band. | ||
UV-Vis absorption spectra collected for 4 in a range of solvents support the CT assignment (Fig. 3b). The lowest energy absorption exhibits negative solvatochromism, suggesting stabilization of the ground-state relative to the excited state of interest with increasing solvent polarity. Fitting the transition energies to Reichardt's ETN function36 leads to a relatively weak correlation (R2 = 0.77; Fig. S4†), which improves when protic and aprotic solvents are treated separately (R2 = 0.96, 0.93) indicating that specific solute–solvent interactions need to be taken into account. Using Catalan's four parameter solvent scale37 to separate contributions of specific solute–solvent interactions (e.g., solvent acidity/basicity) from non-specific interactions (solvent polarizability/dipolarity) produces a much better correlation between calculated and experimental transition energies (Fig. S5†). Given solubility constraints on the range of solvents employed, we attribute the hypsochromic shift of λmax in increasingly polar solvents with the most confidence to solvent dipolarity (i.e., solute–solvent dipole interactions) and solvent acidity (i.e., hydrogen bonding; Tables S1 and S2†). In particular, the large coefficient and positive sign obtained from fitting the solvent dipolarity indicate preferential ground-state stabilization.36 Increasing solvent dipolarity would be expected to stabilize the larger dipole moment typically associated with an excited state of CT character. However, the [M+L]LCT character of 1–4 induces an excited state dipole moment (μe) which is not expected to orient in the same direction as the ground state dipole moment (μg). The Franck–Condon principle necessitates the solvent to be in a ‘frozen’ state; that is, the solvent remains in its ground-state equilibrium orientation around the chromophore. This leads to ‘orientational strain’ on the solvent contributing to the apparent hypsochromic shift in the CT excitation energies with increasing solvent polarity.38 In contrast, ground state stabilization by solvent acidity is made possible by hydrogen bonding to atom(s) contributing to the HOMO, likely through the chloride. Indeed, incorporation of hydrogen-bonding solvents (e.g., CHCl3) with close contacts to the chloride and oxygen of the ligand is observed in the solid-state structure of 2 (Fig. S6†).
As with related Pt(II) complexes chelated by monanionic, tridentate N∧N∧O Schiff-base ligands,26 the novel Pt(II) complexes presented here emit in the orange region of the visible spectrum (λmax ∼ 600 nm; Fig. 4). Each of complexes 1, 3 and 4 are brightly emissive, with quantum yields up to 16% in deoxygenated dichloromethane at room temperature (Table 2), superior to those of the archetypal MLCT emitter [Ru(bpy)3]2+ for example,39 and one to two orders of magnitude larger than those observed for Pt(II) complexes of closely related phenanthridine-based diarylamido ligands.23 In contrast, the 2,6-dimethyl substituted 2 is only very weakly emissive at room temperature, too weak to reliably record a quantum yield or lifetime. Amongst the other three, complex 4 emits with (marginally) the narrowest band structure (FWHM = 2460 cm−1 compared to 2730 cm−1 for 3) and the highest quantum yield. These values far exceed those reported for (N∧N∧O)PtCl complexes based on dipyridylphenolato frameworks, which emit at λem 593–606 nm, with Φ ∼ 1–4% in the solid-state,25 and those for Pt(II) emitters with Schiff-base ligand frameworks (λem 686–735 nm; Φ = 0.5–4.6% in fluid solution for quinoline-based derivatives; λem 580–636 nm for hydrazone derived analogs, with Φ reaching 11% for acetylide derivatives).26 The luminescence of 1, 3 and 4 follows mono-exponential decay kinetics, with a lifetime of around 22 μs in each. Values in the microsecond range are typical of phosphorescence from the triplet state in cyclometallated Pt(II) complexes, although most examples tend to be somewhat shorter-lived, usually <10 μs. Some insight into the longer lifetimes can be gleaned by estimating the radiative kr and non-radiative ∑knr rate constants from the quantum yields and lifetimes (Table 2). The former are around an order of magnitude lower than found for the brightest Pt(II) emitters (though the brightest tend to be green emitters), but not dissimilar to values for [Pt(dqpy)Cl]+, for example (dqpy = 1,3-di(8-quinolyl)pyridine).40 The ∑knr values, meanwhile, are of a magnitude fairly typical for Pt(II) emitters with tridentate ligands.
| Absorption λmax/nm (ε/M−1 cm−1)a | Emission λmax![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b/nm b/nm |
Φ
lum![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c/10−2 c/10−2 |
τ /μs |
k
SQQ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e/108 M−1 s−1 e/108 M−1 s−1 |
/108 M−1 s−1 |
k
r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/103 s−1 f/103 s−1 |
∑knr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/103 s−1 f/103 s−1 |
Emission 77 Kg | ||
|---|---|---|---|---|---|---|---|---|---|---|
| λ max/nm | τ/μs | |||||||||
a In CH2Cl2 at 295 K.
b In deoxygenated CH2Cl2 at 295 K.
c Measured using [Ru(bpy)3]Cl2 (aq) as the standard.
d Values in parenthesis refer to air-equilibrated solution.
e Self-quenching rate constant estimated from concentration dependence of lifetime.
f Radiative kr and non-radiative ∑knr rate constants calculated assuming that the emitting state is formed with unit efficiency, under which conditions kr = Φ/τ and ∑knr = (1 − Φ)/τ.
g In diethyl ether/isopentane/ethanol (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v).
h The emission intensity of complex 2 is too weak to determine the lifetime or a reliable Φlum. 1 v/v).
h The emission intensity of complex 2 is too weak to determine the lifetime or a reliable Φlum.
|
||||||||||
| 1 | 261 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800), 354 (17 800), 354 (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200), 463 (6030) 200), 463 (6030) |
604 | 9.1 | 23 [0.42] | 1.5 | 11 | 4.0 | 40 | 573, 620, 682sh | 64 |
| 2 | 261 (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736), 343 (11 736), 343 (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241), 453 (5424) 241), 453 (5424) |
610 | —h | — | — | — | — | — | 587, 640, 700sh | 36 |
| 3 | 258 (31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800), 354 (16 800), 354 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500), 459 (5080) 500), 459 (5080) |
608 | 6.8 | 22 [0.41] | 2.0 | 11 | 3.1 | 42 | 573, 620, 682sh | 61 |
| 4 | 265 (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600), 360 (16 600), 360 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100), 475 (5980) 100), 475 (5980) |
608 | 16 | 24 [0.48] | 1.1 | 9.3 | 6.7 | 35 | 579, 626, 694sh | 52 |
Given the long lifetimes in fluid solution, it is not surprising to find that the emission is strongly quenched by dissolved molecular oxygen, with bimolecular quenching constants of the order of 109 M−1 s−1 at room temperature. A modest degree of self-quenching is also observed in concentrated solutions, though the self-quenching constants of 1 − 2 × 108 M−1 s−1 are much lower than for systems such as Pt(N∧C∧N-dpyb)Cl and derivatives {dpyb = 1,3-di(2-pyridyl)benzene}.18 Moreover, there is no evidence of excimer emission to lower energy at elevated concentrations, unlike many of the latter group.
To better understand the trends in absorption, emission and electrochemistry, density functional theory (DFT) modelling of 1–4 was performed. Molecular orbital energies from ground-state optimized geometries (Fig. 5 and Tables S5–S8†) corroborate the trends in the HOMO–LUMO gaps gleaned from electrochemistry and electronic absorption spectroscopy (Fig. S7†). In particular, the HOMO energies are slightly stabilized upon deprotonation/metal coordination and mirror the ordering discussed above. In each case, the HOMO has significant contributions from platinum (∼20%), the N∧O donor chelate (∼45%) and the chloride (∼10%), with Pt–Namido/O/Cl π-antibonding character evident in the MO isosurfaces. The LUMO, on the other hand, is largely comprised of the phenanthridinyl π* manifold, with significant contribution from the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N fragment (1 28, 2 31, 3 29, 4 28%), minor delocalization into the N∧O chelate (∼15%) and negligible metal (2%) and halide (0%) contributions. As noted above, comparing the electrochemical data of L1–L4 and 1–4 reveals a more pronounced shift to the potentials associated with reductions of 1–4vs. L1–L4 compared to their respective oxidations. The localization of the LUMO at the C
N fragment (1 28, 2 31, 3 29, 4 28%), minor delocalization into the N∧O chelate (∼15%) and negligible metal (2%) and halide (0%) contributions. As noted above, comparing the electrochemical data of L1–L4 and 1–4 reveals a more pronounced shift to the potentials associated with reductions of 1–4vs. L1–L4 compared to their respective oxidations. The localization of the LUMO at the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N sub-unit apparently amplifies the stabilizing effect of coordination to Pt(II) on the vacant, low-lying orbitals.
N sub-unit apparently amplifies the stabilizing effect of coordination to Pt(II) on the vacant, low-lying orbitals.
 | ||
| Fig. 5 Molecular orbital energy level diagrams, HOMO–LUMO gaps and selected isosurfaces (isovalue = 0.04) for 1–4. | ||
The nature of the frontier orbitals is in line with previously studied transition metal complexes supported by ligand frameworks containing phenanthridinyl moieties, with mixed-character (metal + nN) HOMO and πphen* LUMO frontier orbitals.41,42 It is notable that in the HOMOs, there is no orbital density at the 2-position of the phenanthridinyl ring. The slight perturbation in the HOMO energies thus appears to originate from the weak inductive effect of the substituent, through the orbital density at the 1- and 3-positions. The CH3 substituent at the 6-position did not have any notable effect on the energy of the HOMO of 2 as there is no significant orbital density at the attached carbon or the adjacent nitrogen. In comparison, the LUMOs present orbital density at carbon atoms in both the 6- (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) and 2-positions; thus, the CF3 substituent in 4 stabilizes the vacant MO and enhances the electron-accepting character of the LUMO, while the LUMO of 2 is destabilized compared to 1 as a result of hyperconjugation of the CH3 σC–H with the phenanthridinyl π*HC
N) and 2-positions; thus, the CF3 substituent in 4 stabilizes the vacant MO and enhances the electron-accepting character of the LUMO, while the LUMO of 2 is destabilized compared to 1 as a result of hyperconjugation of the CH3 σC–H with the phenanthridinyl π*HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N orbital.
N orbital.
TDDFT simulations were also carried out. Given the presence of the third-row transition metal ion, we first investigated the impact of spin–orbit coupling (SOC) on the calculated UV-Vis absorption spectra (Fig. S8†) of a representative complex (4). The scalar-only simulated TDDFT spectrum of 4 (Fig. S13†) shows only one particle-hole pair involved in the lowest energy manifold of HOMO → LUMO character (97%; Table S12†) consistent with a mixed (M+L)LCT assignment. A notable absence of transitions is observed in the valley region between the lowest energy (∼460 nm) and mid-energy (∼353 nm) absorption manifolds within the spin-only approximation. Inclusion of SOC (SOC-TDDFT) leads to an increase in the spectral intensity of this region. Previous computational modelling of the UV-Vis absorption spectra of Re(I) carbonyl complexes supported by 8-aminophenanthridines and 4-aminoquinolines indicated that SOC is necessary in accounting for weak, low-energy transitions in the 450–650 nm range of such complexes.43 In addition, a growing body of literature supports the necessity of SOC to properly model the absorption spectra of complexes containing heavy elements, providing a mechanism to account for the direct population of low-lying excited triplet states.43–46
SOC-TDDFT simulated spectra for all four complexes calculated using a polarizable continuum of CH2Cl2 are in excellent agreement with the experimental UV-Vis absorption spectra (Fig. S9–S12 and Tables S9–S12†). In general, our simulations suggest that two important transitions are responsible for the lowest energy manifold of the experimental UV-Vis spectra. For 1–3, one weaker, lower-energy (SOC4, fosc > 0.005) and a stronger, higher-energy transition (SOC7, fosc > 0.049) are prominent, while the weaker SOC4 gains intensity in 4 due to increased participation of S1 (1–3 < 11%, 4 ∼ 40%). Both transitions have largely S1 excited singlet state contributions, while T2 states dominate the excited triplet state. The S1 state is largely HOMO → LUMO; that is, (M+L)LCT, in character. The T2 excited state, on the other hand, has significant contribution from the HOMO−1 → LUMO transition, which comprises a similar (M+L)LCT character but with increased contribution from Pt (%Pt, HOMO−1: 1 32, 2 38, 3 34, 4 46) and reduced Cl (%Cl, HOMO−1: 1 0, 2 12, 3 0, 4 4) contribution. This would suggest that the lowest energy absorption manifold can be reasonably attributed to HOMO → LUMO transitions, which enables us to estimate the Eg from the λmax of this band. This also explains the excellent agreement between the experimental ΔEHOMO–LUMO from electrochemistry and Eg estimated by optical spectroscopy. Thus, the spectral shifts observed between the Pt(II) complexes can be largely attributed to the electronic perturbations identified in the frontier MOs. In either case, relaxation to the lowest-lying triplet state (T1) is expected prior to radiative decay.
The optimized geometries of the T1 state, in each case, show a general contraction of the Pt–Namido (Pt1–N2) and Pt–Cl bond distances (Table S4†). This is consistent with depopulation of an orbital (HOMO) with Pt–Namido/Pt–Cl antibonding character. The increase in bond order reflects the charge-transfer (CT) character of T1, as metal-centered (MC) states would be expected to result in longer metal–ligand bonds thanks to population of metal–ligand anti-bonding orbitals. Similar π-mixing between ligand π-orbitals and metal d-orbitals of appropriate symmetry has been observed in Fe(II) complexes of diarylamido ligands, but not for other metals.47 In the former, depopulation of a highly covalent HOMO with metal–Namido (dπ–pπ)* anti-bonding character is similarly thought to induce a metal–ligand bond contraction in the CT state, with consequences for CT/MC excited state ordering. In comparison, square planar Pt complexes of dithiolene ligands bearing protonated pyrazine units show diminished dπ–pπ hybridization compared to complexes of lighter elements such as Ni.48 Of the four complexes, 2 exhibits the most distortion both in its solid-state structure, and in its optimized ground-state and lowest-lying excited triplet state geometries. This is clear from the calculated τδ parameter (0.16) which indicates a distorted square planar geometry (Fig. 6). The anomalously weak emission from 2 can thus be attributed to competitive non-radiative decay pathways made possible by excited state distortions.49
Finally, for the brightest emitter (4), we probed the excited state dynamics (ESD) via the ESD module implemented in the ORCA software suite,50,51 using the optimized geometries of the ground-state (1GSeq) and lowest-lying triplet excited state (T1). We first estimated the rate of intersystem crossing (kISC) of the scalar-only S1 (the dominant transition in the visible region) and S7 (the dominant transition contributing to the band at 360 nm) states at the 1GS geometry to the lowest-lying excited triplet state at its equilibrium geometry (Table S13†). Rapid and efficient population of the triplet state is calculated with average kISC of 8.870 × 1012 s−1 (S1 → T1) and 1.020 × 1013 s−1 (S7 → T1). This suggests strong coupling between these states and the presumably emissive T1 state, consistent with the strong mixing between the singlet and triplet states through the influence of SOC evident in the UV-Vis absorption spectra, as discussed above. SOC-TDDFT simulations also predict strong mixing between S1 and T2, both of which contribute significantly to the predicted strong, low-energy absorptions in the calculated SOC-TDDFT spectrum (Fig. S12 and Table S12†), and both of which exhibit (M+L)LCT character. This suggests that T2 is also populated upon excitation, and likely undergoes rapid internal conversion to T1.
We also simulated the phosphorescence spectra and decay parameters for 4 (Table S14†). In general, the simulated spectra of 4 at room temperature (Fig. S14†) and 77 K (Fig. S15†) faithfully reproduce the respective experimental spectra, with errors of <0.2 eV. The vibrational progression observed experimentally at 77 K that appears as a low-energy shoulder at 295 K is reproduced in both calculated spectra, indicating the molecule retains rigidity in solution at 295 K with only minimal distortion, as shown by similar values for τδ for both 1GSeq and T1,eq. In contrast, the emission spectrum of 2 is broad and weak at 295 K, but resembles those of 1, 3 and 4 at 77 K (Fig. S16†). This implies that significant distortions occur at elevated temperature, in line with the weakness of the emission. Spin density maps reveal a similar (M+L)LCT character of the emissive triplet state of all four complexes (Fig. S17†).
Conclusions
In summary, multidentate N∧N∧O β-enaminoketonato ligands bearing benzannulated N-heterocyclic phenanthridinyl donor arms can be used to prepare new luminescent Pt(II) complexes under mild conditions. The substitution pattern on the phenanthridinyl ligand lends control over emissive properties by impacting molecular rigidity rather than ligand electronics as shown by DFT calculations, and bright orange emission is observed from three of the four complexes at room temperature with quantum yields reaching 16% for the CF3-substituted 4 and elongated phosphorescence lifetimes on the order of ∼20 μs. In comparison, methyl substitution at the 6-position of the phenanthridinyl ligand leads to quenching of the emissive state, traced by computational analysis to enhanced distortions in both the ground state and excited state. The origin of the photophysical properties of the complexes was further examined by probing the excited state dynamics of 4. These simulations suggested that the emissive triplet state is populated rapidly and efficiently thanks to the participation of Pt(II) in the (M+L)LCT excited states. Strong mixing between low-lying singlet and triplet manifolds, thanks to the high spin–orbit coupling of the 5d transition metal, is similarly evident in TDDFT simulations of the experimental UV-Vis absorption spectra which are most faithfully reproduced with explicit inclusion of SOC. While trailing those of very strongly emissive neutral Pt(II) complexes of 2,6-bis(1H-1,2,4-triazol-5-yl)pyridine-based N−∧N∧N−-ligands,52 when compared with closely related quinoline-containing phenolate N∧N∧O26 and N∧N∧N21–23 Pt(II) emitters, the higher quantum yields and significantly lengthened phosphorescence lifetimes suggests that β-enaminoketonato ligand scaffolds and benzannulated acceptor arms can be combined to access improved photophysical properties under comparably simple synthetic conditions.Experimental section
Air-sensitive manipulations were carried out in a N2-filled glove box or using standard Schlenk techniques under Ar. Platinum dichloride (Millipore Sigma) and other common reagents were purchased from commercial suppliers and used without further purification. L1–L4, 3 and 4 were prepared according to literature procedures.31 Organic solvents were dried and distilled using appropriate drying agents. 1- and 2D NMR spectra were recorded on a Bruker Avance 300 MHz spectrometer or a Bruker Avance 500 MHz spectrometer. 1H and 13C{1H} NMR spectra were referenced to residual solvent peaks. High resolution mass spectra were recorded using a Bruker microOTOF-QIII. For electrochemical analysis, 5–15 mg of each compound investigated was dissolved in 15 mL of 0.1 M [nBu4N][PF6] in CH2Cl2 and purged with Ar before analysis. All electrochemical experiments were conducted under inert (Ar) atmosphere using a CHI 760c bipotentiostat, a 3 mm diameter glassy carbon working electrode, a Ag/Ag+ quasi-non-aqueous reference electrode separated by a Vycor tip, and a Pt wire counter electrode. Cyclic voltammetric (CV) experiments were conducted using scan rates of 100–500 mV s−1. Differential pulse voltammetry (DPV) experiments were also conducted, using a 10 mV increment, 50 mV amplitude, 0.5 s pulse width, 0.0167 s sample width, and 0.5 s pulse period. Upon completion of all CV and DPV analyses, ferrocene (FcH) was added to the solution as an external standard, with all potentials reported versus the FcH0/+ redox couple.Synthesis of [Pt(L1)Cl], 1
A solution of L1 (0.0587 g, 0.113 mmol) in THF (3.5 mL) was added to a suspension of PtCl2 (0.0618 g, 0.232 mmol), Ag2O (0.0293 g, 0.126 mmol) and 4 Å molecular sieves (0.180 g) in THF (3.5 mL). The mixture was protected from light and heated in an oil bath set to 60 °C for 16 h. The mixture was then filtered over Celite then the solvent was evaporated to isolate an orange solid compound. The product was purified by precipitation from a CHCl3 solution using petroleum ether. Isolated yield = 0.0362 g (34%). 1H NMR (CDCl3, 500 MHz, 22 °C): δ 9.97 (s, 1H, 3JPtH = 40 Hz; C1H), 8.46 (d, 3JHH = 8.3 Hz, 1H; C6H), 8.03 (d, 3JHH = 8.0 Hz, 1H; C3H), 7.95 (m, 1H; C5H), 7.81 (s, 1H; C13H), 7.72 (m, 1H; C4H), 7.53 (s, 1H; C11H), 5.28 (s, 1H; C16H), 2.62 (s, 3H; C19H), 2.42 (s, 3H; C20H), 2.07 ppm (s, 3H; C14H). 13C{1H} NMR (CDCl3, 125 MHz, 22 °C): δ 179.8 (C16), 158.1 (C18), 154.7 (C1), 148.8 (C10), 139.1 (C12), 138.9 (C9), 133.5 (C5), 131.9 (C2), 130.0 (C3), 128.9 (C4), 126.3 (C8), 125.5 (C7), 122.6 (C6), 122.6 (C11), 117.9 (C13), 106.7 (C16), 26.2 (C14), 25.7 (C18), 22.6 ppm (C19). HRMS (ESI-TOF) m/z: [M + Na]+ Calcd for [C19H17ClN2OPt + Na]+ 542.0571; Found 542.0532.
Synthesis of [Pt(L2)Cl], 2
An identical procedure to the preparation of 1 was followed using a solution of L2 (0.0612 g, 0.115 mmol) in THF (3.5 mL), and a suspension of PtCl2 (0.0590 g, 0.222 mmol), Ag2O (0.0313 g, 0.135 mmol) and 4 Å molecular sieves (0.122 g) in THF (3.5 mL). After precipitation from CHCl3, the supernatant was further concentrated, and more product was following diffusion of diethylether vapors into the solution. Isolated yield = 0.0519 g (49%). 1H NMR (CDCl3, 500 MHz, 22 °C): δ 8.51 (d, 3JHH = 8.4 Hz, 1H; C6H), 8.21 (d, 3JHH = 8.4 Hz, 1H; C3H), 7.92 (ddd, 3JHH = 8.4, 7.6 Hz, 4JHH = 1.0 Hz, 1H; C5H), 7.78 (s; 1H; C13H), 7.69 (ddd; 3JHH = 8.7, 7.7 Hz; 4JHH = 0.9 Hz; 1H; C4H), 7.19 (s; 1H; C11H), 5.27 (s; 1H; C16H), 3.53 (s; 1H; C19H), 2.56 (s; 1H; C20H), 2.28 (s; 1H; C14H), 2.06 (s; 1H; C18H). 13C{1H} NMR (CDCl3, 125 MHz, 22 °C): δ 179.9 (C19), 167.8 (C1), 158.3 (C17), 148.8 (C10), 140.1 (C9), 137.7 (C12), 133.0 (C5), 131.4 (C7), 128.8 (C4), 127.9 (C3), 127.1 (C2), 124.6 (C8), 122.7 (C6), 121.0 (C11), 117.4 (C13), 106.5 (C16), 26.8 (C19), 25.3 (C18), 23.7 (C14), 22.2 ppm (C20). HRMS (ESI-TOF) m/z: [M]+ Calcd for [C20H19N2OPt]+ 498.1142; Found 498.1130.
X-ray crystallography experimental details
X-ray crystal structure data was collected from multi-faceted crystals of suitable size and quality selected from a representative sample of crystals of the same habit using an optical microscope. Crystals were mounted on MiTiGen loops and data collection carried out in a cold stream of nitrogen (150 K; Bruker D8 QUEST ECO). Diffractometer manipulations were carried out using Bruker APEX3 software.53 Structure solution and refinement was performed using XS, XT and XL software, embedded within the OLEX2.54 For each structure, the absence of additional symmetry was confirmed using ADDSYM incorporated in the PLATON program.55Crystal structure data for 1 (CCDC 2100576†)
X-ray quality crystals were grown following diffusion of diethyl ether vapor into CHCl3 at room temperature. Crystal structure parameters: C19H17ClN2OPt 519.89 g mol−1, monoclinic, space group P21/n; a = 9.2499(5) Å, b = 11.5853(6) Å, c = 15.3470(8) Å, α = γ = 90°, β = 103.623(2)°, V = 1598.36(15) Å3; Z = 4, ρcalcd = 2.160 g cm−3; crystal dimensions 0.16 × 0.14 × 0.02 mm; diffractometer Bruker D8 QUEST ECO CMOS; Mo Kα radiation, 150(2) K, 2θmax = 2.731 to 24.790°; 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 441 reflections, 2739 independent (Rint = 0.0642), direct methods; absorption coeff. (μ = 8.954 mm−1), absorption correction semi-empirical from equivalents (SADABS); refinement (against Fo2) with SHELXTL V6.1, 220 parameters, 0 restraints, R1 = 0.0351 (I > 2σ) and wR2 = 0.0754 (all data), Goof = 1.121, residual electron density 1.745/−1.521 e Å−3.
441 reflections, 2739 independent (Rint = 0.0642), direct methods; absorption coeff. (μ = 8.954 mm−1), absorption correction semi-empirical from equivalents (SADABS); refinement (against Fo2) with SHELXTL V6.1, 220 parameters, 0 restraints, R1 = 0.0351 (I > 2σ) and wR2 = 0.0754 (all data), Goof = 1.121, residual electron density 1.745/−1.521 e Å−3.
Crystal structure data for 2 (CCDC 2100577†)
X-ray quality crystals were grown following diffusion of diethyl ether vapor into CHCl3 at room temperature. Crystal structure parameters: C21H20Cl4N2OPt 653.28 g mol−1, triclinic, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ; a = 11.0564(7) Å, b = 14.0350(9) Å, c = 16.4321(10) Å, α = 113.018(2)°, β = 99.705(2)°, γ = 100.551(2)°, V = 2224.4(2) Å3; Z = 4, ρcalcd = 1.951 g cm−3; crystal dimensions 0.35 × 0.14 × 0.06 mm; diffractometer Bruker D8 QUEST ECO CMOS; Mo Kα radiation, 150(2) K, 2θmax = 2.550 to 30.591°; 61
; a = 11.0564(7) Å, b = 14.0350(9) Å, c = 16.4321(10) Å, α = 113.018(2)°, β = 99.705(2)°, γ = 100.551(2)°, V = 2224.4(2) Å3; Z = 4, ρcalcd = 1.951 g cm−3; crystal dimensions 0.35 × 0.14 × 0.06 mm; diffractometer Bruker D8 QUEST ECO CMOS; Mo Kα radiation, 150(2) K, 2θmax = 2.550 to 30.591°; 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 734 reflections, 13
734 reflections, 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 independent (Rint = 0.0468), direct methods; absorption coeff. (μ = 6.804 mm−1), absorption correction semi-empirical from equivalents (SADABS); refinement (against Fo2) with SHELXTL V6.1, 531 parameters, 0 restraints, R1 = 0.0335 (I > 2σ) and wR2 = 0.652 (all data), Goof = 1.044, residual electron density 1.784/−1.569 e Å−3.
610 independent (Rint = 0.0468), direct methods; absorption coeff. (μ = 6.804 mm−1), absorption correction semi-empirical from equivalents (SADABS); refinement (against Fo2) with SHELXTL V6.1, 531 parameters, 0 restraints, R1 = 0.0335 (I > 2σ) and wR2 = 0.652 (all data), Goof = 1.044, residual electron density 1.784/−1.569 e Å−3.
Crystal structure data for 4 (CCDC 2100578†)
X-ray quality crystals were grown following diffusion of diethyl ether vapor into CHCl3 at room temperature. Crystal structure parameters: C19H14ClF3N2OPt 573.86 g mol−1, monoclinic, space group P21/n; a = 9.5576(6) Å, b = 11.5940(7) Å, c = 15.7469(10) Å, α = γ = 90°, β = 105.381(2)°, V = 1682.43(18) Å3; Z = 4, ρcalcd = 2.266 g cm−3; crystal dimensions 0.1 × 0.08 × 0.05 mm; diffractometer Bruker D8 QUEST ECO CMOS; Mo Kα radiation, 150(2) K, 2θmax = 2.683 to 27.553°; 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565 reflections, 3880 independent (Rint = 0.0828), direct methods; absorption coeff (μ = 8.543 mm−1), absorption correction semi-empirical from equivalents (SADABS); refinement (against Fo2) with SHELXTL V6.1, 231 parameters, 0 restraints, R1 = 0.0436 (I > 2σ) and wR2 = 0.0844 (all data), Goof = 1.115, residual electron density 2.469/−2.433 e Å−3.
565 reflections, 3880 independent (Rint = 0.0828), direct methods; absorption coeff (μ = 8.543 mm−1), absorption correction semi-empirical from equivalents (SADABS); refinement (against Fo2) with SHELXTL V6.1, 231 parameters, 0 restraints, R1 = 0.0436 (I > 2σ) and wR2 = 0.0844 (all data), Goof = 1.115, residual electron density 2.469/−2.433 e Å−3.
Computational modeling
Modeling of all complexes was carried out using ORCA version 4.2.1.50,51 The resolution-of-identity with chain-of-spheres approximation (RIJCOSX56) was used to speed up all calculations. Geometry optimizations were performed in the gas phase with the dispersion corrected (D3BJ57,58) PBE059–61 functional and the def2-TZVP(-f)62,63 on all atoms and the corresponding ECP basis set on Pt; def2/J auxiliary basis sets were used on all atoms in the density fitting. The 1GSeq and T1,eq geometries were optimized for all four complexes to understand the deactivation mechanisms in the Pt(II) complexes. The starting input for ground state (1GSeq) geometries was obtained from the coordinates of each solid-state structure. The following SCF and geometry convergence criteria, DFT grids, COSX grids were used for the optimizations: tightscf, tightopt, grid5, finalgrid6, intaccx (4.34,4.34,4.67), and gridx (2,2,2). Frequency calculations were carried to confirm that all geometries are at a minimum.Single point calculations were conducted using the same dispersion corrected PBE0 functional and inclusion of implicit solvation using the solvation model based on density (SMD,64 solvent = CH2Cl2) on gas-phase optimized geometries. However, to best account for scalar relativistic effects, we employed the zeroth order approximation (ZORA65), ZORA-optimized all-electron relativistic (ZORA-def2-TZVP63 on H, C, N, O, F, and Cl; SARC-ZORA-TZVP on Pt) and the appropriate auxiliary basis sets (SARC/J66,67). We used the same SCF convergence criteria and COS-X grid for all single points (tightscf; intaccx 4.34, 4.34, 4.67; gridx 2,2,2), while the DFT integration grids were increased to grid6 and finalgrid7. We also increased the grid around Pt (specialgridintacc 9). Time-dependent DFT (TDDFT) was used to predict the first 50 Sn,FC ← 1GSeq and Tn,FC ← 1GSeq excitations (FC implies electronic excitations within the Franck–Condon approximation) to simulate the UV-Vis spectra of the complexes without spin–orbit correction. In addition, we also predicted the extent of SOC effects by allowing mixing of Sn and Tn states as implemented in ORCA.
The excited-state dynamics of 4 were probed using the ESD module implemented in ORCA.50,51 The phosphorescence spectrum was simulated and phosphorescence rate constants (kphos, and intersystem crossing rate (kISC) were calculated. The three substates (MS = −1, 0, +1) of the lowest excited triplet state were considered in estimating kphos and kISC at 298 K and 77 K. For kISC, we considered the ground state optimized geometry as the geometry of the populated excited singlet states initially populated upon light excitation. This was performed for both S1(1GSeq) and S7(1GSeq), as these have the strongest oscillator strengths in the absorbance bands at 475 and 360 nm, respectively. The final geometry is of the lowest-lying excited triplet state. For the kphos, initial and final geometries are of the lowest-lying excited triplet state and ground state, respectively.
UV-Visible absorption and luminescence measurements
Absorption spectra were measured on a Biotek Instruments XS spectrometer, using quartz cuvettes of 1 cm pathlength. Steady-state luminescence spectra were measured using a Jobin Yvon FluoroMax-2 spectrofluorimeter, fitted with a red-sensitive Hamamatsu R928 photomultiplier tube; the spectra shown are corrected for the wavelength dependence of the detector, and the quoted emission maxima refer to the values after correction. Samples for emission measurements were contained within quartz cuvettes of 1 cm pathlength modified with appropriate glassware to allow connection to a high-vacuum line. Degassing was achieved via a minimum of three freeze–pump–thaw cycles whilst connected to the vacuum manifold; final vapor pressure at 77 K was <5 × 10−2 mbar, as monitored using a Pirani gauge. Luminescence quantum yields were determined using [Ru(bpy)3]Cl2 in aqueous solution as the standard (Φ = 0.04 ± 0.002).68 The estimated uncertainty on the quantum yields obtained in this way on the instrumentation employed is up to ±20%.Luminescence lifetimes of the complexes in air-equilibrated solutions were measured by time-correlated single-photon counting, following excitation at 405 nm with a pulsed-diode laser. The emitted light was detected at 90° using a Peltier-cooled R928 PMT after passage through a monochromator. The estimated uncertainty in the quoted lifetimes is ±10% or better. Lifetimes in deoxygenated solution and at 77 K were measured following excitation with a microsecond-pulsed xenon lamp and detection using the same PMT operating in multichannel scaling mode. For all measurements, the decays were much longer than the instrument response and data were analyzed by tail fitting to the following equation (rather than by deconvolution of the response function):
I(t) = I(0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kt) + c exp(−kt) + c |
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The following sources of funding are gratefully acknowledged: the Natural Sciences Engineering Research Council of Canada for a Discovery Grant to DEH (RGPIN-2014-03733); the Canadian Foundation for Innovation and Research Manitoba for an award in support of an X-ray diffractometer (CFI #32146); Compute Canada for access to computational resources; and the University of Manitoba for the Bert & Lee Friesen Graduate Scholarship (IBL) and GETS support.References
- W.-Y. Wong and C.-L. Ho, Heavy metal organometallic electrophosphors derived from multi-component chromophores, Coord. Chem. Rev., 2009, 253, 1709–1758 CrossRef CAS.
- H. Yersin, A. F. Rausch, R. Czerwieniec, T. Hofbeck and T. Fischer, The triplet state of organo-transition metal compounds. Triplet harvesting and singlet harvesting for efficient OLEDs, Coord. Chem. Rev., 2011, 255, 2622–2652 CrossRef CAS.
- J. Kalinowski, V. Fattori, M. Cocchi and J. A. G. Williams, Light-emitting devices based on organometallic platinum complexes as emitters, Coord. Chem. Rev., 2011, 255, 2401–2425 CrossRef CAS.
- C. Cebrian and M. Mauro, Recent advances in phosphorescent platinum complexes for organic light-emitting diodes, Beilstein J. Org. Chem., 2018, 14, 1459–1481 CrossRef CAS.
- E. Baggaley, J. A. Weinstein and J. A. G. Williams, Lighting the Way to See Inside the Live Cell With Luminescent Transition Metal Complexes, Coord. Chem. Rev., 2012, 256, 1762–1785 CrossRef CAS.
- M. Mauro, A. Aliprandi, D. Septiadi, N. S. Kehr and L. De Cola, When Self-Assembly Meets Biology: Luminescent Platinum Complexes for Imaging Applications, Chem. Soc. Rev., 2014, 43, 4144–4166 RSC.
- Y. Chen, R. Guan, C. Zhang, J. Huang, L. Ji and H. Chao, Two-photon luminescent metal complexes for bioimaging and cancer phototherapy, Coord. Chem. Rev., 2016, 310, 16–40 CrossRef CAS.
- Q. Zhao, F. Li and C. Huang, Phosphorescent Chemosensors Based on Heavy-Metal Complexes, Chem. Soc. Rev., 2010, 39, 3007–3030 RSC.
- V. W.-W. Yam and A. S.-Y. Law, Luminescent d8 metal complexes of platinum(II) and gold(III): From photophysics to photofunctional materials and probes, Coord. Chem. Rev., 2020, 414, 213298 CrossRef CAS.
- P.-T. Chou, Y. Chi, M.-W. Chung and C.-C. Lin, Harvesting luminescence via harnessing the photophysical properties of transition metal complexes, Coord. Chem. Rev., 2011, 255, 2653–2665 CrossRef CAS.
- K. Li, G. S. M. Tong, Q. Wan, G. Cheng, W.-Y. Tong, W.-H. Ang, W.-L. Kwong and C.-M. Che, Highly phosphorescent platinum(II) emitters: photophysics, materials and biological applications, Chem. Sci., 2016, 7, 1653–1673 RSC.
- A. Haque, L. Xu, R. A. Al-Balushi, M. K. Al-Suti, R. Ilmi, Z. Guo, M. S. Khan, W.-Y. Wong and P. R. Raithby, Cyclometallated tridentate platinum(II) arylacetylide complexes: old wine in new bottles, Chem. Soc. Rev., 2019, 48, 5547–5563 RSC.
- E. C. Constable, R. P. G. Henney, T. A. Leese and D. A. Tocher, Cyclometalation reactions of 5-phenyl-2,2′-bipyridine; a potential C,N,N-donor analog of 2,2′:6′,2′′-terpyridine. Crystal and molecular structure of dichlorobis(6-phenyl-2,2′-bipyridine)ruthenium(II)., J. Chem. Soc., Dalton Trans., 1990, 443–449 RSC.
- S.-W. Lai, M. C.-W. Chan, T.-C. Cheung, S.-M. Peng and C.-M. Che, Probing d8-d8 Interactions in Luminescent Mono- and Binuclear Cyclometalated Platinum(II) Complexes of 6-Phenyl-2,2′-bipyridines, Inorg. Chem., 1999, 38, 4046–4055 CrossRef CAS.
- C. F. Harris, D. A. K. Vezzu, L. Bartolotti, P. D. Boyle and S. Huo, Synthesis, Structure, Photophysics, and a DFT Study of Phosphorescent C*N∧N- and C∧N∧N-Coordinated Platinum Complexes, Inorg. Chem., 2013, 52, 11711–11722 CrossRef CAS.
- Z. Wang, E. Turner, V. Mahoney, S. Madakuni, T. Groy and J. Li, Facile Synthesis and Characterization of Phosphorescent Pt(N∧C∧N)X Complexes, Inorg. Chem., 2010, 49, 11276–11286 CrossRef CAS PubMed.
- D. A. K. Vezzu, D. Ravindranathan, A. W. Garner, L. Bartolotti, M. E. Smith, P. D. Boyle and S. Huo, Highly Luminescent Tridentate N∧C*N Platinum(II) Complexes Featured in Fused Five–Six-Membered Metallacycle and Diminishing Concentration Quenching, Inorg. Chem., 2011, 50, 8261–8273 CrossRef CAS PubMed.
- J. A. G. Williams, The coordination chemistry of dipyridylbenzene: N-deficient terpyridine or panacea for brightly luminescent metal complexes?, Chem. Soc. Rev., 2009, 38, 1783–1801 RSC.
- A. F. Rausch, L. Murphy, J. A. G. Williams and H. Yersin, Improving the Performance of Pt(II) Complexes for Blue Light Emission by Enhancing the Molecular Rigidity, Inorg. Chem., 2012, 51, 312–319 CrossRef CAS PubMed.
- M. Lersch and M. Tilset, Mechanistic Aspects of C−H Activation by Pt Complexes, Chem. Rev., 2005, 105, 2471–2526 CrossRef CAS PubMed.
- K. Hanson, L. Roskop, P. I. Djurovich, F. Zahariev, M. S. Gordon and M. E. Thompson, A Paradigm for Blue- or Red-Shifted Absorption of Small Molecules Depending on the Site of π-Extension., J. Am. Chem. Soc., 2010, 132, 16247–16255 CrossRef CAS PubMed.
- P. Mandapati, J. D. Braun, C. Killeen, R. L. Davis, J. A. G. Williams and D. E. Herbert, Luminescent Platinum(II) Complexes of N∧N−∧N Amido Ligands with Benzannulated N-Heterocyclic Donor Arms: Quinolines Offer Unexpectedly Deeper Red Phosphorescence than Phenanthridines, Inorg. Chem., 2019, 58, 14808–14817 CrossRef CAS PubMed.
- P. Mandapati, J. D. Braun, I. B. Lozada, J. A. G. Williams and D. E. Herbert, Deep-Red Luminescence from Platinum(II) Complexes of N∧N−∧N–Amido Ligands with Benzannulated N–Heterocyclic Donor Arms, Inorg. Chem., 2020, 59, 12504–12517 CrossRef CAS PubMed.
- D. A. Bardwell, J. G. Crossley, J. C. Jeffery, A. G. Orpen, E. Psillakis, E. E. M. Tilley and M. D. Ward, A study of crystal packing in a series of closely related square-planar palladium(II) and platinum(II) complexes., Polyhedron, 1994, 13, 2291–2300 CrossRef CAS.
- C.-C. Kwok, H. M. Y. Ngai, S.-C. Chan, I. H. T. Sham, C.-M. Che and N. Zhu, [(O∧N∧N)PtX] Complexes as a New Class of Light-Emitting Materials for Electrophosphorescent Devices, Inorg. Chem., 2005, 44, 4442–4444 CrossRef CAS PubMed.
- E. V. Puttock, J. D. Fradgley, D. S. Yufit and J. A. G. Williams, A family of readily synthesised phosphorescent platinum(II) complexes based on tridentate N∧N∧O-coordinating Schiff-base ligands, Dalton Trans., 2019, 48, 15012–15028 RSC.
- R. Mondal, I. B. Lozada, R. L. Davis, J. A. G. Williams and D. E. Herbert, Site-Selective Benzannulation of N-Heterocycles in Bidentate Ligands Leads to Blue-Shifted Emission from [(P∧N)Cu]2(μ-X)2 Dimers, Inorg. Chem., 2018, 57, 4966–4978 CrossRef CAS PubMed.
- R. Mondal, I. B. Lozada, R. L. Davis, J. A. G. Williams and D. E. Herbert, Exploiting synergy between ligand design and counterion interactions to boost room temperature phosphorescence from Cu(I) compounds, J. Mater. Chem. C, 2019, 7, 3772–3778 RSC.
- R. Mondal, P. K. Giesbrecht and D. E. Herbert, Nickel(II), Copper(I) and Zinc(II) Complexes Supported by a (4-Diphenylphosphino)phenanthridine Ligand, Polyhedron, 2016, 108, 156–162 CrossRef CAS.
- R. H. Holm, G. W. Everett Jr. and A. Chakravorty, Metal complexes of Schiff bases and β-ketoamines., Prog. Inorg. Chem., 1966, 7, 83–214 CAS.
- I. B. Lozada, B. Huang, M. Stilgenbauer, T. Beach, Z. Qiu, Y. Zheng and D. E. Herbert, Monofunctional Platinum(II) Anticancer Complexes Based on Multidentate Phenanthridine-Containing Ligand Frameworks, Dalton Trans., 2020, 49, 6557–6560 RSC.
- P. Mandapati, P. K. Giesbrecht, R. L. Davis and D. E. Herbert, Phenanthridine-Containing Pincer-like Amido Complexes of Nickel, Palladium, and Platinum, Inorg. Chem., 2017, 56, 3674–3685 CrossRef CAS PubMed.
- M. H. Reineke, M. D. Sampson, A. L. Rheingold and C. P. Kubiak, Synthesis and Structural Studies of Nickel(0) Tetracarbene Complexes with the Introduction of a New Four-Coordinate Geometric Index, τδ, Inorg. Chem., 2015, 54, 3211–3217 CrossRef CAS PubMed.
- J. J. Davidson, J. C. DeMott, C. Douvris, C. M. Fafard, N. Bhuvanesh, C.-H. Chen, D. E. Herbert, C.-I. Lee, B. J. McCulloch, B. M. Foxman and O. V. Ozerov, Comparison of the Electronic Properties of Diarylamido-Based PNZ Pincer Ligands: Redox Activity at the Ligand and Donor Ability Toward the Metal, Inorg. Chem., 2015, 54, 2916–2935 CrossRef CAS PubMed.
- P. K. Giesbrecht, D. B. Nemez and D. E. Herbert, Electrochemical hydrogenation of a benzannulated pyridine to a dihydropyridine in acidic solution, Chem. Commun., 2018, 54, 338–341 RSC.
- C. Reichardt, Solvatochromic Dyes as Solvent Polarity Indicators, Chem. Rev., 1994, 94, 2319–2358 CrossRef CAS.
- J. Catalán, Toward a Generalized Treatment of the Solvent Effect Based on Four Empirical Scales: Dipolarity (SdP, a New Scale), Polarizability (SP), Acidity (SA), and Basicity (SB) of the Medium, J. Phys. Chem. B, 2009, 113, 5951–5960 CrossRef PubMed.
- G. Van der Zwan and J. T. Hynes, Time-dependent fluorescence solvent shifts, dielectric friction, and nonequilibrium solvation in polar solvents, J. Phys. Chem., 1985, 89, 4181–4188 CrossRef CAS.
- J. V. Caspar and T. J. Meyer, Photochemistry of tris(2,2′-bipyridine)ruthenium(2+) ion (Ru(bpy)32+). Solvent effects, J. Am. Chem. Soc., 1983, 105, 5583–5590 CrossRef CAS.
- K. L. Garner, L. F. Parkes, J. D. Piper and J. A. G. Williams, Luminescent Platinum Complexes with Terdentate Ligands Forming 6-Membered Chelate Rings: Advantageous and Deleterious Effects in N∧N∧N and N∧C∧N-Coordinated Complexes, Inorg. Chem., 2010, 49, 476–487 CrossRef CAS PubMed.
- I. B. Lozada, T. Murray and D. E. Herbert, Monomeric zinc(II) amide complexes supported by bidentate, benzannulated phenanthridine amido ligands, Polyhedron, 2019, 161, 261–267 CrossRef CAS.
- J. D. Braun, I. B. Lozada, C. Kolodziej, C. Burda, K. M. E. Newman, J. van Lierop, R. L. Davis and D. E. Herbert, Iron(II) coordination complexes with panchromatic absorption and nanosecond charge-transfer excited state lifetimes, Nat. Chem., 2019, 11, 1144–1150 CrossRef CAS PubMed.
- S. Gaire, R. J. Ortiz, B. R. Schrage, I. B. Lozada, P. Mandapati, A. J. Osinski, D. E. Herbert and C. J. Ziegler, (8-Amino)quinoline and (4-amino)phenanthridine complexes of Re(CO)3 halides, J. Organomet. Chem., 2020, 921, 121338 CrossRef CAS PubMed.
- A. R. G. Smith, P. L. Burn and B. J. Powell, Spin–Orbit Coupling in Phosphorescent Iridium(III) Complexes, ChemPhysChem, 2011, 12, 2429–2438 CrossRef CAS PubMed.
- E. Ronca, F. De Angelis and S. Fantacci, Time-Dependent Density Functional Theory Modeling of Spin–Orbit Coupling in Ruthenium and Osmium Solar Cell Sensitizers, J. Phys. Chem. C, 2014, 118, 17067–17078 CrossRef CAS.
- C. Gourlaouen and C. Daniel, Spin–orbit effects in square-planar Pt(II) complexes with bidentate and terdentate ligands: theoretical absorption/emission spectroscopy, Dalton Trans., 2014, 43, 17806–17819 RSC.
- J. D. Braun, I. B. Lozada and D. E. Herbert, In Pursuit of Panchromatic Absorption in Metal Coordination Complexes: Experimental Delineation of the HOMO Inversion Model Using Pseudo-Octahedral Complexes of Diarylamido Ligands, Inorg. Chem., 2020, 59, 17746–17757 CrossRef CAS PubMed.
- M. Hayashi, Y. Takahashi, Y. Yoshida, K. Sugimoto and H. Kitagawa, Role of d-Elements in a Proton–Electron Coupling of d–π Hybridized Electron Systems, J. Am. Chem. Soc., 2019, 141, 11686–11693 CrossRef CAS PubMed.
- M. Spencer, A. Santoro, G. R. Freeman, Á. Díez, P. R. Murray, J. Torroba, A. C. Whitwood, L. J. Yellowlees, J. A. G. Williams and D. W. Bruce, Phosphorescent, liquid-crystalline complexes of platinum(II): influence of the β-diketonate co-ligand on mesomorphism and emission properties, Dalton Trans., 2012, 41, 14244–14256 RSC.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- M. Mydlak, M. Mauro, F. Polo, M. Felicetti, J. Leonhardt, G. Diener, L. De Cola and C. A. Strassert, Controlling aggregation in highly emissive Pt(II) complexes bearing tridentate dianionic N∧N∧N ligands. Synthesis, photophysics, and electroluminescence., Chem. Mater., 2011, 23, 3659–3667 CrossRef CAS.
- Bruker-AXS, APEX3 v2016.1-0, Madison, Wisconsin, USA, 2016 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- A. L. Spek, PLATON, A Multipurpose Crystallographic Tool, Utrecht University, Utrecht, The Netherlands, 1998 Search PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Ernzerhof and G. E. Scuseria, Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- D. Andrae, U. Huermann, M. Dolg, H. Stoll and H. Preu, Energy-adjustedab initio pseudopotentials for the second and third row transition elements, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- C. van Wüllen, Molecular density functional calculations in the regular relativistic approximation: Method, application to coinage metal diatomics, hydrides, fluorides and chlorides, and comparison with first-order relativistic calculations, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- K. Suzuki, A. Kobayashi, S. Kaneko, K. Takehira, T. Yoshihara, H. Ishida, Y. Shiina, S. Oishi and S. Tobita, Reevaluation of absolute luminescence quantum yields of standard solutions using a spectrometer with an integrating sphere and a back-thinned CCD detector, Phys. Chem. Chem. Phys., 2009, 11, 9850–9860 RSC.
- S. L. Murov, I. Carmichael and G. L. Hug, Handbook of Photochemistry, Marcel Dekker, New York, 2nd edn, 1993 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional UV-Vis absorption and emission spectra; computational data tables; multi-nuclear NMR spectra of all new compounds; crystallographic information files containing all X-ray data. CCDC 2100576–2100578. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1qi01120k |
| This journal is © the Partner Organisations 2022 |