Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Elemental analysis: an important purity control but prone to manipulations†
Wolfgang
Kandioller‡
 a,
Johannes
Theiner‡
b,
Bernhard K.
Keppler
a and
Christian R.
Kowol
a,
Johannes
Theiner‡
b,
Bernhard K.
Keppler
a and
Christian R.
Kowol
 *a
*a
aFaculty of Chemistry, Institute of Inorganic Chemistry, University of Vienna, Waehringer Str. 42, A-1090, Vienna, Austria. E-mail: christian.kowol@univie.ac.at
bFaculty of Chemistry, Microanalytical Laboratory, University of Vienna, Waehringer Str. 42, A-1090, Vienna, Austria
First published on 21st December 2021
Abstract
Elemental analysis provides a powerful analytical tool for purity determination of compounds and is a prerequisite for publication in many journals dealing with (bio)inorganic synthetic chemistry. However, in contrast to other analytical methods, there is no requirement to prove the presented values e.g. with chromatograms, making this essential analysis prone to manipulations. Our personal observation in the review process of numerous manuscripts over the last years revealed that the amount of questionable data is constantly increasing. Within this article we discuss what realistic measured deviations from the theoretical composition of a compound are and present an approach to provide original elemental analysis data to support the listed values in the experimental sections. This would enable reviewers, editors and readers to better judge the presented results in the future.
Introduction
Elemental analysis marks the origin of chemical understanding. It has provided essential information about substances and their composition from the beginning of the development of chemical concepts and science in general. The advancement of organic chemistry (identification of natural substances as well as synthetic approaches) was based on the information about the composition and the molar mass of chemical compounds. Fritz Pregl compiled the methods after adapting them to consume as little as a few milligrams of material for one analysis and founded Organic Elemental Microanalysis (OEM, or simplified: elemental analysis).1 The typically analysed elements are carbon (C), hydrogen (H), nitrogen (N) and sulfur (S), rarely also oxygen (O) is measured.After the invention of mass spectrometry, the introduction of high performance liquid chromatography (HPLC) and the rise of nuclear magnetic resonance (NMR), the importance of elemental analysis in synthetic organic chemistry declined (in contrast to (bio)inorganic chemistry). Of course, elemental analysis seems to be a rather crude technique leading to nothing more than an empirical formula. It delivers only a few values which show little compared to the large amount of information generated from e.g. an NMR spectrum. Nevertheless, these values allow conclusions about the elemental composition and as a consequence the purity of compounds. This is the feature that makes elemental analysis unique among characterisation tools. Inorganic salts like NaCl derived from insufficient purification protocols or co-crystallized water molecules cannot be detected by NMR spectroscopy or HPLC, which easily can lead to errors of about 10–20% in the molar mass. As a consequence, this will generate wrong results when comparing e.g. rate constants (catalysis), biological data (medicinal chemistry) or material properties.
Reviewing elemental analysis data
In contrast to synthetic organic chemistry, elemental analysis is an essential part of substance characterization in the field of (bio)inorganic coordination chemistry. A likely explanation is that characterization of the subclass of paramagnetic compounds by NMR spectroscopy is not meaningful. Thus, in peer-reviewed international (bio)inorganic chemistry journals e.g. Inorganic Chemistry, Inorganic Chemistry Frontiers, Organometallics, Dalton Transactions, Journal of Inorganic Biochemistry, Journal of Biological Inorganic Chemistry, and many more, elemental analyses of newly synthesized compounds are a requirement for publication. Also, in case of multidisciplinary journals like Angewandte Chemie, Journal of American Chemical Society, Chemical Science, Chemistry – A European Journal, etc., this analysis is mandatory for synthetic (bio)inorganic chemistry. Usually, the measured values have to fit the gold standard of ± 0.40% of the calculated values to guarantee sufficient purity (see author guidelines e.g. of Organometallics,2Angewandte Chemie,3Chemistry – A European Journal4). This is essential for all subsequent biological, catalytical and analytical studies, which rely on this information for their accuracy. However, this is where the problems begin. Based on our experience as reviewers in various peer-reviewed journals, there are more and more manuscripts/publications, where the presented values are so perfect that it is extremely hard to believe that real values were actually measured.We checked the deviation of theoretical and experimental elemental analysis values in several issues of bioinorganic and general chemistry journals. About 5–10% of the publications show elemental analysis data where most or all values deviate ≤0.10% from the theoretical calculation. Of course, these data can be of experimental origin, however, it can also be an indication for faked values (especially in the case of a large number of perfectly fitting analyses). When extrapolating our observations to a global publication scale, it can be estimated that the number of publications with questionable elemental analysis data is in the four-digit range. Unfortunately, in contrast to fake biological data (which normally is a serious misconduct), in case of elemental analyses and compound purity it seems that this is largely not of interest or rather perceived as a cavalier offense.
Furthermore, it appears that a lot of referees don't check the elemental analysis data at all during their review process. This can be confirmed by reading the reports of other reviewers which are frequently provided by editors after the review process. However, the main problem is that it is currently not possible to go beyond the presented values as long as no additional information is provided.
Generally, there is no international protocol that regulates Quality Assurance (QA) in elemental analyses. With reference to ISO 9001 rules, “traceability” should be established as one of the corner stones of quality assurance.5 The ISO recommendation to only use validated methods is; however, out of reach as method validation would have to be performed for every single substance. As in synthetic chemistry research, an incredible number of compounds is characterised by the same instrumentation and methods, other strategies are necessary. At the moment there is no requirement to provide any additional information or original/raw data such as detailed experimental setups and/or chromatograms. Under the current conditions publishing fake elemental analysis data is rather easy and it is difficult if not impossible to prove that it has been manipulated. This is in strong contrast to other routinely applied analytical methods such as NMR, HRMS, HPLC, etc. where the spectra frequently have to be provided in the ESI. In addition, journals often prescribe very detailed instructions on how to present virtually any kind of data, but with the exception of elemental analyses where just the final values have to be listed. In case of X-ray analyses, the experimentally collected and refined data even has to be submitted to the Cambridge Crystallographic Data Centre (CCDC) and are deposited at the Cambridge Structural Database (CSD), where they are evaluated for suitability before publication.6 Notably and surprisingly, sometimes the presented NMR spectra in the ESI reveal significant impurities although the elemental analysis data are extremely well fitting (≤0.05% deviation from theory). This is also a strong indication for doubtful elemental analysis values.
What are realistic deviations from theory?
Of course, there might be an exact match occasionally, but no experimental method provides a reproducibility that ends in an exact match throughout a relevant number of substances. As mentioned the tolerance for sufficient purity is generally at ± 0.40%, considering traces of impurities, that the correctness of analysis is not absolute, as well as statistical errors. All these parameters sum up to this estimative reliability.But why are very small deviations throughout a whole series of compounds not realistic? Already co-crystallization of small amounts of water distinctly changes the elemental composition. For example, when 0.5 H2O co-crystallize with oxaliplatin (C8H14N2O4Pt) the difference for C is already 0.54%, which is more than the generally acceptable 0.40% from theory. The oxygen levels would prove the crystal water with a highly significant change from 16.11% to 17.72%. Though oxygen analysis is less widely reported it needs to be pointed out that automated methods are available for most elemental analysers. In case of a small organic molecule e.g. 4-morpholinoaniline (C10H14N2O) the influence of 0.5 H2O is even more dramatic due to the lower molecular mass, leading to a difference of 3.24% (C) and 0.76% (N), respectively. Even 0.1 eq. H2O would shift the values outside the acceptable range (0.68% for C).
Thus, very small amounts of water, organic solvents or inorganic materials can dramatically change the elemental composition. In case of commercially available compounds, the synthetic process is optimized and remaining solvent traces or other impurities are scarce. In contrast, newly developed research compounds are synthesised for the very first time. The respective protocols are not perfectly elaborated and purification processes are not fully optimized. Consequently, the chance that small amounts of remaining solvents or other impurities are present is high, and perfect elemental analysis data cannot be expected. Therefore, such values should be doubted, when a whole series of compounds in a manuscript/publication shows deviations ≤0.05% for all elements.
To prove this estimation, we analysed six commercially available compounds with different elemental composition (for chemical structures see Scheme S1†). Three organic compounds were investigated namely 3-hydroxy-2-methyl-pyr-4-one (maltol; C,H); 8-hydroxyquinoline (C,H,N), N-acetyl-L-cysteine (C,H,N,S) and three metal complexes: ferrocene (C,H), cobalt(II) acetylacetonate (C,H) and bis(8-hydroxyquinolinato)zinc (C,H,N). All have been purchased in high purity (>99%) (for respective NMR spectra see Fig. S1–S5†). The elemental composition of all six compounds was determined in triplicate to elucidate the differences to the theoretical values. First, we measured the compounds using an EA3000 CHNSO elemental analyser manufactured by Eurovector. It can be seen in Table 1 that out of the 48 measured values (18 × C; 18 × H; 9 × N and 3 × S), 42% show deviations from theory ≥0.10% and 77% ≥0.05%.
| 3-hydroxy-2-methyl-pyr-4-one | ||||||||
| C 6 H 6 O 3 | C | H | N | S | ||||
| Theoretical composition | 57.14 | Δ | 4.80 | Δ | 0.00 | Δ | 0.00 | Δ |
| Elemental analysis 1 | 57.29 | 0.15 | 4.87 | 0.07 | <0.05 | <0.02 | ||
| Elemental analysis 2 | 57.22 | 0.08 | 4.85 | 0.05 | <0.05 | <0.02 | ||
| Elemental analysis 3 | 57.23 | 0.09 | 4.86 | 0.06 | <0.05 | <0.02 | ||
| Average | 57.25 | 0.11 | 4.86 | 0.06 | ||||
| σ | 0.04 | 0.01 | ||||||
| 8-hydroxyquinoline | ||||||||
| C 9 H 7 NO | C | H | N | S | ||||
| Theoretical composition | 74.47 | Δ | 4.86 | Δ | 9.65 | Δ | 0.00 | Δ |
| Elemental analysis 1 | 74.80 | 0.33 | 4.91 | 0.05 | 9.75 | 0.10 | <0.02 | |
| Elemental analysis 2 | 74.56 | 0.09 | 4.94 | 0.08 | 9.83 | 0.18 | <0.02 | |
| Elemental analysis 3 | 74.80 | 0.33 | 4.91 | 0.05 | 9.76 | 0.11 | <0.02 | |
| Average | 74.72 | 0.25 | 4.92 | 0.06 | 9.78 | 0.13 | ||
| σ | 0.14 | 0.02 | 0.04 | |||||
| Ferrocene | ||||||||
| C 10 H 10 Fe | C | H | N | S | ||||
| Theoretical composition | 64.56 | Δ | 5.42 | Δ | 0.00 | Δ | 0.00 | Δ |
| Elemental analysis 1 | 64.68 | 0.12 | 5.48 | 0.06 | <0.05 | <0.02 | ||
| Elemental analysis 2 | 64.71 | 0.15 | 5.48 | 0.06 | <0.05 | <0.02 | ||
| Elemental analysis 3 | 64.74 | 0.18 | 5.48 | 0.06 | <0.05 | <0.02 | ||
| Average | 64.71 | 0.15 | 5.48 | 0.06 | ||||
| σ | 0.03 | 0.00 | ||||||
| Cobalt( II ) acetylacetonate | ||||||||
| C 10 H 14 CoO 4 | C | H | N | S | ||||
| Theoretical composition | 46.70 | Δ | 5.49 | Δ | 0.00 | Δ | 0.00 | Δ |
| Elemental analysis 1 | 46.10 | −0.60 | 5.56 | 0.07 | <0.05 | <0.02 | ||
| Elemental analysis 2 | 46.19 | −0.51 | 5.59 | 0.10 | <0.05 | <0.02 | ||
| Elemental analysis 3 | 46.13 | −0.57 | 5.59 | 0.10 | <0.05 | <0.02 | ||
| Average | 46.14 | −0.56 | 5.58 | 0.09 | ||||
| σ | 0.05 | 0.02 | ||||||
| Bis-(8-hydroxyquinolinato)zinc | ||||||||
| C 18 H 12 N 2 O 2 Zn | C | H | N | S | ||||
| Theoretical composition | 61.12 | Δ | 3.42 | Δ | 7.92 | Δ | 0.00 | Δ |
| Elemental analysis 1 | 60.83 | −0.29 | 3.39 | −0.03 | 7.88 | −0.04 | <0.02 | |
| Elemental analysis 2 | 60.85 | −0.27 | 3.39 | −0.03 | 7.90 | −0.02 | <0.02 | |
| Elemental analysis 3 | 60.94 | −0.18 | 3.40 | −0.02 | 7.90 | −0.02 | <0.02 | |
| Average | 60.87 | −0.25 | 3.39 | −0.03 | 7.89 | −0.03 | ||
| σ | 0.06 | 0.01 | 0.01 | |||||
| N-Acetyl-L-cysteine | ||||||||
| C 5 H 9 NO 3 S | C | H | N | S | ||||
| Theoretical composition | 36.80 | Δ | 5.56 | Δ | 8.59 | Δ | 19.65 | Δ |
| Elemental analysis 1 | 36.73 | −0.07 | 5.60 | 0.04 | 8.56 | −0.03 | 20.01 | 0.36 |
| Elemental analysis 2 | 36.74 | −0.06 | 5.61 | 0.05 | 8.57 | −0.02 | 19.94 | 0.29 |
| Elemental analysis 3 | 36.76 | −0.04 | 5.61 | 0.05 | 8.56 | −0.03 | 20.02 | 0.37 |
| Average | 36.76 | −0.06 | 5.61 | 0.05 | 8.55 | −0.03 | 19.99 | 0.34 |
| σ | 0.02 | 0.01 | 0.01 | 0.04 | ||||
Next, we determined the same compound panel on a different instrument (2400 CHNSO from PerkinElmer in the CHN mode; Table S1†). The data were very well comparable with 53% ≥ 0.10% and 78% ≥ 0.05% deviation. In addition, the same compound panel was sent to three independent elemental analysis service facilities. HEKAtech measured the samples also on an EA3000 CHNSO instrument resulting in 40% ≥ 0.10% and 52% ≥ 0.05% deviation from theory for the 48 values (Table S2†) Elementar Analysensysteme measured on a Unicube instrument with 27% ≥ 0.10% and 52% ≥ 0.05% deviation (Table S3;† this company used the best fitting three out of four analyses). The company Solvias measured the six compounds on two different instruments: 56% ≥ 0.10% and 75% ≥ 0.05% for the Unicube instrument (Table S4†) and 48% ≥ 0.10% and 73% ≥ 0.05% deviation from theory on an EA3000 CHNSO elemental analyser (Table S5†). The average over all measurements at the different facilities results in 44% ≥ 0.10% and 69% ≥ 0.05% deviation from the theoretical values.
Except for cobalt(II) acetylacetonate, nearly all values had deviations <0.40% which confirmed the elemental composition and purity of the compounds. The strong deviations of cobalt(II) acetylacetonate can be explained by the hygroscopic behaviour of the substance. After inclusion of 0.25 eq. water to the theoretical composition the measured C and H values fit perfectly. This was proven by determination of the oxygen levels by elemental analysis confirming the presence of 0.25 equivalents of H2O (also the oxygen levels of all other compounds could be proven; Table S6†). The elemental analysis data of the companies indicate that the crystal water increased to 0.5 eq. during transport of cobalt(II) acetylacetonate, again in good agreement with their oxygen analyses (data not shown).
The results impressively show that typical deviations from theory are in the range of 0.05–0.20% even when high purity commercial compounds are analysed. Just in few cases all values of a compound are ≤0.05%. Notably, in ∼40% of the analysed elements already the standard deviation from triplicate measurements is ≥0.05 (Table 1 and Tables S1–S5†). This means when the same sample is measured several times at the same instrument, a difference of ≥0.05% between the individual measurements is not unlikely. Therefore, it is hard to believe that a whole set of compounds in a publication shows perfectly fitting values with ≤0.05% for all elements.
Documentation of elemental analyses as standard for future publications
Despite the data we present that very small deviations from theory are not likely for a larger series of compounds, a discussion between authors and reviewers on this topic is not even possible or would be ineffective since no “proof” of elemental analysis values is required. Hence, the reviewer's hands are tied if they suspect some values in a manuscript to be unrealistic. This problem can only be solved if measured data and parameters are available and the experimental section contains sufficient information for “traceability”. Therefore, a guideline for data presentation is essential and of high urgency. If this guideline becomes a standard the problem with doubtful elemental analysis values could be widely overcome.Recommendations
The experimental part/ESI should contain the following information:(1) the laboratory where the elemental analyses have been performed and the used instrumentation (elemental analyser, balance),
(2) range of the weighted sample amounts and accuracy of weighing (±μg),
(3) limit of quantification for each element,
(4) used standards for calibration (the reference materials should cover the elemental %-range of the measured samples),
(5) are the presented values based on a single measurement or the average of multiple determinations,
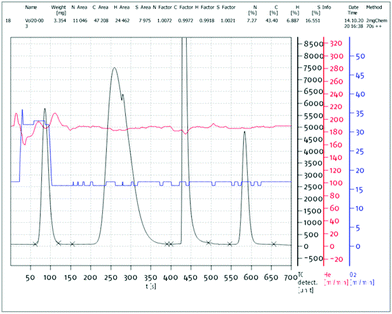
(6) a figure of the original data of each elemental analysis, with the analysis ID, the respective peak integrations and the calibration factors/blank values (e.g.Fig. 1 and 2).
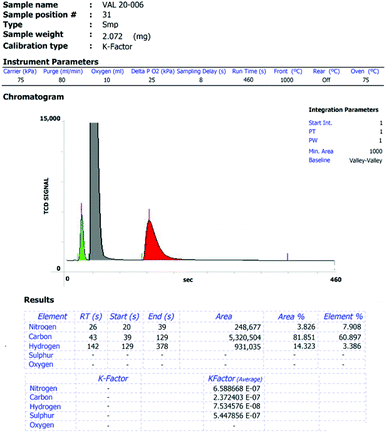 | ||
| Fig. 1 Exemplary elemental analysis report with the respective chromatogram, peak areas and scale factors of an EA3000 CHNSO analyser from Eurovector. | ||
In general, the elemental composition in % can be calculated using the following formula:
An example for the methodological part would be:
Elemental analyses were performed by the Microanalytical Laboratory of the University of Vienna on an EA3000 CHNSO analyser manufactured by Eurovector. Samples were weighed on a Sartorius SEC 2 ultra-micro balance with ± 0.1 μg resolution. Sample weights from 1–3 mg were used. For calibration two NIST-certified reference materials were used: sulfanilamide (C6H8N2O2S) and BBOT (2,5-bis-(5-tert-butyl-2-benzoxazol-2-yl)-thiophenone, C26H26N2O2S). The limit of quantification (LOQ) was 0.05 wt% for C, H, N and 0.02 wt% for S. Also for samples without N and/or S, the content of these elements was determined and verified to be below LOQ. The presented values are the average of determinations in triplicate. The respective chromatograms with peak integrations and scale factors can be found in the ESI.
Parts of the standard analysis report of the EA3000 instrument from Eurovector and the UNICUBE from Elementar are presented in Fig. 1 and 2, respectively. In such a report all necessary data is already collected. Simple copy and paste into the ESI of a publication enables tracking of the presented values.
An alternative read out (from an older devices) can be a line chart of the data (Fig. S6†), including the respective formula to calculate the elemental contents.
Conclusions
The purity of a compound is the basis of reliable and reproducible research. Elemental analysis is still an essential method to guarantee sufficient purity of novel compounds. However, more and more often the elemental analysis values in submitted manuscripts or already accepted publications are doubtful, because the reported deviations from theory are extremely small (≤0.05%), which is hardly possible for all elements in a panel of compounds. As we have shown with six commercially available high purity (>99%) compounds, in ∼70% the values are ≥0.05% and even the standard deviation of repeated analyses is ≥0.05% in 40% of the measurements. Unfortunately, there is currently no possibility to verify presented data in a manuscript or publication. We suggest the following strategy to overcome this problem: A more detailed instrumental and experimental part should be provided by the authors and chromatograms of the performed measurements in the ESI. To include such information is already routine for other analytical methods like NMR spectroscopy. This would raise the reliability of elemental analysis data to a new level and guarantee that the presented research is indeed based on sufficiently pure compounds.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the support by Fabio Manco from Solvias AG, Switzerland; Klaus Hecker from HEKAtech GmbH Germany and Sabine Kraus from Elementar Analysensysteme GmbH Germany who contributed their measurement to this work. We thank Alexander Unterlercher for NMR measurements.References
-
F. Pregel, Die Quantitative Organische Mikroanalyse, Julius Springer, Berlin, 1917 Search PubMed
.
- Author Guidelines – Organometallics, https://publish.acs.org/publish/author_guidelines?coden=orgnd7, (accessed September 10, 2021).
- Notice to Authors – Angewandte Chemie International Edition, http://onlinelibrary.wiley.com/page/journal/15213773/homepage/notice-to-authors, (accessed September 10, 2021).
- Author guidelines – Chemistry – A European Journal, http://onlinelibrary.wiley.com/page/journal/15213765/homepage/2111_guideline.html (accessed September 10, 2021).
- ISO/IEC 17025:2017 International Standard: General requirements for the competence of testing and calibration laboratories, 2017.
- Deposit – The Cambridge Crystallographic Data Centre (CCDC), https://www.ccdc.cam.ac.uk/deposit/upload, (accessed September 10, 2021).
Footnotes |
| † Electronic supplementary information (ESI) available: Structure and NMR spectra of the investigated compounds, experimental part, elemental analyses data. See DOI: 10.1039/d1qi01379c |
| ‡ These authors contributed equally to this work. |
| This journal is © the Partner Organisations 2022 |