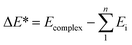Open Access Article
Open Access ArticleImportance of water and intramolecular interaction governs substantial blue shift of Csp2–H stretching frequency in complexes between chalcogenoaldehydes and water†
Nguyen Thi Thanh Cuc a,
Nguyen Truong An
a,
Nguyen Truong An a,
Vu Thi Ngan
a,
Vu Thi Ngan a,
Asit. K. Chandra
a,
Asit. K. Chandra b and
Nguyen Tien Trung
b and
Nguyen Tien Trung *a
*a
aLaboratory of Computational Chemistry and Modelling (LCCM), Department of Chemistry, Faculty of Natural Sciences, Quy Nhon University, Vietnam. E-mail: nguyentientrung@qnu.edu.vn; thanhcuc1501@gmail.com; truongan.spk37@gmail.com; vuthingan@qnu.edu.vn
bDepartment of Chemistry, North-Eastern Hill University, Shillong 793022, Meghalaya, India. E-mail: akchandra@nehu.ac.in
First published on 12th January 2022
Abstract
Geometrical structure, stability and cooperativity, and contribution of hydrogen bonds to the stability of complexes between chalcogenoaldehydes and water were thoroughly investigated using quantum chemical methods. The stability of the complexes increases significantly when one or more H2O molecules are added to the binary system, whereas it decreases sharply going from O to S, Se, or Te substitution. The O–H⋯O H-bond is twice as stable as Csp2–H⋯O and O–H⋯S/Se/Te H-bonds. It is found that a considerable blue-shift of Csp2–H stretching frequency in the Csp2–H⋯O H-bond is mainly determined by an addition of water into the complexes along with the low polarity of the Csp2–H covalent bond in formaldehyde and acetaldehyde. The Csp2–H stretching frequency shift as a function of net second hyperconjugative energy for the σ*(Csp2–H) antibonding orbital is observed. Remarkably, a considerable Csp2–H blue shift of 109 cm−1 has been reported for the first time. Upon the addition of H2O into the binary systems, halogenated complexes witness a decreasing magnitude of the Csp2–H stretching frequency blue-shift in the Csp2–H⋯O H-bond, whereas CH3-substituted complexes experience the opposite trend.
1 Introduction
Understanding non-covalent interactions is essential for elucidating the mysteries of cellular functions in health issues in order to explore new treatments, and to develop new drugs and materials.1 Among non-covalent interactions, the hydrogen bond (H-bond) is an interaction of significant importance in numerous fields of science, such as molecular recognition, protein folding, structural organization of nucleic acids, crystal and polymer packing, self-assembly, supramolecular chemistry, solvation, and even organic synthesis.2,3 The A–H⋯B H-bond is a weak non-covalent interaction, where A and B are usually highly electronegative elements, and B carries a region of high electron density, such as a lone pair, negative charge or π-systems. The red-shifting hydrogen bond (RSHB) is followed by an elongation of the A–H bond and a decrease in its stretching vibrational frequency. The origin of the RSHB, which is mainly an electrostatic attraction between H and B atoms, has been well-comprehended. Since the 1980s, however, the blue-shifting hydrogen bond (BSHB) has been found with the opposite characteristics, including an A–H contraction and a stretching frequency increase in the A–H⋯B H-bond as compared to those in the isolated monomer.4 Although several hypotheses have been proposed to justify this phenomenon;5–10 the origin of BSHB is still a matter of debate. For instance, Wu et al. suggested that the A–H stretching frequency shift was determined by the long-range electrostatic interaction of the A–H bond and B atom, and the short-range hyperconjugative interaction of n(B) → σ*(A–H).11 The competition of these two factors including the A–H covalent and ionic states causes different changes in direction of the A–H stretching frequency, in which the former one tends to shift it to blue, whereas the latter one leads to a red-shifting.12 In another context, Gordon et al. suggested that Pauli repulsion induces an enhancement of its A–H stretching frequency, whereas a lowering of A–H stretching frequency originated from a combination of electrostatic and dispersion forces.9 The long-range electrostatic and Pauli exchange interactions overcoming the total effect of polarization and charge transfer interaction determines the increase of A–H stretching frequency.13 Besides, Hermansson emphasized that the stretching frequency blue shift of C–H bond as a proton donor is related to the presence of a negative dipole moment derivative dμ0/drCH of the H-bond donor molecule.14 Krimm et al. also showed that when the field and dipole derivative are antiparallel, as in the case of C–H⋯O hydrogen bond, the C–H bond length shortens and causes its blue shift of stretching frequency.15 This model was utilized to understand phenomenon on the blue-shifting and red-shifting H-bonds.16,17The C–H⋯B H-bond (C is carbon) is of considerable importance owing to its ubiquity and large diversity in nature. Currently, the organic synthesis approach based on the activation and functionalization of C–H bond has become a key strategy due to its high abundance and rich variety in organic chemistry.10,18,19 In this approach, the presence of H-bonds containing C–H bonds is observed in the intermediates, which facilitates the formation of the desired products.3,20 The first experimental proof for BSHB was discovered by Trudeau et al., who investigated complexes of fluoroparaffins containing –CHF2 groups and several proton acceptors and realized the shortening of the C–H bonds and their stretching frequency shifting to a higher energy level, i.e. a blue-shift.4 Further evidence of increase in stretching frequency of the C–H bonds involving H-bonds was reported upon the complexation between triformylmethane and chloroform, or between chloroform, deuterochloroform, bromoform, and some proton acceptors containing carboxyl, nitro, and sulfo groups.21,22 The C–H stretching frequency blue-shift was measured using infrared (IR) spectroscopy by Boldeskul et al. in 1997 in complexes between haloforms and nitromethane or nitrobenzene.23 Direct evidence of the C–H stretching frequency blue-shift of 14 cm−1 in gas phase was observed in 1999 for the complex between chloroform and fluorobenzene, using double-resonance IR ion-depletion spectroscopy.24 So far, a large variety of BSHB with the involvement of C–H bond as proton donor in C–H⋯O/N/halogen/π H-bonds, of which the C–H⋯O/N H-bonds are most abundantly reported, have been recorded experimentally using IR and Raman spectroscopy.25–33 More recently, in 2019, a very slight C–H blue-shift of 8.7 cm−1 was even observed by Fourier transform IR spectroscopy for the C–H⋯N H-bond in the binary Cl3CH⋯NCCH3 complex.34
Similar to covalent Csp3–H bonds (Csp3 refers to the tetrahedral carbon), the stretching frequency blue-shifts were recently observed in Csp2–H bonds upon the formation of hydrogen-bonded complexes to a larger extent.35,36 Indeed, the data at the B3LYP/6-311++G(d,p) level of theory reported a large increase in the stretching frequency of Csp2–H covalent bond involving in Csp2–H⋯O H-bond of ca. 93 cm−1 upon complexation between CH3CHO and two H2O molecules.35 Nevertheless, the role of H2O that affects the Csp2–H contraction, the cooperativity of H-bond and the strength of the formed complexes has not yet emerged in literature. A considerable Csp2–H blue-shift, up to 81–96 cm−1 in the Csp2–H⋯O H-bonds formed by the interactions of formaldehydes and thioformaldehydes with formic acid has recently been reported.36 In the complexes between HCHO and one or two H2O molecules, the blue-shifts of Csp2–H stretching frequency were found to be 45 and 66 cm−1, respectively,37 which are also significantly greater than those of Csp3–H bond in Cl3CH⋯NCCH3 (ΔνCH = 8.7 cm−1)34 and F3CH⋯OH2 (ΔνCH = 20.3 cm−1).38
Furthermore, the strength and characteristics of O–H⋯S, S–H⋯O/S H-bonds in the systems such as (H2O)2, (H2S)n (n = 2–4), and H2O⋯H2S were realized both computationally and experimentally.39–44 It is noteworthy that a large number of unconventional H-bonds have been found, which demonstrates the pivotal role of H-bonds in biomolecular structure, catalysis, etc. Surprisingly, the O–H⋯Se/Te H-bonds have also been observed experimentally and confirmed by computations.45–53 Nevertheless, a systematic investigation into strength and properties of the O–H⋯Z, with Z being chalcogens such as O, S, Se, and Te, has not been available in the literature.
To date, the intensive investigations of the BSHB have mainly concentrated on the Csp3–H proton donor, while the ability of blue- or red-shift of the Csp2–H vibrational stretching frequency upon complexation has rarely been studied coherently and consistently. Accordingly, in order to clarify the origin of BSHB, it is imperative to explore characteristics of the Csp2–H⋯O H-bond with various polarity of Csp2–H covalent bond, because of the fact that medium Csp2–H bond polarity makes its stretching frequency shift more sensitive to the proton affinity of various proton acceptors. To the best of our knowledge, the hydrogen-bonded complexes of chalcogenoaldehydes RCHZ (R = H, F, Cl, Br, CH3; Z = O, S, Se, Te) with a few water molecules have not yet been reported, especially the ternary and quaternary systems.
In the present work, a theoretical investigation into characteristics of nonconventional and conventional H-bonds and strength of the complexes of chalcogenoaldehydes and waters in gas phase is carried out. One to three water molecules are added in complexes investigated with purpose of clarifying role of water molecule on blue shift of Csp2–H stretching frequency in the Csp2–H⋯O H-bond, cooperativity of H-bonds, and strength of complexes. More importantly, the impact of the O–H⋯O/S/Se/Te H-bonds on the stability of Csp2–H⋯O H-bonds and characteristics of Csp2–H blue shift of stretching frequency in the complexes are investigated thoroughly. In addition, importance of intramolecular and intermolecular electron transfer in the complexes to Csp2–H stretching frequency blue-shift involving H-bonds is also evaluated.
2 Computational methods
All calculations of geometric optimization, harmonic vibrational frequency and thermodynamic parameter for monomers and complexes are performed by means of the Gaussian 09 package.54 The geometrical structure and vibrational spectra are computed using the second-order Moller–Plesset perturbation theory (MP2). The basis set 6-311++G(3df,2pd) is used for all atoms while the aug-cc-pVTZ basis set is utilized for Te atom. Deprotonation enthalpies (DPE) of Csp2–H bonds, proton affinities (PA) at the Z site of XCHZ monomers were evaluated at the same level of theory. In order to enhance the accuracy of energetic parameters, further calculations were carried out at the sophisticated CCSD(T)/6-311++G(3df,2pd) level with the MP2 optimized geometries. The interaction energies (ΔE*) with both zero-point energy (ZPE) and basis set superposition error (BSSE) corrections using the Boys and Bernardi scheme were calculated as follows:55In which Ecomplex is the total energy of the complex, Ei is the single point energy of the monomers, and n is the number of monomers.
The cooperativity of a ternary complex containing A, B, C molecules (ΔEcoop) was computed as:
| ΔEcoop = E(ABC) − E2(AB) − E2(BC) − E2(AC) |
In which, the E(ABC) and E2 values correspond to the total interaction energy and the pairwise interaction energy at the optimized geometry of the ternary system calculated at the CCSD(T)/6-311++G(3df,2pd).
The electron density (ρ(r)) and Laplacian of electron density (∇2ρ(r)) at bond critical points (BCPs) were evaluated at the MP2/6-311+G(3df,2pd) level using the quantum theory of atoms in molecule (AIM)56 as implemented in the AIMALL program.57 The individual energy of each H-bond (EH-bond) was calculated according to the formula of Espinosa–Molins–Lecomte based on the electron density distribution at the BCPs of H-bonds: EH-bond = 0.5V(r),58 in which V(r) was the electronic potential energy density. The natural bond orbital (NBO) analysis was invoked to deeply explore the characteristics of the bonding formation, stability, and the effect of various factors on H-bonds. The orbital occupancies, intramolecular and intermolecular hyperconjugation energies in NBO analysis were performed at the ωB97X-D/6-311++G(3df,2pd) level using NBO 5.G program.59 The range-separated hybrid functional ωB97X-D has been proved to be appropriate for treating non-covalent interactions.60 In addition, NCIplot description was also utilized to visualize the weak interaction.61
3 Results and discussion
3.1 Structure, energetics and AIM analysis
As presented in Fig. 1, the interaction of XCHZ⋯nH2O (X = H, F, Cl, Br, CH3; Z = O, S, Se, Te; n = 1–3) induces 60 stable complexes in three shapes on the potential energy surfaces. The sp2-hybridized carbon atom in XCHZ is hereafter denoted as Csp2. Structures of the binary, ternary and quaternary systems are labelled as XZ-1, XZ-2 and XZ-3, respectively. The XZ-1 is stabilized by intermolecular contacts including O–H⋯Z and Csp2–H⋯O. The addition of H2O molecules into binary complexes to form ternary XZ-2, then quaternary XZ-3 leads to the emergence of an interaction (O–H⋯O) between the two water molecules. The intermolecular distances R1, R2, R3, R4 (cf. Table S1 of ESI†) correspond to O2–H1⋯Z, Csp2–H⋯O2/O5/O8, O5–H4⋯O2 and O8–H7⋯O5 contact as illustrated in Fig. 1.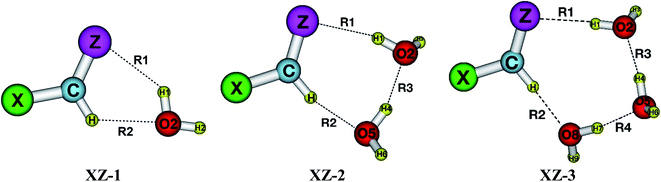 | ||
| Fig. 1 Stable structures of the complexes XCHZ⋯nH2O (with X = H, F, Cl, Br, CH3; Z = O, S, Se, Te; n = 1–3) at MP2/6-311++G(3df,2pd). | ||
The O⋯H, S⋯H, Se⋯H, Te⋯H intermolecular distances in the complexes are in the range of 1.77–2.66 Å; 2.29–2.63 Å; 2.43–2.73 Å; 2.64–2.93 Å, respectively, which are smaller than the sum of van der Waals radii of the corresponding contact atoms of 2.72, 3.00, 3.10, 3.26 Å (cf. Table S1†). These initial results roughly suggest the presence of O–H⋯O/S/Se/Te and Csp2–H⋯O H-bonds in the complexes. Intermolecular contacts are also affirmed by the existence of BCPs with the values of electron density and Laplacian being within the criteria for formation of H-bond (cf. Table S2a–c†),62 except for the contact Csp2–H⋯O in H/CH3O-1 due to low polarity of Csp2–H in HCHO, CH3CHO compared to that in the remaining monomers. Indeed, all values of electron density (ρ(r)) and Laplacian (∇2ρ(r)) at the BCPs in Csp2–H⋯O and O–H⋯Z intermolecular contacts are in the range of 0.0083–0.0366 au and 0.025–0.103 au, respectively. The EH-bond values suggest that the strength of O–H⋯S/Se/Te H-bonds is quite similar to that of Csp2–H⋯O one, and is about a half of the O–H⋯O strength. Indeed, they range from −14.9 to −45.9 kJ mol−1, −7.0 to −22.6 kJ mol−1, −6.7 to −23.3 kJ mol−1 for O–H⋯O, O–H⋯S/Se/Te, Csp2–H⋯O H-bonds, respectively. As a result, it is suggested that the O–H⋯O H-bond plays a substantial role in stabilizing the XO-1 complexes with an additional role of the Csp2–H⋯O H-bonds. For the XS/Se/Te-1 systems, the complexes are contributed by both O–H⋯S/Se/Te and Csp2–H⋯O H-bonds.
In order to examine the effect of proton donor or acceptor ability of the isolated monomers on the strength of intermolecular interactions, deprotonation enthalpies of Csp2–H and proton affinities at the Z sites of XCHZ are calculated and given in Table 1. For the X substitution in XCHZ, the distances R1 in the complexes lessen in the order of F ∼ Cl ∼ Br > H > CH3 substituted derivatives, implying that the strength of O2–H1⋯Z H-bonds rises in this sequence. The electron density and the absolute value of H-bond energies at the BCPs of O2–H1⋯Z H-bonds explain such a trend well (cf. Table S2a–c of ESI†). This arises from a decrease of the Z proton affinity in XCHZ as going from CH3 to H to Br to Cl and F substitution (cf. Table 1). Besides, Csp2–H⋯O2/O5/O8 H-bonds are much more stable for halogenated complexes than for the others. The strength of Csp2–H⋯O H-bonds in the complexes is also directed due to the polarity of Csp2–H bond in XCHZ. Accordingly, the strength of the H-bond following complexation depends on proton affinity of Z and polarity of Csp2–H bond in the isolated XCHZ.
| HCHO | FCHO | ClCHO | BrCHO | CH3CHO | HCHS | FCHS | ClCHS | BrCHS | CH3CHS | |
|---|---|---|---|---|---|---|---|---|---|---|
| a Experimental data. | ||||||||||
| DPE(Csp2–H) | 1684.9 | 1583.8 | 1540.9 | 1505.0 | 1659.9 | 1636.5 | 1581.3 | 1557.7 | 1542.0 | 1629.1 |
| DPE(Csp2–H)a | 1650.7 (ref. 63) | 1645.1 (ref. 64) | ||||||||
| PA(O/S) | 696.6 | 642.2 | 678.2 | 682.5 | 755.6 | 753.1 | 706.8 | 739.3 | 746.1 | 793.4 |
| PA(O)a | 712.9 (ref. 65) | 768.5 (ref. 66) | ||||||||
| HCHSe | FCHSe | ClCHSe | BrCHSe | CH3CHSe | HCHTe | FCHTe | ClCHTe | BrCHTe | CH3CHTe | |
|---|---|---|---|---|---|---|---|---|---|---|
| DPE(Csp2–H) | 1625.9 | 1571.2 | 1554.6 | 1542.2 | 1623.5 | 1611.4 | 1560.1 | 1549.7 | 1540.8 | 1614.4 |
| PA(Se/Te) | 754.2 | 716.9 | 744.8 | 751.3 | 791.4 | 770.2 | 740.0 | 761.7 | 766.9 | 801.2 |
For the same X, on the basis of the EH-bond values it is found that the strength of O–H⋯Z H-bonds decreases in the sequence of O–H⋯O ≫ O–H⋯S > O–H⋯Se > O–H⋯Te. As shown in Table 1, the proton affinities of Te in XCHTe are stronger than those of its lighter congeners. Therefore, electronegativity of the Z atoms could be the reason for the trend of H-bond strength.67 Indeed, the electronegativity of the Z atom decreases as Z goes from O (3.44) to S (2.58), to Se (2.55) and then Te (2.10). This affirms a dominant role of the O atom compared to the S, Se, and Te ones in XCHZ in stabilizing O–H⋯Z H-bonds. In general, the Csp2–H⋯O H-bond is less stable for XO-n than for XS/Se/Te-n, indicating that the strength of Csp2–H⋯O H-bonds is governed by the polarity of Csp2–H covalent bonds in XCHZ (cf. Table 1), except for CH3S/Se/Te-3 with an additional presence of Csp3–H⋯O H-bond.
The EH-bond value becomes more negative when adding H2O molecules into a binary system (cf. Tables S2a–c†). The Csp2–H⋯O and O–H⋯Z H-bonds become more stable as more water molecules are added. A rising strength of the XZ-n systems is induced in going from the binary to ternary and then to quaternary ones. Indeed, at the CCSD(T)/6-311++G(3df,2pd)//MP2/6-311++G(3df,2pd) level, the interaction energies of XZ-3 are about two and four times as negative as those of XZ-2 and XZ-1 (cf. Table 2). This data indicates a key role of O–H⋯O H-bonds in stabilizing the complex.
| Complex | ΔE* | Complex | ΔE* | Ecoop | Complex | ΔE* |
|---|---|---|---|---|---|---|
| HO-1 | −12.5 | HO-2 | −35.4 | −14.1 | HO-3 | −59.6 |
| FO-1 | −12.5 | FO-2 | −38.0 | −13.7 | FO-3 | −63.4 |
| ClO-1 | −12.2 | ClO-2 | −36.9 | −13.4 | ClO-3 | −61.8 |
| BrO-1 | −12.1 | BrO-2 | −36.3 | −13.0 | BrO-3 | −61.4 |
| CH3O-1 | −15.3 | CH3O-2 | −39.1 | −14.7 | CH3O-3 | −64.0 |
| HS-1 | −9.8 | HS-2 | −30.4 | −13.6 | HS-3 | −52.8 |
| FS-1 | −10.6 | FS-2 | −32.0 | −13.2 | FS-3 | −55.0 |
| ClS-1 | −10.5 | ClS-2 | −32.2 | −13.3 | ClS-3 | −55.2 |
| BrS-1 | −10.6 | BrS-2 | −32.0 | −13.2 | BrS-3 | −55.1 |
| CH3S-1 | −11.7 | CH3S-2 | −33.8 | −13.9 | CH3S-3 | −58.6 |
| HSe-1 | −9.8 | HSe-2 | −30.4 | −13.4 | HSe-3 | −52.5 |
| FSe-1 | −11.0 | FSe-2 | −32.5 | −13.2 | FSe-3 | −55.5 |
| ClSe-1 | −11.0 | ClSe-2 | −32.6 | −13.4 | ClSe-3 | −55.6 |
| BrSe-1 | −10.9 | BrSe-2 | −32.5 | −13.3 | BrSe-3 | −55.4 |
| CH3Se-1 | −11.9 | CH3Se-2 | −33.7 | −13.6 | CH3Se-3 | −58.2 |
| HTe-1 | −9.2 | HTe-2 | −29.2 | −12.8 | HTe-3 | −50.8 |
| FTe-1 | −10.8 | FTe-2 | −31.7 | −12.9 | FTe-3 | −54.2 |
| ClTe-1 | −10.8 | ClTe-2 | −31.9 | −13.0 | ClTe-3 | −54.3 |
| BrTe-1 | −10.7 | BrTe-2 | −31.7 | −12.9 | BrTe-3 | −54.3 |
| CH3Te-1 | −11.1 | CH3Te-2 | −32.3 | −13.0 | CH3Te-3 | −55.8 |
For a particular functional group Z, a lessening of strength is found in the order of CH3Z-n > F/Cl/BrZ-n > HZ-n. The stability of H/CH3Z-n is mainly determined by the O–H⋯Z H-bonds while the O–H⋯Z and Csp2–H⋯O H-bonds contribute to the strength of F/Cl/BrZ-n, as halogenation enhances the acidity of the C–H bond. It is noted that the interaction energies for HCHO⋯H2O, FCHO⋯H2O, CH3CHO⋯H2O in the present work are quite close to those at MP2/aug-cc-pVTZ level in ref. 68 For the same substituent X, the stability of complexes tends to decrease sharply in the sequence of XO-n ≫ XS-n ∼ XSe-n ∼ XTe-n (cf. Table 2 and Fig. 2). The significantly larger strength of XO-n compared to XS/Se/Te-n certifies the much higher strength of O2–H1⋯O H-bond over the O2–H1⋯S/Se/Te ones as realized above. This observation is in accordance with the decrease of the complex strength in the order of H2O⋯nHX ≫ H2S/Se⋯nHX (X = F, Cl, Br; n = 1, 2).67 Consequently, the stabilization of complexes is dominated by a larger role of O atom compared to the S, Se, Te ones in XCHZ.
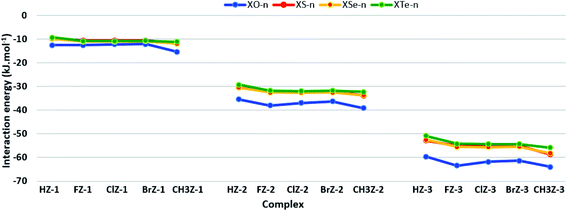 | ||
| Fig. 2 Correlation between interaction energy and the substituent group in different complex series. | ||
In order to compare the structure and strength of XZ-n and (H2O)n complexes, geometrical optimization and interaction energies of (H2O)n (with n = 2–4) complexes are performed at CCSD(T)/6-311++G(3df,2dp)//MP2/6-311++G(3df,2dp). The obtained results show that the most stable structures of (H2O)n are similar to those of XZ-n,69,70 As given in Table S3 of ESI,† it is found that the (H2O)n complexes are more stable than XZ-n ones for the same value of n, indicating that addition of H2O into binary and ternary and quaternary induces larger strength of relevant complexes.
Large negative values of Ecoop from −12.9 to −14.7 kJ mol−1 are estimated in all XZ-2 ternary complexes (cf. Table 2), indicating strong positive cooperativity of intermolecular interactions in the complexes. For the same functional group Z, the negative Ecoop values rise in the sequence of FZ-n ∼ ClZ-n ∼ BrZ-n < HZ-n < CH3Z-n, exhibiting a cooperative decrease in the halogenated complexes and a cooperative increase in CH3-substituted complexes.
For the same X, a declining pattern of positive cooperativity is observed in the order of XO-2 ≫ XS-2 ∼ XSe-2 > XTe-2, which is similar to the trend of interaction energy in the complexes. This shows that the presence of O2–H1⋯O H-bond versus O2–H1⋯S/Se/Te ones in the ternary complexes makes positive cooperativity stronger, leading to the considerably greater strength of XO-n as opposed to the rest of complexes.
3.2 NBO analysis and NCI plot
The selected results of NBO analysis at the ωB97X-D/6-311++G(3df,2pd) level are collected in Table 3. The positive EDT values of XCHZ (1.1–40.7 me) indicate an electron transfer from XCHZ to H2O upon complexation. The intermolecular hyperconjugative interaction energy of electron density transfer from n(O2/O5/O8) to σ*(Csp2–H) orbital is in the range of 0.6–39.2 kJ mol−1, while larger values of 7.2–74.2 kJ mol−1 are observed for the transfer from n(Z) to σ*(O2–H1) orbital. Such data reveal the presence of Csp2–H⋯O and O–H⋯Z H-bonds in the investigated complexes.| HO-1 | FO-1 | ClO-1 | BrO-1 | CH3O-1 | HS-1 | FS-1 | ClS-1 | BrS-1 | CH3S-1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| a For XCHO. | ||||||||||
| EDTa | 15.0 | 4.1 | 4.1 | 2.8 | 18.5 | 17.7 | 6.7 | 8.0 | 7.5 | 20.3 |
| Einter[n(O2) → σ*(Csp2–H)] | 0.6 | 2.7 | 2.1 | 2.0 | 0.7 | 1.7 | 4.2 | 3.8 | 3.3 | 2.1 |
| Einter[n(Z) → σ*(O2–H1)] | 29.1 | 9.7 | 9.3 | 7.2 | 36.3 | 23.5 | 9.9 | 11.5 | 10.9 | 27.8 |
| ΔEintra[n(O) → σ*(Csp2–H)] | −11.2 | −9.6 | −9.9 | −9.4 | −14.8 | −6.0 | −5.6 | −6.2 | −6.1 | −6.8 |
| ΔEintra[n(X) → σ*(Csp2–H)] | — | 0.1 | 0.4 | 0.3 | — | — | −1.3 | −0.5 | −0.1 | — |
| Δσ*(Csp2–H) | −7.4 | −4.9 | −5.3 | −5.2 | −8.3 | −3.9 | −4.1 | −4.4 | −4.3 | −4.4 |
| Δσ*(O2–H1) | 14.7 | 5.1 | 5.5 | 4.6 | 18.1 | 16.3 | 7.6 | 9.0 | 8.7 | 19.2 |
| HSe-1 | FSe-1 | ClSe-1 | BrSe-1 | CH3Se-1 | HTe-1 | FTe-1 | ClTe-1 | BrTe-1 | CH3Te-1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| EDTa | 15.1 | 6.3 | 7.5 | 7.4 | 17.1 | 13.4 | 6.7 | 7.5 | 7.5 | 15.0 |
| Einter[n(O2) → σ*(Csp2–H)] | 1.8 | 4.2 | 3.8 | 3.3 | 1.8 | 1.4 | 3.7 | 3.6 | 3.1 | 1.5 |
| Einter[n(Z) → σ*(O2–H1)] | 20.1 | 10.0 | 11.2 | 10.9 | 23.2 | 17.1 | 10.2 | 11.0 | 10.9 | 19.9 |
| ΔEintra[n(O) → σ*(Csp2–H)] | −4.7 | −4.1 | −4.5 | −4.4 | −5.2 | −3.2 | −2.7 | −2.8 | −2.7 | −3.3 |
| ΔEintra[n(X) → σ*(Csp2–H)] | — | −1.5 | −0.9 | −0.4 | — | — | −1.7 | −1.2 | −0.9 | — |
| Δσ*(Csp2–H) | −2.8 | −3.2 | −3.4 | −3.4 | −3.2 | −1.8 | −2.4 | −2.4 | −2.4 | −2.1 |
| Δσ*(O–H1) | 14.4 | 7.8 | 8.9 | 8.8 | 16.6 | 12.9 | 8.3 | 9.0 | 9.1 | 15.0 |
| HO-2 | FO-2 | ClO-2 | BrO-2 | CH3O-2 | HS-2 | FS-2 | ClS-2 | BrS-2 | CH3S-2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| EDTa | 18.0 | 4.5 | 4.2 | 2.2 | 22.5 | 27.6 | 13.9 | 15.2 | 14.0 | 30.7 |
| Einter[n(O5) → σ*(Csp2–H)] | 13.1 | 21.8 | 21.3 | 21.4 | 12.6 | 16.8 | 24.3 | 24.8 | 24.5 | 14.8 |
| Einter[n(Z) → σ*(O2–H1)] | 51.4 | 32.4 | 30.3 | 27.0 | 60.6 | 50.0 | 36.7 | 38.5 | 36.8 | 54.8 |
| Einter[n(O2) → σ*(O5–H4)] | 52.2 | 49.0 | 48.4 | 47.9 | 54.5 | 52.0 | 50.2 | 50.7 | 50.2 | 53.9 |
| ΔEintra[n(O) → σ*(Csp2–H)] | −23.2 | −20.4 | −21.6 | −20.9 | −28.1 | −12.7 | −11.9 | −12.9 | −12.6 | −13.6 |
| ΔEintra[n(X) → σ*(Csp2–H)] | — | −1.8 | 0.7 | −1.2 | — | — | −4.1 | −3.1 | −2.3 | — |
| Δσ*(Csp2–H) | −9.5 | −4.7 | −5.8 | −5.5 | −11.3 | −2.4 | −2.2 | −2.7 | −2.4 | −4.2 |
| Δσ*(O2–H1) | 23.4 | 13.8 | 14.1 | 12.9 | 27.5 | 31.8 | 23.2 | 25.1 | 24.5 | 34.9 |
| Δσ*(O5–H4) | 21.9 | 20.6 | 20.3 | 20.0 | 22.8 | 21.5 | 20.8 | 21.0 | 20.7 | 22.3 |
| HSe-2 | FSe-2 | ClSe-2 | BrSe-2 | CH3Se-2 | HTe-2 | FTe-2 | ClTe-2 | BrTe-2 | CH3Te-2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| EDTa | 24.3 | 13.6 | 15.2 | 14.3 | 27.1 | 24.1 | 15.8 | 16.9 | 16.4 | 26.2 |
| Einter[n(O5) → σ*(Csp2–H)] | 16.2 | 23.8 | 24.0 | 23.4 | 14.4 | 14.6 | 21.1 | 21.5 | 21.0 | 13.1 |
| Einter[n(Z) → σ*(O2–H1)] | 44.4 | 35.3 | 36.7 | 35.4 | 48.2 | 40.3 | 34.7 | 35.6 | 34.7 | 43.6 |
| Einter[n(O2) → σ*(O5–H4)] | 51.9 | 51.2 | 51.5 | 51.2 | 53.6 | 50.6 | 51.3 | 51.2 | 51.0 | 52.5 |
| ΔEintra[n(O) → σ*(Csp2–H)] | −10.0 | −9.2 | −9.5 | −9.3 | −10.7 | −7.0 | −6.3 | −6.2 | −6.0 | −7.1 |
| ΔEintra[n(X) → σ*(Csp2–H)] | — | −4.6 | −3.8 | −2.8 | — | — | −4.7 | −4.3 | −3.5 | — |
| Δσ*(Csp2–H) | −0.5 | −0.7 | −1.1 | −0.9 | −2.2 | 0.8 | 0.3 | 0.2 | 0.3 | −0.6 |
| Δσ*(O2–H1) | 29.3 | 23.2 | 24.9 | 24.5 | 31.9 | 28.5 | 24.5 | 25.6 | 25.3 | 30.7 |
| Δσ*(O5–H4) | 21.4 | 21.2 | 21.3 | 21.1 | 22.1 | 20.8 | 21.2 | 21.1 | 21.0 | 21.7 |
| HO-3 | FO-3 | ClO-3 | BrO-3 | CH3O-3 | HS-3 | FS-3 | ClS-3 | BrS-3 | CH3S-3 | |
|---|---|---|---|---|---|---|---|---|---|---|
| EDTa | 18.7 | 1.7 | 1.1 | −1.7 | 25.9 | 31.3 | 15.1 | 16.9 | 15.8 | 40.7 |
| Einter[n(O8) → σ*(Csp2–H)] | 21.1 | 37.6 | 37.6 | 39.2 | 17.3 | 21.5 | 32.8 | 32.6 | 32.7 | 2.8 |
| Einter[n(Z) → σ*(O2–H1)] | 61.9 | 42.8 | 40.3 | 36.7 | 74.2 | 50.0 | 46.0 | 48.0 | 46.3 | 64.8 |
| Einter[n(O2) → σ*(O5–H4)] | 73.2 | 69.1 | 68.2 | 66.9 | 75.4 | 69.5 | 67.1 | 67.5 | 67.0 | 67.0 |
| Einter[n(O5) → σ*(O8–H7)] | 67.1 | 71.3 | 70.9 | 71.0 | 65.7 | 65.6 | 68.7 | 68.8 | 68.6 | 61.1 |
| ΔEintra[n(O) → σ*(Csp2–H)] | −27.3 | −24.6 | −25.9 | −25.3 | −31.3 | −14.2 | −13.8 | −14.4 | −14.0 | −9.8 |
| ΔEintra[n(X) → σ*(Csp2–H)] | — | −3.3 | −0.6 | −2.3 | — | — | −5.5 | −4.3 | −3.3 | — |
| Δσ*(Csp2–H) | −9.2 | −2.1 | −3.3 | −2.6 | −11.3 | −1.8 | −1.1 | −1.7 | −1.2 | −4.8 |
| Δσ*(O2–H1) | 27.3 | 17.3 | 17.5 | 16.4 | 33.0 | 37.1 | 27.9 | 30.2 | 29.7 | 42.0 |
| Δσ*(O5–H4) | 29.6 | 28.0 | 27.6 | 27.1 | 30.6 | 28.1 | 27.0 | 27.2 | 27.0 | 27.2 |
| Δσ*(O8–H7) | 27.6 | 29.4 | 29.2 | 29.2 | 26.9 | 26.9 | 28.3 | 28.4 | 28.3 | 24.9 |
| HSe-3 | FSe-3 | ClSe-3 | BrSe-3 | CH3Se-3 | HTe-3 | FTe-3 | ClTe-3 | BrTe-3 | CH3Te-3 | |
|---|---|---|---|---|---|---|---|---|---|---|
| EDTa | 27.7 | 15.3 | 17.3 | 16.4 | 36.5 | 28.5 | 18.5 | 20.2 | 19.8 | 34.6 |
| Einter[n(O8) → σ*(Csp2–H)] | 20.4 | 30.9 | 30.3 | 30.0 | 2.3 | 18.4 | 27.0 | 26.8 | 26.3 | 1.7 |
| Einter[n(Z) → σ*(O2–H1)] | 52.9 | 43.8 | 45.1 | 43.8 | 56.3 | 48.7 | 43.1 | 44.1 | 43.2 | 49.6 |
| Einter[n(O2) → σ*(O5–H4)] | 68.7 | 67.3 | 67.7 | 67.2 | 66.4 | 67.4 | 67.0 | 67.0 | 66.7 | 65.0 |
| Einter[n(O5) → σ*(O8–H7)] | 65.0 | 68.5 | 68.4 | 68.1 | 60.5 | 63.6 | 67.2 | 67.1 | 67.5 | 59.3 |
| ΔEintra[n(O) → σ*(Csp2–H)] | −11.3 | −10.7 | −10.7 | −10.2 | −7.2 | −8.0 | −7.4 | −6.9 | −6.6 | −4.1 |
| ΔEintra[n(X) → σ*(Csp2–H)] | — | −6.0 | −5.0 | −3.9 | — | — | −6.1 | −5.6 | −4.6 | — |
| Δσ*(Csp2–H) | 0.0 | 0.3 | −0.3 | 0.1 | −3.1 | 1.5 | 1.1 | 0.8 | 1.1 | −1.8 |
| Δσ*(O2–H1) | 34.4 | 27.9 | 29.6 | 29.3 | 38.3 | 34.2 | 29.5 | 30.9 | 30.7 | 36.3 |
| Δσ*(O5–H4) | 27.7 | 27.1 | 27.3 | 27.1 | 26.9 | 27.3 | 27.0 | 27.1 | 26.9 | 26.4 |
| Δσ*(O8–H7) | 26.7 | 28.2 | 28.2 | 28.0 | 24.6 | 26.0 | 27.6 | 27.6 | 27.6 | 24.1 |
For the same Z, the Einter[n(O2/O5/O8) → σ*(Csp2–H)] values become larger in going from H/CH3Z-n to F/Cl/BrZ-n. This trend agrees well with the polarity enhancement of Csp2–H covalent bond as changing X of XCHZ in that ordering of substituted derivatives. The proton affinity at the Z site of XCHZ becomes lower (cf. Table 1), while the decreasing order of Einter[n(Z) → σ*(O2–H1)] values is obtained in the sequence of CH3 > H > Br/Cl/F substitution (cf. Table 3). Thus, the strength of O–H⋯Z H-bonds in the complexes also decreases according to the above trend.
For the same X, the larger attractive electrostatic interaction between O and H1 as compared to S/Se/Te and H1 overcoming charge transfer interaction from n(Z) to σ*(O2–H1) causes the larger strength of O2–H1⋯O, as compared to O2–H1⋯S/Se/Te in the complexes. The results in Table 2 show that the XO-n is much more stable than XS-n, XSe-n, and XTe-n. NBO charges at Z atoms in XCHZ at MP2/6-311++G(3df,2pd) given in Table S5 of ESI† support this observation. Indeed, charges of O in XCHO are negative in the range from −0.445 to −0.514 electron, while those of S, Se and Te in XCHS, XCHSe, and XCHTe are positive from 0.075 to 0.337 electron.
From the binary to ternary and then to a quaternary system, the electron density transfers are significantly augmented in going from n(O2/O5/O8) to σ*(Csp2–H) orbital, from n(Z) to σ*(O2–H1), n(O2) to σ*(O5–H4) and from n(O5) to σ*(O8–H7) orbital. This observation implies a much higher magnitude of the Csp2–H⋯O, O–H⋯Z and O–H⋯O interaction in the ternary and quaternary complexes when adding H2O molecules into the binary systems. For the same Z and n, the trend of H-bond strength is in the order of O5–H4⋯O2 > O8–H7⋯O5 > O2–H1⋯Z in H/CH3Z-n while the halogenated complexes are stabilized by H-bonds in the sequence of O8–H7⋯O5 > O5–H4⋯O2 > O2–H1⋯Z contacts (cf. Table 3). This result might arise from the larger strength of Csp2–H⋯O H-bonds in F/Cl/BrZ-n as compared to H/CH3Z-n.
NCI (non-covalent interaction) calculations have recently been found to be very useful for visualizing weak non-covalent interactions present in molecules.61,71 NCI calculations show the correlation between reduced density gradient (RDG or s(r)) and electron density (ρ(r)) for identification and characterization of interactions with different strengths from the characteristics of the s(r) versus sign(λ2)ρ(r) plots. The s(r) diagrams and the 2D plots using the sign(λ2)ρ(r) are displayed in Fig. S1a–c of ESI.† Two spikes in the binary complexes are found in the negative region, yet again affirming the presence of the O–H⋯Z and Csp2–H⋯O H-bonds. The O–H⋯Z connectivity is assigned by the spike lying at the more negative region. Two overlapping pikes of the halogenated derivatives suggest the comparable strength of O–H⋯S/Se/Te and Csp2–H⋯O. For the case of H/CH3 substituted derivatives, green-colored isosurfaces of the O–H⋯Z H-bond are darker than those of the Csp2–H⋯O one, and even turn to blue ones. This evidences the larger strength of O–H⋯Z versus Csp2–H⋯O in H/CH3Z-n, in accordance with the trend reported by Lei et al. in trifluoroacetophenone·H2O complex.72
From n = 1 to 3, the spikes shift to the more negative region, showing the sharply increasing strength of the H-bonds when the H2O molecule is added. For the same Z, the O–H⋯Z peaks tend to deviate to the left in CH3Z-n compared to F/Cl/BrZ-n, in contrast to the case of the Csp2–H⋯O ones. With the same X, NCIplot results display growth in the strength of Csp2–H⋯O H-bonds in the sequence of XO-n < XS/Se/Te-n and a fall in the O–H⋯Z strength in the order of O–H⋯O ≫ O–H⋯S > O–H⋯Se > O–H⋯Te. The spikes nearest to the zero point on the positive region in the complexes correspond to weakly attractive dispersion interaction arising from H-bond mediated rings.
3.3 Shift of bond length and stretching frequency for the Csp2–H and O–H bonds
In order to clarify characteristics of H-bond interactions upon complexation, the changes of Csp2–H and O–H bond lengths (Δr, in mÅ) and their corresponding stretching frequencies (Δν, in cm−1) for XZ-n are estimated at the MP2/6-311++G(3df,2pd) level of theory as tabulated in Table S4 of ESI.† The blue-shift of the Csp2–H stretching frequencies in Csp2–H⋯O are observed in the XZ-1, XO-2, HO-3 and CH3Z-2,3 complexes. On the contrary, an elongation of Csp2–H bond length and a red-shift of stretching frequency are induced in the complexes including XS-2, XSe-2, XTe-2, and XZ-3 (except for X = CH3 and HO-3).The Csp2–H contraction of 0–7.4 mÅ in the Csp2–H⋯O H-bonds, accompanied by an increase in their stretching frequencies of ca. 4.6–109.0 cm−1, occurs upon complexation. Remarkably, the Csp2–H blue-shift of stretching frequency as large as 109 cm−1 in CH3O-3 has rarely been found in literature. Indeed, a brief summary of the experimental and theoretical reports on the stretching frequencies of Csp2–H, Csp–H and Csp3–H bonds is collected in Table S6 of ESI† affirms this observation. These results also show the large blue shifts of Csp2–H compared to Csp3–H bonds in various complexes.
The Csp2–H stretching frequency blue-shifts of 81–96 cm−1 and 53 cm−1 in the Csp2–H⋯O H-bonds were indeed reported for the interactions of formaldehydes and thioformaldehydes with formic acid and nitrosyl hydride.36,73 It is noteworthy that smaller magnitudes of the Csp3–H stretching frequency blue-shifts were suggested for Cl3CH⋯NCCH3 (8.7 cm−1),30 F3CH⋯OH2 (20.3–32.3 cm−1),38 CHX3⋯NH2Y (X = F, Cl; Y = H, F, Cl, Br) (9.4–36.3 cm−1),74 and DMSO⋯H2O/CO2 (8.4–44.5 cm−1),75 despite the lower polarity of Csp3–H than Csp2–H covalent bond. These results indicate the important role of adding one or more H2O molecules into the binary systems, which contributes to a significant increase of Csp2–H stretching frequencies in Csp2–H⋯O H-bonds. Accordingly, it is suggested that a contraction of Csp2–H bond lengths, and a substantial increase of its stretching frequencies depend on role of H2O addition as well as presence of O–H⋯O H-bond in complexes beside low polarity of Csp2–H covalent bond in isolated isomer.
For the O–H⋯O/S/Se/Te H-bonds, the elongation of the O–H bond lengths in the range of 3.4–18.0 mÅ and a considerable decrease of its stretching frequencies of 60.0–354.2 cm−1 are observed, which characterize them as red-shifting H-bonds. The large red-shift of the O–H stretching frequencies in O–H⋯Y (Y = O, S, Se) H-bonds were also observed in the complexes of rhodanine⋯YH2 (97–144 cm−1),76 C6H5OH⋯Y(CH3)2 (119–326 cm−1),46 and 4-H–C6H4–OH+⋯YH2 (740–836 cm−1).50
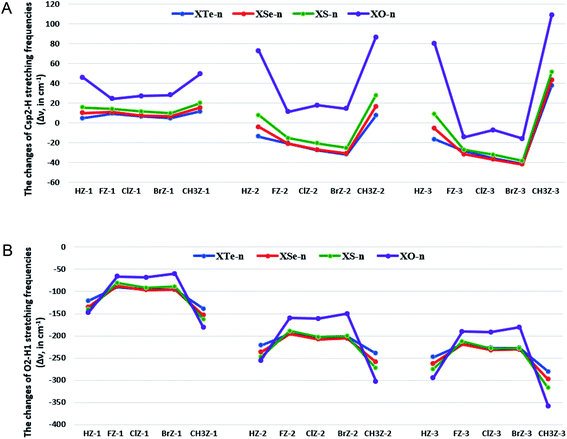
Correlations of the changes of Csp2–H stretching frequencies with substituents in different complexes are displayed in Fig. 3a. For the same Z, a sharp change in Csp2–H stretching frequency is recorded when the n value of XZ-n goes from n = 1 to n = 3. This indicates that the addition of H2O molecules leads to a significant enhancement of Csp2–H stretching frequency involving Csp2–H⋯O H-bonds in the complexes. For the Csp2–H⋯O, an increase of Csp2–H stretching frequency is witnessed as X to be CH3, H, while a decrease of its stretching frequency is induced as X being halogen. A larger decrease in the population of σ*(Csp2–H) in HZ-n and CH3Z-n as compared to that in the remaining XZ-n causes a larger contraction of Csp2–H bond length and a considerable increase of its stretching frequency in HZ-n and CH3Z-n. This is taken from the smaller Einter[n(O) → σ*(Csp2–H)] values and the more negative ΔEintra[n(Z) → σ*(Csp2–H)] values in CH3Z-n and HZ-n. Therefore, the difference in redistribution of electron density in the σ*(Csp2–H) orbitals could be the reason for this observation.
A larger decrease of σ*(Csp2–H) electron densities in HO-n and CH3Z-n as compared to that in the remaining XZ-n gives rise to a larger blue-shift in HO-n and CH3Z-n. This is evidenced by the smaller Einter[n(O2/O5/O8) → σ*(Csp2–H)] values and the more negative ΔEintra[n(Z) → σ*(Csp2–H)] values in CH3Z-n and HO-n (cf. Table 3). A significant decrease of the σ*(Csp2–H) electron density induces the largest blue-shift of Csp2–H stretching frequency in the CH3-substituted complexes. On the other hand, the Csp2–H⋯O bonds in the halogenated complexes, such as XS-2, XSe-2, XTe-2, and XZ-3, are classified as red-shifting H-bonds. This results from the larger positive values of Δσ*(Csp2–H) in such complexes, owing to the larger values of Einter[n(O) → σ*(Csp2–H)] as compared to ΔEintra[n(Z/X) → σ*(Csp2–H)] absolute values.
For the same substituent X, for XZ-1, XO-2, HO-3 and CH3Z-2,3, the Csp2–H blue-shift of stretching frequency in the Csp2–H⋯O H-bond decreases as replacing O atom in XCHO by S, Se, and Te. Indeed, the stretching frequency enhancement of Csp2–H bond involving the Csp2–H⋯O is 24.4–49.4 cm−1 with Z = O, 9.7–19.9 cm−1 with Z = S, 6.5–15.4 cm−1 with Z = Se, and 4.6–11.5 cm−1 with Z = Te in XZ-1. This observation is determined by a decrease of electron density in the σ*(Csp2–H) orbital, as compared to that in the corresponding monomer. The ΔEintra[n(Z/X) → σ*(Csp2–H)] values in XO-1, XO-2, and CH3O-2,3 are significantly more negative than those in XS/Se/Te-1, CH3S/Se/Te-2,3, which might be for the growing magnitude of Δσ*(Csp2–H) values as going from O to S, Se, and Te. Consequently, the large blue-shift of Csp2–H stretching frequencies in Csp2–H⋯O H-bonds is found in XO-1, XO-2, and H/CH3O-3, especially in H/CH3-substituted complexes up to 80.1–109.0 cm−1. For XS-2, XSe-2, XTe-2 and XZ-3 (except for HO-3 and X = CH3), the red-shift of Csp2–H stretching frequencies in Csp2–H⋯O H-bonds rises when going from Z = O to Z = S, Se, Te, which arises from the more positive Δσ*(Csp2–H) values as O in XCHO replaced by S, Se, and Te ones.77–79 The obtained results indicate a dominant role of the decrease of intramolecular electron transfer predominating intermolecular one in contributing to the blue-shift of Csp2–H stretching frequency in the Csp2–H⋯O H-bonds upon complexation. The shift of Csp2–H stretching frequency (Δν(Csp2–H)) can be expressed as a function of net second hyperconjugative energy of electron transfer to σ*(Csp2–H) orbital in the XZ-n complexes as: Δν(Csp2–H) = −2.8142(Einter + 1.5ΔEintra) + 1.9458 (R2 = 0.91), and the correlation diagram is presented in Fig. S2 of ESI.† A competition of intramolecular interaction decreases, and intermolecular interaction causes a change of Csp2–H bond length and its stretching frequency, in which the Csp2–H blue-shift occurs as the former is predominant. This supports the pivotal role of H2O addition to significant blue shifts of Csp2–H stretching frequencies in the complexes.
Correlation of the changes in the O2–H1 stretching frequencies with different substituents in complexes is presented in Fig. 3b. The changes in length of O5–H4 and O8–H7 bonds and their corresponding stretching frequencies are tabled in Table S4 of ESI.† For the same Z and n, the red-shift of O2–H1 stretching frequencies in the O2–H1⋯Z for the H/CH3-substituted complexes is larger than that for the halogenated ones, which is related to the larger proton affinity at Z in HCHZ and CH3CHZ molecules than in the remaining monomers.73,80,81 The magnitude of O5–H4 stretching frequency red-shift in the O5–H4⋯O2 is found to increase in the sequence of F/Cl/BrZ-2,3 < H/CH3Z-2,3. Besides, the larger red-shift of O8–H7 stretching frequency in the O8–H7⋯O5 is achieved with X being a halogen compared to H/CH3. With the same Z and X, the magnitude of stretching frequency red-shifts of O2–H1 or O5–H4, or O8–H7 bonds involving the O2–H1⋯Z or O5–H4⋯O2, or O8–H7⋯O5 in XZ-n grows considerably from n = 1 to 2 and then to 3, which is consistent with an increase of Δσ*(O2–H1/O5–H4/O8–H7) values. In other words, the red-shift of O2–H1⋯Z, O5–H4⋯O2 and O8–H7⋯O5 H-bonds rises sharply as the number of H2O molecules in the complexes rises. For the same X and n, the red-shift magnitude of the O2–H1⋯Z H-bonds tends to be lower for HZ-n and CH3Z-n while being higher for the halogenated ones as Z changes from O to S to Se, and then to Te. This shows that a larger role of electrostatic attraction between Z = O and H as compared to Z = S, Se, Te is observed in H/CH3Z-n, while a prominent role of electron density transfer from n(Z) to σ*(O2–H1) is suggested in the halogenated ones. The red-shift magnitude of the O5–H4⋯O2 and O8–H7⋯O5 H-bonds becomes weaker in going from Z = O to Z = S, Se, Te. This is associated with a decrease of Δσ*(O5–H4) and Δσ*(O8–H7) values.
4 Concluding remarks
Sixty stable structures of XCHZ⋯nH2O (n = 1–3; Z = O, S, Se, Te, X = H, F, Cl, Br, CH3) complexes are located on the potential energy surfaces. The individual energy of Csp2–H⋯O (from −6.7 to −23.3 kJ mol−1) approximates O–H⋯S/Se/Te (from −7.0 to −22.6 kJ mol−1) and is ca. half of O–H⋯O ones (from −14.9 to −45.9 kJ mol−1). Following complexation, the O–H⋯Z bond strength is determined by proton affinity at the Z atom of XCHZ while the polarity of Csp2–H covalent bonds in XCHZ plays a decisive role in stabilizing Csp2–H⋯O H-bonds.The strength of complexes is enhanced upon the addition of extra H2O molecules into binary systems. With the same substituent X, the strength of Csp2–H⋯O H-bonds in XO-n is observed to be weaker than that in XS/Se/Te-n. The significantly larger stability of O–H⋯O H-bonds compared to O–H⋯S/Se/Te ones causes a sharp decrease in the strength of complexes from XO-n to XS/Se/Te-n. The obtained result emphasizes the key role of the O atom with respect to the S, Se, and Te ones in XCHZ for the stabilization of complexes. With the same functional group Z, the stability of complexes rises in the consequence of HZ-n < F/Cl/BrZ-n < CH3Z-n. The Csp2–H stretching frequency in Csp2–H⋯O H-bond experiences an enhancement upon the substitution of one H in XCHZ by a CH3 group, while an inverse trend is detected as substituted by a halogen atom. The largest blue-shift of Csp2–H stretching frequency in the Csp2–H⋯O up to 109.0 cm−1 is found for CH3O-3, which is one of the highest values in literature up to date. It is found that a crucial role of H2O addition into complexes and low polarity of Csp2–H covalent bond in HCHO and CH3CHO monomers induces a substantial blue-shift of Csp2–H stretching frequency in the Csp2–H⋯O H-bond. The decrease of intramolecular electron transfer predominating intermolecular one to the σ*(Csp2–H) orbital results in the blue-shift of Csp2–H stretching frequency following complexation.
The results show that all the O–H bonds in the O–H⋯O/S/Se/Te H-bonds are the red-shifting H-bonds. For the same substituent X and the same complex size n, the O–H stretching frequency red-shift in the O–H⋯Z H-bond in H, CH3-substituted complexes decreases as Z from O to S, Se and Te, and an inverse trend is observed in the case of halogenated complexes. The magnitude of O–H elongation in O2–H1⋯Z and O5–H4⋯O2 H-bonds becomes greater in the sequence of F/Cl/BrZ-n < H/CH3Z-n for the same Z and n, while an inverse trend is detected in the O8–H7⋯O5 H-bond. Moreover, the magnitude of O–H stretching frequency red-shifts in these H-bonded complexes keeps growing as the number of H2O molecules added to the XCHO molecule increases.
Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 104.06-2020.28.References
- J. M. Lehn and J. Sanders, Angew. Chem., 1995, 34, 2563 Search PubMed.
- I. G. Kaplan, Intermolecular interactions: physical picture, computational methods and model potentials, John Wiley & Sons, 2006 Search PubMed.
- R. E. Plata, D. E. Hill, B. E. Haines, D. G. Musaev, L. Chu, D. P. Hickey, M. S. Sigman, J.-Q. Yu and D. G. Blackmond, J. Am. Chem. Soc., 2017, 139, 9238–9245 CrossRef CAS PubMed.
- G. Trudeau, J. M. Dumas, P. Dupuis, M. Guérin and C. Sandorfy, Top. Curr. Chem., 1980, 93, 91–125 CrossRef CAS PubMed.
- J. Joseph and E. D. Jemmis, J. Am. Chem. Soc., 2007, 129, 4620–4632 CrossRef CAS PubMed.
- I. V. Alabugin, M. Manoharan, S. Peabody and F. Weinhold, J. Am. Chem. Soc., 2003, 125, 5973–5987 CrossRef CAS PubMed.
- O. Donoso-Tauda, P. Jaque and J. C. Santos, Phys. Chem. Chem. Phys., 2011, 13, 1552–1559 RSC.
- X. Li, L. Liu and H. B. Schlegel, J. Am. Chem. Soc., 2002, 124, 9639–9647 CrossRef CAS PubMed.
- Y. Mao and M. Head-Gordon, J. Phys. Chem. Lett., 2019, 10, 3899–3905 CrossRef CAS PubMed.
- V. C. C. Wang, S. Maji, P. P.-Y. Chen, H. K. Lee, S. S. F. Yu and S. I. Chan, Chem. Rev., 2017, 117, 8574–8621 CrossRef CAS PubMed.
- Y. Mo, C. Wang, L. Guan, B. Braida, P. C. Hiberty and W. Wu, Chem.– Eur. J., 2014, 20, 8444–8452 CrossRef CAS PubMed.
- X. Chang, Y. Zhang, X. Weng, P. Su, W. Wu and Y. Mo, J. Phys. Chem. A, 2016, 120, 2749–2756 CrossRef CAS PubMed.
- C. Wang, D. Danovich, S. Shaik and Y. Mo, J. Chem. Theory Comput., 2017, 13, 1626–1637 CrossRef CAS PubMed.
- K. Hermansson, J. Phys. Chem. A, 2002, 106, 4695–4702 CrossRef CAS.
- W. Qian and S. Krimm, J. Phys. Chem. A, 2002, 106, 6628–6636 CrossRef CAS.
- W. Wang, N.-B. Wong, W. Zheng and A. Tian, J. Phys. Chem. A, 2004, 108, 1799–1805 CrossRef CAS.
- J. S. Murray, M. C. Concha, P. Lane, P. Hobza and P. Politzer, J. Mol. Model., 2008, 14, 699–704 CrossRef CAS PubMed.
- R. H. Crabtree and A. Lei, Chem. Rev., 2017, 117, 8481–8482 CrossRef CAS PubMed.
- B. Yang, J.-F. Cui and M. K. Wong, RSC Adv., 2017, 7, 30886–30893 RSC.
- L. S. Sremaniak, J. L. Whitten, M. J. Truitt and J. L. White, J. Phys. Chem. B, 2006, 110, 20762–20764 CrossRef CAS PubMed.
- M. Budesinsky, P. Fiedler and Z. Arnold, Synthesis, 1989, 858–860 CrossRef CAS.
- R. Taylor and O. Kennard, J. Am. Chem. Soc., 1982, 104, 5063–5070 CrossRef CAS.
- I. Boldeskul, I. Tsymbal, E. Ryltsev, Z. Latajka and A. Barnes, J. Mol. Struct., 1997, 436, 167–171 CrossRef.
- P. Hobza, V. r. Špirko, Z. Havlas, K. Buchhold, B. Reimann, H.-D. Barth and B. Brutschy, Chem. Phys. Lett., 1999, 299, 180–186 CrossRef CAS.
- B. Reimann, K. Buchhold, S. Vaupel, B. Brutschy, Z. Havlas, V. Špirko and P. Hobza, J. Phys. Chem. A, 2001, 105, 5560–5566 CrossRef CAS.
- B. Reimann, K. Buchhold, S. Vaupel and B. Brutschy, Z. Phys. Chem., 2001, 215, 777–793 CAS.
- B. J. Van der Veken, W. A. Herrebout, R. Szostak, D. N. Shchepkin, Z. Havlas and P. Hobza, J. Am. Chem. Soc., 2001, 123, 12290–12293 CrossRef CAS PubMed.
- S. N. Delanoye, W. A. Herrebout and B. J. Van der Veken, J. Am. Chem. Soc., 2002, 124, 7490–7498 CrossRef CAS PubMed.
- W. A. Herrebout, S. N. Delanoye, B. U. Maes and B. J. van der Veken, J. Phys. Chem. A, 2006, 110, 13759–13768 CrossRef CAS PubMed.
- P. R. Shirhatti and S. Wategaonkar, Phys. Chem. Chem. Phys., 2010, 12, 6650–6659 RSC.
- P. R. Shirhatti, D. K. Maity and S. Wategaonkar, J. Phys. Chem. A, 2013, 117, 2307–2316 CrossRef CAS PubMed.
- W. A. Herrebout, S. M. Melikova, S. N. Delanoye, K. S. Rutkowski, D. N. Shchepkin and B. J. van der Veken, J. Phys. Chem. A, 2005, 109, 3038–3044 CrossRef CAS PubMed.
- K. Rutkowski, S. Melikova, M. Rospenk and A. Koll, Phys. Chem. Chem. Phys., 2011, 13, 14223–14234 RSC.
- B. Behera and P. K. Das, J. Phys. Chem. A, 2019, 123, 1830–1839 CrossRef CAS PubMed.
- A. K. Chandra and T. Zeegers-Huyskens, J. At. Mol. Phys., 2012, 2, 1–8 Search PubMed.
- N. T. Trung, P. N. Khanh, A. J. P. Carvalho and M. T. Nguyen, J. Comput. Chem., 2019, 40, 1387–1400 CrossRef CAS PubMed.
- A. K. Chandra and T. Zeegers-Huyskens, J. Comput. Chem., 2012, 33, 1131–1141 CrossRef CAS PubMed.
- R. Gopi, N. Ramanathan and K. Sundararajan, Chem. Phys., 2016, 476, 36–45 CrossRef CAS.
- B. Nelander, J. Chem. Phys., 1978, 69, 3870–3871 CrossRef.
- B. J. Mintz and J. M. Parks, J. Phys. Chem. A, 2012, 116, 1086–1092 CrossRef CAS PubMed.
- A. Barnes, R. Bentwood and M. Wright, J. Mol. Struct., 1984, 118, 97–102 CrossRef CAS.
- A. J. Tursi and E. R. Nixon, J. Chem. Phys., 1970, 53, 518–521 CrossRef CAS.
- R. D. Amos, Chem. Phys., 1986, 104, 145–151 CrossRef CAS.
- S. Sarkar and B. Bandyopadhyay, Phys. Chem. Chem. Phys., 2019, 21, 25439–25448 RSC.
- K. K. Mishra, S. K. Singh, S. Kumar, G. Singh, B. Sarkar, M. S. Madhusudhan and A. Das, J. Phys. Chem. A, 2019, 123, 5995–6002 CrossRef CAS PubMed.
- K. K. Mishra, S. K. Singh, P. Ghosh, D. Ghosh and A. Das, Phys. Chem. Chem. Phys., 2017, 19, 24179–24187 RSC.
- V. R. Mundlapati, D. K. Sahoo, S. Ghosh, U. K. Purame, S. Pandey, R. Acharya, N. Pal, P. Tiwari and H. S. Biswal, J. Phys. Chem. Lett., 2017, 8, 794–800 CrossRef CAS PubMed.
- A. Chand and H. S. Biswal, J. Indian Inst. Sci., 2020, 100, 77–100 CrossRef.
- M. Hou, Q. Z. Li and S. Scheiner, ChemPhysChem, 2019, 20, 1–7 CrossRef PubMed.
- B. Das, A. Chakraborty and S. Chakraborty, Comput. Theor. Chem., 2017, 1102, 127–138 CrossRef CAS.
- A. Chand, D. K. Sahoo, A. Rana, S. Jena and H. S. Biswal, Acc. Chem. Res., 2020, 53, 1580–1592 CrossRef CAS PubMed.
- K. K. Mishra, S. K. Singh, S. Kumar, G. Singh, B. Sarkar, M. Madhusudhan and A. Das, J. Phys. Chem. A, 2019, 123, 5995–6002 CrossRef CAS PubMed.
- D. K. Sahoo, S. Jena, J. Dutta, A. Rana and H. S. Biswal, J. Phys. Chem. A, 2019, 123, 2227–2236 CrossRef CAS PubMed.
- M. Frisch, G. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision D. 01, Gaussian Inc, Wallingford CT, 2009 Search PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- R. F. W. Bader, Atoms in molecules: a quantum theory, Oxford University Press, Oxford, 1990 Search PubMed.
- R. F. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- I. Mata, I. Alkorta, E. Espinosa and E. Molins, Chem. Phys. Lett., 2011, 507, 185–189 CrossRef CAS.
- E. D. Glendening, J. K. Badenhoop, A. E. Read, J. E. Carpenter, A. J. Bohmann, and F. Weinhold, GenNBO 5.G, University of Wisconsin: Madison, Wisconsin, USA, 2001 Search PubMed.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- I. Alkorta, I. Rozas and J. Elguero, Chem. Soc. Rev., 1998, 27, 163–170 RSC.
- K. K. Murray, T. M. Miller, D. G. Leopold and W. Lineberger, J. Chem. Phys., 1986, 84, 2520–2525 CrossRef CAS.
- M. R. Nimlos, J. Soderquist and G. B. Ellison, J. Am. Chem. Soc., 1989, 111, 7675–7681 CrossRef CAS.
- K. Kimura, Handbook of HeI photoelectron spectra of fundamental organic molecules, Halsted Press, 1981 Search PubMed.
- E. P. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656 CrossRef CAS.
- H. Liu, R. Man, Z. Wang, J. Liao, X. Li, S. Ma and P. Yi, J. Theor. Comput. Chem., 2014, 13, 1450037 CrossRef.
- A. Karpfen and E. S. Kryachko, J. Phys. Chem. A, 2007, 111, 8177–8187 CrossRef CAS PubMed.
- M. Masella, N. Gresh and J.-P. Flament, J. Chem. Soc., Faraday Trans., 1998, 94, 2745–2753 RSC.
- S. S. Xantheas and T. H. Dunning Jr, J. Chem. Phys., 1993, 99, 8774–8792 CrossRef CAS.
- E. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- J. Lei, S. Alessandrini, J. Chen, Y. Zheng, L. Spada, Q. Gou, C. Puzzarini and V. Barone, Molecules, 2020, 25, 4899 CrossRef CAS PubMed.
- N. T. Trung, T. T. Hue and M. T. Nguyen, J. Phys. Chem. A, 2009, 113, 3245–3253 CrossRef CAS PubMed.
- N. Thi Hong Man, P. Le Nhan, V. Vo, D. Tuan Quang and N. Tien Trung, Int. J. Quantum Chem., 2017, 117, 1–8 CrossRef.
- P. N. Khanh, C. T. D. Phan, D. Q. Ho, Q. Van Vo, V. T. Ngan, M. T. Nguyen and N. T. Trung, J. Comput. Chem., 2019, 40, 464–474 CrossRef CAS PubMed.
- M. Guin, K. Rautela, R. Roopa, C. Shantharam and S. B. Elavarasi, Comput. Theor. Chem., 2021, 1196, 113134 CrossRef CAS.
- N. T. Trung, T. T. Hue, M. T. Nguyen and T. Zeegers-Huyskens, Phys. Chem. Chem. Phys., 2008, 10, 5105–5113 RSC.
- N. T. Trung, T. T. Hue, T. Zeegers-Huyskens and M. T. Nguyen, Phys. Chem. Chem. Phys., 2009, 11, 926–933 RSC.
- N. T. Trung, T. T. Hue and M. T. Nguyen, Can. J. Chem., 2010, 88, 849–857 CrossRef CAS.
- N. T. Trung, N. P. Hung, T. T. Hue and M. T. Nguyen, Phys. Chem. Chem. Phys., 2011, 13, 14033–14042 RSC.
- N. N. Tri, N. T. H. Man, N. Le Tuan, N. T. T. Trang, D. T. Quang and N. T. Trung, Theor. Chem. Acc., 2017, 136, 1–12 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tables and figures list of contact distances, the AIM analysis, NCI plot, length changes and stretching frequency shifts of the Csp2–H and O–H bonds in the complexes. See DOI: 10.1039/d1ra07444j |
| This journal is © The Royal Society of Chemistry 2022 |