Open Access Article
Open Access ArticleBonding and stability of dinitrogen-bonded donor base-stabilized Si(0)/Ge(0) species [(cAACMe–Si/Ge)2(N2)]: EDA-NOCV analysis†
Harsha S. Karnamkkott,
Sai Manoj N. V. T. Gorantla ,
Kavita Devi,
Geetika Tiwari and
Kartik Chandra Mondal
,
Kavita Devi,
Geetika Tiwari and
Kartik Chandra Mondal *
*
Department of Chemistry, Indian Institute of Technology Madras, Chennai 600036, India. E-mail: csdkartik@iitm.ac.in
First published on 1st February 2022
Abstract
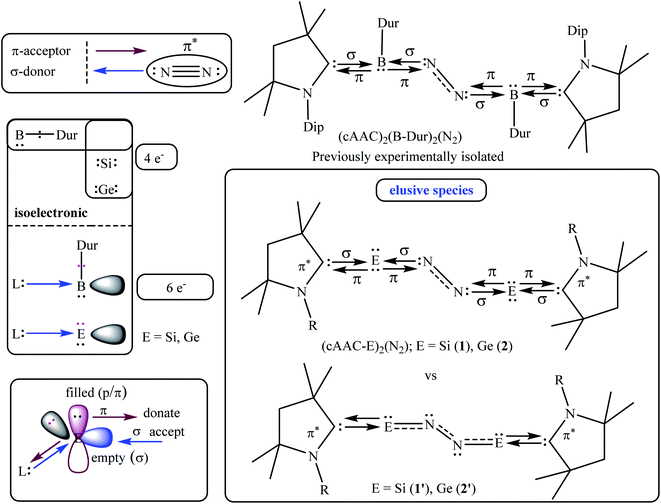
Recently, dinitrogen (N2) binding and its activation have been achieved by non-metal compounds like intermediate cAAC-borylene as (cAAC)2(B-Dur)2(N2) [cAAC = cyclic alkyl(amino) carbene; Dur = aryl group, 2,3,5,6-tetramethylphenyl; B-Dur = borylene]. It has attracted a lot of scientific attention from different research areas because of its future prospects as a potent species towards the metal free reduction of N2 into ammonia (NH3) under mild conditions. Two (cAAC)(B-Dur) units, each of which possesses six valence electrons around the B-centre, are shown to accept σ-donations from the N2 ligand (B ← N2). Two B-Dur further provide π-backdonations (B → N2) to a central N2 ligand to strengthen the B–N2–B bond, providing maximum stability to the compound (cAAC)2(B-Dur)2(N2) since the summation of each pair wise interaction accounted for the total stabilization energy of the molecule. (cAAC)(B-Dur) unit is isolobal to cAAC–E (E = Si, Ge) fragment. Herein, we report on the stability and bonding of cAAC–E bonded N2-complex (cAAC–E)2(N2) (1–2; Si, Ge) by NBO, QTAIM and EDA-NOCV analyses (EDA-NOCV = energy decomposition analysis coupled with natural orbital for chemical valence; QTAIM = quantum theory of atoms in molecule). Our calculation suggested that syntheses of elusive (cAAC–E)2(N2) (1–2; Si, Ge) species may be possible with cAAC ligands having bulky substitutions adjacent to the CcAAC atom by preventing the homo-dimerization of two (cAAC)(E) units which can lead to the formation of (cAAC–E)2. The formation of E![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E bond is thermodynamically more favourable (E = Si, Ge) over binding energy of N2 inbetween two cAAC–E units.
E bond is thermodynamically more favourable (E = Si, Ge) over binding energy of N2 inbetween two cAAC–E units.
Introduction
The activation of small molecules1 from natural resources has been an endless effort from scientists around the globe since the products could be utilised in certain ways for the survival of the human race2 on earth and could even help to colonise the exo-planets in the future.3 Small molecules like H2, O2, N2, CO2, CH4, and others have initially been activated by different chemical species in the laboratory, and later on, some of the processes have been extended to the industrial scale.4 Among the above-mentioned species, activations of N2 and CH4 have been considered to be the toughest due to their non-polar nature and kinetic inertness.5 The N–N σ- and π-bonds of N2, and C–H σ-bond of CH4 are extremely stable and possess very high bond dissociation energies.5 In addition, the electron pairs (bonding/anti-bonding electrons) which are available for σ-donation from these species (N2 and CH4) are quite low in energy and hence thermodynamically less favourable for the formation of new bonds with the acceptors. Various research groups have isolated N2-bonded complexes of early and late transition metals over the last two decades.5c The N–N triple bond in these complexes is stated to be activated and hence elongated due to the flow of electron densities from the metal's d-orbital to the π* of the N2 ligand (Fig. 1).5c These metal complexes are engrossing since N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond of a bonded N2 complex is further elongated by stepwise additions of electrons and finally protons, leading to the formation of hydrazine (N2H4) or ammonia (NH3).5a,c The former is utilised as a rocket fuel and the latter has a huge application in the fertiliser industry. Nitrogen containing fertilisers and bio-molecules are the most desired products for plants and micro-organisms or animals.6 Azotobacter, which forms colonies in the roots of the plants, has the special and captivating ability to directly utilise aerial N2 and reduce it to NH3 catalysed by the inorganic cluster MoFe7S9C1− (FeMoco) nitrogenase enzyme.7,8 This process is linked to another cofactor, 4Fe–4S (P-cluster) residing within the same enzyme. The P-cluster provides the required number of electrons for the reduction of N2 into NH3. The overall process costs 16 Mg-ATP at ambient conditions.7,8 This process has a huge impact on the survival of life on the planet, supplying billions of tonnes of nitrogen products by direct fixation of aerial N2. A century ago, the Haber–Bosch process is the only industrial process by which 174 million tonnes of NH3 are annually produced at present.9 However, this process is energy-inefficient since it needs extreme conditions like high temperature and pressure (leading to the global warming via carbon emission). Several research groups have synthesised N2-bonded main group elements complexes10 and N2-bonded metal complexes of different metal ions.11–35 Most of them can catalytically reduce N2 into NH3 under mild conditions with low yield in the laboratory.
N bond of a bonded N2 complex is further elongated by stepwise additions of electrons and finally protons, leading to the formation of hydrazine (N2H4) or ammonia (NH3).5a,c The former is utilised as a rocket fuel and the latter has a huge application in the fertiliser industry. Nitrogen containing fertilisers and bio-molecules are the most desired products for plants and micro-organisms or animals.6 Azotobacter, which forms colonies in the roots of the plants, has the special and captivating ability to directly utilise aerial N2 and reduce it to NH3 catalysed by the inorganic cluster MoFe7S9C1− (FeMoco) nitrogenase enzyme.7,8 This process is linked to another cofactor, 4Fe–4S (P-cluster) residing within the same enzyme. The P-cluster provides the required number of electrons for the reduction of N2 into NH3. The overall process costs 16 Mg-ATP at ambient conditions.7,8 This process has a huge impact on the survival of life on the planet, supplying billions of tonnes of nitrogen products by direct fixation of aerial N2. A century ago, the Haber–Bosch process is the only industrial process by which 174 million tonnes of NH3 are annually produced at present.9 However, this process is energy-inefficient since it needs extreme conditions like high temperature and pressure (leading to the global warming via carbon emission). Several research groups have synthesised N2-bonded main group elements complexes10 and N2-bonded metal complexes of different metal ions.11–35 Most of them can catalytically reduce N2 into NH3 under mild conditions with low yield in the laboratory.
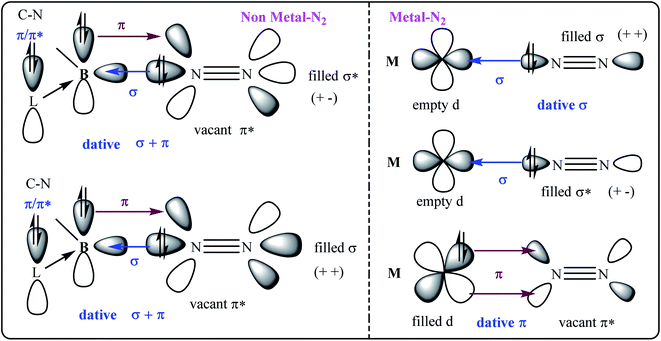 | ||
| Fig. 1 The σ- and π-orbital interactions between orbitals of B and N2 (left; non-metal–N2); and, M and N2 (right; metal–N2). L = cAAC. | ||
The compounds of main group elements have been unable to bind with N2 for decades until recently an intermediate cAAC-borylene species of the general formula (cAAC)(B-Dur)36 has been shown to bind with N2 to produce (cAAC)2(B-Dur)2(N2) [cAAC = cyclic alkyl(amino)carbene;37 Dur = aryl group, 2,3,5,6-tetramethylphenyl; B-Dur = borylene].36 This remarkable species can be further treated with electron and proton sources to produce NH3. However, this process is not cyclic possibly due to the stronger covalent bonding interaction between B- and N-atoms. There is a constant search for compounds of other or heavier main group elements that can mimic the N2 reduction into NH3 under milder conditions.
The E–N bond of heavier main group elements like Si and Ge are expected to be comparatively more dative in nature (E = Si, Ge) than the boron-analogue. In the past, carbene ligands (cAAC and/or NHC; NHC = N-hetero cyclic carbene) have been shown to form adducts [(L) → ECl4−n; E Si, Ge; n = 0, 1, 2] with ECl4/ECl2. These adducts have been shown to be important synthons for the syntheses of Si2 and Ge2 units when the precursors have been reacted with suitable reducing agents. The cAAC has been established as a redox non-innocent and a stronger, π-accepting donor base ligand. It is not impossible to generate intermediate species cAAC → E (E = Si, Ge) which can possibly undergo dimerization and trimerization to produce cAAC → E = E ← cAAC and (cAAC)3E3 (E = Si).38,39 The cAAC–E intermediate is isolobal with (cAAC)(B-Dur) (Fig. 2, left) and thus can be tested by the EDA-NOCV method40 to predict the stability of dinitrogen bonded dimeric species (cAAC–E)2(N2) (1–2; E = Si, Ge; Fig. 2; right) (EDA-NOCV = energy decomposition analysis coupled with natural orbital for chemical valence). EDA-NOCV is a very powerful tool that can predict the quantum mechanical stability of chemical bonds41 and hence can often predict the synthetic viability of a chemical species, although it cannot suggest a chemical route for the synthesis. There are several new classes of reactive species like carbone,42 silylone and germylone whose stability has been predicted before their synthetic success. They were later synthesised and isolated in the laboratory; (NHC)2C(0).43 Similarly, Frenking et al.44a predicted the stabilisation of a borylene-containing bulky ligand (B–R) via coordination with two CO ligands, and Braunschweig et al.44b have isolated it.
Computational methods
The optimizations of equilibrium geometries of 1 and 2 in singlet electronic states have been carried out at the BP86-D3(BJ)/Def2TZVPP level.45 The absence of imaginary frequencies assures the minima on the potential energy surface. All the calculations have been performed using Gaussian 16 program package.46 NBO47 calculations have been performed using NBO 6.0 (ref. 48) program to evaluate partial charges, Wiberg bond indices (WBI) and natural bond orbitals (NBO). The nature of Si–N2 and Ge–N2 bonds of 1–2 have been analysed by energy decomposition analysis (EDA)49 coupled with natural orbital for chemical valence (NOCV)50 using ADF 2018.105 program package.51 EDA-NOCV calculations were carried out at the BP86-D3(BJ)/TZ2P52 level using the geometries optimized at BP86-D3(BJ)/TZ2PP level. EDA-NOCV method involves the decomposition of the intrinsic interaction energy (ΔEint) between two fragments into four energy components as follows:| ΔEint = ΔEelstat + ΔEPauli + ΔEorb + ΔEdisp | (1) |
| ΔEorb = ∑ΔEr | (2) |
The combined EDA-NOCV method is able to partition the total orbital interactions into pairwise contributions of the orbital interactions which is important in providing a complete picture of the bonding. The charge deformation Δρk(r), which comes from the mixing of the orbital pairs ψk(r) and ψ−k(r) of the interacting fragments, gives the magnitude and the shape of the charge flow due to the orbital interactions (eqn (3)), and the associated orbital energy ΔEorb presents the amount of orbital energy coming from such interaction (eqn (4)).
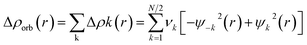 | (3) |
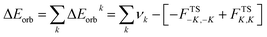 | (4) |
Readers are further referred to the recent reviews articles to know more about the EDA-NOCV method and its application.41
Structure description
Geometry optimizations of (cAAC–Si)2(N2) (1) and (cAAC–Ge)2(N2) (2) at the BP86-D3(BJ)/Def2TZVPP level of theory revealed that both species have a singlet spin ground state (Fig. 3). The triplet states of both the species (1–2) are higher in energy by 12.2 (2) to 15 (1) kcal mol−1. A notable observation is the disconnection of one Ge–N bond of (cAAC–Ge)2(N2) (2) in its triplet state (Fig. S1†).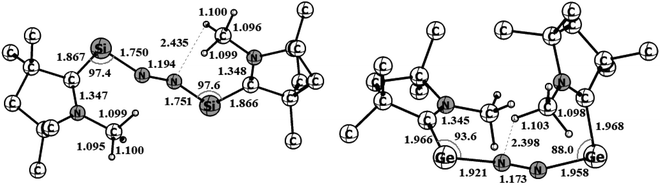 | ||
| Fig. 3 Optimized equilibrium geometries of (cAAC–Si)2(N2) (1) and (cAAC–Ge)2(N2) (2) in singlet states at the BP86-D3(BJ)/TZ2P level of theory. | ||
A μ-N2 ligand has been coordinated by two cAACMe–E units in end-on fashion (E = Si, Ge). Si–N/Ge–N bond distances of 1/2 (1.75/1.96) are in between a covalent single bond and a double bond. The lengths of the N–N bonds in 1–2 (1.194/1.173) are significantly longer than those of the free N2 ligand (1.102). The CcAAC–Si/Ge–N angles are in the range of 90° to 100° [97.4 (Si), 93.6(Ge)] which are significantly smaller than silylone/germylone (∼117°; (cAAC)2E; E = Si, Ge).39b The Si/Ge–N–N bond angles are 154.18° (Si) and 163.58° (Ge) suggesting that E–N2–E unit is not perfectly linear. The E–N–N–E torsion angles are 109.68° (Si; 1) and 140.19° (Ge; 2). The CcAAC–Si⋯Si–CcAAC and CcAAC–Ge⋯Ge–CcAAC torsion angles are 107.81° (ref. 39a) and 67.19°, respectively, suggesting pseudo-cis orientations of cAACMe ligands with respect to the central E2N2 unit. The CcAAC–N distances of the cAACMe ligands in 1–2 are nearly 1.35 Å suggesting the presence of π-backdonation38,39 from E to CcAAC-atom (Table 1).39 The Me groups of two cAACMe ligands are trans to each other with respect to the central E–N2–E unit (Fig. 3). The calculation of dissociation energy of E–N bond suggests that ((cAAC–E)2N2 → 2 cAAC–E + N2; E = Si, Ge) Si–N bond (53.7 kcal mol−1) in 1 is thermodynamically more stable than two Ge–N (35.7 kcal mol−1) bonds in 2 by 18 kcal mol−1. The Gibbs energy values of 28.3 kcal mol−1 (1) and 7.9 kcal mol−1 (2) indicates the endergonic nature of N2 dissociation. A marginal increase in one of the C–H distances of N substituted methyl 1.100 (1) and 1.103 (2) is observed, indicating N–HC interaction.
| Bond distance (Å) | (cAAC–Si)2(N2) (1); E = Si | (cAAC–Ge)2(N2) (2); E = Ge |
|---|---|---|
| C–N | 1.347/1.348 | 1.345/1.349 |
| C–E | 1.867/1.866 | 1.966/1.968 |
| E–N | 1.750/1.751 | 1.921/1.958 |
| N–N | 1.194 | 1.173 |
| Bond angles (°) | (cAAC–Si)2(N2) (1); E = Si | (cAAC–Ge)2(N2) (2); E = Ge |
|---|---|---|
| C–C–N | 108.17 | 108.25 |
| C–C–E | 117.61 | 116.49 |
| N–C–Si | 134.22 | 135.11 |
| C–E–N | 97.42 | 93.61 |
| E–N–N | 154.18 | 163.58 |
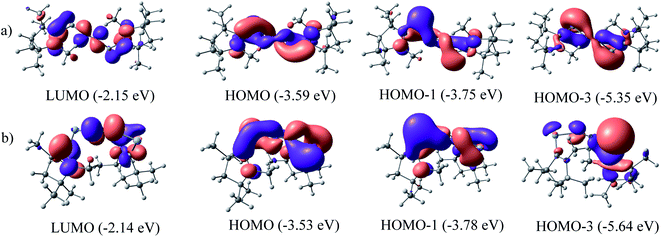
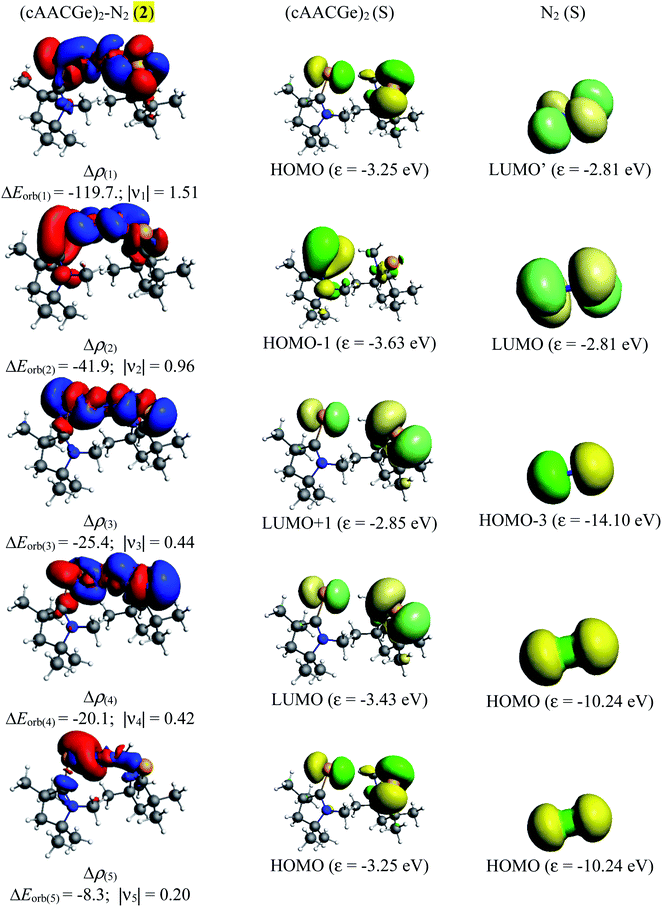
The NBO calculations reveal that the Wiberg bond indexes (WBI) of Si/Ge–N bonds of 1–2 fall in the range of 0.71–0.91, while the same of N–N bonds of 1 and 2 are 1.82 and 2.04 respectively (Table 2). The reduced bond order of N–N bond is in accordance with the calculated bond lengths, suggesting the significant π-backdonation from the filled orbital of E (Si, Ge) to the vacant π*-orbital of the bridging N2 unit. NBO analysis shows an electron occupancy of 1.97 e for the both Si–N bonds of 1, which is polarised towards the nitrogen atom (84%). The results reveal an occupancy in the range of 1.98–1.99 e for the N–N bond in both species, with equal participation of both nitrogen atoms in the bond. The occupancy for the Ge–N bond of complex 2 was not provided by the NBO calculation, which could be due to low occupancy orbitals not exceeding the occupancy threshold value. The Ge–N bond might be a coordinate polar bond rather than a covalent coordinate donor–acceptor σ/π-bond (π Ge → NN2; σ Ge ← NN2). Further calculations show the concentration of charge on the N2 unit in 1 (−0.846) and 2 (−0.636), signifying the flow of electrons from the E (Si, Ge) to N2. Further, the positive partial charge on Si/Ge atoms agrees with the π-backdonation of electrons to the bonded N2. However, cAAC ligands of compound 1 show overall positive charge, whereas the cAAC ligands of 2 show negative charge denoting a probable stronger cAAC ← Ge π-backdonation in 2. The LUMO of 1 and 2 majorly represents the antibonding π*-orbitals on N2 which are separated by nodes from two terminal E–CcAAC–NcAAC units. HOMO and HOMO−1 suggest the lone pair of the Si/Ge atoms interact with the π* orbital on the CcAAC-atom as well as the central N2 unit. HOMO−3 of 1 significantly denotes the interaction of a lone pair orbital with the N2 π*-orbital, whereas in 2 HOMO−3 indicates the presence of a germanium lone pair orbital (Fig. 4). The HOMO–LUMO gap between these two species is in the range of 1.38–1.45 eV, indicating moderate electronic stability. In general, intra/inter molecular interaction may have effect on the conformations of these molecules. The intra molecular CcAAC⋯CcAAC distances are 6.48 (1) and 5.08 (2) Å connecting themselves by a non-linear E–N2–E chain. Any intramolecular favourable interaction can bring some molecular units close to each other. NBO analyses show that the partial charges on N-atoms are −0.423 (1) and −0.318 (2). Significant CHN–Me⋯NN2 short contact (NN2⋯H 2.49/2.51 (1), 2.39/2.55 (2); NN2⋯C 2.81 (1), 2.80 (2) Å) is present. It might have brought two cAAC units of 1–2 relatively close to each other.
| Complex | Bond | ON | Polarisation and hybridisation (%) | WBI | qN | qE2 | qcAAC2 | |
|---|---|---|---|---|---|---|---|---|
| (cAAC–Si)2(N2) 1 | Si′–N | 1.97 | Si′: 16 s(12), p(87), d(1) | N: 84 s(58.6), p(41.4) | 0.91 | −0.423 | 1.055 | 0.624 |
| Si′–N | 1.97 | Si′: 16 s(12), p(87), d(1) | N: 84 s(58.6), p(41.4) | 0.91 | ||||
| N–N σ | 1.99 | N: 50 s(41), p(59) | N: 50 s(41), p(59) | 1.82 | ||||
| N–N π | 1.98 | N: 49.6 s(1.2), p(98.8) | N: 50.4 s(1.3), p(98.7) | |||||
| N–Nπ | 1.98 | N: 50.3 s(1), p(99) | N: 49.7 s(1), p(99) | |||||
| (cAAC–Ge)2(N2) 2 | Ge′–N | — | — | — | 0.76 | −0.318 | 0.905 | −0.539 |
| Ge′–N | — | — | — | 0.71 | ||||
| N–N σ | 1.99 | N: 49.9 s(41), p(59) | N: 50.1 s(41), p(59) | 2.04 | ||||
| N–N π | 1.98 | N: 49.2 s(0.2), p(99.8) | N: 50.1 s(0.2), p(99.8) | |||||
| N–N π | 1.98 | N: 52.5 s(0.2), p(99.8) | N: 47.5 s(0.5), p(99.5) | |||||
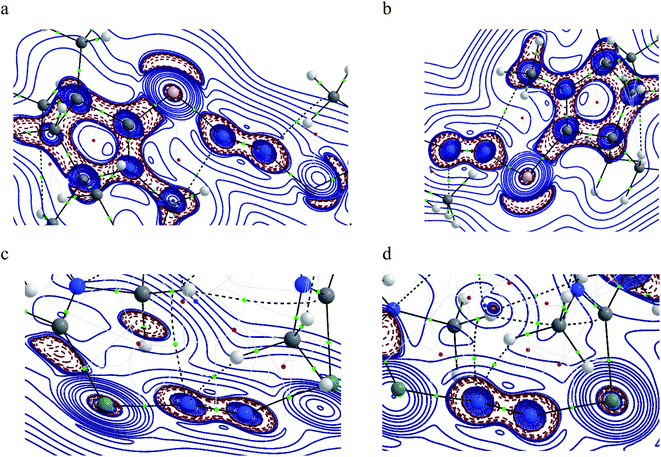
The QTAIM analysis of species 1–2 shows (Fig. 5 and Table 3) a higher positive value of Laplacian along the Si–N bond of complex 1 compared to the Ge–N bond of complex 2 denoting the depletion of electron density along the BCP, whereas the higher value of electron densities, ρ(r) on the N–N bond of both complexes supports the charge migration calculated from NBO analysis. Besides, contour plots also reflect the higher concentration of electron densities on nitrogen atoms than on E (Si, Ge) atoms of both complexes. An imaginary bond path between the N2 unit and the hydrogen of N-bound methyl group of cAAC in 1 and 2 is observed, indicating a possible N⋯HCN–Me interaction. The C–HN–Me bond lengths are in the range of 1.099 to 1.100 Å. The proximity to N-atom has been shown in optimized geometries of 1–2 in Fig. 1. This NN2 (δ−)⋯(δ+) HCN–Me interaction could an electrostatic interaction since the partial charges on N-atoms of 1–2 significantly negative (Table 2).
| Species | Bond | ρ(r) | ∇2ρ(r) | H(r) | V(r) | G(r) | εBCP | η |
|---|---|---|---|---|---|---|---|---|
| (cAAC–Si)2(N2) 1 | Si′–N | 0.107 | 0.538 | −0.036 | −0.207 | 0.171 | 0.155 | 0.190 |
| Si′′–N | 0.107 | 0.541 | −0.036 | −0.207 | 0.171 | 0.154 | 0.190 | |
| N–N | 0.524 | −1.508 | −1.031 | −1.156 | 0.125 | 0.001 | 1.274 | |
| (cAAC–Ge)2(N2) 2 | Ge′–N | 0.099 | 0.391 | −0.027 | −0.152 | 0.125 | 0.140 | 0.199 |
| Ge′′–N | 0.093 | 0.327 | −0.026 | −0.133 | 0.107 | 0.127 | 0.206 | |
| N–N | 0.554 | −1.652 | −0.848 | −1.284 | 0.435 | 0.005 | 1.33 |
The positive value of Laplacian at (3, −3) at topological point indicates a possible closed shell Si/Ge–N interaction. It is to be noted that the negative Laplacian for a covalent bond does not always hold true for bonds involving heavier elements like Si or Ge. However, the value of |V(rc)| less than 2G(rc)53 and η value less than 1.0, further supports the Si/Ge–N closed shell interaction. The covalent nature of the N–N bond obtained from the negative value of its Laplacian and the total energy, denotes the bond stabilisation of the N2 unit majorly through potential energy. Bond ellipticity is a measure of π character which is given by (ε = (λ1/λ2) − 1) at the topological point (3, −1).54 For a single bond and triple bond, it reaches a value close to zero. The ellipticity value of the Si/Ge–N bond in both complexes indicates the possibility of the partial double bond character, whereas the value of N–N (0.001 and 0.005) indicates the cylindrically symmetric distribution of electron densities as expected for the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond.
N bond.
NBO and QTAIM analyses however, cannot provide proper bonding scenarios and also cannot distinguish between an electron sharing covalent and a dative covalent bond. EDA-NOCV analyses of (cAAC)2Si2N2 (1) and (cAAC)2Ge2N2 (2) were carried out using methods similar to those reported for other species at the BP86/Def2TZVPP level of theory.40–42,44a The N2-bonded silicon species (cAAC)2Si2N2 (1) have been studied by two bonding scenarios (a) donor–acceptor dative (σ Si ← N2, π Si → N2; 1) bond between (cAACMe–Si)(Si–cAACMe) and N2 fragments in their singlet states, and (b) both σ- and π-electron sharing (Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) bond (E) between (cAACMe–Si)(Si–cAACMe) and N2 fragments in their quintet states [like cAACMe–Si
N–) bond (E) between (cAACMe–Si)(Si–cAACMe) and N2 fragments in their quintet states [like cAACMe–Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–N
N–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si–cAACMe; 1′] (Fig. 2; middle). The minimum ΔEorb is obtained (Table 4) for the former bonding scenario, confirming the preference of both dative (D) σ- and π-bonds between Si- and N-atoms of 1 over the electron sharing double bond as suggested for previously reported (cAAC)2(B-Dur)2(N2) species.36 A similar bonding scenario is expected for the comparatively more electron positive Ge-analogue (2). This correlates well with the charge distribution from the NBO analysis and closed shell bonding suggestion from the QTAIM results.
Si–cAACMe; 1′] (Fig. 2; middle). The minimum ΔEorb is obtained (Table 4) for the former bonding scenario, confirming the preference of both dative (D) σ- and π-bonds between Si- and N-atoms of 1 over the electron sharing double bond as suggested for previously reported (cAAC)2(B-Dur)2(N2) species.36 A similar bonding scenario is expected for the comparatively more electron positive Ge-analogue (2). This correlates well with the charge distribution from the NBO analysis and closed shell bonding suggestion from the QTAIM results.
| Molecule | Bond type | Fragments | ΔEint | ΔEPauli | ΔEelec | ΔEdis | ΔEorb |
|---|---|---|---|---|---|---|---|
| (cAAC–Si)2(N2) | D | 2cAAC–Si (S) + N2 (S) | −68.1 | 395.6 | −182.2 | −6.6 | −274.9 |
| E | 2cAAC–Si (Q) + N2 (Q) | −424.1 | 354.5 | −240.9 | −6.6 | −531.0 |
The bonding and stability of (cAAC)2E2 by EDA-NOCV analyses have been previously studied by Frenking et al.55,56 The (cAAC)2 fragment has been shown to form two strong dative σ-bonds with the E2 unit [cAAC → E2 ← cAAC]. In addition, there are two π-bonds (π-backdonation) between E2 and (cAAC)2 [cAAC ← E2 → cAAC; E = Si, Ge]. The total intrinsic interaction energy is nearly −140 (E = Si)/−100 (E = Ge) kcal mol−1.55,56 The CcAAC–N bond lengths in 1–2 are close to 1.35 Å which signifies moderate π-backdonation from E to cAAC [E2 → cAAC].38,39 The bonding interactions between (cAAC) and E have not been studied further here, as they have already been established (E = Si, Ge) before by Frenking et al.55,56
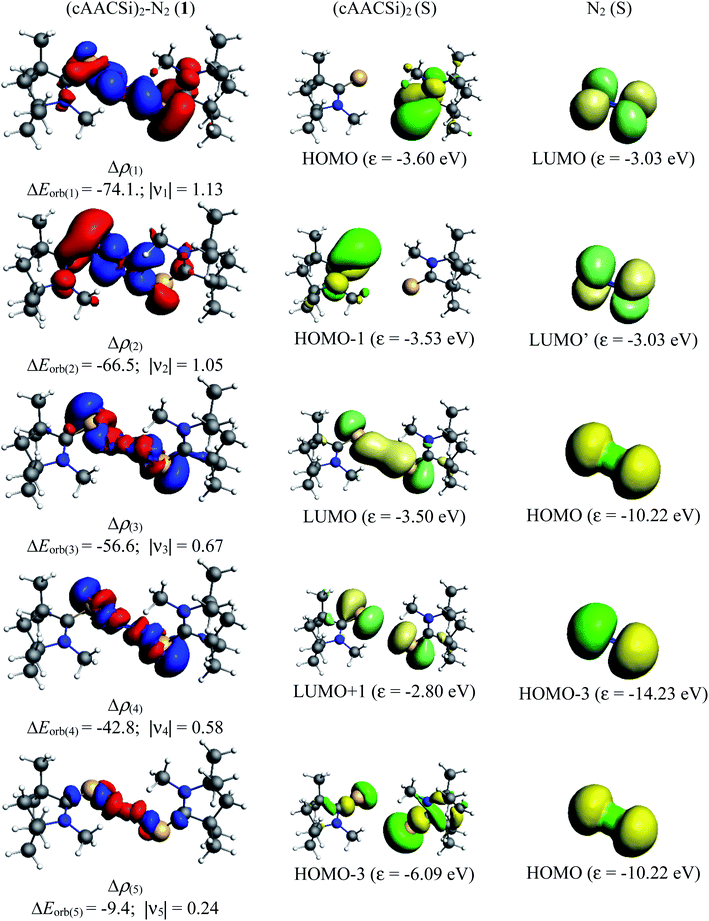
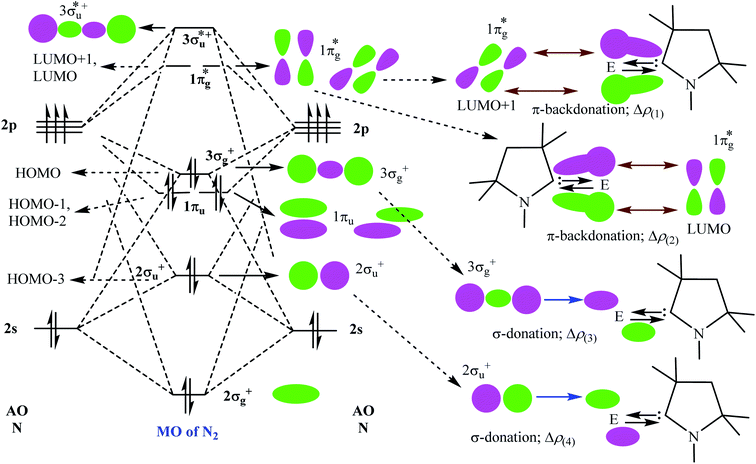
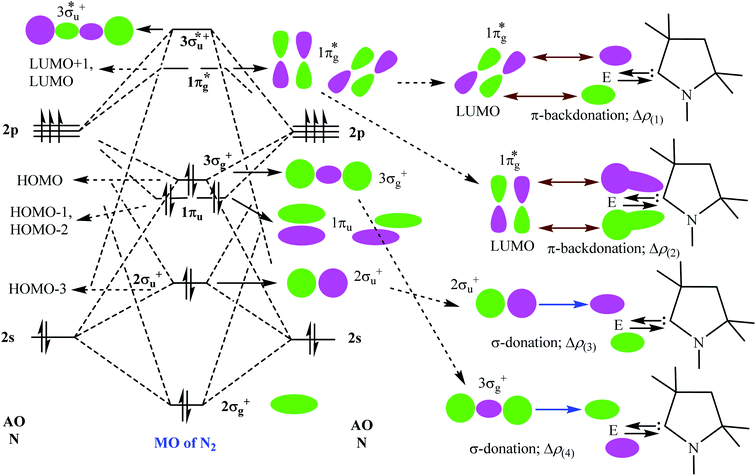
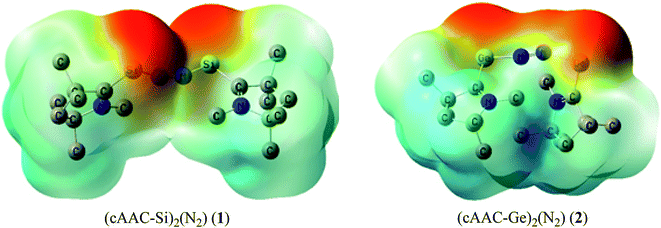
Table 5 shows that the intrinsic interaction energies of silicon and germanium species (1–2) are −68 to −70 kcal mol−1, respectively. The Si-analogue (1) possesses significantly higher Pauli repulsion energy than Ge-containing species (2). Both the coulombic and orbital interactions in 1 contribute higher stabilization energies than those in 2. Overall, ΔEint indicates that Ge-species is slightly more stable (2 kcal mol−1) than Si-species. The contribution due to orbital interaction (ΔEorb) is significantly (∼59%) higher than coulombic (∼40%) interactions in both species 1–2. EDA-NOCV provides an additional feature called pairwise orbital interaction which shows the interacting orbitals of the fragments (Fig. 6 and 7). The total ΔEorb is split into several major interacting sub-energies. The major orbital stabilization in 1 due to the formation E–N bonds comes from four significant orbital interactions [cAAC–E → N2 ← E–cAAC, HOMO, HOMO−1 of (cAAC–E)2 fragment to LUMO+1 and LUMO (doubly degenerate 1πg) of central N2; Fig. 6–8]. These π-backdonations in 1–2 contribute 51% (1) and 69% (2), respectively, of total orbital interaction (ΔEorb) (Fig. 6 and 7). The π-backdonations correlate well with the ellipticity values from QTAIM analysis. The MESP plots (Fig. 10) shows the charge accumulation (red region) in the E–N2–E region while the charge shifted from cAAC ligands (bluish-green region). The σ-donations in 1–2 contribute ∼35% (1) and ∼20% (2), respectively, of total orbital interaction (ΔEorb). The σ-charge polarizations in 1–2 contribute ∼9% (1) and ∼8% (2), respectively. In addition, 8–9% of the total interaction arises from other types of orbital interactions which are not negligible. The EDA-NOCV analyses suggest that cAAC–E unit can act as strong π-donor (π-orbital of N–C–E unit) towards the binding of molecule N2 in 1–2.
| Energy (kcal mol−1) | Interaction (σ E ← N2, π E → N2) | (cAAC–Si)2 (S) + N2 (S) 1 | (cAAC–Ge)2 (S) + N2 (S) 2 |
|---|---|---|---|
| a The values in the parentheses show the contribution to the total attractive interaction ΔEelstat + ΔEorb + ΔEdisp.b The values in parentheses show the contribution to the total orbital interaction ΔEorb. | |||
| ΔEint | −68.1 | −70.1 | |
| ΔEPauli | 395.6 | 329.4 | |
| ΔEdispa | −6.6 (1.4%) | −7.6 (1.9%) | |
| ΔEelstata | −182.2 (39.3%) | −157.2 (39.4%) | |
| ΔEorba | −274.9 (59.3%) | −234.6 (58.7%) | |
| ΔEorb(1)b | (cAAC–E)2 → N2 π-backdonation | −74.1 (27.0%) | −119.7 (51.0%) |
| ΔEorb(2)b | (cAAC–E)2 → N2 π-backdonation | −66.5 (24.2%) | −41.9 (17.9%) |
| ΔEorb(3)b | (cAAC–E)2 ← N2 σ-donation | −56.6 (20.6%) | −25.4 (10.8%) |
| ΔEorb(4)b | (cAAC–E)2 ← N2 σ-donation | −42.8 (15.5%) | −20.1 (8.6%) |
| ΔEorb(5)b | (cAAC–E)2–N2 σ-polarization | −9.4 (3.4%) | −8.3 (3.5%) |
| ΔEorb(rest)b | −25.5 (9.3%) | −19.2 (8.2%) | |
Finally, we tried to optimize the geometries of (cAACMe–Si)2(N2) (1) and (cAACMe–Ge)2(N2) (2) compounds with the ligands trans to each other. In case of compound 1, two cAACMe ligands remained trans to each other through the optimization steps, though there were slight changes in the final low energy geometry. However, for compound 2, the attempt to optimize trans-geometry interestingly resulted in a final cis-geometry. The plots of energy vs. optimization steps have been shown in Fig. S2 and S3† to illustrate the changes in the geometries at the key steps (higher energy local minima) until the final global minima (optimized geometry). The energies of the geometries at key steps (Fig. S2 and S3†) were calculated relative to the energy of the optimized geometry. The central Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si unit38,39a,57 of the reported cAACDip–Si
Si unit38,39a,57 of the reported cAACDip–Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si–cAACDip showed the presence of different conformers in the solid state while in solution it maintains an average equilibrium geometry which has been studied by solid state/solution 29Si NMR and temperature dependent X-ray structure determination.57 At 23 K the cyclohexyl functionalized cAACDip analogue Cy–cAACDip–Si
Si–cAACDip showed the presence of different conformers in the solid state while in solution it maintains an average equilibrium geometry which has been studied by solid state/solution 29Si NMR and temperature dependent X-ray structure determination.57 At 23 K the cyclohexyl functionalized cAACDip analogue Cy–cAACDip–Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si–Cy–cAACDip possesses a centre of inversion between two Si-atoms while the molecule is non centero-symmetric at 100 K.38 Thus, the central E–N–N–E unit of 1Dip–2Dip [(cAACDip–Si)2(N2) (1Dip), (cAACDip–Si)2(N2) (2Dip)] may also possess some thermal movement around its equilibrium position in between two cAAC ligands. The void space around E–N–N–E unit may allow it to have some thermal movement.
Si–Cy–cAACDip possesses a centre of inversion between two Si-atoms while the molecule is non centero-symmetric at 100 K.38 Thus, the central E–N–N–E unit of 1Dip–2Dip [(cAACDip–Si)2(N2) (1Dip), (cAACDip–Si)2(N2) (2Dip)] may also possess some thermal movement around its equilibrium position in between two cAAC ligands. The void space around E–N–N–E unit may allow it to have some thermal movement.
The cAAC ligands with a Dip-group on the N-atom (Dip = 2,4-isopropylphenyl; cAACDip) are regularly employed as an efficient coordinating/anchoring ligand.36–39 The bonding and stability remain almost unaltered if the geometries of the species with smaller substituents on the cAAC ligand do not change significantly on choosing smaller substituents on cAAC part for simplification. The Si-analogue of 1 (cAAC = cAACMe) having a Dip-group (cAAC = cAACDip) on cAAC has been optimized in the same level of theory [(cAACDip–Si)2(N2) (1Dip)]. The central Si–N–N–Si non-linear chain of 1Dip has been shielded by two cAACDip ligands (see space filling model in Fig. 11 and S4†). The cAACDip ligands are oriented nearly trans (CcAAC–Si–Si–CcAAC torsion of 152.67° in 1Dip vs. 107.81° in 1) to each other with respect to the central Si–N–N–Si chain. The CcAAC–Si–N angle widens by 3° (100.89° in 1Dip vs. 97.4/97.6° in 1). The bond length slightly changes at third decimal suggesting that the Si–N2 interaction energies (ΔEint) of 1Dip is expected to be very close to that of 1. C–HiPr⋯N weak interactions are observed (2.479/2.543 Å; see Fig. 11) in 1Dip. Further calculations indicate that the cAACDip ligands of 2Dip [(cAACDip–Si)2(N2) (2Dip)] also arrange themselves trans to each other with respect to the central Ge–N–N–Ge unit like Si-compound.
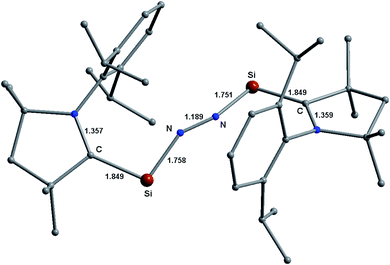 | ||
| Fig. 11 Optimized equilibrium geometries of (cAACDip–Si)2(N2) (1Dip) in the singlet state at the BP86-D3(BJ)/TZ2P level of theory. | ||
The precursor (Me/Cy–cAACDip)SiCl4 has been reduced with KC8 in different molar ratios to produce (Me/Cy–cAACDip)SiCl3 radical, (Me/Cy–cAACDip)2Si2Cl4, (Me/Cy–cAACDip)2Si2Cl2, (Me/Cy–cAACDip)2Si2 in THF controlling the initiation temperatures of the reactions.38 The (Me/Cy–cAACDip)GeCl2 is isolated in small quantity by directly reacting GeCl2(dioxane) adduct with cAAC ligand in the presence of an anionic compound to avoid the formation of cAACH+ GeCl3−.58 The adduct (bulky group-cAACbulky group)SiCl4 can be utilized as a precursor under reduced (KC8) condition to prevent the dimerization of (bulky group-cAACbulky group)Si unit under dinitrogen atmosphere. In recent time, several bulky cAAC ligands59,60 have been synthesized, isolated and utilized for catalytic organic transformation.60 The bulky substituents around CcAAC–atom is suggested here to prevent the dimerization of 2cAAC–E to (cAAC–E)2 creating the possibility of N2 binding by two cAAC–E fragments under suitable reaction condition via the prevention of self dimerization of 2 cAAC–E units. The later process is thermodynamically more favourable over binding of N2 by 2 cAAC–E units.
Conclusion
The stability and bonding of N2-bonded species (cAAC–E)2(N2) (1–2; Si, Ge) have been studied by DFT calculations [NBO, QTAIM and EDA-NOCV analyses]. The cAAC bonded E(0) [cAAC–E; E = Si, Ge] can act as a very good π-donor ligand. The major stability of E–N2–E bonds in 1–2 arise from stronger π-backdonations (E → N2; cAAC–E → N2 ← E–cAAC) which are nearly 1.5 (Si) and 3 (Ge) times higher than σ-donations (E ← N2; cAAC–E ← N2 → E–cAAC) in 1 and 2, respectively. The bonding interactions have been clearly shown in Fig. 8 and 9. The σ-charge polarization from E to N2 is not negligible. The London dispersion force is only 1–2% of the total stabilization energy. Significant intrinsic interaction energies (∼68–70 kcal mol−1) of E–N E–N2–E bonds in 1–2 suggest that species 1–2 may be synthesized and isolated in the laboratory.Conflicts of interest
Authors do not have any conflict of interest.Acknowledgements
S. M. thanks CSIR for SRF. K. C. M. thanks SERB for the ECR grant (ECR/2016/000890) and IIT madras for seed grant.References
- C. Shan, S. Yao and M. Driess, Chem. Soc. Rev., 2020, 49, 6733 RSC.
- (a) J. Cribb, Surviving the 21st Century, Humanity's Ten Great Challenges and How We Can Overcome Them, Springer International Publishing, 2017, eBook ISBN 978-3-319-41270-2 CrossRef; (b) R. Walsh, Staying Alive: The Psychology of Human Survival, 1984, New Science Library, USA, Boston, Massachusetts, U.S.A, 1984-09 ISBN 13: 9780394726908 Search PubMed.
- (a) A. Marshall, Development and Imperialism in Space, Space Policy, 1995, 11, pp. 41–52 Search PubMed; (b) D. Deudney, Dark Skies: Space Expansionism, Planetary Geopolitics, and the Ends of Humanity, Oxford University Press, 2020, ISBN 978-0-19-009024-1. OCLC 1145940182 CrossRef.
- J. A. Kent. Riegel's Handbook of Industrial Chemistry, CBS Publishers & Distributors, January 1, 1997, ISBN-13: 978-8123905440 Search PubMed.
- (a) A. W. Pierpont and T. R. Cundari, J. Coord. Chem., 2011, 64, 3123 CrossRef CAS; (b) A. Nandy and H. J. Kulik, ACS Catal., 2020, 10, 15033 CrossRef CAS; (c) Y. Nishibayashi, Transition Metal-Dinitrogen Complexes: Preparation and Reactivity, John Wiley & Sons, ISBN: 978-3-527-34425-3, 2019, 352734425X, 9783527344253 CrossRef.
- (a) B. K. Burgess and D. J. Lowe, Chem. Rev., 1996, 96, 2983 CrossRef CAS PubMed; (b) V. Smil, Enriching the Earth: Fritz Haber, Carl Bosch and the Transformation of World Food Production, MIT Press, Cambridge, 2001 Search PubMed.
- B. M. Hoffman, D. R. Dean and L. C. Seefeldt, Acc. Chem. Res., 2009, 42, 609 CrossRef CAS PubMed.
- J. L. Crossland and D. R. Tyler, Coord. Chem. Rev., 2010, 254, 1883 CrossRef CAS.
- (a) M. Appl, The Haber–Bosch Process and the Development of Chemical Engineering. A Century of Chemical Engineering, Plenum Press, New York, 1982, pp. 29–54, ISBN 978-0-306-40895-3 Search PubMed; (b) P. H. Pfromm, J. Renewable Sustainable Energy, 2017, 9, 034702 CrossRef.
- (a) C.-H. Wang, Z.-B. Yin, J. Wei, W. X. Zhang and Z. Xi, Tetrahedron, 2020, 76, 131703 CrossRef CAS; (b) H. Song and E. Lee, Chem.–Asian J., 2021, 16, 2421–2425 CrossRef CAS PubMed; (c) Q. Zhu, R. Qiu, S. Dong, G. Zeng and J. Zhu, Chem.–Asian J., 2021, 16, 2063–2067 CrossRef CAS PubMed; (d) X. Yu, P. Han, Z. Wei, L. Huang, Z. Gu, S. Peng, J. Ma and G. Zheng, Joule, 2018, 2, 1610–1622 CrossRef CAS; (e) A. M. Rouf, C. Dai, S. Dong and J. Zhu, Inorg. Chem., 2020, 59, 11770–11781 CrossRef CAS PubMed; (f) A. M. Rouf, Y. Huang, S. Dong and J. Zhu, Inorg. Chem., 2021, 60, 5598–5606 CrossRef CAS PubMed.
- (a) Z.-J. Lv, J. Wei, W.-X. Zhang, P. Chen, D. Deng, Z.-J. Shi and Z. Xi, Natl. Sci. Rev., 2020, 7, 1564 CrossRef CAS PubMed; (b) S. Kin, F. Loose and P. J. Chirik, Chem. Rev., 2020, 120, 5637–5681 CrossRef PubMed; (c) R. J. Burford, A. Yaeo and M. D. Fryzuk, Coord. Chem. Rev., 2017, 334, 84–99 CrossRef CAS; (d) R. J. Burford and M. D. Fryzuk, Nat. Rev. Chem., 2017, 1, 26 CrossRef CAS; (e) H.-P. Jia and E. A. Quadrelli, Chem. Soc. Rev., 2014, 43, 547–564 RSC.
- (a) T. Yamabe, K. Hori, T. Minato and K. Fukui, Inorg. Chem., 1980, 19, 2154–2159 CrossRef CAS; (b) D. L. M. Suess, C. Tsay and J. C. Peters, J. Am. Chem. Soc., 2012, 134, 14158–14164 CrossRef CAS PubMed; (c) M. T. Whited, N. P. Mankad, Y. Lee, P. E. Oblad and J. C. Peters, Inorg. Chem., 2009, 48, 2507 CrossRef CAS PubMed.
- B. D. Matson and J. C. Peters, ACS Catal., 2018, 8, 1448 CrossRef CAS PubMed.
- J. Fajardo, Jr and J. C. Peters, J. Am. Chem. Soc., 2017, 139, 16105 CrossRef PubMed.
- J. Rittle and J. C. Peters, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15898 CrossRef CAS PubMed.
- N. P. Mankad, M. T. Whited and J. C. Peters, Angew. Chem., Int. Ed., 2007, 46, 5768 CrossRef CAS PubMed.
- Y. Lee, N. P. Mankad and J. C. Peters, Nat. Chem., 2010, 2, 558 CrossRef CAS PubMed.
- S. E. Creutz and J. C. Peters, J. Am. Chem. Soc., 2014, 136, 1105 CrossRef CAS PubMed.
- M. D. Zott and J. C. Peters, J. Am. Chem. Soc., 2021, 143, 7612–7616 CrossRef CAS PubMed.
- N. B. Thompson, M. T. Green and J. C. Peters, J. Am. Chem. Soc., 2017, 139, 15312 CrossRef CAS PubMed.
- Q. J. Bruch, G. P. Connor, N. D. McMillion, A. S. Goldman, F. Hasanayn, P. J. Holland and A. J. M. Miller, ACS Catal., 2020, 10, 10826 CrossRef CAS.
- G. Ung and J. C. Peters, Angew. Chem., Int. Ed., 2015, 54, 532 CAS.
- P. J. Hill, L. R. Doyle, A. D. Crawford and W. K. Myers, J. Am. Chem. Soc., 2016, 138, 13521 CrossRef CAS PubMed.
- T. A. Bazhenova and A. E. Shilov, Coord. Chem. Rev., 1995, 144, 69 CrossRef CAS.
- S. Kuriyama, K. Arashiba, K. Nakajima, Y. Matsuo, H. Tanaka, K. Ishii, K. Yoshizawa and Y. Nishibayashi, Nat. Commun., 2016, 7, 12181 CrossRef CAS PubMed.
- S. F. McWilliams, D. L. J. Broere, C. J. V. Halliday, S. M. Bhutto, B. Q. Mercado and P. L. Holland, Nature, 2020, 584, 221 CrossRef CAS PubMed.
- Y. Lee, F. T. Sloane, G. Blondin, K. A. Abboud, R. García-Serres and L. J. Murray, Angew. Chem., Int. Ed., 2015, 54, 1499 CrossRef CAS PubMed.
- I. Čorić and P. L. Holland, J. Am. Chem. Soc., 2016, 138, 7200 CrossRef PubMed.
- L. A. Wickramasinghe, T. Ogawa, R. R. Schrock and P. Müller, J. Am. Chem. Soc., 2017, 139, 9132 CrossRef CAS PubMed.
- B. M. Lindley, R. S. van Alten, M. Finger, F. Schendzielorz, C. Würtele, A. J. M. Miller, I. Siewert and S. Schneider, J. Am. Chem. Soc., 2018, 140, 7922 CrossRef CAS PubMed.
- Y. Sekiguchi, K. Arashiba, H. Tanaka, A. Eizawa, K. Nakajima, K. Yoshizawa and Y. Nishibayashi, Angew. Chem., Int. Ed., 2018, 57, 9064 CrossRef CAS PubMed.
- Y. Yao, S. Zhu, H. Wang, H. Li and M. Shao, J. Am. Chem. Soc., 2018, 140, 1496 CrossRef CAS PubMed.
- S. Ye, E. Bill and F. Neese, Inorg. Chem., 2016, 55, 3468 CrossRef CAS PubMed.
- R. Bjornsson, F. Neese and S. DeBeer, Inorg. Chem., 2017, 56, 1470 CrossRef CAS PubMed.
- I. Čorić, B. Q. Mercado, E. Bill, D. J. Vinyard and P. L. Holland, Nature, 2015, 526, 96 CrossRef PubMed.
- (a) E. Welz, I. Krummenacher, B. Engels and H. Braunschweig, Science, 2018, 359, 896 CrossRef PubMed; (b) M. A. Légaré, M. Rang, G. Bélanger-Chabot, J. I. Schweizer, I. Krummenacher, R. Bertermann, M. Arrowsmith, M. C. Holthausen and H. Braunschweig, Science, 2019, 363, 1329 CrossRef PubMed; (c) M. A. Legare, G. Belanger-Chabot, M. Rang, R. D. Dewhurst, I. Krummenacher, R. Bertermann and H. Braunschweig, Nat. Chem., 2020, 12, 1076 CrossRef CAS PubMed; (d) H. Braunschweig, I. Krummenacher, M. A. Legare, A. Matler, K. Radacki and Q. Ye, J. Am. Chem. Soc., 2017, 139, 1802 CrossRef CAS PubMed.
- V. Lavallo, Y. Canac, C. Präsang, B. Donnadieu and G. Bertrand, Angew. Chem., Int. Ed., 2005, 44, 5705 CrossRef CAS PubMed.
- K. C. Mondal, S. Roy and H. W. Roesky, Chem. Soc. Rev., 2016, 45, 1080 RSC.
- (a) K. C. Mondal, P. P. Samuel, H. W. Roesky, R. R. Aysin, L. A. Leites, S. Neudeck, J. Lübben, B. Dittrich, M. Hermann and G. Frenking, J. Am. Chem. Soc., 2014, 136, 8919 CrossRef CAS PubMed; (b) K. C. Mondal, S. Roy, B. Dittrich, D. M. Andrada, G. Frenking and H. W. Roesky, Angew. Chem., Int. Ed., 2016, 55, 3158 CrossRef CAS PubMed.
- L. Zhao, S. Pan, N. Holzmann, P. Schwerdtfeger and G. Frenking, Chem. Rev., 2019, 119, 8781 CrossRef CAS PubMed.
- (a) G. Frenking and F. M. Bickelhaupt, The Chemical Bond 1. Fundamental Aspects of Chemical Bonding, chap. The EDA Perspective of Chemical Bonding, Wiley-VCH, Weinheim, 2014, vol 121 CrossRef; (b) L. M. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 1345 Search PubMed; (c) L. Zhao, M. Hermann, W. H. E. Schwarz and G. Frenking, Nat. Rev. Chem., 2019, 3, 48 CrossRef CAS; (d) S. Pan and G. Frenking, Angew. Chem., Int. Ed., 2020, 59, 8756 CrossRef CAS PubMed; (e) J. Andrés, P. W. Ayers, R. A. Boto, R. Carbó-Dorca, H. Chermette, J. Cioslowski, J. Contreras-García, D. L. Cooper, G. Frenking, C. Gatti, F. Heidar-Zadeh, L. Joubert, Á. M. Pendás, E. Matito, I. Mayer, A. J. Misquitta, Y. Mo, J. Pilmé, P. L. A. Popelier, M. Rahm, E. Ramos-Cordoba, P. Salvador, W. H. E. Schwarz, S. Shahbazian, B. Silvi, M. Solà, K. Szalewicz, V. Tognetti, F. Weinhold and É. L. Zins, J. Comput. Chem., 2019, 40, 2248 CrossRef PubMed; (f) W. Yang, K. E. Krantz, L. A. Freeman, D. Dickie, A. Molino, G. Frenking, S. Pan, D. J. D. Wilson and R. J. Gilliard, Jr, Angew. Chem., Int. Ed., 2020, 59, 3850 CrossRef CAS PubMed; (g) S. M. N. V. T. Gorantla, P. Parameswaran and K. C. Mondal, J. Comput. Chem., 2021, 42, 1159 CrossRef CAS PubMed; (h) S. M. N. V. T. Gorantla, S. Pan, K. C. Mondal and G. Frenking, Chem.–Eur. J., 2020, 26, 14211 CrossRef CAS PubMed; (i) L. Zhao, S. Pan, M. Zhou and G. Frenking, Science, 2019, 365, eaay5021 CrossRef CAS PubMed; (j) R. Saha, S. Pan, P. K. Chattaraj and G. Merino, Dalton Trans., 2020, 49, 1056 RSC.
- R. Tonner and G. Frenking, Angew. Chem., Int. Ed., 2007, 46, 8695 CrossRef CAS PubMed.
- (a) C. A. Dyker, V. Lavallo, B. Donnadieu and G. Bertrand, Angew. Chem. Int. Ed., 2008, 47, 3206 CrossRef CAS PubMed; (b) A. Fürstner, M. Alcarazo, R. Goddard and C. W. Lehmann, Angew. Chem., Int. Ed., 2008, 47, 3210 CrossRef PubMed.
- (a) M. A. Celik, R. Sure, S. Klein, R. Kinjo, G. Bertrand and G. Frenking, Chem.–Eur. J., 2012, 18, 5676 CrossRef CAS PubMed; (b) H. Braunschweig, R. D. Dewhurst, F. Hupp, M. Nutz, K. Radacki, C. W. Tate, A. Vargas and Q. Ye, Nature, 2015, 522, 327 CrossRef CAS PubMed.
- (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3099 CrossRef CAS PubMed; (b) J. P. Perdew, Phys. Rev. B: Solid State, 1986, 33, 8822–8823 CrossRef PubMed; (c) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed; (d) S. Grimme, J. Antony, S. Ehrlich and H. A. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed; (e) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC; (f) F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- M. J. Frisch, et al., Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- (a) F. Weinhold and C. Landis, Valency and Bonding, A Natural Bond Orbital Donor – Acceptor Perspective, Cambridge University Press, Cambridge, 2005 Search PubMed; (b) C. R. Landis and F. Weinhold, The NBO View of Chemical Bonding. The Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH, Weinheim, 2014, pp. 91–120 Search PubMed; (c) F. M. Bickelhaupt and E. J. Baerends, Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry, in Rev. Comput. Chem., ed. K. B. Lipkowitz and B. D. Boyd, Wiley-VCH, New York, 2000, vol. 15, pp. 1–86 Search PubMed.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS.
- (a) M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576–6580 CrossRef CAS; (b) M. Mitoraj and A. Michalak, J. Mol. Model., 2008, 14, 681–687 CrossRef CAS PubMed.
- (a) ADF2017, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed; (b) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- (a) E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142 CrossRef CAS PubMed; (b) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS; (c) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS.
- P. S. V. Kumar, V. Raghavendra and V. Subramanian, J. Chem. Sci., 2016, 128, 1527 CrossRef CAS.
- S. Jenkins, L. Blancafort, S. R. Kirk and M. J. Bearpark, Phys. Chem. Chem. Phys., 2014, 16, 7115 RSC.
- N. Holzmann, D. M. Andrada and G. Frenking, J. Orgmet. Chem., 2015, 792, 139 CrossRef CAS.
- A. Sidiropoulos, C. Jones, A. Stasch, S. Klein and G. Frenking, Angew. Chem., Int. Ed., 2009, 48, 9701 CrossRef CAS PubMed.
- K. C. Mondal, S. Roy, B. Dittrich, B. Maity, S. Dutta, D. Koley, S. K. Vasa, R. Linser, S. Decherta and H. W. Roesky, Chem. Sci., 2015, 6, 5230 RSC.
- Y. Li, K. C. Mondal, H. W. Roesky, H. Zhu, P. Stollberg, R. Herbst-Irmer, D. Stalke and D. M. Andrada, J. Am. Chem. Soc., 2013, 135, 12422 CrossRef CAS PubMed.
- D. Pichon, M. Soleilhavoup, J. Morvan, G. P. Junor, T. Vives, C. Crévisy, V. Lavallo, J.-M. Campagne, M. Mauduit, R. Jazzar and G. Bertrand, Chem. Sci., 2019, 10, 7807 RSC.
- J. Morvan, M. Mauduit, G. Bertrand and R. Jazzar, ACS Catal., 2021, 11, 1714 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Tables, Figures, QTAIM, and optimized coordinates. See DOI: 10.1039/d1ra07714g |
| This journal is © The Royal Society of Chemistry 2022 |