Open Access Article
Open Access ArticleQuasi-bound states in the continuum with high Q-factors in metasurfaces of lower-index dielectrics supported by metallic substrates
Kwang-Hyon Kim * and
Il-Pong Kim
* and
Il-Pong Kim
Institute of Physics, State Academy of Sciences, Unjong District, Pyongyang, Democratic People's Republic of Korea. E-mail: kwang-h.kim@star-co.net.kp
First published on 12th January 2022
Abstract
For observing high-Q quasi-bound states in the continuum (BIC), the metasurfaces should be made of high-index materials, restricting their applications due to the limited material functionalities. In this work, we demonstrate that high-Q quasi-BIC can also be obtained by using lower-index dielectrics, provided that the metasurfaces are supported by metallic substrates. Strong field confinement assisted by plasmon excitation on the surface of metallic substrate enables realizing quasi-BIC even when using the lower-index materials such as zinc oxide. The numerical results show that high Q-factors in the order of several hundreds can be obtained with such metasurfaces of lower-index materials. They do not exhibit, however, quasi-BIC when supported by dielectric substrates due to the strong mode leakage originating from the low index contrast. Quite interestingly, metasurfaces made of high-index dielectrics supported by metallic substrates exhibit lower Q-factors compared with the metasurfaces of lower-index dielectrics due to the stronger penetration of mode field into the metallic substrate. The presented results can find important applications for photonic purposes, including efficient UV generation and low-threshold lasing from the lower-index dielectric metasurfaces.
Introduction
Dielectric nanophotonics1–4 has recently shown rapid progress due to the advantage of low optical loss, which is required for most nanophotonic processes such as efficient nonlinear generation5 and low-threshold nanolasing.6 For obtaining strong enhancement of local field and high Q-factor, the photonic structures should be made of high-index materials such as silicon and germanium.7 Unfortunately, they exhibit strong optical losses in the short wavelength range from blue to ultraviolet,7 leading to the low harmonic generation efficiency. Besides, by using only high-index materials one cannot employ the diverse functionalities of photonic materials. For solving this problem, lower-index dielectric materials have been considered as the materials for constructing photonic nanostructures, when the major attention should be paid to avoiding leakage of local mode field originating from the low index (see e.g. ref. 8). Ensuring high index contrast between the nanoparticles and substrates8 or using metallic substrates9–11 prevent the mode leakage and support strong field confinement even with the lower-index materials.Bound states in the continuum (BIC)12–15 have recently attracted great attention in the field of photonics and have found numerous applications, including low-threshold lasing,16–18 efficient nonlinear processes,19–25 sensing and imaging,26–30 circular dichroism and vortex beam generation,31–35 photonic quantum-spin Hall effect,36 and negative refraction.37 Taking the structures exhibiting the symmetry-protected BIC (see e.g. ref. 12 and 38) as examples, they support completely dark states with infinitely high Q-factor which are unable to couple to the far-field due to the structural symmetry. When the symmetry of the systems is broken, one obtains quasi-BIC with high Q-factor,39–41 the magnitude of which depends on the asymmetry parameter: in metasurfaces with broken in-plane symmetry, the Q-factor is inversely proportional to the square of asymmetry parameter.39 In the preceding results, most of metasurfaces exhibiting high-Q quasi-BIC have been made of high-index dielectric materials (see e.g. ref. 15). If quasi-BIC can be realized by using the metasurfaces of lower-index dielectrics, we can enjoy their diverse functionalities compared with the cases of using only high-index materials, which is the motivation of this study.
In this work, we reveal that the dielectric metasurfaces made of lower-index materials can also exhibit high-Q quasi-BIC, provided that they are supported by metallic substrates, taking the metasurfaces consisting of parallel dielectric nanorods in their unit cells, as examples. Assisted by plasmon excitation in the interface between dielectric nanorods and metallic substrate surface, strongly anti-coupled dipole modes are excited in the dielectric nanorods with different lengths, leading to the strong resonant reflection dip with narrow linewidth due to quasi-BIC. When the dielectric nanorods are identical, the dipoles exactly cancel each other, resulting in completely dark BIC. Such a behaviour cannot be observed when the metasurfaces are supported by dielectric substrates. The influences of structural parameters on the characteristics of quasi-BIC are numerically investigated. The metasurfaces of high-index dielectrics supported by metallic substrates have the lower Q-factor compared with the case the lower-index metasurfaces, which is attributed to the stronger penetration of mode field into the metallic substrates: using metallic substrates is preferable only for the metasurfaces made of lower-index dielectrics. As an example of possible applications of lower-index metasurfaces exhibiting quasi-BIC, we numerically show efficient third-harmonic generation (THG) in the ultraviolet range, which is unobtainable with high-index dielectric metasurfaces due to their strong optical losses in this spectral range. The proposed scheme for obtaining high-Q quasi-BIC with lower-index dielectrics paves the way towards broader photonic applications by employing diverse photonic functionalities of materials.
Quasi-bound states in the continuum in metasurfaces of lower-index dielectrics supported by metallic substrates
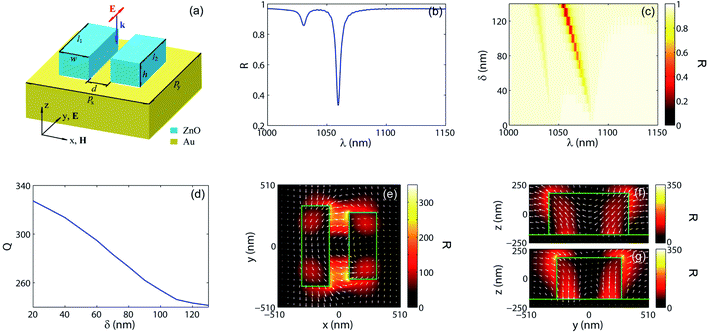
In this section, we examine the optical responses of metasurfaces consisting of two lower-index dielectric nanorods in their unit cells, which are supported by metallic substrates. Here, the lower-index dielectrics indicate that their refractive indices are much lower than high-index materials such as silicon and germanium. As examples, we take metasurfaces made of zinc oxide (ZnO),42 the refractive of which is approximately 1.9 in the visible-infrared range, supported by gold substrate.Fig. 1a presents the unit cell structure of the metasurface, where the incident light is polarized parallel to the nanorods. The dielectric functions of ZnO and gold are taken from ref. 42 and 43, which have the values of εZnO = 3.68 and εAu = −47.27 + 3.62i at 1050 nm, respectively. Fig. 1b presents the reflection spectrum of the metasurface for the following structural parameters: the widths of nanorods are w = 240 nm, their lengths are l1 = 680 and l2 = 560, corresponding to the asymmetry parameter δ = l1 − l2 of 120 nm, the spacing between the nanorods is d = 160 nm, the periods along the x- and y-directions are px = pv = 1020 nm, respectively. In this work, we study the electromagnetic responses by using the numerical tool FDTD Lumerical Solutions. We calculate Q-factor by using the built-in analysis tool of the FDTD software, which determines its magnitude from the slope of decaying envelope. The mesh sizes along x-, y-, and z-directions are taken as 10 nm, respectively. As the figure shows, at around 1060 nm a strong reflection dip appears, the spectral width (FWHM) of which amounts to 4.36 nm, corresponding to the Q-factor of around 243. In Fig. 1c, the dependence of reflection spectrum on the asymmetry parameter δ as the color density map. The figure shows the reflection dip blue-shifts and becomes stronger with increasing the magnitude of asymmetry parameter δ, revealing the symmetry-protectedness. The dependence of Q-factor on δ is shown in Fig. 1d. From the figure, we can see that the asymmetry parameter dependence of Q-factor does not follow the rule ∝ δ−2 inherent to the in-plane symmetry broken all-dielectric metasurfaces.39 Such a tendency is attributed to the additional optical loss due to the plasmon excitation on the surface of metallic substrate. Despite of plasmon-induced loss, the resultant magnitude of Q-factor is larger than 200 (Fig. 1d), which is still comparable to the systems made of high-index materials exhibiting quasi-BIC and practically valuable for most of photonic applications: even in all-dielectric photonic structures without metallic losses, the surface roughness and the inherent structural asymmetry due to the existence of dielectric substrate limit the magnitude of Q-factor down to the order of around 300 (see e.g. ref. 44). The above shown quasi-BIC results from the anti-symmetric coupling of dipoles excited in the dielectric nanorods as shown in Fig. 1e–g.
For further confirming the nature as the symmetry-protected BIC, we proceed the eigenmode analysis. Fig. 2a illustrates the distribution of eigenmode for the case of δ = 0, where color density map represents the intensity distribution and the arrows show the distribution of the electric mode field. As the figure shows, the completely symmetric structure of double parallel nanorods supports the local field induced by antiparallel dipoles with identical strengths, thus the far-field cannot couple to this mode and clearly shows the symmetry protectedness of the BIC. Fig. 2b presents the result of eigenfrequency analysis, where blue line shows the wavelength corresponding to the eigenfrequency as the function of the asymmetry parameter δ. The result shown in Fig. 2b well agrees with the spectral dip in the reflection spectrum of the metasurface shown in Fig. 1c, revealing the excitation of eigenmode of the metasurface structure by the far-field. Fig. 2c and d presents the charge distributions on the surfaces of gold substrate, from which we can confirm again that the BIC is induced by anti-symmetric coupling of dipole modes excited in the dielectric nanorods.
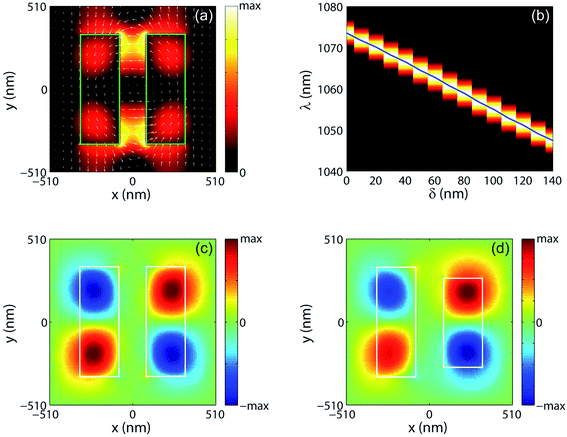 | ||
| Fig. 2 The results of eigenmode analysis and charge distributions on the metallic substrate. In (a), the eigenmode distribution is shown, where the intensity distribution is shown as color map and the eigenmode field as arrows, respectively. In (b), the wavelength corresponding to the eigenfrequency is shown as the function of the asymmetry parameter δ, where color map is the result of band structure analysis calculated by using the FDTD numerical tool. In (c) and (d), the charge distributions of the eigenmode for δ = 0 and the resonant mode for δ = 120 nm are shown on the surface of gold substrate, respectively. The other structural and material parameters are the same as in Fig. 1. | ||
From the results shown in this section, we can conclude that high-Q quasi-BIC can be obtained even with lower-index dielectrics, provided that the metasurfaces are supported by metallic substrates, by the assistance of plasmon excitation. Although the surface plasmon plays the important role in the appearance of quasi-BIC, the resultant Q-factor is high enough for photonic applications due to the major confinement of electromagnetic energy into the dielectric nanorods rather than the substrate.
Parameter dependence
Next, we study the parameter dependence of optical responses of the proposed metasurfaces. Fig. 3a shows the reflection spectra for different nanorod width w = 340, 360, and 380 nm, respectively, and Fig. 3b for different lengths l1 = 640, 680, and 720 nm of the longer nanorod for a constant value of δ = 120 nm, where the other structural and material parameters are the same as in Fig. 1b. The figures show that the resonant wavelength red-shifts for the increase of both nanorod width and length. When the refractive index of nanorods increases, the spectral position of reflection dip also red-shifts and the resonance dip becomes stronger.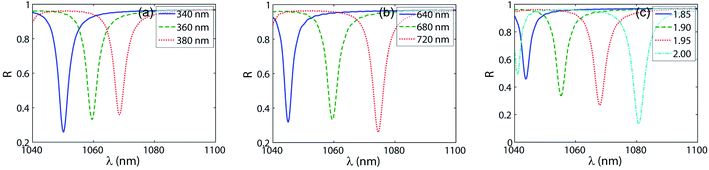 | ||
| Fig. 3 The influence of structural and material parameters on the reflectance. In (a) and (b), the dependencies on the nanorod widths w and the length l1 of the longer nanorod are shown, respectively. In (b), δ = 120 nm is kept to be constant and the length of the shorter nanorods is taken as l2 = l1 − δ. In (c), the reflectance is shown for different refractive indices of the dielectric nanorods. The other structural and material parameters are the same as in Fig. 1b. | ||
As the metasurface is made of dielectric material with refractive index much lower than silicon or germanium, the material parameter of substrate significantly influences on the generation and performance of quasi-BIC. Fig. 4a presents the reflection and transmission spectra of the metasurface, which is the same as in Fig. 1b but supported by silica substrate. The dielectric function of silica is taken from ref. 45. The figure shows that the lower-index dielectric metasurface supported by dielectric substrate does not show a strong resonance by quasi-BIC, which is attributed to strong mode leakage due to the low index contrast between the nanorods and substrate. The reflection spectra calculated for the substrates of different metals show that the silver substrate provides the similar result as the gold, while the reflection dip appears at a shorter wavelength and its spectral width becomes much wider when using aluminium as the substrate material (see Fig. 4b). For detailed study of the influence of the metallic substrate, we calculate the reflectance depending on the plasma frequency ωp and collision frequency γ, being Drude parameters describing the dielectric function ε = 1 − ωp2/(ω2 + iγω) of metals, where ω is the angular frequency of the incident light. Fig. 4c presents the influence of the reflectance on ωp, showing that the reflection dip blue-shifts and the linewidth decreases for the increase of ωp. From the boundary condition for the normal components of the electric induction (as shown in Fig. 1f and g, the local field in the vicinity of metallic substrate is normal to its surface) and considering that the higher ωp results in the larger absolute value of the real part of the dielectric function of Drude metal, we can see that the field weaker penetrates into the metallic substrate for higher ωp and, resultantly, the spectral width of the reflection dip becomes narrower due to the smaller loss in the substrate. Fig. 4d–g intuitively shows the above behaviour: for ωp = 0.8 × 1016 rad s−1 (Fig. 4d and e) the intensity in the metallic region is much higher than the case of ωp = 1.4 × 1016 rad s−1 (Fig. 4f and g). For the increase of collision frequency γ, optical loss in metallic substrate becomes stronger, resulting in the increased linewidth and decreased Q-factor (Fig. 4h). Now we reconsider the optical responses of the metasurfaces supported by the substrates of different metals, which is presented in Fig. 4b. Although the absolute value of the real part of the dielectric function of Al is much larger than gold and silver, the linewidth of reflection dip is wider, which seems to be inconsistent with the result shown in Fig. 4c. However, the imaginary part of the dielectric function of Al, determined by collision frequency, is so large compared with Au and Ag that the influence of ohm's loss in the substrate exceeds the linewidth narrowing by the large plasma frequency, resulting in the wider spectral width of reflection dip and the reduced Q-factor.
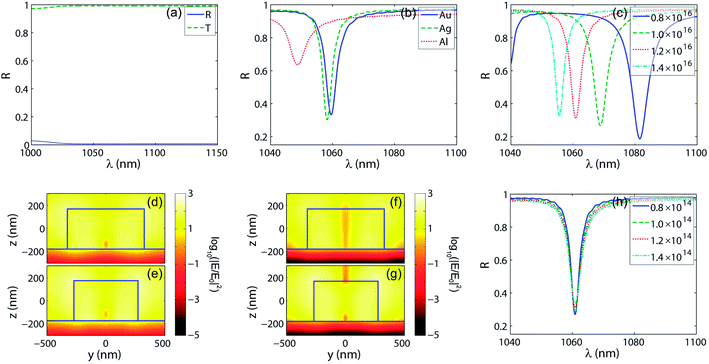 | ||
| Fig. 4 The influence of substrate. In (a), the reflection and transmission spectra are shown for the metasurface as shown in Fig. 1b, but supported by silica substrate. In (b), the reflection spectra for the substrates of different metals are illustrated. In (c), the dependence on the plasma frequency of the substrate is presented. The intensity distributions in two nanorods for different plasma frequencies of the metallic substrate are shown in (d–g): (d and e) the distributions of intensity enhancement for ωp = 0.8 × 1016 rad s−1, (f and g) intensity enhancements for ωp = 1.4 × 1016 rad s−1, respectively. The dependence of the reflectance on the collision frequency γ is shown in (h). The other structural and material parameters are the same as in Fig. 1b. | ||
Examining the dependence of optical responses on the dielectric materials, which the metasurfaces are made of, is of great importance for practical applications. Fig. 5a presents the refractive indices of some typical dielectric materials: silicon (Si), gallium phosphide (GaP), diamond, and zinc oxide (ZnO), the refractive indices of which amount to around 3.5, 3.1, 2.4, and 1.9 in the near-infrared range from 1000 nm to 1500 nm,45 respectively. For the structural parameters as shown in Fig. 1b, the wavelengths λ0 at the reflection dips induced by quasi-BIC are presented in Fig. 5b and the corresponding Q-factors in Fig. 5c as the functions of the asymmetry parameter δ. Fig. 5b shows that the resonant wavelength increases from around 1070 nm to 1500 nm for the increase of refractive index of the dielectric material constructing the metasurface from 1.9 to 3.5. Quite interestingly, with the lower-index dielectrics the higher Q-factors are obtained, which is attributed to the weaker penetration the mode field due to the higher contrast of absolute values of the dielectric functions of the dielectric materials and the substrates as discussed above (see Fig. 2c–g). Note that using metallic substrates is not always preferable for generating high-Q quasi-BIC: for the structural parameters the same as in Fig. 1b, the numerical result shows that the Q-factor of 209 is obtained in silicon metasurface supported by silica substrate, while the magnitude of Q-factor reaches only 153 (see Fig. 5c) in the same metasurface but supported by gold substrate. Such a tendency originates from that the electromagnetic field is strongly confined in nanorods of high-index materials even without metallic substrate, which results in additional loss, leading to the lower Q-factor compared with the case of using dielectric substrate. Thus, we can see that using metallic substrate is preferable only for the lower-index metasurfaces.
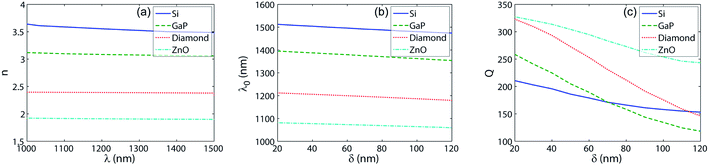 | ||
| Fig. 5 Characteristics of quasi-BIC in metasurfaces made of different dielectric materials, supported by gold substrate. The refractive indices of the dielectric materials are shown as the function of light wavelength in (a). In (b) and (c), the resonant wavelength λ0 and Q-factor Q are shown as the functions of the asymmetry parameter δ for different dielectric materials, which the metasurfaces are made of. The structural parameters are the same as in Fig. 1. The dielectric functions of Si, GaP, and diamond have been taken from ref. 45. | ||
In the final part of this work, we show the advantage of high-Q quasi-BIC in the lower-index metasurfaces supported by metallic substrates, by taking efficient THG in the ultraviolet range from the metasurface shown in Fig. 1b, as an example. The central wavelength, pulse duration, and peak intensity of pump are 1060 nm, 1 ps, and 11.95 GW cm−2, respectively. In Fig. 6, the resultant power spectrum (blue solid line) reflected from the metasurface is shown at the logarithmic scale, where the red dashed line indicates the spectrum of the pump wave. The calculated efficiency of THG at 353 nm is calculated to be 0.11%, being the highest record obtained from the metasurfaces in the ultraviolet range, to the best of our knowledge. As is well known, such an efficient nonlinear generation of ultraviolet cannot be realized with metasurfaces of high-index materials due to their strong optical losses. Dielectric metasurfaces of lower-index materials exhibiting high-Q quasi-BIC proposed in this work can find important photonic applications by employing their diverse functionalities.
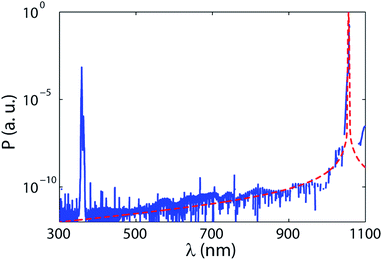 | ||
| Fig. 6 Third-harmonic spectrum generated from the metasurface shown in Fig. 1b. The central wavelength, peak intensity and pulse duration of pump are 1060 nm, 11.95 GW cm−2, and 1 ps, respectively. The efficiency of THG is calculated to be 0.11%. Here, blue solid line shows the spectrum of third-harmonic wave and red dashed one the spectral shape of pump. | ||
Conclusion
In this work, we have shown that high-Q quasi-BIC can be obtained in the metasurfaces of lower-index dielectrics, provided that they are supported by metallic substrates. Strong dipoles, which are excited in the dielectric nanorods by the assistance of plasmon excitation on the metallic substrate, anti-couple to form quasi-BIC. Although the plasmon excitation plays an important role, the practically acceptable high Q-factors in the order of 200–350 are obtained, since the majority of energy is confined in the dielectric nanorods rather than in the metallic substrate. Taking the metasurfaces containing a couple of parallel ZnO nanorods in their unit cells supported by gold substrate as examples, we have shown strong resonances with high-Q factors can be obtained by quasi-BIC which evolves from symmetry-protected BIC by in-plane inversion symmetry breaking. Through the numerical calculations, we have shown the parameter dependence of reflectance of the metasurface. Using metallic substrates is not the universal measure for obtaining quasi-BIC with higher Q-factors and only preferable for the lower-index dielectric metasurface: high-index dielectric metasurfaces supported by metallic substrates generate quasi-BIC with Q-factors lower than the case of using dielectric substrates, which is attributed to the additional plasmonic losses in metallic substrates. As an example of employing high-Q quasi-BIC in lower-index dielectric metasurfaces, we have shown efficient ultraviolet generation by third-order nonlinear process: for pumping at 1060 nm with a peak intensity of around 12 GW cm−2 and a pulse duration of 1 ps, the efficiency of THG at 353 nm reaches 0.11%, being the highest record of nonlinear generation efficiency in the ultraviolet spectral range. With high-index dielectrics, such a high efficiency cannot be obtained due to their strong material losses. The results presented in this work pave the way towards various photonic applications of high-Q quasi-BIC by employing the diverse functionalities of lower-index dielectric materials.Conflicts of interest
Authors declare no conflicts of interest.References
- S. Jahani and Z. Jacob, All-Dielectric Metamaterials, Nat. Nanotechnol., 2016, 11, 23–36 CrossRef CAS PubMed.
- P. Genevet, F. Capasso, F. Aieta, M. Khorasaninejad and R. Devlin, Recent Advances in Planar Optics: from Plasmonic to Dielectric Metasurfaces, Optica, 2017, 4, 139–152 CrossRef CAS.
- Y. Kivshar, All-Dielectric Meta-Optics and Non-linear Nanophotonics, Natl. Sci. Rev., 2018, 5, 144–158 CrossRef CAS.
- S. M. Kamalia, E. Arbabia, A. Arbabi and A. Faraon, A Review of Dielectric Optical Metasurfaces for Wavefront Control, Nanophotonics, 2018, 7, 1041–1068 Search PubMed.
- B. Sain, C. Meier and T. Zentgraf, Nonlinear optics in all-dielectric nanoantennas and metasurfaces: a review, Adv. Photonics, 2019, 1, 024002 CAS.
- S. T. Ha, Y. H. Fu, N. K. Emani, Z. Pan, R. M. Bakker, R. Paniagua-Domínguez and A. I. Kuznetsov, Directional Lasing in Resonant Semiconductor Nanoantenna Arrays, Nat. Nanotechnol., 2018, 13, 1042–1047 CrossRef CAS PubMed.
- D. G. Baranov, D. A. Zuev, S. I. Lepeshov, O. V. Kotov, A. E. Krasnok, A. B. Evlyukhin and B. N. Chichkov, All-Dielectric Nanophotonics: The Quest for Better Materials and Fabrication Techniques, Optica, 2017, 4, 814–825 CrossRef CAS.
- K.-H. Kim and W.-S. Rim, Anapole Resonances Facilitated by High-Index Contrast between Substrate and Dielectric Nanodisk Enhance Vacuum Ultraviolet Generation, ACS Photonics, 2018, 5, 4769–4775 CrossRef CAS.
- K.-H. Kim, Low-Index Dielectric Metasurfaces Supported by Metallic Substrates for Efficient Second-Harmonic Generation in the Blue-Ultraviolet Range, Phys. Chem. Chem. Phys., 2020, 22, 7300–7305 RSC.
- K.-H. Kim and J.-R. Kim, Dielectric Chiral Metasurfaces for Second-Harmonic Generation with Strong Circular Dichroism, Ann. Phys., 2020, 532, 2000078 CrossRef CAS.
- J.-K. An and K.-H. Kim, Efficient Non-Perturbative High-Harmonic Generation from Nonlinear Metasurfaces with Low Pump Intensity, Opt. Laser Technol., 2021, 135, 106702 CrossRef CAS.
- C. W. Hsu, B. Zhen, A. D. Stone, J. D. Joannopoulos and M. Soljačić, Bound States in the Continuum, Nat. Rev. Mater., 2016, 1, 16048 CrossRef CAS.
- K. Koshelev, A. Bogdanov and Y. Kivshar, Meta-Optics and Bound States in the Continuum, Sci. Bull., 2019, 64, 836–842 CrossRef.
- K. Koshelev, G. Favraud, A. Bogdanov, Y. Kivshar and A. Fratalocchi, Nonradiating Photonics with Resonant Dielectric Nanostructures, Nanophotonics, 2019, 8, 725–745 Search PubMed.
- S. I. Azzam and A. V. Kildishev, Photonic Bound States in the Continuum: from Basics to Applications, Adv. Opt. Mater., 2021, 9, 2001469 CrossRef CAS.
- A. Kodigala, T. Lepetit, Q. Gu, B. Bahari, Y. Fainman and B. Kanté, Lasing Action from Photonic Bound States in Continuum, Nature, 2017, 541, 196–199 CrossRef CAS PubMed.
- A. Pavlov, I. Zabkov and V. Klimov, Lasing Threshold of the Bound States in the Continuum in the Plasmonic Lattices, Opt. Express, 2018, 26, 28948–28962 CrossRef CAS PubMed.
- W. Bi, X. Zhang, M. Yan, L. Zhao, T. Ning and Y. Huo, Low-Threshold and Controllable Nanolaser Based on Quasi-BIC Supported by an All-Dielectric Eccentric Nanoring Structure, Opt. Express, 2021, 29, 12634–12643 CrossRef CAS PubMed.
- L. Carletti, K. Koshelev, C. De Angelis and Y. Kivshar, Giant Nonlinear Response at the Nanoscale Driven by Bound States in the Continuum, Phys. Rev. Lett., 2018, 121, 033903 CrossRef CAS PubMed.
- Z. Liu, Y. Xu, Y. Lin, J. Xiang, T. Feng, Q. Cao, J. Li, S. Lan and J. Liu, High-Q Quasibound States in the Continuum for Nonlinear Metasurfaces, Phys. Rev. Lett., 2019, 123, 253901 CrossRef CAS PubMed.
- K. Koshelev, Y. Tang, K. Li, D.-Y. Choi, G. Li and Y. Kivshar, Nonlinear Metasurfaces Governed by Bound States in the Continuum, ACS Photonics, 2019, 6, 1639–1644 CrossRef CAS.
- L. Carletti, S. S. Kruk, A. A. Bogdanov, C. De Angelis and Y. Kivshar, High-Harmonic Generation at the Nanoscale Boosted by Bound States in the Continuum, Phys. Rev. Res., 2019, 1, 023016 CrossRef CAS.
- E. N. Bulgakov and D. N. Maksimov, Nonlinear Response from Optical Bound States in the Continuum, Sci. Rep., 2019, 9, 7153 CrossRef.
- A. P. Anthur, H. Zhang, R. Paniagua-Dominguez, D. Kalashnikov, S. T. Ha, T. W. W. Mass, A. I. Kuznetsov and L. Krivitsky, Continuous Wave Second Harmonic Generation Enabled by Quasi-Bound-States in the Continuum on Gallium Phosphide Metasurfaces, Nano Lett., 2020, 20, 8745–8751 CrossRef CAS PubMed.
- J. S. Ginsberg, A. C. Overvig, M. M. Jadidi, S. C. Malek, G. N. Patwardhan, N. Swenson, N. Yu and A. L. Gaeta, Enhanced Harmonic Generation in Gases Using an All-Dielectric Metasurface, Nanophotonics, 2021, 10, 733–740 CAS.
- S. Romano, G. Zito, S. Torino, G. Calafiore, E. Penzo, G. Coppola, S. Cabrini, I. Rendina and V. Mocella, Label-free sensing of ultralow-weight molecules with all-dielectric metasurfaces supporting bound states in the continuum, Photonics Res., 2018, 6, 726–733 CrossRef CAS.
- F. Yesilkoy, E. R. Arvelo, Y. Jahani, M. Liu, A. Tittl, V. Cevher, Y. Kivshar and H. Altug, Ultrasensitive Hyperspectral Imaging and Biodetection Enabled by Dielectric Metasurfaces, Nat. Photonics, 2019, 13, 390–396 CrossRef CAS.
- L. Xu, K. Z. Kamali, L. Huang, M. Rahmani, A. Smirnov, R. Camacho-Morales, Y. Ma, G. Zhang, M. Woolley, D. Neshev and A. E. Miroshnichenko, Dynamic Nonlinear Image Tuning through Magnetic Dipole Quasi-BIC Ultrathin Resonators, Adv. Sci., 2019, 6, 1802119 CrossRef PubMed.
- D. N. Maksimov, V. S. Gerasimov, S. Romano and S. P. Polyutov, Refractive Index Sensing with Optical Bound States in the Continuum, Opt. Express, 2020, 28, 38907–38916 CrossRef CAS PubMed.
- Y. Wang, Z. Han, Y. Du and J. Qin, Ultrasensitive Terahertz Sensing with High-Q Toroidal Dipole Resonance Governed by Bound Sates in the Continuum in All-Dielectric Metasurface, Nanophotonics, 2021, 10, 1295–1307 CrossRef.
- M. V. Gorkunov, A. A. Antonov and Y. S. Kivshar, Metasurfaces with Maximum Chirality Empowered by Bound States in the Continuum, Phys. Rev. Lett., 2020, 125, 093903 CrossRef CAS PubMed.
- A. Overvig, N. Yu and A. Alù, Chiral Quasi-Bound States in the Continuum, Phys. Rev. Lett., 2020, 126, 073001 CrossRef.
- B. Wang, W. Liu, M. Zhao, J. Wang, Y. Zhang, A. Chen, F. Guan, X. Liu, L. Shi and J. Zi, Generating Optical Vortex Beams by Momentum-Space Polarization Vortices Centred at Bound States in the Continuum, Nat. Photonics, 2020, 14, 623–628 CrossRef CAS.
- M. Gandolfi, A. Tognazzi, D. Rocco, C. De Angelis and L. Carletti, Near-Unity Third-Harmonic Circular Dichroism Driven by Quasi-BIC in Asymmetric Silicon Metasurfaces, Phys. Rev. A, 2021, 104, 023524 CrossRef CAS.
- K.-H. Kim and J.-R. Kim, High-Q Chiroptical Resonances by Quasi-Bound States in the Continuum in Dielectric Metasurfaces with Simultaneously Broken in-Plane Inversion and Mirror Symmetries, Adv. Opt. Mater., 2021, 9, 2101162 CrossRef CAS.
- G. Zito, S. Romano, S. Cabrini, G. Calafiore, A. C. D. Luca, E. Penzo and V. Mocella, Observation of Spin-Polarized Directive Coupling of Light at Bound States in the Continuum, Optica, 2019, 6, 1305–1312 CrossRef CAS.
- Z. Zhang, F. Qin, Y. Xu, S. Fu, Y. Wang and Y. Qin, Negative Refraction Mediated by Bound States in the Continuum, Photonics Res., 2021, 9, 1592–1597 CrossRef.
- L. Cong and R. Singh, Symmetry-Protected Dual Bound States in the Continuum in Metamaterials, Adv. Opt. Mater., 2019, 7, 1900383 CrossRef.
- K. Koshelev, S. Lepeshov, M. Liu, A. Bogdanov and Y. Kivshar, Asymmetric Metasurfaces with High-Q Resonances Governed by Bound States in the Continuum, Phys. Rev. Lett., 2018, 121, 193903 CrossRef PubMed.
- I. Volkovskaya, L. Xu, L. Huang, A. I. Smirnov, A. E. Miroshnichenko and D. Smirnova, Multipolar Second-Harmonic Generation from High-Q Quasi-BIC States in Subwavelength Resonators, Nanophotonics, 2020, 9, 3953–3963 CrossRef CAS.
- D. R. Abujetas, Á. Barreda, F. Moreno, A. Litman, J.-M. Geffrin and J. A. Sánchez-Gil, High-Q Transparency Band in All-Dielectric Metasurfaces Induced by a Quasi Bound State in the Continuum, Laser Photonics Rev., 2021, 15, 2000263 CrossRef.
- X. W. Sun and H. S. Kwok, Optical Properties of Epitaxially Grown Zinc Oxide Films on Sapphire by Pulsed Laser Deposition, J. Appl. Phys., 1999, 86, 408–411 CrossRef CAS.
- P. B. Johnson and R. W. Christy, Optical Constants of the Noble Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 6, 4370–4379 CrossRef CAS.
- Z. F. Sadrieva, I. S. Sinev, K. L. Koshelev, A. Samusev, I. V. Iorsh, O. Takayama, R. Malureanu, A. A. Bogdanov and A. V. Lavrienko, Transition from optical bound states in the continuum to leaky resonances: role of substrate and roughness, ACS Photonics, 2017, 4, 723–727 CrossRef CAS.
- E. D. Palik, Handbook of Optical Properties of Solids, Academic Press, New York, 1985 Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |