 Open Access Article
Open Access ArticleComments on “Removal of methylene blue dye using nano zerovalent iron, nanoclay and iron impregnated nanoclay – a comparative study” by M. M. Tarekegn, R. M. Balakrishnan, A. M. Hiruy and A. H. Dekebo, RSC Adv., 2021, 11, 30109
Jean-Claude Bollinger *a,
Hai Nguyen Tran
*a,
Hai Nguyen Tran bc and
Eder C. Lima
bc and
Eder C. Lima d
d
aGroupement de Recherches Eau, Sol, Environnement, Faculté des Sciences, Université de Limoges, 87060 Limoges, France. E-mail: jean-claude.bollinger@unilim.fr
bInstitute of Fundamental and Applied Sciences, Duy Tan University, Ho Chi Minh City, 70000, Vietnam. E-mail: trannguyenhai@duytan.edu.vn
cFaculty of Environmental and Chemical Engineering, Duy Tan University, Da Nang, 550000, Vietnam
dInstitute of Chemistry, Federal University of Rio Grande do Sul (UFRGS), 91501-970, Porto Alegre, RS, Brazil. E-mail: eder.lima@ufrgs.br
First published on 16th February 2022
Abstract
The study mentioned in the title of this comment paper contains some calculations/results that disagree with some basic chemistry concepts. These misleading calculations include (i) both kinetic and isotherm modelling through linear equations, and (ii) calculating the thermodynamic parameters for the adsorption processes. Thus, we run through the correct way to make these calculations. In our opinion, it is very confusing to continue to disseminate erroneous methods as applied in the original paper.
1. Introduction
Recently, the above-cited paper (hereafter also called ‘the original paper’) was published in RSC Advances by Tarekegn et al.1 The objective of the paper is ambitious, and this detailed study of the preparation and characterization of nZVI, nanoclay and iron-impregnated nanoclay, and their use for adsorbing the methylene blue (MB) dye in batch mode, is worthy of interest.Unfortunately, some shortfalls limit the scientific value of this study. Indeed, due to many years experience in adsorption studies, both as authors and reviewers, we consider that several parts of the modelling methods and their subsequent discussions should be reconsidered.
2. Discussion
Here we will mainly focus on subsection ‘3.4 Adsorption isotherms, kinetics and thermodynamics’ in the original paper,1 where several fundamental errors can be discovered.2.1. Adsorption experiments
In their original paper, the authors should add information about the number of replicates for all experiments (including preparation of the solid adsorbent material, and MB concentration determination), hence the corresponding standard deviation. Then in all figures the experimental data points should contain their respective error bars.Moreover, the MB ‘removal (adsorption) efficiency’ given according to the original eqn (3), i.e.:
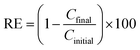 | (1) |
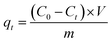 | (2) |
2.2. Kinetic modelling
Firstly, from a logical point of view, kinetics should be realized before isotherms to select the best contact time. In the original paper, the authors used the linear regression method to calculate the parameters of the kinetic models, where pseudo-first-order, or the so-called Lagergren equation (PFO) and pseudo-second-order (PSO) kinetics equations are written as the original eqn (19) and (20), respectively:
ln(qe − qt) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe − k1t qe − k1t
| (3) |
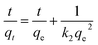 | (4) |
However, several studies2,3 have demonstrated that non-linear regression is more appropriate to obtain the parameters of kinetic models, rather than linear regression. This shortcoming is because transformations of non-linear equations to linear forms implicitly alter their error structure and may also violate standard least-squares error variance and normality assumptions. In this setting, the non-linear method provides a mathematically rigorous method for determining model parameter values; fortunately, we all now have easy access to computer programs with non-linear least-squares (NLLS) adjustments, to be applied in the present case in place of linear regression analyses, with the full non-linear qt = f(t) forms of PFO and PSO equations, respectively:
| qt = qe[1 − exp(−k1t)] | (5) |
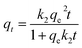 | (6) |
Lima et al.,3 in a study with 252 kinetic results, showed that the values of k1 and k2 obtained from linear fitting do not match the values of these parameters obtained by non-linear fitting. The value of qe obtained by a linear approach of the PSO model matched with the value of non-linear fitting. This is the main reason that authors insist on using linear fitting for kinetic treatment. Also, using the linear fitting, the 252 experiments were better fitted to a linear PSO model. However, when non-linear fitting was utilized, more than 50% of the kinetic results were better fitted to a non-linear PFO model. Therefore, this study demonstrates that high values of R2 in linear fitting are not a good statistical tool to establish a kinetic model.
Consequently, the content of the original Table 4 should be changed to new values calculated from the NLLS method.
2.3. Isotherm modelling
Similarly, in the original paper, isotherm data have been modelled with the linear forms of Langmuir and Freundlich equations (original eqn (17) and (18), respectively):
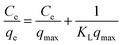 | (7) |
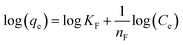 | (8) |
Of course, here also the non-linear forms are better,4 written as:
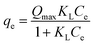 | (9) |
| qe = KFCe1/nF | (10) |
Therefore, we suggest that the original Fig. 20 and 21 could be deleted and changed into the direct isotherm curves qe = f(Ce), allowing one to obtain information about the formation of a plateau. Moreover, the parameters given in the original Tables 3 and 4 should be recalculated under the NLLS method. Then, the authors could better discuss their results as a comparison of the three solid adsorbents is concerned.
2.4. Thermodynamic parameters
The calculation of the thermodynamic parameters for MB adsorption onto each solid adsorbent was done from the classical thermodynamic relationships (eqn (22)–(24) in the original paper). However, contrary to the assertion of the authors of the original paper, Ke from their eqn (21) cannot be considered as ‘the adsorption equilibrium constant’; indeed, this is the distribution coefficient
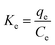 | (11) |
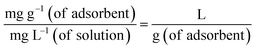 | (12) |
Thus, Ke cannot be introduced in place of K0Eq within the definition of the standard Gibbs energy
ΔG° = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(K0Eq) ln(K0Eq)
| (13) |
Because one can only take the logarithm of a dimensionless parameter, moreover, when calculating an equilibrium constant, the only unit for the amount of substance should be mol L−1 (not g or mg or any other) to make the logarithm of the so-called ‘thermodynamic equilibrium constant’ K0Eq unitless. Although this should be a well-known topic,4–7 it is too often forgotten.
Therefore, it is impossible to introduce the distribution coefficient Ke to calculate the thermodynamic parameters.
2.5. The Langmuir constant
We have another puzzling point to note about the calculation of these thermodynamic parameters. A net discrepancy appears between the values of the Langmuir adsorption constant KL in Table 3 (probably at T = 303 K) and in Table 5; moreover, the data points in Fig. 22 do not seem to be consistent with this Table 5.Again, KL (with its unit in L mg−1 of adsorbate) cannot allow the calculation of the Gibbs energy for the adsorption process directly; it should be transformed by calculating the corresponding (dimensionless) thermodynamic Langmuir constant K0L To do this calculation, we kindly suggest the use of the following relationship:5,6,8
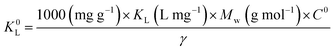 | (14) |
This is eqn (12) in Mouni et al.9 (quoted as ref. 80 in the original paper) where MMB = 319.85 g mol−1 is the MB molar mass, C0 = 1 mol L−1 corresponding to the solution standard state, and the factor 1000 allows converting g to mg; and assuming the activity coefficient of the MB dye solution as unitary for infinite dilution.8
Now, one can easily and rigorously calculate the Gibbs energy ΔG°, and obtain the other thermodynamic parameters ΔH° and ΔS° from data at various temperatures according to the non-linear van’t Hoff relationship:8,10
ΔG° = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(K0L) ln(K0L)
| (15) |
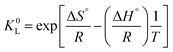 | (16) |
In any case, the comments in the original paper about the sign, the magnitude and the significance of the thermodynamic parameters should be moderated with reference to Salvestrini et al.5
3. Conclusion
It is of course important to emphasize that this ‘Comment’ paper should not discredit the work by Tarekegn et al.1 On the contrary, the original published article is really interesting and contributes to scientific knowledge; however, as indicated above, some corrections should be conducted and published by the original authors. Furthermore, the present authors hope that these comments will be read in the spirit in which they are intended; that is, constructive criticism to produce a better final scientific paper, and to avoid the dissemination of undesirable and overlooked mistakes into the scientific literature, as discussed for example in several recent critical papers, here cited within the Discussion section.Author contributions
All authors have made equal contributions to this paper.Conflicts of interest
There are no conflicts to declare.References
- M. M. Tarekegn, R. M. Balakrishnan, A. M. Hiruy and A. H. Dekebo, RSC Adv., 2021, 11, 30109 RSC.
- J.-P. Simonin, Chem. Eng. J., 2016, 300, 254–263 CrossRef CAS.
- E. C. Lima, F. Sher, A. Guleria, M. R. Saeb, I. Anastopoulos, H. N. Tran and A. Hosseini-Bandegharaei, J. Environ. Chem. Eng., 2021, 9, 104813 CrossRef CAS.
- H. N. Tran, S.-J. You, A. Hosseini-Bandegharaei and H.-P. Chao, Water Res., 2017, 120, 88–116 CrossRef CAS PubMed.
- S. Salvestrini, V. Leone, P. Iovino, S. Canzano and S. Capasso, J. Chem. Thermodyn., 2014, 68, 310–316 CrossRef CAS.
- X. Zhou and X. Zhou, Chem. Eng. Commun., 2014, 201, 1459–1467 CrossRef CAS.
- J.-C. Bollinger, Environ. Pollut., 2019, 261, 113824 CrossRef PubMed.
- E. C. Lima, A. Hosseini-Bandegharaei, J. C. Moreno-Piraján and I. Anastopoulos, J. Mol. Liq., 2019, 273, 425–434 CrossRef CAS.
- L. Mouni, L. Belkhiri, J.-C. Bollinger, A. Bouzaza, A. Assadi, A. Tirri, F. Dahmoune, K. Madani and H. Remini, Appl. Clay Sci., 2018, 153, 38–45 CrossRef CAS.
- E. C. Lima, A. A. Gomes and H. N. Tran, J. Mol. Liq., 2020, 311, 113315 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |
