Open Access Article
Open Access ArticleEffect of sequence distribution of block copolymers on the interfacial properties of ternary mixtures: a dissipative particle dynamics simulation†
Dongmei Liu a,
Ye Lin*a,
Huifeng Boa,
Deyang Lia,
Kai Gonga,
Zhanxin Zhanga and
Sijia Li*b
a,
Ye Lin*a,
Huifeng Boa,
Deyang Lia,
Kai Gonga,
Zhanxin Zhanga and
Sijia Li*b
aSchool of Science, North China University of Science and Technology, Tangshan, 063210, P. R. China. E-mail: linye315317@163.com
bSchool of Intelligence Policing, People's Police University of China, Langfang 065000, P. R. China. E-mail: lisijia@cppu.edu.cn
First published on 24th January 2022
Abstract
In this paper, the dissipative particle dynamics (DPD) simulations method is used to study the effect of sequence distribution of block copolymers on the interfacial properties between immiscible homopolymers. Five block copolymers with the same composition but different sequence lengths are utilized for simulation. The sequence distribution is varied from the alternating copolymer to the symmetric diblock copolymer. Our simulations show that the efficiency of the block copolymer in reducing the interfacial tension is highly dependent on both the degree of penetration of the copolymer chain into the homopolymer phase and the number of copolymers at the interface per area. The linear block copolymers AB with the sequence length of τ = 8 could both sufficiently extend into the homopolymer phases and exhibit a larger number of copolymers at the interface per area. Thereby the copolymer with the sequence length τ = 8 is more effective in reducing the interfacial tension compared to that of diblock copolymers and the alternating copolymers at the same concentration. This work offers useful tips for copolymer compatibilizer selection at the immiscible homopolymer mixture interfaces.
1. Introduction
Polymer mixing is a cost-efficient method to develop new materials with excellent and synergistic properties, which has attracted considerable attention from researchers for a long time.1 However, as chemically different polymers are usually incompatible, most polymer mixtures tend to macroscopically phase separate, which results in poor adhesion and mechanical properties and thereby limits their potential applications.2 To overcome this limitation, adding copolymer compatibilizers into the immiscible mixtures becomes a highly important method.3 Copolymer compatibilizers segregate preferentially at the interfaces between the immiscible homopolymers, which reduces the interfacial tension4 and increases the interfacial adhesion.5 Therefore leads to a stable interface with improved mechanical strength.6 Though the simplest diblock copolymer has been widely used to improve the performance of the interfaces, some investigations found that the sequence distribution7 of the linear copolymer compatibilizers could change significantly the phase behaviors and interfacial properties of the mixtures.8In the past decades, studies of the influence of the sequence distribution of a block copolymer on its compatibilization ability in a ternary mixture were extensively performed.9–18 Balazs and DeMeuse10 explored the influence of the copolymer sequence on the miscibility of the ternary mixture A/AB/B, where A and B represent the immiscible homopolymers, AB represents the copolymer compatibilizer. They found that the sequence distribution of the copolymer compatibilizers had a significant effect on the phase behavior of the mixtures and the diblock copolymers were not always the most efficient thermodynamic compatibilizers. Balazs and Lyatskaya11 initially reported that the random copolymer localized at the interface between the incompatible homopolymers and therefore reduced the interfacial tension. When the molecular weight was fixed, as the added compatibilizers were diblock copolymers, the interfacial tension was lower. Whereas as the molecular weight was varied, the longer random copolymers were more efficient than the shorter diblock copolymers.10 Kramer and Dai12 also reported the same result that the long random copolymer was more effective in strengthening the interface than the short block copolymer. Brown and Deline13 reported that the styrene–methyl methacrylate random copolymers reinforce the polystyrene/poly(methyl methacrylate) interface effectively. They also proposed that the random copolymer organized itself so as to make multiple trips across the interface. Dadmun14 employed Monte Carlo simulation to examine the effect of copolymer architecture on the interfacial structure and miscibility of the homopolymer/copolymer/homopolymer mixture. They found that the sequence distribution can dramatically change the ability of the copolymer to compatibilized the interface. Both the diblock and alternating copolymer showed a promise as compatibilizers, whereas the random copolymer had the weakest effectiveness in reinforcing the interface. They also found that the variation of the sequence distribution could dramatically affect the ability of the copolymer to compatibilized the interface. Subsequently, Dadmun and Eastwood15 studied the ability of styrene and methyl methacrylate copolymers with different architectures to compatibilized the polystyrene and poly(methyl methacrylate) mixtures. They found that the pentablock copolymers [S-M-S-M-S(30) and M-S-M-S-M(30)] provided the strongest interfaces, where S and M represent the styrene and methyl methacrylate monomer, respectively.
Previous studies mainly focused on the phase behaviors and the structural properties of the interfaces for the mixtures containing the diblock, the triblock, the random, and the alternating copolymers,6 whereas the study of the dependence of the mechanical and microscopic structural properties of interfaces on the sequence distributions of copolymers remains limited. Therefore, the microscopically detailed investigation of the effect of the sequence distributions of the block copolymers on the interfacial and structural properties is necessary for the design of high-efficient compatibilizers.
In our preceding papers, we explored the compatibilization ability of the diblock and the triblock copolymers.19–23 As predicted by Noolandi,24 when the diblock and triblock copolymers are placed at a biphasic interface, they will align perpendicular to the interface and form a dumbbell-shaped conformation. In the present work, dissipative particle dynamics (DPD) simulations are employed to examine the interfacial and structure properties of ternary mixtures composed of different sequence block copolymers. The model and simulation details are described in the next section. Then, the simulation results are presented. Our work elucidates the fundamental mechanism for the mixtures with sequence length τ = 8 exhibits a lower interfacial tension than the diblock copolymers and the alternating copolymers. In the final section, a brief summary and some concluding remarks are offered.
2. Method
For nearly 20 years, dissipative particle dynamics (DPD) simulation technology has been greatly developed, which could not only calculate macroscopic mechanical properties of the interfaces but also provide valuable microscopic insights into them.25 Many researchers have used DPD simulation to study the interfacial structure and tension of immiscible ternary mixtures.26–37 Motivated by these DPD simulations and the Density Functional Theory (DFT)38,39 simulation studies, we constructed the model of this work, which we briefly introduce as follows.2.1. Model
The DPD simulation method is a powerful coarse-grained mesoscopic simulation technology,40,41 especially useful for large and complex polymers and biomacromolecules systems as compared to the full-atomistic MD simulations.42,43 In a simulation system, all DPD beads interact through a soft potential.44 The motion of all beads abide by Newton's second law,
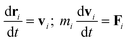 | (1) |
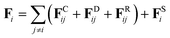 | (2) |
The conservative force FCij is a soft repulsion force, which generally follows45
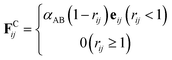 | (3) |
The dissipative force FDij and the random force FRij commonly follow
| FDij = −γωD(rij)(vijeij)eij | (4) |
| FRij = σijωR(rij)ξijΔt−1/2eij | (5) |
| ωD(rij) = [ωR(rij)]2, σij2 = 2γkBT | (6) |
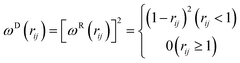 | (7) |
The DPD interaction parameter αAB depends on the Flory–Huggins parameter χAB through the relationship45
| αAB ≈ αAA + 3.50χAB | (8) |
The interaction parameter between the same type of beads is taken as αAA = αBB = 25 and between different ones are taken as αAB = 40.25
The harmonic spring force FSi is introduced to link adjacent beads on a polymer backbone46
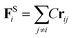 | (9) |
2.2. Simulation details
In this work, the ternary mixtures composed of A, B homopolymers and AB copolymers are simulated using the DPD method. The A, B homopolymers consist of 10 A beads and 10 B beads, respectively. The AB copolymer consists of 16 A and 16 B beads. We change the sequence distribution of block copolymers by varying the sequence length of block copolymers. The sequence length τ of the AB copolymer is defined by its periodicity as follows: a copolymer with a sequence that alternates between A and B beads has a sequence length τ = 2, and a copolymer that has 8 A beads followed by 8 B beads has a sequence length τ = 16. Schematic representations of AB copolymers with different sequence lengths are shown in Fig. 1. | ||
| Fig. 1 Schematic representations of AB copolymers with sequence lengths τ = 2, 4, 8, 16, 32, where the blue and green spheres denote bead A and bead B respectively. | ||
DPD simulations are accomplished in NVT ensembles using the DPD module embedded in the Materials Studio package. All simulations in this work are performed in a 30 × 30 × 30 cubic box with periodic boundary conditions in DPD reduced units. The interaction radius of different beads rc = 1. The simulation box contains approximately 81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 beads with a number density of beads ρ = 3, that is, the ratio of the total number of beads to the volume of the simulation box is 3. The time step Δt = 0.05 in DPD reduced units and the friction coefficient γ = 4.5 in DPD reduced units.
000 beads with a number density of beads ρ = 3, that is, the ratio of the total number of beads to the volume of the simulation box is 3. The time step Δt = 0.05 in DPD reduced units and the friction coefficient γ = 4.5 in DPD reduced units.
Equilibration is carried out for 2.0 × 105 time steps, which has been proved long enough for this system.23,47 After that, sampling is performed for 5.0 × 104 time steps. In this work, data of 103 to 104 independent samples from 5 parallel simulation runs are averaged to achieve good statistics.
The interfacial tension is an indispensable parameter to predict the mechanical properties of the interfaces for polymer mixtures. As the interfaces are normal to the x-axis, the interfacial tension can be calculated according to the Irving–Kirkwood equation in our DPD simulations48
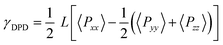 | (10) |
We also calculate the mean-square radius of gyration 〈Rg2〉 of the copolymer across the interfaces and its components in three directions 〈Rg2〉x, 〈Rg2〉y and 〈Rg2〉z. The orientation parameter q is obtained by the difference between the normal and the transverse component of the mean-square radius of gyration 〈Rg2〉25
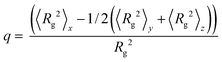 | (11) |
In addition, the interfacial width w between the immiscible homopolymers is calculated according to the study of Guo et al.,26 which is examined by fitting the function tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h((x + d)/w) to the (ρA(x) − ρB(x))/ρ(x) across the two interfaces, where d is the shift of the interface center along the x-axis.
h((x + d)/w) to the (ρA(x) − ρB(x))/ρ(x) across the two interfaces, where d is the shift of the interface center along the x-axis.
3. Results and discussion
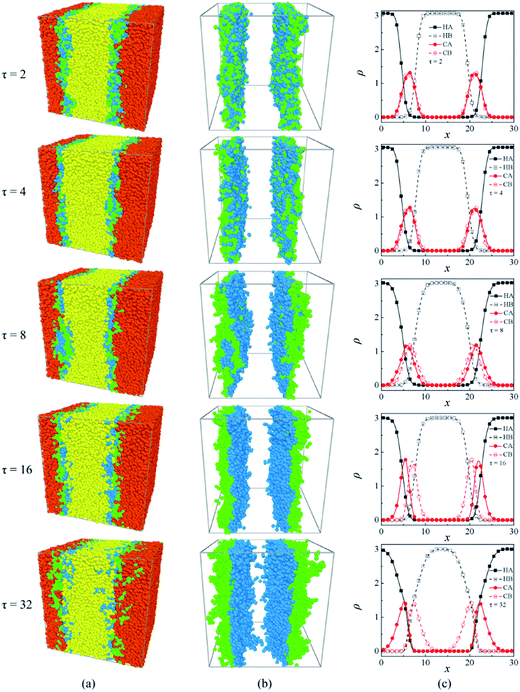
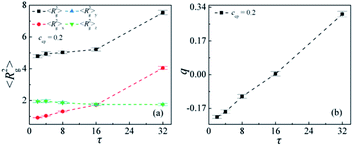
In this section, the effects of the sequence distributions of linear block copolymer AB on the interfacial and structural properties of the ternary mixtures A/AB/B are analyzed and discussed. Fig. 2 shows the morphology snapshots and the density profiles of the ternary mixtures, where the sequence length of block copolymer AB varies from τ = 2 to τ = 32, the copolymer concentration is fixed at ccp = 0.2 (ccp is the ratio of the number of copolymer beads to the total number of beads). These morphology snapshots and density profiles provide a picture of the local concentration gradients in the systems, which can help us to visualize the locations of homopolymers and copolymers and the extent to which the copolymer chains penetrate into the homopolymer domains.11 According to the morphology snapshots, there are two interfaces in all the mixtures because of the periodic boundary conditions, and it is obvious that all the AB copolymers used are located at the interfaces regardless of the copolymer sequence and that they then play the role of compatibilizer, thereby stabilizing the interfaces. This is consistent with the experimental results of PS/PS-b-PMMA/PMMA mixtures by Russell et al.49 However, the morphologies and bead distributions of the copolymers across the interfaces change significantly with the copolymer sequence length. For τ = 2, beads A and B of the alternating copolymers distributed disorderly at the interfaces as shown in the morphologies in Fig. 2(a) and (b), they aggregate and achieve completely the same density peaks just at the centers of the interfaces as shown in the density profiles in Fig. 2(c). This indicates that the alternating copolymers hardly penetrate into the homopolymer phases11 and thereby just lie on the interfaces. For τ = 4, although beads A and B of the copolymers remain disorderly distributed at the interfaces, the density peaks in the profiles are no longer completely overlapped but slightly segregated [Fig. 2(c)]. For τ = 8, beads A and B of the copolymers tend to become separated at the interfaces, and their density peaks move towards the compatible phases of the homopolymers, which shows that the copolymers tend to penetrate into the homopolymer domains. It is worthwhile to note that the copolymers with the sequence length τ = 8 form micelles at the interfaces, suggesting that the interfaces have reached saturation.6 For τ = 16, the locations of the density peaks of the copolymer beads A and B become more separated and the values of the density peaks rise higher. This result indicates that the copolymers beads of the same type aggregate more intensively and thus the copolymer segments become more orderly across the interfaces. Whereas as the sequence length of the copolymers further increases to τ = 32, the degree of penetration of the diblock copolymers into the homopolymer phases increases,15 resulting in a wider width of the copolymer beads spread across the interfaces and lower density peaks. These results can be used to predict the density distribution of the M-S-M(50), M-S-M-S-M(30), M-S-M-S-M-S-M(21) copolymers in the experiment by Eastwood and Dadmun.15Fig. 3 shows the detailed conformation of the AB copolymers at the interfaces against the sequence length τ. It can be seen that the orientation of the copolymers at the interface significantly depends upon the sequence length of the copolymer. The mean-square radius of gyration 〈Rg2〉, and the orientation parameter q of the copolymer versus the sequence length τ are given in Fig. 3(a) and (b), respectively. With increasing the sequence length τ, the 〈Rg2〉 and its x components 〈Rg2〉x and the q increase, whereas the y and z components of the 〈Rg2〉 decrease slightly. From this result, it is conjectured that the alternating copolymers (τ = 2) stretch least, whereas the diblock copolymers (τ = 32) stretch most across the interfaces. Thus, the degree of penetration into the homopolymer phase for the diblock copolymer is far larger than that of the alternating copolymers. This is the reason why the diblock copolymers barely cover the interfaces. As τ < 16 the x component of 〈Rg2〉 is smaller than the components in y and z directions, which suggests that copolymer volumes for these sequences are shaped like a pancake,8 and the AB copolymers at the interfaces per area exhibit a higher number. As τ = 16, 〈Rg2〉x = 〈Rg2〉y = 〈Rg2〉z, the x component of 〈Rg2〉 is equal to the components in y, and z-direction, and the orientation q of the copolymer is close to 0. As τ = 32, the x component of 〈Rg2〉 is greater than the components in y and z directions, which implies that the two blocks of the diblock copolymer adopt a mushroom-type configuration,8 and the diblock copolymer volume is shaped like a cylinder at the interfaces. Therefore, we can conclude that the copolymer compatibilizers with dumbbell-shaped conformations require more material to cover a given interfacial area than with pancake-shaped conformations.15
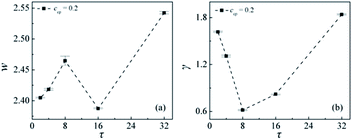
To quantitatively examine the efficiency of the AB copolymer compatibilizers with different sequence distributions, we calculated the interfacial width w, interfacial tension γ at different copolymer sequence lengths τ, as shown in Fig. 4. Fig. 4(a) and (b) show the interfacial width w and the interfacial tension γ at different sequence lengths of the copolymers when ccp = 0.2. We found that with the sequence length τ increases from 2 to 8, the interfacial width w exhibits an increase, then decrease as τ increases from 8 to 16, whereas increases again as τ further increases from τ = 16 to 32. We inferred that the change of the interfacial widths w with the sequence length increases from τ = 2 to 32 is related to the distribution of copolymers A + B beads [see Fig. S1†]. That is, as the sequence length increases from τ = 2 to 8, the density A + B beads of the copolymers at the center of the interface decrease, the distributions of beads A + B of copolymers broaden, the degree of penetration of the A and B beads of copolymers into homopolymer phase increases [as shown in Fig. S1†], thus the interfacial width w increases. However, as τ = 16, the density of A + B beads of the copolymers at the center of the interfaces increases, the distributions of beads A + B of copolymers narrow [the down triangle in Fig. S1†], which results in a reduced interfacial width w. As the copolymer sequence length further increases to τ = 32, density profiles of beads A + B of copolymers across the interface again broaden significantly [the diamond in Fig. S1†], and the broader distributions of the diblock copolymer result in a larger interfacial width w. Fig. 4(b) shows that the mechanical properties of the interfaces also depend strongly upon the copolymer sequence distributions. Specifically, the interfacial tensions γ of the mixtures rapidly decrease with increasing the sequence length from 2 to 8, whereas as the sequence length of the AB copolymers further increases from 8 to 32, the interfacial tension γ increases. This funding indicates that diblock copolymers are not always the optimal thermodynamic compatibilizers for the immiscible homopolymers mixtures, which is consistent with the theoretical calculation results by DeMeuse,10 whereas concurs with the report of Lyatskaya.11 The reason that the lower interfacial tension γ for the mixtures of A/AB (τ = 8)/B can be that with increasing the sequence length of AB copolymers from 2 to 8 the copolymers at the interface of penetration into the homopolymer phase increases [as illustrated in Fig. 2(a) and (c) τ = 8], which results in a lower interfacial tension and an improvement of the interfacial adhesion.6 This result confirms that the sequence length of the linear copolymer must be above a minimum value to effectively extend into the homopolymer phases and strengthen the interface. However, as the sequence length of the AB copolymers increases from 8 to 32, the penetration of the AB copolymers into the homopolymer phase further increases, which leads to the number of the AB copolymers at the interface per area decreases,25 thus the interfacial tension γ increases. From the above observation, the compatibilization efficiency can be related to the conformation of copolymer at the interfacial region. It seems that both the penetration degree of the copolymer chain into the homopolymer phase and the number of the copolymers at the interface per area can be important factors for evaluating the compatibilization efficiency. The larger penetration degree of chains leads to a decrease in the number of the diblock copolymers at the interface per area and thereby results in a reduction of compatibilization efficiency. However, the linear block copolymers AB with the sequence length of τ = 8 could both sufficiently extend into the homopolymer phases and exhibit a larger number of copolymers at the interface per area. The increased compatibilization efficiency of the AB (τ = 8) in comparison with the diblock copolymers also can be explained according to Noolandi24 by their different conformations at the interface (“pancakes” unlike “dumbbells”).50 It should be noted that the smaller the interfacial tension γ the more stable the interfaces. Therefore, we can conclude that the interfacial stability varies significantly with the copolymer sequence length, and the mixture of A/AB (τ = 8)/B exhibits more stable interfaces.
4. Conclusions
In this paper, the effects of the sequence distributions of block copolymer on the interfacial properties of A/AB/B ternary mixtures are investigated by the dissipative particle dynamics (DPD) simulations.By comparing the interfacial properties for the A/AB/B mixtures with different copolymer sequence distributions (the sequence lengths τ = 2, 4, 8, 16, 32) at copolymer concentration ccp = 0.2, we found that both the penetration degree of the copolymer chain into the homopolymer phase and the number of the copolymers at the interface per area can be important factors for evaluating the compatibilization efficiency. The alternating copolymers just lie on the interfaces, which hardly extend into the homopolymer phase, thereby couldn't effectively strengthen the interface. The diblock copolymers penetrate deeply into the homopolymer phase, which leads to a decrease in the number of copolymers at the interface per area and thereby results in a reduction of compatibilization efficiency. However, the linear block copolymers AB with the sequence length of τ = 8 could both sufficiently extend into the homopolymer phases and exhibit a larger number of copolymers at the interface per area. Hence the addition of the block copolymers AB with the sequence length τ = 8 results in a more reduced interfacial tension, which indicates the better performance of the copolymer with τ = 8 in maintaining the stability of the ternary polymer mixtures compared to that of the copolymers with other sequence lengths.
Our studies indicate that the compatibilization efficiency of the block copolymers is highly dependent on the sequence distributions of block copolymers, which provide important guidelines for designing and synthesizing high-effective copolymer compatibilizers.
Author contributions
Conceptualization, D. L.; methodology, D. L.; validation, D. L.; formal analysis, D. L.; resources, Y. L., K. G.; data curation, D. L., Y. L.; writing – original draft preparation, D. L.; writing – review and editing, D. L., S. L.; supervision, D. L., Y. L., H. B., D. L., Z. Z.; project administration, D. L., Y. L., H. B.; funding acquisition, Y. L., and S. L.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financially supported by the Basic Scientific Research Project of Hebei Provincial Department of Education (grant JQN2020021), the National Natural Science Foundation of China (grant 22073093), the Natural Science Foundation in Hebei Province, China, Grant No. B2020507044, the Research Project of Statistical Science in Hebei Province, China, Grant No. 2021HL17, the Project of Science and Technology in Langfang, China, Grant No. 2020029050. We are grateful for the essential supports of Hebei Key Laboratory of Data Science and Application and School of Materials of Sun Yat-sen University.Notes and references
- C. Konig, M. Van Duin, C. Pagnoulle and R. Jerome, Prog. Polym. Sci., 1998, 23, 707 CrossRef.
- M. Lorenzo and M. Frigione, J. Polym. Eng., 1997, 17, 429 Search PubMed.
- H. Retsos, I. Margiolaki, A. Messaritaki and S. H. Anastasiadis, Macromolecules, 2001, 34, 5295 CrossRef CAS.
- H. Retsos, S. H. Anastasiadis, S. Pispas, J. W. Mays and N. Hadjichristidis, Macromolecules, 2004, 37, 524 CrossRef CAS.
- S. H. Anastasiadis, I. Gancarz and J. T. Koberstein, Macromolecules, 1989, 22, 1449 CrossRef CAS.
- T. Lemos, C. Abreu and J. C. Pinto, Macromol. Theory Simul., 2020, 29, 1900042 CrossRef CAS.
- L. W. Chang, T. K. Lytle, M. Radhakrishna, J. J. Madinya, J. Vélez, C. E. Sing and S. L. Perry, Nat. Commun., 2017, 8, 1273 CrossRef PubMed.
- R. Malik, C. K. Hall and J. Genzer, Macromolecules, 2010, 43, 5149 CrossRef CAS.
- D. Rigby, J. L. Lin and R. J. Roe, Macromolecules, 1985, 18, 2269 CrossRef CAS.
- A. C. Balazs and M. T. Demeuse, Macromolecules, 1989, 22, 4260 CrossRef CAS.
- Y. Lyatskaya, D. Gersappe, N. A. Gross and A. C. Balazs, J. Phys. Chem., 1996, 100, 1449 CrossRef CAS.
- C. A. Dai, B. J. Dair, K. H. Dai, C. K. Ober, E. J. Kramer, C. Y. Hui and L. W. Jelinski, Phys. Rev. Lett., 1994, 73, 2472 CrossRef CAS PubMed.
- H. R. Brown, K. Char, V. R. Deline and P. F. Green, Macromolecules, 1993, 26, 4155 CrossRef CAS.
- M. Dadmun, Macromolecules, 1996, 29, 3868 CrossRef CAS.
- E. A. Eastwood and M. Dadmun, Macromolecules, 2002, 35, 5069 CrossRef CAS.
- M. J. Ko, S. H. Kim and W. H. Jo, Polymer, 2000, 41, 6387 CrossRef CAS.
- R. Malik, C. K. Hall and J. Genzer, Macromolecules, 2013, 46, 4207 CrossRef CAS.
- D. M. Liu, X. Z. Duan, T. F. Shi, F. Jiang and H. Z. Zhang, Chem. Res. Chin. Univ., 2015, 36, 2532–2539 CAS.
- D. M. Liu, L. J. Dai, X. Z. Duan, T. F. Shi and H. Z. Zhang, Chem. Res. Chin. Univ., 2015, 36, 1752–1758 CAS.
- D. M. Liu, K. Gong, Y. Lin, T. Liu, Y. Liu and X. Z. Duan, Polymers, 2021, 13, 1516 CrossRef CAS PubMed.
- D. M. Liu, K. Gong, Y. Lin, H. F. Bo, T. Liu and X. Z. Duan, Polymers, 2021, 13, 2333 CrossRef CAS PubMed.
- D. M. Liu, M. Y. Yang, D. P. Wang, X. Y. Jing, Y. Lin and X. Duan, Polymers, 2021, 13, 2866 CrossRef CAS PubMed.
- D. M. Liu, Y. Lin, K. Gong, H. F. Bo, D. Y. Li, Z. X. Zhang and W. D. Chen, RSC Adv., 2021, 11, 38316 RSC.
- J. Noolandi, Macromol. Theory Simul., 1992, 1, 295 CrossRef CAS.
- H. J. Qian, Z. Y. Lu, L. J. Chen, Z. S. Li and C. C. Sun, J. Chem. Phys., 2005, 122, 187907 CrossRef PubMed.
- H. X. Guo and M. O. Cruz, J. Chem. Phys., 2005, 123, 174903 CrossRef PubMed.
- A. D. Goodson, G. L. Liu, M. S. Rick, A. W. Raymond, M. F. Uddin, H. S. Ashbaugh and J. N. L. Albert, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 794 CrossRef CAS.
- C. R. Catarino, R. A. Bustamante-Rendon and J. S. Hernandez-Fragoso, J. Mol. Model., 2017, 23, 306 CrossRef PubMed.
- Y. Z. Zhang, J. B. Xu and X. F. He, Mol. Phys., 2018, 116, 1851 CrossRef CAS.
- X. P. Liang, J. Q. Wu, X. G. Yang, X. B. Tu and Y. Wang, Colloids Surf., A, 2018, 546, 107 CrossRef CAS.
- S. Wang, S. W. Yang, R. C. Wang, R. C. Tian, X. Y. Zhang, Q. J. Sun and L. L. Liu, J. Pet. Sci. Eng., 2018, 169, 81 CrossRef CAS.
- F. Goodarzi and S. Zendehboudi, Ind. Eng. Chem. Res., 2019, 58, 8817 CrossRef CAS.
- F. Goodarzi, J. Kondori, N. Rezaei and S. Zendehboudi, J. Mol. Liq., 2019, 295, 111357 CrossRef CAS.
- B. Y. Li, L. Zhao and Z. Y. Lu, Phys. Chem. Chem. Phys., 2020, 22, 5347 RSC.
- A. G. Schlijper, P. J. Hoogerbrugge and C. W. Manke, J. Rheol., 1995, 39, 567 CrossRef CAS.
- Y. Lin, A. Boker, J. B. He, K. Sill, H. Q. Xiang, C. Abetz, X. F. Li, J. Wang, T. Emrick, S. Long, Q. Wang, A. Balazs and T. P. Russell, Nature, 2005, 434, 55 CrossRef CAS PubMed.
- Z. H. Hong, N. Xiao, L. Li and X. N. Xie, J. Food Eng., 2020, 276, 109877 CrossRef CAS.
- G. K. Gueorguiev, C. Goyenola, S. Schmidt and L. Hultman, Chem. Phys. Lett., 2011, 516, 62 CrossRef CAS.
- G. K. Gueorguiev, Z. Czigany, A. Furlan, S. Stafstrom and L. Hultman, Chem. Phys. Lett., 2011, 501, 400 CrossRef CAS.
- P. J. Hoogerbrugge and J. Koelman, Europhys. Lett., 1992, 19, 155 CrossRef.
- J. Koelman and P. J. Hoogerbrugge, Europhys. Lett., 1993, 21, 363 CrossRef CAS.
- K. Shi, C. Lian, Z. Bai, S. Zhao and H. Liu, Chem. Eng. Sci., 2015, 122, 185 CrossRef CAS.
- H. Rezaei and H. Modarress, Chem. Phys. Lett., 2015, 620, 114 CrossRef CAS.
- J. W. Zhang, L. Chen, A. L. Wang and Z. C. Yan, Ind. Eng. Chem. Res., 2020, 59, 763 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1998, 107, 4423 CrossRef.
- Z. Q. Bai and H. X. Guo, Polymer, 2013, 54, 2146 CrossRef CAS.
- Y. Zhou, X. P. Long and Q. X. Zeng, J. Appl. Polym. Sci., 2012, 125, 1530 CrossRef CAS.
- J. Irving and J. G. Kirkwood, J. Chem. Phys., 1950, 18, 817 CrossRef CAS.
- P. F. Green and T. P. Russell, Macromolecules, 1991, 24, 2931–2935 CrossRef CAS.
- D. Hlavata, Z. Horak, F. Lednicky, J. Hromadkova, A. Pleska and Y. Z. Zanevskii, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 931 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra08936f |
| This journal is © The Royal Society of Chemistry 2022 |