Open Access Article
Open Access ArticleThe unique sandwich K6Be2B6H6 cluster with a real borozene B6H6 core†
Ying-Jin Wang *ab,
Lin-Yan Fengab,
Miao Yana,
Chang-Qing Miaoa,
Su-Qin Fenga and
Hua-Jin Zhai
*ab,
Lin-Yan Fengab,
Miao Yana,
Chang-Qing Miaoa,
Su-Qin Fenga and
Hua-Jin Zhai *b
*b
aDepartment of Chemistry, Xinzhou Teachers University, Xinzhou 034000, Shanxi, China. E-mail: yingjinwang@sxu.edu.cn; hj.zhai@sxu.edu.cn
bNanocluster Laboratory, Institute of Molecular Science, Shanxi University, Taiyuan 030006, China
First published on 18th March 2022
Abstract
Theoretical evidence is reported for a boron-based K6Be2B6H6 sandwich cluster, showing a perfectly D6h B6H6 ring, being capped by two tetrahedral K3Be ligands. Due to the comfortable charge transfer, the sandwich is viable in [K3Be]3+[B6H6]6−[BeK3]3+ ionic complex in nature. The [B6H6]6− core with 6π aromaticity vividly imitates the benzene (C6H6), occurring as a real borozene. In contrast, the tetrahedral [K3Be]3+ ligand is 2σ three-dimensional aromatic, acting as the simple superatom. Thus, this complex possesses a collectively three-fold 2σ/6π/2σ aromaticity. The interlaminar interaction is governed by the robust electrostatic attraction. The unique chemical bonding gives rise to interesting dynamic fluxionality.
1. Introduction
The electron-deficiency of boron leads to unconventional structures in its allotropes and compounds,1–11 which is quite different from its neighbour carbon. The pure boron clusters favor the (quasi-)planar geometries over a wide range of sizes. Most of the planar boron clusters are controlled by the double (σ + π) aromaticity, especially, their π frameworks are analogous to those in benzene1,12,13 or polycyclic aromatic hydrocarbons (PAHs).14–17 The planar B73−, B82−, and B9− clusters12,18–22 are representative, possessing the identical 6π aromaticity to C5H5−, C6H6, and C7H7+. Thus, they are endowed a relevant name of “borozene” by L. S. Wang, albeit that they are 6σ aromatic as well.23 The “borozene” was first proposed for the planar B12H6 cluster by N. G. Szwacki.24 Moreover, the metal-doped boron molecular wheels25–30 and various inorganic benzene analogues31,32 with double aromaticity are also widely investigated.Strictly speaking, the real “borozene” is corresponding to the planar and aromatic B6H66− ring, assuming as a derivative of C6H6 by replacing the C atom with B−, just like the CH4 and BH4− anion. However, the boron hydrides and their dianion species like forming the three-dimensional (3D) geometries, the latter are extremely stable with the 3D aromaticity.33 Thus, it is more challenging to flatten the boron hydrides in chemistry. Additionally, the repulsion in highly charged B6H66− is drastic, need to neutralize with the counter-cations. In 2003, A. I. Boldyrev computationally investigated the Li6B6H6 cluster in the spirit of C6H6, providing a theoretical proof for existence of aromatic B6H66− motif, albeit with a somewhat low D2h symmetry.34,35 The chemists have paid a lot of efforts into designing the transition metal centred M©B6H6 molecular wheels. Unfortunately, none of B6H6 motifs can be recognized as real “borozene” in view of the strong covalent interaction between the central metal atom and B6H6 ring, and abnormal charge distribution.36–39 Last year, the author computationally reported a “Big Mac” sandwich of Rb6Be2B6 cluster, consisting of a hexagonal B6 ring and two tetrahedral Rb3Be ligands, which skilfully mimics the style of ferrocene. The hexagonal B6 core exists in the B66− charge state with double 6π/6σ aromaticity, being sufficiently stable in the cationic field provided by two [Rb3Be]3+ ligands.40 The bare planar B6 ring as a structural motif has been found in the crystal structure of a solid state phase (Ti7Rh4Ir2B8),41 and be discovered in some inverse sandwich clusters.28,42,43 One interesting question arises, whether the planar [B6H6]6− ring can be stabilized in the similar field of counter-cation? If it is feasible, the real “borozene” will be achieved.
The target of present work lies in probing the viability of aromatic [B6H6]6− in K6Be2B6H6 cluster, which is consist of a perfectly planar B6H6 ring and two tetrahedral K3Be ligands. The natural charge analyses show that K6Be2B6H6 cluster is a typical ionic complex, can be described by [K3Be]3+[B6H6]6−[BeK3]3+ formula. The perfectly planar [B6H6]6− ring possesses the 6π aromaticity merely, occurring as a real “borozene”. In contrast, the tetrahedral [K3Be]3+ ligand with 2σ delocalized electrons has the 3D aromaticity (or spherical aromaticity), serving as the superatom. Thus, this sandwich cluster has a collectively three-fold 2σ/6π/2σ aromaticity, whose three components are hold together via the robust electrostatic attraction. We believe that the stabilization of [B6H6]6− borozene in K6Be2B6H6 complex is not an individual case. The planar aromatic [B5H5]6− and [B7H7]6− ring might be viable in such sandwich complexes.
2. Methods
We have theoretically designed a quaternary K6Be2B6H6 sandwich cluster basing on the concept of charge transfer and multi-fold aromaticity. The potential energy surface scan for K6Be2B6H6 cluster was performed using the Coalescence Kick (CK) algorithm44,45 at the B3LYP/6-31G level, aiding with the manual constructions. Various possible initial structures were explored and fully reoptimized at the PBE0/6-311+G(d,p) level.46 Vibrational frequencies were checked at the same level to guarantee that all presented isomers are true minima. The accurate energies of top five low-lying isomers at the PBE0/6-311+G(d,p) level were further estimated at the single-point CCSD(T)/6-311+G(d,p)//PBE0/6-311+G(d,p) level.47 The transition state (TS) structures were searched using the QST2 method, and verified by intrinsic reaction coordinate (IRC) calculations.For interpreting the stabilization of K6Be2B6H6 cluster, we have performed the Wiberg bond indices (WBIs) and natural atomic charges calculation using the NBO 6.0 program48 at the PBE0/6-311+G(d,p) level. Chemical bonding was elucidated using the canonical molecular orbital (CMO), electron localization functions (ELFs),49,50 and adaptive natural density partitioning (AdNDP) methods.51 The AdNDP calculations were performed at the PBE0/6-31G level due to the low sensitivity to the theoretical level. The ELFs and AdNDP data were visualized using Molekel 5.4.0.8.52 The nucleus-independent chemical shifts (NICSs)53 were calculated at the PBE0/6-311+G(d,p) level. Born–Oppenheimer molecular dynamics (BOMD) simulations were performed at the PBE0/6-31G* level at the temperature of 300 and 600 K.54 All electronic structure calculations and BOMD simulation were done using the Gaussian 09 package.55
3. Results and discussion
3.1. Geometric structures
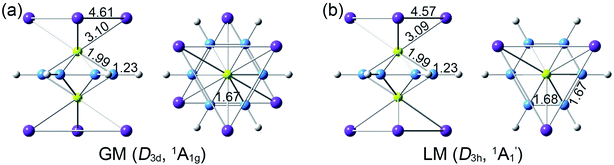
Extensive structural searches and density functional theory calculations at the PBE0/6-311+G(d,p) level suggest that the K6Be2B6H6 cluster possesses two almost degenerated isomers (Fig. 1), the global minimum (GM) (D3d, 1A1g) and the closest low-lying isomer (LM) . Both isomers adopt the fascinating sandwich architectures, featuring a perfectly D6h B6H6 ring being jammed by two tetrahedral K3Be ligands. As a whole, two isomers are ingeniously assembled on the basis of the hierarchy of electronegativity. They are discrepant in assembling style of K3Be ligands, a staggered fashion for GM and eclipsed one for LM. Their cartesian coordinates are given in Table S1 (ESI†). At the PBE0/6-311+G(d,p) level, D3d (1A1g) GM is marginally more stable by 0.04 eV than
. Both isomers adopt the fascinating sandwich architectures, featuring a perfectly D6h B6H6 ring being jammed by two tetrahedral K3Be ligands. As a whole, two isomers are ingeniously assembled on the basis of the hierarchy of electronegativity. They are discrepant in assembling style of K3Be ligands, a staggered fashion for GM and eclipsed one for LM. Their cartesian coordinates are given in Table S1 (ESI†). At the PBE0/6-311+G(d,p) level, D3d (1A1g) GM is marginally more stable by 0.04 eV than  LM with the zero-point energy (ZPE) corrections. Noted the dispersion corrections are not sensitive for present system according to the results at the PBE0-D3/6-311+G(d,p) level. The relative energies of two degenerated isomers were further refined at the CCSD(T)/6-311+G(d,p)//PBE0/6-311+G(d,p) level, which gives an energy distinction of 0.05 eV merely. The T1 diagnostic factors of CCSD(T) for the GM and LM are 0.019, indicating the reliable CCSD(T) data. The other low-lying isomers (see Fig. S1, ESI†) are highly unstable, being at least 0.34 eV above the GM at the CCSD(T) level. Frankly, given the extremely complicated potential energy surface, we cannot completely ensure the true global minimum of the quaternary system. We have performed the minima hopping (MH)56 search for this system (about 500 stationary points) as well, and did not find more stable isomers than the D3d (1A1g) GM structure.
LM with the zero-point energy (ZPE) corrections. Noted the dispersion corrections are not sensitive for present system according to the results at the PBE0-D3/6-311+G(d,p) level. The relative energies of two degenerated isomers were further refined at the CCSD(T)/6-311+G(d,p)//PBE0/6-311+G(d,p) level, which gives an energy distinction of 0.05 eV merely. The T1 diagnostic factors of CCSD(T) for the GM and LM are 0.019, indicating the reliable CCSD(T) data. The other low-lying isomers (see Fig. S1, ESI†) are highly unstable, being at least 0.34 eV above the GM at the CCSD(T) level. Frankly, given the extremely complicated potential energy surface, we cannot completely ensure the true global minimum of the quaternary system. We have performed the minima hopping (MH)56 search for this system (about 500 stationary points) as well, and did not find more stable isomers than the D3d (1A1g) GM structure.
3.2. The bond distances, Wiberg bond indices and natural atomic charges
The bond distances for D3d (1A1g) GM and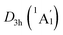 LM at the PBE0 level are shown in Fig. 1. Two structures have almost identical bond distances, all of them are within 0.01 Å, apart from the K–K bonds (0.04 Å). Specifically, the B–B distances are 1.67 Å in the GM and 1.68/1.67 Å in the LM, respectively, being slightly shorter than the standard B–B single bond (1.70 Å).57 The B–H bond distances are 1.23 Å. The B–Be/Be–K/K–K bond distances are distinctly longer than their referenced single bonds, suggesting the weak covalent interaction of them.
LM at the PBE0 level are shown in Fig. 1. Two structures have almost identical bond distances, all of them are within 0.01 Å, apart from the K–K bonds (0.04 Å). Specifically, the B–B distances are 1.67 Å in the GM and 1.68/1.67 Å in the LM, respectively, being slightly shorter than the standard B–B single bond (1.70 Å).57 The B–H bond distances are 1.23 Å. The B–Be/Be–K/K–K bond distances are distinctly longer than their referenced single bonds, suggesting the weak covalent interaction of them.
The WBIs for GM and LM structures are in accordance with the bond distances. The B–B bonds have the WBIs of 1.34 for the D3d (1A1g) GM (Fig. S2(a), ESI†) and 1.35/1.33 for 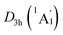 LM (Fig. S2(c), ESI†), being intermediate between the single and double bonds. Thus, they are dominated by the delocalized bonds apart from the two-center two-electron (2c–2e) σ bond. The WBIs of B–H bonds is 0.93, representing the normal single bond. The Be–K/K–K bonds with the nonnegligible WBIs of 0.21/0.13 have somewhat strong covalent interaction than B–Be bonds, the WBIs of latter is negligible (only 0.07), which leads to an integrally tetrahedral K3Be ligands in two isomers. Furthermore, the Be–K and K–K bonds in K3Be ligand have a collective WBIs of 1.02, being in line with one four-center two-electron (4c–2e) bond.
LM (Fig. S2(c), ESI†), being intermediate between the single and double bonds. Thus, they are dominated by the delocalized bonds apart from the two-center two-electron (2c–2e) σ bond. The WBIs of B–H bonds is 0.93, representing the normal single bond. The Be–K/K–K bonds with the nonnegligible WBIs of 0.21/0.13 have somewhat strong covalent interaction than B–Be bonds, the WBIs of latter is negligible (only 0.07), which leads to an integrally tetrahedral K3Be ligands in two isomers. Furthermore, the Be–K and K–K bonds in K3Be ligand have a collective WBIs of 1.02, being in line with one four-center two-electron (4c–2e) bond.
As for the natural atomic charges, the D6h B6H6 rings in D3d (1A1g) GM and 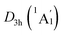 LM have the same charge distribution (−0.91|e| for B and −0.02|e| for H, see Fig. S2(b and d), ESI†). Thus, the B6H6 rings exist in the [B6H6]6− charged state, being isoelectronic with C6H6. The Be and K atom carries a positive charge of +0.94|e| and +0.63/0.62|e|, respectively. The tetrahedral K3Be ligand has a collectively positive charge of +2.83/2.80|e|, being in line with [K3Be]3+ species. Thus, both GM and LM could be viewed as the [K3Be]3+[B6H6]6−[BeK3]3+ ionic complexes, in which the electron-deficiency of B6H6 is reasonably compensated by two tetrahedral K3Be ligands.
LM have the same charge distribution (−0.91|e| for B and −0.02|e| for H, see Fig. S2(b and d), ESI†). Thus, the B6H6 rings exist in the [B6H6]6− charged state, being isoelectronic with C6H6. The Be and K atom carries a positive charge of +0.94|e| and +0.63/0.62|e|, respectively. The tetrahedral K3Be ligand has a collectively positive charge of +2.83/2.80|e|, being in line with [K3Be]3+ species. Thus, both GM and LM could be viewed as the [K3Be]3+[B6H6]6−[BeK3]3+ ionic complexes, in which the electron-deficiency of B6H6 is reasonably compensated by two tetrahedral K3Be ligands.
3.3. Chemical bonding
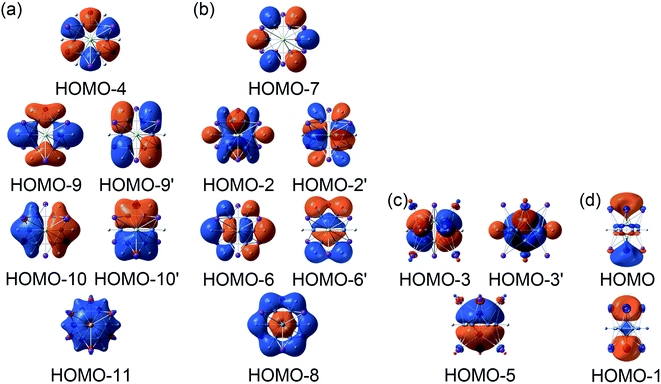
In order to interpret the unique geometries and stability of the D3d GM (1A1g) and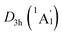 LM sandwiches, we performed the systematic chemical bonding analyses for them. The D3d GM (1A1g) has 34 valence electrons in total, occupying 17 CMOs (Fig. 2). According to their constituent atomic orbitals (AOs), these occupied CMOs are reasonably sorted into four subsets. In subset (a), there are six σ CMOs composed by the B 2s/2p AOs, which can be directly recombined as six Lewis 2c–2e B–B σ bonds. The six CMOs in subset (b) originated from the radical B 2p AOs and H 1s AOs are shown one-to-one correspondence with those in subset (a), which describes the six Lewis 2c–2e B–H σ bonds in nature. The subset (c) exhibits a perfectly π sextet on the D6h B6H6 ring, faithfully mimicking that in organic benzene, although the degenerated HOMO−3/HOMO−3′ π CMOs have slight hybridization with the HOMO−2/HOMO−2′ σ CMOs in subset (b). Thus, the B6H6 ring possesses 6π aromaticity according to the (4n + 2) Hückel rule. These 15 CMOs in subsets (a–c) with 30 occupying electrons are located on the B6H6 motif, supporting the assertation of [B6H6]6− charge state of NBO results. Two CMOs in subset (d) are clearly located on the two tetrahedral K3Be ligands, which can be directly recombined into two 4c–2e σ bonds, one on each K3Be tetrahedron. Thus, the tetrahedral K3Be ligand has the 2σ 3D aromaticity according to 2(n + 1)2 electron counting rule.58 It can also be viewed as a superatom.59,60
LM sandwiches, we performed the systematic chemical bonding analyses for them. The D3d GM (1A1g) has 34 valence electrons in total, occupying 17 CMOs (Fig. 2). According to their constituent atomic orbitals (AOs), these occupied CMOs are reasonably sorted into four subsets. In subset (a), there are six σ CMOs composed by the B 2s/2p AOs, which can be directly recombined as six Lewis 2c–2e B–B σ bonds. The six CMOs in subset (b) originated from the radical B 2p AOs and H 1s AOs are shown one-to-one correspondence with those in subset (a), which describes the six Lewis 2c–2e B–H σ bonds in nature. The subset (c) exhibits a perfectly π sextet on the D6h B6H6 ring, faithfully mimicking that in organic benzene, although the degenerated HOMO−3/HOMO−3′ π CMOs have slight hybridization with the HOMO−2/HOMO−2′ σ CMOs in subset (b). Thus, the B6H6 ring possesses 6π aromaticity according to the (4n + 2) Hückel rule. These 15 CMOs in subsets (a–c) with 30 occupying electrons are located on the B6H6 motif, supporting the assertation of [B6H6]6− charge state of NBO results. Two CMOs in subset (d) are clearly located on the two tetrahedral K3Be ligands, which can be directly recombined into two 4c–2e σ bonds, one on each K3Be tetrahedron. Thus, the tetrahedral K3Be ligand has the 2σ 3D aromaticity according to 2(n + 1)2 electron counting rule.58 It can also be viewed as a superatom.59,60
On the whole, the CMOs in subsets (a) and (b) describe the interactions of B–B and B–H of B6H6 ring, being in line with its six localized B–B and B–H σ bonds. The CMOs in subsets (c) and (d) represent the delocalized frameworks, including of the 6π aromaticity on B6H6 ring and 2σ aromaticity on two K3Be tetrahedrons, which collectively renders the three-fold (2σ/6π/2σ) aromaticity for the [K3Be]3+[B6H6]6−[BeK3]3+ complex. The three-fold aromaticity underlies the stability of the GM structure. Moreover, the orbital component analysis suggests that HOMO-5 has a 14.2% Be 2s AOs contribution, in which two Be 2s AOs pretends to be the “pz” style, taking part in the globally delocalized π bonding. As for the degenerated HOMO−3/HOMO−3′, there is a 12.0% Be 2px/2py AOs contribution, being bonding to the B 2pz AOs of B6H6 ring. The minimal contribution of Be 2s/2px/2py AOs to three π CMOs is responsible for the extremely weak covalent interaction of B–Be bonds. The CMOs pattern of  LM is similar to that in D3d (1A1g) GM, and its degenerated π CMOs with less hybridization are more elegant (Fig. S3, ESI†).
LM is similar to that in D3d (1A1g) GM, and its degenerated π CMOs with less hybridization are more elegant (Fig. S3, ESI†).
The above CMOs bonding images of D3d (1A1g) GM and  LM are fully supported by the AdNDP analyses. As shown in Fig. 3, the AdNDP result for the D3d (1A1g) GM clearly reproduces six localized 2c–2e B–B and B–H σ bonds, as well as two delocalized 4c–2e σ bonds on tetrahedral K3Be ligands and three delocalized six-center two-electron (6c–2e) π bonds on B6H6 ring. All the occupation numbers (ONs) are ideal. The delocalized σ and π frameworks further confirm the three-fold (2σ/6π/2σ) aromaticity of the system. Note that the scheme of 4c–2e σ bond in K3Be tetrahedron is more rational than the alternative three-center two-electron (3c–2e) σ bond on K3 triangle, the latter gives rise to a rather low ON of 1.48|e|. It means that Be atom has a remarkable 20.4% contribution to the 4c–2e σ bond, being close to K atom (26.5%).40 The identical AdNDP bonding pattern is observed in the
LM are fully supported by the AdNDP analyses. As shown in Fig. 3, the AdNDP result for the D3d (1A1g) GM clearly reproduces six localized 2c–2e B–B and B–H σ bonds, as well as two delocalized 4c–2e σ bonds on tetrahedral K3Be ligands and three delocalized six-center two-electron (6c–2e) π bonds on B6H6 ring. All the occupation numbers (ONs) are ideal. The delocalized σ and π frameworks further confirm the three-fold (2σ/6π/2σ) aromaticity of the system. Note that the scheme of 4c–2e σ bond in K3Be tetrahedron is more rational than the alternative three-center two-electron (3c–2e) σ bond on K3 triangle, the latter gives rise to a rather low ON of 1.48|e|. It means that Be atom has a remarkable 20.4% contribution to the 4c–2e σ bond, being close to K atom (26.5%).40 The identical AdNDP bonding pattern is observed in the  LM (Fig. S4†).
LM (Fig. S4†).
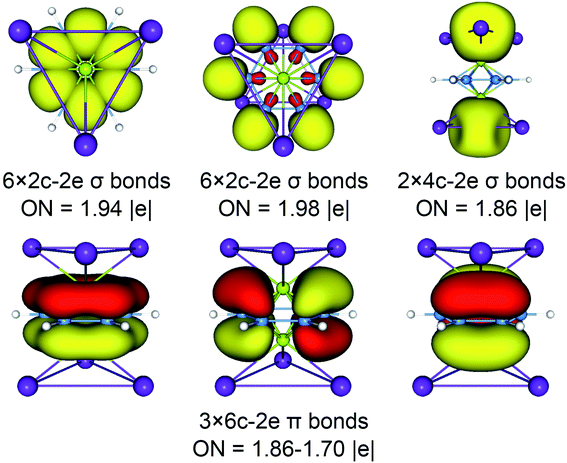 | ||
| Fig. 3 Adaptive natural density partitioning (AdNDP) bonding pattern of D3d (1A1g) GM for K6Be2B6H6 cluster. Occupation numbers (ONs) are indicated. | ||
3.4. Interaction between B6H6 ring and tetrahedral K3Be ligands
As mentioned above, the B6H6 ring and two tetrahedral K3Be ligands are viable in hexavalent anion [B6H6]6− and trivalent cation [K3Be]3+, respectively. The interaction between the B6H6 ring and tetrahedral K3Be ligands should be mainly dominated by the robust electrostatic attraction. We qualitatively estimate the ionic interaction by manually expanding the distances of two Be atoms to 10 Å, and subsequently performing a single-point calculation at the same level of theory. In this case, the energy difference with respect to the ground state structure is mainly attributed to the electrostatic attraction. The calculated ionic interaction energies are as high as 18.35 eV for the D3d (1A1g) GM and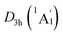 LM. Thus, the sandwiches are quite stable against dissociation. Alternatively, we also estimated the electrostatic attraction between the Be2B6H6 inverse sandwich and the two K3 rings by separating the K3 rings to 10 Å distance, which are 5.09 eV for the GM and 5.01 eV for LM, respectively.
LM. Thus, the sandwiches are quite stable against dissociation. Alternatively, we also estimated the electrostatic attraction between the Be2B6H6 inverse sandwich and the two K3 rings by separating the K3 rings to 10 Å distance, which are 5.09 eV for the GM and 5.01 eV for LM, respectively.
Furthermore, we calculated the dissociation energy of [K3Be]3+ units in K6Be2B6H6 cluster according to the following formula, [K3Be]3+[B6H6]6−[BeK3]3+ (D3d, 1A1g) = [K3Be]3+[B6H6]6−[BeK2]2+ (Cs, 1A′) + K+. The [K3Be]3+[B6H6]6−[BeK2]2+ (Cs, 1A′) is obtained from the GM structure by removing a K atom, and performing a fully optimization using its anion state at the same level. Such calculation can be used to evaluate quantitatively the energetics of the combination of [K2Be]2+ and K+ with respected to the tetrahedral [K3Be]3+ ligands in K6Be2B6H6 cluster. The result suggests that the dissociation energy of tetrahedral [K3Be]3+ is as high as 4.90 eV, hinting the tetrahedral [K3Be]3+ ligands is enough stable, and against disintegrating into the [BeK2]2+ and K+ components.
3.5. The B6H6 ring in K6Be2B6H6 complex: a real borozene
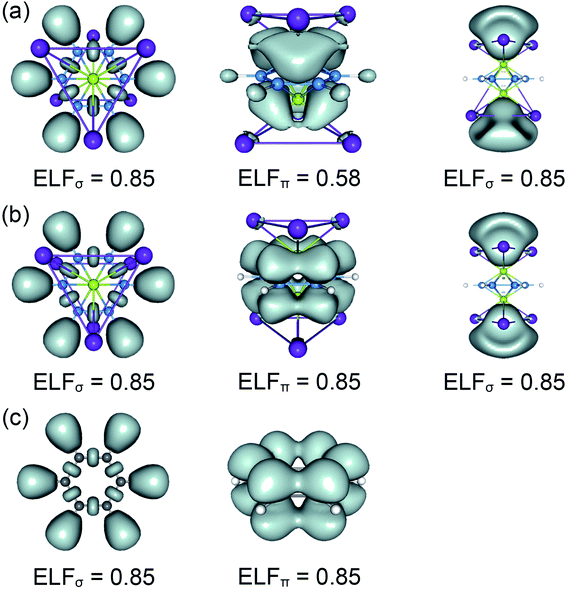
The real “borozene” should accurately imitate the C6H6 in both molecular structure and chemical bonding. Bonding analyses indicate that the K6Be2B6H6 cluster can be described as [K3Be]3+[B6H6]6−[BeK3]3+ complex. Here, the D6h [B6H6]6− ring is isoelectronic with C6H6, possessing the identical π sextet and Lewis B–B/B–H σ bond skeletons with the C6H6 (Fig. 2(c) and 3). Actually, it is an example of electronic transmutation, the boron atom acquiring an extra electron is transmutated into the carbon.61 Therefore, it truly occurs as a “borozene”. The ELFs data provide the further theoretical proof. As shown in Fig. 4, the D6h [B6H6]6− ring in the D3d (1A1g) GM and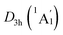 LM exhibit the identical bonding patterns (ELFσ and ELFπ) with the C6H6, despite the bifurcation value of ELFπ for the [B6H6]6− ring in D3d (1A1g) GM is somewhat lower (0.58) (Fig. 4(a)), which is mainly attributed to the weak hybridization of π CMOs (as indicated above). Interestingly, the [B6H6]6− ring in
LM exhibit the identical bonding patterns (ELFσ and ELFπ) with the C6H6, despite the bifurcation value of ELFπ for the [B6H6]6− ring in D3d (1A1g) GM is somewhat lower (0.58) (Fig. 4(a)), which is mainly attributed to the weak hybridization of π CMOs (as indicated above). Interestingly, the [B6H6]6− ring in 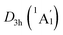 LM presents an ideal bifurcation value (Fig. 4(b)), which positively confirms the 6π aromaticity of [B6H6]6− ring. Compared with the C6H6 (Fig. 4(c)), the D3d (1A1g) GM and
LM presents an ideal bifurcation value (Fig. 4(b)), which positively confirms the 6π aromaticity of [B6H6]6− ring. Compared with the C6H6 (Fig. 4(c)), the D3d (1A1g) GM and 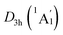 LM have two additional 4c–2e σ bonds on tetrahedral [K3Be]3+ ligands, being in line with their three-fold (2σ/6π/2σ) aromaticity, which are responsible for the stabilization for B6H6 and K3Be components. The three-fold (2σ/6π/2σ) aromaticity in D3d (1A1g) GM cluster is confirmed independently by the NICS calculation at the PBE0/6-311+G(d,p) level. The calculated NICS and NICSzz values are enough negative: −19.8 and −25.4 ppm for the center of K3Be ligand, and −16.0 and −22.8 ppm for 0.5 Å above the center of B6H6 ring.
LM have two additional 4c–2e σ bonds on tetrahedral [K3Be]3+ ligands, being in line with their three-fold (2σ/6π/2σ) aromaticity, which are responsible for the stabilization for B6H6 and K3Be components. The three-fold (2σ/6π/2σ) aromaticity in D3d (1A1g) GM cluster is confirmed independently by the NICS calculation at the PBE0/6-311+G(d,p) level. The calculated NICS and NICSzz values are enough negative: −19.8 and −25.4 ppm for the center of K3Be ligand, and −16.0 and −22.8 ppm for 0.5 Å above the center of B6H6 ring.
3.6. The dynamic fluxionality
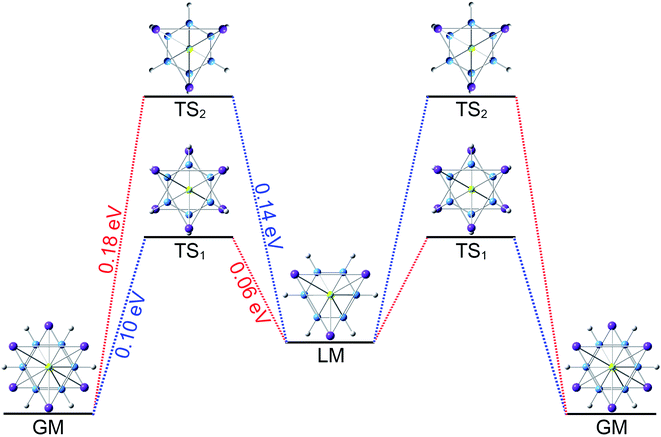
The three-fold (2σ/6π/2σ) aromaticity and robust electrostatic attraction in the [K3Be]3+[B6H6]6−[BeK3]3+ complex would facilitate interesting dynamic fluxionality of the cluster.62–64 We obtained two TS structures (Fig. 5), D3d (1A1g) TS1 and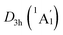 TS2, along with the displacement vectors for two soft vibrational modes of 46.2 and 24.7 cm−1 of the GM (Fig. S5(a)†). The TS1 and TS2 can be located from the GM by an independent rotation of 30° for B6H6 ring or an opposite rotation of 30° for each tetrahedral BeK3 ligand with the B6H6 ring fixation, respectively. Alternatively, they also can be located from the LM by the similar operation. The LM structure has two soft vibrational modes of 58.8 and 8.9 cm−1 (Fig. S5(b)†), relating to the intramolecular rotations. At the PBE0/6-311+G(d,p) level, the TS1 and TS2 structures are 0.10 and 0.18 eV above the GM with the ZPE corrections, which are refined to 0.14 and 0.23 eV at the single point CCSD(T) level. The small energy barriers imply that the clusters are dynamically fluxional at room temperature. The structural evolution process is illustrated in Fig. 5. Two pathways are demonstrated for the rotation of B6H6 ring (blue line) and the opposite rotation of two tetrahedral K3Be ligands (red line). The BOMD simulation performed at the temperature of 300 K at the PBE0/6-31G* level faithfully confirm the above assessment (see the video in the ESI†), vividly demonstrating the fascinating dynamic structural fluxionality of the system. It should be noted that the structural integrity of K6Be2B6H6 cluster is maintained consistently even at the higher temperature of 600 K.
TS2, along with the displacement vectors for two soft vibrational modes of 46.2 and 24.7 cm−1 of the GM (Fig. S5(a)†). The TS1 and TS2 can be located from the GM by an independent rotation of 30° for B6H6 ring or an opposite rotation of 30° for each tetrahedral BeK3 ligand with the B6H6 ring fixation, respectively. Alternatively, they also can be located from the LM by the similar operation. The LM structure has two soft vibrational modes of 58.8 and 8.9 cm−1 (Fig. S5(b)†), relating to the intramolecular rotations. At the PBE0/6-311+G(d,p) level, the TS1 and TS2 structures are 0.10 and 0.18 eV above the GM with the ZPE corrections, which are refined to 0.14 and 0.23 eV at the single point CCSD(T) level. The small energy barriers imply that the clusters are dynamically fluxional at room temperature. The structural evolution process is illustrated in Fig. 5. Two pathways are demonstrated for the rotation of B6H6 ring (blue line) and the opposite rotation of two tetrahedral K3Be ligands (red line). The BOMD simulation performed at the temperature of 300 K at the PBE0/6-31G* level faithfully confirm the above assessment (see the video in the ESI†), vividly demonstrating the fascinating dynamic structural fluxionality of the system. It should be noted that the structural integrity of K6Be2B6H6 cluster is maintained consistently even at the higher temperature of 600 K.
4. Conclusions
We have computationally designed a boron-based K6Be2B6H6 sandwich cluster, featuring a B6H6 ring being sandwiched by two tetrahedral K3Be ligands. There is significant charge transfer from the K3Be tetrahedrons to B6H6 ring (three electrons for each K3Be), yielding the [K3Be]3+[B6H6]6−[BeK3]3+ complex. The [B6H6]6− ring (with 6π delocalized electrons) precisely mimics the benzene in both geometry and chemical bonding, occurring as a real borozene. The tetrahedral [K3Be]3+ ligand with 2σ delocalized electrons possesses the three-dimensional aromaticity, serving as a superatom in essence. Overall, the sandwich cluster is a three-fold 2σ/6π/2σ aromatic system. The multi-fold aromaticity and robust electrostatic attraction among three motifs facilitates interesting dynamic fluxionality.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (21873058), the Natural Science Foundation of Shanxi Province (2018103), the Top Science and Technology Innovation Teams of Xinzhou Teachers University and the Fund for Shanxi “1331 Project” Key Subjects Construction.References
- H. J. Zhai, B. Kiran, J. Li and L. S. Wang, Nat. Mater., 2003, 2, 827–833 CrossRef CAS.
- S. Pan, J. Barroso, S. Jalife, T. Heine, K. R. Asmis and G. Merino, Acc. Chem. Res., 2019, 52, 2732–2744 CrossRef CAS PubMed.
- A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, Coord. Chem. Rev., 2006, 250, 2811–2866 CrossRef CAS.
- T. Jian, X. Chen, S. D. Li, A. I. Boldyrev, J. Li and L. S. Wang, Chem. Soc. Rev., 2019, 48, 3550–3591 RSC.
- E. Oger, N. R. M. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503–8506 CrossRef CAS PubMed.
- W. Huang, A. P. Sergeeva, H. J. Zhai, B. B. Averkiev, L. S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202–206 CrossRef CAS PubMed.
- H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727–731 CrossRef CAS.
- Y. J. Wang, Y. F. Zhao, W. L. Li, T. Jian, Q. Chen, X. R. You, T. Ou, X. Y. Zhao, H. J. Zhai, S. D. Li, J. Li and L. S. Wang, J. Chem. Phys., 2016, 144, 064307 CrossRef.
- W. N. Lipscomb, Science, 1977, 196, 1047–1055 CrossRef CAS.
- H. Braunschweig, R. D. Dewhurst and V. H. Gessner, Chem. Soc. Rev., 2013, 42, 3197–3208 RSC.
- E. D. Jemmis, M. M. Balakrishnarajan and P. D. Pancharatna, Chem. Rev., 2002, 102, 93–144 CrossRef CAS.
- H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2003, 42, 6004–6008 CrossRef CAS.
- Y. J. Wang, X. Y. Zhao, Q. Chen, H. J. Zhai and S. D. Li, Nanoscale, 2015, 7, 16054–16060 RSC.
- A. P. Sergeeva, D. Y. Zubarev, H. J. Zhai, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2008, 130, 7244–7246 CrossRef CAS.
- A. P. Sergeeva, Z. A. Piazza, C. Romanescu, W. L. Li, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 18065–18073 CrossRef CAS PubMed.
- Z. A. Piazza, H. S. Hu, W. L. Li, Y. F. Zhao, J. Li and L. S. Wang, Nat. Commun., 2014, 5, 3113 CrossRef.
- Q. Chen, G. F. Wei, W. J. Tian, H. Bai, Z. P. Liu, H. J. Zhai and S. D. Li, Phys. Chem. Chem. Phys., 2014, 16, 18282–18287 RSC.
- A. N. Alexandrova, H. J. Zhai, L. S. Wang and A. I. Boldyrev, Inorg. Chem., 2004, 43, 3552–3554 CrossRef CAS.
- T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, J. Chem. Phys., 2011, 135, 104301 CrossRef.
- P. W. Fowler and B. R. Gray, Inorg. Chem., 2007, 46, 2892–2897 CrossRef CAS.
- L. L. Pan, J. Li and L. S. Wang, J. Chem. Phys., 2008, 129, 024302 CrossRef PubMed.
- T. T. Chen, W. L. Li, T. Jian, X. Chen, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2017, 56, 6916–6920 CrossRef CAS.
- W. L. Li, T. T. Chen, W. J. Chen, J. Li and L. S. Wang, Nat. Commun., 2021, 12, 6467 CrossRef CAS.
- N. G. Szwacki, V. Weber and C. J. Tymczak, Nanoscale Res. Lett., 2009, 4, 1085–1089 CrossRef.
- W. L. Li, C. Romanescu, T. R. Galeev, Z. A. Piazza, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 165–168 CrossRef CAS.
- W. L. Li, T. T. Chen, D. H. Xing, X. Chen, J. Li and L. S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6972−E6977 Search PubMed.
- W. L. Li, T. Jian, X. Chen, T. T. Chen, G. V. Lopez, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2016, 55, 7358–7363 CrossRef CAS PubMed.
- W. L. Li, L. Xie, T. Jian, C. Romanescu, X. Huang and L. S. Wang, Angew. Chem., Int. Ed., 2014, 53, 1288–1292 CrossRef CAS.
- Z. H. Cui, W. S. Yang, L. Zhao, Y. H. Ding and G. Frenking, Angew. Chem., Int. Ed., 2016, 55, 7841–7846 CrossRef CAS PubMed.
- C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Acc. Chem. Res., 2013, 46, 350–358 CrossRef CAS.
- D. Z. Li, H. Bai, Q. Chen, H. Lu, H. J. Zhai and S. D. Li, J. Chem. Phys., 2013, 138, 244304 CrossRef PubMed.
- L. Y. Feng, R. Li and H. J. Zhai, Phys. Chem. Chem. Phys., 2019, 21, 20523–20537 RSC.
- J. Aihara, J. Am. Chem. Soc., 1978, 100, 3339–3342 CrossRef CAS.
- A. N. Alexandrova, K. A. Birch and A. I. Boldyrev, J. Am. Chem. Soc., 2003, 125, 10786–10787 CrossRef CAS.
- A. N. Alexandrova and A. I. Boldyrev, Inorg. Chem., 2004, 43, 3588–3592 CrossRef CAS.
- L. F. Li, C. Xu, B. K. Jin and L. J. Cheng, J. Chem. Phys., 2013, 139, 174310 CrossRef PubMed.
- L. F. Li, C. Xu and L. J. Cheng, Comput. Theor. Chem., 2013, 1021, 144–148 CrossRef CAS.
- J. Hou, Q. Duan, J. Qin, X. Shen, J. Zhao, Q. Liang, D. Jiang and S. Gao, Phys. Chem. Chem. Phys., 2015, 17, 9644–9650 RSC.
- H. L. Yu, R. L. Sang and Y. Y. Wu, J. Phys. Chem. A, 2009, 113, 3382–3386 CrossRef CAS PubMed.
- Y. J. Wang, L. Y. Feng, L. Xu, X. R. Hou, N. Li, C. Q. Miao and H. J. Zhai, Phys. Chem. Chem. Phys., 2020, 22, 20043–20049 RSC.
- B. P. T. Fokwa and M. Hermus, Angew. Chem., Int. Ed., 2012, 51, 1702–1705 CrossRef CAS.
- Y. J. Wang, C. Q. Miao, J. J. Xie, Y. R. Wei and G. M. Ren, New J. Chem., 2019, 43, 15979–15982 RSC.
- Y. J. Wang, M. M. Guo, G. L. Wang, C. Q. Miao, N. Zhang and T. D. Xue, Phys. Chem. Chem. Phys., 2020, 22, 20362–20367 RSC.
- M. Saunders, J. Comput. Chem., 2004, 25, 621–626 CrossRef CAS.
- P. P. Bera, K. W. Sattelmeyer, M. Saunders, H. F. Schaefer III and P. v. R. Schleyer, J. Phys. Chem. A, 2006, 110, 4287–4290 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- R. J. Bartlett and M. Musial, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- E. D. Glendening, C. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2013 Search PubMed.
- B. Silvi and A. Savin, Nature, 1994, 371, 683–686 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- U. Varetto, Molekel 5.4.0.8, Swiss National Supercomputing Center, Manno, Switzerland, 2009 Search PubMed.
- P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS.
- T. Helgaker, E. Uggerud and H. J. A. Jensen, Chem. Phys. Lett., 1990, 173, 145–150 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 09, revision D.01, Gaussian Inc., Wallingford, Connecticut, 2009 Search PubMed.
- S. Goedecker, J. Chem. Phys., 2004, 120, 9911–9917 CrossRef CAS PubMed.
- P. Pyykkö, J. Phys. Chem. A, 2015, 119, 2326–2337 CrossRef PubMed.
- M. Bühl and A. Hirsch, Chem. Rev., 2001, 101, 1153–1183 CrossRef PubMed.
- A. C. Reber and S. N. Khanna, Acc. Chem. Res., 2017, 50, 255–263 CrossRef CAS.
- P. Jena and Q. Sun, Chem. Rev., 2018, 118, 5755–5870 CrossRef CAS PubMed.
- X. Zhang, K. A. Lundell, J. K. Olson, K. H. Bowen and A. I. Boldyrev, Chem.–Eur. J., 2018, 24, 9200–9210 CrossRef CAS PubMed.
- J. O. C. Jiménez-Halla, R. Islas, T. Heine and G. Merino, Angew. Chem., Int. Ed., 2010, 49, 5668–5671 CrossRef PubMed.
- Y. J. Wang, J. C. Guo and H. J. Zhai, Nanoscale, 2017, 9, 9310–9316 RSC.
- J. C. Guo, L. Y. Feng, Y. J. Wang, S. Jalife, A. Vásquez-Espinal, J. L. Cabellos, S. Pan, G. Merino and H. J. Zhai, Angew. Chem., Int. Ed., 2017, 56, 10174–10177 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary Table S1 and Fig. S1–S5, as well as a short movie for dynamic fluxionality extracted from the BOMD simulation. See DOI: 10.1039/d2ra00692h |
| This journal is © The Royal Society of Chemistry 2022 |