A combined crystallography and DFT study on ring-shaped Cucurbit[n]urils: structures, surface character, and host–guest recognition

Abstract

A combined crystallography and DFT study of cucurbit[n]urils (n = 5–8, 10) was carried out, and PBE0 was certified to be the most rational density functional method for optimization task. Steric hindrance and electronic effect of the hindered lone pair electrons in cucurbit[n]urils were qualitatively measured by bond order analysis, lone pair electron (LP) visualization and electrostatic potential (ESP) study. Together with energy decomposition analysis of some selected host–guest systems, we quantitatively verified the effect of size/cavity and noncovalent interaction in host–guest recognition. This solid study revealed that lone pairs electrons affect not only on host–guest identification mode but also on geometry stability, which pave the avenue for further sophisticated applications.

---

Introduction

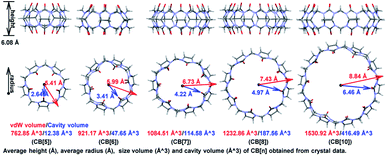
The first preparation of Cucurbit[n]uril (CB[n]) can be dated back to 1904 by Behrend and co-workers,^1a who reported the condensation reaction of formaldehyde and glycoluril. However, limited by the poor solubility and difficulty in crystallization, the single crystal structure of the condensed product was not obtained until 1981,^1b which hindered the understanding and application of CB[n]s. In the past twenty years, 7 more homologues were synthesized and CB[n] family now contains skeletons with 5 to 15 glycoluril units.^1a,c–g As shown in Fig. 1, CB[n]s (n ≤ 10) has pumpkin-like shapes. Crystallography study shows that all the single-ring CB[n]s have a congenial height approximate to 6.08 Å, and their inner/outer diameters range from 2.64 Å/5.41 Å to 6.46 Å/8.84 Å. Thanks to the hydrophobic cavities with adjustable volumes (from 12.38 ų to 416.49 ų, more details in Fig. S1†), CB[n]s have been widely applied in catalysis,^2a photochemistry,^2b drug delivery,^2c biosensing,^2d gas storage,^2e and separation science,^2f etc.^2g–k

Fig. 1 Structural parameters of the reported ring-shaped CB[n]s.

With the prosperity of porous materials in the past decades, scientists have gained developing understandings of the recognition mode between CB[n]s and guest molecules. And some more sophisticated applications were developed as a result. Liu group³ prepared the syn/anti-excimer complexes by assembling dipolar dyes styrylpyridiniums into CB[n] (n = 7 or 8), which performed reversibly tunable white-light emissions capability when opposite stacking orientations embedded. Agasti and co-worker⁴ exploited dynamic supramolecular recognition between fluorescently labelled guest molecules and complementary CB[7] hosts, based on which a super-resolution imaging method for live-cell microscopy was established. Among these applications, cavity size and noncovalent interactions provided the vital contribution, and it's believed that theoretical calculation would supply more detailed information to the mechanism.

However, to the best of our knowledge, little theoretical studies on CB[n]s were conducted. Most reported theoretical studies focused on explaining the solubility or host–guest bonding strength of CB[n]s by referring to energies, while a general comparison about the similarity/difference among different CB[n]s was rarely discussed. What's more, we deemed that crystal structures should be paid more attention when theoretical study was involved, for which supplied the most solid information about CB[n] species. In this paper, we carried out our investigation on CB[n]s (n ≤ 10) through combining crystallography and ab initio calculation. By focusing on the structure, surface character, and host–guest binding properties, a deeper understanding of the host–guest recognition was achieved, which provided fundamental ideas for designing of such supramolecular self-assembly systems.

Computational details

Gaussian 16 package^5a and xtb program^5b,c were applied in the calculation. Original structures were set up based on single crystals structures obtained from CCDC database.^6a–h Semi-empirical method of PM7 (ref. 7a) and GFN2-xTB,^5b together with DFT methods including B3LYP,^7b PBE0,^7c wB97-D3,^7d M06-2X,^7e and B3LYP combined D3 version of Grimme's dispersion^7f were applied in geometry optimization, using 6-31G(d) basis set.^7g All the geometry optimization tasks were performed in vacuum to reproduce the crystal environment for CB[n]s. Single point energies were calculated at M06-2X/def-TZVP^7h (SDD for I) level for the optimized structures and host–guest systems extracted from crystal structures. Wavefunction analysis including Mayer bond orders,^8a Mulliken charge population,^8b LP distribution,^8c ESP, energy decomposition analysis (EDA) and non-covalent interaction (NCI) analysis were performed by Multiwfn program,^5d using the fchk files generated in M06-2X/def-TZVP level. RDSM calculation and the visualization of structures and isosurface were carried out by VMD program.^5e

Results and discussion

Structural information

Firstly, some commonly used density functional methods were screened for the geometry optimization task, and the single point energies of the optimized structures were summarized. As shown in Table 1, the relative energies of the optimized structures were much lower than those of crystal structures, which implied that the monomer structure extract from periodic crystal structure was not the minimal point and geometry optimization was prerequisite for ab initio study. As shown in the first raw, energies of CB[n]s optimized by semi-empirical method PM7 were much higher (about 40 kcal mol⁻¹) than those optimized by DFT methods, implying insufficient precision of PM7 for CB[n]s optimization task. Comparatively, GFN2-xTB provided a much better result with accuracy approaching to B3LYP. Considering of the calculation cost and hardware dependencies, GFN2-xTB is suitable and recommended for pre-optimized calculation. Among the selected DFT methods, B3LYP-D3, PBE0, and M06-2X showed similar capabilities for geometry optimization, while wB97-D3 was much inferior (about 8 kcal mol⁻¹ higher). The B3LYP functional did not combine D3 version of Grimme's dispersion raised energies about 2 kcal mol⁻¹ higher than those calculated from B3LYP-D3, inferring dispersion correction had a certain impact on the optimization of CB[n]s structures. By combining with the RMSD data (see Table S1†), it can be seen that PBE0 changed the crystal structure in the minimal level. In order to fit the crystal structures to the greatest extent, structures optimized by PBE0 were chosen for the following wavefunction analysis.

Table 1 Relative energies of CB[n] optimized by selected theoretical methods. Basis set 6-31G(d) was applied for geometry optimizations; energies calculated at M06-2X/def-TZVP level, and setting the calculated energy of crystal as zero point

ΔG (kcal mol^−1)	CB[5]	CB[6]	CB[7]	CB[8]	CB[10]
PM7	−196.2	−234.9	−179.6	−301.2	−403.4
GFN2-xTB	−236.4	−288.1	−242.6	−376.7	−502.9
B3LYP	−236.1	−287.1	−241.5	−375.1	−502.0
B3LYP-d3(BJ)	−238.0	−288.8	−243.9	−377.6	−504.9
PBE0	−239.0	−290.1	−245.2	−379.3	−507.2
wB97-D	−233.1	−282.9	−236.7	−369.6	−494.9
M06-2X	−239.7	−290.9	−246.1	−380.5	−508.6

---

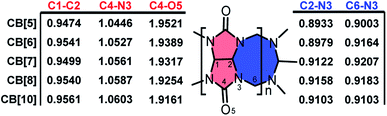
With the optimized structures in hand, bond order index analysis was then performed. Bond connection in CB[n] skeletons could be summarized in 5 types, as shown in Scheme 1, which are C1–C2, C2–N3, C4–N3, C4–O5, and C6–N3. With n enlarging, bond order indexes of C4–O5 significantly decreased (from 1.9521 to 1.9161), while those of C1–C2 and C4–N4 tinnily increased (from 0.9474 to 0.9561 and from 1.0446 to 1.0603). Specially, bond order indexes of C2–N3 and C6–N3 held a tendency to increase first and then decrease (0.8999 → 0.9158 → 0.9103 and 0.900 3 → 0.9207 → 0.9103). As the chemical structures shown on the right, eight-membered rings (blue ring) constituted of C2–N3 and C6–N3, and five-membered rings (red ring) constituted of C1–C2, C2–N3, and C4–N3, hence the rigidity of the ring could be described by the involved bond order indexes. In other word, the growth of the bond order indexes of C1–C2 and C4–N3 implied the stability raised in the five-membered rings with n increasing. And eight-membered rings were most stable when n equalled to 7. As a result, CB[7] was less deformed than other CB[n]s, and CB[7] should be the most stable and rigid compound among the selected structures.

Scheme 1 Mayer bond order index variation of CB[n] skeletons with n enlarging.

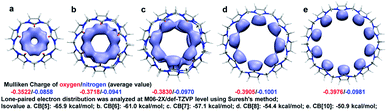
Apparently, the bond order index changes of C1–C2, C2–N3, C4–N3, and C6–N3 were closely related to those of C4–O5, and we assumed that the bond order index decreases of C4–O5 as n increasing were associated with the LP and ring tension. As shown in Fig. 2, the LP were visualized by Suresh's method,^8c where isosurface value equalled to the minimal add 10 kcal mol⁻¹ were drawn. Apparently, owing to the limitation of the ring size, LP overlapped in CB[5] and CB[6]. The LP overlapping reserved electrons in high density and made hydrogen bond prone to form with those doners contributing hydrogen. Similar to steric effect, the overlap of LP brought repulsive force, which pressed on the C4–O5 bond and shorten it. In addition, the overlap of LP might squeeze each other and force the electrons to reflow to the C4–O5 bond. With the ring size enlarging, the overlap of LP gradually decreased in CB[7] and CB[8], and finally became independent in CB[10]. Ring enlargement decreased LP overlap and made room for keeping LP, which determined the Mulliken charges population of oxygen as CB[5] owned the minimal negative value (−0.3522) while CB[10] owned the maximum negative one (−0.3976). Ring tension decreased with n enlarging (more evidences in Fig. S2†), leading to enhancement of coplanarity of the urea functional groups, thus improved the conjugation of C=N bonds. Hence, those electrons formerly restricted to C=O bonds could be more shared by the urea functional groups, resulting in the decrease and increase of bond order indexes of C4–O5 and C4–N3 respectively, and Mulliken charge population of nitrogen became more negative (−0.0858 to −0.0981).

Fig. 2 Lone pair electron distribution in CB[n]s.

Surface character

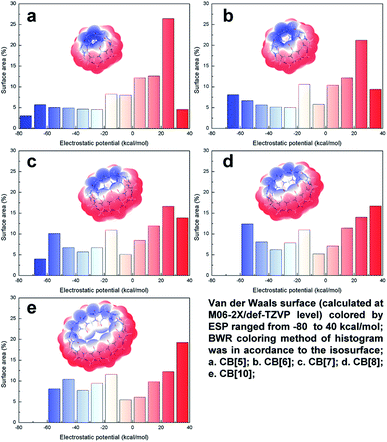
ESP plays an important role in the noncovalent interaction for polarized structures, which determines both the interaction area and strength of the electrostatics and inductive force. Thus, ESP study brings insight into more in-depth understanding of host–guest recognition. The van der Waals surface map colored by ESP of CB[n]s (n = 5, 6, 7, 8, 10) were summarized in Fig. 3. It can be clearly identified that the negative ESP value distributed in the both ends, above/below the carbonyl oxygen, and the positive ESP value distributed in the middle of the structures, on the outside of hydrogen. The up-down distributed negative ESP area were electron-rich, where cation or electron-deficient species were prone to be trapped. Owing to the enlargement of the pumpkin-like shape from CB[5] to CB[10], the surface outside of hydrogens expanded, resulting in gradually increasing ratio of the positive ESP surface area (the red area increased in histogram). However, the same change brought opposite effect to the negative ESP surface. The enlargement of the CB[n]s departed the carbonyl oxygen, which decreased their LP overlap and made negative ESP value less negative (the blue area shifted to 0 in histogram). Combined with the LP distribution analysis above, we can infer that electron density increased because of ring tensions in compact rings. Therefore, electrostatic attraction held a greater strength among the smaller CB[n]s. By influence of the distances and angles of the LP, CB[5] and CB[6] usually preferred to co-crystallize with cations. On the other hand, the electron-neutral ESP value mostly distributed inside the structures. The inner surface gradually became larger with the enlargement of CB[n]s, leading those low-polarized structures tended to be trapped into the cavity. Lots of crystallographic examples support these conclusions, which will be further discussed below.

Fig. 3 Electrostatic potential (ESP) character of CB[n]s.

Host–guest recognition

Independent gradient model (IGM)^9a takes advantages in analysing host–guest interaction by dividing the integral complex into fragments and visualizes the noncovalent interaction between fragments optionally, which have been widely applied in pioneer's work.^9b–d As shown in Fig. 4, IGM isosurface of some typical ion/neutral molecule-CB[n] complex structures were presented with attachment of the result of EDA based on AMBER force field¹⁰ and Merz–Kollmann ESP fitting atomic charge.¹¹ The selected host–guest systems can be treated as typical representatives of several types, which were described as metal ion (cluster) outside of CB[n] (Mg²⁺(H₂O)₄@CB[6]), organic ion outside of CB[n] (NH₄⁺@CB[5]*), polarized molecule outside of CB[n] (H₂O@CB[5]*), charged organic compound inside of CB[n] (Az⁺@CB[8]), polarized molecule inside of CB[n] (CO₂@CB[5]*), and non-polarized molecule inside of CB[n] (I₂@CB[6]).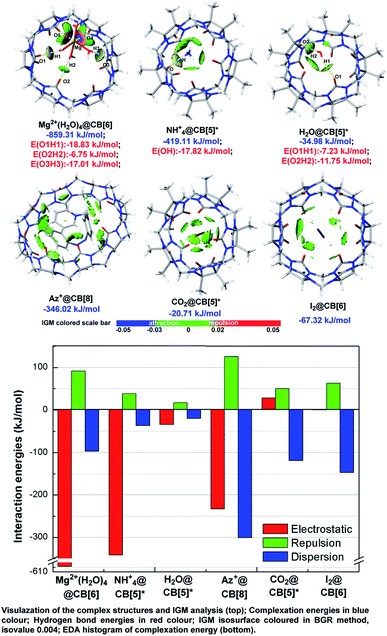

Fig. 4 Independent gradient model (IGM) analysis and energy decomposition analysis (EDA) of the selected host–guest systems.

Consistent with the above conclusions, ions and hydrogen bond doners, such as Mg²⁺, NH₄⁺, and H₂O were caught by carbonyl oxygens. Hydrogen bonds formed in these complexes as the IGM isosurface showed (colored in pale bule and blue-green). According to the hydrogen bond energies (noted in red), hydrogen bond strength was slightly stronger in charged complexes than that in neutral ones (−17.82 vs. −11.75 kJ mol⁻¹). Strong attraction (isosurface colored in deep blue) and repulsion (isosurface colored in deep red) existed between Mg²⁺(H₂O)₄ and CB[6] of Mg²⁺(H₂O)₄@CB[6], and we inferred it should be a manifestation of strong coordination bonds. Neutral molecules and those compounds which cannot donor hydrogen to form hydrogen bonds preferred to be trapped within the cavities and form complex structures, for example, CO₂@CB[5]*, I₂@CB[6], and Az⁺@CB[8]. IGM pointed out the repulsion and dispersion betwixt the host and guest in CO₂@CB[5]* and I₂@CB[6] were in medium intensity (isosurface mostly colored in bright green and bright grey-green), whose isosurface were tattered and in small area. Relatively, isosurface in Az⁺@CB[8] was much more diffuse, and coloured method showed that the host–guest interactions were stronger (isosurface colored in green and dark grey-green).

The result of EDA qualitatively matched with the basis set superposition error (BSSE) corrected complexation energies. The value of EDA/corrected complexation energies were −859.31/−609.56, −419.11/−340.59, −34.98/−37.66, −346.02/−408.79, −20.71/−40.05, and −67.32/−84.04 (kJ mol⁻¹) for Mg²⁺(H₂O)₄@CB[6], NH₄⁺@CB[5]*, H₂O@CB[5]*, Az⁺@CB[8], CO₂@CB[5]*, and I₂@CB[6], respectively. Generally, ions held a 5 to 10-times of electrostatic intensity than neutral molecules did, and electrostatic force was a vital factor to keep polarized guest outside the host's cavity. On the other hand, dispersion was related to molecular volume and interaction surface area, and dispersion was the main contributor for maintaining guest trapped in cavities.

EDA histogram indicated that electrostatic force played a negative role in stabilizing the complex structures for CO₂@CB[5]*, which could be ascribed to LP repulsion. Carbonyl oxygens of CB[5]* in both ends were in negative ESP value (Fig. 3), the same as oxygens of CO₂. Groups with same charge repels each other and repels and raises up energy. Therefore, the most stable conformation was formed when CO₂ was stuck inside the cavity, where electrostatic repulsion of the both ends offset each other out and dispersion can be improved to the maximum level as the largest contact surface was achieved.

The interaction modes found in these complex structures consistent with the conclusions drawn by ESP analysis, that is high-polarized structures tended to interact at both end of CB[n]s while low-polarized structures preferred to be trapped in the central cavities. The example of I₂@CB[6] implied that non-polarized molecule trapped inside the cavity could be stabilized without electrostatic, and maintained only by van der Waals forces. And the example of Az⁺@CB[8] disclosed that dispersion intensity could be expanded remarkably when fully-trapped guests owned large VDW surface. Hence, more attention should be paid for the contribution of dispersion, which was even more effective in reducing the energy of the system than electrostatics when large-sized molecular were trapped in CB[n]s. The effect of dispersion was a key role in the applications such as drug delivery, molecular recognition and separation science for CB[n]s, and it was the first time discussed by visualization method in qualitative/quantitative.

Conclusions

In summary, we confirmed that the PBE0 was suitable for geometry optimization task of CB[n]s, which got the balance between least structural changes and lowest relative energies. We disclosed that the eight-membered ring became more flexible while five-membered glycoluril ring turned to be firmer with ring size enlarging, which was controlled by the conjugation effect, ring tension, and LP repulsion. To address, LP repulsion in CB[n] was carefully discussed for the first time, which not only effect on the geometry structures, but also on the electrostatics potential distribution. Combined with IGM and EDA analysis, we revealed how electrostatic dominated polar host–guest recognition in both ends of CB[n]s and dispersion played an important role in stabilizing guests trapped in cavities, in qualitative/semi-quantitative. These studies provided solid evidences and clear understandings of the CB[n]-guest recognition mode/mechanism, bringing insight to the further research and sophisticated applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the following funding: Education Commission of Guangdong Province (2020ZDZX2077), Science and Technology Planning Project of Guangzhou (202102021119) and Special Fund Projects of Guangdong Academy of Sciences for the Construction of Domestic First-class Research Institutions (2021GDASYL-20210103035).

Notes and references

1. Papers on the development of CB[n], see: (a) R. Behrend, E. Meyer and F. Rusche, Justus Liebigs Ann. Chem., 1905, 339, 1–37; (b) W. A. Freeman, W. L. Mock and N. Y. Shih, J. Am. Chem. Soc., 1981, 103, 7367–7368; (c) X.-J. Cheng, L.-L. Liang, K. Chen, N.-N. Ji, X. Xiao, J.-X. Zhang, Y. Zhang, S.-F. Xue, Q.-J. Zhu, X.-L. Ni and Z. Tao, Angew. Chem., Int. Ed., 2013, 52, 1–5; (d) Q. Li, S. C. Qiu, J. Zhang, K. Chen, Y. Huang, X. Xiao, Y. Zhang, F. Li, Y. Q. Zhang, S. F. Xue, Q. J. Zhu, Z. Tao, L. F. Lindoy and G. Wei, Org. Lett., 2016, 18, 4020–4023; (e) J. Lagona, P. Mukhopadhyay, S. Chakrabarti and L. Isaacs, Angew. Chem., Int. Ed., 2005, 44, 4844–4870; (f) J. Kim, I.-S. Jung, S.-Y. Kim, E. Lee, J.-K. Kang, S. Sakamoto, K. Yamaguchi and K. Kim, J. Am. Chem. Soc., 2000, 122, 540–541; (g) A. I. Day, R. J. Blanch, A. P. Arnold, S. Lorenzo, G. R. Lewis and I. Dance, Angew. Chem., Int. Ed., 2002, 41, 275–277.
2. For selected papers on the applications of CB[n], see: (a) B. C. Pemberton, N. Barooah, D. K. Srivatsava and J. Sivaguru, Chem. Commun., 2010, 46, 225–227; (b) A. A. Elbashir and H. Y. Aboul-Enein, Crit. Rev. Anal. Chem., 2014, 45, 52–61; (c) S. Walker, R. Oun, F. J. McInnes and N. J. Wheate, Isr. J. Chem., 2011, 51, 616–624; (d) L. C. Smith, D. G. Leach, B. E. Blaylock, O. A. Ali and A. R. Urbach, J. Am. Chem. Soc., 2015, 137, 3663–3669; (e) H. Kim, Y. Kim, M. Yoon, S. Lim, S. M. Park, G. Seo and K. Kim, J. Am. Chem. Soc., 2010, 132, 12200–12202; (f) H. Zheng, Z. Li, J. Zhang, J. Ma, Y. Zhou and Q. Jia, RSC Adv., 2015, 5, 5850–5857; (g) X. Wu, Y. Chen, Q. Yu, F. Q. Li and Y. Liu, Chem. Commun., 2019, 55, 4343–4346; (h) Y. H. Liu, Y. M. Zhang, H. J. Yu and Y. Liu, Angew. Chem., Int. Ed., 2021, 60, 3870–3880; (i) S. Li, H. Chen, X. Yang, D. Bardelang, I. W. Wyman, J. Wan, S. M. Y. Lee and R. Wang, ACS Med. Chem. Lett., 2015, 6, 1174–1178; (j) S. Murkli, J. Klemm, A. T. Brockett, M. Shuster, V. Briken, M. R. Roesch and L. Isaacs, Chem.–Eur. J., 2021, 27, 3098–3105; (k) Y. Sun, Z. Wang, L. Yue, Q. Huang, Q. Cheng and R. Wang, J. Am. Chem. Soc., 2020, 142, 16523–16527.
3. S. H. Li, X. Xu, Y. Zhou, Q. Zhao and Y. Liu, Org. Lett., 2017, 19, 6650–6653.
4. R. Sasmal, N. Das Saha, F. Schueder, D. Joshi, V. Sheeba, R. Jungmann and S. S. Agasti, Chem. Commun., 2019, 55, 14430–14433.
5. Software and program involved in this paper, see: (a) M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. L. F. Ding, J. G. F. Egidi, B. Peng, A. Petrone, , D. R. T. Henderson, V. G. Zakrzewski, J. Gao, N. Rega, , W. L. G. Zheng, M. Hada, M. Ehara, K. Toyota, R. Fukuda, , M. I. J. Hasegawa, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, , K. T. T. Vreven, J. A. Montgomery Jr, J. E. Peralta, , M. J. B. F. Ogliaro, J. J. Heyd, E. N. Brothers, K. N. Kudin, , T. A. K. V. N. Staroverov, R. Kobayashi, J. Normand, , A. P. R. K. Raghavachari, J. C. Burant, S. S. Iyengar, , M. C. J. Tomasi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, , R. L. M. J. W. Ochterski, K. Morokuma, O. Farkas, and D. J. F. J. B. Foresman, Gaussian 16, Gaussian, Inc., Wallingford CT, 2016; (b) C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671; (c) G. Stefan, B. Christoph and S. Philip, J. Chem. Theory Comput., 2017, 13, 1989–2009; (d) T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592; (e) H. William, D. Andrew and S. Klaus, J. Mol. Graphics, 1996, 14, 33–38.
6. Single crystals included in this paper were obtained from CCDC database, see: (a) M. M. Ayhan, H. Karoui, M. Hardy, A. Rockenbauer, L. Charles, R. Rosas, K. Udachin, P. Tordo, D. Bardelang and O. Ouari, J. Am. Chem. Soc., 2015, 137, 10238–10245; (b) O. Danylyuk and V. P. Fedin, Cryst. Growth Des., 2011, 12, 550–555; (c) J. del Barrio, P. N. Horton, D. Lairez, G. O. Lloyd, C. Toprakcioglu and O. A. Scherman, J. Am. Chem. Soc., 2013, 135, 11760–11763; (d) H. S. El-Sheshtawy, B. S. Bassil, K. I. Assaf, U. Kortz and W. M. Nau, J. Am. Chem. Soc., 2012, 134, 19935–19941; (e) C. Liu, R. Gao, Y. Zhang, Q. Zhu and Z. Tao, Chin. Chem. Lett., 2021, 32, 362–366; (f) Y. Miyahara, K. Abe and T. Inazu, Angew. Chem., Int. Ed., 2002, 41, 3020–3023; (g) J. Wang, Y. Jang, J. K. Khedkar, J. Y. Koo, Y. Kim, C. J. Lee, Y. M. Rhee and K. Kim, Chemistry, 2016, 22, 15791–15799; (h) M. Liu, M. Yang, Y. Yao, Y. Zhang, Y. Zhang, Z. Tao, Q. Zhu, G. Wei, B. Bian and X. Xiao, J. Mater. Chem. C, 2019, 7, 1597–1603.
7. Methods applied in DFT calculations, see: (a) J. J. P. Stewart, J. Mol. Model., 2013, 19, 1–32; (b) P. J. Stephens, F. J. Devlin, C. F. Chabalowsk and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627; (c) A. Carlo and B. Vincenzo, J. Chem. Phys., 1999, 110, 6158–6170; (d) Y. S. Lin, G. D. Li, S. P. Mao and J. D. Chai, J. Chem. Theory Comput., 2013, 9, 263–272; (e) Z. Yan and D. G. Truhlar, Theor. Chem. Acc., 2006, 120, 215–241; (f) S. Grimmea, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104; (g) M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797–2803; (h) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
8. Methods applied in wavefunction analysis, see: (a) I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274; (b) R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840; (c) P. V. Bijina, C. H. Suresh and S. R. Gadre, J. Comput. Chem., 2018, 39, 488–499.
9. For selected papers on the applications of IGM method, see: (a) C. Lefebvre, H. Khartabil, J. C. Boisson, J. Contreras-Garcia, J. P. Piquemal and E. Henon, Chemphyschem, 2018, 19, 724–735; (b) J. Gutiérrez-Flores, S. E. Pérez-Figueroa, R. M. d. Castillo, A. Martínez, L. E. Sansores and E. Ramos, Struct. Chem., 2020, 32, 775–785; (c) H. Khartabil, L. Doudet, I. Allart-Simon, M. Ponce-Vargas, S. Gerard and E. Henon, Org. Biomol. Chem., 2020, 18, 6840–6848; (d) X. Yang, Q. Wang, P. Hu, C. Xu, W. Guo, Z. Wang, Z. Mao, Z. Yang, C. Liu, G. Shi, L. Chen, B. Xu and Z. Chi, Mater. Chem. Front., 2020, 4, 941–949.
10. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197.
11. U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed results and coordinates of the optimized species. See DOI: 10.1039/d2ra00797e

---