Open Access Article
Open Access ArticleDoes the inclusion of electronic polarisability lead to a better modelling of peptide aggregation?†
Batuhan Kav a and
Birgit Strodel
a and
Birgit Strodel *ab
*ab
aInstitute of Biological Information Processing: Structural Biochemistry (IBI-7), Forschungszentrum Jülich, 52428 Jülich, Germany. E-mail: b.strodel@fz-juelich.de
bInstitute of Theoretical and Computational Chemistry, Heinrich Heine University Düsseldorf, 40225 Düsseldorf, Germany
First published on 21st July 2022
Abstract
Simulating the process of amyloid aggregation with atomic detail is a challenging task for various reasons. One of them is that it is difficult to parametrise a force field such that all protein states ranging from the folded through the unfolded to the aggregated state are represented with the same level of accuracy. Here, we test whether the consideration of electronic polarisability improves the description of the different states of Aβ16–22. Surprisingly, the CHARMM Drude polarisable force field is found to perform worse than its unpolarisable counterpart CHARMM36m. Sources for this failure of the Drude model are discussed.
1 Introduction
The aggregation of the amyloid-β peptide (Aβ) into amyloid fibrils is one of the defining features of Alzheimer's disease. In order to understand the molecular basis of that disease, one has to elucidate the aggregation process of Aβ. To this end, a multitude of experimental methodologies as well as molecular dynamics (MD) simulations are applied to this problem.1 However, the results of biomolecular MD simulations depend sensitively on the force field used to model the system in question.2 We and others demonstrated this problem for both monomeric Aβ3 and amyloid aggregation where the fragment Aβ16–22 was used as a test case.4–6 This peptide has the sequence KLVFFAE, containing the hydrophobic residues 17–21 which play a major role in the aggregation of Aβ,7,8 and it is known to aggregate into amyloid fibrils with an antiparallel β-sheet architecture.9 The conclusion of the various force field evaluations was that the accurate modelling of peptide aggregation requires a reliable representation of the monomeric peptide structures and a fine balance between the peptide–peptide and peptide-water interactions. These two conditions are currently best realized in the CHARMM36m (C36m) force field.10A shortcoming of C36m and the other typical protein force fields is that they are not able to capture the effects of electronic polarisation, as they are non-polarisable force fields that assign point charges to the atoms which are unchangeable during a simulation.11 With such a static charge distribution, the atoms cannot respond to the changes in the local electric field. However, peptides undergoing self-assembly encounter changes in the dielectric constants of their surroundings as they pass from the aqueous solution phase with a high dielectric constant to the aggregated state which is characterised by lower dielectric constants. Therefore, our assumption is that the accurate modelling of such systems requires the inclusion of electronic polarisability, which is accomplished with polarisable force fields like the CHARMM-Drude (C-Drude) force field.11 It allows for electronic polarisability via induced dipoles, which are realised through so-called Drude particles that are connected via harmonic springs to the polarisable non-hydrogen atoms and carry point charges of opposite sign, but same magnitude as their parent atoms. This, however, implies an increased computational cost as both the simulated system size almost doubles and a smaller timestep for integrating the equations of motion must be used, which is one of the reasons that thus far prevented the widespread use of polarisable force fields. Nonetheless, thanks to methodological advancements this started to change.11–14 For instance, with regard to Aβ, the C-Drude 2013 force field15 has been employed to study the unfolding dynamics of the Aβ17–25 fragment16 and the stability of an Aβ42 fibrillar structure.17
Here, we address the question whether polarisable force fields are indeed better at modelling the process of peptide aggregation than their non-polarisable counterparts. To this end, we apply the C-Drude 2019 force field18 to the dimerisation of Aβ16–22. As aggregation pathways are tightly coupled to the conformations of the aggregating entities, we also assess the performance of C-Drude to model the Aβ16–22 monomer. As a reference, we apply the C36m force field to the same problems and use experimental observations to judge the simulation results.7–9
2 Materials and methods
2.1 Simulation details
2.2 Analysis of the simulations
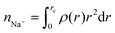 where rc is the cutoff distance; this integration can also be accomplished with the gmx rdf command in combination with its -cn option. The volume density of the sodium ions around Aβ16–22 was calculated using VMD.34
where rc is the cutoff distance; this integration can also be accomplished with the gmx rdf command in combination with its -cn option. The volume density of the sodium ions around Aβ16–22 was calculated using VMD.34The secondary structure assignment has been performed using an in-house script which uses the backbone torsion angles ϕ and ψ. Here, an amino acid is assumed to adopt a β-strand conformation if the (ϕ, ψ) pairs are within the polygon with vertices at (−180°, 180°), (−180°, 126°), (−162°, 126°), (−162°, 108°), (−144°, 108°), (−144°, 90°), (−50°, 90°), and (−50°, 180°). An amino acid is assumed to adopt an α-helical conformation if the (ϕ, ψ) pairs are within the polygon with the vertices at (−90°, 0°), (−90°, − 54°), (−72°, − 54°), (−72°, − 72°), (−36°, − 72°), (−36°, − 18°), (−54°, − 18°), and (−54°, 0°). All other (ϕ, ψ) pairs are assigned as random coil.36
Peptide–water hydrogen bonds were computed using MDAnalysis37,38 by applying a 0.35 nm distance cutoff between the donor and acceptor atoms and a ± 30° angle cutoff for the deviation of the donor-hydrogen-acceptor angle from linearity. In addition, various RDFs of water around selected peptide groups were evaluated and the resulting distributions integrated to obtain hydration numbers, nH2O. To this end, the same tools as applied to the RDF calculations involving Na+ were used.
The translational diffusion constant (D) of the peptide was calculated using the Einstein relation,
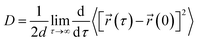 | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0072_20d1.gif) (τ) and
(τ) and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0072_20d1.gif) (0) are the particle positions at time τ and time zero. The angle brackets denote average over time. The quantity in the square brackets is the mean squared displacement (MSD). The MSD was determined using rolling windows with a length of τ = 20 ns time and a lag time of σ = 20 ns, i.e., the next window started where the previous finished. We arrived at this window length and lag time from calculating the normalized autocorrelation function of the squared displacement (SD),39
(0) are the particle positions at time τ and time zero. The angle brackets denote average over time. The quantity in the square brackets is the mean squared displacement (MSD). The MSD was determined using rolling windows with a length of τ = 20 ns time and a lag time of σ = 20 ns, i.e., the next window started where the previous finished. We arrived at this window length and lag time from calculating the normalized autocorrelation function of the squared displacement (SD),39
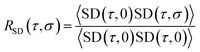 | (2) |
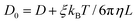 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 297 is a dimensionless constant, η is the solvent viscosity, T is the temperature, kB is the Boltzmann constant, and L is the size of the simulation box.
297 is a dimensionless constant, η is the solvent viscosity, T is the temperature, kB is the Boltzmann constant, and L is the size of the simulation box.
The secondary structure was calculated using the backbone ϕ and ψ angles as explained for the monomer and the results were averaged over both peptides. We used the ATTRANET script, which is available at https://github.com/strodel-group/ATRANET, for calculating the networks. The resulting networks are visualized using Gephi v0.92.43
3 Results and discussion
3.1 Peptide–ion interactions
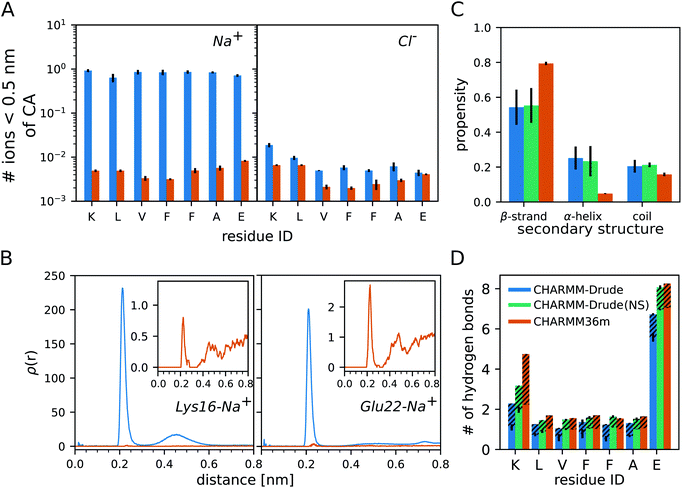
The analysis of the monomer simulations with C-Drude revealed a strong binding of Na+ to Aβ16–22. This is demonstrated by the average number of sodium ions that are within a distance of 0.5 nm from the Cα atoms of the peptide residues (Fig. 1A). The Na+ ions of the C-Drude model interact with Aβ16–22 almost 100 times more frequently than in the case of C36m, which is confirmed by the radial distributions of Na+ around the carbonly-oxygen atoms that are shown in Fig. 1B for K16 and E22 taken as examples. Integrating these radial distributions yields the cumulative sums of Na+ around the carbonly-oxygen atoms (shown in ESI Fig. S3† for K16 and E22) and till a distance of 0.35 nm, which only includes the directly bound Na+, one obtains the numbers shown in Table S2.† Summing up these numbers, we find that about 1.855 Na+ (out of 12) are on average bound to CO of the peptide backbone with C-Drude, while this number is only 0.014 (out of 13 Na+) with C36m. These numbers are a lower bound for the number of peptide-bound Na+ as they ignore the ion binding to other parts of the peptide, such as the termini and side chains. In the case of E22, binding to the side chain is of particular relevance, which can be seen from the volumetric isosurface of the sodium ions around the Aβ16––22 peptide and their radial distributions for the side chains of K16 and E22 (ESI Fig. S4†). Therefore, about 2 Na+ (out of 12 in total) are bound to Aβ16–22 when modelled with C-Drude, whereas this number is only ≈ 0.02 (out of 13 Na+) for C36m.In order to assess which of the two peptide–Na+ binding predictions better reflects reality, we referred to experimental findings. For instance, using conductivity measurements it was shown for RNase A, a protein with 124 residues, that one protein molecule binds one to two Na+ ions.44 However, a direct comparison to the current study is difficult. The salt concentrations in the cited experimental work on RNase A was only 1 mM to 45 mM, which is 3 to 100 times less than the concentration of 150 mM used in our simulations. Thus, the higher salt concentrations in our work might lead to higher Na+ binding. This, on the other hand, is not supported by the work on RNase A as the sodium-ion binding to RNase binding did not increase much beyond NaCl concentrations of 25 mM. Another complicating fact is the different size of the two proteins, with RNase A having about 18 times more residues than Aβ16–22 and 9 times more negatively charged residues, which play an important role in Na+ binding.44 Based on this one might expect an order of magnitude fewer Na+ being bound to Aβ16–22 than to RNase A, suggesting that C-Drude overestimates the sodium-ion binding to the peptide. This is supported by a study by Abelein et al. who performed a series of 1H–15N-heteronuclear single quantum spectra (HSQC) of Aβ1–40 at 0, 50, 100, and 150 mM NaF to characterize the effect of ionic strength on the amyloid-β peptide.45 They observed only minute changes to the chemical shift spectra indicating that no significant Na+ binding occurred on an intermediate exchange rate. This result is further verified by other MD studies of Aβ that found no significant Na+ binding,46–48 which is in line with our C36m results.
A large accumulation of ions around protein surfaces has been previously reported for C-Drude.49 Although the ion–protein interactions have been updated in the C-Drude 2019 force field18 used here, we still find a strong Na+ accumulation around the Aβ16–22 peptide. The overestimation of ion–peptide interactions with C-Drude is limited to the cation, as the numbers of bound Cl− are similar, yet still somewhat larger with C-Drude (Fig. 1A).
3.2 Structure of the monomeric Aβ16–22 peptide
Next, we assess the secondary structure adopted by the monomeric Aβ16–22 peptide, where we considered the possibility that the overestimated Na+–peptide binding in the C-Drude simulations can affect the peptide structure and therefore repeated the 3 × 1 μs simulations without NaCl being added. We determined the secondary structure based on the ϕ and ψ angles of the peptide backbone. This allows us to separate random coil structures into extended structures falling into the β-basin of the Ramachandran space and more collapsed random coil structures, which is not possible if one uses a method that assigns secondary structures based on hydrogen bonds (H-bonds). Independent of the force field and whether or not NaCl is present, monomeric Aβ16–22 prefers to adopt extended β-strand conformations (Fig. 1C). However, with C-Drude the β-strand propensity is ≈ 15% less than with C36m. Instead, Aβ16–22 has an increased tendency for ϕ and ψ to adopt conformations that fall into the α-helix basin. With a helix propensity of about 20%, C-Drude stabilises helices in Aβ16–22 more than other force fields do.5,6 This gives rise to more intrapeptide contacts between residues that are further away from each other, including the K16–E22 salt bridge, as the contact map analysis in ESI Fig. S5† reveals.The removal of NaCl has no effects on the structural preferences of the peptide modelled by C-Drude. This is different from the results of Ngo et al. who found that Drude polarisable ions induced conformational changes in model peptides, as opposed to the CHARMM non-polarisable ion models that had no effects.49 Their observation was with the C-Drude 2013 force field, while we used the revised C-Drude 2019 force field, where the effects caused by the ions are already smaller despite the still too strong Na+–peptide binding.
3.3 Peptide–water interactions
A consequence – or cause – of the altered secondary structure propensities are changes in the number of H-bonds that formed between the peptide and water (Fig. 1D). For all of the residues, C36m predicts more H-bonds than C-Drude does, in particular for K16 where more than twice as many H-bonds are modelled with C36m, which explains the higher preference for intrapeptide contacts found with C-Drude. However, in the absence of NaCl the H-bond numbers obtained with C-Drude are very similar to those obtained with C36m (with salt). K16 is the only residue where the difference remains quite large. To understand the sources of the disparate H-bond propensities, we distinguished between the peptide residues acting as hydrogen donor (via backbone NH or side-chain NH3+ groups, dashed areas in Fig. 1D) or as hydrogen acceptor (via backbone CO or side-chain COO− groups, solid areas in Fig. 1D). Two observations can be made. First, if C-Drude was applied in the presence of NaCl, it is the number of H-bonds where the peptide provides the hydrogen acceptor that is being reduced compared to C36m and also C-Drude without salt. This implies that Na+ and H2O compete for interaction with CO and COO−. This is supported by the radial distributions of the H atoms of water around the O atoms of E22 (ESI Fig. S6†). For both the backbone and side chain, the radial distributions with C-Drude (with NaCl) are smaller than for C36m (with salt), while it was the other way round for ρ(r) of Na+ with respect to CO of E22 (Fig. 1B). This changes in the C-Drude simulation without NaCl; here the radial distribution with respect to CO of E22 is similar to that from the C36m simulation and even higher for the COO− group. However, the latter finding only applies to the first peak of ρ(r) (ESI Fig. S6†), while the second peak with C36m is higher and appears at a smaller distance. Surprisingly, the difference in the heights of the peaks cancel each other for C-Drude without salt and C36m, leading to the same number of H-bonds.The second finding is that in the case of K16, the number of H-bonds with K16 serving as hydrogen donor is larger for C36m than for C-Drude, independent of whether or not NaCl was included in the simulation. This difference is also reflected in the corresponding radial distributions of the O atoms of water around the NH group of the backbone and the NH3+ group of the side chain of K16 (ESI Fig. S7†). Importantly, we observe that the location of the first minimum of ρ(r), corresponding to the end of the first solvation shell, is shifted to surprisingly larger distances with C-Drude compared to with C36m: to ≈ 0.37 nm versus ≈ 0.27 nm for the backbone NH and to ≈ 0.27 nm versus ≈ 0.23 nm for the side-chain NH3+. This results in coordination numbers, calculated from the volume integrals of the RDFs, of nH2O = 2.2 with C-Drude and nH2O = 0.9 with C36m around NH and nH2O = 5.1 with C-Drude and nH2O = 1.3 with C36m around NH3+. That is, C-Drude yields a higher hydration around the K16, which is in line with a recent report49 but is contrary to our H-bond results. However, at the cutoff distance of 0.35 nm applied during the H-bond analysis, C-Drude yields fewer number of water molecules around the NH group (1.8 for C-Drude and 1.9 for C36m), whereas the same number of water molecules results for the NH3+ group (4.2 for both force fields). The considerably smaller number of H-bonds between K16 acting as H-bond donor and water seen for C-Drude can thus not be explained by the larger distance between K16 and the first solvation shell adopted in this force field. However, it can be concluded that the first solvation shell around the NH group of K16 is not correctly modelled with C-Drude, as the NH–water distance is too large. This seems to be a particular effect of the positively charged residue causing this, because for F19, E22 and also the C-terminal capping group, the radial distributions of water around NH are very similar for C36 and C-Drude (Fig. S7†). Moreover, these distributions are not affected by the presence of NaCl.
In addition to the general hydration when testing for the existence of H-bonds, one also needs to analyse the donor(D)–H–acceptor(A) angles. Since this might further explain the different H-bond numbers generated by C-Drude and C36m for the water–Aβ16–22 interactions, we calculated the probability distribution of the D–H–A angle at the cutoff D–A distance of 0.35 nm (ESI Fig. S8†). An H-bond is typically assumed to be present when this angle deviates less than 30° from linearity, which is indicated by a dashed line for 150° in ESI Fig. S8.† Because of symmetry, only the results between 0 and 180° are shown. In the case of the peptide providing the acceptor groups, the distribution profiles are very similar, with a higher density obtained with C36m and C-Drude without NaCl compared to C-Drude with NaCl for angles >100° and a lower one for C36m compared to both C-Drude with and without NaCl for angles below 100°. Therefore, the smaller H-bond numbers modelled with C-Drude (with NaCl) for the peptide residues as acceptors have two causes: a generally lower hydration around CO and COO− groups as well as a preference of D–H–A angles deviating considerably from linearity. Both can be explained to a large extent by Na+ occupying the same position that the H atoms of H2O would like to fill. The larger deviation from linearity also plays a role for the H-donating NH and NH3+ groups of the peptide, where the N–H–OH2 angles around 100° are considerably more populated when C-Drude (with and without NaCl) was applied, while the C-Drude angle probability is decreased for > rbin150° but also for ≈ 50°. Since in these cases the different H-bond numbers could neither be explained by the presence of Na+ nor the general hydration levels, the conclusion is that there seem to be problems with the orientation of the Drude particle representing the lone pairs of the water oxygen atom in the N–H···OH2 H-bonds, explaining the smaller number of H-bonds counted in these cases.
Finally, we analysed the effects of the water model and the peptide–water interactions on the translational diffusion constant of monomeric Aβ16–22 (Table 1), which was reported to have an experimental value 0.353 × 10−5 cm2 s−1.50 The predictions from the C-Drude simulations are closer to the experimental value. This is mainly due to the fact that the viscosity of the SWM4-NDP water model is closer to the real water viscosity than that of the CHARMM-modified TIP3P water model. The presence of NaCl does not alter the translational diffusion constant predicted by the C-Drude force field. When correcting for the differently underestimated viscosities of the water models by scaling the translational diffusion constants by 1/2.81 for C36m and by 1/1.29 for C-Drude,25,51 C36m predicts a diffusion constant that is closer to the experimental value. This suggests that C36m provides a better description of the peptide–water interactions. Nonetheless, the overestimation of the peptide's translational diffusion when TIP3P is used as a water model is likely to have an impact on the aggregation speed of Aβ16–22, which requires further investigation.
| D0 (10−5 cm2 ns−1) | |
|---|---|
| CHARMM-Drude | 0.260 ± 0.002 [0.202 ± 0.002] |
| CHARMM-Drude NS | 0.267 ± 0.009 [0.208 ± 0.007] |
| CHARMM36m | 0.870 ± 0.010 [0.309 ± 0.004] |
3.4 Dimerisation of Aβ16–22
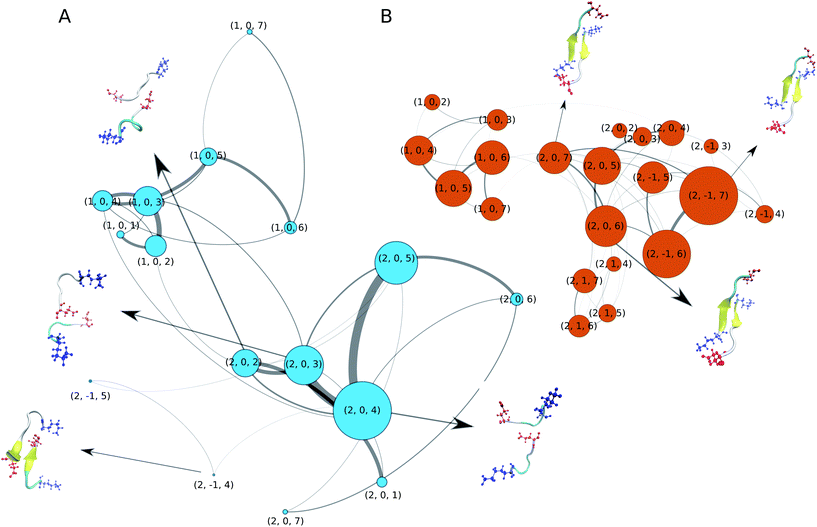
We now turn our attention to the dimerisation of Aβ16–22. In our previous study we analysed this process in detail based on a 10 μs MD simulation that employed a variant of the C36m force field that employs increased protein–water interactions.52 To elucidate the aggregation pathway we calculated Markov state models and transition networks (TNs), finding the latter to reveal more information. Therefore, we apply the same analysis method here. For building the TNs, we characterised the conformation of each MD snapshot using three descriptors: (i) the oligomer size (1 or 2), (ii) the nematic order parameter of the alignment of the two Aβ16–22 peptides with respect to each other (−1 for antiparallel, 0 for disordered, and 1 for parallel), (iii) the peptide-averaged number of residues in β-strand configuration based on ϕ and ψ (from 0 to 7). The resulting TNs are shown in Fig. 2A and B for C-Drude and C36m, respectively. Both TNs contain a few nodes that represent unbound monomers of different secondary structure, reproducing the structural preferences seen for the single peptide (Fig. 1C). With C36m, there are more monomers that adopt extended structures. Interestingly, these are the monomer states that preferentially associate and form an initial dimer state, which is represented by node (2, 0, 7) where the β-strands are not properly aligned yet. This state evolves to antiparallel β-sheets, which are contained in nodes (2, −1, 6) and (2, −1, 5). This observation agrees with our previous findings52 and is consistent with the antiparallel β-sheet architecture of Aβ16–22 fibrils.9 The antiparallel alignment is achieved by hydrophobic interactions between residues L17–A21 and salt bridges between K16 and E22. These terminal salt bridges can stabilise an off-register β-sheet, as the representative dimer structures in Fig. 2B show. However, the longer simulations in our previous study revealed that these off-register β-sheets eventually transform into in-register β-sheets that are compatible with the fibril structure.52The dimers and aggregation pathways found with C-Drude are largely different from those produced by C36m (Fig. 2A). C-Drude yields mostly disordered dimers without alignment between the peptides and without β-sheet formation. As for the monomer, the polarisable force field predicts a lower tendency for extended structures. As a result, node (2, 0, 4) corresponds to the most populated state. The representative structure for that node and the one for node (2, 0, 3) show that not many interpeptide contacts are formed in these dimers, especially not between the hydrophobic residues that are known to be of high importance for the aggregation of Aβ16–22.7 Moreover, there were also almost no interpeptide salt bridges established between K16 and E22. Due to the missing hydrophobic and salt–bridge interactions, hardly any β-sheets were formed. The two states where (antiparallel) β-sheets are present, (2, −1, 4) and (2, −1, 5), are only marginally populated and the β-sheets are off-register by 2 or 3 residues.
In order to check if the strong Na+ binding modelled by C-Drude affects the aggregation behavior, we run an additional 3 × 1 μs dimer simulations for the C-Drude force field without the presence of NaCl. The resulting TN (ESI Fig. S9†) shows that also without the presence of the sodium ions, the C-Drude force field predicts disordered dimers. This result suggests that the discrepancies of the aggregation behaviour of the Aβ16–22 peptide modelled with the C-Drude force field from that simulated with C36m and also from the experimental observations originate from the protein and water force field parameters but not from the too strong Na+ binding.
4 Conclusions
The question we set out to answer was whether the inclusion of electronic polarisation in the force field would increase the accuracy of the modelling of amyloid aggregation. Based on the experimental data that is available for the structures of the Aβ16–22 amyloid fibrils9 and the intermediates aggregates,8 our conclusion is that C-Drude does not provide a correct model of the Aβ16–22 monomer and its dimerisation. Bera et al. followed the assembly of Aβ16–22 over time using circular dichroism (CD) spectroscopy.8 The initial peptide structure is a random coil conformation, which agrees to our findings made with C36m for the monomer. Even though we assigned this as a β-strand as the Aβ16–22 peptide adopts a mostly extended random coil structure, there is no β-sheet present in the monomer.52 The CD spectrum of Aβ16–22 is devoid of α-helical traces, also during the aggregation process,8 which renders the C-Drude model of Aβ16–22 as less accurate than that of C36m. The results of Bera et al. further show that the complete transition from random coil to β-sheet is a slow process, taking hours,8 which suggests that C36m may overestimate the amyloid aggregation speed by predicting Aβ16–22 to almost directly develop into an antiparallel β-sheet. The higher aggregation rate is thought to be linked to the increased translational diffusion of Aβ16–22 modelled by C36m, a known problem of the TIP3P water model used together with C36m (Table 1).53 On the other hand, the Thioflavin T (ThT) fluorescence assay of Aβ16–22 amyloid aggregation shows that this process takes place without a lag time because there is already substantial ThT fluorescence present at time zero.8 This indicates that a certain amount of amyloid fibrils are formed instantly, while the transformation of all peptides into the amyloid fold requires hours.Based on these various considerations we conclude that C36m provides a better model of Aβ16–22 and its aggregation than C-Drude does. This conclusion is further supported by the fact that with C36m the aggregation end product, i.e., Aβ16–22 fibrils are stable when being simulated. In our previous study, where we tested different nonpolarisable force fields for their ability to simulate the aggregation of Aβ16–22, the force fields that failed to model the dimerisation of Aβ16–22 into an antiparallel β-sheet, also failed in modelling stable fibrillar structures.6 Nonetheless, it remains to be shown whether or not C-Drude is able to model the fibrillar Aβ16–22 structure. Though we anticipate problems there, given that C-Drude overestimates the helical propensity of Aβ16–22, while not being successful in simulating the formation of hydrophobic contacts and salt bridges between the peptides. On the other hand, this expectation might also be wrong as in the context of 1,3,5-trisamidocyclohexane self-assembly into long ordered fibers, it has been found that while the C-Drude force field failed to model the dimerisation of this molecule, the simulations that started from pre-ordered fibrils yielded stable structures.54 Nonetheless, a further simulation study that also identified shortcomings of the C-Drude force field should be mentioned.55 In that study, the reorganisation energies between stable structures of the serine dipeptide were determined with C-Drude and compared to the respective quantum mechanical energies. C-Drude was not successful to correctly model the peptide's structural preferences 55. We can therefore conclude that the inability of C-Drude to correctly capture the behaviour of Aβ16–22 as a monomer and dimer is not limited to this peptide. Further studies using preformed Aβ16–22 fibrils and other peptides will be required to fully understand C-Drude's capability of modelling aggregation.
In summary, in its current state, the C-Drude force field is not suitable yet for modelling the aggregation of the Aβ16–22 peptide. A main problem of this force field that we identified here is an overbinding of Na+, which leads to an underestimation of the H-bonding with water when water and Na+ compete for the same interaction sites at the peptide. For the positively charged K16 there seems to a be problem of the orientation of the lone pairs of the oxygen atom of water with respect to the NH3+ group, leading to an underreporting of H-bonds that is independent of the presence of Na+. Moreover, for both charged peptide residues, we spotted deviations between C-Drude and C36m with regard to the preferred distances between the respective side-chain terminal and water. The reduced H-bond propensity between peptide and water gives rise to more intrapeptide residue–residue contacts and in turn affects the structures of the Aβ16–22 aggregates.
However, this is not to say that the inclusion of electronic polarisation is the culprit here: C-Drude contains further energy terms (atomic polarisability and Thole screening factors)11 that could also influence the delicate balance between the peptide–water and peptide–peptide interactions. We are still convinced that only the inclusion of polarisability will lead to an improved description of peptide aggregation, but several rounds of reparameterisations are expected to be required to obtain a polarisable force field that can accurately model the different protein forms, such as folded and unfolded proteins, as well as conformational transitions, including protein folding and aggregation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Jennifer Loschwitz and Mohammed Khaled for fruitful discussions. Computing resources granted by RWTH Aachen University under project rwth0565 are gratefully acknowledged.Notes and references
- P. H. Nguyen, A. Ramamoorthy, B. R. Sahoo, J. Zheng, P. Faller, J. E. Straub, L. Dominguez, J.-E. Shea, N. V. Dokholyan and A. De Simone, et al., Chem. Rev., 2021, 121, 2545–2647 CrossRef CAS PubMed.
- B. Strodel, Curr. Opin. Struct. Biol., 2021, 67, 145–152 CrossRef CAS PubMed.
- A. Paul, S. Samantray, M. Anteghini, M. Khaled and B. Strodel, Chem. Sci., 2021, 12, 6652–6669 RSC.
- M. Carballo-Pacheco, A. E. Ismail and B. Strodel, J. Chem. Theory Comput., 2018, 14, 6063–6075 CrossRef CAS PubMed.
- V. H. Man, X. He, P. Derreumaux, B. Ji, X.-Q. Xie, P. H. Nguyen and J. Wang, J. Chem. Theory Comput., 2019, 15, 1440–1452 CrossRef PubMed.
- S. Samantray, F. Yin, B. Kav and B. Strodel, J. Chem. Inf. Model., 2020, 60, 6462–6475 CrossRef CAS.
- F. T. Senguen, T. M. Doran, E. A. Anderson and B. L. Nilsson, Mol. BioSyst., 2011, 7, 497–510 RSC.
- S. Bera, E. Arad, L. Schnaider, S. Shaham-Niv, V. Castelletto, Y. Peretz, D. Zaguri, R. Jelinek, E. Gazit and I. W. Hamley, Chem. Commun., 2019, 55, 8595–8598 RSC.
- J. J. Balbach, Y. Ishii, O. N. Antzutkin, R. D. Leapman, N. W. Rizzo, F. Dyda, J. Reed and R. Tycko, Biochemistry, 2000, 39, 13748–13759 CrossRef CAS.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. De Groot, H. Grubmüller and A. D. MacKerell, Nat. Methods, 2017, 14, 71–73 CrossRef CAS PubMed.
- J. A. Lemkul, Progress in Molecular Biology and Translational Science, Elsevier, 2020, vol. 170, pp. 1–71 Search PubMed.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht and R. A. DiStasio Jr, et al., J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- Y. Shi, Z. Xia, J. Zhang, R. Best, C. Wu, J. W. Ponder and P. Ren, J. Chem. Theory Comput., 2013, 9, 4046–4063 CrossRef CAS PubMed.
- A. M. Salsbury and J. A. Lemkul, Curr. Opin. Struct. Biol., 2021, 67, 9–17 CrossRef CAS PubMed.
- P. E. M. Lopes, J. Huang, J. Shim, Y. Luo, H. Li, B. Roux and A. D. MacKerell, J. Chem. Theory Comput., 2013, 9, 5430–5449 CrossRef CAS PubMed.
- J. A. Lemkul, J. Huang and A. D. MacKerell Jr, J. Phys. Chem. B, 2015, 119, 15574–15582 CrossRef CAS.
- D. S. Davidson, A. M. Brown and J. A. Lemkul, J. Mol. Biol., 2018, 430, 3819–3834 CrossRef CAS PubMed.
- F.-Y. Lin, J. Huang, P. Pandey, C. Rupakheti, J. Li, B. Roux and A. D. MacKerell Jr, J. Chem. Theory Comput., 2020, 16, 3221–3239 CrossRef CAS PubMed.
- L. L. C. Schrödinger, The PyMOL Molecular Graphics System, Version 1.8, 2015 Search PubMed.
- A. A. Kognole, J. Lee, S.-J. Park, S. Jo, P. Chatterjee, J. A. Lemkul, J. Huang, A. D. MacKerell Jr and W. Im, J. Comput. Chem., 2022, 43, 359–375 CrossRef CAS PubMed.
- W. Jiang, D. J. Hardy, J. C. Phillips, A. D. MacKerell Jr, K. Schulten and B. Roux, J. Phys. Chem. Lett., 2011, 2, 87–92 CrossRef CAS PubMed.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- G. Lamoureux, E. Harder, I. V. Vorobyov, B. Roux and A. D. MacKerell Jr, Chem. Phys. Lett., 2006, 418, 245–249 CrossRef CAS.
- Y. Luo, W. Jiang, H. Yu, A. D. MacKerell and B. Roux, Faraday Discuss., 2013, 160, 135–149 RSC.
- H. Yu, T. W. Whitfield, E. Harder, G. Lamoureux, I. Vorobyov, V. M. Anisimov, A. D. MacKerell Jr and B. Roux, J. Chem. Theory Comput., 2010, 6, 774–786 CrossRef CAS PubMed.
- F.-Y. Lin, P. E. Lopes, E. Harder, B. Roux and A. D. MacKerell Jr, J. Chem. Inf. Model., 2018, 58, 993–1004 CrossRef CAS PubMed.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan and C. D. Stern, et al., PLoS Comput. Biol., 2017, 13, e1005659 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- A. D. MacKerell Jr, D. Bashford, M. Bellott, R. L. Dunbrack Jr, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo and S. Ha, et al., J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- S. Páll, M. J. Abraham, C. Kutzner, B. Hess and E. Lindahl, International Conference on Exascale Applications and Software, 2014, pp. 3–27 Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernández, C. R. Schwantes, L.-P. Wang, T. J. Lane and V. S. Pande, Biophys. J., 2015, 109, 1528–1532 CrossRef CAS.
- M. H. Viet, S. T. Ngo, N. S. Lam and M. S. Li, J. Phys. Chem. B, 2011, 115, 7433–7446 CrossRef CAS.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, J. Domanski, D. L. Dotson, S. Buchoux, I. M. Kenney and O. Beckstein, 2019.
- G. Pranami and M. H. Lamm, J. Chem. Theory Comput., 2015, 11, 4586–4592 CrossRef CAS PubMed.
- B. Dünweg, J. Chem. Phys., 1993, 99, 6977–6982 CrossRef.
- B. Dünweg and K. Kremer, J. Chem. Phys., 1993, 99, 6983–6997 CrossRef.
- I.-C. Yeh and G. Hummer, J. Phys. Chem. B, 2004, 108, 15873–15879 CrossRef CAS.
- M. Bastian, S. Heymann and M. Jacomy, Gephi: An Open Source Software for Exploring and Manipulating Networks, 2009, http://www.aaai.org/ocs/index.php/ICWSM/09/paper/view/154 Search PubMed.
- L. Vrbka, J. Vondrášek, B. Jagoda-Cwiklik, R. Vácha and P. Jungwirth, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15440–15444 CrossRef CAS PubMed.
- A. Abelein, J. Jarvet, A. Barth, A. Gräslund and J. Danielsson, J. Am. Chem. Soc., 2016, 138, 6893–6902 CrossRef CAS PubMed.
- M. D. Smith and L. Cruz, J. Phys. Chem. B, 2013, 117, 6614–6624 CrossRef CAS.
- M. D. Smith and L. Cruz, J. Phys. Chem. B, 2013, 117, 14907–14915 CrossRef CAS.
- D. Huraskin and A. H. Horn, J. Mol. Model., 2019, 25, 1–11 CrossRef CAS.
- V. A. Ngo, J. K. Fanning and S. Y. Noskov, Adv. Theory Simul., 2019, 2, 1800106 CrossRef.
- J. Danielsson, J. Jarvet, P. Damberg and A. Gräslund, Magn. Reson. Chem., 2002, 40, S89–S97 CrossRef CAS.
- E. E. Ong and J.-L. Liow, Fluid Phase Equilib., 2019, 481, 55–65 CrossRef CAS.
- A.-M. Illig and B. Strodel, J. Chem. Theory Comput., 2020, 16, 7825–7839 CrossRef CAS PubMed.
- Y. Mao and Y. Zhang, Chem. Phys. Lett., 2012, 542, 37–41 CrossRef CAS.
- T. K. Piskorz, A. De Vries and J. H. Van Esch, J. Chem. Theory Comput., 2021, 18, 431–440 CrossRef PubMed.
- G. König and S. Riniker, Interface Focus, 2020, 10, 20190121 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Simulation details Table S1, Fig. S1–S2, diffusion results. See https://doi.org/10.1039/d2ra01478e |
| This journal is © The Royal Society of Chemistry 2022 |