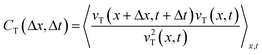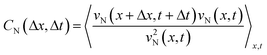Collective motion of epithelial cells along a wrinkled 3D-buckled hydrogel

Abstract

Epithelial cells migrate autonomously by aligning and inducing a collective motion. Controlling the collective motion of epithelial cells in geometrically confined environments is important for understanding physiological processes such as wound healing and self-organized morphogenesis. However, collective migration under a three-dimensional (3D) curved surface resembling living epithelial tissue has not yet been explored. In this study, we investigated the collective motion of a 3D-buckled polyacrylamide (PAAm) gel that mimics the shape of folds and wrinkles of epithelial tissue to understand the geometric effects of collective motion. We found that the velocity correlation in the space near the hydrogel boundary showed a periodic change that correlated with the wrinkled folding of the hydrogel pattern. Furthermore, the characteristic length of the velocity correlation increased proportionally with the wavelength of wrinkled folding. These observations indicated that the hydrogel pattern could steer the collective motion of epithelial cells over long distances. Our study also suggests that the wrinkled design of the hydrogel is a versatile platform for studying the geometric effect of a curved surface on complex epithelial cell dynamics.

---

Introduction

Active matter showing autonomous motion while consuming energy has attracted considerable attention for understanding out-of-equilibrium dynamics,^1,2 which are common to a wide variety of materials, including swimming bacteria,^3,4 cytoskeletons driven by motor proteins,^5,6 epithelial cells,^7,8 active colloidal particles,⁹ and swimming droplets.¹⁰ One of the most important properties inherent in the active matter is that collective motions appear with an ordered velocity correlation in space and time as the density increases.^11,12 With polar interactions, in which the direction of motion is aligned parallel among self-propelling particles, active turbulence,¹³ vortex pairing,¹⁴ vortex lattices,¹⁵ and the jammed phase¹⁶ appear in their collective motion. The emergence of these out-of-equilibrium structures, induced by the autonomous motion and orientation interaction of dense active matter, is a unique characteristic distinct from that of conventional passive materials.

A fascinating property of a group of active matter is the geometry-induced self-organization in collective motion; in the collective motions of epithelial cells, emergent vortices have a characteristic size.^17–22 The control of collective motion under such designed boundaries has also enabled the discovery of geometrical rules governing ordered structures. For instance, a single active vortex of microswimmers can be extracted when boundary conditions comparable to this size are imposed on swimmer suspensions,⁴ and the control of the active vortex lattice has been studied using microdevices in a two-dimensional plane.^3,6,14 The geometry of collective dynamics can provide essential insights into how cells and microswimmers spontaneously form ordered structures. The geometrical rule that controls the formation of vortex pairs with the same and opposite rotation directions was also clarified. A detailed understanding of active matter has been obtained by revealing how these active vortexes interact with theoretical models.^4,14 However, most previous experiments were conducted in ideal artificial environments, such as two-dimensional flat surfaces with rigid substrates. In the case of collective motion exhibited by epithelial cells, more complex geometries, not just in the two-dimensional plane, would also propagate their biological self-organization in living tissues.

On a three-dimensionally deformed substrate, cells can be mechanically stimulated according to the curvature of the substrate, leading to cell orientation and differentiation. Since the surface geometry of multicellular morphogenesis is a three-dimensional (3D) constraint with viscoelastic properties, exploring the self-organized collective motion of epithelial cells under a curved elastic substrate^23–25 is needed to further understand the physical basis of tissue mechanics. In particular, structures such as wrinkles and folds are often formed upon tissue swelling and local proliferation. The geometric dependence of their collective dynamics under complex curved confinement can be analyzed by determining how cells exhibit collective dynamics in motion and morphology while under the wrinkled structures of epithelial tissues.

In this study, we fabricated a 3D-buckled hydrogel film with a wrinkled surface deformation similar to that of biological tissues. A thin film of polyacrylamide (PAAm) gel, whose swelling and mechanical properties can be controlled, was used as a substrate model for cell culture. By partially bonding the PAAm gel film to a glass substrate and subsequently swelling it, a 3D-folded structure based on buckling instability can be easily and reproducibly obtained.²⁶ The 3D-buckled hydrogel was then used to analyze the collective motion of Madin–Darby canine kidney (MDCK) epithelial cells under 3D spatial confinement. We found that the velocity of collective motion was affected by the periodic pattern of the wrinkled structure near the wrinkled patterns. Furthermore, the wrinkled pattern of the hydrogel extended the velocity correlation of the collective movement and enabled the formation of emergent patterns aligned over a longer distance. Such a spatial correlation in collective motion may be relevant for guiding a group of epithelial cells and their complex morphogenesis during development.

Materials and methods

Chemical reagents

3-(Trimethoxysilyl)propyl methacrylate (TMSPMA), as a covalent anchor between the PAAm gel and the glass substrate, was purchased from Sigma-Aldrich. Acrylamide (AAm), as a monomer for PAAm gel, N,N′-methylenebis[acrylamide] (MBAA), as a cross-linker for PAAm gels, and lithium phenyl (2,4,6-trimethylbenzoyl)phosphinate (LAP), as a UV initiator for the polymerization, were purchased from Tokyo Kasei Co., Ltd. Fluorescein o-acrylate (FL), as a fluorescent monomer for visualizing hydrogel 3D morphology, was purchased from Sigma-Aldrich. Sulfosuccinimidyl 6-(4′-azido-2′-nitrophenylamino)hexanoate (sulfo-SANPAH), as a heterobifunctional cross-linker for the surface modification of the hydrogels to attach cells, and type I collagen, as an extracellular matrix (ECM), were purchased from Sigma-Aldrich. The chemicals used in this study were used as received without further purification.

3D Buckled hydrogel fabrication

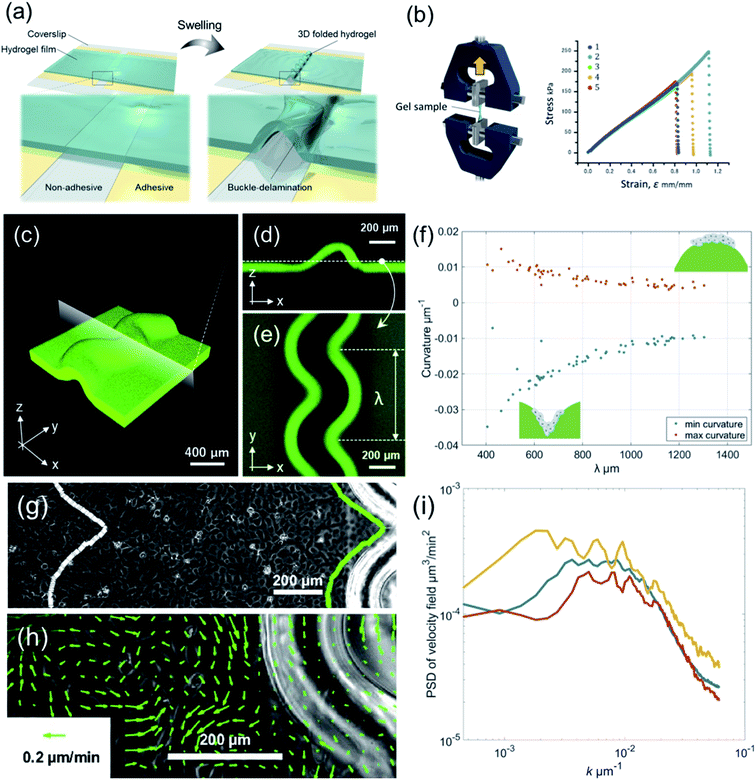
3D-Buckled hydrogels were fabricated as described previously.^26,27 Briefly, cleaned coverslips (18 × 18 mm) were chemically modified with TMSPMA to covalently bind the coverslips to hydrogels. Striped silanized coverslips (400–1400 μm-wide line pattern) were obtained using conventional photolithography and oxygen plasma etching. The reaction cell was assembled by attaching a 60 μm-thick Scotch tape (4 mm-wide, 3 M) as a spacer between the cleaned coverslip and the silanized coverslip. Next, 18 μL of the pre-gel solution containing 4 M AAm, 0.04 M MBAA, 0.004 M LAP, and 0.05 wt% FL in pure water was injected into the reaction cell. After UV light irradiation (5.4 mW cm⁻²) at 365 nm for 3 min (HLDL-150UV365, CCS Inc.), the PAAm gel/coverslip layer composite with interfacial adhesion defined by the TMSPMA pattern was prepared. Finally, the composites were immersed in a large amount of pure water to form wavy folds with buckling instabilities (Fig. 1(a)).

Fig. 1 Epithelial cell monolayer on 3D-buckled hydrogel. (a) Schematic of a 3D-buckled hydrogel. (b) Mechanical properties of PAAm gel. (b, left) Schematic of tensile testing and tensile stress–strain curves of PAAm gel. (b, right) Young’s modulus was calculated from the initial slope of the plot for each sample. (c–e) Fluorescent microscopic images of the 3D-buckled hydrogel. Representative folded pattern with a peeling width of 600 μm and crosslinking density of 1 mol%. The wavelength λ is defined as the peak-to-peak distance. (f) The mean curvature of the concave (blue) and convex (red) sides of the wrinkled patterns with various wavelengths λ. (g) Microscopic image of MDCK epithelial cell monolayer far from the wrinkled patterns (white line) and near the wrinkled patterns (green line). Scale bars: 200 μm. (h) Velocity field of collective motion of MDCK cells near the wrinkled patterns. Green arrows indicate the velocity field v(x,t). (i) Power spectrum density (PSD) of the velocity field of MDCK cells, analyzed using the velocity field at a point far from the wrinkled pattern of the hydrogel. The data from three independent experiments are shown as different colored curves.

The elastic modulus of the PAAm gel used in this study was evaluated using uniaxial tensile tests. Uniaxial tensile tests were performed on a water-swollen PAAm gel using a tensile-compressive tester (STB-1225S, A&D Co. Ltd.). All the samples were cut into specific dimensions of 12 × 2 × 0.75 mm; the gauge length was 12 mm. All the samples were stretched along their lengths at an extension rate of 100 mm min⁻¹. The tensile strain ε is defined as (l − l₀)/l₀, where l₀ and l are the lengths of the gel before and during elongation, respectively. The resulting elastic modulus is 218 kPa (Fig. 1(b)).

Cell culture

Prior to the spreading and growth of cell culture, type-I collagen was immobilized on the surface of the 3D-buckled hydrogels using sulfo-SANPAH. The gel surface was covered with 200 μL of 2 mM sulfo-SANPAH solution. The solution was then irradiated with UV light at 365 nm for 10 min to allow it to react chemically with the gel surface. Subsequently, 200 μL of type-I collagen solution (0.3 wt%) was added to the gel surfaces, which were incubated at room temperature for 1 h. Finally, the gel surface was washed three times with pure water and incubated in the culture medium at 37 °C for 1 h.

The epithelial cells used in this study were MDCK cells (NBL-2, JCRB9029), grown at 37 °C in a CO₂ incubator with 5% CO₂ and 90% humidity. The growth medium used was Dulbecco’s modified Eagle’s medium (11965092, Thermo Fisher Scientific) supplemented with 10% fetal bovine serum (173012, NICHIREI Biosciences). The cell density was determined using a cell counter (TC20, Bio-Rad). For inverted microscopic observations, we used a glass-bottom dish (φ35 mm, IWAKI) for the chamber.

Microscopy

Time-lapse recordings of the collective motion of the MDCK cell monolayer were obtained at intervals of 5 min for 72 h. An inverted fluorescent microscope (IX73, Olympus) equipped with a CMOS camera (Zyla, Andor Technology) was used with a phase-contrast imaging setup. The temperature of the microscopic stage was maintained at 37 °C, and the concentration of CO₂ gas was maintained at 5% using a stage-top cultivation chamber (STXG-IX3WX, TOKAI-Hit). The geometric pattern of the hydrogel was determined by visualizing the green fluorescent dye inside it. The microscopic stage was motorized with a BIOS-Light driver (Sigma Koki), and the multipoint acquisition was performed using the Metamorph software. All microscopic images were analyzed, and image processing and calculation of the autocorrelation function were performed using MATLAB software. In particular, we carried out particle image velocimetry (PIV) analysis using ImageJ software with iterative PIV-plugin to obtain the velocity field of collective motion of MDCK cells. The size of the captured images used in PIV was 4160 μm on the vertical axis and 3510 μm on the horizontal axis, the interrogation window size was 20.5 μm and the search window size was 61.5 μm. The correlation threshold of iterative PIV was set at 0.60.

Statistical analysis

Statistical analysis was performed using MATLAB software. The p-values were determined using Student’s t-test. The p-value threshold for statistical significance is 0.05. We also performed the Jarque–Bera test to confirm that the data set used for Student’s t-test can be assumed as a normal distribution.

Results

When the PAAm hydrogel film swelled in the adhesion-free area, it detached and formed wavy folds with buckling instability (Fig. 1(a)). We used this 3D-buckled hydrogel with periodically deformed wrinkles to investigate the effect of curved boundaries on the collective motion of epithelial cells. To determine the outline of the hydrogel folds by projecting them onto a two-dimensional plane, we added a green fluorescent monomer to the PAAm hydrogel (Fig. 1(c)) and extracted the boundary shape of the wrinkled patterns using a fluorescence microscope (Fig. 1(d) and (e)). We binarized the image of the hydrogel wrinkling pattern to determine the boundaries where the deformation started. The wavelengths of these wrinkled folds were evaluated using the peak-to-peak distance λ (Fig. 1(e)). The hydrogels used in this study had periodic wrinkle designs from λ = 405.4 μm (peeling width 400 μm) to 1303.5 μm (peeling width 1400 μm). In addition, the height of the area under the swelling also varied from 189.5 μm (in peeling width 400 μm) to 423.2 μm (in peeling width 1400 μm), providing the boundary condition for the wrinkled folding. The curvature of the gel boundary due to buckling tended to be large for hydrogels with small periodic lengths, whereas the curvature became smaller as the periodic length increased (Fig. 1(f)).

MDCK cells were seeded at a density of 2.0 × 10⁵ cells per mL, and time-lapse observation at 10 min intervals was started after establishing sufficient adhesion to the substrate. PIV analysis was performed on the captured images to calculate the velocity field v(x,t) of MDCK cells. The velocity fields were then analyzed at two positions: the first was v(x,t), near the boundary along the outline of the hydrogel folds, and the second was v(x,t), along the same outline shape 1 mm away from the wrinkled pattern (Fig. 1(g)). Fig. 1(h) shows a vector representation of the obtained velocity field. By analyzing the power spectrum of the velocity field, we can see that a peak appeared at k⁻¹ ∼600 μm, which is the typical correlation length of v(x,t) in the MDCK cell monolayer (Fig. 1(i)). This length scale also suggests that a distance of 1 mm is suitable for testing cases without velocity correlation.

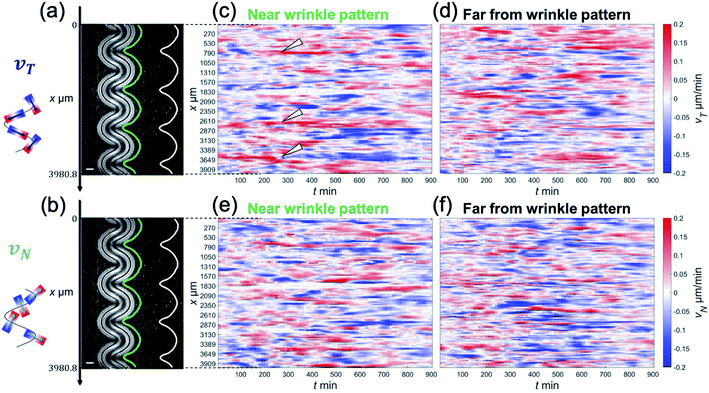
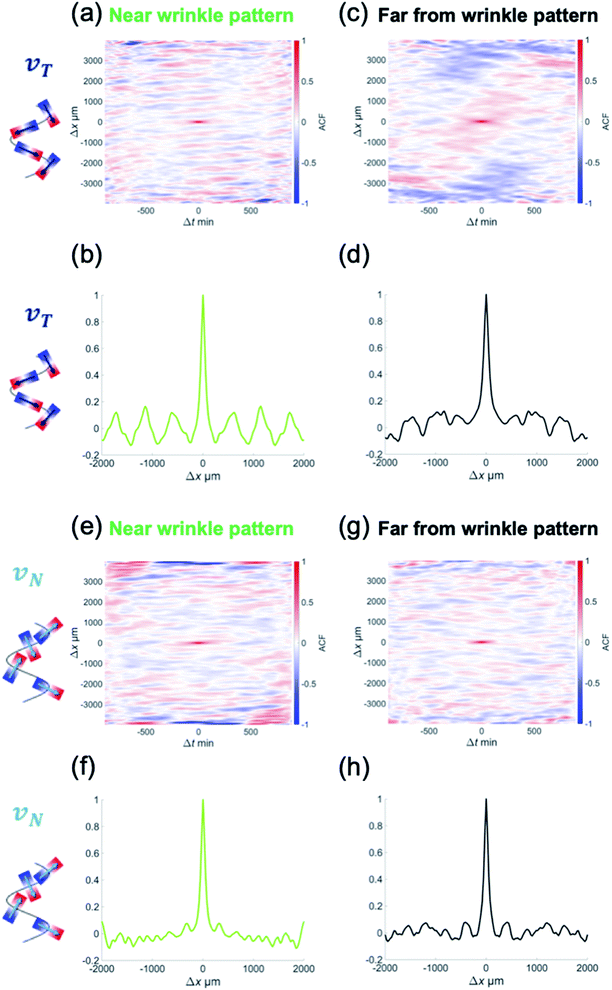
The focus of this study was to reveal how the wrinkled hydrogel fold guides the collective motion of MDCK cells. Hence, we decomposed the velocity of the collective movement in the tangential direction v_T(x,t) and the normal direction v_N(x,t), along the wrinkled patterns, and analyzed their spatiotemporal evolution (Fig. 2(a) and (b)). The velocity in the tangential direction v_T indicates the collective motion along parallel to the wrinkled pattern, whereas the normal velocity v_N represents the component of the motion of the cell vertical upwards along the wrinkled pattern. To calculate v_T, we defined unit vector t(x) in one direction along the tangential direction of the boundary. This unit vector t(x) allowed us to obtain the tangential velocity, v_T = v·t (Fig. 2(a)). In addition, we defined the normal unit vector n(x) that points outward from the wrinkled folding and makes an angle of 90° with vector t(x) (Fig. 2(b)). The velocity v_N in the normal direction was defined as v_N = v·n. As shown in Fig. 2(c), close to the wrinkled folds of a hydrogel pattern with a wavelength of λ = 1008.4 μm, the position showing the greater speed of v_T tended to be localized on the concave side (Fig. 2(c), white arrowhead), where the curvature was larger along the boundary. Furthermore, v_T near the wrinkle pattern does not vary significantly with respect to time, and its spatial patterns were preserved. In contrast, the tangential velocity v_T at a distance far from the wrinkled patterns showed substantial changes with space and time, and reversal of the tangential velocity was occasionally observed (Fig. 2(d)). These results suggest that a spatial correlation in tangential velocity could exist under the wrinkled hydrogel pattern. Next, we analyzed the normal velocity v_N(x,t) along the wrinkled hydrogel. Near the boundary of the wrinkled hydrogel, the normal velocity v_N exhibited temporal and spatial variations, and the locations with large velocities tended to fluctuate over time (Fig. 2(e)). In the region far from the gel, v_N also showed temporal variation and spatial irregularity (Fig. 2(f)), as in the case of the tangential velocity (Fig. 2(f)).

Fig. 2 Velocity field of epithelial cell monolayer along the tangential direction and the normal direction of 3D-buckled hydrogel. (a) Schematic of tangential direction along the wrinkle pattern. The wave-like deformation of the folded hydrogel has a wavelength (λ) of 1008.4 μm. (b) Schematic of normal direction along the hydrogel pattern. (c and d) Tangential velocity v_T(x,t) near the wrinkle pattern (c) and far from the wrinkle pattern (d). The white arrowhead in (c) indicates the position showing the greater speed of v_T locally on the concave side. (e and f) Normal velocity v_N(x,t) near the wrinkle pattern (e) and far from the wrinkle pattern (f).

To further analyze the geometric dependence of the collective motion along the hydrogel or normal to the hydrogel, we calculated the autocorrelation function (ACF) in space and time. The following equations were used to calculate the ACFs of v_T(x,t) and v_N(x,t), respectively,

and
where 〈·〉_x,t represents the ensemble average over space and time.²⁸ The ACF revealed the temporal and spatial similarities of the velocity deviation from the mean value (〈v_T〉_x,t = 0 and 〈v_N〉_x,t = 0).

To determine the correlation in the velocity of collective motion, we examined C_T(Δx,Δt) at two positions, as noted earlier: one at a point 1 mm away from the hydrogel pattern and the other near the wrinkled patterns. Interestingly, C_T(Δx,Δt) near the wrinkled patterns showed periodic changes in the correlation pattern over long Δx and Δt (Fig. 3(a) and (b)). This ACF pattern indicates that the direction of each velocity component can be switched to the opposite direction over time. Furthermore, by examining how C_T(Δx,Δt) changed spatially at the same time (Δt = 0), we found that the periodic change was more significant in the ACF near the wrinkled patterns (Fig. 3(c) and (d)). As for the normal velocity component, the C_N(Δx,Δt) tended to show unclear periodic changes both near the wrinkled patterns (Fig. 3(e)) and far from the wrinkled patterns (Fig. 3(f)). The peak of C_N(Δx,0) was only weakly correlated with periodic changes, which was different from the spatial periodicity in the tangential direction (Fig. 3(h)). The characteristic length in the correlation of the tangential velocity (k⁻¹_T) was 624 μm (from C_T(Δx,0), Fig. 3(d)), and the length scale in the correlation of the normal velocity (k⁻¹_N) was 332 μm (from C_N(Δx,0), Fig. 3(h)). These were shorter than the wavelength of the wrinkled hydrogel folds (λ = 1008 μm), but the characteristic length in the tangential direction k⁻¹_T was comparable to the characteristic length in the velocity correlation without the hydrogel pattern (k⁻¹ ∼600 μm, Fig. 1(g)).

Fig. 3 The autocorrelation function of velocity in the tangential direction and normal direction along the 3D-buckled hydrogel. (a–d) The ACF of tangential velocity v_T(x,t) near the wrinkled pattern (a and b) and far from the wrinkle pattern (c and d). (a and c) The ACF of v_T(x,t) and (b and d) the plot of the ACF extracted at Δt = 0. (e–h) The ACF of normal velocity v_N(x,t) near the wrinkle pattern, near the wrinkled pattern (e and f), and far from the wrinkle pattern (g and h). (e and g) The ACF of v_N(x,t) and (f and h) the plot of the ACF extracted at Δt = 0.

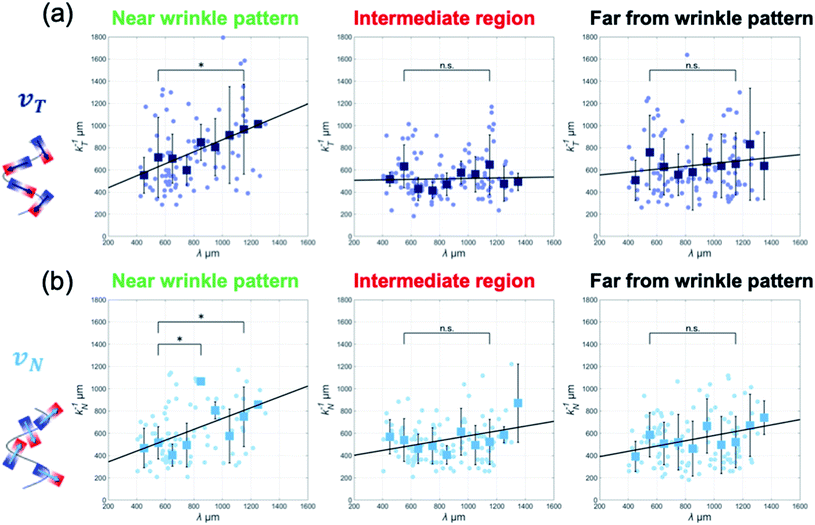
Moreover, to determine whether this model correctly captures the periodic changes in the collective motion, we conducted experiments using hydrogels whose folds varied in periodicity from λ = 405.4 μm to 1303.5 μm and analyzed collective motion on wrinkled hydrogels having various wavelength patterns. By analyzing the ACF of the velocity and extracting the spatial periodicity in the tangential direction k⁻¹_T, we found that the collective motion near the wrinkled pattern exhibited a linear dependence between the periodicity of k⁻¹_T and the wrinkle wavelength λ (Fig. 4(a)). As the wavelength of the wrinkled folds increased, the correlation length of the ACF patterns increased linearly. This enlarged correlation length along the boundary implies that the emergent pattern of collective motion is guided by wrinkling geometry in the vicinity of hydrogel folds.

Fig. 4 The linear dependence of velocity correlation length on the wavelength of folded hydrogel pattern. (a) The characteristic length of the tangential velocity (k⁻¹_T) and (b) the characteristic length of the normal velocity (k⁻¹_N) at various wrinkled patterns. In each figure, from left to right, k⁻¹_T and k⁻¹_N in the vicinity of the pattern (near the wrinkle pattern, left), 500 μm farther away (intermediate region, middle) and 1 mm farther away (far from the wrinkle pattern, right) are shown. The statistical analysis was carried out using λ = 500–550 μm as the standard, and significant differences were found when λ = 1100–1150 μm was reached. The p-value was determined by Student's t-test (*p < 0.05, n.s. represents no significant difference). The black line is drawn by the least-square fitting.

A similar linear relationship between the two characteristic lengths also appeared in the periodicity of the normal direction C_N(Δx,Δt) only near the wrinkled pattern (Fig. 4(b)).

It is important to know whether the tendency of the correlation length of the velocity correlations to extend farther away from the wrinkled patterns is affected by collective motion along the boundary. Therefore, we plotted k⁻¹_T and k⁻¹_N with respect to λ at positions farther from the boundary. The plots in the intermediate region and far from the wrinkled patterns (500 μm and 1 mm away from the wrinkled pattern, respectively) show that the characteristic length of the velocity correlation was k⁻¹_T = 500–600 μm, regardless of the wavelength of the wrinkled patterns, which is close to the correlation length of v(x,t) (∼600 μm) (Fig. 4(a) and (b)). These analyses indicate that the influence of the gel boundary did not exceed the correlation distance. A proportional relationship was found only in collective motion near the wrinkled pattern, suggesting that MDCK cells can collectively move along the hydrogel folds in a wrinkle-size-dependent manner.

Discussion

We investigated the collective motion of an epithelial cell monolayer of MDCK cells close to a 3D-buckled hydrogel mimicking a complex tissue shape. The spatial correlation in velocity can be found only near the wrinkled boundary of the hydrogel, and this correlation extends proportionally to the wavelength of the wrinkling pattern of the hydrogel. The periodic changes in the velocity correlation suggest that the wrinkled folds in the hydrogel substrate could steer the direction of collective motion. We assume the following mechanism to account for this spatial correlation: the wrinkled hydrogel has a gradient in the height direction, and there are regions where the gradient is too steep to migrate upward (Fig. 1(c)–(e)). MDCK cells facing the shallow gradient move up the folds, while cells facing the apex of the wrinkled folds move sideways to avoid a steep gradient. Then, MDCK cells can show collective motion consistent with the boundary shape, such that they move according to the periodic changes in the folds.

In addition to periodic changes in the ACF reflecting the velocity correlation in space, we also found that the velocity correlations in the vicinity of the gel changed little over time. In particular, the high-velocity region tended to be localized on the concave side of the gel wrinkle, as shown in Fig. 2(c). This further suggests that the collective motion in the vicinity of the wrinkled pattern shows little change in the direction along the gel. Interestingly, the characteristic lengths of the velocity correlation, k⁻¹_T and k⁻¹_N, did not perfectly match the wavelength of the wrinkled pattern λ. However, the correlation lengths k⁻¹_T and k⁻¹_N were slightly shorter. This could be because the wrinkle of the hydrogel has a height difference, and the hydrogel becomes a vertically standing wall at long wavelengths. When the wavelength in such vertical walls becomes longer than the correlation length of the collective motion, the velocity correlation is less likely to extend to the cells near the boundary of wrinkled patterns.

Notably, past studies have suggested that the orientation of epithelial cells changes along with the geometry of the 3D curved surface and that a geometry-driven flow can occur.²⁹ Since the buckled 3D gel can also provide suitable geometric confinement in the height direction, the analysis of collective motion on the 3D buckled gel surface remains a future challenge. In addition, unlike the PDMS elastomers used in previous studies, hydrogels can be stretched and contracted to provide mechanical stimulation to epithelial cell populations, making it possible to validate mechanical response stimulation.^24,25 Moreover, MDCK cells exhibit ordered orientation in space, known as topological defects.^30,31 Certain types of topological defects cause mechanical stress to accumulate because of the large cell density. As topological defects appear even in 3D boundary geometries, a future challenge would be to elucidate the geometric properties of collective motion under 3D constraints to understand the epithelial development of multicellular organisms.

Author contributions

Y. T. M. designed research, K. S. and T. F. performed research, R. T., A. T. and K. B. contributed to microfabrication and analytical tools, Y. T. M. wrote the manuscript. K. S. and T. F. contributed equally to this work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by NTT-Kyushu Univ. collaborative grant. Y. T. M. also thanks the support from Grant-in-Aid for Scientific Research on Innovative Areas JP18H05427, Grant-in-Aid for Scientific Research (B) JP20H01872, Grant-in-Aid for Challenging Research JP21K01872.

References

1. M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. Aditi Simha, Hydrodynamics of soft active matter, Rev. Mod. Phys., 2013, 85, 1143.
2. R. Alert and X. Trepat, Physical Models of Collective Cell Migration, Annu. Rev. Condens. Matter Phys., 2020, 11, 77–101.
3. H. Wioland, F. G. Woodhouse, J. Dunkel and R. E. Goldstein, Ferromagnetic and antiferromagnetic order in bacterial vortex lattices, Nat. Phys., 2016, 12, 341–345.
4. K. Beppu, Z. Izri, T. Sato, Y. Yamanishi, Y. Sumino and Y. T. Maeda, Edge current and pairing order transition in chiral bacterial vortex, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2107461118.
5. T. Sanchez, D. T. N. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Spontaneous motion in hierarchically assembled active matter, Nature, 2012, 491, 431–434.
6. S. Araki, K. Beppu, A. M. R. Kabir, A. Kakugo and Y. T. Maeda, Controlling collective motion of kinesin-driven microtubules via patterning of topographic landscapes, Nano Lett., 2021, 21, 10478–10485.
7. T. E. Angelini, E. Hannezo, X. Trepat, M. Marquez, J. J. Fredberg and D. A. Weitz, Glass-like dynamics of collective cell migration, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4714–4719.
8. G. Duclos, C. Blanch-Mercader, V. Yashunsky, G. Salbreux, J.-F. Joanny, J. Prost and P. Silberzan, Spontaneous shear flow in confined cellular nematics, Nat. Phys., 2018, 14, 728–732.
9. A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Emergence of macroscopic directed motion in populations of motile colloids, Nature, 2013, 503, 95–98.
10. Z. Izri, M. N. van der Linden, S. Michelin and O. Dauchot, Self-Propulsion of Pure Water Droplets by Spontaneous Marangoni-Stress-Driven Motion, Phys. Rev. Lett., 2014, 113, 248302.
11. G. Duclos, C. Blanch-Mercader, V. Yashunsky, G. Salbreux, J.-F. Joanny, J. Prost and P. Silberzan, Spontaneous shear flow in confined cellular nematics, Nat. Phys., 2018, 14, 728–732.
12. M. Deforet, V. Hakim, H. G. Yevick, G. Duclos and P. Silberzan, Emergence of collective modes and tri-dimensional structures from epithelial confinement, Nat. Commun., 2014, 5, 3747.
13. R. Alert, J. Casademunt and J.-F. Joanny, Active Turbulence, Annu. Rev. Condens. Matter Phys., 2022, 13, 143–170.
14. K. Beppu, Z. Izri, J. Gohya, K. Eto, M. Ichikawa and Y. T. Maeda, Geometry-driven collective ordering of bacterial vortices, Soft Matter, 2017, 13, 5038–5043.
15. Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chaté and K. Oiwa, Large-scale vortex lattice emerging from collectively moving microtubules, Nature, 2012, 483, 448–452.
16. D. Bi, X. Yang, M. C. Marchetti and M. L. Manning, Motility-Driven Glass and Jamming Transitions in Biological Tissues, Phys. Rev. X, 2016, 6, 021011.
17. W. Xi, S. Sonam, T. B. Saw, B. Ladoux and C. T. Lim, Emergent patterns of collective cell migration under tubular confinement, Nat. Commun., 2017, 8, 1517.
18. S.-Z. Lin, D. Bi, B. Li and X.-Q. Feng, Dynamic instability and migration modes of collective cells in channels, J. R. Soc., Interface, 2019, 16, 20190258.
19. V. Petrolli, et al., Confinement-Induced Transition between Wavelike Collective Cell Migration Modes, Phys. Rev. Lett., 2020, 122, 168101.
20. S. R. K. Vedula, M. C. Leong, T. L. Lai, P. Hersen, A. J. Kabla, C. T. Lim and B. Ladoux, Emerging modes of collective cell migration induced by geometrical constraints, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12974–12979.
21. J. Fouchard, T. P. J. Wyatt, A. Proag, A. Lisica, N. Khalilgharibi, P. Recho, M. Suzanne, A. Kabla and G. Charras, Curling of Epithelial Monolayers Reveals Coupling between Active Bending and Tissue Tension, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 9377–9383.
22. H. G. Yevick, G. Duclos, I. Bonnet and P. Silberzan, Architecture and Migration of an Epithelium on a Cylindrical Wire, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5944–5949.
23. J.-F. Rupprecht, K. H. Ong, J. Yin, A. Huang, H.-H.-Q. Dinh, A. P. Singh, S. Zhang, W. Yu and T. E. Saunders, Geometric Constraints Alter Cell Arrangements within Curved Epithelial Tissues, Mol. Biol. Cell, 2017, 28, 3582–3594.
24. N. Harmand, A. Huang and S. Hénon, 3D Shape of Epithelial Cells on Curved Substrates, Phys. Rev. X, 2021, 11, 031028.
25. E. Latorre, et al., Active Superelasticity in Three-Dimensional Epithelia of Controlled Shape, Nature, 2018, 563, 203–208.
26. R. Takahashi, H. Miyazako, A. Tanaka and Y. Ueno, Dynamic Creation of 3D Hydrogel Architectures via Selective Swelling Programmed by Interfacial Bonding, ACS Appl. Mater. Interfaces, 2019, 11, 28267–28277.
27. R. Takahashi, H. Miyazako, A. Tanaka, Y. Ueno and M. Yamaguchi, Tough, permeable and biocompatible microfluidic devices formed through the buckling delamination of soft hydrogel films, Lab Chip, 2021, 21, 1307–1317.
28. Y. T. Maeda, J. Inose, M. Y. Matsuo, S. Iwaya and M. Sano, Ordered patterns of cell shape and orientational correlation during spontaneous cell migration, PLoS ONE, 2008, 3, e3734.
29. S. Bell, S.-Z. Lin, J.-F. Rupprecht and J. Prost, Active nematic flows on curved surfaces, arXiv:2203.05644, 2022.
30. A. Doostmohammadi, J. Ignés-Mullol, J. M. Yeomans and F. Sagués, Active nematics, Nat. Commun., 2018, 9, 3246.
31. G. Duclos, et al., Topological structure and dynamics of three-dimensional active nematics, Science, 2020, 367, 1120–1124.

---

Footnote

† Equally contributed to this work.

---