Open Access Article
Open Access ArticleHot carrier dynamics of BiTeI with large Rashba spin splitting
Hongze Denga,
Chenhui Zhangb,
Weizheng Liang *a,
Xi-Xiang Zhang
*a,
Xi-Xiang Zhang b and
Sheng-Nian Luo
b and
Sheng-Nian Luo c
c
aThe Peac Institute of Multiscale Sciences, Chengdu, Sichuan, People's Republic of China. E-mail: wzliang@pims.ac.cn
bPhysical Science and Engineering Division, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia
cSchool of Materials Science and Engineering, Southwest Jiaotong University, Chengdu, Sichuan, People's Republic of China
First published on 5th June 2022
Abstract
We present a time-resolved ultrafast optical spectroscopy study on BiTeI, a noncentrosymmetric semiconductor with large spin–orbit splitting. By tuning the pump photon energy, hot carriers can be excited into different energy bands, and the hot carriers decay dynamics are measured. The hot carriers excited by an 1.544 eV photon induce a positive differential reflectivity following a single exponential decay, while the hot carriers excited by an 1.651 eV photon show a negative reflectivity following two exponential decays, i.e., the hot carriers excited by 1.544 eV and 1.651 eV photons show different decay dynamics. We also investigate hot carrier dynamics in each Rashba splitting band at the 1.544 eV and 1.651 eV photon pump, and there is no difference in hot carrier decay between the left and right Rashba splitting bands for both cases.
1 Introduction
The Rashba effect originates from the spin–orbit interaction, and has been rarely explored since the energy band splitting is normally too small,1–4 except for such substances as bismuth tellurohalides BiTeX (X= I, Br, and Cl) with strong Rashba spin–orbit coupling.5–12 Given the lack of spatial inversion symmetry in its lattice, BiTeI has demonstrated the strongest spin–orbit coupling, which gives rise to large Rashba spin splitting in both bulk and surface states.13–17 Such spin splitting was also observed in materials such as PtBi2, which have potential applications in novel spintronic devices.18The layered non-centrosymmetric semiconductor BiTeI is a van der Waals layer material. Each van der Waals layer contains three atomic layers, i.e., the Bi, Te and I layers. The Bi layer is inserted between the Te and I layers [Fig. 1(a)]. The I layer is negatively charged, while the (BiTe)+ layer, containing the Bi and Te layers, is positively charged.19–24 The intrinsic polarity between the I− and (BiTe)+ layers, coupled with the strong spin–orbit interaction of Bi, leads to a huge Rashba effect.2,23,25 The energy band splitting of BiTeI near the Fermi energy has been measured with angle resolved photoemission spectroscopy (ARPES),19,26,27 and the relationship between the band splitting in bulk/surface states and the giant Rashba effect has been established with the help of the first-principles calculations23,28–31(Fig. 1(b)). Both the bulk and surface states of BiTeI are split.20,32–34
Here, we employ femtosecond time-resolved optical spectroscopy (FTOS) to investigate photoexcited hot carrier decay dynamics of BiTeI. By tuning the pump photon energy, we excite hot carriers into different energy bands, and their decay dynamics are measured. On the other hand, the hot carrier decay dynamics show no difference between the left and right Rashba splitting bands.
2 Experiments
Single crystals of BiTeI were grown by the Bridgman method. High pure powders of bismuth, tellurium and iodine with the molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were mixed in a quartz ampoule which was sealed in vacuum. Then the quartz ampoule was inserted into a tubular furnace. After melting the sealed powders above 900 K, the ampoule was pulled with a speed of 1 mm hour−1 toward the lower-temperature region to obtain the single crystals BiTeI. The crystal structure of the BiTeI sample was characterized with X-ray diffraction (XRD) (PANalytical Empyrean). Raman spectrum was also measured in a home-make Raman system. We measured the absorbance of BiTeI using a UV-visible-near infrared spectrophotometer (UV-3600). Before being loaded on a cooling stage for the FTOS experiments, a BiTeI single crystal is cleaved with scotch tape to obtain a fresh surface. Fig. 1(c) show a schematic of the FTOS, and the detail setup was presented elsewhere.35 We use a Ti:sapphire laser with a temporal solution of ∼35 fs, and a repetition rate of 80 MHz. A beam splitter splits the laser beam into a pump beam and a probe beam. The pump beam is modulated by an acoustic optical modulator. A delay stage is set in the probe light path to tune the delay time. The center wavelength of the Ti:sapphire laser can be tuned between 1.544 eV and 1.651 eV. These two beam spots overlap on the sample surface (the spot diameter ∼ 30 μm). For all the pump photon energies and temperatures explored, the pump fluence is fixed at 9 μJ cm−2, and the probe fluence, at 0.9 μJ cm−2. By tuning the polarization of the femtosecond pump laser (left circular (↺), right circular (↻) or linear (↔) polarization), we can selectively excite the hot carriers into the left side, the right side, or both sides of the Rashba spin splitting bands[Fig. 1(b)]. The probe laser is fixed at the s-polarization in all the measurements. For both the left circular polarization (↺) and the right circular polarization (↻) explored, the pump fluence is fixed at 9 μJ cm−2, and the probe fluence, at 0.9 μJ cm−2. The sample temperature is controlled with a Montana cryostation.
1 were mixed in a quartz ampoule which was sealed in vacuum. Then the quartz ampoule was inserted into a tubular furnace. After melting the sealed powders above 900 K, the ampoule was pulled with a speed of 1 mm hour−1 toward the lower-temperature region to obtain the single crystals BiTeI. The crystal structure of the BiTeI sample was characterized with X-ray diffraction (XRD) (PANalytical Empyrean). Raman spectrum was also measured in a home-make Raman system. We measured the absorbance of BiTeI using a UV-visible-near infrared spectrophotometer (UV-3600). Before being loaded on a cooling stage for the FTOS experiments, a BiTeI single crystal is cleaved with scotch tape to obtain a fresh surface. Fig. 1(c) show a schematic of the FTOS, and the detail setup was presented elsewhere.35 We use a Ti:sapphire laser with a temporal solution of ∼35 fs, and a repetition rate of 80 MHz. A beam splitter splits the laser beam into a pump beam and a probe beam. The pump beam is modulated by an acoustic optical modulator. A delay stage is set in the probe light path to tune the delay time. The center wavelength of the Ti:sapphire laser can be tuned between 1.544 eV and 1.651 eV. These two beam spots overlap on the sample surface (the spot diameter ∼ 30 μm). For all the pump photon energies and temperatures explored, the pump fluence is fixed at 9 μJ cm−2, and the probe fluence, at 0.9 μJ cm−2. By tuning the polarization of the femtosecond pump laser (left circular (↺), right circular (↻) or linear (↔) polarization), we can selectively excite the hot carriers into the left side, the right side, or both sides of the Rashba spin splitting bands[Fig. 1(b)]. The probe laser is fixed at the s-polarization in all the measurements. For both the left circular polarization (↺) and the right circular polarization (↻) explored, the pump fluence is fixed at 9 μJ cm−2, and the probe fluence, at 0.9 μJ cm−2. The sample temperature is controlled with a Montana cryostation.
3 Results and discussion
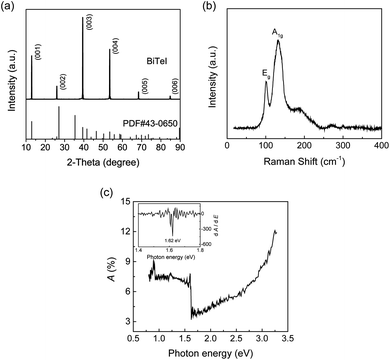
The XRD θ − 2θ scan in Fig. 2(a) shows only the (00L) peaks, indicating that the BiTeI sample is indeed single-crystal and its surface is perpendicular to the c axis. The Raman spectrum of BiTeI sample show two phonon model at 102 cm−1 and 133 cm−1, indicate its pure phase. Photon energy-dependent reflectance of BiTeI at 300 K was shown in Fig. 2(c). Sharp reflectance change is observed near 1.62 eV, i.e., the electronic transition near 1.651 eV induce strong reflectance change.We conduct the pump-probe experiments first with the linearly polarized (↔) femtosecond pump laser. The linear polarization (↔) can be considered as the combination of the left circular polarization (↺) and the right circular polarization (↻). The ↺- and ↻-polarized light have an angular momentum +1 and −1, respectively. The electron hopping between the energy bands is governed by the conservation of angular momentum.36 For example, a ↺-polarized light pump can only excite a spin electron from the 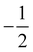 -branch of the valence band into the
-branch of the valence band into the 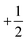 -branch of the conduction band, i.e., the change of angular momentum Δ
-branch of the conduction band, i.e., the change of angular momentum Δ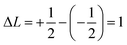 . We assign the spins of the electrons on the left surface/bulk Rashba splitting band in the valence and conduction bands as
. We assign the spins of the electrons on the left surface/bulk Rashba splitting band in the valence and conduction bands as 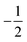 and
and 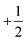 , respectively, and the spins of the electrons on the right surface/bulk Rashba splitting band in the valence and conduction bands as
, respectively, and the spins of the electrons on the right surface/bulk Rashba splitting band in the valence and conduction bands as 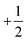 and
and 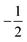 , respectively [Fig. 1(b)]. Hence, the ↺-polarized light pump can only excite electrons from the left surface/bulk Rashba splitting valence band
, respectively [Fig. 1(b)]. Hence, the ↺-polarized light pump can only excite electrons from the left surface/bulk Rashba splitting valence band  into the left surface/bulk Rashba splitting conduction band
into the left surface/bulk Rashba splitting conduction band  [Fig. 1(b)]. It is similar for the excitation of electrons by the ↻-polarized light pump. Hence, a linearly polarized (↔) laser can simultaneously excite the hot carriers into both the left side and the right side of the Rashba spin-splitting bands for both the surface and bulk states.
[Fig. 1(b)]. It is similar for the excitation of electrons by the ↻-polarized light pump. Hence, a linearly polarized (↔) laser can simultaneously excite the hot carriers into both the left side and the right side of the Rashba spin-splitting bands for both the surface and bulk states.
Fig. 3 shows the ΔR(t)/R0 time series of single-crystal BiTeI collected at 5 K and 300 K with a linearly polarized (↔) laser and the pump photon energy varied from 1.544 eV to 1.651 eV. At 5 K [Fig. 3(a)], the ΔR(t)/R0 curve has a strong positive peak at a pump photon energy of 1.544 eV. With increasing pump photon energy, the positive peak becomes weaker and disappears completely at 1.651 eV, while a negative peak emerges at ∼1.574 eV and continues to grow. The complete sign reversal occurs at 1.651 eV. However, the sign reversal at 300 K [Fig. 3(b)] is not complete even at the highest pump photon energy allowed by the system (1.651 eV), and there is only a weak negative peak in the ΔR(t)/R0 time series at high pump photon energies.
 | ||
| Fig. 3 ΔR(t)/R0 time series at (a) 5 K and (b) 300 K for different pump energies as noted. The femtosecond pump laser is linearly polarized (↔). | ||
The temperature dependence of the ΔR(t)/R0 time series collected with linearly polarized (↔) femtosecond laser pump is explored within 5–300 K at fixed pump photon energies (1.544 eV and 1.651 eV; Fig. 4). At 1.544 eV, the ΔR(t)/R0 time series show a pronounced positive peak at 5 K, and its amplitude decreases with increasing temperature [Fig. 4(a)]. At 1.651 eV, the ΔR(t)/R0 time series shows a strong negative peak at 5 K, and as heating proceeds, this negative peak weakens and a positive component emerges, grows and becomes dominant at high temperatures.
 | ||
| Fig. 4 ΔR(t)/R0 time series collected with a pump photon energy of (a) 1.544 eV and (b) 1.651 eV at different temperatures as noted. The femtosecond pump laser is linearly polarized (↔). | ||
4 Discussion
The different ΔR(t)/R0 time series are observed at 5 K when BiTeI is pumped with different photon energies (1.544 eV versus 1.651 eV), since the photonexcited hot carriers are excited into different energy levels. Fresnel equations can be used to describe the reflectivity of the materials, it have been used to study the 2-dimensional materials, such as MoS2, MoSe2, WS2, WSe2 and CrCl3.37,38 Here, we invite it to investigate the reflectivity of BiTeI. Reflectivity of a material under consideration can be described as R = (n − n0)/(n + n0) = 1 − 2n0/(n + n0), with n0 = 1, and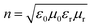 .39 Here n, ε0, εr, μ0 and μr are refractive index, dielectric coefficient in vacuum, relative dielectric coefficient, magnetic permeability in vacuum, and relative magnetic permeability, respectively. For a non-magnetic material, μr ≈ 1,
.39 Here n, ε0, εr, μ0 and μr are refractive index, dielectric coefficient in vacuum, relative dielectric coefficient, magnetic permeability in vacuum, and relative magnetic permeability, respectively. For a non-magnetic material, μr ≈ 1, 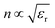 , and
, and 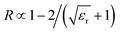 . The ΔR(t)/R0 time series collected at 1.544 eV and 5 K has a positive peak, revealing that the hot carriers excited by 1.544 eV photon induce an increase in εr. On the other hand, the ΔR(t)/R0 time series collected at 1.651 eV and 5 K shows a negative peak, indicating that the hot carriers excited by 1.651 eV photon induce a reduction in εr.
. The ΔR(t)/R0 time series collected at 1.544 eV and 5 K has a positive peak, revealing that the hot carriers excited by 1.544 eV photon induce an increase in εr. On the other hand, the ΔR(t)/R0 time series collected at 1.651 eV and 5 K shows a negative peak, indicating that the hot carriers excited by 1.651 eV photon induce a reduction in εr.
The ΔR(t)/R0 time series collected at 1.544 eV can be described with a single exponential decay (denoted with subscripts a), while the ΔR(t)/R0 time series collected at 1.651 eV can be described with the combination of two exponential decays (denoted with subscripts b1 and b2),
 | (1) |
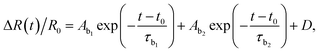 | (2) |
Here A and τ are amplitude and relaxation time of a hot carrier decay, respectively, C and D are fitting constant. Fig. 5 shows examples of fitting to the ΔR(t)/R0 time series collected at 5 K with pump photon energies of 1.544 eV and 1.651 eV; the two exponential components are shown as well. For the hot carrier excited by 1.544 eV photon, only one decay process was observed and τa = 1.175 ± 0.012 ps at 5 K. For the hot carrier excited by 1.651 eV photon, a fast decay and a slow decay, τb1 = 1.541 ± 0.011 ps and τb2 = 6.043 ± 0.032 ps were observed, respectively.
 | ||
| Fig. 5 Exponential fittings to the ΔR(t)/R0 time series (empty circles) collected with a pump photon energy of (a) 1.544 eV and (b) 1.651 eV at 5 K. | ||
We investigate the temperature dependence of amplitude A and decay rate τ−1 of the hot carriers excited by 1.544 eV (Fig. 6) and 1.651 eV (Fig. 7) photon.
 | (3) |
 | (4) |
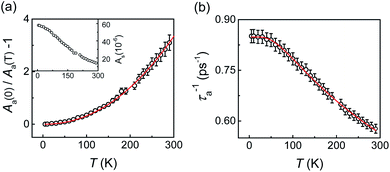 | ||
| Fig. 6 (a) [Aa(0)/Aa(T) − 1] and (b) decay rate τ−1a as a function of temperature. The inset of (a) shows the temperature dependence of Aa. The red lines are fitting with eqn (3) and (4). | ||
For the hot carrier excited by an 1.544 eV photon, Aa and τ−1a are well fitted with eqn (3) and (4) [Fig. 6(a) and (b)]. For the hot carrier excited by by an 1.651 eV photon, we extract the temperature-dependences of Ab1, τb1−1, Ab2 and τb2−1 from 5 K to 300 K and conduct fitting with eqn (3) and (4). The fitting is good for the b1 decay process [Fig. 7(a) and (b)]. However, the b2 decay process does not follow eqn (3) and (4) [Fig. 7(c) and (d)]. The different temperature-dependences of Ab1, τb1−1, Ab2 and τb2−1 indicate different scattering mechanisms which give rise to the b1 and b2 decay processes. The decay process, which can be well fitted with eqn (3) and (4), are normally origin from the electron-phonon scattering. So, we attribute the τa decay and the τb1 decay to the electron-phonon scattering. The scattering mechanisms of the b2 decay processes is unclear now, it may be due the inter-band hopping of the hot carrier.
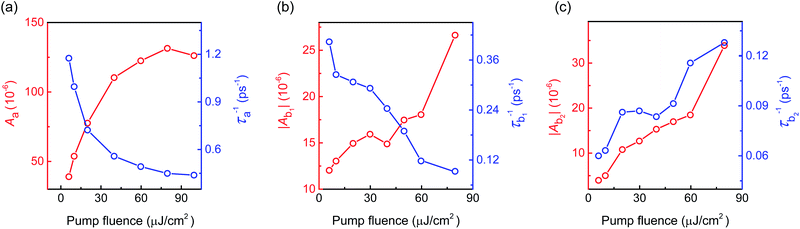
We change the fluence of the ↔-polarized pump light and collect the ΔR(t)/R0 time series at 5 K with 1.544 eV and 1.651 eV photon energy, and the results are presented in Fig. 8. At 1.544 eV, the intensity of the ΔR(t)/R0 time series increases with increasing pump fluence (F). At 1.651 eV, the intensity also increases with increasing F; a positive peak appears at F ≥ 19.9 μJ cm−2 and its intensity increases with increasing F as well. Higher pump fluence induce heat accumulation in the surface of BiTeI and result in lattice expansion, which give rise to the band shifts of BiTeI. The appearance of the positive peak for the 1.651 eV pump is due to the energy band shift as F increased.
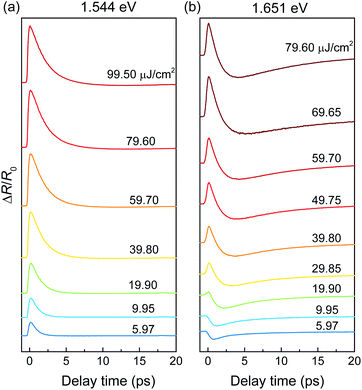 | ||
| Fig. 8 Pump-fluence dependent ΔR(t)/R0 time series collected with a pump photon energy of (a) 1.544 eV and (b) 1.651 eV at 5 K. The femtosecond pump laser is linearly polarized (↔). | ||
The pump fluence dependent ΔR(t)/R0 time series collected at 1.544 eV can be well fitted with eqn (1) and the results are shown in Fig. 9. Aa increases with increasing pump fluence in the low pump fluence regime, and becomes saturated in the high pump fluence region; τ−1a decreases rapidly in the low pump fluence regime with increasing pump fluence, and then becomes insensitive to F in the high pump fluence regime. However, the ΔR(t)/R0 time series collected at 1.651 eV can only be well fitted with the combination of eqn (1) and (2). Fig. 9(b) and (c) show the pump fluence dependent Ab1, τb1−1, Ab2 and τb2−1. Both Ab1 and Ab2 increase with increasing pump fluence in the low pump fluence regime, and do not saturate in the high pump fluence region. τb1−1 decreases rapidly in the low pump fluence regime with increasing pump fluence, while τb2−1 increases with increasing pump fluence in the 3.0–78.0 μJ cm−2 pump fluence regime.
The increase in Aa in the low pump fluence regime indicates that the carrier excitation is more pronounced with increasing pump fluence; its saturation in the high pump fluence region is a result of the limited density of state in the electronic energy band which the hot carriers were excited to, since sufficient excited electrons occupy the a energy band and their number is limited by the Pauli exclusion principle. In this case, increasing pump fluence F does not lead to an increase in the number density of laser excited carriers.
For the hot carrier excited by 1.651 eV photon, Ab1 and Ab2 increase with increasing pump fluence, since both the number densities of laser excited carriers decaying through the τb1 and τb2 decays increase with increasing F. Ab1 and Ab2 show no sign of saturation in the high pump fluence region, that may be due to the energy band which the hot carriers were excited to has a much higher density of state in the electronic energy band and can accommodate more laser excited carriers. τb1−1 decreases with increasing pump fluence (Fig. 9(b)), similar to the case of τ−1a in the low pump fluence region. However, τb2−1 unexpectedly increases with increasing pump fluence (Fig. 9(c)). Here, the different pump-fluence dependences of τb1−1 and τb2−1 are likely associated with different scattering mechanisms.
For the hot carrier decay via electron-phonon coupling,40,41
 | (5) |
In the FTOS measurements, increasing pump fluence induces higher population of hot carriers, and hence gives rise to a higher Te and a smaller τ−1 (eqn (5)). τ−1a and τb1−1 decrease as increasing pump fluence [Fig. 9(a) and (b)], indicating τa and τb1 decays are induced by the electron-phonon coupling. Hot carriers can also decay via interband hopping,42 and increasing the population of hot carriers usually promotes this decay process and results in a larger τ−1. The τb2−1 process is likely induced by the hot carriers decay via interband hopping.
To investigate hot carrier decay in the Rashba split bands of BiTeI, we use polarized pump light with one of the three polarizations: linear (↔), left circular (↺), and right circular (↻). Fig. 10 shows the ΔR(t)/R0 time series collected with different pump laser polarizations, at 1.544 eV and 1.651 eV. For the ΔR(t)/R0 time series collected at 1.651 eV and 1.544 eV, the signal intensities of ΔR(t)/R0 time series for the ↺- and ↻-polarized are nearly half and 70% that for the linear polarization, respectively. Such a reduction induced by a circular polarization is a result of the conservation of angular momentum. The ↔-polarized pump light can excite the electrons in both the left and right sides of the Rashba splitting valence band, while the ↺-polarized (↻-polarized) light can only excite the electrons in the left (right) side of the band, respectively. We note that the intensities of ΔR(t)/R0 time series for the ↺- and ↻-polarized are about 70% that for the linear polarization at 1.544 eV which is not half for the one of the linear polarization, that may be due to the defect energy levels near 1.544 eV which have not chirality.
The ΔR(t)/R0 time series collected with the ↺- and ↻-polarized pump light show negligible differences at 1.544 eV [Fig. 10(a)], and are fitted with eqn (1); such ΔR(t)/R0 time series collected with ↺- and ↻-polarized pump light also show a single exponential component, and the decay times are τa = 1.152 ± 0.013 and 1.167 ± 0.015 ps at 5 K, respectively. The decay times are comparable to that with the ↔-polarized light. The ΔR(t)/R0 time series collected with ↺- and ↻-polarized light at 1.651 eV show minor tips near t = 0 ps [inset in Fig. 10(b)]. These tips show opposite signs for the ↺- and ↻-polarized pump light, and are not observed in the ↔-polarized case linear. We fit the ΔR(t)/R0 time series with eqn (2), and obtain τb1 = 1.522 ± 0.016 ps and 1.536 ± 0.017 ps, τb2 = 6.102 ± 0.033 ps and 6.115 ± 0.035 ps at 5 K for the ↺- and ↻-polarized light, respectively. The decay times are very close to those collected with the ↔-polarized light, indicating that the Rashba splitting does not affect hot carrier decay.
The tips at the ΔR(t)/R0 time series collected with circularly polarized pump at 1.651 eV arise from the decay of spin polarization of BiTeI. Since the excitation of electrons by circularly polarized light is selective, the electrons with opposite spin directions transport to a selected Rashba splitting subbands to conserve angular momentum, hence giving rise to distinct spin polarizations. The decay of the spin polarization may be very rapid. Mauchain et al.,43 by using the dichroic map acquired by switching the circular polarization of a pump beam, demonstrated that the decay of spin polarization can be as fast as 80 fs, comparable to the time scale of the tips in our measurements. We confirm that the two transient oscillation signals are derived from spin polarization, and many-body scattering erases the orbital and spin polarization within the duration of the pump pulse.43
5 Conclusions
In summary, we have investigated the hot carrier dynamics of BiTeI at the laser pump with 1.544 eV and 1.651 eV photon energy with time-resolved optical spectroscopy. By tuning the pump photon energy, the ΔR(t)/R0 time series at different energy bands are obtained, and show opposite signs, indicating the distinct hot carrier dynamics. We also investigate the hot carrier decay in the Rashba splitting bands, and no difference is observed between the left and right Rashba splitting bands for both the 1.544 eV and 1.651 eV pump photon energy.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was sponsored by Southwest Jiaotong University.Notes and references
- Y. A. Bychkov and I. Rashba, JETP Lett., 1984, 39, 78–81 Search PubMed
.
- L. Demkó, G. Schober, V. Kocsis, M. Bahramy, H. Murakawa, J. Lee, I. Kézsmárki, R. Arita, N. Nagaosa and Y. Tokura, Phys. Rev. Lett., 2012, 109, 167401 CrossRef PubMed
.
- G. Landolt, S. V. Eremeev, Y. M. Koroteev, B. Slomski, S. Muff, T. Neupert, M. Kobayashi, V. N. Strocov, T. Schmitt and Z. S. Aliev, et al., Phys. Rev. Lett., 2012, 109, 116403 CrossRef PubMed
.
- G. Schober, H. Murakawa, M. Bahramy, R. Arita, Y. Kaneko, Y. Tokura and N. Nagaosa, Phys. Rev. Lett., 2012, 108, 247208 CrossRef CAS PubMed
.
- Y. Ma, Y. Dai, W. Wei, X. Li and B. Huang, Phys. Chem. Chem. Phys., 2014, 16, 17603–17609 RSC
.
- L. Moreschini, G. Autès, A. Crepaldi, S. Moser, J. Johannsen, K. Kim, H. Berger, P. Bugnon, A. Magrez and J. Denlinger, et al., J. Electron Spectrosc. Relat. Phenom., 2015, 201, 115–120 CrossRef CAS
.
- D. Hvazdouski, M. Baranava and V. Stempitsky, IOP Conf. Ser.: Mater. Sci. Eng., 2018, 012017 Search PubMed
.
- A. Zeugner, M. Kaiser, T. V. Menshchikova, I. P. Rusinov and A. Isaeva, Chem. Mater., 2017, 29, 1321–1337 CrossRef CAS
.
- D. Hajra, R. Sailus, M. Blei, K. Yumigeta, Y. Shen and S. Tongay, ACS Nano, 2020, 14, 15626–15632 CrossRef PubMed
.
- S. Bordács, M. Orlita, M. Šikula, H. Murakawa and Y. Tokura, Phys. Rev. B, 2019, 100, 155203 CrossRef
.
- J. I. Facio, D. Efremov, K. Koepernik, J. S. You, I. Sodemann and V. D. B. Jeroen, Phys. Rev. Lett., 2018, 121, 246403 CrossRef CAS PubMed
.
- A. Shikin, A. Rybkina, I. Klimovskikh, O. Tereshchenko, A. Bogomyakov, K. Kokh, A. Kimura, P. Skirdkov, K. Zvezdin and A. Zvezdin, 2D Mater., 2017, 4, 025055 CrossRef
.
- K. Ishizaka, M. Bahramy, H. Murakawa, M. Sakano, T. Shimojima, T. Sonobe, K. Koizumi, S. Shin, H. Miyahara and A. Kimura, et al., Nat. Mater., 2011, 10, 521–526 CrossRef CAS PubMed
.
- S. V. Eremeev, I. A. Nechaev, Y. M. Koroteev, P. M. Echenique and E. V. Chulkov, Phys. Rev. Lett., 2012, 108, 246802 CrossRef CAS PubMed
.
- M. Tran, J. Levallois, P. Lerch, J. Teyssier, A. Kuzmenko, G. Autes, O. Yazyev, A. Ubaldini, E. Giannini and D. van Der Marel, et al., Phys. Rev. Lett., 2014, 112, 047402 CrossRef CAS PubMed
.
- Y. Qi, W. Shi, P. G. Naumov, N. Kumar, R. Sankar, W. Schnelle, C. Shekhar, F. C. Chou, C. Felser and B. Yan, Adv. Mater., 2017, 29, 1605965.1–1605965.7 Search PubMed
.
- S. Schwalbe, R. Wirnata, R. Starke, G. Schober and J. Kortus, Phys. Rev. B, 2016, 94, 205130 CrossRef
.
- Y. Feng, Q. Jiang, B. Feng, M. Yang, T. Xu, W. Liu, X. Yang, M. Arita, E. F. Schwier and K. Shimada, et al., Nat. Commun., 2019, 10, 1–8 CrossRef PubMed
.
- H. Maaß, H. Bentmann, C. Seibel, C. Tusche, S. V. Eremeev, T. R. Peixoto, O. E. Tereshchenko, K. A. Kokh, E. V. Chulkov and J. Kirschner, et al., Nat. Commun., 2016, 7, 1–7 Search PubMed
.
- B. Fülöp, Z. Tajkov, J. Pető, P. Kun, J. Koltai, L. Oroszlány, E. Tóvári, H. Murakawa, Y. Tokura and S. Bordács, et al., 2D Mater., 2018, 5, 031013 CrossRef
.
- C. J. Butler, H.-H. Yang, J.-Y. Hong, S.-H. Hsu, R. Sankar, C.-I. Lu, H.-Y. Lu, K.-H. O. Yang, H.-W. Shiu and C.-H. Chen, et al., Nat. Commun., 2014, 5, 1–6 Search PubMed
.
- S.-D. Guo, X.-S. Guo, Z.-Y. Liu and Y.-N. Quan, J. Appl. Phys., 2020, 127, 064302 CrossRef CAS
.
- F. Sebastian, S. V. Eremeev, V. A. Golyashov, A. K. Kaveev, O. E. Tereshchenko, K. A. Kokh, E. V. Chulkov, B. Hendrik and R. Friedrich, New J. Phys., 2018, 20, 063035 CrossRef
.
- J. Kim, K. M. Rabe and D. Vanderbilt, Phys. Rev. B, 2019, 100, 104115 CrossRef CAS
.
- Y. Chen, X. Xi, W.-L. Yim, F. Peng, Y. Wang, H. Wang, Y. Ma, G. Liu, C. Sun and C. Ma, et al., J. Phys. Chem. C, 2013, 117, 25677–25683 CrossRef CAS
.
- A. Crepaldi, L. Moreschini, G. Autes, C. Tournier-Colletta, S. Moser, N. Virk, H. Berger, P. Bugnon, Y. Chang and K. Kern, et al., Phys. Rev. Lett., 2012, 109, 096803 CrossRef CAS PubMed
.
- A. S. Ketterl, B. Andres, M. Polverigiani, V. Voroshnin, C. Gahl, K. A. Kokh, O. E. Tereshchenko, E. V. Chulkov, A. Shikin and M. Weinelt, Phys. Rev. B, 2021, 103, 085406 CrossRef CAS
.
- M. Bahramy, R. Arita and N. Nagaosa, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 041202 CrossRef
.
- S. D. Guo and J. L. Wang, J. Phys. D: Appl. Phys., 2016, 49, 215107 CrossRef
.
- Q. Liu, X. Zhang, J. A. Waugh, D. S. Dessau and A. Zunger, Phys. Rev. B, 2016, 94, 125207 CrossRef
.
- S. Güler-Kl and E. Kl, Phys. Rev. B, 2016, 94, 165203 CrossRef
.
- A. Manchon, H. C. Koo, J. Nitta, S. Frolov and R. Duine, Nat. Mater., 2015, 14, 871–882 CrossRef CAS PubMed
.
- A. Crepaldi, F. Cilento, M. Zacchigna, M. Zonno, J. Johannsen, C. Tournier-Colletta, L. Moreschini, I. Vobornik, F. Bondino and E. Magnano, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 125408 CrossRef
.
- M. Bahramy, B.-J. Yang, R. Arita and N. Nagaosa, Nat. Commun., 2012, 3, 1–7 Search PubMed
.
- N. Li, W. Liang and S.-N. Luo, Phys. Rev. B, 2020, 101, 014304 CrossRef CAS
.
- V. Iyer, Y. P. Chen and X. Xu, Phys. Rev. Lett., 2018, 121, 026807 CrossRef CAS PubMed
.
- C. Hsu, R. Frisenda, R. Schmidt, A. Arora, S. M. De Vasconcellos, R. Bratschitsch, H. S. van der Zant and A. Castellanos-Gomez, Adv. Opt. Mater., 2019, 7, 1900239 CrossRef
.
- S. Kazim, R. Gunnella, M. Zannotti, R. Giovannetti, T. Klimczuk and L. Ottaviano, J. Microsc., 2021, 283, 145–150 CrossRef CAS PubMed
.
- M. Born and E. Wolf, Principles of optics: electromagnetic theory of propagation, interference and diffraction of light, Elsevier, 2013 Search PubMed
.
- P. B. Allen, Phys. Rev. Lett., 1987, 59, 1460 CrossRef CAS PubMed
.
- C. Gadermaier, V. Kabanov, A. Alexandrov and D. Mihailovic, J. Appl. Phys., 2012, 111, 112605 CrossRef
.
- R. P. Prasankumar and A. J. Taylor, Optical techniques for solid-state materials characterization, CRC press, 2016 Search PubMed
.
- J. Mauchain, Y. Ohtsubo, M. Hajlaoui, E. Papalazarou, M. Marsi, A. Taleb-Ibrahimi, J. Faure, K. Kokh, O. Tereshchenko and S. Eremeev, et al., Phys. Rev. Lett., 2013, 111, 126603 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2022 |