 Open Access Article
Open Access ArticleDiffusion of dyes in polyelectrolyte-surfactant hydrogels
Martina Klučáková*,
Martina Havlíková,
Filip Mravec and
Miloslav Pekař
Brno University of Technology, Faculty of Chemistry, Purkyňova 118, 612 00 Brno, Czech Republic. E-mail: klucakova@fch.vutbr.cz
First published on 3rd May 2022
Abstract
In this work, hydrogels formed by interaction of biopolymeric electrolytes and oppositely charged surfactants are studied from the point of view of their ability to incorporate model hydrophobic dyes in their micelle-like structure. Two types of hydrogels were investigated. The first type was based on cationized dextran cross-linked by sodium dodecylsulphate. The second type was prepared by interactions of hyaluronan with carbethoxypendecinium bromide (septonex). Nile red and Atto488 were used as model dyes for the diffusion experiments. The dyes were dissolved in two different media: surfactant and physiological saline. The diffusion of dyes into hydrogel was monitored over time. Effective diffusion coefficients were determined. It was found that their values are strongly influenced by the hydrogel character, the types of dye used and the solvent. The obtained effective coefficients were higher in comparison with the values determined for the diffusion in the opposite direction (release from the hydrogel). The dyes are presented as free in physiological saline and in the form of micelles or micelle aggregates in surfactants. During diffusion into the hydrogel, they can be gradually incorporated in a “pearl necklace structure” which suppresses their mobility. In contrast, this partial immobilization of dyes can increase the concentration gradient which is a driving force of diffusion. Also, the gradual incorporation of dyes into hydrogel structures influences the values of the effective diffusion coefficients.
1. Introduction
The development of drug delivery systems is the line of investigation of many research teams. Hydrogels as systems similar to biological tissues are widely studied for medicinal purposes1–4 because they can prolong drug action and reduce side effects.5–8 Oh et al.9 described the development of microgel/nanogel particles as drug delivery carriers and various synthetic strategies for their preparation. Hydrogels are biocompatible due to their high content of water but their capabilities for solubilisation of hydrophobic compounds are very scarce. This problem can be solved by means of incorporation of hydrophobic (nano)domains into the hydrogel structure.4,8,9 The combination of polyelectrolytes with oppositely charged surfactants can result in the complex containing surfactant self-assemblies which can enhance the ability of the hydrogel to solubilize hydrophobic solutes. The binding strength depends on the surfactant's hydrophobicity and the charge density of the polyelectrolyte.10,11Hyaluronan and dextran can be used for these purposes for functional groups suitable for cross-linking.8,12–15 Their combination with oppositely charged surfactants can provide systems characteristic of their biocompatibility, biodegradability and solubilization ability.13–24 Perhaps the first study on gelation in hyaluronan-alkyltrimethylammonium halide systems was published by Thalberg and Lindman.13 They confirmed the formation of mixed micelles between surfactant molecules and carboxylate groups of hyaluronan as well as solubilization of hydrophobic dye Orange OT in prepared systems. The formed micelles, self-diffusion and phase separation in those systems were studied in detail in their subsequent works.16–19 Dong et al. dealt with hydrogels based on dextran and sodium dodecylsulphate.20 The important improvement of the solubility of drug camptothecin and prolonged drug release caused by the formation of sodium dodecylsulphate micelles in agarose hydrogel were observed by Liu and Li.21 Similarly, the solubility of dye murexide was increased in dextran–epichlorohydrin hydrogel.22
In our previous work,8 the hyaluronan and cationized dextran were used as naturally occurring polyelectrolytes. They were combined with opposite charged surfactants: cationic carbethopendecinium bromide (septonex) for hyaluronan and anionic sodium dodecyl sulfate (SDS) for dextran. The model diffusion probe (Nile red) was incorporated in the hydrogels in their preparations. Then its release from hydrogels into corresponding surfactant solutions and physiological saline was studied. We assumed that Nile red was present in micelle-like nano-containers in hydrogels and in the form of free micelles or micelle aggregates. Therefore, the release of dye can be strongly influenced by the strength of their binding in structures of hydrogels as well as size of micelles and micelle aggregates. It was found that the mobility of Nile red increased with increasing charge ratio between surfactant and biopolymer. It was relatively surprising because our primal assumption was that higher charge ratio should result in more compact structure with higher degree of cross-linking. In fact, the structure of hydrogels enables to incorporate Nile red into the network nodes and micelles in pore solution. It is also probable that dye can be in the form of free molecules if capacities of nodes and micelles are exhausted. On the basis of these findings, we decided to enrich our research with the study of diffusion from solutions into hydrogels. The form of dye molecules thus can be controlled by the choice of solvent. The penetration of dye will be studied in the form of micelles (if surfactant is used as solvent) and as free molecules in physiological saline. Nile red was chosen as a model hydrophobic diffusion probe used also in our previous study.8 Atto 488 was chosen as hydrophilic dye with good solubility in water and aqueous solutions. Therefore, the effect of the form of diffusion probes as well as their hydrophilic/hydrophobic characters on the migration of dyes in hydrogels will be investigated in detail.
2. Materials and methods
In this work, hyaluronan and cationized dextran were used as polyelectrolytes. Hyaluronan (the sodium form) was obtained from Contipro (Czech Republic) and used in two different molecular weights. The exact molecular weights were determined in our previous work8 as 309 ± 4 kDa and 1247 ± 5 kDa. Diethylaminoethyl-dextran hydrochloride (Sigma-Aldrich, Czech Republic; DEAED) was used in one molecular weight 729 ± 3 kDa.8Carbethopendecinium bromide (septonex, Czech Pharmacopoeia quality) was supplied by GBNchem Company (Czech Republic) and used as a surfactant for hyaluronan. Sodium dodecyl sulfate (SDS, ≥99.0%) was purchased from Sigma Aldrich (Czech Republic) and used as a surfactant for dextran.
Nile red and Atto 488 purchased from Sigma-Aldrich and used as diffusion probes. NaCl was purchased from Penta (Czech Republic).
All solutions were prepared in 0.15 M NaCl solution using purified water (Purelab ELGA system). Salt solution was used because preliminary experiments showed that a non-zero ionic strength on the aqueous medium is important for obtaining gel-like materials.8,12,25 Samples were prepared by mixing polyelectrolyte and surfactant stock solutions in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio. The concentrations of initial solutions of polyelectrolytes and surfactants are given in Table 1. Hydrogels were equilibrated (24 h) and then separated from the liquid residue by centrifugation at 4000 rpm for 15 min.
1 volume ratio. The concentrations of initial solutions of polyelectrolytes and surfactants are given in Table 1. Hydrogels were equilibrated (24 h) and then separated from the liquid residue by centrifugation at 4000 rpm for 15 min.
| Hydrogel | Polyelectrolyte | Concentration of polyelectrolyte (% w/v) | Surfactant | Concentration of surfactant (mM) |
|---|---|---|---|---|
| D-I | Cationized dextran | 4 | SDS | 400 |
| D-II | Cationized dextran | 4 | SDS | 100 |
| H-I | HMW hyaluronan | 2 | Septonex | 200 |
| H-II | HMW hyaluronan | 2 | Septonex | 100 |
| L-I | LMW hyaluronan | 2 | Septonex | 200 |
| L-II | LMW hyaluronan | 2 | Septonex | 100 |
Centrifuged hydrogels were covered by 5 mL of solution containing diffusion probe. In relation to hydrophobic character of Nile red, it was dissolved in surfactant used in the preparation of hydrogels (SDS for dextran hyaluronan hydrogels and septonex for hyaluronan hydrogels). Concentrations of surfactants were equal to half of the values used in preparation because of the mixing polyelectrolyte and surfactant stock solutions in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio. Hydrophilic dye Atto 488 was dissolved in surfactant (similarly as Nile red) or in 0.15 M NaCl solution. The diffusion probes (Nile red and Atto 488) were used in ten different initial concentrations listed in Table 2.
1 volume ratio. Hydrophilic dye Atto 488 was dissolved in surfactant (similarly as Nile red) or in 0.15 M NaCl solution. The diffusion probes (Nile red and Atto 488) were used in ten different initial concentrations listed in Table 2.
| Designation | Concentration (μM) |
|---|---|
| a | 2 |
| b | 3 |
| c | 4 |
| d | 5 |
| e | 6 |
| f | 7 |
| g | 8 |
| h | 9 |
| i | 10 |
| j | 15 |
The time development of concentration of diffusion probes in solutions was monitored by means of UV/VIS spectrometry (Hitachi U-3300). Confocal Fluorescence Microscope MicroTime 200, PicoQuant GmbH was used for the determination of dye contents in hydrogels.
3. Results and discussion
In the beginning of this study, we decided to extend previous results8 and measure the contents of diffusion probe (Nile red) directly in hydrogels. This measurement was realized in diffusion experiments described in ref. 8, it means in hydrogels with Nile red incorporated in their structure in preparation and then the release of dye from hydrogels into solutions was monitored. The following equations8,26–28 can be used for the description of the diffusion of Nile red from hydrogels. The time development of the total diffusion flux mh→s can be expressed as:
 | (1) |
 | (2) |
Both equations assume that there is no accumulation of the diffusion probe at the interface, i.e. the diffusion flux from the hydrogel to the interface is equal to the diffusion flux from the interface into the solution. Eqn (2) was used for the calculation of time developments of concentrations profiles in hydrogels and the “model” profiles were compared with experimental data. In Fig. 1, the concentrations of Nile red in hyaluronic hydrogels L-I and dextran hydrogels D-I measured in the distance of 5 μm from the interface and values calculated using eqn (2) are compared. The values of Def,h determined in ref. 8 were used for the calculation of dye concentrations in hydrogels. The comparison of experimental data with calculated values resulted in the conclusion that the used mathematical model can fit data relatively well in the case of the release into physiological saline. In contrast, the diffusion rate is overvalued if the hyaluronic hydrogel is covered with surfactant and undervalued in the case of dextran and SDS. Similar results were obtained for all studied hydrogels: the model provided lower values for hyaluronic hydrogels and higher values for dextran hydrogels in comparison with experimental data. Without regard to the ratio of charges between polyelectrolyte and surfactant. It is not easy to explain this discrepancy. Nile red is a hydrophobic dye probe which is “visible”, if it is incorporated in micelles. It means that this dye does not fluoresce in polar solvents as water.29 It seems that the formation of micelles plays a key role in the dye release because no discrepancy between experimental data and calculated values was observed in the case of physiological saline. It is not clear why deviations of model from experimental data of dye release into surfactants are different for hyaluronan and dextran hydrogels. In spite of the fact, that Nile red is hydrophobic dye, it seems that its behaviour can be influenced by chemical character and charge of used surfactant and polyelectrolytes. It is assumed that an incessant disruption of equilibrium between individual forms of dye in hydrogels and surfactants and new equilibration is occurring. We suppose the aggregation of micelles if dye diffuses into surfactant as described in ref. 13 and 16–18.
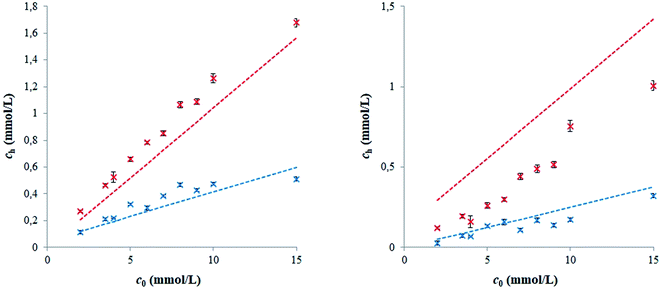 | ||
| Fig. 1 The comparison of the concentration of Nile red in L-I (left) and D-II (right) hydrogels (5 μm from interface) with values predicted according to eqn (2): release into surfactant (red) and physiological saline (blue). | ||
Therefore, we decided to investigate an opposite problem – the diffusion of dye probe from solution into hydrogel. Both surfactants as well as physiological saline were used as solvents in donor solutions.
In the case of opposite situation, when the dye diffuses from solution into hydrogel, the time development of the total diffusion flux ms→h can be expressed as:8,26
 | (3) |
 | (4) |
No accumulation of the diffusion probe at the interface between hydrogel and solution is assumed similarly as in the previous case. In general, the effective diffusion coefficient Def,h can be assumed as an indicator of hydrogel structure and interactions between hydrogel and dye probe.26–28,30,31 If probe diffuses through hydrogel, interactions are realized by means of so-called active sites and they presence in hydrogel causes that the hydrogel is reactive. In contrast, non-reactive hydrogel consists of no active site and the diffusion of probe is affected only by the structure of hydrogel. The structure parameter is then the ratio between the hydrogel porosity and the tortuosity. Since we assume that the probe can diffuse only in pore structure and its diffusion in the hydrogel network is negligible, the porosity φ represents the area of interface accessible for dye. It is reduced in the comparison with the solution where whole interface area is free for the diffusion. The tortuosity τ relates to the shape of pore which can “meander” in hydrogel (in various directions). The structure parameter μ (=φ/τ) thus represents a limitation in dye movement in hydrogel. In the case of non-reactive hydrogel, it can be calculated as the ratio between Def,h and Ds. In this work, a diffusion coefficient of 4.9 × 10−10 m2 s−1 for NR in aqueous solution32 was used as the value of Ds. If the hydrogel contains active sites able to interact with dye probe, the interactions can be included in the values of Def,h and can by expressed as:26,27,33–35
 | (5) |
As mentioned above, φ is the porosity, it means the ratio of the effective diffusive cross section, which is available for transport of dye probe to the bulk cross section. The tortuosity τ is a value characterizing the longer distance traversed in the pores. The parameter μ represents the influences of the structure of hydrogel and its local geometry in the diffusion. K in eqn (5) represents the influence of interactions of dye probe with active sites in hydrogel. In the simple equilibrium between probe bound to active site and non-reacted dye, the equilibrium constant K is equal to the ratio between immobilized probe (cim) and free dye particles (cfree) in hydrogel:
 | (6) |
We assume that chemical interactions are much faster than the diffusion. Therefore the constant K represents a local dynamic equilibrium between immobilized and free probe (Pfree ↔ Pim).27,33–35 In consideration of a complexity of possible interaction, the value of K represents an apparent or effective equilibrium constant characterizing the effect of interactions on the diffusion of probe into hydrogel.
Interactions proceeding during the diffusion thus can influence the rate of transport. At first sight, the diffusion rate is reduced because the effective diffusion coefficient Def,h is lower than Ds. The diffusion rate is dependent on the diffusion coefficient and the concentration gradient. If dye can interact with hydrogel during diffusion the concentration of free movable dye decreases because a part is immobilized. It resulted in increase in the concentration gradient and support of diffusion. Interactions can thus influence the diffusion rate by two opposite ways and final effect depends on the affinity between dye and hydrogel.
In Fig. 2, the dependencies of total diffusion fluxes on the square root of time for both dextran hydrogels are shown as examples of experimental data. The data were fitted by eqn (3) and the values of Def,h were calculated for all hydrogels (on the basis of obtained slopes). The results are listed in Table 3. We can see that values of Def,h obtained for the diffusion from solution into hydrogels are higher in order of magnitude in comparison with values obtained for release experiments.8 The increase in the diffusivity is affected by the type of used polyelectrolyte and surfactant as well as their ratio of charges. The highest diffusivity was observed for dextran hydrogels. The difference between diffusion coefficients obtained for these two hydrogels is not too high. It indicates that the degree of cross-linking of hydrogels can be similar for different charge ratios between polyelectrolyte and surfactant. We believe that charges of dextran and SDS are compensated by means of cross-linking which corresponds with the theoretical ratio of charges between surfactant and biopolymer equal to 1. It means that the density of cross-linking is not affected by the ratio of charges. In the case of D-II hydrogel, the ratio of charges between surfactant and polyelectrolyte was equal to 1 and SDS was exhausted by cross-linking. If the ratio of charges is higher than 1 (other hydrogels), the surfactant can form micelles and dye can be incorporated into them. The critical micellar concentration must by exceeded.
 | ||
| Fig. 2 The examples of data fitting (eqn (3)) for D-I (left) and D-II (right) hydrogels. | ||
| Hydrogel | Def,h (m2 s−1) |
|---|---|
| D-I | (3.81 ± 0.12) × 10−10 |
| D-II | (3.63 ± 0.22) × 10−10 |
| H-I | (2.16 ± 0.06) × 10−10 |
| H-II | (3.25 ± 0.11) × 10−10 |
| L-I | (3.34 ± 0.06) × 10−10 |
| L-II | (2.16 ± 0.10) × 10−10 |
In Fig. 3, the comparison of diffusion coefficients obtained for NR release and its diffusion into hydrogel is shown. This comparison is expressed as the ratio λ between Def,h obtained for the diffusion from surfactant into hydrogel and its value for NR release from hydrogel into surfactant. We can see that the coefficient λ is lower if the ratio between surfactant and polyelectrolyte is higher (D-I, H-I, L-I). Theoretical ratios of charges between surfactant (SDS, septonex) and biopolymer (cationized dextran, hyaluronan) are ∼4 for D-I, H-I, L-I; ∼2 for H-II and L-II; and ∼1 for D-II.8 We assume that the majority of surfactant is consumed for the cross-linking of the hydrogel if the charge ratio is approximately equal to 1. It means that the content of surfactant in the pores of D-II hydrogel is very low. In the case of other hydrogels, their pores should be filled by surfactant solutions, because only a proportion of the surfactant can be exhausted for the formation of hydrogel networks. The excess of surfactant can result in the formation of micelles. The micellization is conditioned by the exceeding of the critical micellar concentration, which is around ∼8 mM for SDS36–38 and ∼0.8 mM for septonex.38–41 The highest values of Def,h were obtained for D-I hydrogel (for both experimental arrangements: release of NR from hydrogel in our previous study8 and diffusion from surfactant into hydrogel in this study). In contrast to our previous study,8 the lowest values of Def, were obtained for H-I and L-II hydrogels. Striking increases of diffusivity (in comparison with release studied in ref. 8) were observed for D-II and H-II hydrogels. Increase found for other hydrogels were comparable. Obtained results showed that we have many values with different orders for the release of NR from hydrogels and for the diffusion from surfactant into hydrogels. The questions are why the values differ in order of magnitude from different experimental arrangements, why the increase is conspicuously higher for two particular hydrogels, and why the order of Def,h values are different if we change experimental arrangement. Our hypothesis is that answers should be search in the micellization of surfactant and incorporation of NR into micelles. In previous work,8 the dye was incorporated in the hydrogel directly in its preparation. In general, charges of polyelectrolyte and surfactant should be compensated as result of cross-linking which corresponds with the theoretical ratio of charges between surfactant and biopolymer equal to 1. Therefore, a proportion of the surfactant can be exhausted for the formation of hydrogel networks. As mentioned above, the surfactant is exhausted and NR can be present in the hydrogel structure in the form of free molecules, if the ratio of charges between the used surfactant and biopolymer is ∼1 (hydrogel D-II). A concentration excess of surfactant was used in the preparations of other hydrogels therefore micelles can be formed in hydrogel pores and the so-called “pearl necklace structure” can be formed by the combination of polyelectrolytes with surfactants.42–46 This structure is characteristic mainly for longer chains.13,16 Nile red then be incorporated into these “nano-containers”. In hydrogel pores, the dye can occur as free particles and in the cores of micelles formed by surfactant.46–50 To resolve observed discrepancies in the release of NR from hydrogels were not easy.8 Therefore, we studied here the opposite problem the diffusion of dye from solution into hydrogel. In view of the fact, that the concentrations of surfactants are much higher than critical micellar concentrations of SDS36–38 and septonex,38–41 we can assume that Nile red is in the solutions incorporated in micelles and our problem can be simpler in comparison with previous study.8 In this study, the diffusion of Nile red into hydrogels can be affected by hydrogel structure (e.g., degree of cross-linking) as well as the size of micelles or micelle aggregates and potential interactions between hydrogels and diffusing particles. If we analyse results listed in Table 3, we can see that the diffusivity of NR decreased with lower concentrations of surfactants for dextran and hyaluronan of low molecular weight. In contrast, higher molecular weight of hyaluronan resulted in the increase of diffusivity for less concentrated surfactant. The structure of hydrogels is not fully understood but micelles are believed to form the (electrostatic) crosslinks of the hydrogel network and to connect the polymer chains.8 At first sight, it seems that the use of more concentrated surfactant should result in more cross-linked hydrogel network and lower permeability for diffusion probes. In contrast, many obtained results do not agree with this assumption. Hoffmann et al.46,51 observed the decrease in viscosity for the excess of surfactant charges caused the decrease in viscosity in semi-dilute solutions. They stated that the polyelectrolyte formed relatively large and densely packed clusters near the phase boundary on the surfactant rich side, thereby occupying less space and reducing the viscosity. In contrast, the increase in the viscosity while an excess of polyelectrolyte in semi-dilute solutions caused by the cross-links formed between polyelectrolyte chains.8,46,51 Rheological study on hyaluronan hydrogels12 showed that samples prepared with the 300 kDa hyaluronan and 200 mM septonex (as L-I) had the elastic modulus lower than the viscous modulus throughout the whole tested frequency range and the cross-over of moduli curves was not observed in contrast to the samples prepared with higher molecular weight of hyaluronan. No correlation was found between the rheological properties of hydrogels and the charge ratio between surfactant and biopolymer. Our hypothesis (formulated in ref. 8) is that the concentration of surfactant cannot affect the degree of cross-linking if the ratio between charges of surfactant and polyelectrolyte is ≥1. The surfactant which was not exhausted for the formation of hydrogel networks remains in pores of hydrogel and can affect the behaviour of diffusion probes. According to this assumption, lower contents of surfactants are in pores of hydrogels labelled as D-II, H-II and L-II. We can see that this lower content agrees with the considerable increase in diffusivity of dye in hydrogels based on dextran and hyaluronan of high molecular weight. In contrast, this effect is relatively small in the case of hyaluronan of low molecular weight. Simultaneously, we assume that dye in solutions is incorporated in micelles because the concentrations of surfactants are above the critical micellar concentration.36–41 We believe that the diffusion ability of micelles is lower than that of free dye molecules.
 | ||
| Fig. 3 The ratio λ between Def,h obtained for the diffusion from surfactant into hydrogel and its value for the release of Nile red from hydrogels into surfactants. | ||
In contrast to Nile red, the Atto 488 is hydrophilic dye with high water solubility.52 Therefore, it can be used as the diffusion probe in the form of free molecule as well as in micellar form. In consideration of its hydrophilic character, this dye cannot be placed in the core of micelles but closed to its surface layer. Diffusion experiments were realized from surfactant and physiological saline, therefore the difference between micellar and molecular forms can be studied. Effective diffusion coefficients were determined similarly as in the case of Nile red. The decrease in concentration of dye in solution was measured and the calculation of Def,h values were based on eqn (3). The calculated values are listed in Table 4. We can see that the highest Def,h values were obtained for the diffusion into D-I and D-II hydrogels. Results obtained for D-I were lightly higher in the comparison with D-II hydrogel in spite of the fact that D-I hydrogel should contain an excess of surfactant non-consumed by the cross-linking in the preparation of hydrogel. Theoretical ratios of charges between SDS and dextran is 1/1 for D-II and 4/1 for D-I. The values determined for free Atto 488 molecules diffusing from physiological saline were higher than the values for its micellar form in SDS. Our results obtained for both dextran hydrogels are similar as the value published by Zhang et al.36 and Dertinger et al.:53 4 × 10−10 m2 s−1. Values of Def,h obtained for hyaluronan hydrogels are lower. Theoretical ratios of charges between septonex and hyaluronan were 4/1 for H-I and L-I and 2/1 for H-II and L-II hydrogels. Hydrogels based on hyaluronan with a ratio of charges equal to 1/1 were not prepared because of our previous experimental experience8,12,39,54 and the cloudiness of studied solutions. Diffusivities were also lower for the diffusion of micellar dyes from surfactant. Similarly as in the case of Nile red, the highest Def,h values were obtained for the diffusion into H-II and L-I hydrogels (both from SDS and physiological saline). In contrast to Nile red, experimental data obtained for the diffusion of Atto 488 agreed with concentrations of dye in hydrogel (5 μm from interface) with values predicted according to eqn (4) (see Fig. 4). As mentioned above, the effective diffusion coefficient includes the influences of pore structure of hydrogel represented by the structure parameter μ and interactions between hydrogel and dye represented by the apparent equilibrium constant K (see eqn (5)). The value of Def,h is also influenced by the size of micelles, which should be much greater for SDS (in comparison with septonex surfactant). We are not able to prevent from interactions and to study the diffusion in the same but non-reactive hydrogel, therefore the structure parameter cannot be calculated simply as he ratio between Def,h and Ds. However, these ratios are different for the diffusion from surfactants and physiological saline (see Fig. 5). In this work, a diffusion coefficient of 4.9 × 10−10 m2 s−1 for Nile red32 was used as the value of Ds and 4.0 × 10−10 m2 s−136 for Atto 488. The lowest ratios were obtained for the diffusion of Nile red from surfactants, the highest values for the diffusion of Atto 488 from physiological saline, but the differences are not too high and are affected both by pore structure and interactions of dyes with hydrogels. On the other hand, if we assume that charges of polyelectrolyte and surfactant are compensated as result of cross-linking with the ratio of charges between surfactant and biopolymer equal to 1/1, the density of hydrogel networks based on the same surfactant and polyelectrolyte should be also the same with the same structure parameter μ (D-I And D-II hydrogels; H-I and H-II hydrogels; L-I and L-II hydrogels). Differences should be caused by different excesses of surfactant in hydrogels (according to the ratios between charges). If we mark quantities belonging to X-I hydrogel with index I and (similarly) quantities belonging to X-II hydrogel with index I. We can write
 | (7) |
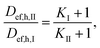 | (8) |
| Hydrogel | Def,h (m2 s−1) – surfactant | Def,h (m2 s−1) – physiological saline |
|---|---|---|
| D-I | (3.66 ± 0.17) × 10−10 | (3.81 ± 0.19) × 10−10 |
| D-II | (3.58 ± 0.12) × 10−10 | (3.68 ± 0.16) × 10−10 |
| H-I | (1.81 ± 0.06) × 10−10 | (1.85 ± 0.04) × 10−10 |
| H-II | (3.14 ± 0.16) × 10−10 | (3.51 ± 0.15) × 10−10 |
| L-I | (3.38 ± 0.16) × 10−10 | (3.48 ± 0.08) × 10−10 |
| L-II | (1.83 ± 0.11) × 10−10 | (1.96 ± 0.07) × 10−10 |
 | ||
| Fig. 4 The comparison of the concentration of Nile red in H-I (left) and L-I (right) hydrogels (5 μm from interface) with values predicted according to eqn (4): release into surfactant (red) and physiological saline (blue). | ||
 | ||
| Fig. 5 The ratio between Def,h and Ds obtained for the diffusion of Nile red from surfactant (red), Atto 488 from surfactant (grey) and Atto 488 from physiological saline (blue) into hydrogels. | ||
4. Conclusions
The diffusion of Nile red and Atto 488 as model dyes from surfactant solutions and physiological saline into hydrogels based on a combination of polyelectrolyte and opposite charged surfactant was studied. The mobility of dyes in hydrogels are affected by several factors. The dyes can be present in the form of free molecules, free mobile micelles or micelle aggregates. Their forms depend on the used solvent and potential excess of surfactant in pore structure of hydrogel. It was found that the behaviour of dyes differed if the hydrogel was based on the hyaluronan of high molecular weight. In this case, type of surfactant, type and form of dye resulted in more noticeable differences in obtained results. Hydrogels based on dextran and hyaluronan of low molecular weight are not probably able to immobilize higher amounts of dyes and higher part of them remained mobile.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Czech Science Foundation, project No. 16-12477S.References
- H. Liu, C. Wang, C. Li, Y. Qin, Z. Wang, F. Yang, Z. Li and J. Wang, RSC Adv., 2018, 8, 7533–7549 RSC.
- B. J. Kong, A. Kim and S. N. Park, Carbohydr. Polym., 2016, 147, 473–481 CrossRef CAS PubMed.
- S. Zhang, J. Ermann, M. D. Succi, A. Zhou, M. J. Hamilton, R. Langer and J. M. Karp, Sci. Transl. Med., 2015, 7, 300 Search PubMed.
- M. Pekař, Front. Mater., 2015, 1, 35 Search PubMed.
- C. Ju, J. Sun, P. Zi, X. Jin and C. Zhang, J. Pharm. Sci., 2013, 102, 2707–2717 CrossRef CAS PubMed.
- C. T. Huynh, M. K. Nguyen and D. S. Lee, Macromolecules, 2011, 44, 6629–6636 CrossRef CAS.
- W. Shi, Y. Ji, X. Zhang, S. Shu and Z. Wu, J. Pharm. Sci., 2011, 100, 886–895 CrossRef CAS PubMed.
- M. Klučáková, S. Jarábková, T. Velcer, M. Kalina and M. Pekař, Colloids Surf., A, 2019, 573, 73–79 CrossRef.
- J. K. Oh, R. Drumright, D. J. Siegwart and K. Matyjaszewski, Prog. Polym. Sci., 2008, 33, 448–477 CrossRef CAS.
- L. Piculell, Langmuir, 2013, 29, 10313–10329 CrossRef CAS PubMed.
- D. Li and N. J. Wagner, J. Am. Chem. Soc., 2013, 135, 17547–17555 CrossRef CAS PubMed.
- T. Venerová and M. Pekař, Carbohydr. Polym., 2017, 170, 176–181 CrossRef PubMed.
- K. Thalberg and B. Lindman, J. Phys. Chem., 1989, 93, 1478–1483 CrossRef CAS.
- J. Krouská, M. Pekař, M. Klučáková, B. Šarac and M. Bešter-Rogač, Carbohydr. Polym., 2017, 157, 1837–1843 CrossRef PubMed.
- M. S. Lindblad, J. Sjoeberg, A. C. Albertsson and J. Hartmann, ACS Symp. Ser., 2007, 954, 153–167 CrossRef CAS.
- K. Thalberg and B. Lindman, Langmuir, 1991, 7, 277–283 CrossRef CAS.
- K. Thalberg, B. Lindman and G. Karlström, J. Phys. Chem., 1991, 95, 3370–3376 CrossRef CAS.
- K. Thalberg, B. Lindman and G. Karlström, J. Phys. Chem., 1991, 95, 6004–6011 CrossRef CAS.
- T. C. Wong, K. Thalberg, B. Lindman and H. Gracz, J. Phys. Chem., 1991, 95, 8850–8857 CrossRef CAS.
- J. Dong, L. Chen, Y. Ding and W. Han, Macromol. Chem. Phys., 2005, 206, 1973–1980 CrossRef CAS.
- J. Liu and L. Li, Eur. J. Pharm. Sci., 2005, 25, 237–244 CrossRef CAS PubMed.
- C. Demirbilek and C. O. Dinç, Desalin. Water Treat., 2015, 57, 1–10 Search PubMed.
- G. Bai, V. Castro, M. Nichifor and M. Bastos, J. Therm. Anal., 2010, 100, 413–422 CrossRef CAS.
- A. O. Abioye and A. Kola-Mustapha, Drug Dev. Ind. Pharm., 2016, 42, 39–59 CrossRef CAS PubMed.
- T. Pilgrová, T. Venerová, F. Mravec and M. Pekař, Int. J. Biol. Macromol., 2018, 112, 241–249 CrossRef PubMed.
- M. Klučáková and M. Pekař, Colloids Surf., A, 2009, 349, 96–101 CrossRef.
- J. Crank, The Mathematics of Diffusion, Clarendon Press, Oxford, 1975 Search PubMed.
- E. L. Cussler, Diffusion, Mass Transfer in Fluid Systems, Cambridge University Press, Cambridge, 1997 Search PubMed.
- J. Jin, E. A. Morin, D. M. Henn, Z. Cao, J. W. Woodcock, S. Tang, W. He and B. Yhao, Biomacromolecules, 2013, 14, 2713–2723 CrossRef PubMed.
- P. Sedláček, J. Smilek and M. Klučáková, React. Funct. Polym., 2013, 73, 1500–1509 CrossRef.
- P. Sedláček, J. Smilek and M. Klučáková, React. Funct. Polym., 2014, 75, 41–50 CrossRef.
- S. A. Chowdhury and M. Lim, J. Korean Chem. Soc., 2011, 55, 746–749 CrossRef CAS.
- M. Klučáková, M. Kalina, P. Sedláček and L. Grasset, J. Soils Sediments, 2014, 14, 368–376 CrossRef.
- M. Klučáková and M. Kalina, Colloids Surf., A, 2015, 483, 162–170 CrossRef.
- F. A. L. Dullien, Porous Media, Fluid Transport and Pore Structure, Academic Press, San Diego, 1992 Search PubMed.
- X. Zhang, A. Poniewierski, A. Jelinska, A. Zagozdzon, A. Wisniewska, S. Hou and R. Holyst, Soft Matter, 2016, 12, 8186–8194 RSC.
- E. Dutkiewicz and A. Jakubowska, Colloid Polym. Sci., 2002, 280, 1009–1014 CrossRef CAS.
- S. S. Shah, N. U. Jamroz and Q. M. Sharif, Colloids Surf., A, 2001, 178, 199–206 CrossRef CAS.
- A. Kargerová and M. Pekař, Carbohydr. Polym., 2019, 204, 17–23 CrossRef PubMed.
- J. Fischer and P. Jandera, J. Chromatogr. B: Biomed. Sci. Appl., 1996, 681, 3–19 CrossRef CAS PubMed.
- J. Oremusová and O. Greksáková, Tenside, Surfactants, Deterg., 2003, 4, 35–39 Search PubMed.
- L. Shi, F. Carn, F. Boue and E. Buhler, Phys. Rev. E, 2016, 94, 032504 CrossRef PubMed.
- A. M. Rumyantsev, A. Johner and J. J. de Pablo, ACS Macro Lett., 2010, 10, 1048–1054 CrossRef PubMed.
- S. Uyaver and C. Seidel, J. Phys. Chem. B, 2004, 108, 18804–18814 CrossRef CAS.
- R. Schweins and K. Huber, Macromol. Symp., 2004, 211, 25–42 CrossRef CAS.
- I. Hoffmann, P. Heunemann, S. Prevost, R. Schweins, N. J. Wagner and M. Gradzielski, Langmuir, 2011, 27, 4386–4396 CrossRef CAS PubMed.
- H. D. Burrows, A. J. M. Valente, T. Costa, B. Stewart, M. J. Tapia and U. Scherf, J. Mol. Liq., 2015, 210, 82–99 CrossRef CAS.
- M. K. Cowman, C. Spagnoli, D. Kudasheva, M. Li, A. Dyal, S. Kanai and E. A. Balazs, Biophys. J., 2005, 88, 590–602 CrossRef CAS PubMed.
- M. Goswami, J. M. Borreguero, P. A. Pincus and B. G. Sumpter, Macromolecules, 2015, 48, 9050–9059 CrossRef CAS.
- O. D. Iakobson, A. V. Dobrodumov, N. N. Saprykina and N. N. Shevchenko, Macromol. Chem. Phys., 2017, 218, 1600523 CrossRef.
- I. Hoffmann, M. Simon, B. Farago, R. Schweins, P. Falus, O. Holderer and M. Gradzielski, J. Chem. Phys., 2016, 145, 124901 CrossRef PubMed.
- A. Borodavka, E. C. Dykeman, W. Schrimpf and D. C. Lamb, eLife, 2017, 6, e27453 CrossRef PubMed.
- T. Dertinger, A. Loman, B. Ewers, C. B. Mulle, B. Kramer and J. Enderlein, Opt. Express, 2008, 16, 14353–14368 CrossRef PubMed.
- A. Kargerová and M. Pekař, Langmuir, 2014, 30, 11866–11872 CrossRef PubMed.
- I. Hoffmann, P. Heunemann, S. Prevost, R. Schweins, N. J. Wagner and M. Gradzielski, Langmuir, 2011, 27, 4386–4396 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |

