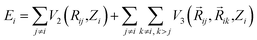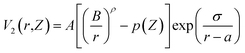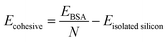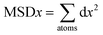Open Access Article
Open Access ArticleFeasibility study of Mg storage in a bilayer silicene anode via application of an external electric field†
Sumaiyatul Ahsan‡
a,
Abrar Rauf‡a,
M. F. N. Taufique b,
Hasan Al Jamea,
Saugata Sarkera,
Sadiq Shahriyar Nishatc,
Md Tohidul Islamd,
Azmain Faek Islame,
Md Rafsun Jania,
Md Shafiqul Islama,
Kazi Md Shorowordia and
Saquib Ahmed
b,
Hasan Al Jamea,
Saugata Sarkera,
Sadiq Shahriyar Nishatc,
Md Tohidul Islamd,
Azmain Faek Islame,
Md Rafsun Jania,
Md Shafiqul Islama,
Kazi Md Shorowordia and
Saquib Ahmed *f
*f
aDepartment of Materials and Metallurgical Engineering (MME), Bangladesh University of Engineering and Technology (BUET), East Campus, Dhaka, 1000, Bangladesh
bPacific Northwest National Laboratory, Richland, WA 99354, USA
cDepartment of Materials Science and Engineering (MSE), Rensselaer Polytechnic Institute, 110 8th Street, Troy, NY 12180, USA
dDepartment of Materials Design and Innovation, University at Buffalo, Buffalo, NY 14260, USA
eSchool of Mechanical and Materials Engineering, Washington State University, Pullman, Washington 99163, USA
fDepartment of Mechanical Engineering Technology, SUNY – Buffalo State, 1300 Elmwood Avenue, Buffalo, NY 14222, USA. E-mail: ahmedsm@buffalostate.edu; Fax: +1-716-878-3033; Tel: +1-716-878-6006
First published on 21st July 2022
Abstract
With the goal of developing a Si-based anode for Mg-ion batteries (MIBs) that is both efficient and compatible with the current semiconductor industry, the current research utilized classical Molecular Dynamics (MD) simulation in investigating the intercalation of a Mg2+ ion under an external electric field (E-field) in a 2D bilayer silicene anode (BSA). First principles density functional theory calculations were used to validate the implemented EDIP potentials. Our simulation shows that there exists an optimum E-field value in the range of 0.2–0.4 V Å−1 for Mg2+ intercalation in BSA. To study the effect of the E-field on Mg2+ ions, an exhaustive spread of investigations was carried out under different boundary conditions, including calculations of mean square displacement (MSD), interaction energy, radial distribution function (RDF), and trajectory of ions. Our results show that the Mg2+ ions form a stable bond with Si in BSA. The effects of E-field direction and operating temperature were also investigated. In the X–Y plane in the 0°–45° range, 15° from the X-direction was found to be the optimum direction for intercalation. The results of this work also suggest that BSA does not undergo drastic structural changes during the charging cycles with the highest operating temperature being ∼300 K.
1 Introduction
The 21st century marked a rapid adoption of electrochemical energy storage in all walks of life – this fact in turn calls for the immediate development of next-generation batteries. Rechargeable lithium-ion batteries (LIBs), which are undoubtedly the most popular energy storing devices, are no longer able to adequately meet the required energy or safety requirements;1–3 additionally, large-scale production of LIBs is dependent on raw materials produced in countries with geopolitical risks.4 Among post-LIB alternatives,5–7 rechargeable magnesium-ion batteries (MIBs) offer the best replacement technology. MIBs utilize divalent Mg2+ as charge carriers, which have smaller ionic radii than Li+ while offering a higher volumetric energy density due to their capability of storing two electrons per ion, and the natural advantage of utilizing earth-abundant materials.5,6,8–11 Mg undergoes safer reversible dendrite-free deposition in Mg metal anodes5,6,11 which is why most research on MIBs is done utilizing metallic Mg anodes, with a focus on developing the cathode materials10,12 and electrolytes.10Despite all the benefits of metallic Mg anode, it is impractical for practical usage due to its incompatibility with conventional electrolytes used in batteries. It can result in undesirable electrode–electrolyte reactions, resulting in the formation of a blocking layer12 and leading to poor cycling ability and battery voltage. To solve this issue, a large focus of current MIB research has been on developing an anode material that is compatible with conventional battery materials,13–19 instead of developing new electrolytes and cathode. There is no doubt that a critical requirement for the success of the MIB technology is in the development of a suitable anode material.
Due to the high natural abundance of silicon and its synergy with existing electrochemical and semiconductor industry, Si-based anode is a very attractive material for the MIB technology. Many variations of Si-based anode are currently being tested such as bulk Si,13 nano-Si,16 Al doped Si20 etc. In our current investigation, we probe 2D bilayer silicene, which is a 2D allotrope of silicon (similar to graphene being the 2D allotrope of carbon). The reasons behind our choice of material are three-fold.
Firstly, most other variations of Si-based anode for MIBs have been tested already either theoretically or experimentally and found inadequate in resolving the storage problem.13,16,20 Even though bulk Si might seem very promising13 due to having a very high specific capacity (3817 mA hg−1) and low average insertion voltage (close to 0.15 eV vs. Mg), for Mg storage, it shows a very significant lattice expansion (nearly 216%). Mg intercalation into nano-Si anode has been proven to be inadequate,15,21 and this will be further discussed in later sections.
Secondly, there exists a strong correlation between lowering the particle size of the anode particle and enhancing the intercalation process in MIBs. Strong evidence in favour of size reduction of anode particles was highlighted through a study utilizing nano-Sn anode for MIBs, where commercial Sn nanoparticles (∼150 nm) were shown to take up to ∼3 weeks to store Mg. By decreasing the particle size to sub-50 nm range, this charging process time dramatically decreased to a few hours.15,16,21 This correlation between size and performance can easily be explained. Mg storage in silicon is a diffusion-controlled process and the divalent nature of Mg already results in a sluggish diffusion process compared to monovalent counterparts (Li, Na). This means that lowering the characteristic particle size for anodes is critical to decreasing lattice expansion, increasing diffusion & storage rate. A similar experimental study in search for the critical size for nano-Si anode for MIBs was done to address the drawbacks associated with bulk Si;16 it was shown that for oxide-free nanostructured Si with size in the range of ∼100 nm, roughly 91.7% of Mg was removed during deintercalation. This result demonstrated a successful electrochemical path for deintercalation of Mg from nano-Si. Unfortunately, so far, attempts to reverse the process by electrochemically storing (intercalation) Mg in nano-Si anode during charging have been unsuccessful. These failures have been attributed to the relatively larger nano Si particle sizes (∼100 nm) compared to nano-Sn (∼30–50 nm) that does show successful Mg storage.15,21 Hence, we understand only reducing particle size of nano-Si is not the answer. Due to the buckled honeycomb structure of silicene,22–25 diffusion should be enhanced drastically compared to nano-Si particles. Silicene additionally showcases some unique properties including: (a) beneficial mechanical and electronic properties;26,27 (b) zero-band gap,28 and (c) high influence on the future electronic industry.29
Lastly, silicene is easier to manufacture compared to oxide-free nano-Si.22–25 However, experimental measurements show that there exists a strong hybridization between Si and a given substrate (such as Ag(111)30) that influences the monolayer silicene heavily. This influence can be reduced by using multilayer silicene (starting from bilayer) where stronger inter-silicene layer coupling overrides the silicene–substrate interaction.22,31 In short, bilayer silicene showcases enhanced stability. Fortunately, synthesis of stabilized bilayer silicene has been successfully seen on CaF2 substrate.32 Bilayer silicene anode (BSA) has already been extensively researched for LIBs using molecular dynamics (MD) simulation and shows favourable reversible reactions.33–35 The current research has focused on investigating bilayer silicene with ABAB stacking as an anode material for storing Mg.
One of the key factors in determining the storing capability will be investigating diffusion and bond formation of Mg2+ ion in the anode. To that end, this research introduces external E-field to simulate the charging process of MIBs and study the effect on ion diffusion.33,36,37 A singular Mg2+ ion was introduced into BSA and calculations of mean square displacement (MSD), interaction energy, and accurate trajectory through the anode were carried out to assess the feasibility of Mg storage in this unique anode structure.
2 Methods
2.1 Molecular dynamics simulation
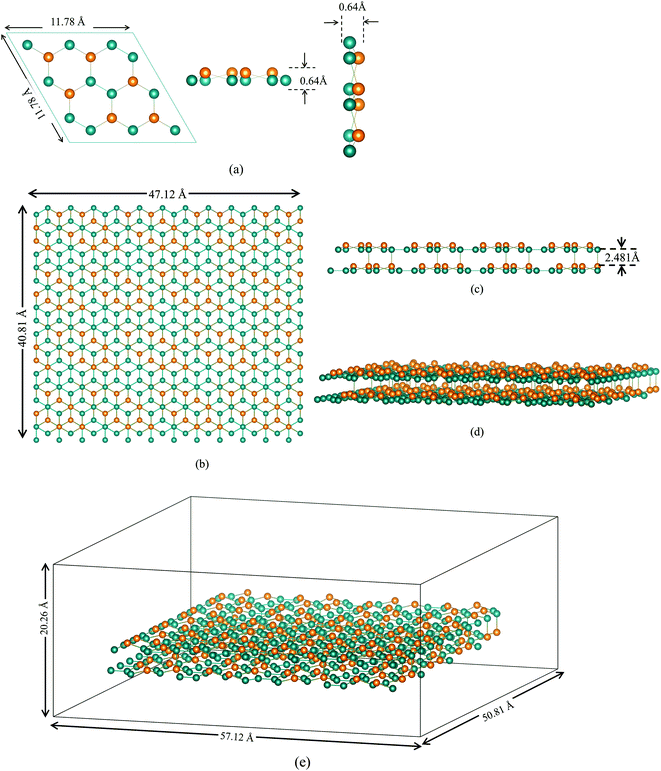
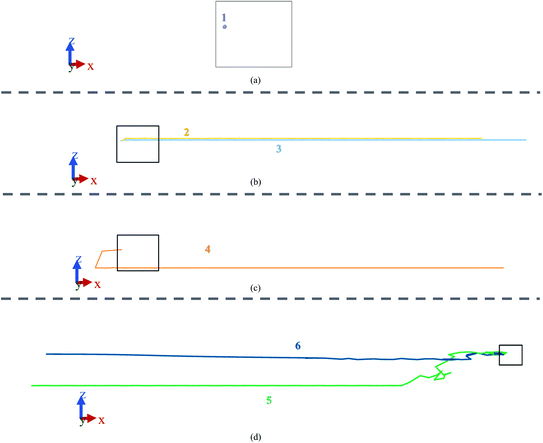
In the current experiment, a bilayer silicene with 4 × 4 phase was created using experimentally validated lattice parameters.35,38–40 This bilayer was constructed by placing two monolayer silicene unit cells shown in Fig. 1(a) on top of each-other in ABAB stacking.The final BSA structure shown in Fig. 1(b) has a total of 576 Si atoms in the system. At t = 0, the distance of the wall from Si atoms is set to a minimum value of 5 Å (in x and y directions), while the distance from the Si atoms of the upper sheet of silicene to the upper and lower walls of the container were set to be 11.5 Å and 5 Å respectively.34 Fig. 1(e) represents the simulation box after the inclusion of vacuum.
It is important to enumerate here that this study follows a methodology of 4 × 4 surface construction – a process that is validated through experimental studies of silicene grown on Ag substrate41,42 – and which is distinctly different from the more theoretical free standing silicene structure. Published literature23,41,42 often have conflicting information, as well as being minimal in content, on the surface configuration of the second layer of silicene. In this study, both layers were made in the 4 × 4 phase, which were then energy minimized to get a more stable configuration. Furthermore, Ag substrate does not undergo chemical reaction with ions while inter-silicene layer coupling overrides the effect of substrate layers on silicene.22,31 This study therefore eliminates simulating the substrate and uses a wall potential to account for the structural effect in accordance with standard practice.33,43,44 This final unit cell, shown in Fig. 2, closely resembles the unit cell grown on Ag(111) substrate under ultrahigh vacuum (UVH) chamber.23,45 Details on energy minimization process is provided in the latter part of the Methodology section.
The current work on bilayer silicene utilizes the EDIP (Environment Dependent Interatomic Potential)46 force field. Here the energy of the configuration is expressed as a sum over single-atom energy,
| p(Z) = e−βZ2 |
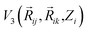 represents radial and angular factors.46 There are 13 empirical parameters in EDIP potential, and they are provided in Table 1.
represents radial and angular factors.46 There are 13 empirical parameters in EDIP potential, and they are provided in Table 1.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| A | 7.9821730 eV | γ | 1.1247945 Å |
| B | 1.5075463 Å | λ | 1.4533108 eV |
| a (cutoff) | 3.1213820 Å | μ | 0.6966326 |
| c (cutoff) | 2.5609104 Å | ρ | 1.2085196 |
| α | 3.1083847 | σ | 0.5774108 Å |
| β | 0.0070975 | Q0 | 312.1341346 |
| η | 0.2523244 |
Previously this potential parameters have been used in accurately calculating Young's modulus,47 mechanical,48 thermal transport in silicene.49 With regards to simulating the interactions between Mg–Si and Mg–Mg, the current research utilized a modified Morse potential50 – a choice validated by previous work as being accurate for this function. Periodic boundary conditions (PBC) were applied along all three dimensions (x, y, z). To avoid the rotation of the 2D anode a weakly attractive Lennard-Jones (LJ) potential (12-6) was applied on all 6 walls of the simulation cell. Parameters of Morse & LJ potential for different interactions are given in Table 2.
Geometric minimization of potential energy was performed in our structure followed by a dynamic relaxation with 0.0001 ps timestep. The first step in this process was to eliminate any remaining hot spots; to that end, the structure was equilibrated under 4 K temperature for 20 ps using NVT ensemble.51 The structure was then slowly heated from 4 K to 293 K under NVT ensemble over 120 ps with a heating rate of 2.41 K ps−1. Finally, another equilibration under NVT ensemble for 220 ps was run at 293 K.
We applied a considerably larger E-field (0.2 V Å−1, 0.4 V Å−1, 0.6 V Å−1, 0.8 V Å−1, 1.0 V Å−1) compared to what is applied in a commercial setting. This was done to accelerate the intercalation process in an effort to complete the computation in a reasonable time; this procedure and the range of E-field utilized are standard methods in MD simulation and have been published extensively before where the E-field range falls typically in the 0 V Å−1 to 1.5 V Å−1 range.36,52–56 Hence the simulation times used in this work and the experimental times in commercial batteries should not be compared directly as they are measured in different scales.
While applying external E-fields in MD simulation, an unmodified thermostat can generate faulty results due to interference. In a previous study, a modified Nose–Hoover (NH) thermostat and a CSVR thermostat which use non-Hamiltonian and Hamiltonian dynamics, respectively, were employed to account for this interference.55 In the present simulation, three thermostats were employed to run MD simulation under the same E-field strength to check the consistency of the results: (a) “Nose–Hoover” ensemble (NVT) (results included in ESI†);51 (b) modified “Nose–Hoover” ensemble (NVT) (results included in ESI†) where the thermostat only calculates temperature based upon kinetic energy-resolved in directions normal to the E-field;57 (c) CSVR thermostat58 with a separate time integrator, NVE. With high congruence in results between the three thermostat modes providing further validation of the accuracy of the executed methodology, this current work has focused on results derived using the CSVR thermostat, as it has been shown to be the least likely to manifest the “flying ice cube effect”59 (ESI 1.1†) or develop problematic results due to interaction with E-field.55 The quantitative details supporting these procedures have been included in the ESI file.†
The large-scale atomic/molecular massively parallel simulator (LAMMPS)60 program developed by Plimpton et al. was utilized to perform simulations to calculate relevant properties and predict the behavior of the Mg2+ ion in the BSA channel. The Verlet algorithm was used to integrate Newton's equations of motion. A very small timestep of 0.00001 ps or 0.01 fs (1 × 10−17 s) was utilized and the simulation was run for 50 ps. A small time step of 0.01 fs was used to accurately calculate the trajectories because during velocity rescaling in MD, using larger time steps could result in larger atomic jumps in between consecutive time steps leading to a faultier trajectory. Time step values in the range of 0.01–2 fs can be seen in published literature.25,44,55,56,61–65
2.2 First-principle calculations
In this study, first-principle calculations were performed to further verify the validity of utilizing the EDIP potential and the modified Morse potential for capturing the physics of silicene and Si–Mg interactions respectively. To this end, Density Functional Theory (DFT) calculations were carried out within the framework of the Vienna Ab initio Software Package (VASP).66,67 The approximations to the exchange–correlation functional were computed using the Generalized Gradient Approximation (GGA)68 together with the Perdew–Burke–Ernzerhof functional. The DFT-D3 method69 was employed to accurately describe the van der Waals interactions. The governing Kohn–Sham equations were solved using the projector wave augmented method.70 Since DFT is more computationally expensive, a smaller unit cell containing 72 Si atoms was used to model the BSA structure and for Mg-intercalation a single Mg-ion was placed within the bilayer of this silicene cell.The ground state electronic density and corresponding ground state energies were computed using a plane-wave basis set energy cut-off of 700 eV and a 3 × 2 × 1 gamma-centered Monkhorst–Pack K-point grid. The lattice of the BSA was relaxed via the force-based conjugate gradient approach71 with an energy convergence tolerance of 10−8 eV and a force/ion tolerance of 0.02 eV Å−1. To perform validation studies, the per atomic cohesive energy of pure silicene was computed using DFT using the following equation,
EDIP provides the closest agreement to the DFT computed cohesive energy, with Tersoff potential being a close second. On the other hand, Morse potential is very inaccurate in modeling the silicene structure as it predicts positive cohesive energy which would constitute a repulsive interaction between the silicene atoms. This validates the choice of EDIP potential as a suitable inter-atomic potential for modeling the physics of the silicene bilayer.
This study also uses a modified Morse potential to capture the Si–Mg interaction for Mg intercalation within the bilayer silicene. To demonstrate that the hybrid EDIP and modified Morse potential are sufficient in describing the Mg–silicene system, the absorption energy of Mg within BSA was computed using both MD & DFT. The following equation was employed for the calculation of absorption energy,
| Eabsorption = EBSA–Mg − Epristine–BSA − μMg |
| Absorption energy (eV) | |
|---|---|
| DFT | MD |
| −0.111 | −0.081 |
These results validate the use of modified Morse potential in hybrid form along with EDIP to capture the physics of Mg–Si interaction in a bilayer silicene anode.
3 Results and discussion
3.1 Effect of E-field
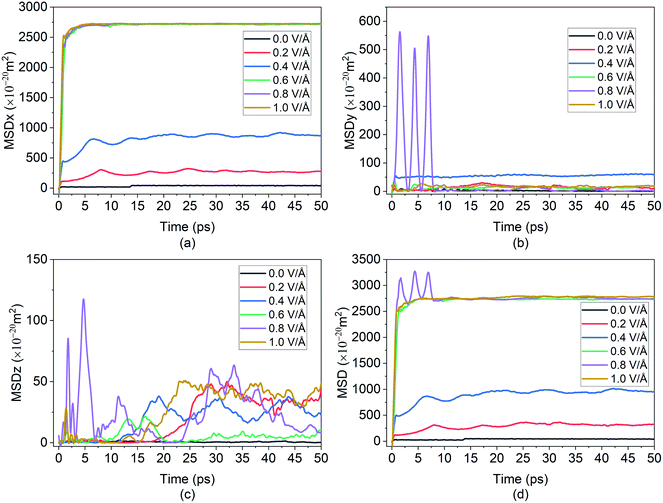
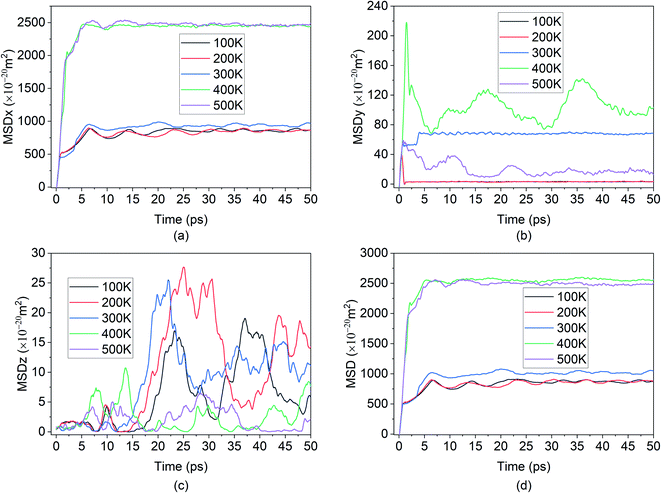
The fourth element is the total squared displacement, i.e. (dx × dx + dy × dy + dz × dz), summed and averaged over atoms in the group. The deviation of position for MSD calculation is taken with respect to the initial position of the Mg2+ ion. Smoothed MSD vs. time curves presented in Fig. 3 demonstrate the trends clearly by eliminating minute vibrations; the unsmoothed curves can be found in the ESI section (refer to ESI: 1†).
In the present experiment, an external E-field was applied in the x-direction. This led, as expected, to the distinctive movement of the Mg2+ ion in the x-direction as shown in Fig. 3(a), and with some degree of random motion observed in the y and z directions shown in Fig. 3(b) and (c) respectively. This serves as a validation of E-field being the primary contributor for the diffusion of Mg2+ in BSA.
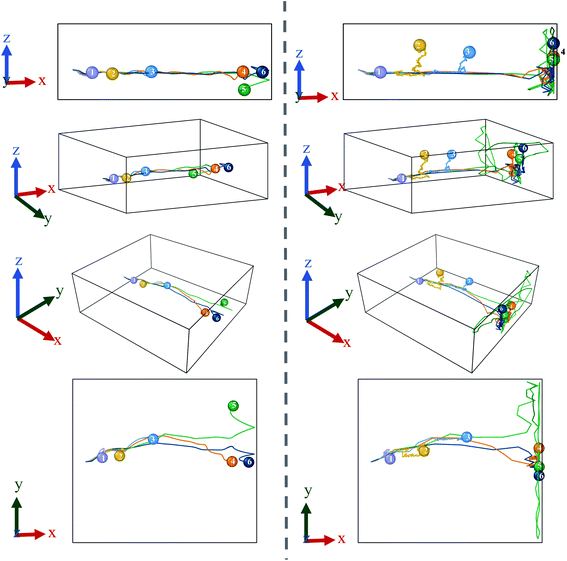
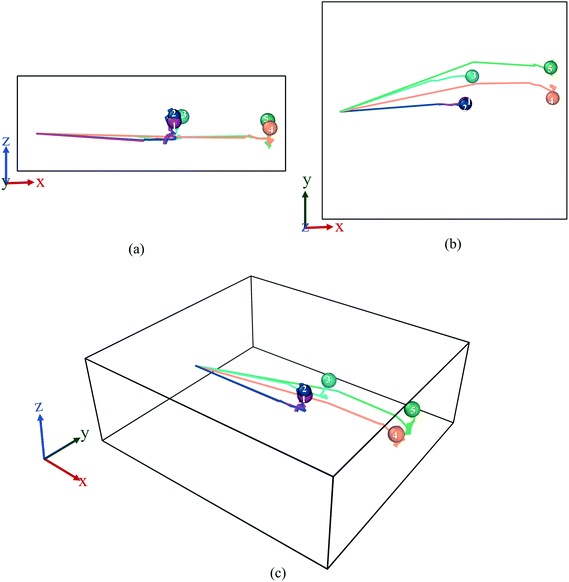
From the graph in Fig. 3(a), it can be observed that there is little to no changes in the Mg2+ ion position in the absence of an E-field (highest value for MSD ∼49 × 10−20 m2). In the absence of E-field, diffusion of ion is solely dependent on thermal contribution and hence Fig. 3(a) indicates that the thermal contribution for the Mg2+ ion displacement is very trivial. This phenomenon is better observed in Fig. 4 where the trajectory of Mg2+ ion under 0 V Å−1 represented by trajectory 1 shows barely any movement with time. Now, applying 0.2 V Å−1 at the same temperature (∼293 K) (hence with the same thermal contribution) leads to a large jump in MSD (∼300 × 10−20 m2) and larger movement in x direction in trajectory 2 shown in Fig. 4. As can be observed from both the MSD curve in x direction and trajectory profile given in Fig. 3(a) and 4 respectively, with increasing E-field strength Mg2+ ion travels larger distance. The most significant impact occurs when 0.6 V Å−1 is applied – four times larger in magnitude compared to the MSD value when an E-field of 0.4 V Å−1 is applied (∼900 × 10−20 m2 at 0.4 V Å−1 vs. ∼2710 × 10−20 m2 at 0.6 V Å−1). Moreover, we can see that prior to 0.6 V Å−1, increase in E-field (from 0.2 V Å−1 to 0.4 V Å−1) results in a comparatively smaller increase in MSD – with a difference in values ∼600 × 10−20 m2. From Fig. 4, the trajectory profile of Mg2+ ion under 0.6 V Å−1 represented by trajectory 4 at both 1 ps and 50 ps shows significantly larger movement compared to trajectory 1, 2 & 3 representing Mg2+ movement at 0, 0.2, 0.4 V Å−1 respectively. The reason becomes apparent in Fig. 4, where at a lower E-field strength, the ion can only move a few nanometres (<10 nm) of distance inside the BSA channel. On the other hand, under the influence of a higher E-field strength (≥0.6 V Å−1), the ion reaches the end portion of the anode with ease (within 1 ps).
It can be further seen from the trajectory profile in Fig. 4 that within the first ∼1 ps, the Mg2+ ion under all E-field strength finds its equilibrium position, and this distance travelled is directly proportional to the E-field strength (the higher the strength, it is clearly seen that the more the distance the ion traverses). To further prove this assertion, we provide the MSD and interaction energy curve with respect to time in Fig. 5(a) and (b) respectively, where we can see even though there are fluctuations in data prior to reaching 1 ps, the trends stabilize and show clear sign of reaching their equilibrium position. A detailed discussion on interaction energy can be found in later section.
 | ||
| Fig. 5 Smoothed curve: (a) total MSD vs. time (b) interaction energy vs. time for first 1 ps of simulation. | ||
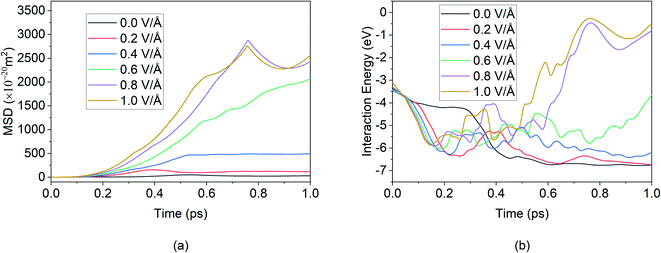
Furthermore in Fig. 4, it can be noticed that after 50 ps of simulation, the ion is locked into a fixed x-position. The only changes in position observed are in the z direction – this can be attributed to the movement of the entire bilayer silicene in that z direction. Movement of BSA corresponds to the lack of structural support in z direction as unlike the bulk, the 2D material has vacuum surrounding it. In a real system, this movement will be limited due to anode being confined by surrounding insulating material, or neighbour 2D layers. In this present work a similar effect was simulated by applying the LJ (12-6) potential in wall in an effort to minimized and limit in the z direction. Similarly, from Fig. 6(a), it can be further observed, after the initial jump in MSD in x direction upon application of an E-field of 0.6 V Å−1, further increase in the E-field strength does not have a noticeable impact on MSD. The dense and large oscillating MSD curves (in the top zoomed-in graph of Fig. 3(a)) are indicative of the same conclusion, interaction of the ion with the wall potential. It is noticed however that after a while, the ion demonstrates fewer oscillations and reaches a saturation level. It is known that saturation in any given MSD curve is characteristic of solid phase behaviour, where the ion remains in its fixed position and undergoes vibration.56 It can thus be clearly stated here that the Mg2+ ion in the current system has formed strong bonds with the Si atoms in BSA and has thereby become locked-in within the solid matrix and the MSD shows a saturation instead of growth. This fact implies that in the presence of a barrier, the ion can form bonds with BSA even at high E-field values.
 | ||
| Fig. 6 MSD in x direction of Mg2+ ion in BSA for 100 ps in the absence of applied boundary condition. | ||
As ion movement is primarily seen in x direction, total MSD curve shown in Fig. 3(d) naturally resembles the MSD behaviour in that direction. An interesting deviation is observed under 0.8 V Å−1 where a significant contribution of MSD in y and z directions under 0.8 V Å−1. This is also observed in Fig. 4, where comparing trajectory 5 & 6 representing Mg2+ ion movement under 0.8 V Å−1 and 1.0 V Å−1 we can notice a significant movement is seen in y as well as z directions i.e., highest overall random motion in trajectory 5. This behaviour does not correspond to the movement of entire BSA; rather, it is an effect of the free movement of the Mg2+ ion after it leaves the channel and the E-field is not strong enough to keep the ion motion confined in the direction of field (x direction). However, after ∼10 ps when Mg2+ ion loses its momentum and come close to BSA, it finally forms bond and becomes locked in an equilibrium position as well.
While a consistent expectation would be that 1 V Å−1 producing trajectory 6 showcases a similar, if not higher randomness, compared to trajectory 5, the results show an opposite behaviour. A logical hypothesis for this phenomenon could be that a higher E-field (1 V Å−1) overrides the randomness of the Mg2+ ion, forcing it to move primarily in the x direction, and to ultimately face restrictions only on the face of boundary. This is further validated as the largest x-direction displacement is observed under 1 V Å−1 and can be seen in trajectory (Fig. 4) and MSD in x direction (Fig. 3(a)). It therefore appears that an E-field of 0.8 V Å−1, showcasing trajectory 5, is an inflexion point in the spatial behaviour of the Mg2+ within the BSA.
Now, as mentioned earlier, at higher E-field (≥0.6 V Å−1) and below ∼1 ps, the ion leaves the BSA channel; it can therefore be extrapolated that the bond formation was largely assisted via the presence of boundary. In a real-life situation, for a battery under a larger charging voltage together with complex interactions between several ions present in the system, the interaction between boundary and individual ions might be much more complicated.
Given this context, we removed the vacuum in the x and y directions and removed the wall potentials and then ran the simulation for 100 ps under periodic boundary condition. In the absence of the applied boundary condition the changes in MSD curve in x direction is given in Fig. 6.
Here we notice that the MSD of Mg2+ ion in x direction keeps on growing, in contrast to Fig. 3(a) that showed that the MSD curve in x direction stopped growing within the first few picoseconds when boundary condition was applied. However, in Fig. 6, the growth is seen even below 0.6 V Å−1 where they supposedly didn't interact with wall potential previously. To investigate this phenomenon further, trajectory profile for 100 ps in absence of boundary conditions is given in Fig. 7, where we can visualize that, this movement is actually attributed to the entire BSA movement under applied E-field in x direction, as in the absence of a boundary condition, a 2D material will have no support to hold it in place. As the trajectory profile was generated under PBC conditions (unwarped), movement of entire system (BSA & Mg2+ ion) is represented by lines moving forward from the simulation cell, whereas in case when movement of only ion is present, lines appear backward moving. From trajectory profiles given in Fig. 7(a), we can see at 0.0 V Å−1 there's no movement in the system. In Fig. 7(b), we notice trajectory 2 & 3 under E-field strength 0.2 V Å−1 and 0.4 V Å−1 respectively, the entire system moves towards the E-field. As BSA is charge neutral, movement of BSA only occurs when it forms strong bonds with cation Mg2+. We also notice trajectory 3 is greater than trajectory 2. We see an interesting phenomenon for trajectory 4 given in Fig. 7(c) under E-filed strength 0.6 V Å−1, at first trajectory moves backwards for first ∼18.56 ps, signifying Mg2+ ion doesn't form any bonds during this period. After this initial random movement, Mg2+ ion indeed finds an equilibrium position and form bonds; hence trajectory 4 shows forward movement for the rest of the simulation period. A stark contrast is observed at Fig. 7(d) where trajectory 5 and 6 under the E-field value of 0.8 V Å−1 and 1.0 V Å−1 shows only backward movement, signifying ions don't form bonds in the system. MSD curve in Fig. 6 also shows that at E-field ≥ 0.8 V Å−1, the MSD curve grows significantly more than that is observed under 0.6 V Å−1, which signifiest higher diffusion rate of Mg2+ ion, which makes it harder to form bonds.
In consistent with our previous observation of 0.8 V Å−1 being the inflexion point of spatial movement, here as well we notice higher random movement for trajectory 5 compared with rest including trajectory 6.
3.2 Interaction energy
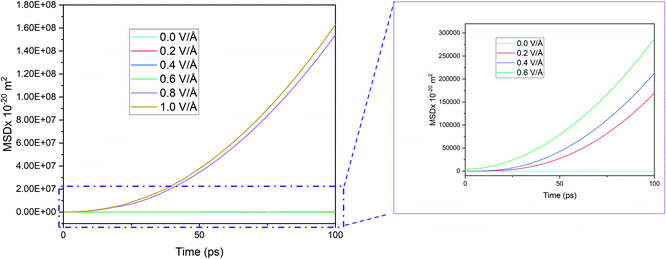
The interaction energy is the total energy of interactions between Mg2+ ion with all the Si atoms in BSA based on the pair potentials acting between these two species. Thus, the computed interaction energy plots represent the total energies of interaction between a single Mg and surrounding silicon atoms as it travels through the channel. Further proof of the presence of an inflexion point and dependence of E-field strength on Mg2+ ion diffusion in BSA can be observed from the interaction energy graph given in Fig. 8, where interaction energy of the Mg2+ ion with silicene depends directly on the position of the ion inside the BSA channel or beyond it.33 This energy therefore indirectly depends on the E-field strength determining the motion of the ion in the channel. Naturally at higher E-field, ion motion will be higher and hence more interaction energy will be expected which proves right for E-field values 0.0–0.6 V Å−1, as can be observed in Fig. 8.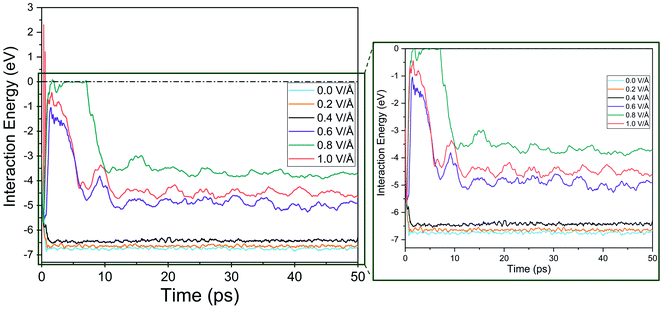 | ||
| Fig. 8 Interaction energy between Mg2+ ion and bi-layer silicene anode with respect to increasing electric field. | ||
It is noticed that interaction energy is higher at an E-field strength of 0.8 V Å−1 compared to that at 1 V Å−1. As discussed previously, after 0.8 V Å−1, the Mg2+ ion leaves the anode easily and shows random motion in y and z direction. Again, while it is a reasonable expectation that at 1 V Å−1 similar, if not higher, randomness and MSD in y, z would be observed, the reality does not show that. This is because a higher E-field beyond the critical inflexion point of 0.8 V Å−1 overrides the randomness of the Mg2+ ion, leading to its movement primarily in the x direction, leading ultimately for it to face restrictions on the face of the wall boundary.
At 0.8 V Å−1, prior to 10 ps, 0 eV energy between Mg2+ and silicene is observed. This indicates that during this time period, the Mg2+ ion leaves the BSA channel and moves randomly till coming close enough again to start interacting with silicene and forming bonds. Similar phenomenon is also noticeable for 0.6 V Å−1 and 1 V Å−1 but with less severity (prior to 10 ps, and with the energy never reaching 0 eV). At 0.6 V Å−1, the ion leaves the channel and returns instantaneously as the provided E-field is not enough to propel it further; at 1 V Å−1, only movement is seen at x direction where bonds between Mg–Si are formed.
3.3 Radial distribution function (RDF)
For successful intercalation of ion, it not only needs to have easy diffusion capability in anode but also the ability to form bond and stay bonded for a required period of time (during charging). Finally, after adequate analysis on diffusivity of Mg2+ ion, we need to focus on bond formation of ion in anode, to that end we provide RDF analysis which will reveal the probability of finding a given particle at a distance from another tagged particle. In this section we include RDF analysis under applied boundary condition, as boundary conditions doesn't alter RDF much due to the analysis being limited to mostly the nearest neighbour shells. The RDF analysis in Fig. 9(a), reveals distribution of Si atoms around Mg2+ ion and the first major peak indicates the nearest neighbour (NN) distances from central atom (Mg2+ ion).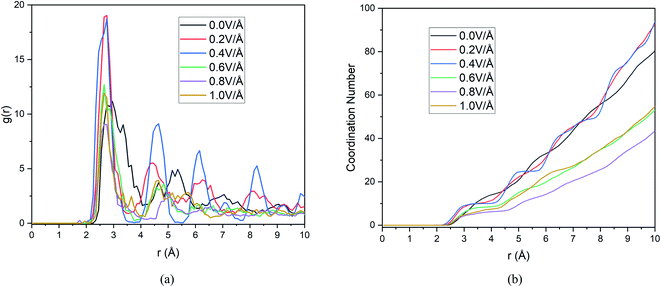 | ||
| Fig. 9 Changes in (a) RDF analysis & (b) coordination number (CN) under the effect of different electric field. | ||
These results and the CN numbers of first NN shell is summarized in Table 5, which reveals that NN bond distance decreases with increasing E-field. The calculated bond distance under E-field application 2.75 Å is closely comparable to experimental73 and first principal calculation,50,73,74 this serves as a validation step for our current result. However, we notice the highest probability of finding NN atoms is observed under 0.2 & 0.4 V Å−1 and further increase in E-field decreases the probability drastically. We also notice that ≤0.4 V Å−1 peaks seen in Fig. 9(a) is much more ordered that is indicative of solid phase.
| Data source | Mg–Si bond length (Å) | ||
|---|---|---|---|
| Experimental73 | 2.664, 2.733, 2.861 | ||
| First-principal calculation | 2.7552 (ref. 50) | ||
| 2.77 (ref. 74) | |||
| 2.620, 2.697, 2.726 (ref. 73) | |||
| Simulation | E-field strength | Bond length (Å) | Coordination number (nearest neighbour shell around Mg2+ ion) |
| 0.0 V Å−1 | 2.95 | 8.0396 | |
| 0.2 V Å−1 | 2.75 | 10.08911 | |
| 0.4 V Å−1 | 2.75 | 9.9703 | |
| 0.6 V Å−1 | 2.65 | 8.33663 | |
| 0.8 V Å−1 | 2.65 | 5.09901 | |
| 1.0 V Å−1 | 2.65 | 5.51485 | |
Now, in Fig. 9(b) we include the coordination number as a function of cut off distance. In consistent with RDF analysis, we observe highest growth of CN at 0.2 & 0.4 V Å−1, increasing the E-field any further decreases CN to a lower value than that of CN at 0.0 V Å−1. As we know, higher CN value indicates higher chance of bond formation, as Mg2+ ion will be surrounded by more Si atom in its NN shell. Hence bond formation is highest at the E-field range of 0.0–0.4 V Å−1. Therefore, we conclude that, even though diffusion increases at higher E-field strength, bond formation doesn't take place beyond 0.4 V Å−1. On the other hand, even though in the absence of E-field, bond formation takes place as can be seen from RDF graph, we notice from Section 3.1.1, diffusion doesn't take place in the absence of E-field for any boundary condition. This indicates that there exist an optimum E-field range, in our case 0.2–0.4 V Å−1, where E-field is strong enough to ensure diffusion as seen in Section 3.1.1 and weak enough to ensure bond formation with highest CN numbers. This synergy between diffusion and bond formation, will play an important role in defining E-field parameter, even in experimental setup to ensure the intercalation of Mg2+ ion in BSA.
3.4 Effect of temperature
The effect of temperature on the Mg intercalation in the BSA was investigated by running the same simulation set-up at temperatures of 100 K, 200 K, 300 K, 400 K & 500 K. From the temperature-dependent MSD curves given in Fig. 10, it is clear that there exists an inflection point between 300 K & 400 K where the extent of diffusion is greatly increased. There is a clear jump in the total MSD for temperatures of 400 K & 500 K (∼2500 × 10−20 m2) relative to the total MSD at the lower temperatures of 100 K, 200 K & 300 K (∼1000 × 10−20 m2). Similar to the previous section, the contribution to the total MSD is dominated by the MSD in the x-direction, which is to be expected since the E-field was applied in that direction. The saturation of all five of the curves seems to indicate that Mg–Si coordination and bond formation took place in all five cases, however, the trajectories paint a different picture.It can be seen from Fig. 11, that for the higher temperatures 400 K & 500 K, the Mg-ions reached the edge of the BSA simulation cell and was only stopped due to interaction with the wall potential. Thus, successful intercalation did not take place.
This is further corroborated by the RDF shown in Fig. 12. For the temperature values of 100 K, 200 K & 300 K, the peaks of the RDF overlap indicating the same coordination number and extent of bond formation between Si and Mg for these temperatures.
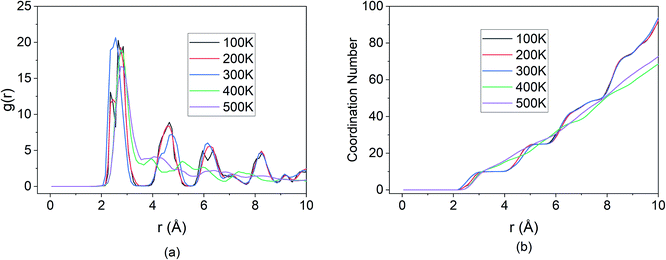 | ||
| Fig. 12 Changes in (a) RDF analysis & (b) coordination number (CN) under the effect of different temperature. | ||
However, beyond the inflection point, for temperature values of 400 K & 500 K, only the first peak of the RDF is well defined. The subsequent peaks that were present in the lower temperatures are no longer visible at higher temperatures. The first peak results from the boundary condition imposed on the wall and is representative of the Mg-ion interacting with the wall potential. However, due to the absence of Si atoms beyond the boundary, the coordination with other nearest neighbour atoms does not take place. This indicates that for the BSA structure, operating at temperatures higher than 300 K, causes the diffusion rates to increase beyond the threshold at which bond formation between Si and Mg can slow down Mg diffusion. Thus, the maximum operating temperature for the simulated BSA cell exists in the 300–400 K temperature range.
3.5 Effect of E-field directions
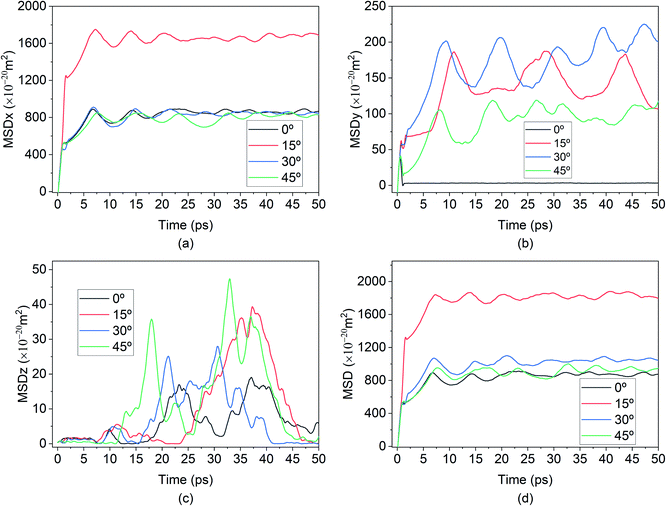
The behaviours of the Mg-ion within the BSA channel doesn't only depend on the magnitude of the E-field but also on the direction in which it is applied. This direction dependency can be investigated within the framework of our MD study. Since this study is focused on the motion of the Mg-ion through the channel, the variations of the E-field will have to remain confined to the X–Y plane. To illustrate how the behaviour Mg-interaction changes with the E-field direction, 0.4 V Å−1 E-fields were applied at respectively 0°, 15°, 30° & 45° from the positive X-axis in the X–Y plane at a constant 100 K temperature.As discussed before, the saturation behaviour of the MSD curve illustrated on Fig. 13, denotes the bond formation between Mg–Si within the BSA. It is therefore clear from Fig. 13(d), which denotes the total MSD behaviour of Mg-ion with respect to time and E-field direction, that the most optimal direction for Mg-ion transport within the channel is 15° with respect to the positive-X direction. This is inferred from the higher MSD value (∼1800 × 10−20 m2) at which saturation is achieved for Mg-ions traveling at 15°, relative to the other three directions as shown in Fig. 13(d). This contribution to the total MSD is mainly dominated by the increase in the MSD in the X-axis. Therefore, even though the MSD in the Y-axis is largest for E-field in the 30° direction (∼175 × 10−20 m2), it is only slightly larger than that for the E-field in the 15° direction (∼150 × 10−20 m2). However, in the x-axis, the MSD in the 15° (∼1600 × 10−20 m2) is significantly higher compared to the 0°, 30° & 45° directions. This is further confirmed by the visualization of the trajectories of the Mg atom within the BSA as shown in Fig. 14. Even though the same E-field was applied in all 4 directions, it can be clearly seen that the distance travelled by the Mg-ion in the 15° as indicated by the orange path, is the farthest distance relative to all other three directions. The trajectories also confirm the fact that the intercalation did take place within the BSA simulation cell and that the saturation in the MSD curves was not brought on by the Mg-ion hitting the wall potential at the edge of the simulation box.
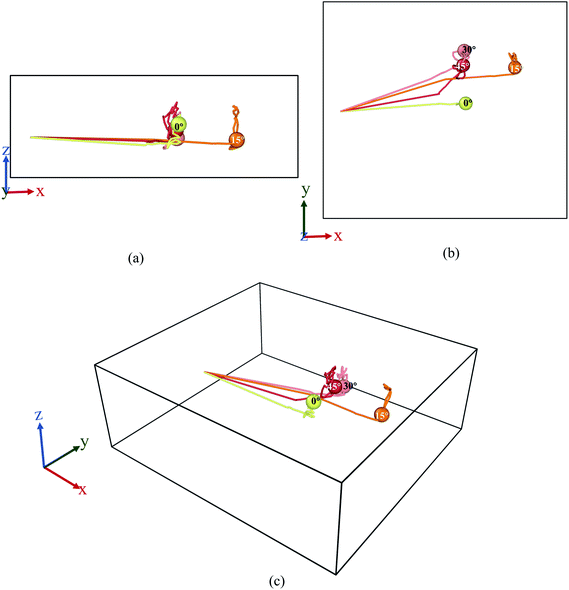 | ||
| Fig. 14 Trajectory profile for 50 ps where data was taken every 0.1 ps. Here, (a) front, (b) top, (c) perspective view ((1) yellow-0°, (2) orange-15°, (3) pink-30°, (4) red-45°). | ||
Additionally, the RDF shown in Fig. 15 demonstrates that while the MSD and travel path for the 15° E-field is significantly greater than the other three directions, the extent of bond formation between the Mg and Si is not affected by altering the E-field direction.
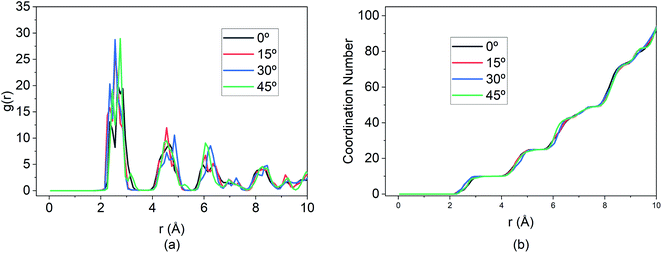 | ||
| Fig. 15 Changes in (a) RDF analysis & (b) coordination number (CN) under the effect of different direction of E-field. | ||
The peaks of the first, second and so on, nearest neighbours overlap for all three directions indicating that the coordination number is the same for all four cases. This illustrates that, at optimal E-field magnitude, altering the direction of the field can enhance the diffusion of Mg within the BSA while still ensuring similar intercalation behaviour as shown by RDF and coordination number.
4 Conclusions
While previous research on MIBs showcase a high rate of de-intercalation (∼91.7%) of Mg from nano-Si anode, the reverse process of intercalation has never been achieved, with the prime reason being attributed to large particle sizes. In this current research, it has been shown that by decreasing dimensionality in 2D porous BSA, Mg2+ ion can be successfully stored (intercalated). Results further show that there exists an optimum E-field strength that's strong enough to ensure diffusion of ion in BSA and weak enough to let ion form bonds. For our current simulation setup this E-field value ranges from 0.2 to 0.4 V Å−1. Hence, in the development of a Si-based anode investigation should focus on E-field parameters alongside investigating particle sizes and dimensions.Mg2+ ion under 0.8 V Å−1 shows some interesting results, with the highest displacement in y and z direction as seen from MSD curves and trajectory, also shows the highest interaction energy. Our conclusion is that the ion leaves the channel readily under this high E-field same as an ion under 1 V Å−1; however, unlike 1 V Å−1, this E-field strength is not strong enough to override its tendency to move randomly and hence at 0.8 V Å−1, the ion moves more freely.
Additionally, for a given E-field magnitude, varying the direction of the field changes the diffusion behavior as seen from the direction dependent MSD and trajectory. It has been demonstrated that among the range of directions between 0° and 45°, the highest diffusion is achieved in the 15° direction. However, the RDF and CN illustrated that the change in field direction did not alter the extent of Si–Mg bond formation and thus led to successful intercalation in all cases.
Furthermore, the effect of temperature has also been investigated leading to the conclusion that there is a maximum operating temperature beyond which the thermal contribution to the diffusion will prevent the bond formation and storage of Mg within the BSA. For the present simulated cell, this inflection point exists between 300 K & 400 K.
The significance of the present research has been in proving the potential of a Si based anode for MIBs that is both inexpensive and highly efficient. Moreover, the compatibility of the silicene material with currently well-established silicon-based semiconductor industry opens the door for using current commercial electrolytes and cathode materials with the demonstrated MIB system.
Author contributions
S. Ahsan and A. R. conceptualized the project, designed the methodology, did formal analysis, investigation, visualization and wrote the paper. S. Ahsan, A. R. and M. F. N. T. validated the model, curated data and software usage. S. Ahmed supervised the project and revised the manuscript. H. A. J., S. S., S. S. N., M. T. I., A. F. I., M. R. J., M. S. I., K. M. S. provided resources. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Notes and references
- A. Manthiram, ACS Cent. Sci., 2017, 3, 1063–1069 CrossRef CAS PubMed.
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243–3262 RSC.
- H. D. Yoo, E. Markevich, G. Salitra, D. Sharon and D. Aurbach, Mater. Today, 2014, 17, 110–121 CrossRef CAS.
- C. Vaalma, D. Buchholz, M. Weil and S. Passerini, Nat. Rev. Mater., 2018, 3, 18013 CrossRef.
- Y. Liang, H. Dong, D. Aurbach and Y. Yao, Nat. Energy, 2020, 5, 646–656 CrossRef CAS.
- H. D. Yoo, I. Shterenberg, Y. Gofer, G. Gershinsky, N. Pour and D. Aurbach, Energy Environ. Sci., 2013, 6, 2265–2279 RSC.
- J. W. Choi and D. Aurbach, Nat. Rev. Mater., 2016, 1, 16013 CrossRef CAS.
- R. Attias, M. Salama, B. Hirsch, Y. Goffer and D. Aurbach, Joule, 2019, 3, 27–52 CrossRef CAS.
- R. Mohtadi and F. Mizuno, Beilstein J. Nanotechnol., 2014, 5, 1291–1311 CrossRef PubMed.
- H. Dong, O. Tutusaus, Y. Liang, Y. Zhang, Z. Lebens-Higgins, W. Yang, R. Mohtadi and Y. Yao, Nat. Energy, 2020, 5, 1043–1050 CrossRef CAS.
- D. Aurbach, Z. Lu, A. Schechter, Y. Gofer, H. Gizbar, R. Turgeman, Y. Cohen, M. Moshkovich and E. Levi, Nature, 2000, 407, 724–727 CrossRef CAS PubMed.
- D. Aurbach, I. Weissman, Y. Gofer and E. Levi, Chem. Rec., 2003, 3, 61–73 CrossRef CAS PubMed.
- O. I. Malyi, T. L. Tan and S. Manzhos, J. Power Sources, 2013, 233, 341–345 CrossRef CAS.
- L. Wang, S. S. Welborn, H. Kumar, M. Li, Z. Wang, V. B. Shenoy and E. Detsi, Adv. Energy Mater., 2019, 9, 1–7 Search PubMed.
- H. Yaghoobnejad Asl, J. Fu, H. Kumar, S. S. Welborn, V. B. Shenoy and E. Detsi, Chem. Mater., 2018, 30, 1815–1824 CrossRef CAS.
- D. Zhang, J. Fu, Z. Wang, L. Wang, J. S. Corsi and E. Detsi, J. Electrochem. Soc., 2020, 167, 050514 CrossRef CAS.
- T. S. Arthur, N. Singh and M. Matsui, Electrochem. Commun., 2012, 16, 103–106 CrossRef CAS.
- N. Singh, T. S. Arthur, C. Ling, M. Matsui and F. Mizuno, Chem. Commun., 2013, 49, 149–151 RSC.
- Y. Shao, M. Gu, X. Li, Z. Nie, P. Zuo, G. Li, T. Liu, J. Xiao, Y. Cheng, C. Wang, J. G. Zhang and J. Liu, Nano Lett., 2014, 14, 255–260 CrossRef CAS PubMed.
- F. Legrain and S. Manzhos, J. Power Sources, 2015, 274, 65–70 CrossRef CAS.
- L. R. Parent, Y. Cheng, P. V. Sushko, Y. Shao, J. Liu, C. M. Wang and N. D. Browning, Nano Lett., 2015, 15, 1177–1182 CrossRef CAS PubMed.
- R. Yaokawa, T. Ohsuna, T. Morishita, Y. Hayasaka, M. J. S. Spencer and H. Nakano, Nat. Commun., 2016, 7, 6–11 Search PubMed.
- P. Vogt, P. Capiod, M. Berthe, A. Resta, P. De Padova, T. Bruhn, G. Le Lay and B. Grandidier, Appl. Phys. Lett., 2014, 104, 4–9 CrossRef.
- C. L. Lin, R. Arafune, K. Kawahara, N. Tsukahara, E. Minamitani, Y. Kim, N. Takagi and M. Kawai, Appl. Phys. Express, 2012, 5, 5–8 Search PubMed.
- M. De Crescenzi, I. Berbezier, M. Scarselli, P. Castrucci, M. Abbarchi, A. Ronda, F. Jardali, J. Park and H. Vach, ACS Nano, 2016, 10, 11163–11171 CrossRef CAS PubMed.
- R. E. Roman and S. W. Cranford, Comput. Mater. Sci., 2014, 82, 50–55 CrossRef CAS.
- C. Grazianetti, D. Chiappe, E. Cinquanta, G. Tallarida, M. Fanciulli and A. Molle, Appl. Surf. Sci., 2014, 291, 109–112 CrossRef CAS.
- Z. Ni, Q. Liu, K. Tang, J. Zheng, J. Zhou, R. Qin, Z. Gao, D. Yu and J. Lu, Nano Lett., 2012, 12, 113–118 CrossRef CAS.
- G. Le Lay, Nat. Nanotechnol., 2015, 10, 202–203 CrossRef PubMed.
- S. Cahangirov, M. Audiffred, P. Tang, A. Iacomino, W. Duan, G. Merino and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 035432 CrossRef.
- Y. Yao, A. Liu, J. Bai, X. Zhang and R. Wang, Nanoscale Res. Lett., 2016, 11, 371 CrossRef PubMed.
- T. N. Do, G. Gumbs, P. H. Shih, D. Huang, C. W. Chiu, C. Y. Chen and M. F. Lin, Sci. Rep., 2019, 9, 1–15 CrossRef CAS PubMed.
- A. E. Galashev, Y. P. Zaikov and R. G. Vladykin, Russ. J. Electrochem., 2016, 52, 966–974 CrossRef CAS.
- A. Y. Galashev and Y. P. Zaikov, J. Appl. Electrochem., 2019, 49, 1027–1034 CrossRef CAS.
- A. Y. Galashev and K. A. Ivanichkina, ChemElectroChem, 2019, 6, 1525–1535 CrossRef CAS.
- V. Ponce, D. E. Galvez-Aranda and J. M. Seminario, Phys. Chem. Chem. Phys., 2021, 23, 597–606 RSC.
- A. E. Galashev and Y. P. Zaikov, Russ. J. Phys. Chem. A, 2015, 89, 2243–2247 CrossRef CAS.
- A. E. Galashev, O. R. Rakhmanova and K. A. Ivanichkina, J. Struct. Chem., 2018, 59, 877–883 CrossRef CAS.
- W. Rui, W. Shaofeng and W. Xiaozhi, J. Appl. Phys., 2014, 116, 024303 CrossRef.
- A. Bourke, R. P. Lynch and D. N. Buckley, ECS Trans., 2013, 53, 59 CrossRef.
- H. X. Zhong, R. G. Quhe, Y. Y. Wang, J. J. Shi and J. Lü, Chin. Phys. B, 2015, 24, 087308 CrossRef.
- Y. Yamada-Takamura and R. Friedlein, Sci. Technol. Adv. Mater., 2014, 15, 64404 CrossRef PubMed.
- A. Y. Galashev and A. S. Vorob'ev, J. Solid State Electrochem., 2018, 22, 3383–3391 CrossRef CAS.
- A. Y. Galashev and K. A. Ivanichkina, Phys. Lett. A, 2017, 381, 3079–3083 CrossRef CAS.
- A. Curcella, R. Bernard, Y. Borensztein, A. Resta, M. Lazzeri and G. Prévot, Phys. Rev. B, 2016, 94, 1–6 CrossRef.
- J. F. Justo, M. Z. Bazant and E. Kaxiras, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 2539–2550 CrossRef CAS.
- Y. Jing, Y. Sun, H. Niu and J. Shen, Phys. Status Solidi B, 2013, 250, 1505–1509 CrossRef CAS.
- X. Yuan, G. Lin and Y. Wang, Mol. Simul., 2016, 42, 1157–1164 CrossRef CAS.
- M. Hu, X. Zhang and D. Poulikakos, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 1–11 Search PubMed.
- R. Yu, P. Zhai, G. Li and L. Liu, J. Electron. Mater., 2012, 41, 1465–1469 CrossRef CAS.
- D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074 CrossRef CAS.
- L. A. Selis and J. M. Seminario, RSC Adv., 2019, 9, 27835–27848 RSC.
- N. Kumar and J. M. Seminario, J. Phys. Chem. C, 2016, 120, 16322–16332 CrossRef CAS.
- D. E. Galvez-Aranda, V. Ponce and J. M. Seminario, J. Mol. Model., 2017, 23, 120 CrossRef PubMed.
- R. Clark, M. Von Domaros, A. J. S. Mcintosh, A. Luzar, B. Kirchner and T. Welton, J. Chem. Phys., 2019, 151, 164503 CrossRef PubMed.
- V. Ponce, D. E. Galvez-Aranda and J. M. Seminario, J. Phys. Chem. C, 2017, 121, 12959–12971 CrossRef CAS.
- J. Petravic and J. Delhommelle, J. Chem. Phys., 2003, 118, 7477–7485 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101, DOI:10.1063/1.2408420.
- E. Braun, S. M. Moosavi and B. Smit, J. Chem. Theory Comput., 2018, 14, 5262–5272 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. Zhao, Y. Xiong, S. Ma, J. Zhang, B. Xu and J.-J. Kai, Acta Mater., 2021, 219, 117233 CrossRef CAS.
- M. M. Ghosh, J. Nanosci. Nanotechnol., 2013, 13, 2961–2966 CrossRef CAS PubMed.
- O. Folorunso, Y. Hamam, R. Sadiku, S. S. Ray and G. J. Adekoya, Eng. Solid Mech., 2021, 9, 311–322 CrossRef.
- K. Sau and T. Ikeshoji, J. Phys. Chem. C, 2020, 124, 20671–20681 CrossRef CAS.
- Z. Zhuo, X. Wu and J. Yang, Nanoscale, 2018, 10, 1265–1271 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. E. Blöchl, J. Kästner and C. J. Först, in Handbook of Materials Modeling, Springer Netherlands, Dordrecht, 2005, pp. 93–119 Search PubMed.
- S. Fischer and M. Karplus, Chem. Phys. Lett., 1992, 194, 252–261 CrossRef CAS.
- G. P. P. Pun and Y. Mishin, Phys. Rev. B, 2017, 95, 224103 CrossRef.
- R. Vissers, M. A. van Huis, J. Jansen, H. W. Zandbergen, C. D. Marioara and S. J. Andersen, Acta Mater., 2007, 55, 3815–3823 CrossRef CAS.
- A. G. Frøseth, R. Høier, P. M. Derlet, S. J. Andersen and C. D. Marioara, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 1–11 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Detailed information on thermostating, smooth and unsmoothed curves and trajectories generated by using Nose–Hoover and modified NVT thermostats and unsmoothed curves using CSVR thermostats. Crystallographic information file (cif) on bilayer silicene, and all experimental data from simulation is provided. See https://doi.org/10.1039/d2ra02475f |
| ‡ Sumaiyatul Ahsan and Abrar Rauf equally contributed to this work. |
| This journal is © The Royal Society of Chemistry 2022 |