Angle distortion model for predicting enediyne activation towards Bergman cyclization: an alternate to the distance theory

Abstract

The kinetics of Bergman cyclization (BC) of enediynes into 1,4-benzene diradicals (also known as p-benzynes) have attracted interest ever since the discovery of natural enediynes which pointed out a surprising reactivity profile difference across enediynes with varying structural architectures. From the analysis of experimental kinetic data, several models were proposed to have a structure-kinetics correlation, out of which, the cd-distance model and the transition state model are the most accepted ones. Recently, Houk et al. introduced a distortion model to explain the regioselectivity of nucleophilic addition to unsymmetrical o-benzynes based on the geometry of the transition state. In the case of BC, since the reaction is endothermic, the transition state geometrically resembles the product structure which implies that in the reaction pathway, the sp-carbons of enediynes are transformed into the trigonal sp² carbons of the benzenoid product. Thus, greater bending of the interior angles at the proximal alkyne carbons in the enediynes will lead to a lower activation barrier for the BC and hence faster cyclization. This hypothesis has been tested on a series of enediynes including natural product surrogates and the extent of deviation correlates well with the kinetic results. A cut-off value for the average internal proximal angles has been proposed to categorize enediynes as per their reactivity under ambient conditions. We believe that this distortion theory offers an alternative model in designing new unnatural enediynes with desired kinetic stabilities.

---

Introduction

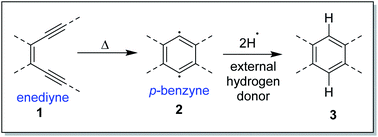
The Bergman cycloaromatization¹ (Scheme 1) involves the conversion of enediynes 1 into highly reactive para-benzynes, mainly present in the benzenoid 1,4-diradical form 2. The p-benzynes are capable of abstracting two hydrogen atoms from H-donors like the sugar backbones of complementary strands of DNA² leading to double strand DNA cleavage followed by self-programmed cell death (apoptosis). Bergman cyclization has also been extensively applied to the development of polymeric materials with valuable thermal/electrical properties and to the synthesis of polynuclear aromatic compounds.³ The enormous utility of this cycloaromatization in medicine and materials science has driven a series of continuous research efforts towards exploring enediyne chemistry including synthesis, reactivity, quantum chemical theory, thermodynamics and kinetics studies.⁴ A literature survey reveals that Bergman cylization still remains a dynamic field for further exploration as manifested through many of the on-gonging endeavours. Luxon et. al. theoretically studied the singlet and triplet energy surfaces for the Bergman cyclization of (Z)-hex-3-ene-1,5-diyne using coupled-cluster methods.⁵ The cyclization of the triplet enediyne was exothermic with a C₂-symmetric transition state while the singlet enediyne showed endothermic cyclization with a C_2v-symmetric transition state. The analysis of the frontier orbitals of each stationary point led to the conclusion that the triplet pathway is energetically unfavoured as compared to the singlet pathway. This was in-line with the conclusion drawn by Turro and workers regarding the non-feasibility of the triplet pathway.⁶ Our group recently reported⁷ the highly regioselective halide addition to the para-benzynes obtained from the Bergman cyclization of ortho substituted naphtho-fused cyclic azaenediyne to give halo naphtho tetrahydroisoquinolines in high yields. Steric hindrance to the trajectory of the nucleophile imposed by the peripheral hydrogen atom (close to the site of nucleophilic attack) was found to be the major driving force behind the observed regioselectivity. Also, the differential electrostatic potential as well as distortions at reactive centres played a minor role in controlling the regioselectivity. Binder and co-workers reported⁸ the synthesis of main-chain diamino enediyne embedded polymers and showed that these polymers in solution exert a chain-length dependent DNA cleavage activity under physiological conditions, which is additionally tuneable by modulating the stereoelectronic environment via their substitution patterns. Photochemical activation of such systems led to the formation of long-lived free radicals.

Scheme 1 Bergman cyclization.

The core structure of the enediyne 1 is constituted of a double bond flanked by two acetylenic moieties for which the out-of-plane orbitals are in conjugation with the double bond. The intrinsic reactivity of enediynes, controlled in the general sense, through either strain or electronic effects, has intrigued the chemists for decades and that has driven a lot of experimental and theoretical studies towards delineating the structural parameters of enediynes that govern the stability and reactivity of enediynes towards Bergman cyclization.⁹ One such seminal work (cd-distance theory)^9a,b was reported by Nicolaou and co-workers where it was empirically shown that the distance between carbon atoms c and d (c and d are the acetylenic carbons remote from double bond of the enediyne, also designated as the alkyne termini as shown in Fig. 1) plays a crucial role in determining the rate of p-benzyne formation.

Fig. 1 Labelling of the crucial carbon atoms and angles in the enediyne scaffold.

Upon correlating the cd-distances between the termini of the triple bonds of the enediyne systems and the rate of cycloaromatization, it was revealed that a decreased cd-distance and a consequent greater proximity between the acetylenic termini made the systems more prone towards Bergman reaction in order to relieve the torsional strain arising out of the alkyne electron cloud repulsion. A critical upper limit for the cd-distance of around 3.2–3.3 Å in the ground state, was proposed for the reaction to occur at a measurable rate at ambient temperatures.^9d These studies provide an explanation of why naturally occurring enediyne antibiotics contain either 9 or 10 membered cyclic enediyne cores as their cd-distances fall below or within the critical limit and thus they can be easily cycloaromatized under ambient conditions after removal of a so-called locking device. Subsequently, Snyder,¹⁰ Tipsword,¹¹ Magnus and co-workers,¹² based on molecular mechanics calculations and experimental data pointed out the limitation of the cd-distance rule and suggested that the reactivity of an enediyne is dependent not only on the strain energy of the ground state but also on that of the transition state – the ease of cycloaromatization of an enediyne is critically determined by the difference in the strain energy between the ground state and the transition state. An enediyne with a smaller strain energy difference between the ground and transition states undergoes easier cycloaromatization.

In 2010, Houk and co-workers proposed an interesting theoretical model known as the aryne distortion model¹³ based on experimental and theoretical studies which explained the regioselectivity of nucleophilic addition reactions to unsymmetrical o-benzynes. According to this model, the nucleophilic addition to unsymmetrical benzynes was found to be favoured for attack at that aryne carbon which requires the minimum geometrical and energetic change in going from the aryne to the TS structure. Thus, closer the aryne bond angle to linearity, greater was the reactivity observed for that centre. This observation may be exemplified through the results of the computational and synthetic studies on the regioselectivity of nucleophilic attack on 5,6-indolyne (Scheme 2). The aryne carbon (as shown in 5,6-indolyne) undergoing nucleophilic addition gets flattened in the corresponding transition state (5a – due to attack at C-5; 6a – due to attack at C-6). The slightly greater linearity of C-5 (interior angle = 130°) than at C-6 (interior angle = 127°) in 4, increased the susceptibility of C-5 towards the nucleophilic attack as that would require lesser geometric and energetic change upon going to the transition state 5a than C-6 nucleophilic attack leading to the transition state 6a. Flattening of the aryne carbon (C-5) also induces significant p-character of the in-plane hybrid orbital at the site of attack and a slight positive charge (attributed to electron withdrawal by indolyl nitrogen at para-position, as shown for structure 5b), while the adjacent angle is compressed (C-6), leading to increased s-character of the in-plane hybrid orbital to stabilize the developing carbanion. These promising results obtained from correlating the angular distortion with the observed regioselectivity in the aryne systems led to the inception of our current work.

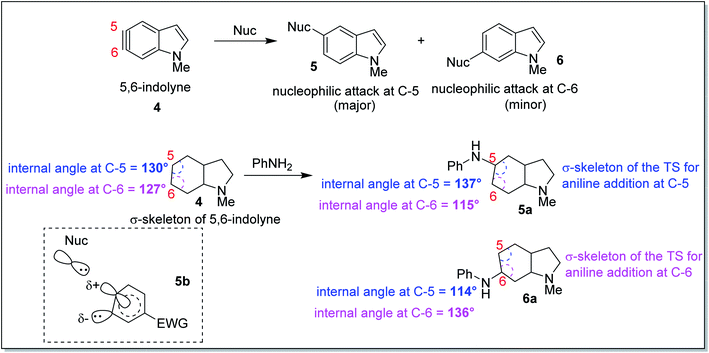Scheme 2 Aryne distortion model to explain the regioselectivity in nucleophilic addition to indolyne systems.

It is well known that in a multistep reaction, the activation energy of the rate-determining step controls the over-all rate of the process.¹⁴ Generally, the first step of Bergman cyclization involving formation of the 1,4-benzenoid diradical is the slow rate determining step and is an endothermic process.¹ Subsequent hydrogen atom abstraction step follows a much faster kinetics. So, the transition state for the rate determining step would resemble the diradical species (late transition state) in accordance to Hammond's postulate.¹⁵ Theoretical studies¹⁶ on the transition state of Bergman cyclization support this postulation as well. Thus, it is a reasonable assumption that the interior C–C–C bond angles in the transition state will get reduced in order to facilitate the attainment of an of 120° as the hybridization state of the acetylenic carbons change from sp to sp² upon formation of the p-benzynes. Extrapolation of the distortion model to enediyne system leads to the hypothesis that greater the deviation of the alkyne interior angle from linearity and closer it is towards trigonal geometry, greater will be the extent of mimicking the transition state, consequently lesser will be the difference in energy between the ground state and the transition state (lower activation energy) and hence faster should be the rate of cycloaromatization (Scheme 3). One may however argue that decreasing the internal acetylene angles should accompany a concomitant decrease in cd-distance, however this is not always true as shown by example 14 and 15 described later. It is interesting to note the for regioselective nucleophilic addition to o-arynes, distortion model predicts that greater the angular shift from trigonal to linear geometry, higher the reactivity; whereas in case of Bergman cyclization of enediynes, greater the angular shift from linear to trigonal geometry, higher should be the reactivity.

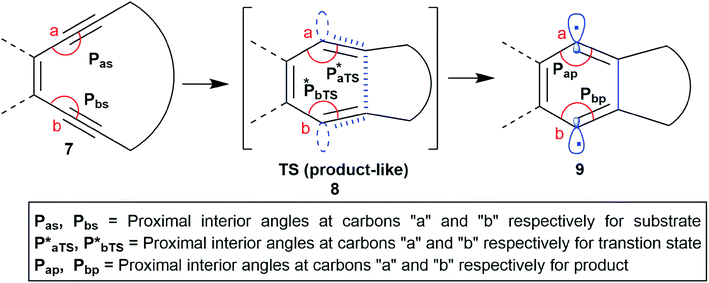Scheme 3 The changes in the interior angles P_a and P_b during the formation of the p-benzyne diradical via BC.

Basis of the present work

Based on the above preamble, we carried out geometry optimization for a series of enediynes using DFT-method and an attempt was made to establish a correlation between their experimentally obtained half-lives with their respective angular distortions. The hypothesis was indeed supported by the kinetic data and could be reasonably extrapolated to systems for which the kinetic studies have not been done yet. It was found that among structurally similar enediynes, increase in the interior angular distortions (less than 180° and closer to 120°) of the acetylenic carbons at positions a and b of the enediyne motif, leads to decrease in half-life indicating an increase in reactivity. Distortions in enediyne core were primarily quantified through the proximal interior angles at alkyne carbons a and b mainly due to the following reasons: (i) in Bergman cyclization, the transition state is diradical-like in nature and atoms a and b become the diradical centres in the diradical-product; (ii) these atoms are not bonded to any substituent which is not a part of the enediyne core; (iii) unlike atoms c and d, a and b do not participate in any new bond formation. To further consider the combined effect of angular distortions over both the proximal alkyne carbons (a and b), we calculated the average interior proximal angle [(P_a + P_b)/2].^1,17 Subsequently, a threshold-value was proposed for this average parameter which has been successfully used to distinguish enediynes which cycloaromatize under ambient conditions from those which do not. It was gratifying to note that for all the studied systems, this threshold value was found to be consistent in categorizing the enediynes into either of the two categories (discussed later) as per their reactivity under ambient conditions.

However, the extent of angular deviations, either for individual proximal alkyne carbon atoms (P_a and P_b) or the average parameter [(P_a + P_b)/2], should not be correlated to their individual reactivity order for the dissimilar enediynes. For such structurally different systems, the correlation may or may not hold good.

Thus, in addition to other major theories like the cd-distance model and transition-state model, this one offers a very simple yet alternative theoretical approach towards predicting the reactivity of enediynes. The results of our study are described in this paper.

Results and discussion

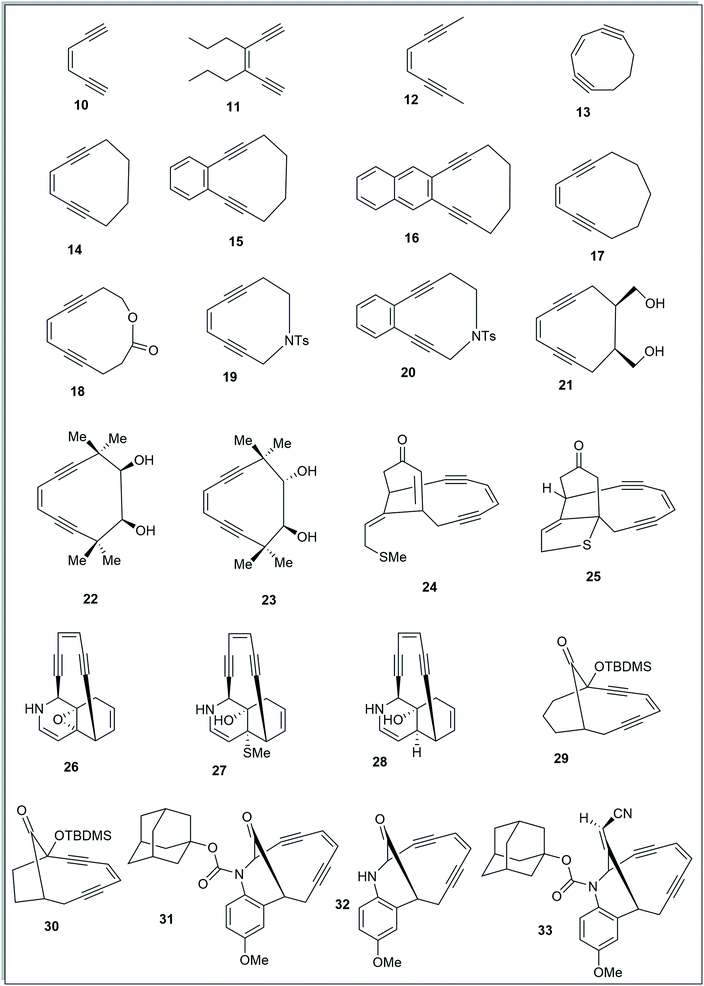
To study the effect of angular distortions, present in the enediynes on their reactivity, several different enediynes (10-33) were selected (Fig. 2) including two truncated structures of natural enediyne retaining the core enediyne structure along the trigging device in antibiotics calicheamicin γ1 (24) and dynemicin A (26).

Fig. 2 Enediynes geometry optimized using DFT-based calculations.

The ground state equilibrium structures of all the molecules were computed with DFT using B3LYP/6-31G+(d,p) and B3LYP/6-311G++(d,p) levels of theory, in gas phase, considering the singlet state (since we are dealing with the thermal mode of Bergman cyclization),^5,6,18 using the Gaussian 09 (Revision-A.02)¹⁹ program package. It is to be noted that the output obtained from using B3LYP/6-31G+(d,p) optimization was used as the input geometry while using B3LYP/6-311G++(d,p).²⁰

For each molecule, the basis set 6-311G++(d,p) furnished lowest energy values (included in ESI†). The following parameters were computed (Table 1 – acyclic and monocyclic enediyne; Table 2 – polycyclic enediyne) for each of the geometry optimized structures: (a) non-bonded distances between carbons a–b, c–d; (b) angles P_a, P_b, D_c and D_d; (c) energy values.

Table 1 Distance between the carbon atoms c–d and angles P_a, P_b computed for the acyclic (10–12) and monocyclic (13–23) enediynes using DFT-calculation

Entry	Enediyne molecule (along with their reactivities)	c–d (distance in Å)	Bond angle (in degrees)		Entry	Enediyne molecule (along with their reactivities)	c–d (distance in Å)	Bond angle (in degrees)
			Pa	Pb				Pa	Pb
a B3LYP/6-31G+(d,p) theory level.b B3LYP/6-311G++(d,p) theory level. Refer to the ESI for the corresponding values for a–b distance, angles Dc, Dd and the energy (at both the theory levels).
A	10	4.488^a	182.26^a	182.27^a	H	17	3.763^a	171.88^a	170.56^a
	Stable at 25 °C^1	4.463^b	182.06^b	182.04^b		Stable at 25°C^9a,21	3.748^b	171.76^b	170.29^b
B	11	4.171^a	183.62^a	183.62^a	I	18	4.168^a	177.45^a	177.87^a
	Stable at 25 °C^1	4.152^b	183.39^b	183.39^b		Stable at 25°C^9a,21,23	4.149^b	177.07^b	177.62^b
C	12	4.518^a	182.41^a	182.41^a	J	19	3.339^a	164.24^a	166.38^a
	Not reported, expected to cyclize only at high temperature	4.490^b	182.06^b	182.06^b		t1/2 = 72 h at 23 °C^24	3.338^b	164.72^b	166.53^b
D	13	2.918^a	156.80^a	156.51^a	K	20	3.348^a	166.64^a	167.68^a
	Expected to cyclize at ambient temperature^9b	2.930^b	157.55^b	157.52^b		t1/2 = 52 h at 65 °C^24	3.345^b	167.02^b	167.77^b
E	14	3.376^a	165.40^a	165.40^a	L	21	3.298^a	163.81^a	164.23^a
	t1/2 = 18 h at 25°C^21,9a-b	3.383^b	165.89^b	165.89^b		t1/2 = 11.8 h at 37°C^9a,b,21	3.310^b	164.54^b	164.97^b
F	15	3.353^a	166.90^a	166.90^a	M	22	3.441^a	166.33^a	166.25^a
	ca t1/2 = 10 h at 84 °C^22	3.357^b	167.34^b	167.34^b		t1/2 = 4 h at 50 °C^21,25	3.436^b	166.60^b	166.43^b
G	16	3.350^a	167.10^a	167.11^a	N	23	3.482^a	167.01^a	167.01^a
	Not reported, but expected to be stable because of benzannulation	3.352^b	167.53^b	167.54^b		t1/2 = 22 h at 50 °C^21,25	3.470^b	167.10^b	167.05^b

---

Table 2 Distance between the carbon atoms c–d and angles P_a, P_b computed for the polycyclic enediynes (24–33) using DFT-calculation

Entry	Enediyne molecule (along with their reactivities)	c–d (distance in Å)	Bond angle (in degrees)		Entry	Enediyne molecule (along with their reactivities)	c–d (distance in Å)	Bond angle (in degrees)
			Pa	Pb				Pa	Pb
a B3LYP/6-31G+(d,p) theory level.b B3LYP/6-311G++(d,p) theory level. Refer to the ESI for the corresponding values for a–b distance, angles Dc, Dd and the energy (at both the theory levels).
O	24	3.504^a	168.15^a	168.11^a	T	29	3.418^a	168.62^a	164.93^a
	Not reported, but expected to be stable at physiological (ambient) temperature	3.490^b	168.14^b	167.83^b		t1/2 = 2.1 h at 71 °C^12	3.414^b	168.71^b	165.29^b
P	25	3.171^a	161.92^a	162.59^a	U	30	3.468^a	168.99^a	166.68^a
	Not reported, but expected to cycloaromatize at physiological (ambient) temperature	3.182^b	162.68^b	163.41^b		Reported to cycloaromatize 650 times slower than 29 at 124 °C^12	3.456^b	168.73^b	166.87^b
Q	26	3.654^a	170.17^a	168.98^a	V	31	3.434^a	167.53^a	166.67^a
	Not reported, but expected to be stable at physiological (ambient) temperature	3.628^b	169.46^b	168.69^b		t1/2 = 10.9 h at 81 °C^26	3.429^b	167.58^b	166.93^b
R	27	3.300^a	163.21^a	164.90^a	W	32	3.420^a	167.17^a	166.49^a
	Not reported, but expected to cycloaromatize at physiological (ambient) temperature	3.309^b	163.87^b	165.60^b		Reported to cycloaromatize 1.6 times faster than 31, and at 65 °C^26	3.416^b	167.22^b	166.73^b
S	28	3.252^a	163.36^a	162.98^a	X	33	3.315^a	165.33^a	164.73^a
	Not reported, but expected to cycloaromatize at physiological (ambient) temperature	3.260^b	164.23^b	163.47^b		Reported to cycloaromatize 500 times faster than 31 at 37 °C, t1/2 = 15.3 h at 37 °C^26	3.317^b	165.62^b	165.29^b

---

Observing the trend in the theoretically calculated structural parameters from the geometry optimized structures revealed that along with the cd-distance, the interior angles subtended at carbon atoms a, b, c and d (P_a, P_b, D_c and D_d respectively) also undergo a gradual change corresponding to the change in the rate of cycloaromatization. Correlating the literature reported experimental half-lives with the calculated P_a and P_b values depicted that for geometrically similar enediynes, there occurs a decrease in these angles (P_a and P_b) with increase in their reactivity (Tables 1 and 2). Consequently, the average internal angles were also found to decrease with increase in reactivity (Table 3).

Table 3 Classification of enediynes based on their average interior proximal angles

Molecule	Theory level: B3LYP/6-31G+(d,p) average interior proximal angle [(Pa + Pb)/2] (in degrees)	Theory level: B3LYP/6-311G++(d,p) average interior proximal angle [(Pa + Pb)/2] (in degrees)
CATEGORY-I: average interior proximal angle is less than 166° (expected to cyclize at ambient temperatures)
13	156.66	157.54
14	165.40	165.89
19	165.31	165.63
21	164.02	164.76
25	162.26	163.05
27	164.06	164.74
28	163.17	163.85
33	165.03	165.46
CATEGORY-II: average interior proximal angle is less than 166° (expected to be stable at ambient temperatures)
10	182.27	182.05
11	183.62	183.39
12	182.41	182.06
15	166.90	167.34
16	167.11	167.54
17	171.22	171.03
18	177.66	177.35
20	167.16	167.40
22	166.29	166.52
23	167.01	167.08
24	168.13	167.99
26	169.58	169.08
29	166.78	167.00
30	167.84	167.80
31	167.10	167.26
32	166.83	166.98

---

The acyclic enediynes are highly unreactive as compared to their cyclic analogues. This is substantiated by the corresponding very high values of P_a and P_b (entries A–C in Table 1) for molecules 10–12. Among the simple unsubstituted cyclic enediynes, nine membered (13) is so reactive^9b that it has not been isolated (as it readily cyclizes under ambient condition) and it showed the lowest values (Fig. 3) for P_a and P_b (entry D in Table 1) among the molecules studied. A subsequent increase in the ring size in molecules 14 and 17^9b,27 (ring sizes 10 and 11 respectively) decreases its reactivity manifested through a consequent increase in the values of P_a and P_b (entries E and H respectively, in Table 1). Experimental studies^22,24 suggested that fusion of aryl rings with the cyclic enediyne scaffold leads to a decrease in their reactivity. This trend was supported by the increased P_a and P_b values in presence of fused phenyl or naphthyl rings in the ten-membered carbocyclic enediyne 14 to form molecules 15 and 16 respectively (entries F and G in Table 1).²² Similarly, increase in half-life was found to be accompanied by the increase in the values of P_a and P_b upon going from ten-membered aza-enediyne 19 to it's for the benzo-fused derivative 20 (entries J and K respectively, in Table 1).²⁴ It is interesting to note that the computed cd-distances decreased with subsequent fusion of aromatic ring(s) in molecules 15 and 16 (as compared to simple ten-membered cyclic enediyne 14) which contradicted the order of their reactivities as per Nicolaou's distance theory.

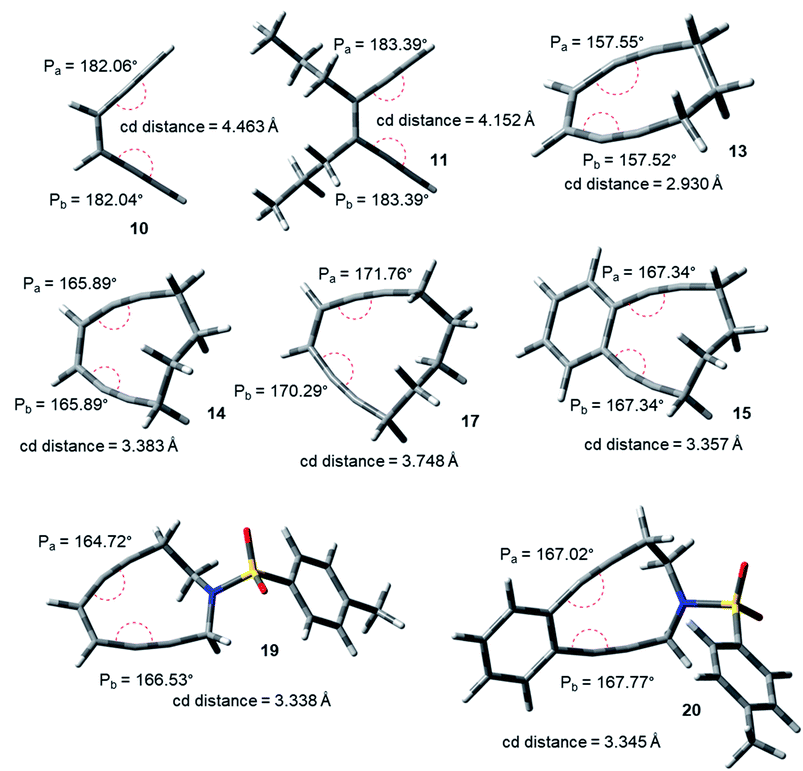Fig. 3 Geometry optimized structures of a few representative enediynes (10,11, 13, 14, 15, 17, 19 and 20) at B3LYP/6-311G++(d,p) level.

Among the studied diols^9a,21,25 (entries L–N, in Table 1), molecule 21 was found to be most reactive while 23 was found to be least reactive (as reflected from their experimentally reported half-lives). The proposed distortion theory as manifested through the proximal interior angles (P_a and P_b) supported their reactivity order as the angular distortion was found to be highest for 21 and lowest for 23.

The idea of correlating reactivity with extent of bond angle distortion was further validated on the simplified structural analogues of two well established enediyne antibiotics – calicheamicin γ¹ and dynemicin A.^2g The enediyne functionality of both these molecules are locked within rigid bridged ring systems awaiting activation to undergo the Bergman cyclization. Calicheamicin γ¹ has a bicyclic aglycon enediyne unit that is triggered for the cycloaromatization through a conjugate addition of thiolate to the proximate α, β-unsaturated carbonyl system. On the other hand, dynemicin A is activated through NADPH or glutathione induced epoxide ring opening reaction. The newly induced strain makes the triggered form much more reactive (activated) than the untriggered form. We selected the surrogates (truncated and simplified structural analogues due to computational constraints) of calicheamicin γ1 (represented by molecule 24, entry O in Table 2) and dynemicin A (represented by 26, entry Q in Table 2) as our model systems. The activated form of calicheamicin γ1 (conjugate addition product) was represented in its simplified form by molecule 25. For the dynemicin A analogue, two simplified analogues of its activated forms were considered: (a) epoxide ring opened by sulphur based nucleophilic attack (represented by molecule 27); (b) epoxide ring opened by hydride attack (represented by molecule 28). For both calicheamicin γ¹ (24) and dynemicin A analogues (26), as expected, the values of angles P_a and P_b were found to be closer to trigonal geometry (Table 2) upon their activation (Fig. 4).

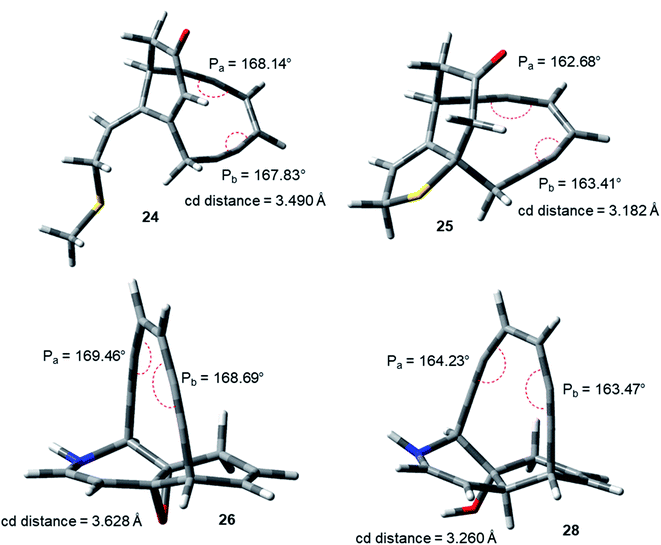Fig. 4 Geometry optimized structures of natural product analogues 24, 25, 26 and 28 at B3LYP/6-311G++(d,p) level.

During the course of work, our attention was drawn to the interesting relative reactivity profiles of a few bicyclic enediynes 29 to 33 (entries T–X, in Table 2). Magnus reported¹² that although the cd-distance is lower for 12-ketobicyclo[7.2.1]enediyne (30) than 13-ketobicyclo[7.3.1] enediyne (29), yet 30 cycloaromatizes 650 times slower than 29 which has a half-life of 2.1 h at 71 °C. This observation by Magnus was in disagreement with the cd-distance theory proposed by Nicolaou. Our theoretical studies²⁸ revealed that the interior proximal angles P_a and P_b are slightly higher (Table 2, entries T and U) for 30 than that for 29 (Fig. 5). Also, the average interior angle (Table 3) is higher for 30 than 29. Thus, the angle distortion parameters are successfully able to rationalize the reactivity order. Interestingly, unlike Magnus' report, our optimization studies revealed a marginal increase in the cd-distance upon going from 29 to 30 (Table 2, entries T and U), which also extended support to the distance theory.²⁹

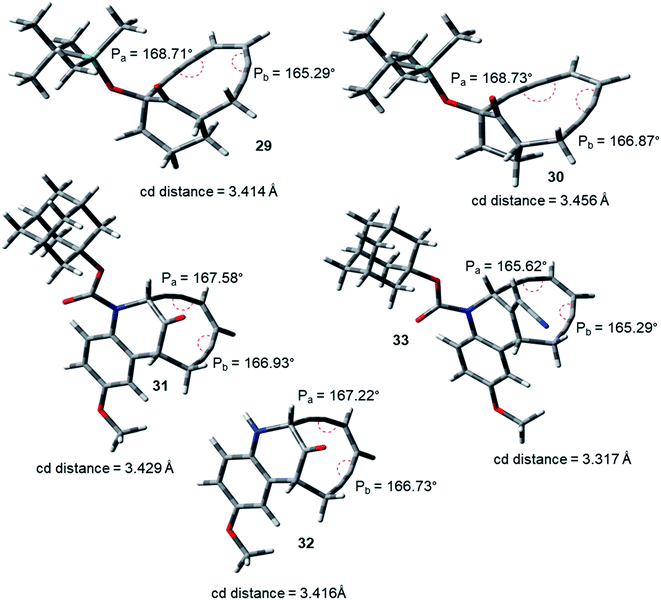Fig. 5 Geometry optimized structures of a few representative enediynes (10,11, 13, 14, 15, 17, 19 and 20) at B3LYP/6-311G++(d,p) level.

For dynemicin core azabicyclo[7.3.1]enediynes (31, 32 and 33),²⁶ Magnus reported that the reactivity increase (as revealed from their kinetic studies) upon going from 31 to 33 in spite of having almost same cd-distance. Our optimization studies revealed that upon going from 31 to 33, increase in reactivity was accompanied by a concomitant decrease in the interior proximal angles (Table 2, entries V to X) as well as average internal proximal angles (Table 3). Thus, the angle distortion hypothesis was able to justify the order of experimental half-lives. The cd-distance obtained at B3LYP/6-31G+(d,p) and B3LYP/6-311G++(d,p) levels of theory, were found to decrease upon going from 31 to 33 (Table 2, entries V to X). Thus, like molecules 29 and 30, the theoretically obtained cd-distances for 31, 32 and 33 are in accordance to the cd-distance theory.

Based on our studies, we envisaged that the enediynes may be broadly classified into the following two categories depending on their reactivity: (i) category I – those which undergo Bergman cyclization under ambient conditions (at temperature ≤ 37 °C); (ii) category II – those which are relatively stable under ambient conditions and undergo Bergman cyclization at higher temperatures (at temperature > 37 °C). Keeping this in perspective, the scope of our hypothesis was further extended by proposing an empirical cut-off value of 166° for the average interior proximal angle [(P_a + P_b)/2]. It was found that the enediynes having this average value less than 166° belonged to category I, and the ones having this average value greater than 166° belonged to category II (Table 3). None of the studied enediynes was found to violate this empirical threshold value. Further, this threshold value was also successful in uniformly classifying the enediynes into the two categories, in accordance to their reactivities, irrespective of their structural similarity/dissimilarity.

It is interesting to note that the benzannulated enediynes 15, 16 and 20 (entries F, G and K respectively, in Table 1) defied the modified cd-distance range of 3.4–2.9 Å that was proposed by Schreiner^9d for spontaneous cyclization, as these systems showed a cd-distance within the proposed range, yet they cyclized only under higher temperature conditions. On the other hand, the threshold value of the average interior proximal angle (166°) as proposed in this work, was able to categorize (category II in Table 3) them as stable molecules under ambient conditions.³⁰

Conclusion

A novel and simple theoretical approach has been proposed to correlate the reactivity of enediynes with their angular distortions at the proximal alkyne carbon atoms. Since the p-benzyne formation during Bergman cyclization adopts a late transition state, so substrates which mimic the corresponding p-benzyne follow a faster reaction kinetics. For the structurally similar kind of enediyne systems, it was observed that greater the angular deviation of the proximal alkyne carbons from linearity, lower is their experimental half-lives. A threshold value of 166° was empirically proposed for the composite parameter of average interior proximal angle to distinguish the potentially reactive enediynes from the unreactive ones. Although activation energy calculation for the respective cyclization pathway has the potential to probably give a more accurate correlation between the structure and reactivity than the results obtained via the proposed semi-quantitative distortion model, considering the advantage of the latter in terms of computational resources and time, the current hypothesis is a viable trade-off which may be used to design various enediyne scaffolds with controlled reactivities.

Computational details

All of the computations were performed in gas phase with the Gaussian 09 (Revision-A.02)¹⁹ software package and calculation of the structural parameters were done using Gauss View 6.0.³¹ Becke's three-parameter hybrid functional,³² the correlation functional of Lee, Yang, and Parr³³ and split-valence basis sets 6-31G+(d,p)³⁴ and 6-311G++(d,p)³⁵ were used.³⁶ Electronic energies in atomic unit (Hartrees) and Cartesian coordinates of the optimized geometries of enediynes are reported in the ESI.† The nature of the stationary point was characterized by the absence of imaginary frequency in the vibrational frequency analysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The Indian National Science Academy is acknowledged for supporting A. B. under the INSA Senior Scientist Programme. The authors also thank Dr Sangita Sen, IISER Kolkata, for helpful discussion.

Notes and references

1. (a) R. G. Jones and R. G. Bergman, p-Benzyne. Generation as an Intermediate in a Thermal Isomerization Reaction and Trapping Evidence for the 1,4-Benzenediyl Structure, J. Am. Chem. Soc., 1972, 94, 660–661; (b) R. G. Bergman, Reactive 1,4-Dehydroaromatics, Acc. Chem. Res., 1973, 6, 25–31; (c) T. P. Lockhart and R. G. Bergman, Evidence for the Reactive Spin State of 1,4-Dehydrobenzenes, J. Am. Chem. Soc., 1981, 103, 4091–4096; (d) For a comprehensive overview on cycloaromatizaton reactions leading to the formation of diradicals including the relevant discussion on electronic effects, molecular orbital analysis, ionic and zwitterionic pathways, metal catalyzed cycloaromatizations and secondary aromaticity effects, refer to the following book chapter: A. Campbell, P. W. Peterson and I. G. Alabugin, Cycloaromatization reactions, in AROMATICITY Modern Computational Methods and Application, 1st edn, Elsevier, 2021, pp. 339–375.
2. (a) A. L. Smith and K. C. Nicolaou, The Enediyne Antibiotics, J. Med. Chem., 1996, 39, 2103–2117; (b) K. C. Nicolaou and A. L. Smith, Molecular Design, Chemical Synthesis, and Biological Action of Enediynes, Acc. Chem. Res., 1992, 25, 497–503; (c) J. W. Grissom, G. U. Gunawardena, D. Klingberg and D. Huang, The Chemistry of Enediynes, Enyne Allenes and related Compounds, Tetrahedron, 1996, 52, 6453–6518; (d) S. Caddick, V. M. Delisser, V. E. Doyle, S. Khan, A. G. Avent and S. Vile, Studies toward the Synthesis of Natural and Unnatural Dienediynes 1. Approaches to a Functionalised Bicyclic Ring System, Tetrahedron, 1999, 55, 2737–2754; (e) Enediyene Antibiotics as Antitumor Agents, ed. Border, D. B. and Doyle, T. W., Marcel Dekker, New York, 1995; (f) R. Gleiter and D. Kratz, Conjugated Enediynes—An old topic in a different light, Angew. Chem., Int. Ed. Engl., 1993, 32, 842–845; (g) K. C. Nicolaou and W.-M. Dai, Chemistry and Biology of the Enediyne Anticancer Antibiotics, Angew. Chem., Int. Ed. Engl., 1991, 30, 1387–1416.
3. (a) X. Chen, L. Tolbert, D. W. Hess and C. Henderson, A Bergman Cyclization Approach to Polymers for Thin-Film Lithography, Macromolecules, 2001, 34, 4104–4108; (b) H. V. Shah, D. A. Babb and D. W. Smith, Bergman Cyclopolymerization Kinetics of bis- Ortho -Diynylarenes to Polynaphthalene Networks. A comparison of Calorimetric Methods, Polymer, 2000, 41, 4415–4422; (c) J. A. John and J. M. Tour, Synthesis of Polyphenylenes and Polynaphthalenes by Thermolysis of Enediynes and Dialkynylbenzenes, J. Am. Chem. Soc., 1994, 116, 5011–5012; (d) D. M. Bowles, G. J. Palmer, C. A. Landis, J. L. Scott and J. E. Anthony, The Bergman Reaction as a Synthetic Tool: Advantages and Restrictions, Tetrahedron, 2001, 57, 3753–3760; (e) D. M. Bowles and J. E. Anthony, A Reiterative Approach To 2,3-Disubstituted Naphthalenes and Anthracenes, Org. Lett., 2000, 2, 85–87; (f) Y. Xiao and A. Hu, Bergman Cyclization in Polymer Chemistry and Material Science, Macromol. Rapid Commun., 2011, 32, 1688–1698.
4. (a) J. M. Zaleski and D. S. Rawat, Geometric and Electronic Control of Thermal Bergman Cyclization, Synlett, 2004, 3, 393–421; (b) M. Klein, T. Walenzyk and B. König, Electronic Effects on The Bergman Cyclisation of Enediynes. A Review, Collect. Czech. Chem. Commun., 2004, 69, 945–965; (c) A. Basak, S. Mandal and S. S. Bag, Chelation-Controlled Bergman Cyclization: Synthesis and Reactivity of Enediynyl Ligands, Chem. Rev., 2003, 103, 4077–4094; (d) J. C. Santos, J. Andres, A. Aizman, P. Fuentealba and V. A. Polo, Theoretical Study on the Reaction Mechanism for the Bergman Cyclization from the Perspective of the Electron Localization Function and Catastrophe Theory, J. Phys. Chem. A, 2005, 109, 3687–3693; (e) A. A. Taherpour and P. Ghasemi, Bergman cyclization reactions in fused enediynes: a DFT study, J. Iran. Chem. Soc., 2019, 16, 1965–1976; (f) I. V. Alabugin, M. Manoharan and S. V. Kovalenko, Tuning Rate of the Bergman Cyclization of Benzannelated Enediynes with Ortho Substituents, Org. Lett., 2002, 4, 1119–1122; (g) J. W. Grissom, T. L. Calkins, H. A. McMillen and Y. Jiang, Determination of the Activation Parameters for the Bergman Cyclization of Aromatic Enediynes, J. Org. Chem., 1994, 59, 5833–5835; (h) T. A. Zeidan, S. V. Kovalenko, M. Manoharan and I. V. Alabugin, Ortho Effect in the Bergman Cyclization: Comparison of Experimental Approaches and Dissection of Cycloaromatization Kinetics, J. Org. Chem., 2006, 71, 962–975; (i) K. C. Nicolaou, W.-M. Dai, Y. P. Hong, K. K. Baldridge, J. S. Siegel and S. C. Tsay, Molecular design, chemical synthesis, kinetic studies, calculations, and biological studies of novel enediynes equipped with triggering, detection, and deactivating devices. Model dynemicin A epoxide and cis-diol systems, J. Am. Chem. Soc., 1993, 115, 7944–7953; (j) I. V. Alabugin and M. Manoharan, Reactant Destabilization in the Bergman Cyclization and Rational Design of Light- and pH-Activated Enediynes, J. Phys. Chem. A, 2003, 107, 3363–3371; (k) T. A. Zeidan, M. Manoharan and I. V. Alabugin, Ortho Effect in the Bergman Cyclization: Interception of p-Benzyne Intermediate by Intramolecular Hydrogen Abstraction, J. Org. Chem., 2006, 71, 954–961; (l) F. C. Pickard IV, R. L. Shepherd, A. E. Gillis, M. E. Dunn, S. Feldgus, K. N. Kirschner, G. C. Shields, M. Manoharan and I. V. Alabugin, Ortho Effect in the Bergman Cyclization: Electronic and Steric Effects in Hydrogen Abstraction by 1-Substituted Naphthalene 5,8-Diradicals, J. Phys. Chem. A, 2006, 110, 2517–2526.
5. A. R. Luxon, N. Orms, R. Kanters, A. I. Krylov and C. A. J. Parish, An ab Initio Exploration of the Bergman Cyclization, J. Phys. Chem. A, 2018, 122, 420–430.
6. N. J. Turro, A. Evenzahav and K. C. Nicolaou, Photochemical Analogue of the Bergman Cycloaromatization Reaction, Tetrahedron Lett., 1994, 35, 8089–8092.
7. M. Singha, P. Bhattacharya, D. Ray and A. Basak, Sterically hindering the trajectory of nucleophilic attack towards p-benzynes by a properly oriented hydrogen atom: an approach to achieve regioselectivity, Org. Biomol. Chem., 2021, 19, 5148–5154.
8. Y. Cai, F. Lehmann, E. Peiter, S. Chen, J. Zhu, D. Hinderberger and W. H. Binder, Bergman cyclization of main-chain enediyne polymers for enhanced DNA cleavage, Polym. Chem., 2022, 13, 3412–3421.
9. (a) K. C. Nicolaou, G. Zuccarello, C. Riemer, V. A. Estevez and W.-M. Dai, Design, synthesis, and study of simple monocyclic conjugated enediynes. The 10-membered ring enediyne moiety of the enediyne anticancer antibiotics, J. Am. Chem. Soc., 1992, 114, 7360–7371; (b) K. C. Nicolaou, Y. Ogawa, G. Zuccarello, E. J. Schweiger and T. J. Kumazawa, Cyclic conjugated enediynes related to calicheamicins and esperamicins: calculations, synthesis, and properties, J. Am. Chem. Soc., 1988, 110, 4866–4868; (c) K. Iida and M. J. Hirama, Synthesis and Characterization of Nine-Membered Cyclic Enediynes, Models of the C-1027 and Kedarcidin Chromophores: Equilibration with a p-Benzyne Biradical and Kinetic Stabilization, J. Am. Chem. Soc., 1995, 117, 8875–8876; (d) Later, Schreiner has modified the Nicolaou's empirically determined “critical range” of 3.31−3.2 Å, where spontaneous cyclization should occur at room temperature, to the range 3.4−2.9 Å. See: Monocyclic Enediynes: Relationships between Ring Sizes, Alkyne Carbon Distances, Cyclization Barriers, and Hydrogen Abstraction Reactions. Singlet−Triplet Separations of Methyl-Substituted p-Benzynes P. Schreiner, J. Am. Chem. Soc., 1998, 17, 4184–4190.
10. (a) J. P. Snyder, The cyclization of calicheamicin-esperamicin analogs: a predictive biradicaloid transition state, J. Am. Chem. Soc., 1989, 111, 7630–7632; (b) J. P. Snyder, Monocyclic enediyne collapse to 1,4-diyl biradicals: a pathway under strain control, J. Am. Chem. Soc., 1990, 112, 5367–5369.
11. J. P. Snyder and G. E. Tipsword, Proposal for blending classical and biradical mechanisms in antitumor antibiotics: dynemicin A, J. Am. Chem. Soc., 1990, 112, 4040–4042.
12. P. Magnus, P. Carter, J. Elliott, R. Lewis, J. Harling, T. Pitterna, W. E. Bauta and S. Fortt, Synthetic and mechanistic studies on the antitumor antibiotics esperamicin A1 and calicheamicin gamma.1: synthesis of 2-ketobicyclo[7.3.1.]enediyne and 13-ketocyclo[7.3.1]enediyne cores mediated by .eta.2]dicobalt hexacarbonyl alkyne complexes. Cycloaromatization rate studies, J. Am. Chem. Soc., 1992, 114, 2544–2559.
13. P. H.-Y. Cheong, R. S. Paton, S. M. Bronner, G.-Y. J. Im, N. K. Garg and K. N. Houk, Indolyne and Aryne Distortions and Nucleophilic Regioselectivites, J. Am. Chem. Soc., 2010, 132, 1267–1269.
14. J. R. Murdoch, What is the rate-limiting step of a multistep reaction?, J. Chem. Educ., 1981, 58, 32.
15. G. S. A. Hammond, Correlation of Reaction Rates, J. Am. Chem. Soc., 1955, 77, 334–338.
16. (a) S. Feldgus and G. C. Shields, An ONIOM study of the Bergman reaction: a computationally efficient and accurate method for modeling the enediyne anticancer antibiotics, Chem. Phys. Lett., 2001, 347, 505–511; (b) W. C. Chen, N.-Y. Chang and C.-H. Yu, Density Functional Study of Bergman Cyclization of Enediynes, J. Phys. Chem. A, 1998, 102, 2584–2593; (c) A. C. Scheiner, H. F. Schaefer and B. Liu, The ∼X1A1 and ∼a3B2 states of o-benzyne: a theoretical characterization of equilibrium geometries, harmonic vibrational frequencies, and the singlet-triplet energy gap, J. Am. Chem. Soc., 1989, 111, 3118–3124; (d) A. Nicolaides and W. T. Borden, CI calculations on didehydrobenzenes predict heats of formation for the meta and para isomers that are substantially higher than previous experimental values, J. Am. Chem. Soc., 1993, 115, 11951–11957; (e) R. Lindh and B. J. Persson, Ab Initio Study of the Bergman Reaction: The Autoaromatization of Hex-3-ene-1,5-diyne, J. Am. Chem. Soc., 1994, 116, 4963–4969; (f) R. Lindh, T. J. Lee, A. Bernhardsson, B. J. Persson and G. Karlstroem, Extended ab Initio and Theoretical Thermodynamics Studies of the Bergman Reaction and the Energy Splitting of the Singlet o-, m-, and p-Benzynes, J. Am. Chem. Soc., 1995, 117, 7186–7194; (g) E. Kraka, D. Cremer, G. Bucher, H. Wandel and W. Sander, A CCSD(T) and DFT investigation of m-benzyne and 4-hydroxy-m-benzyne, Chem. Phys. Lett., 1997, 268, 313–320; (h) U. Ryde, M. Schutz and R. Lindh, On the significance of the trigger reaction in the action of the calicheamicin gamma 1 anti-cancer drug, Theor. Chem. Acc., 1997, 97, 203–210; (i) R. J. McMahon, R. J. Halter, R. L. Fimmen, R. J. Wilson, S. A. Peebles, R. L. Kuczkowski and J. F. Stanton, Equilibrium Structure of cis-Hex-3-ene-1,5-diyne and Relevance to the Bergman Cyclization, J. Am. Chem. Soc., 2000, 122, 939–949; (j) G. B. Jones and P. M. Warner, Electronic Control of the Bergman Cyclization: The Remarkable Role of Vinyl Substitution, J. Am. Chem. Soc., 2001, 123, 2134–2145; (k) C. J. Bergman Cramer, Aza-Bergman, and Protonated Aza-Bergman Cyclizations and Intermediate 2,5-Arynes: Chemistry and Challenges to Computation, J. Am. Chem. Soc., 1998, 120, 6261–6269; (l) W. T. G. Johnson, M. B. Sullivan and C. J. Cramer, meta and para substitution effects on the electronic state energies and ring-expansion reactivities of phenylnitrenes, Int. J. Quantum Chem., 2001, 85, 492–508; (m) W. T. G. Johnson and C. J. Cramer, Substituent effects on benzyne electronic structures, J. Phys. Org. Chem., 2001, 14, 597–603; (n) C. J. Cramer and J. Thompson, Quantum Chemical Characterization of Singlet and Triplet Didehydroindenes, J. Phys. Chem. A, 2001, 105, 2091–2098; (o) E. Kraka and D. Cremer, The para-Didehydropyridine, para-Didehydropyridinium, And Related Biradicals-a contribution to the chemistry of enediyne antitumor drugs, J. Comput. Chem., 2000, 22, 216–229; (p) C. F. Logan and P. Chen, Ab Initio Calculation of Hydrogen Abstraction Reactions of Phenyl Radical And P-Benzyne, J. Am. Chem. Soc., 1996, 118, 2113–2114; (q) M. J. Schottelius and P. Chen, 9,10-Dehydroanthracene: P-Benzyne-Type Biradicals Abstract Hydrogen Unusually Slowly, J. Am. Chem. Soc., 1996, 118, 4896–4903.
17. The consideration of average interior proximal angle to compare the reactivities of enediynes offers us the following advantages – (a) In some cases, the individual changes in P_a and P_b are not consistent in accordance with the change in reactivity, however the change in average interior proximal angles have been found to be reasonably more consistent.; (b) The average interior proximal angles give a more rational basis to compare dissimilar enediynes due to the confusion that may arise in individually labelling ‘a’ and ‘b’ to the alkyne carbons for dissimilar systems..
18. (a) M. Nath, M. Pink and J. M. Zaleski, Controlling Both Ground-and Excited-State Thermal Barriers to Bergman Cyclization with Alkyne Termini Substitution, J. Am. Chem. Soc., 2005, 127, 478–479; (b) I. D. Cambell and G. Eglinton, A Novel Photochemical Cyclisation of OBisiodoethynylbenzene to Substituted Naphthalenes, J. Chem. Soc. C., 1968, 2120–2121; (c) A. Evenzahav and N. J. Turro, Photochemical Rearrangement of Enediynes: Is a “Photo-Bergman” Cyclization a Possibility?, J. Am. Chem. Soc., 1998, 120, 1835–1841; (d) P. Papp, P. Neogrady, P. Mach, J. Pittner, I. Huba and S. Wilson, Many-Body Brillouin–Wigner Second-Order Perturbation Theory: An Application to the Autoaromatisation of Hex-3-Ene-1,5-Diyne (the Bergman Reaction), Mol. Phys., 2008, 106, 57–74; (e) J. Kagan, X. Wang, X. Chen, K. Y. Lau, I. V. Batac, R. W. Tuveson and J. B. Hudson, DNA Cleavage, Antiviral and Cytotoxic Reactions Photosensitized by Simple Enediyne Compounds, J. Photochem. Photobiol., B, 1993, 21, 135–142.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
20. As input geometry, 3 different feasible structures with conformational differences were optimized and the lowest energy output was selected for further analysis. Also, it was observed that the corresponding variations in the structural parameters were negligible within the experimental error range.
21. K. C. Nicolaou, A. L. Smith and E. W. Yue, Chemistry and Biology of Natural and Designed Enediynes, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 5881–5888.
22. M. F. Semmelhack and R. Sarpong, Kinetic Analysis of a Reactive Model Enediyne, J. Phys. Org. Chem., 2004, 17, 807–813.
23. D. Guillerm and G. Linstrumelle, Catalysed Cyclisation of an (Z)-Ene-Diyne Hydroxy Acid Precursor, Tetrahedron Lett., 1985, 26, 3811–3812.
24. A. Basak, J. C. Shain, U. K. Khamrai, K. R. Rudra and A. Basak, Nitrogen Substituted Cyclic Enediynes: Synthesis, Thermal Reactivity and Complexation with Metal Ions, J. Chem. Soc., Perkin Trans. 1, 2000, 12, 1955–1964.
25. K. C. Nicolaou, E. J. Sorensen, R. Discordia, C.-K. Hwang, R. G. Bergman, R. E. Minto and K. N. Bharucha, Ten-Membered Ring Enediynes with Remarkable Chemical and Biological Profiles, Angew. Chem., Int. Ed. Engl., 1992, 31, 1044–1046.
26. P. Magnus and R. A. Fairhurst, Relative Rates of Cycloaromatization of Dynemicin Azabicyclo [7.3.l]enediyne Core Structures. An Unusual Change in ΔS^≠, J. Chem. Soc., Chem. Commun., 1994, 1541–1542.
27. For the crystal structure compound 17, refer to reference number 5b. For this compound, the values for the average internal proximal angles obtained from the crystal, optimized models using B3LYP/6-31G+(d,p) and B3LYP/6-311G++(d,p) are 171.03°, 171.22° and 171.03° respectively. The cd-distance obtained from the crystal, optimized model using B3LYP/6-31G+(d,p) and B3LYP/6-311G++(d,p) are 3.661Å, 3.763Å and 3.748 Å respectively. For the comparison regarding other vital structural parameters, refer to the ESI.†.
28. For the crystal structure of compound 29, refer to reference number 8. For this compound, the values for the average internal proximal angles obtained from the crystal, optimized models using B3LYP/6-31G+(d,p) and B3LYP/6-311G++(d,p) are 167.19°, 166.78° and 167.00° respectively. The cd-distance obtained from the crystal, optimized model using B3LYP/6-31G+(d,p) and B3LYP/6-311G++(d,p) are 3.391Å, 3.418Å and 3.414 Å respectively. For the comparison regarding other vital structural parameters, refer to the ESI.†.
29. The optimization studies were done in gas phase considering a single molecule; on the other hand, crystals were obtained in suitable solvents and many such molecules are closely packed in a crystal lattice where they primarily interact through various non-covalent interactions. In some cases, these factors may lead to the small difference in the results obtained from the crystallographic and the theoretical studies.
30. Just like the proximal internal angles (P_a and P_b) and average internal angle parameters, we tried to find any existing correlation between the force constants (k values obtained from the frequency calculations) corresponding to symmetric bends in the alkynes (C-C_a-C and C-C_b-C). Assignment of the respective vibrations were done by visualizing through Gauss View. It was apparent that in many of the cases, the vibrations were of hybrid nature having contributions from different kinds of bonds within the molecule. In our case, for simple enediynes of similar nature, force constant seemed to increase with increase in reactivity. However, this observation is not a generalized one and extensive study over a larger number of examples with structural diversity needs to be carried out to draw any substantial conclusion on this.
31. R. D. Dennington II, T. A. Keith and J. M. Millam, GaussView, version 6.0.16; Semichem, Inc.: Shawnee Mission KS, 2016.
32. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
33. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
34. (a) W. J. Hehre, R. Ditchfield and J. A. Pople, Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 1972, 56, 2257–2261; (b) P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222; (c) G. W. Spitznanel, T. Clark, J. Chandrasekhar and P. V. R. Schlever, Stabilization of methyl anions by first-row substituents. The superiority of diffuse function-augmented basis sets for anion calculations, J. Comput. Chem., 1982, 3, 363–371.
35. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72, 650–654.
36. As per the suggestion of one of the reviewers, geometry optimization using B3LYP/6-311G(d,p) was also done for a few compounds for which the average internal proximal angle were close to 166°. The basis set was so chosen to ignore the effect of diffusivity factor and only consider the polarization effect. Optimization results revealed that the for these enediynes, basis sets 6-311G(d,p) and 6-311G++(d,p) yielded results that are quantitatively very close to each other. Further, the proposed threshold value of 166° was also found to be consistent with results obtained by using this new basis set. Refer to ESI for the comparative table (page number S61)†.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra03193k

---