Open Access Article
Open Access ArticleLattice dynamic stability and electronic structures of ternary hydrides La1−xYxH3 via first-principles cluster expansion
Prutthipong Tsuppayakorn-aek ab,
Wiwittawin Sukmasab,
Prayoonsak Pluengphon
ab,
Wiwittawin Sukmasab,
Prayoonsak Pluengphon c,
Burapat Inceesungvorn
c,
Burapat Inceesungvorn d,
Piya Phansuke*e,
Pungtip Kaewtubtime,
Rajeev Ahuja
d,
Piya Phansuke*e,
Pungtip Kaewtubtime,
Rajeev Ahuja fg,
Thiti Bovornratanaraks
fg,
Thiti Bovornratanaraks *ab and
Wei Luo
*ab and
Wei Luo f
f
aExtreme Conditions Physics Research Laboratory and Center of Excellence in Physics of Energy Materials (CE:PEM), Department of Physics, Faculty of Science, Chulalongkorn University, Bangkok 10330, Thailand. E-mail: thiti.b@chula.ac.th
bThailand Center of Excellence in Physics, Ministry of Higher Education, Science, Research and Innovation, 328 Si Ayutthaya Road, Bangkok 10400, Thailand
cDivision of Physical Science, Faculty of Science and Technology, Huachiew Chalermprakiet University, Samutprakarn 10540, Thailand
dDepartment of Chemistry, Center of Excellence in Materials Science and Technology and Materials Science Research Centre, Faculty of Science, Chiang Mai University, Chiang Mai, 50200, Thailand
eDepartment of Science, Faculty of Science and Technology, Prince of Songkla University, Pattani, 94000, Thailand. E-mail: piya.p@psu.ac.th
fMaterials Theory, Department of Physics and Materials Science, Uppsala University, Box 530, SE-751 21, Uppsala, Sweden
gDepartment of Physics, Indian Institute of Technology (IIT) Ropar, Rupnagar 140001, Punjab, India
First published on 21st September 2022
Abstract
Lanthanum hydride compounds LaH3 become stabilized by yttrium substitution under the influence of moderate pressure. Novel materials with a wide range of changes in the structural properties as a function of hydrogen are investigated by means of the first-principles cluster expansion technique. Herein, the new compounds La1−xYxH3, where 0 ≤ x ≤ 1, are determined to adopt tetragonal structures under high-pressure with the compositions La0.8Y0.2H3, La0.75Y0.25H3, and La0.5Y0.5H3. The corresponding thermodynamic and dynamical stabilities of the predicted phases are confirmed by a series of calculations including, for example, phonon dispersion, electronic band structure, and other electronic characteristics. According to the band characteristics, all hydrides except that of I41/amd symmetry are semiconductors. The tetragonal La0.5Y0.5H3 phase is found to become semi-metallic, as confirmed by adopting the modified Becke–Johnson exchange potential. The physical origins of the semiconductor properties in these stable hydrides are discussed in detail. Our findings provide a deeper insight into this class of rare-earth ternary hydrides.
1 Introduction
Hydrogen-rich materials have attracted considerable attention thanks to their potential applications, especially in hydrogen storage,1–3 as well as the changes in physical and chemical properties as a function of the hydrogen concentration.4–8 The electronic structures of several rare-earth hydrides have been widely investigated,9–17 for example, the metal–semiconductor transition in lanthanum dihydride and lanthanum trihydride.9 Also, lanthanum deuterium was observed by neutron diffraction measurements18 to form NaCl-type LaD at high pressures as a result of pressure-induced decomposition of LaH2.3 via dismutation. This phase separation19 is due to the influence of H atoms moving into the empty O-sites of the surrounding LaH2.3. Following this, by means of first-principles calculations, LaH was predicted to become thermodynamically and dynamically stable at a pressure of 15 GPa. The pressure-dependent disproportionation reaction of LaH2 was also observed by high-pressure infrared reflection and Raman scattering measurements. Reportedly, at frequency ranging from 14 to 30 GPa, the absorption peaks found are similar to those observed in LaH3.20In recent years, both experimental and theoretical studies of rare-earth trihydrides have been reported. Face-centered cubic ScH3, YH3, and LaH3 rare-earth trihydrides were predicted to be dynamically stable and become superconducting at high pressures.21,22 The fcc YH3 superconducts at a relatively high superconducting transition temperature (Tc) close to 40 K at 18 GPa.21 According to the aforementioned experimental findings9 and recent extensive studies by first-principles calculations,23,24 LaH3 was demonstrated to have an energy gap of 0.8–0.9 eV. Moreover, the LaH3 and YH3 compounds were confirmed theoretically to be structurally stable at 11 GPa and 18 GPa, respectively.21,22 At this stage, alloying these mentioned rare-earth elements, by means of the cluster expansion (CE) technique, might give rise to new hydrides with novel physical properties. To thoroughly investigate electronic properties in the candidate structure of La1−xYxH3, calculations should be conducted at moderate pressures, as consistent with the reports on LaH3 being thermodynamically stable up to at least 20 GPa.18 As a consequence, first-principles CE will be performed at 20 GPa for the new class of La1−xYxH3 substituted rare-earth hydrides. In this regard, we attempt to (i) search for stable compositions and favored atomic configurations of La1−xYxH3, (ii) to look for signs of superconducting properties in these stable compositions, and (iii) to better understand any changes in the materials' properties induced by the substitution of the Y atom.
Herein, we make use of the first-principles CE based on density functional theory as a starting point to first define the stable La1−xYxH3 alloy(s). CE is conducted at 20 GPa due to the possible chemical reaction between LaH3 and YH3 solid solution achievable at 15 GPa and 18 GPa, respectively.18,21 Then the concentration x is varied from 0 to 1, while the GS structures of the La–Y–H system as well as their formation energies are determined correspondingly. Based on the density functional theory (DFT), CE calculations output ground-state candidate structures along the convex hull.3,25,26 Note that the CE calculation is associated with a set of lattice sites appointed as an occupation variable in a crystal structure. Clearly, an occupation variable in a given crystal structure leads to a decrease in the crystal symmetry. In our case, the role of the Y atom induces the decrease in symmetry of fcc-LaH3, which is expected to exhibit structural phase transitions under pressure. The resulting semiconducting properties of the La–Y–H systems are then compared and discussed.
2 Computational details
A substitution of an atomic type can be determined by the cluster expansion (CE) method,27 while the energy of which is reported as a function of substituted occupation. This is done by using the MIT Ab initio Phase Stability (MAPS) code,28 as implemented in the Alloy-Theoretic Automated Toolkit (ATAT).29 These codes are available in the Quantum Espresso (QE) package.30 The technical details of the CE calculations have been described extensively in ref. 3, 26, 31 and 32. The plane-wave energy cutoff of 60 Ry and k-point meshes of 4000 were used. The generalized gradient approximation proposed by Perdew, Burke, and Ernzerhof (GGA-PBE)33 was used as the exchange–correlation functional. All structures were calculated by imposing lattice dynamics, by means of a supercell approach, as implemented in Cambridge Serial Total Energy Package (CASTEP) code.34 As for the band structure evaluation, the modified Becke–Johnson (mBJ) exchange potential35 in conjunction with the GGA functional were used to determine the energy gap, as implemented in the Vienna ab initio simulation package (VASP) code.36 The nature of chemical bonding was further demonstrated by evaluating the electron localization function (ELF),37 as also implemented in VASP code, together with the projected crystal orbital overlap population (pCOOPs),38 which is implemented in the LOBSTER code.393 Results and discussion
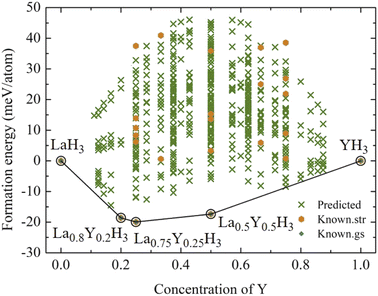
We explored the effect of Y substitution on the face-centered cubic LaH3 at 20 GPa by means of the first-principles CE. Structures predicted from CE have yet to be confirmed by DFT. The stable compositions are determined in terms of minimum free energy along the function of atomic occupation, which is defined by eqn (1).
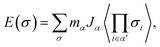 | (1) |
According to Fig. 1, the most relatively stable structures along the convex hull are those of La0.8Y0.2H3, La0.75Y0.25H3, and La0.5Y0.5H3. These candidate alloys undergo a structural relaxation calculated based on DFT under the pressure of 20 GPa. The optimized structural parameters of which are reported in Table 1. Markedly, substituting Y into the fcc-LaH3 significantly affects its structural behaviour, that is, the fcc structure with space group of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m successively transitions from high- to low-symmetry structures (i.e. Fm
m successively transitions from high- to low-symmetry structures (i.e. Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m → I4/m, Fm
m → I4/m, Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m → I4/mmm, and Fm
m → I4/mmm, and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m → I41/amd), as can be seen in Fig. 2. Note that for all our calculations regarding the La1−xYxH3 alloys, all the corresponding structures are evaluated without taking into consideration the entropy (S) contributions due to the fact that DFT works at 0 K and is capable of determining compounds closely resembling those found in experiment.40–46
m → I41/amd), as can be seen in Fig. 2. Note that for all our calculations regarding the La1−xYxH3 alloys, all the corresponding structures are evaluated without taking into consideration the entropy (S) contributions due to the fact that DFT works at 0 K and is capable of determining compounds closely resembling those found in experiment.40–46
| Space group | Pressure (GPa) | Lattice parameters (Å, °) | Atomic coordinates (fractional) |
|---|---|---|---|
| I4/m | 20 | a = 8.096 b = 8.096 c = 4.992 | Y1 (0, 0, 0) |
| α = 90 β = 90 γ = 90 | La1 (0.203, 0.6018, 0) | ||
| H1 (0.1909, 0.092, 0.5) | |||
| H2 (0.388, 0.192, 0.50) | |||
| H3 (0, 0.5, 0.25) | |||
| H4 (0, 0, 0.25) | |||
| I4/mmm | 20 | a = 5.073 b = 5.073 c = 10.723 | Y1 (0, 0, 0) |
| α = 90 β = 90 γ = 90 | La1 (0.5, 0, 0.25) | ||
| La2 (0, 0, 0.5) | |||
| H1 (0, 0, 0.730) | |||
| H2 (0.265, 0.265, 0.620) | |||
| H3 (0.5 0, 0) | |||
| I41/amd | 20 | a = 5.078 b = 5.078 c = 10.749 | Y1 (0.5, 0.5, −0.5) |
| α = 90 β = 90 γ = 90 | La1 (0, 0.5, −0.25) | ||
| H1 (0.5, 0.5, −0.233) | |||
| H2 (0.25, 0.726, −0.625) |
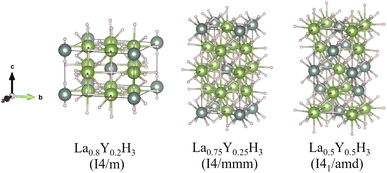 | ||
| Fig. 2 Structures of the La–Y–H system. The pink, dark green, and light green spheres represent hydrogen, lanthanum, and yttrium atoms, respectively. | ||
At this stage, it is worth mentioning once again that at the pressure of 20 GPa, La0.8Y0.2H3, La0.75Y0.25H3, and La0.5Y0.5H3 have negative energies of formation relative to those of LaH3 and YH3. Although formation energy suggests thermodynamic stability, it does not suffice to guarantee the existence of such compounds. Thus, it is of utmost importance to also conduct phonon calculations to ensure dynamical stability for the candidate compounds. Fig. 3 reports the phonon dispersions at 20 GPa of La0.8Y0.2H3 (a), La0.75Y0.25H3 (b), and La0.5Y0.5H3 (c), which are clearly stable due to the absence of imaginary frequencies of any dispersion branches. As for the possibility of such compounds to form at varying temperatures, thermal effects on the dynamical stability must be taken into account in phonon calculations.47
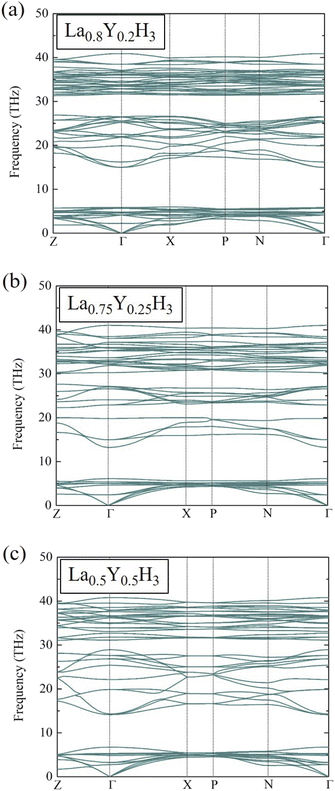 | ||
| Fig. 3 Phonon dispersions of (a) La0.8Y0.2H3 at 20 GPa, (b) La0.75Y0.25H3 at 20 GPa, and (c) La0.5Y0.5H3 at 20 GPa. | ||
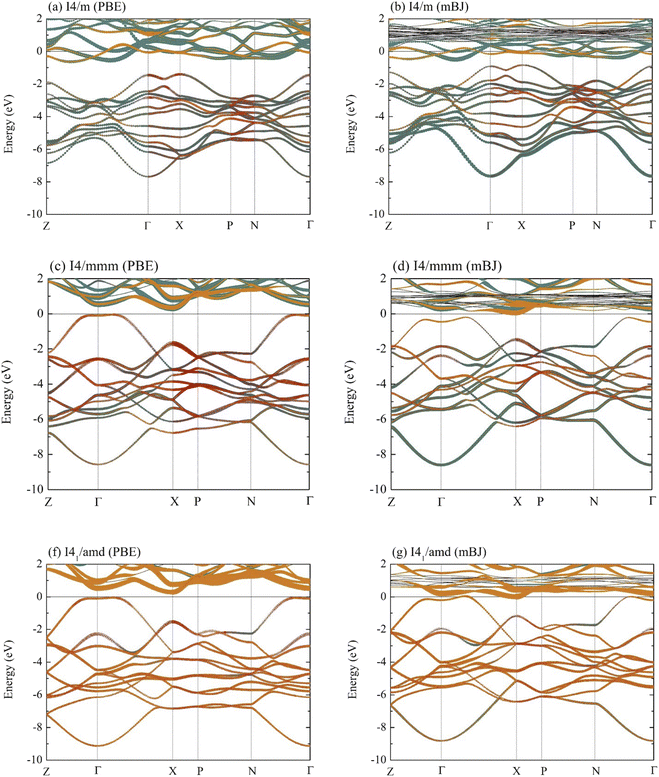
Now, the electronic characteristics of the I4/m, I4/mmm, and I41/amd La–Y–H systems are thoroughly investigated to look for signs of possible superconductivity in these materials. The corresponding electronic band structures of these compounds are shown in Fig. 4, all of which are determined using the GGA-PBE exchange–correlation functional. As a result, the I4/m, I4/mmm, and I41/amd structures become semiconductors with indirect band gaps of 0.765, 0.382, and 0.335 eV, respectively. Note that GGA underestimates band gaps in many semiconducting systems. Therefore, we additionally perform the calculation based on the hybrid exchange–correlation functional to correct the mentioned discrepancy. Despite being considered to be one of the most effective functionals capable of accurately determining band gaps, the Heyd–Scuseria–Ernzerhof (HSE06) functional is itself computationally expensive. Thus, we opt for the modified Becke–Johnson (mBJ) exchange potential35 in conjunction with the GGA functional, owing to the fact that the former determines band gaps even of strongly correlated systems with an acceptable level of accuracy, yet with fewer resources compared to HSE06.48–51 According to Fig. 4(b), the band dispersion of the I4/m structure, calculated by the mBJ exchange potential, clearly indicates a semiconducting phase with an indirect energy gap of 0.346 eV, whereas it is 0.252 eV in the case of the I4/mmm structure (Fig. 4(d)). Markedly, the I41/amd La–Y–H (Fig. 4(g)) turns out to be semimetallic due to the presence of states across the Fermi level (EF). A plausible explanation of which might be attributable to the strongly correlated nature of electrons in Y atoms when substituted into the compound, as highlighted by the increased size of dispersion branches above EF (Fig. 4(g)).
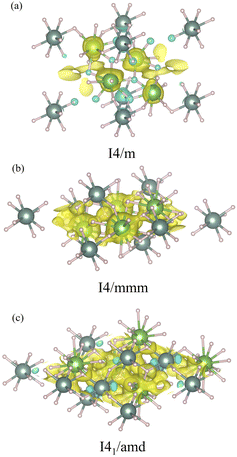
Also we further analyze the electronic structures by means of the charge density differences of the I4/m, I4/mmm, and I41/amd structures, which are illustrated in Fig. 5. The charge density difference in the La–Y–H systems is expressed as,
| ρnet = ρLa1−xYxH3 − ρY − ρH, | (2) |
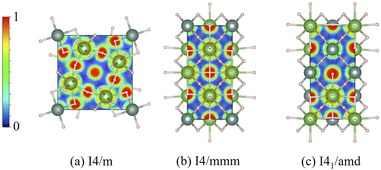
Another aspect that needs to be considered is the nature of chemical bonding, which can be observed in theory via the electron localization function (ELF)37 and the projected crystal orbital overlap population (pCOOPs), both of which play a crucial role in describing the electron accumulation and determining anti-bonding and bonding characteristics.52 As a consequence, the calculations of ELF for all the I4/m, I4/mmm, and I41/amd ternary hydrides are made and reported in Fig. 6. In the case of I4/m (Fig. 6(a)), it is noticeable that electrons tend to accumulate around H atoms which also display some electronic distribution in the vicinity of both La and Y atoms, indicating the possibility of weak bonding between the first nearest-neighbor (NN) La–H (2.2584 Å) and the second NN Y–H (2.0980 Å). On the other hand, electrons tend to localize around each metal in the cases of I4/mmm and I41/amd, as can be seen in the Fig. 6(b) and (c).
It is clear that, according to the ELF in all cases, H atoms are unlikely to chemically bond with La and Y atoms. Thus, we further investigate the bond characteristics by performing the pCOOP calculations53–56 for all materials in question. As a result, the pCOOP calculations for all La–Y–H hydrides are reported in Fig. 7. Shown in Fig. 7(a), I4/m largely consists of anti-bonding between La–H pairs at energies ranging from −0.65 eV to −0.05 eV, while the La–Y pairs dominate at energies ranging from −0.65 eV and all the way up to EF. A lesser contribution from the Y–H pairs and the H–H pairs can be found from −0.64 eV to the Fermi level and −0.54 eV to −0.05 eV, respectively, both of which are anti-bonding states. As for the I4/mmm structure, the La–Y pairs displayed a higher degree of the anti-bonding states starting from −2.20 eV to the Fermi level and so do the Y–H pairs. On the contrary, the La–H and the H–H pairs characterized by ionic states are noticeable from −2.25 eV to −0.05 eV and −2.15 eV to −0.05 eV, respectively (Fig. 7(b)). Lastly, a larger amount of the anti-bonding states attributed from the La–Y pairs dwell at energies ranging from −2.34 eV to the Fermi level. Similar bond characteristics are observable for those of La–H and La–Y pairs, whereas the Y–H and H–H pairs tend to have a lesser degree of ionic states from 2.34 eV to −0.1 eV, as can be seen in Fig. 7(c).
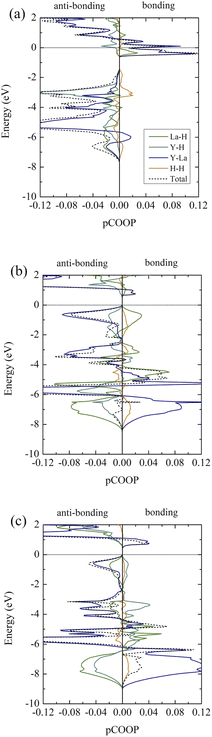 | ||
| Fig. 7 Projected crystal orbital overlap populations (pCOOPs) of (a) the I4/m structure at 20 GPa, (b) the I4/mmm structure at 20 GPa, and (c) the I41/amd structure at 20 GPa, respectively. | ||
4 Conclusion
In summary, we report novel rare-earth substituted La1−xYxH3 alloys under the influence of moderate pressure by adopting the first-principles cluster expansion technique. The relatively lowest energy structures along the convex hull are La0.8Y0.2H3, La0.75Y0.25H3, and La0.5Y0.5H3, all of which are confirmed dynamically stable at 20 GPa. By adopting the modified Becke–Johnson (mBJ) exchange potential, band characteristics of such materials are determined. Also, charge density difference, localization function, and projected crystal orbital overlap population are evaluated to further investigate the corresponding electronic behaviors. However, the stable structures of La0.8Y0.2H3, La0.75Y0.25H3, and La0.5Y0.5H3 have yet to be observed experimentally. We believe that our findings will urge further first-principles calculations as well as experiments for the exploration of this class of rare-earth substituted hydride superconductors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research project is supported by the Second Century Fund (C2F), Chulalongkorn University. We gratefully acknowledge computational resources from the Swedish National Infrastructure for Computing, SNIC (2021/1-42). R. A. and W. L. acknowledge the support from the Swedish Research Council (Grant no. VR-2020-04410) and Gust. Richert stiftelse, Sweden (2021-00665). This project is funded by National Research Council of Thailand (NRCT): (NRCT5-RSA63001-04). This work is partially supported by the Center of Excellence in Materials Science and Technology, Chiang Mai University.Notes and references
- P. Pluengphon, T. Bovornratanaraks, P. Tsuppayakorn-aek, U. Pinsook and B. Inceesungvorn, Int. J. Hydrogen Energy, 2019, 44, 21948–21954 CrossRef CAS.
- P. Pluengphon, P. Tsuppayakorn-aek, B. Inceesungvorn and T. Bovornratanaraks, Int. J. Hydrogen Energy, 2020, 45, 25065–25074 CrossRef CAS.
- P. Pluengphon, P. Tsuppayakorn-aek, B. Inceesungvorn, R. Ahuja and T. Bovornratanaraks, J. Phys. Chem. C, 2021, 125, 1723–1730 CrossRef CAS.
- J. L. Braun, S. W. King, E. R. Hoglund, M. A. Gharacheh, E. A. Scott, A. Giri, J. A. Tomko, J. T. Gaskins, A. Al-kukhun, G. Bhattarai, M. M. Paquette, G. Chollon, B. Willey, G. A. Antonelli, D. W. Gidley, J. Hwang, J. M. Howe and P. E. Hopkins, Phys. Rev. Mater., 2021, 5, 035604 CrossRef CAS.
- M. Nordio, S. A. Wassie, M. V. S. Annaland, D. A. P. Tanaka, J. L. V. Sole and F. Gallucci, Int. J. Hydrogen Energy, 2021, 46, 23417–23435 CrossRef CAS.
- A. Drexler, C. Bergmann, G. Manke, V. Kokotin, K. Mraczek, S. Leitner, M. Pohl and W. Ecker, J. Alloys Compd., 2021, 856, 158226 CrossRef CAS.
- Q. Cheng, C. Hu, G. Wang, Z. Zou, H. Yang and L. Dai, J. Am. Chem. Soc., 2020, 142, 5594–5601 CrossRef CAS PubMed.
- S. Jiang, R. Zhang, H. Liu, Y. Rao, Y. Yu, S. Chen, Q. Yue, Y. Zhang and Y. Kang, J. Am. Chem. Soc., 2020, 142, 6461–6466 CrossRef CAS PubMed.
- D. K. Misemer and B. N. Harmon, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 5634–5644 CrossRef CAS.
- Y. Yao and D. D. Klug, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 140104 CrossRef.
- H. Liu, I. I. Naumov, R. Hoffmann, N. W. Ashcroft and R. J. Hemley, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6990–6995 CrossRef CAS.
- Z. M. Geballe, H. Liu, A. K. Mishra, M. Ahart, M. Somayazulu, Y. Meng, M. Baldini and R. J. Hemley, Angew. Chem., Int. Ed., 2018, 57, 688–692 CrossRef CAS PubMed.
- H. Liu, I. I. Naumov, Z. M. Geballe, M. Somayazulu, J. S. Tse and R. J. Hemley, Phys. Rev. B, 2018, 98, 100102 CrossRef CAS.
- A. P. Drozdov, P. P. Kong, V. S. Minkov, S. P. Besedin, M. A. Kuzovnikov, S. Mozaffari, L. Balicas, F. F. Balakirev, D. E. Graf, V. B. Prakapenka, E. Greenberg, D. A. Knyazev, M. Tkacz and M. I. Eremets, Nature, 2019, 569, 528–531 CrossRef CAS PubMed.
- T. Sakai, M. Sakai, T. Kobayashi, M. Yasutake, S. Akisato, R. Mikami, N. Suganuma, Y. Takahashi, Y. Nakajima and M. Tokuda, et al., Thin Solid Films, 2019, 669, 288–293 CrossRef CAS.
- R. Kataoka, T. Kimura, K. Sakaki, M. Nozaki, T. Kojima, K. Ikeda, T. Otomo, N. Takeichi and A. Kamegawa, Inorg. Chem., 2019, 58, 13102–13107 CrossRef CAS PubMed.
- P. Tsuppayakorn-aek, U. Pinsook, W. Luo, R. Ahuja and T. Bovornratanaraks, Mater. Res. Express, 2020, 7, 086001 CrossRef CAS.
- A. Machida, M. Honda, T. Hattori, A. Sano-Furukawa, T. Watanuki, Y. Katayama, K. Aoki, K. Komatsu, H. Arima, H. Ohshita, K. Ikeda, K. Suzuya, T. Otomo, M. Tsubota, K. Doi, T. Ichikawa, Y. Kojima and D. Y. Kim, Phys. Rev. Lett., 2012, 108, 205501 CrossRef CAS.
- A. Machida, T. Watanuki, D. Kawana and K. Aoki, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 054103 CrossRef.
- Y. Sakurai, A. Machida and K. Aoki, Solid State Commun., 2011, 151, 815–817 CrossRef CAS.
- D. Y. Kim, R. H. Scheicher, H.-k. Mao, T. W. Kang and R. Ahuja, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2793–2796 CrossRef CAS PubMed.
- A. P. Durajski and R. Szcześniak, Supercond. Sci. Technol., 2014, 27, 115012 CrossRef.
- E. K. Chang, X. Blase and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 155108 CrossRef.
- J. A. Alford, M. Y. Chou, E. K. Chang and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 125110 CrossRef.
- M. Amsler, Phys. Rev. B, 2019, 99, 060102 CrossRef CAS.
- P. Tsuppayakorn-aek, P. Phansuke, P. Kaewtubtim, R. Ahuja and T. Bovornratanaraks, Comput. Mater. Sci., 2021, 190, 110282 CrossRef CAS.
- J. M. Sanchez, F. Ducastelle and D. Gratias, Physica A, 1984, 128, 334–350 CrossRef.
- A. van de Walle and G. Ceder, J. Phase Equilib., 2002, 23, 348–359 CrossRef CAS.
- A. Van De Walle, M. Asta and G. Ceder, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2002, 26, 539–553 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- A. Ektarawong, T. Bovornratanaraks and B. Alling, Phys. Rev. B, 2020, 101, 134104 CrossRef CAS.
- P. Tsuppayakorn-aek, P. Pluengphon, P. Phansuke, B. Inceesungvorn, W. Busayaporn, P. Kaewtubtim and T. Bovornratanaraks, Sci. Rep., 2021, 11, 1–7 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2006, 124, 221101 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed.
- P. Tsuppayakorn-aek, W. Luo, R. Ahuja and T. Bovornratanaraks, Sci. Rep., 2018, 8, 3026 CrossRef PubMed.
- P. Tsuppayakorn-aek, W. Luo, T. Watcharatharapong, R. Ahuja and T. Bovornratanaraks, Sci. Rep., 2018, 8, 5278 CrossRef PubMed.
- P. Tsuppayakorn-aek, W. Luo, W. Pungtrakoon, K. Chuenkingkeaw, T. Kaewmaraya, R. Ahuja and T. Bovornratanaraks, J. Appl. Phys., 2018, 124, 225901 CrossRef.
- P. Tsuppayakorn-aek, W. Chaimayo, U. Pinsook and T. Bovornratanaraks, AIP Adv., 2015, 5, 097202 CrossRef.
- P. Jimlim, P. Tsuppayakorn-aek, T. Pakornchote, A. Ektarawong, U. Pinsook and T. Bovornratanaraks, RSC Adv., 2019, 9, 30964–30975 RSC.
- K. Kotmool, P. Tsuppayakorn-aek, T. Kaewmaraya, U. Pinsook, R. Ahuja and T. Bovornratanaraks, J. Phys. Chem. C, 2020, 124, 14804–14810 CrossRef CAS.
- P. Tsuppayakorn-aek, J. Zhang, W. Luo, Y. Ding, R. Ahuja and T. Bovornratanaraks, Phys. Status Solidi B, 2021, 258, 2000279 CrossRef CAS.
- M. Di Gennaro, S. K. Saha and M. J. Verstraete, Phys. Rev. Lett., 2013, 111, 025503 CrossRef.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- K. Boulenouar, M. Bouslama, A. Mokadem, S. Vizzini, Z. Lounis, A. Abdellaoui, B. Reguad, M. Bedrouni, K. Hamaida, T. Guenouna and M. Ghaffour, J. Phys. Chem. C, 2017, 121, 8345–8352 CrossRef CAS.
- F. Tran and P. Blaha, J. Phys. Chem. A, 2017, 121, 3318–3325 CrossRef CAS PubMed.
- T. Bovornratanaraks, R. Ahuja and P. Tsuppayakorn-aek, Mater. Res. Express, 2021, 8(10), 105901 CrossRef CAS.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef CAS PubMed.
- Z. Wu, R.-D. Hoffmann, D. Johrendt, B. D. Mosel, H. Eckert and R. Pöttgen, J. Mater. Chem., 2003, 13, 2561–2565 RSC.
- E. M. Seibel, L. M. Schoop, W. Xie, Q. D. Gibson, J. B. Webb, M. K. Fuccillo, J. W. Krizan and R. J. Cava, J. Am. Chem. Soc., 2015, 137, 1282–1289 CrossRef CAS PubMed.
- S. Lotfi, A. O. Oliynyk and J. Brgoch, Inorg. Chem., 2018, 57, 10736–10743 CrossRef CAS.
- A. A. Adeleke, E. Stavrou, A. O. Adeniyi, B. Wan, H. Gou and Y. Yao, Phys. Rev. B, 2020, 102, 134120 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |