Open Access Article
Open Access ArticleMultiscale modelling of the radical-induced chemistry of acetohydroxamic acid in aqueous solution†
Jacy K. Conrad *a,
Corey D. Pilgrim
*a,
Corey D. Pilgrim a,
Simon M. Pimblott
a,
Simon M. Pimblott a,
Stephen P. Mezyk
a,
Stephen P. Mezyk b and
Gregory P. Horne
b and
Gregory P. Horne *a
*a
aCenter for Radiation Chemistry Research, Idaho National Laboratory, 1955 N. Fremont Ave., Idaho Falls, ID 83415, USA. E-mail: jacy.conrad@inl.gov; gregory.horne@inl.gov
bDepartment of Chemistry and Biochemistry, California State University Long Beach, 1250 Bellflower Blvd., Long Beach, CA 90840, USA
First published on 18th October 2022
Abstract
Acetohydroxamic acid (AHA) is a small organic acid with a wide variety of industrial, biological, and pharmacological applications. A deep fundamental molecular level understanding of the mechanisms responsible for the radical-induced reactions of AHA in these environments is necessary to predict and control their behaviour and elucidate their interplay with other attendant chemical species, for example, the oxidative degradation products of AHA. To this end, we present a comprehensive, multiscale computer model for interrogating the radical-induced degradation of AHA in acidic aqueous solutions. Model predictions were critically evaluated by a systematic experimental radiation chemistry investigation, leveraging time-resolved electron pulse irradiation techniques for the measurement of new radical reaction rate coefficients, and steady-state gamma irradiations for the identification and quantification of AHA degradation products: acetic acid, hydroxylamine, nitrous oxide, and molecular hydrogen, with formic acid and methane as minor products. Excellent agreement was achieved between calculation and experiment, indicating that this fundamental model can accurately predict the degradation pathways of AHA under irradiation in acidic aqueous solutions.
Introduction
Hydroxamic acids have distinct chemical properties that have been extensively leveraged for industrial, biological, and pharmacological applications.1–3 For example, due to its strong bidentate metal chelating properties,4 acetohydroxamic acid (AHA, CH3CONHOH) has been proposed for use in used nuclear fuel reprocessing technologies for the reduction and complexation of plutonium and neptunium ions.5–8 AHA is also used as an oral drug to treat struvite kidney stones,9 urinary tract infections,10 metal poisoning,11 and to complex metalloenzymes related to cancer progression.1,12,13 In addition, hydroxamic acids are prevalent in creating new pharmaceuticals via the promising strategy of linked hybrid bioactive fragments.14–16 In each of these applications, the stability of AHA is an important consideration. Hydroxamic acids are subject to degradation via hydrolysis under acidic conditions. The hydrolysis of AHA yields acetic acid (CH3COOH) and hydroxylamine (HA, NH3OH+) products:17–19| CH3CONHOH + H3O+ → CH3COOH + NH3OH+, k1 = 3.92 × 10−5 M−1 s−1. | (1) |
AHA will also interact with radiolysis products arising from the intense, multi-component, radiation fields present in used nuclear fuel reprocessing solvent systems, and with free radical species generated in the human body. Further, the oxidative decomposition of hydroxamic acids is important for considerations in wastewater treatment, either by the use of polyhydroxamic acids as metal chelators and flocculating agents for treatment,20 or for its disposal via advanced oxidation processes (AOPs), many of which leverage hydroxyl radical (·OH) and/or hydrogen peroxide (H2O2) mediated chemistry to promote complete mineralization of organic contaminants.21–26
Consequently, a quantitative understanding of these hydroxamic acid oxidation and reduction processes at a fundamental molecular level is necessary to facilitate their prediction and control in various macroscopic systems and processes. This complete level of mechanistic understanding can readily be attained by utilizing radiation chemistry, a powerful means for directly characterizing the redox behavior of various transient and steady-state radicals, ions, and molecules. For aqueous solutions, the radiolysis of water produces a suite of primary radiolysis products, many of which are redox active (i.e., eaq−, H˙, ˙OH, and H2O2):27
H2O ![[long arrow, wavy then straight]](https://www.rsc.org/images/entities/char_e0f6.gif) (0.27) eaq−, (0.27) ˙OH, (0.06) H˙, (0.04) H2, (0.08) H2O2, (0.27) Haq+. (0.27) eaq−, (0.27) ˙OH, (0.06) H˙, (0.04) H2, (0.08) H2O2, (0.27) Haq+.
| (2) |
There have been a few studies that characterized the overall products from the gamma irradiation of AHA in concentrated nitric acid solutions for applications in used nuclear fuel reprocessing, but these works did not attempt to determine specific reaction mechanisms.30,31 In addition to those, Samuni and Goldstein measured second-order rate coefficients (k) for the reactions of AHA with ˙OH, ˙CO3−, azide (˙N3), and nitrite (NO2˙) radicals using time-resolved electron pulse radiolysis techniques to show that the product of these radical-induced AHA one-electron oxidations was always a nitroxide radical, CH3CONHO˙, and that no reaction occurs between AHA and the O2˙− radical.32 The structure of the nitroxide radical has been established using electron paramagnetic resonance (EPR) methods.33,34 A mechanism was proposed for the disproportionation of the transient nitroxide radical to form AHA and an unstable acyl nitroso intermediate (CH3CON![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O):32
O):32
CH3CONHO˙ + CH3CONHO˙ → CH3CONHOH + CH3CON![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, k3 = (1.51 ± 0.02) × 109 M−1 s−1. O, k3 = (1.51 ± 0.02) × 109 M−1 s−1.
| (3) |
To this end we present a new, comprehensive, multiscale computer model for the prediction of the free radical-induced mechanistic behavior of AHA in acidic aqueous solutions. The approach combines a stochastic model of the radiation track structure35–37 with a deterministic homogeneous bulk chemistry model, both pieces of which are essential to fully represent the system behavior. This model accounts for different solute concentrations, varying radical production rates, and pH, and has been validated and verified by comparison with experimental results from a new systematic study of the steady-state gamma radiolysis of AHA in pure water and aqueous perchloric acid solutions, in which the concentrations of AHA, and its potential final degradation products: acetic acid, HA, nitrite/nitrous acid (NO2−/HNO2), formic acid (HCOOH), molecular hydrogen (H2), nitrous oxide (N2O), and methane (CH4) were analyzed. These data augment the hydrolysis kinetics previously established for AHA,17–19 providing a complete model for the loss of this acid under different aqueous conditions.
Methods
Chemicals and analytical methods
Details of the chemicals used and the UV-visible spectroscopy, ion chromatography (IC), gas chromatography (GC), and proton nuclear magnetic resonance (1H-NMR) spectroscopy methods are given in the ESI.†Time-resolved electron pulse radiolysis
Radical reaction kinetics were measured for AHA and HA by transient absorption spectroscopy using the Brookhaven National Laboratory (BNL) picosecond Laser Electron Accelerator Facility (LEAF)38 and the Notre Dame Radiation Laboratory (NDRL) nanosecond electron pulse linear accelerator facility.39,40 Dosimetry to determine absolute radical yields per electron pulse was performed using the thiocyanate dosimeter solution (λmax = 470 nm, using G* ε = 5.2 × 10−4 m2 J−1).41 Isolation and measurement of specific radical species was achieved using the following solution conditions:• Hydrated electron (eaq−): direct transient decay kinetics of the eaq− were observed at 720 nm using N2- or Ar-saturated aqueous solutions of 0.5 M tBuOH at pH 4.0 or 9.8 buffered by 10 mM phosphate with pH adjusted by concentrated HClO4 or NaOH.
• Hydrogen atom (H˙): the growth kinetics of the pCBA radical adduct ([pCBA-H]˙) were monitored at 365 nm in N2-saturated aqueous solutions containing 100 μM pCBA, 20 mM tBuOH, and 3.0 M HClO4.
• Hydroxyl radical (˙OH): competition kinetics with SCN− were performed by monitoring the (SCN)2˙− transient absorption at 470 nm in N2O-saturated aqueous solutions using 0.1 mM KSCN at pH 4.0 for protonated AHA, pH 9.8 for deprotonated AHA, and pH 4.0 for HA, buffered by 10 mM phosphate with pH adjusted by concentrated HClO4 or NaOH.
All transient absorption measurements were made using 1 cm optical pathlength quartz cells at ambient room temperature (23–24 °C). Kinetic traces were the average of 8–15 individual measurements. Second-order rate coefficients (k) were derived from pseudo-first-order exponential fits (k′) to raw kinetic data by plotting k′ against the reactant concentration weighted by the inverse squares of the experimental uncertainties. Quoted errors for the presented second-order reaction rate coefficients are a combination of measurement precision and sample concentration errors.
Steady-state gamma irradiations
Gamma irradiations were performed on aqueous solutions of 0.50 M AHA with doses up to 100 kGy using the Idaho National Laboratory (INL) Center for Radiation Chemistry Research (CR2) Foss Therapy Services Model 812 Cobalt-60 Gamma Irradiator. The dose rates (Gy min−1) for different positions in the irradiator were determined to be 50–250 Gy min−1 using Fricke dosimetry42 subsequently corrected for the decay of cobalt-60 (60Co, τ1/2 = 5.27 years, Eγ1 = 1.17 MeV and Eγ2 = 1.33 MeV) throughout the duration of this study. Solution temperatures were monitored in situ during irradiation using a K-type thermocouple and found to be 35–45 °C. Samples for irradiation consisted of aqueous solutions of 0.50 M AHA in water or in 0.20 M HClO4 sealed in screw-cap glass vials or flame-sealed glass ampoules. The HClO4 solutions were chosen to probe the effects of pH on the reactivity and distribution of water radiolysis products, since ClO4− is essentially radiolytically inert.43Multiscale computational modelling
A combination of Monte Carlo radiation track35,36 and independent reaction times (IRT)37 models, in conjunction with a deterministic kinetic model, were used to construct a multiscale predictive computer model for the radical-induced oxidative and reductive behavior of AHA in aqueous solutions.44,45 Calculated stochastic radiation track yields, listed in ESI Table S1† were used as inputs for the deterministic kinetic model, which represents chemical mechanistic reactions as coupled differential equations that are solved numerically using the FACSIMILE kinetic modelling software package.46 The chemical kinetic reaction set used by these calculations consisted of an existing reaction scheme for water radiolysis28 supplemented by radical reactions for AHA and its degradation products, as summarized in ESI Table S2.† Where available, Arrhenius parameters were incorporated to accommodate for changes in temperature between irradiations. Gas partitioning between the aqueous and gaseous phases was accounted for using a simple stagnant two-film model47 with standard Henry's law coefficients48 and temperature-dependent diffusion parameters.49–52Results and discussion
Radical reaction kinetics
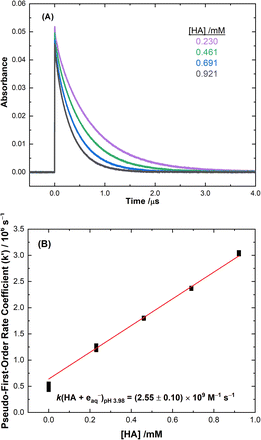
The radiolytic degradation of AHA is driven by a combination of radical-induced oxidation and reduction processes in the aqueous solutions investigated by this work. The second-order rate coefficients (k) of these radical-induced reactions with the protonated and deprotonated forms of AHA (pKa = 8.7 at 25 °C) and its major degradation product HA, were determined, or re-evaluated, at different pHs to quantify their relative contributions. The radical-induced chemical reactions of acetic acid, the other major AHA hydrolysis product (eqn (1)), have been well-studied and their rates are considered established, therefore they did not require measurement for inclusion in the model developed in this work.53–61 Although there are a few possible isomers of AHA, only the Z-amide is considered in this work as it is the most stable form in aqueous solution.62,63Typical data from the electron pulse kinetic measurements from this study are presented in Fig. 1 for the reaction of HA with the eaq−. All other kinetic data are given in ESI Fig. S4–S8.† The second-order rate coefficients derived from these measurements are listed in Table 1. These rate values were incorporated into the multiscale modelling chemical kinetic reaction set, as outlined in the ESI.†
| Radical species | Second-order rate coefficient (k, M−1 s−1) | ||
|---|---|---|---|
| CH3CONHOH | CH3CONHO− | NH3OH+ | |
| eaq− | (6.02 ± 0.86) × 108 | — | (2.55 ± 0.10) × 109 |
| H˙ | (5.43 ± 0.56) × 106 | — | (4.01 ± 0.43) × 105 |
| ˙OH | (4.75 ± 0.76) × 108 | (3.86 ± 0.11) × 109 | (1.59 ± 0.06) × 109 |
Radical-induced degradation mechanism of acetohydroxamic acid
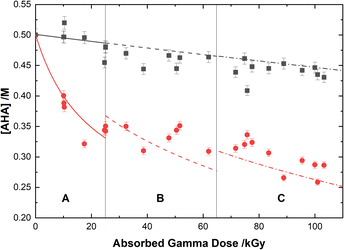
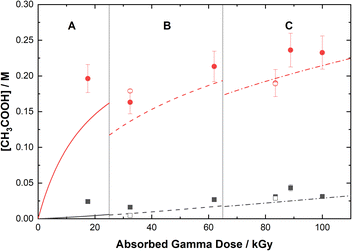
The loss of 0.50 M AHA under gamma irradiation in aerated water and 0.20 M HClO4 aqueous solution is shown in Fig. 2. Multiscale computer model predictions are plotted alongside the experimental data and are in excellent agreement for both solutions. Model predictions are broken into three distinct ‘regions’ chosen as representatives for the specific experimental conditions under which these measurements were performed: Region A, from 0–25 kGy is for a constant temperature of T = 36 °C at 51 Gy min−1; Region B from 25–65 kGy is for a constant temperature of T = 40 °C at 150 Gy min−1; and Region C from 65–110 kGy is for a constant temperature of T = 42 °C at 250 Gy min−1. These three sets of experimental conditions were chosen to keep the hydrolysis time relatively consistent between irradiations. The different regions are separated by vertical lines in Fig. 2, and the change in model conditions are indicated by changes in the line style (solid, dash, and dash–dot) used in the plot. AHA is consumed as a function of absorbed gamma dose and time in both aqueous solutions because of a combination of radiolysis and hydrolysis. This behavior is linear as a function of dose for H2O, but the loss is much more rapid in the HClO4 solution due to the hydrolysis reaction (eqn (1)).The mechanisms for the radical-induced degradation of AHA can be better understood from viewing the cumulative reaction outputs, i.e., the sum concentration of products produced by a given reaction, as shown in Fig. 3. For AHA in aerated water, Fig. 3(A), the radiolytic loss of AHA proceeds primarily via its reaction with the major radical products from water radiolysis (i.e., AHA is lost by reaction with the ˙OH radical (48.7%), eaq− (46.5%), and H˙ atom (4.6%), at 100 kGy) according to the reactions:
| CH3CONHOH + ˙OH → H2O + CH3CONHO˙, k4 = (4.75 ± 0.76) × 108 M−1 s−1, | (4) |
| CH3CONHOH + eaq− → CH3C˙(O−)NHOH, k5 = (6.02 ± 0.86) × 108 M−1 s−1, | (5) |
| CH3CONHOH + H˙ → CH3C˙(OH)NHOH, k6 = (5.43 ± 0.56) × 106 M−1 s−1, | (6) |
| CH3C˙(OH)NHOH → CH3CHO + NH2O˙, k7 = 1 × 107 M−1 s−1. | (7) |
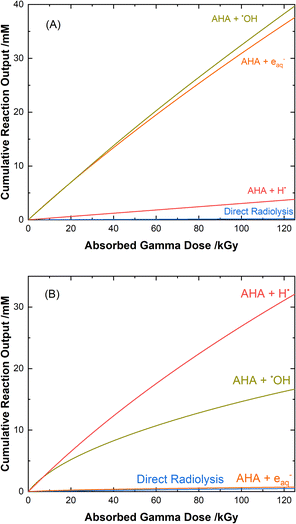 | ||
| Fig. 3 Multiscale model calculated cumulative reaction outputs for the major pathways involved in the radical-induced loss of 0.5 M AHA for 51 Gy min−1 at 36 °C in (A) water and (B) 0.20 M HClO4. | ||
The rate coefficient for k7 is approximated by the rates of similar reactions.67,69,70 The acetaldehyde (CH3CHO) that is formed is expected to react with the primary radiolysis products of water,55,71,72 primarily by oxidizing to acetic acid, and to speciate via its own equilibria73 and acidic degradation reactions74 in solution.
AHA is also expected to react with other minor radical products generated in the solution such as ˙CH2COOH, ˙CH3, and ˙CONHOH. The transient nitroxide radical (CH3CONHO˙), formed in the AHA reaction with the ˙OH radical and other minor carbon radical species undergoes bimolecular combination according to eqn (3), resulting in an acyl nitroso (CH3CON![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O). Acyl nitroso compounds are unstable and have been shown to undergo hydrolysis as follows:75,76
O). Acyl nitroso compounds are unstable and have been shown to undergo hydrolysis as follows:75,76
H2O + CH3CON![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O → HNO + CH3COOH, k8 = 1 s−1. O → HNO + CH3COOH, k8 = 1 s−1.
| (8) |
The HNO formed undergoes bimolecular combination with itself to ultimately yield H2O and N2O according to:77–79
| HNO + HNO → N2O + H2O, k9 = 8 × 106 M−1 s−1.79 | (9) |
Finally, there is also a small contribution from the direct radiolysis of AHA, i.e., the direct deposition of ionizing radiation energy into the electrons of AHA. Calculations based on the electron density of AHA predict that less than 4% of the gamma radiation would interact directly with AHA molecules.29 From these interactions, the AHA can become excited or ionized, resulting in different breakdown pathways to form a variety of products. One pathway suggested in the literature is:31
CH3CONHOH ![[long arrow, wavy then straight]](https://www.rsc.org/images/entities/char_e0f6.gif) CH3CONHOH* → ˙CONHOH + ˙CH3, CH3CONHOH* → ˙CONHOH + ˙CH3,
| (10) |
the products of which ultimately result in the formation of HA, HCOOH, and CH4, all of which were detected in the characterization methods used by this work. The G-value for this pathway was found to be 0.05 μmol J−1 in H2O, and 0.21 μmol J−1 in HClO4 by optimizing to fit the HCOOH and CH4 detected experimentally, as shown in ESI Fig. S9.†
Fig. 3(B) shows the cumulative reaction yields for the radiation-induced degradation of AHA in 0.20 M HClO4. Since the perchlorate anion is essentially radiolytically inert under the given conditions,43 the reaction set here is much the same as for water, and proceeds via the same primary radical species. One major difference, however, is the low solution pH (∼0.7). At low pH, the excess of protons (Haq+) alters the suite of water radiolysis products (ESI Table S1†), predominantly converting the yield of the eaq− into H˙ atom via the fast reaction:
| eaq− + Haq+ → H˙, k11 = 2.3 × 1010 M−1 s−1.27 | (11) |
Although both the eaq− and H˙ atom can be powerful reductants, the H˙ atom can undergo addition and abstraction reactions with organic molecules, resulting in different product distributions.27 Further, under these acidic conditions the majority of AHA loss in solution is due to hydrolysis (eqn (1)) as opposed to radical-induced processes. As shown in Fig. 4, the predicted relative contributions of hydrolysis and radiolysis as a function of absorbed dose for 0.50 M AHA in 0.20 M HClO4 irradiated at a rate of 51 Gy min−1 at 36 °C amounts to 85% and 15%, respectively at 100 kGy.
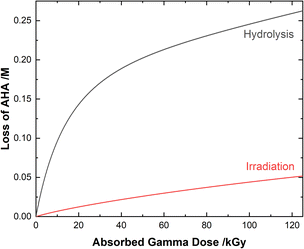 | ||
| Fig. 4 Multiscale model calculated relative contributions of hydrolysis and gamma radiolysis reactions to the cumulative loss of 0.50 M AHA for 51 Gy min−1 at 36 °C in 0.20 M HClO4. | ||
Overview of aqueous degradation products
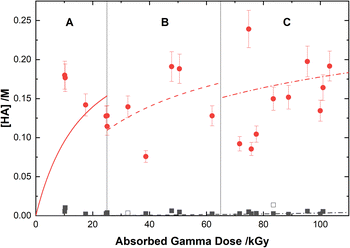
Based on the above reaction schemes, the major aqueous products of AHA degradation under the given conditions are acetic acid and HA, formed from both the radiolysis and hydrolysis processes. Although the yields of these two species from hydrolysis are equimolar, HA is negligibly produced from the radiolysis reactions. Further, both hydrolysis products react at different rates with the various aforementioned radicals, resulting in differences in their overall steady-state yields and subsequent degradation product distributions. The in-growth of acetic acid and HA from the degradation of 0.50 M AHA in water and 0.20 M HClO4 are shown in Fig. 5 and 6, respectively. Our multiscale model predictions are plotted alongside experimental data and again are in excellent agreement. In both solutions there is more acetic acid formed than HA, consistent with the stoichiometry predicted by Sanchez-Garcia et al.80 As expected, more acetic acid and HA are formed in the HClO4 solution than in water due to the increased rate of AHA hydrolysis. There was no NO2− or HNO2 detected in these systems by IC or UV-vis methods.Radical-induced degradation mechanism of hydroxylamine
The cumulative reaction yields for the loss of HA as a function of absorbed gamma dose for each of the two solution conditions are shown in Fig. 7. The primary contributors to the degradation of HA in water, as shown in Fig. 7(A), are its reaction with the eaq− (53% at 100 kGy), the ˙OH radical (45% at 100 kGy), and its molecular reaction with H2O2 (2% at 100 kGy):| NH3OH+ + eaq− → ˙OH + NH3, k12 = (2.55 ± 0.10) × 109 M−1 s−1, | (12) |
| NH3OH+ + ˙OH → H2O + NH3O˙+, k13 = (1.59 ± 0.06) × 109 M−1 s−1, | (13) |
| NH3OH+ + H2O2 → NH3O˙+ + ˙OH + H2O, k14 = 2.2 × 10−4 M−1 s−1,81 | (14) |
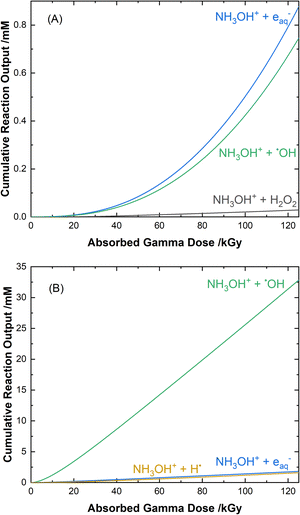 | ||
| Fig. 7 Calculated cumulative reaction yields for the major pathways involved in the radiolytic loss of HA for 51 Gy min−1 gamma irradiation at 36 °C in 0.5 M AHA in (A) water, and (B) 0.20 M HClO4. | ||
For 0.20 M HClO4, as shown in Fig. 7(B), a significant portion of the eaq− yield is converted to H˙ atom (eqn (11)). This allows for its reaction with HA to have an additional contribution to the overall loss of HA:
| NH3OH+ + H˙ → H2 + NH3O˙+, k15 = (4.01 ± 0.43) × 105 M−1 s−1. | (15) |
The HA radical formed in these reactions was originally proposed to take the form ˙NHOH/˙NH2OH+.82,84,85 However, it has since been shown by EPR studies and quantum chemical calculations that the more thermodynamically stable isomer is NH2O˙/NH3O˙+.81,86,87 Decay of NH2O˙ proceeds by one of several competing pathways, yielding either N2 or N2O as gaseous products. Under anoxic conditions, we have:88
| NH2O˙ + NH2O˙ → N2 + 2H2O, k16 = 4.5 × 108 M−1 s−1,82 | (16) |
and under aerated conditions, the following reactions must also be considered:88
| NH2O˙ + O2 → HNO + HO2˙, k17 = 1 × 104 M−1 s−1, | (17) |
| NH2O˙ + H2O2 → HNO + ˙OH + H2O, k18 = 10 M−1 s−1, | (18) |
| NH3O˙+ + H2O2 → HNO + ˙OH + H2O + Haq+, k19 = 150 M−1 s−1. | (19) |
Although reactions eqn (17)–(19) have been proposed in the literature,81,82,84,88 their rates have not been reported. In our model, the rates of these reactions were optimized to match the experimental production of N2O. In agreement with these optimized values, Simic and Hayon suggest that the rate coefficient for reaction eqn (18) is likely slower than eqn (19),82 and Karpel Vel Leitner et al.88 found that eqn (19) did not occur significantly under their experimental conditions.
The HNO produced in eqn (17)–(19) undergoes bimolecular combination according to eqn (9) and therefore, in both solutions, the HA that reacts is primarily converted into N2O and H2O.
Overview of gaseous degradation products
The measured G-values (yields) for the gaseous species resulting from the irradiation of aqueous solutions of AHA are listed in Table 2. The yield of CH4 is very low, as it is produced only from the direct radiolysis of AHA (eqn (10)), which, based on electron fraction calculations, should receive less than 4% of the total gamma radiation at a concentration of 0.50 M. The relative order of magnitude of the G-values for the three gaseous products agree with the volume fraction ratios suggested by Wang et al.31| Experimental gas yields (G-values) in μmol J−1 | ||
|---|---|---|
| Water | 0.20 M HClO4 | |
| N2O | 0.076 ± 0.003 | 0.061 ± 0.005 |
| H2 | 0.045 ± 0.002 | 0.139 ± 0.015 |
| CH4 | 0.0016 ± 0.0002 | 0.0075 ± 0.0005 |
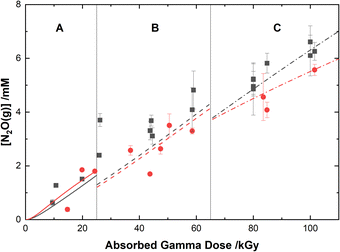
The experimental yields of the major gaseous products, N2O and H2, are shown with our computer model predictions in Fig. 8 and 9, respectively. As shown in Fig. 8, the calculations agree well with the measured yields of N2O and demonstrate a small reduction in this yield for the HClO4 solutions as compared to pure water.
 | ||
Fig. 9 Yields of H2 from the gamma irradiation of 0.50 M AHA in water ( ) and 0.20 M HClO4 ( ) and 0.20 M HClO4 ( ). The experimental data are divided into three regions: (A) 51 Gy min−1 at 36 °C (solid curve), (B) 150 Gy min−1 at 40 °C (dashed curve), and (C) 250 Gy min−1 at 42 °C (dash–dot curve). Lines are predicted values from multiscale modelling calculations using eqn (20) ( ). The experimental data are divided into three regions: (A) 51 Gy min−1 at 36 °C (solid curve), (B) 150 Gy min−1 at 40 °C (dashed curve), and (C) 250 Gy min−1 at 42 °C (dash–dot curve). Lines are predicted values from multiscale modelling calculations using eqn (20) ( , , 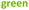 ) and eqn (21) ( ) and eqn (21) ( , ,  ) for the reaction of AHA + H˙ in 0.20 M HClO4 and H2O respectively. ) for the reaction of AHA + H˙ in 0.20 M HClO4 and H2O respectively. | ||
Our cal culations show that H2 is primarily produced from water radiolysis. These radiolytic yields have been extensively investigated in aqueous systems and are attributed to a series of reactions involving H2O, the eaq−, and the H˙ atom.89 Our model predicts higher H2 yields at lower pH, as expected due to an increase in H˙ atom yield under these conditions (as per eqn (11)). In the presence of AHA, there are additional contributions to the yield of H2 from H-atom abstraction reactions with the hydrolysis products acetic acid and HA, and with the radiolytic product acetaldehyde. Wang et al.31 proposed an analogous H-abstraction reaction for AHA:
| CH3CONHOH + H˙ → H2 + CH3CONHO˙, | (20) |
However, our model predicts that if the products of this reaction included H2, the G-value for H2 in water would be ∼1.5× the experimentally determined value of 0.045 μmol J−1. This result is demonstrated by the blue and green curves in Fig. 9 for 0.20 M HClO4 and H2O respectively. Therefore, considering the level of agreement between multiscale model calculations and experiment demonstrated thus far, the pathway proposed by Wang et al.31 is not considered to be the major mechanism. Furthermore, in an experiment measuring CH3CONHO˙ Samuni and Goldstein32 were unable to assign products to the reaction between H˙ and AHA, and therefore the nitroxide radical is also unlikely to be significantly produced. Accordingly, the reaction of AHA and H˙ is proposed to proceed primarily via:
| CH3CONHOH + H˙ → CH3C˙(OH)NHOH, | (21) |
which yields more accurate H2 yields for 0.50 M AHA in water and 0.20 M HClO4. The radical formed in this reaction is the same as the protonated form of the radical from the reaction of AHA and the eaq−, and it will react primarily according to eqn (7) under the given conditions.
All these reactions together provide a detailed picture of the degradation of AHA in acidic aqueous solutions via free radical reactions. The foundational aqueous solution model developed in this work can be further developed to apply to specific applications, as this model has been shown to agree with changes in pH and rate of radical generation at moderate temperatures above ambient conditions. For example, this model could be adapted for use under physiological conditions where the primary radicals generated are reactive oxygen and nitrogen species, because radicals like O2− and ˙NO2 do not react with AHA, and RO˙ species like ˙CO3− will yield the same AHA oxidation product as ˙OH.32
Conclusions
A multiscale computer model has been developed and rigorously evaluated against experimental results for the prediction of the radical-induced behavior of AHA in aqueous solutions. Both calculations and experiment demonstrate that: (i) the major products of AHA degradation in acidic aqueous solution are acetic acid, HA, N2O, and H2, with formic acid and CH4 as additional minor products; (ii) hydrolysis plays a more significant role in the decomposition of AHA than radiolysis under highly acidic conditions; (iii) the radical-induced AHA degradation occurs predominantly through oxidation by the ˙OH radical and reduction by the eaq−, with an increasing contribution from the H˙ atom with decreasing pH. The computational model developed in this work can be used to accurately predict the degradation behavior of AHA in simple acidic aqueous solutions.Beyond the current work, this modelling methodology has been shown to be extremely effective in providing quantitative mechanistic insight into the radiation chemistry occurring over multiple time and distance regimes—from the point of energy deposition, through the lifetime of the non-homogenous radiation chemical track, and ultimately bulk solution—for several aqueous systems including nitrate and nitric acid in the absence44 and presence of neptunium90 and americium91 ions, and for organic molecules, including diglycolamides.92 The proof of principle of these multiscale models has again been demonstrated by the agreement here between calculation and experiment over changes in pH, temperature, and dose rate. This ultimately demonstrates the power of this type of modelling methodology, which will be expanded in future works to apply to different types of chemistry occurring in aqueous solutions and beyond.
Author contributions
Jacy K. Conrad played the lead role in developing experimental methodology for the analytical techniques, steady state gamma irradiation data collection and analysis, kinetic model development and validation, and writing the original draft. Corey D. Pilgrim conducted the NMR data collection and analysis. Simon M. Pimblott developed the stochastic model and calculated the radiolytic escape yields. Simon M. Pimblott and Gregory P. Horne developed the multiscale model foundation. Gregory P. Horne and Stephen P. Mezyk collected the electron pulse radiolysis kinetic data and added valuable insights in the reaction mechanisms and the writing review and editing. Gregory P. Horne played a supervisory role in the kinetic model development and validation and lead the funding acquisition and conceptualization.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research has been funded by U.S. Department of Energy (DOE) Assistant Secretary for Nuclear Energy, under the Material Recovery and Waste Form Development Campaign, DOE-Idaho Operations Office Contract DE-AC07-05ID14517. This research made use of the resources of the High Performance Computing Center at Idaho National Laboratory, which is supported by the DOE Office of Nuclear Energy of the U.S. Department of Energy and the Nuclear Science User Facilities under Contract No. DE-AC07-05ID14517. Most of the electron pulse irradiation experiments took place at the Laser-Electron Accelerator Facility of the Brookhaven National Laboratory Accelerator Center for Energy Research, which is supported by the DOE Office of Science, Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences under contract DE-SC0012704. The Notre Dame Radiation Laboratory, in which some of the electron pulse irradiation experiments were performed, is also supported by the Division of Chemical Sciences, Geosciences and Biosciences, Basic Energy Sciences, DOE Office of Science, through Award No. DE-FC02-04ER15533. We acknowledge Cathy Rae and Kastli D. Schaller for establishing the GC and IC analysis methods and for their training on using each instrument.References
- S. Goldstein and A. Samuni, in Advances in Inorganic Chemistry, ed. R. van Eldik and J. A. Olabe, Academic Press, 2015, vol. 67, ch. 8, pp. 315–333 Search PubMed.
- Z. Syed, K. Sonu, A. Dongre, G. Sharma and M. Sogani, Int. J. Biol. Biomed., 2020, 14, 75–88 Search PubMed.
- B. R. Kant, B. S. Kant, B. T. Chand and B. A. Kumar, in Microbial Applications, ed. V. Kalia, Springer, Cham, 2017, vol. 2 Search PubMed.
- J. Keth, T. Johann and H. Frey, Biomacromolecules, 2020, 21, 2546–2556 CrossRef CAS PubMed.
- R. J. Taylor, I. May, A. L. Wallwork, I. S. Denniss, N. J. Hill, B. Y. Galkin, B. Y. Zilberman and Y. S. Fedorov, J. Alloys Compd., 1998, 271, 534–537 CrossRef.
- I. May, R. J. Taylor and G. Brown, J. Alloys Compd., 1998, 271, 650–653 CrossRef.
- I. May, R. J. Taylor, I. S. Denniss, G. Brown, A. L. Wallwork, N. J. Hill, J. M. Rawson and R. Less, J. Alloys Compd., 1998, 275, 769–772 CrossRef.
- P. Tkac, B. Matteson, J. Bruso and A. Paulenova, J. Radioanal. Nucl. Chem., 2008, 277, 31–36 CrossRef CAS.
- C. Marwick, JAMA, 1983, 250, 321–322 CrossRef CAS PubMed.
- W. N. Fishbein and P. P. Carbone, J. Biol. Chem., 1965, 240, 2407–2414 CrossRef CAS PubMed.
- J. L. Domingo, Reprod. Toxicol., 1998, 12, 499–510 CrossRef CAS PubMed.
- M. E. Neganova, S. G. Klochkov, Y. R. Aleksandrova and G. Aliev, Curr. Med. Chem., 2021, 28, 8139–8162 CrossRef PubMed.
- C. Adamson, H. Kajino, S. A. Kawashima, K. Yamatsugu and M. Kanai, J. Am. Chem. Soc., 2021, 143, 14976–14980 CrossRef CAS PubMed.
- V. N. Osipov, D. S. Khachatryan and A. N. Balaev, Med. Chem. Res., 2020, 29, 831–845 CrossRef CAS.
- D. V. Stanisheva, G. Atanasov, M. D. Aposstolova and O. I. Petrov, Curr. Bioact. Compd., 2021, 17, 59–66 CrossRef CAS.
- A. Citarella, D. Moi, L. Pinzi, D. Bonanni and G. Rastelli, ACS Omega, 2021, 6, 21843–21849 CrossRef CAS PubMed.
- F. P. L. Andrieux, C. Boxall and R. J. Taylor, J. Solution Chem., 2008, 37, 1511–1527 CrossRef CAS.
- F. P. L. Andrieux, C. Boxall, H. M. Steele and R. J. Taylor, J. Solution Chem., 2014, 43, 608–622 CrossRef CAS.
- I. Sanchez-Garcia, L. J. Bonales, H. Galan, J. M. Perlado and J. Cobos, Spectrochim. Acta, Part A, 2020, 229, 117877–117883 CrossRef CAS PubMed.
- Y. Arun, M. Daifa and A. J. Domb, Polym. Adv. Technol., 2021, 32, 842–852 CrossRef CAS.
- Y. J. Chen, J. S. Ye, Y. Chen, H. Hu, H. L. Zhang and H. S. Ou, Chem. Eng. J., 2019, 356, 98–106 CrossRef CAS.
- G. Moussavi, E. Fathi and M. Moradi, Process Saf. Environ. Prot., 2019, 126, 259–268 CrossRef CAS.
- W. J. Cooper, S. P. Mezyk, J. R. Peller, S. K. Cole, W. H. Song, B. J. Mincher and B. M. Peake, Ozone: Sci. Eng., 2008, 30, 58–64 CrossRef CAS.
- P. Gehringer and H. Eschweiler, in Environmental Applications of Ionizing Radiation, ed. W. J. Cooper, R. D. Curry and K. E. O'Shea, Wiley Interscience, New York, 1998, ch. 20, pp. 325–341 Search PubMed.
- T. Oppenländer, Photochemical Purification of Water and Air: Advanced Oxidation Processes (AOPs) – Principles, Reaction Mechanisms, Reactor Concepts, Wiley-VCH Verlag, Weinheim, Germany, 2007 Search PubMed.
- H. Zhou and D. W. Smith, J. Environ. Eng. Sci., 2002, 1, 247–264 CrossRef CAS.
- G. V. Buxton, C. L. Greenstock, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1988, 17, 513–886 CrossRef CAS.
- A. J. Elliot and D. M. Bartels, The Reaction Set, Rate Constants and G-Values for the Simulation of the Radiolysis of Light Water Over the Range 20° to 350 °C Based on Information Available in 2008, Report 153-127160-450-001, AECL Nuclear Platform Research and Development, 2009 Search PubMed.
- J. W. T. Spinks and R. J. Woods, Introduction to Radiation Chemistry, John Wiley & Sons Inc., Canada, 3rd edn, 1990 Search PubMed.
- D. G. Karraker, Radiation Chemistry of Acetohydroxamic Acid in the UREX Process, United States, 2002 Search PubMed.
- J. H. Wang, C. Li, Q. Li, M. H. Wu, W. F. Zheng and H. He, Nucl. Sci. Technol., 2018, 29, 27–35 CrossRef.
- A. Samuni and S. Goldstein, J. Phys. Chem. A, 2011, 115, 3022–3028 CrossRef CAS PubMed.
- M. Gabricevic, E. Besic, M. Birus, A. Zahl and R. van Eldik, J. Inorg. Biochem., 2006, 100, 1606–1613 CrossRef CAS PubMed.
- W. Chamulitrat, R. P. Mason and D. Riendeau, J. Biol. Chem., 1992, 267, 9574–9579 CrossRef CAS PubMed.
- S. M. Pimblott, J. A. LaVerne and A. Mozumder, J. Phys. Chem., 1996, 100, 8595–8606 CrossRef CAS.
- S. M. Pimblott and J. A. LaVerne, J. Phys. Chem. A, 2002, 106, 9420–9427 CrossRef.
- P. Clifford, N. J. B. Green, M. J. Oldfield, M. J. Pilling and S. M. Pimblott, J. Chem. Soc., Faraday Trans. 1, 1986, 82, 2673–2689 RSC.
- J. F. Wishart, A. R. Cook and J. R. Miller, Rev. Sci. Instrum., 2004, 75, 4359–4366 CrossRef CAS.
- G. L. Hug, Y. C. Wang, C. Schoneich, P. Y. Jiang and R. W. Fessenden, Radiat. Phys. Chem., 1999, 54, 559–566 CrossRef CAS.
- K. Whitman, S. Lyons, R. Miller, D. Nett, P. Treas, A. Zante, R. W. Fessenden, M. D. Thomas and Y. Wang, Linear accelerator for radiation chemistry research at Notre Dame, Proceedings of the '95 Particle Accelerator Conference and International Conference on High Energy Accelerators, Dallas, Texas, USA, 1996 Search PubMed.
- G. V. Buxton and C. R. Stuart, J. Chem. Soc., Faraday Trans., 1995, 91, 279–281 RSC.
- H. Fricke, E. J. Hart and H. P. Smith, J. Chem. Phys., 1938, 6, 229–240 CrossRef CAS.
- M. Domae, Y. Katsumura, P. Y. Jiang, R. Nagaishi, K. Ishigure, T. Kozawa and Y. Yoshida, J. Chem. Soc., Faraday Trans., 1996, 92, 2245–2250 RSC.
- G. P. Horne, T. A. Donoclift, H. E. Sims, R. M. Orr and S. M. Pimblott, J. Phys. Chem. B, 2016, 120, 11781–11789 CrossRef CAS PubMed.
- G. Garaix, G. P. Horne, L. Venault, P. Moisy, S. M. Pimblott, J. L. Marignier and M. Mostafavi, J. Phys. Chem. B, 2016, 120, 5008–5014 CrossRef CAS PubMed.
- MCPA Software FACSIMILE Kinetic Modeling Software Package Search PubMed.
- W. G. Whitman, Chem. Metall. Eng., 1923, 26, 146–148 Search PubMed.
- R. Sander, Henry's Law Constants, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 2018 Search PubMed.
- D. T. Kallikragas, A. Y. Plugatyr and I. M. Svishchev, J. Chem. Eng. Data, 2014, 59, 1964–1969 CrossRef CAS.
- A. Tamimi, E. B. Rinker and O. C. Sandall, J. Chem. Eng. Data, 1994, 39, 330–332 CrossRef CAS.
- W. J. Massman, Atmos. Environ., 1998, 32, 1111–1127 CrossRef CAS.
- H. Moradi, H. Azizpour, H. Bahmanyar, M. Mohammadi and M. Akbari, Heliyon, 2020, 6, 5385 CrossRef PubMed.
- D. Razem and W. H. Hamill, J. Phys. Chem., 1977, 81, 1625–1631 CrossRef CAS.
- J. K. Thomas, Trans. Faraday Soc., 1965, 61, 702–707 RSC.
- P. Neta, R. W. Fessenden and R. H. Schuler, J. Phys. Chem., 1971, 75, 1654–1666 CrossRef.
- M. Exner, H. Herrmann and R. Zellner, J. Atmos. Chem., 1994, 18, 359–378 CrossRef CAS.
- M. J. Davies, B. C. Gilbert, C. B. Thomas and J. Young, J. Chem. Soc., Perkin Trans., 1985, 2, 1199–1204 RSC.
- G. Kohler, S. Solar, N. Getoff, A. R. Holzwarth and K. Schaffner, J. Photochem., 1985, 28, 383–391 CrossRef.
- P. Neta and R. H. Schuler, J. Phys. Chem., 1972, 76, 2673–2679 CrossRef CAS.
- R. L. Willson, C. L. Greenstock, G. E. Adams, R. Wageman and L. M. Dorfman, Int. J. Radiat. Phys. Chem., 1971, 3, 211–220 CrossRef.
- P. Neta and R. H. Schuler, J. Phys. Chem., 1975, 79, 1–6 CrossRef CAS.
- M. L. Senent, A. Nino, C. M. Caro, S. Ibeas, B. Garcia, J. M. Leal, F. Secco and M. Venturini, J. Org. Chem., 2003, 68, 6535–6542 CrossRef CAS PubMed.
- S. Tolosa, N. Mora-Diez, A. Hidalgo and J. A. Sanson, RSC Adv., 2014, 4, 44757–44768 RSC.
- J. A. Howard and J. E. Bennett, Can. J. Chem., 1972, 50, 2374–2377 CrossRef CAS.
- G. A. Russell, J. Am. Chem. Soc., 1957, 79, 3871–3877 CrossRef CAS.
- L. M. Smith, H. M. Aitken and M. L. Coote, Acc. Chem. Res., 2018, 51, 2006–2013 CrossRef CAS PubMed.
- P. Neta and A. B. Ross, J. Phys. Chem. Ref. Data, 1990, 19, 413–512 CrossRef CAS.
- E. Suáres and M. Rodriguez, in Radicals in Organic Synthesis, ed. P. Renaud and M. P. Sibi, Wiley-VCH, Weinheim, 2001, vol. 2, p. 440 Search PubMed.
- M. Murakami and N. Ishida, Chem. Lett., 2017, 46, 1692–1700 CrossRef CAS.
- M. Bietti, O. Lanzalunga and M. Salamone, J. Org. Chem., 2005, 70, 1417–1422 CrossRef CAS PubMed.
- C. S. Satterfield and L. C. Case, Ind. Eng. Chem., 1954, 998–1001 CrossRef CAS.
- G. Duplatre and C. D. Jonah, Radiat. Phys. Chem., 1984, 24, 557–565 CrossRef CAS.
- R. R. Michelsen, S. F. M. Ashbourn and L. T. Iraci, J. Geophys. Res., 2004, 109, D23205 CrossRef.
- P. E. Sorensen and W. P. Jencks, J. Am. Chem. Soc., 1987, 109, 4675–4690 CrossRef CAS.
- E. Maimon, A. Lerner, A. Samuni and S. Goldstein, J. Phys. Chem. A, 2018, 122, 7006–7013 CrossRef CAS PubMed.
- A. S. Evans, A. D. Cohen, Z. A. Gurard-Levin, N. Kebede, T. C. Celius, A. P. Miceli and J. P. Toscano, Can. J. Chem., 2011, 89, 130–138 CrossRef CAS.
- Y. Izato, K. Shiota and A. Miyake, Sci. Technol. Energ. Mater., 2019, 80, 212–221 Search PubMed.
- K. Q. Zhang and S. T. Thynell, J. Phys. Chem. A, 2017, 121, 4505–4516 CrossRef CAS PubMed.
- V. Shafirovich and S. V. Lymar, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 7340–7345 CrossRef CAS PubMed.
- I. Sanchez-Garcia, L. J. Bonales, H. Galan, J. M. Perlado and J. Cobos, Radiat. Phys. Chem., 2021, 183, 109402 CrossRef CAS.
- L. W. Chen, X. C. Li, J. Zhang, J. Y. Fang, Y. M. Huang, P. Wang and J. Ma, Environ. Sci. Technol., 2015, 49, 10373–10379 CrossRef CAS PubMed.
- M. Simic and E. Hayon, J. Am. Chem. Soc., 1971, 93, 5982–5986 CrossRef CAS.
- P. Neta, P. Maruthamuthu, P. M. Carton and R. W. Fessenden, J. Phys. Chem., 1978, 82, 1875–1878 CrossRef CAS.
- M. Lefort and X. Tarrago, J. Inorg. Nucl. Chem., 1961, 16, 169–186 CrossRef CAS.
- D. Behar, D. Shapira and A. Treinin, J. Phys. Chem., 1972, 76, 180–186 CrossRef CAS.
- R. Musat, J. L. Marignier, C. Le Naour, S. Denisov, L. Venault, P. Moisy and M. Mostafavi, Phys. Chem. Chem. Phys., 2020, 22, 5188–5197 RSC.
- J. Lind and G. Merenyi, J. Phys. Chem. A, 2006, 110, 192–197 CrossRef CAS PubMed.
- N. Karpel Vel Leitner, P. Berger, G. Dutois and B. Legube, J. Photochem. Photobiol., A, 1999, 129, 105–110 CrossRef.
- A. J. Elliot, Radiat. Phys. Chem., 1989, 34, 753–758 CrossRef CAS.
- G. P. Horne, T. S. Grimes, B. J. Mincher and S. P. Mezyk, J. Phys. Chem. B, 2016, 120, 12643–12649 CrossRef CAS PubMed.
- G. P. Horne, T. S. Grimes, W. F. Bauer, C. J. Dares, S. M. Pimblott, S. P. Mezyk and B. J. Mincher, Inorg. Chem., 2019, 58, 8551–8559 CrossRef CAS PubMed.
- G. P. Horne, A. Wilden, S. P. Mezyk, L. Twight, M. Hupert, A. Stark, W. Verboom, B. J. Mincher and G. Modolo, Dalton Trans., 2019, 48, 17005–17013 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Chemicals, analytical techniques and calibration curves, experimental and computational methodologies, escape yields calculated from stochastic model, kinetic chemical reaction set used, and rate coefficients determined in this work. See DOI: https://doi.org/10.1039/d2ra03392e |
| This journal is © The Royal Society of Chemistry 2022 |