Open Access Article
Open Access ArticleStructure of benzene from mass-correlated rotational Raman spectroscopy†
In Heo‡ ,
Jong Chan Lee‡
,
Jong Chan Lee‡ ,
Begüm Rukiye Özer
,
Begüm Rukiye Özer and
Thomas Schultz
and
Thomas Schultz *
*
UNIST (Ulsan National Institute of Science and Technology), Advanced Materials Research Building 103-413, 50 UNIST-gil, Eonyang-eup, Ulju-gun, Ulsan, 44919, South Korea. E-mail: schultz@unist.ac.kr; Tel: +82-52-217-5455
First published on 3rd August 2022
Abstract
We present high resolution rotational Raman spectra and derived geometry parameters for benzene. Rotational Raman spectra with sub-5 MHz resolution were obtained via high-resolution mass-correlated rotational alignment spectroscopy. Isotopologue spectra for C6H6, 13C–C5H6, C6D6, and 13C–C5D6 were distinguished through their correlated mass information. Spectra for 13C6H6 were obtained with lower resolution. Equilibrium and effective bond lengths were estimated from measured inertial moments, based on explicit assumptions and approximations. We discuss the origin of significant bias in previously published geometry parameters and the possibility to derive H,D isotope-specific bond lengths from purely experimental data.
1 Introduction
Rotationally resolved spectroscopy can readily resolve rotational constants and corresponding molecular inertial moments (MIM) with relative uncertainties in the 10−6 range. The MIM are directly related to atomic positions within the molecule and allow to assign high-resolution molecular structures. For larger molecules, this analysis requires rotational spectra for multiple molecular isotopologues, pinpointing the position of substituted atoms in the molecular frame. We recently developed mass-correlated rotational alignment spectroscopy (CRASY), a method for the mass-selective measurement of rotational Raman spectra with broad spectral range and MHz resolution.1,2 The resolution represents an order-of-magnitude improvement over that of preceding rotational Raman or Fourier-transform IR spectroscopy (FTIR)3,4 and the mass-correlation facilitates the analysis of multiple isotopologue spectra in a single data-set. Here we present rotational spectra for five benzene isotopologues, estimate effective and equilibrium bond lengths, discuss the possibility to determine isotope-specific bond lengths, and explain why preceding literature values were biased.A straightforward derivation of effective (r0) molecular structure from measured MIM is possible under the assumption that isotopic substitution does not affect the molecular geometry5,6 (isotopic invariance approximation, IIA). Equilibrium geometries can be determined if isotope-specific rovibrational corrections are included in the analysis.7–14
Kunishige et al. recently used an interesting approach to directly estimate isotope-dependent r0 bond lengths in benzene from deuterated benzene MIM.15 Because the isotope effect for substituting hydrogen with deuterium is much larger than that for substituting 12C with 13C carbon, Kunishige first used the IIA approximation to estimate the C–C bond lengths to good approximation. He then separately refined hydrogen and deuterium bond lengths using data from a series of deuterated isotopologue measurements. The authors concluded that the C–H and C–D bonds in benzene were identical to within less than one mÅ, based on a fortuitous canceling of vibrational isotope effects associated with C–H/D stretch and bend modes. A model calculation by Hirano et al. supported this explanation.16
The absence of a structural H/D isotope effect in benzene stands in marked contrast to the 3 mÅ to 5 mÅ bond contraction observed in small deuterated molecules9 and a widely accepted “Laurie-type correction” of similar magnitude in rotational structure analysis.13,14 We must therefore raise the question whether (a) benzene (and other hydrocarbon aromatic molecules) represent a special class of molecules with unexpected rovibrational properties; (b) H,D isotope effects were generally misinterpreted in the past, or (c) the data presented by Kunishige and Hirano is compatible with the traditionally expected H,D isotope effect.
Benzene has sixfold rotational symmetry (D6h-symmetry) and two geometry parameters, rC–C and rC–H, are sufficient to describe its structure. Benzene has been thoroughly investigated with spectroscopy and ab initio theory and here we only give a brief summary of the relevant literature. Raman, rovibronic, and rovibrational measurements were used to characterize the rotational spectrum of benzene.2,17–38 Unresolved K-splitting may explain the surprising divergence of rotational constants reported in the literature.2
FTIR was used to characterize fully deuterated benzene C6D6,28,39,40 the 13C6H6 isotopologue,28 the 13C–C5H6 isotopologue at natural abundance,31 and the 13C6D6 isotopologue.41 Asymmetrically deuterated isotopologues have a small permanent dipole moment and were studied by high-resolution Fourier-transform microwave spectroscopy (FTMW).15,42,43
1.1 Structure determination from isotopologue inertial moments
Measured rotational constants A, B, C and the corresponding MIM Ia,b,c for a molecule with N atoms are directly related to the squared distance 〈rα,i2〉 of each atomic mass mi to the α rotation axis:
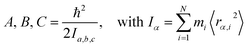 | (1) |
More information is required to solve the structure of larger molecules: generally, each atomic position must be specified within a three-dimensional molecular reference frame. For an asymmetric molecule, (N-6) structural parameters are required to describe all atomic positions relative to the center-of-mass (COM). Only three MIM can be measured for a molecule (one for each spatial axis) and we can only formulate three eqn (1) and solve for three structural parameters. This is insufficient for de novo structure analysis, except in trivial cases. Symmetry can reduce the number of required structural parameters§ but concurrently reduces the number of independently measurable MIM.
Within the IIA, i.e., the assumption of rX = rY for substituting isotope X with isotope Y, we can explicitly solve eqn (1) for the r0 position of an isotopically substituted atom. The complete molecular structure can be solved if a sufficient number of isotopologue MIM are determined. Multiple isotopic substitutions of the same (or a symmetry-equivalent) atom does not add new information and will not increase the number of accessible structure parameters, but can help to confirm the symmetry of the molecule and to establish confidence limits on fitted parameters.
The investigation of a complete set of isotopic substitutions (unsubstituted molecule + substitution of each symmetry-unique atom) allows us to formulate more eqn (1) than required to solve the r0 molecular structure and we can introduce an additional structural parameter, e.g., an isotope-dependent bond length. This is only useful if we can identify one structural parameter that removes a significant error in the IIA approximation. In benzene, effects of zero-point vibration are almost entirely localized on the C–H bond stretch46 and, following the lead of Kunishige et al., we can attempt to extract isotope-dependent C–H and C–D bond lengths under the assumption that the heavier carbon atoms show negligible isotope effects. Note that, except in trivial cases, the investigation of additional isotopologues can never yield enough information to characterize isotope-dependent bond lengths for all atoms, because any information gained through additional isotopic substitution will introduce a corresponding number of additional isotope-dependent geometry parameters.
The IIA approximation ignores that the effective bond lengths are isotope-dependent due to rovibrational coupling. This introduces a significant uncertainty in experimentally determined structures, e.g., up to 10 mÅ difference in the r0 bond lengths calculated for OCS (see chapter 13.7 in ref. 45). Kraitchman proposed to calculate substitution structure parameters rs based on the MIM differences I0α,iso1 − I0α,iso2 between pairs of isotopologues:6,7,45 the rovibrational coupling terms cancel in the MIM differences if they are similar for all observed isotopologues. The resulting rs parameters should become isotopologue-independent and fall between r0 values and the equilibrium bond lengths re. Costain established a straightforward estimate for the bond length uncertainty σrs = 0.0015 Å/rs that separates rs parameters from re and r0 values.7,47
Instead of solving discrete equations for individual r0 or rs atomic positions, iterative optimization procedures allow to determine multiple atomic positions simultaneously.48–50 If the fit is over-determined (i.e., the number of isotopologue MIM exceed the minimum required to solve the molecular structure), the fit approach allows to analyze parameter confidence ranges and to identify outliers in the experimental data.
Watson introduced mass-dependent rovibrational correction terms10,13 to obtain r(1)m (first order approximation¶) and r(2)m (second-order approximation) geometry parameters. As presented in eqn (2), the rm analysis requires the fitting of calculated MIM Iα,m to measured values Iα,0, including rovibrational correction parameters cα (first order correction) and dα (second order correction) for each rotational axis. The correction terms represent the sum of rovibrational effects with respect to rotation around the corresponding axis α. Resulting rm geometry parameters approximate corresponding equilibrium values re.
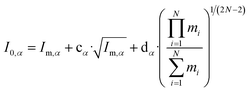 | (2) |
The orientation of principal rotational axes within the molecular frame can differ between isotopologues. This can be rectified within the first-order approximation by including off-diagonal correction terms 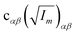 , which project the corrections into an invariant molecular coordinate frame.|| Resulting geometry parameters are labeled r(1r)m and r(2r)m. Fitting of rm geometry parameters represents the current state-of-the-art for estimating equilibrium bond lengths from isotopologue rotational constants, was found to reproduce synthetic data with high accuracy, and was used to obtain meaningful bond parameters from experimental data.13,14,51
, which project the corrections into an invariant molecular coordinate frame.|| Resulting geometry parameters are labeled r(1r)m and r(2r)m. Fitting of rm geometry parameters represents the current state-of-the-art for estimating equilibrium bond lengths from isotopologue rotational constants, was found to reproduce synthetic data with high accuracy, and was used to obtain meaningful bond parameters from experimental data.13,14,51
The large and localized effects of hydrogen-atom substitution can be separately addressed by a Laurie-type correction,9,13 substituting the bond length for each X–H bond length (H = H, D, T) with the mass-corrected value in eqn (3). The Laurie coefficient was found to have a fairly universal value of δH ∼ 10 Å u1/2. Laurie-corrected fit methods and geometry parameters are marked with a superscript (L).
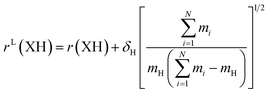 | (3) |
2 Experimental part
The experimental technique of correlated rotational alignment spectroscopy is described in detail in our previous work.1,52 Briefly, a pump pulse (800 nm, 100 μJ, 1 ps) from a 1 kHz amplified femtosecond Ti:Sa laser excited a coherent superposition of rotational states via rotational Raman excitation, creating a rotational wave packet. A time-delayed probe pulse (200 nm, 1 μJ, 45 fs) from a second 1 kHz Ti:Sa amplifier probed the evolution of the rotational wave packet via resonance enhanced two-photon ionization. Resulting ions were detected in a Wiley McLaren time-of-flight mass spectrometer. Interference between the coherent rotational quantum states modulated the ionization efficiency, leading to delay dependent signal modulation in the ion signals. The rotational Raman frequencies encoded in the signal modulation were analyzed by Fourier-transformation of the delay dependent ion signals.Helium carrier gas flowed through a sample holder containing a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of benzene (Sigma Aldrich, HPLC grade) and D6-benzene (Sigma Aldrich, 99% deuterated) or benzene and 13C6-benzene (Sigma Aldrich, 99 atom%). The benzene–helium mixture, at 5 bar pressure, was expanded through a pulsed valve (Even Lavie, E.L-7-4-2007-HRR), running at 500 Hz. The resulting cold molecular beam passed through a skimmer and reached the spectrometer region, where it interacted with pump and probe laser pulses. The time delay between pump and probe pulses was controlled by a combination of an opto-mechanical delay line (folded length of 4.8 m) and an electronic pulse-selection delay. The electronic pulse selection added discrete delays in multiples of 12.5 ns, corresponding to the pulse-to-pulse delay in the Ti:Sa laser oscillator. The oscillator repetition rate was measured against a GPS-stabilized clock to calibrate the time delay axis with relative uncertainties Δt/t ≪ 10−9. Resulting rotational Raman spectra can therefore be considered as absolute frequency spectra within the statistical uncertainty. For details about the absolute frequency calibration (a time domain equivalent to frequency comb spectroscopy), we refer the reader to our earlier work.1
50 mixture of benzene (Sigma Aldrich, HPLC grade) and D6-benzene (Sigma Aldrich, 99% deuterated) or benzene and 13C6-benzene (Sigma Aldrich, 99 atom%). The benzene–helium mixture, at 5 bar pressure, was expanded through a pulsed valve (Even Lavie, E.L-7-4-2007-HRR), running at 500 Hz. The resulting cold molecular beam passed through a skimmer and reached the spectrometer region, where it interacted with pump and probe laser pulses. The time delay between pump and probe pulses was controlled by a combination of an opto-mechanical delay line (folded length of 4.8 m) and an electronic pulse-selection delay. The electronic pulse selection added discrete delays in multiples of 12.5 ns, corresponding to the pulse-to-pulse delay in the Ti:Sa laser oscillator. The oscillator repetition rate was measured against a GPS-stabilized clock to calibrate the time delay axis with relative uncertainties Δt/t ≪ 10−9. Resulting rotational Raman spectra can therefore be considered as absolute frequency spectra within the statistical uncertainty. For details about the absolute frequency calibration (a time domain equivalent to frequency comb spectroscopy), we refer the reader to our earlier work.1
The data presented for C6H6, 13C–C5H6, C6D6, and 13C–C5D6 was obtained by sampling 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mass spectra over a delay range of 200 ns. Delays were sampled in random multiples of 1 ps (10% random sparse sampling). The data presented for 13C6H6 was obtained by sampling 20
000 mass spectra over a delay range of 200 ns. Delays were sampled in random multiples of 1 ps (10% random sparse sampling). The data presented for 13C6H6 was obtained by sampling 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 mass spectra over a delay range of 20.153 ns, with constant 1 ps step size. Rotational Raman spectra were obtained by Fourier-transformation of mass-selected, delay-dependent signal amplitudes after suitable baseline corrections. Resulting rotational Raman spectra had a 500 GHz spectral range and a non-apodized full-width-at-half-maximum (FWHM) resolution limit3 of 3.1 MHz (30 MHz) for the first (second) sample. A break-down of the laser system kept us from measuring higher resolution spectra for the second sample. In the latter case, the delay range was insufficient for calibration against the external clock and we calibrated residual CS2 signals against literature values.
153 mass spectra over a delay range of 20.153 ns, with constant 1 ps step size. Rotational Raman spectra were obtained by Fourier-transformation of mass-selected, delay-dependent signal amplitudes after suitable baseline corrections. Resulting rotational Raman spectra had a 500 GHz spectral range and a non-apodized full-width-at-half-maximum (FWHM) resolution limit3 of 3.1 MHz (30 MHz) for the first (second) sample. A break-down of the laser system kept us from measuring higher resolution spectra for the second sample. In the latter case, the delay range was insufficient for calibration against the external clock and we calibrated residual CS2 signals against literature values.
3 Results
3.1 Spectroscopic results
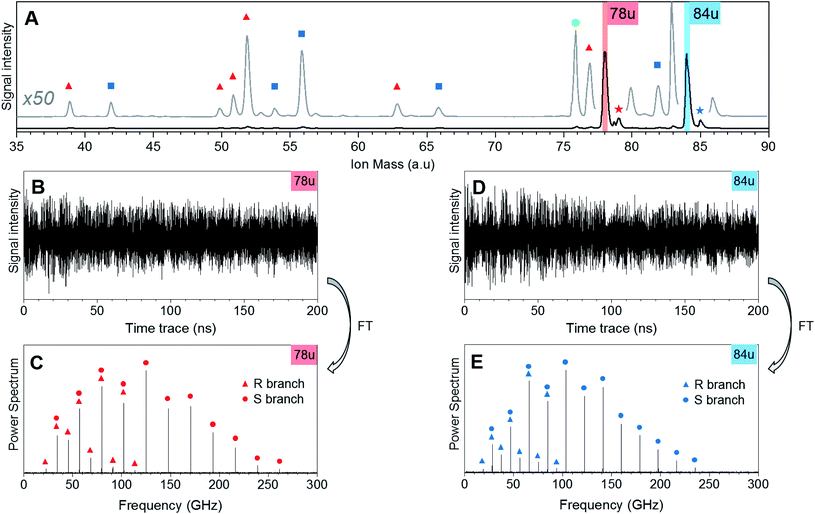
Fig. 1 shows CRASY experimental data for the first sample. Results from other data sets with different sampling of the delay axis gave comparable results. The integrated mass spectrum in Fig. 1A shows parent ions and fragments for C6H6 and C6D6, as well as weak signals for naturally occurring 13C isotopologues. Molecular fragments were assigned to parent species through a comparison of their correlated rotational spectra, as described in more detail below, and mass peaks are marked accordingly. Ion signals at mass 78 u and 79 u stem from C6H6 and its 13C-isotopologue. Masses 84 u and 85 u stem from C6D6 and its 13C-isotopologue. Further mass signals in the range 80 u to 86 u were due to additional benzene isotopologues but were not strong enough to assign correlated rotational spectra. A signal at 76 u, stems from carbon disulfide, which remained in the sample line from earlier measurements.The fragments of the undeuterated and deuterated benzene isotopologues appeared as pairs with an integer mass spacing reflecting the number of hydrogen/deuterium atoms in the fragments: 39 u and 42 u (C3H3 and C3D3), 51 u and 54 u (C4H3 and C4D3), 52 u and 56 u (C4H4 and C4D4), 63 u and 66 u (C5H3 and C5D3), 77 u and 82 u (C6H5 and C6D5). The mass channel 50 u (C4H2) showed a benzene fragment but the corresponding deuterated signal at mass 52 u could not be assigned due to the dominant C4H4 fragment signal at this mass.
Fig. 1B and D show the ion mass signal modulations for C6H6 and C6D6 as a function of the 200 ns pump-probe time delay. The time traces were Fourier-transformed to obtain their frequency-domain rotational Raman spectra as shown in Fig. 1C and E, respectively. R-branch (ΔJ = ±1) and S-branch (ΔJ = ±2) transitions were assigned and are marked in the spectra. No bands were observed in the higher frequency region (300–500 GHz) of the spectrum. The experimental FWHM resolution for all bands was close to 4.5 MHz.
Note that the excitation and probing of the rotational Raman wave packets occurs in the neutral ground state, before electronic excitation and ionization induces molecular fragmentation. The rotational spectra correlated to ionic fragments is therefore identical to the parent spectrum and allows an unambiguous assignment of each fragment to its parent species. Fig. 2 compares sections of the rotational Raman spectrum correlated to mass 78 u (C6H6) to those of all mass peaks marked by red triangles in Fig. 1A. The spectra are identical and transition frequencies agree with deviations well below 1 MHz. All marked ion signals can therefore be assigned as fragmentation products of C6H6.
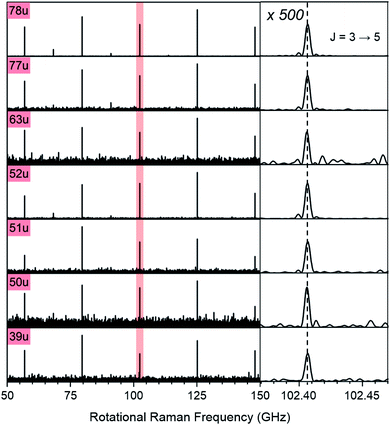 | ||
| Fig. 2 Section of the rotational Raman spectra for C6H6 (78 u) and its six cationic fragments (39 u, 50 u, 51 u, 52 u, 63 u, 77 u, marked with red triangles in Fig. 1A). The enlarged inset on the right shows the J = 3 ↔ 5 transition at 102.406 GHz with 500-fold enlarged abscissa to illustrate the exact correspondence of peak positions. | ||
In Fig. 3, we compare the rotational Raman spectrum correlated with mass 84 u (C6D6) to that correlated with all ion signals marked by blue squares in Fig. 1A. The spectra are identical and all corresponding ion signals can therefore be assigned as fragmentation products of C6D6.
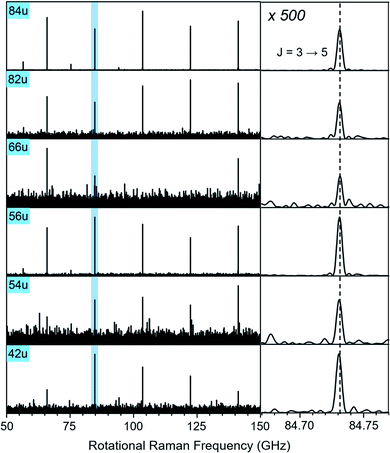 | ||
| Fig. 3 Section of the rotational Raman spectra for C6D6 (84 u) and its five cationic fragments (42 u, 54 u, 56 u, 66 u, 82 u, marked with blue squares in Fig. 1A). The enlarged inset on the right shows the J = 3 ↔ 5 transition at 84.731 GHz with 500-fold enlarged abscissa to illustrate the exact correspondence of peak positions. | ||
Our experiment was sensitive enough to resolve naturally occurring 13C isotopologues (13C abundance of 1.1%) for the benzene species. Fig. 4 shows rotational Raman spectra for the 1-13C carbon isotopologues of benzene and D6-benzene, compared to corresponding simulations created in the PGOPHER program.53
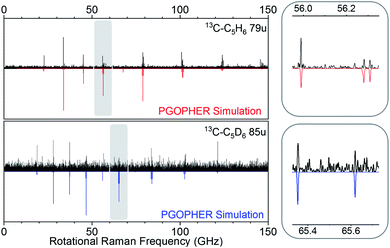 | ||
| Fig. 4 Comparison of experimental simulated spectra for heavy carbon isotopologues at 79 u (top, 13C–C5H6) and 85 u (bottom, 13C–C5D6). | ||
The measurements performed on sample containing 13C6H6 gave spectra with lower resolution and signal quality. Because the parent ion signals were in saturation, we analyzed the rotational spectrum correlated to the sum of fragment species at mass 42 u, 56 u, and 68 u. The relevant mass- and rotational spectra are shown in the ESI† (section 1).
Rotational transitions for all observed benzene isotopologue species were assigned by comparison with simulated spectra in the PGOPHER program.53 PGOPHER was then used to fit rotational constants to the assigned lines. Resulting spectroscopic constants for symmetric and asymmetric isotopologues are listed in Tables 1 and 2. Because we only observed low rotational states in our cold molecular beam, uncertainties for fitted distortion constants were sometimes excessively large and we held corresponding values to calculated distortion constants obtained from MP2 calculations with aug-cc-pVTZ basis set (obtained using the Freq = (vibrot) keyword in Gaussian54). For line-lists and details on the line assignments and fits, see sections (1) and (2) in the ESI,† section 1.
| C6H6 | C6D6 | 13C6H6 | |
|---|---|---|---|
| a Values from MP2 aug-cc-pVTZ calculation. | |||
| B0 | 5689.2855(54) | 4707.3175(34) | 5337.884(51) |
| DJ | 0.79(19) × 10−3 | 0.64(10) × 10−3 | 0.84(74) × 10−3 |
| DJK | −0.78(51) × 10−3 | −0.93(27) × 10−3 | −4.1(23) × 10−3 |
| DK | a[0.935 × 10−3] | a[0.536 × 10−3] | a[0.838 × 10−3] |
| HJ | −5.1(20) × 10−6 | −1.38(92) × 10−6 | |
| HJK | −8.1(91) × 10−6 | −5.2(41) × 10−6 | |
| HKJ | 55(17) × 10−6 | 0.221(74) × 10−6 | |
| Lines | 16 | 18 | 16 |
| 13C–C5H6 | 13C–C5D6 | |
|---|---|---|
| a Values from MP2 aug-cc-pVTZ calculation. | ||
| A0 | 5689.474(18) | 4707.541(36) |
| B0 | 5568.473(23) | 4624.188(31) |
| C0 | 2868.6(73) | 2332(16) |
| ΔJ | 2.77(53) × 10−3 | a[0.709 × 10−3] |
| ΔJK | −10.3(29) × 10−3 | a[-1.169 × 10−3] |
| ΔK | a[0.902 × 10−3] | a[0.521 × 10−3] |
| δJ | a[16.906 × 10−6] | a[8.121 × 10−6] |
| δK | a[276.963 × 10−6] | a[0.164 × 10−3] |
| Assigned lines | 35 | 28 |
The rotational constant for benzene determined here was significantly higher than that reported in ref. 2. This is due to the assignment of higher rotational transitions (here up to J = 11 ↔ 13), which requires the inclusion of higher-order distortion constants. Omitting higher J transitions reduced the fitted rotational constant and brought it closer to literature values. Because, at current resolution, the K-splitting in symmetric benzene isotopologues is not resolved, the distortion constants remain badly determined and we cannot give definitive, ‘correct’ rotational constants. But the achieved accuracy is sufficient for a structure analysis, as described below.
3.2 Structure analysis
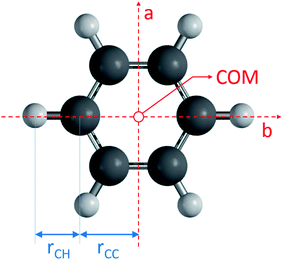
All code used for the structure analysis is available in form of two Python scripts. The first script gives a step-by-step derivation of the relevant equations (ESI,† section 3.1) and the second script offers optimized code and a graphical user-interface for structure fitting (ESI,† section 3.2). Fig. 5 shows the structure and relevant structural parameters of benzene. For the D6h-symmetric planar oblate-top molecules C6H6 and C6D6, it is straightforward to write eqn (1) that relate inertial moments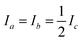 to bond lengths rCC and rCH:
to bond lengths rCC and rCH:| Ib = 3mCrCC2 + 3mH(rCC + rCH)2 | (4) |
| I′b = 3mCrCC2 + 3mD(rCC + rCD)2 | (5) |
Within the IIA approximation (rCH = rCD), and using the inertial moments 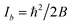 corresponding to rotational constants in Table 1, eqn (2) and (3) can be solved analytically to obtain bond lengths r0,CH = 1.0804(12) Å and r0,CC = 1.3971(11) Å (ESI,† section 3.1.3). The propagated uncertainties from the measured rotational constants were extremely small and values in brackets instead give the Costain errors for the corresponding last digits,7,12 which accounts for the expected uncertainty range between r0, rs, and re parameters. We also solved the corresponding equations for the isotopologue pair C6H6 and 13C6H6 and obtained bond lengths r0,CH = 1.1058(12) Å and r0,CC = 1.3938(11) Å. The bond lengths calculated for the two isotopologue pairs differ by a value far greater than the Costain uncertainty. This illustrates the inadequacy of the IIA assumption and should not be surprising: Costain's original manuscript already stated that “equations […] could not be satisfied unless the H and D atoms were assumed to have different effective positions.”
corresponding to rotational constants in Table 1, eqn (2) and (3) can be solved analytically to obtain bond lengths r0,CH = 1.0804(12) Å and r0,CC = 1.3971(11) Å (ESI,† section 3.1.3). The propagated uncertainties from the measured rotational constants were extremely small and values in brackets instead give the Costain errors for the corresponding last digits,7,12 which accounts for the expected uncertainty range between r0, rs, and re parameters. We also solved the corresponding equations for the isotopologue pair C6H6 and 13C6H6 and obtained bond lengths r0,CH = 1.1058(12) Å and r0,CC = 1.3938(11) Å. The bond lengths calculated for the two isotopologue pairs differ by a value far greater than the Costain uncertainty. This illustrates the inadequacy of the IIA assumption and should not be surprising: Costain's original manuscript already stated that “equations […] could not be satisfied unless the H and D atoms were assumed to have different effective positions.”
To obtain results beyond the IIA approximation, we fitted a variety of geometric parameters to measured inertial moments I0 (ESI,† section 3.1.5). Atomic coordinates were calculated from a minimal set of geometry parameters while assuming D6h symmetry for all benzene isotopologues. Molecular moments-of-inertia tensors Iαβ (α, β ∈ a, b, c) were calculated from atomic masses and coordinates. The corresponding principal moments of inertia Icalc. were obtained as eigenvalues of the secular equation Iαβ − Icalc.,α,α (ESI,† section 3.1.4, see also Chapter 2 of Gordy & Cook45 or ref. 6). A Levenberg–Marquardt nonlinear fit was used to determine geometric parameters that minimized the squared residuals (I0 − Icalc.)2. To account for very different uncertainties σ in experimental MIM, we used a weight function wi = (σi2 + b2)−1 with b = 0.0005 μÅ2, as suggested by Eijck.47**
We fitted the benzene structure based on our own rotational constants, as summarized in Tables 1 and 2, and also based on additional rotational constants from the literature.15,28,31,32,39–41,43,55 If corresponding authors published multiple values for the same isotopologue, we only used the newest or most accurate published values. A summary of relevant literature constants is given in Table 3.
| Isotopologue | A0 | B0 | C0 | Symmetry | Author | Ref. |
|---|---|---|---|---|---|---|
| a Kunishige's15 re-evaluated constants from Oldani1988,43 with distortion constants DJ, DJK, and DK fixed to the averaged values of C6H6 and C6D6.b Kunishige's15 re-evaluated constants from Oldani1988,43 including one additional transition and with distortion constants DJ, DJK, and DK fixed to the averaged values of C6H6 and C6D6.c Distortion constants DJ, DJK, and DK fixed to the averaged values of C6H6 and C6D6. | ||||||
| C6H6 | — | 5688.9220(060) | — | Oblate pl. | Pliva1990 | 28 |
| C6H6 | — | 5689.2664(060) | — | Oblate pl. | Hollenstein1990 | 31 |
| C6H6 | — | 5689.2781(010) | — | Oblate pl. | Juntilla1991 | 32 |
| C6H6 | — | 5689.2120(009) | — | Oblate pl. | Doi2004 | 55 |
| C6H6 | — | 5689.2670(005) | — | Oblate pl. | Lee2019 | 2 |
| C6H6 | — | 5689.2855(005) | — | Oblate pl. | In2021 | This work |
| 13C–C5H6 | 5689.474(018) | 5568.473(023) | 2868.600(730) | Planar | In2021 | This work |
| D1-C6H5 | 5689.144(006) | 5323.934(006) | 2749.674(006) | Planar | Oldani1984 | 42 |
| D1-C6H5a | 5689.143(006) | 5323.933(006) | 2749.675(006) | Planar | Kunishige2015 | 15 |
| o-D2-C6H4 | 5498.062(004) | 5164.242(004) | 2662.496(004) | Planar | Oldani1988 | 43 |
| o-D2-C6H4b | 5498.032(009) | 5164.213(009) | 2662.466(006) | Planar | Kunishige2015 | 15 |
| m-D2-C6H4 | 5502.669(007) | 5152.057(006) | 2660.358(006) | Planar | Oldani1988 | 43 |
| m-D2-C6H4a | 5502.667(009) | 5152.053(009) | 2660.352(009) | Planar | Kunishige2015 | 15 |
| o-D3-C6H3c | 5168.017(015) | 5151.933(060) | 2579.579(006) | Planar | Kunishige2015 | 15 |
| o-D4-C6H2c | 5163.715(006) | 4846.814(006) | 2499.792(003) | Planar | Kunishige2015 | 15 |
| m-D4-C6H2c | 5151.993(120) | 4850.312(120) | 2497.902(030) | Planar | Kunishige2015 | 15 |
| o-D5-C6H1c | 4998.170(150) | 4707.221(150) | 2423.972(060) | Planar | Kunishige2015 | 15 |
| C6D6 | — | 4707.125(006) | — | Oblate pl. | Doi2004 | 55 |
| C6D6 | — | 4707.312(052) | — | Oblate pl. | Pliva1989 | 39 |
| C6D6 | — | 4707.327(006) | — | Oblate pl. | Snels2002 | 40 |
| C6D6 | — | 4707.318(003) | — | Oblate pl. | In2021 | This work |
| 13C–C5D6 | 4707.541(036) | 4624.188(031) | 2332(16) | Planar | In2021 | This work |
| 13C6H6 | — | 5337.925(060) | — | Oblate pl. | Pliva1990 | 28 |
| 13C6H6 | — | 5337.884(051) | — | Oblate pl. | In2021 | This work |
| 13C6D6 | — | 4464.371(024) | — | Oblate pl. | Pliva1991 | 41 |
In a first approach, we fitted effective bond lengths r0 (ESI,† section 3.1.5). We implemented a two-parameter fit of rCC (=rC13C) and rCH (=rCD), corresponding to the IIA approximation, a three parameter fit of rCC (=rC13C), rCH, and rCD, and a four parameter fit with distinct rCH, rCD, rCC, and rC13C. Fit results and related literature values are summarized in Table 4. For r0 structure analysis, we only fitted a and b axis constants because meaningful c-axis constants were only available for deuterated isotopologues and showed large systematic deviations due to the inertial defect. A Monte-Carlo analysis was performed to evaluate the propagation of experimental uncertainties (ESI,† section 3.1.6).
| Fit of effective geometry parameters | ||||
|---|---|---|---|---|
| Row | Fit type | rC (Å) | rCH (Å) | rCD (Å) |
| a Based on A, B constants presented in Tables 1 and 2.b Based on A, B constants in Table 3.c Based on B constants for 12C, 13C isotopologues in Table 3.d Based on A, B, C constants for deuterated isotopologues in ref. 15.e Based on A, B, C constants as listed in Table 3.f Reference values from the CCCBDB database56 for a coupled-cluster (full) calculation with aug-cc-pVTZ basis. | ||||
| 1 | r0, 2-parametersa | 1.3971(11) | 1.0806(14) | |
| 2 | r0, 2-parametersb | 1.3971(11) | 1.0804(14) | |
| 3 | r0, 2-parametersc | 1.3938(2) | 1.1059(7) | |
| 4 | r0, 3-parametersa | 1.3945(12) | 1.1003(45) | 1.0917(28) |
| 5 | r0, 3-parametersb | 1.3937(11) | 1.1069(28) | 1.0953(19) |
| 6 | r0, 3-parametersd | 1.3972(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 410![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525) 525) |
1.0804(10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 881 881![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 503) 503) |
1.0804(6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 149 149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 729) 729) |
| 7 | r(L)0b | 1.3937(10) | 1.1066(233) | 1.0952(18) |
| Geometry fit using mass-weighted rovibrational and Laurie corrections | ||||
|---|---|---|---|---|
| Row | Fit type | rCC (Å) | rCH (Å) | δH (Å u1/2) |
| 7′ | r(L)0b | 1.3937(11) | 1.0671(15) | 0.0393(21) |
| 8 | r(1)me | 1.3912(4) | 1.0817(5) | |
| 9 | r(1L)me | 1.3939(27) | 1.0660(136) | 0.0421(432) |
| 10 | r(2)me | 1.3913(2) | 1.0814(3) | |
| 11 | r(2L)me | 1.3921(15) | 1.0769(76) | 0.012(24) |
| Literature values | ||||
|---|---|---|---|---|
| Row | Fit type | rCC (Å) | rCH (Å) | rCD (Å) |
| 12 | r0, Kunishige2015 | 1.3971 | 1.0805 | 1.0805 |
| 13 | r0, Doi2004 | 1.3971 | 1.0807 | |
| 14 | r0, Pliva1990 | 1.3969 | 1.0815 | |
| 15 | r0, Baba2011 | 1.3969 | 1.0817 | |
| 16 | re, Kunishige2015 | 1.3892 | 1.0864 | |
| 17 | re, Pliva1990 | 1.3893 | 1.0857 | |
| 18 | re, Pliva1991 | 1.3902 | 1.0862 | |
| 19 | re, CCSD(T)f | 1.3920 | 1.0802 | |
The two parameter fit of our own isotopologue rotational constants (Table 4, row 1) closely reproduced the results from the analytical calculation for the C6H6 and C6D6 isotopologue pair and are in good agreement with literature values (Table 4, rows 12–15). Including additional literature constants in the analysis led only to slight changes in the fitted bond lengths (Table 4, row 2). The fitted r0 bond lengths changed significantly if we removed all deuterated isotopologue data from the fit, with the fit result converging to that from the analytical calculation for the C6H6, 13C6H6 isotopologue pair (Table 4, row 3). The latter values represent the best estimates for the actual r0 bond lengths: the isotope dependence for the C–H/D bond length is expected to be much larger than that for the C–C bond length on account of the larger amplitude vibrational motion of the light hydrogens as compared to the heavier carbons. The approximation rCH = rCD required for the analysis of deuterated benzenes is therefore significantly worse than the approximation rCC = rC13C required for the analysis of 13C, 12C isotopologues.
The three parameter fits (Table 4, rows 4 and 5) indicated a significant difference between C–H and C–D bond lengths, with rCH − rCD = 8.6(4.9) mÅ (our data) or 11.5(2.8) mÅ (including literature data). Note that the rC and rCH bond lengths agree well with our best estimates from the 2-parameter fit (Table 4, row 3) but not with results obtained from deuterated isotopologue data (Table 4, rows 1, 2, 12–15). This confirms our assumptions about the severity of the IIA approximation for H/D versus 12C/13C isotopologues. Our results are in clear contradiction to the absence of an H,D geometric isotope effect discussed by Kunishige15 and Hirano.16 If we perform our 3-parameter fit with the deuterated isotopologue data-set reported by Kunishige et al. we reproduce their fit result but find excessive parameter uncertainties (Table 4, row 6).
In the four parameter fit, geometry parameters for r12C/13C and rH/D were strongly correlated and fit results remained badly determined. This fit approach required an assumption about how much of the effective displacement of a 13C versus 12C atom leads to a corresponding displacement of the attached H-atom.†† Treating this as an independent fit parameter gave an optimized H displacement value of 0.4 times the displacement of the bonded carbon atom, but the uncertainty of this parameter and of fitted bond lengths exceed the parameter values themselves. We conclude that a direct fit of isotope dependent r0 parameters for all atoms is not feasible. This agrees with our expectations outlined in the introduction: isotope-dependent bond lengths can not be obtained for all substituted atoms, because any information gained through additional isotopic substitution will introduce a corresponding number of additional geometry parameters.
The difficulty to determine H,D isotope-specific bond lengths from purely deuterated benzene data-sets can be understood from a consideration of the underlying mathematical model: the fit must solve a set of equations that relate measured inertial moments to atomic positions. A solution is only possible when the number of equations is identical, or larger, than the number of unknown parameters. At first glance this should not be an issue because we have rotational constants for 8 different deuterated benzene isotopologues at our disposal. But H atoms in benzene are equivalent by symmetry and the resulting equations are linearly dependent to very high degree.‡‡ The large parameter uncertainty is therefore a direct consequence of the limited data-set. With our experimental data for 13C substituted benzenes, we added a set of linearly independent equations and therefore obtained well-determined r0 geometry parameters for C–C, C–H and C–D bonds. We conclude that the absence of an H,D geometric isotope effect reported by Kunishige is an artefact of a highly undetermined fit.
The assumption of different, but isotopologue-independent CH and CD bond lengths in the 3-parameter fits ignores that the isotopologue masses are different: not only the H/D mass affects the vibrational amplitude, but also the mass of the remainder of the molecule. The Laurie-correction (eqn (3)) properly accounts for the reduced mass of the vibrational modes. Including the Laurie correction in the fitting of effective r0 bond length gave an excessively large Laurie parameter of δH = 39 mÅ u1/2 (Table 4, rows 7 and 7′) and correspondingly large values for rCH and rCD.
Results from Monte Carlo analyses (ESI,† section 3.1.6) agreed with the fit results and gave propagated uncertainties well below the fit uncertainties. This indicates that model errors dominate in our analysis. We found a strong linear correlation between fit parameters in 3 and 4 parameter fits. Fitting of synthetic data verified that this is a fundamental limitation of the fit model and is not due to inaccuracies in the available isotopologue rotational constants (ESI,† section 3.1.7).
Watson's rm formalism13 accounts for the mass-dependence of rovibrational correction terms (ESI,† sections 3.1.8 and 3.2). This fit approach models the magnitude of rovibrational corrections based on our physical understanding (within first- and second-order approximations) of rovibrational effects and allows us to estimate equilibrium bond lengths. To account for the symmetry of benzene, we removed redundant in-plane rovibrational correction terms. Some fit uncertainty arose from the choice of axes along which the rovibrational correction terms were applied.§§ We obtained stable (angle-independent) results with two methods: (a) we randomized the isotopologue coordinate definitions in r(1rL)m, r(2r)m, or r(2rL)m fits to minimize the correlation between axes for rovibrational and Laurie correction terms. (b) We aligned isotopologue coordinate definitions to be symmetric with respect to the a- and b-rotational axes and mapped rovibrational correction terms onto invariant principal axes. Note that method (b) exploits the symmetry of benzene and cannot be generalized to other molecules. In Table 4, rows 8–11, we give values obtained via method (b). The full list of fit parameters and parameter correlation tables are given in the ESI,† section 3.2.6.
The r(2)m parameters should be considered as the best estimate for re equilibrium bond lengths. In this case, two sets of rovibrational correction parameters (c,d parameters) account for the effective rovibrational displacements of rC and rH. The r(1)m fit only includes first-order rovibrational corrections but gave very similar results. We point out the excellent agreement between the r(2)m bond lengths and ab initio reference values in Table 1, row 19.
The fitting of an additional Laurie parameter δH allowed us to explore whether the isotope-dependent bond lengths for C–H and C–D bonds can be distinguished. Unfortunately, rH and δH parameters in r(1L)m and r(2L)m fits were highly correlated, leading to large parameter uncertainties. This is an obvious sign of an under-determined fit. The r(2L)m fit gave a value δH = 12 Å 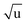 , close to the generally expected value of δH ≈ 10 Å
, close to the generally expected value of δH ≈ 10 Å 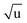 . Note that the fit uncertainty for δH was large and strongly depended on the fitted data-set.
. Note that the fit uncertainty for δH was large and strongly depended on the fitted data-set.
4 Discussion
Our high-resolution rotational Raman data for symmetric benzene isotopologues complements high-resolution FTMW data for asymmetrically deuterated isotopologues in the literature. Table 3 gives a summary of benzene isotopologue rotational constants and highlights our contributions. Preceding data for symmetric isotopologues, where available, were based on FTIR or laser excitation spectra with significantly lower resolution.Mass correlation in our CRASY measurements allowed the unambiguous separation of signals from different molecular species. Up to 5 different spectra (for C6H6, 13C–C5H6, C6D6, 13C–C5D6, and CS2) were assigned in a single data set. The correlation of spectra in parent and fragment mass channels allowed the direct assignment of fragments to their parent species, confirming expected fragmentation channels.
Fitted isotopologue rotational constants and the corresponding MIM allowed us to derive structure parameters r0, rs, and rm. A two parameter fit of r0(H) (=r0(D)) and r0(C) (=r0(13C)) positions reproduced published r0 estimates with high fidelity. A three parameter fit of distinct r0(H), r0(D), and r0(C) (=r0(13C)), positions indicated a significant isotope effect of rCH − rCD > 8 mÅ. This result is in direct contradiction to a corresponding analysis by Kunishige et al.,15 who found that the H and D bond lengths are identical to within a fraction of a mÅ.
The r0(C) bond lengths obtained by two- and three-parameter fits differ considerably (cf. Table 4, rows 2 and 5) and only the former is in agreement with literature estimates.15,28 The origin of this discrepancy becomes clear when we compare both values to two-parameter fit results based on a data set excluding deuterated isotopologues (cf. Table 4, rows 2 and 5 versus 3): the assumption of equal bond lengths for C–H and C–D leads to a significant bias in the fit results, which is removed by fitting only heave carbon isotopologue data or by the three parameter fit. The origin of this bias is obvious: the H,D isotope effect is large due to the large H,D mass difference and the large CH vibrational amplitude. The corresponding 12C,13C isotope effect is much smaller. The fit results based on 12C,13C isotopologue data should therefore be considered as best estimate for the r0 bond lengths.
As outlined in the introduction, it should not be possible to determine isotope-specific bond lengths for all investigated isotope-specific bonds except in particular trivial cases: additional information gained through added isotopic substitution is inherently tied to a corresponding number of additional isotope-dependent geometry parameters. In our three parameter fit, we resolved this issue with the inclusion of 13C substituted isotopologue data and the assumption of 12C,13C isotopologue-independent bond lengths. By omitting 13C isotopologue data from our fit, we could reproduce the results from Kunishige et al.15 (Table 4, row 6). But in this case the fit parameters became undetermined with uncertainties exceeding the fitted parameter values by factors ≫100. The result presented by Kunishige et al. therefore represents a highly undetermined solution that is equivalent to the result of the two parameter fit but contains an additional under-determined parameter.
The assumption of r0(12C) = r0(13C) in our three parameter analysis is not exact and explains the overly large apparent H,D isotope effect. Fits with independent r0(12C) and r0(13C) bond lengths should resolve this issue but run afoul of our caveat that we cannot fit isotope-specific bond lengths for all isotopologues. We nevertheless attempted several four-parameter fits based on further assumptions (details in the ESI†) but did not obtain robust geometry parameters. We conclude that the determination of effective isotope-specific r0 bond lengths based purely on rotational constants is unfeasible, except for the trivial case of linear molecules.
Watson10,13 introduced explicit assumptions about the mass-dependent scaling of rovibrational corrections, based on the quantum mechanical understanding of rovibrational coupling, which allows us to estimate isotope-independent equilibrium bond lengths. For benzene, results from r(2)m fits were very robust and gave bond lengths of r(2)m(C–C) = 1.3913 Å and r(2)m(C–H) 1.0814 Å. Fitted bond lengths were stable against exclusion of particular data points,¶¶ with parameter variations well below 1 mÅ. We therefore consider these values to be the best current estimate for the re bond lengths in benzene.
We must address the significant difference between previous literature estimates for re and our best estimate, based on the r(2)m analysis (Table 4, row 8 versus 16–18). Pliva et al.28 used a first-order rovibrational correction, based on the determination of a single correction parameter, to estimate equilibrium constants. Kunishige et al.15 applied an identical correction to their results. Our r(2)m analysis added second-order rovibrational correction terms, included distinct correction parameters for different rotational axes, and used a significantly larger and more diverse set of rotational data for the analysis. Our r(2)m estimate is very close to results from a coupled-cluster reference calculation (Table 4, row 8 versus 19).
Additional Laurie-corrections to the r(2)m fits greatly increased parameter uncertainties. This is not surprising: three sets of rovibrational correction parameters correct for rovibrational displacements of only two symmetry-unique bonds within the presumed D6h symmetry. The fitted Laurie parameters and r(2L)m(C–H) bond length were no longer robust against exclusion of particular data points. We therefore cannot interpret the fitted Laurie correction terms as a definite estimate for the C–H/D isotope-dependent bond length. But our r(2L)m result of δH = 12 Å 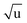 is close to the generally expected Laurie correction value57 of δH = 10 Å
is close to the generally expected Laurie correction value57 of δH = 10 Å 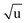 and corresponds to a reasonable ∼3 mÅ bond contraction upon H → D substitution.
and corresponds to a reasonable ∼3 mÅ bond contraction upon H → D substitution.
The propagation of experimental uncertainties with a Monte-Carlo simulation revealed that fitted parameter uncertainties were not due to uncertainties in the experimental data but due to parameter correlation and model errors in our fit models. The rotational data, although measured to high precision, is not sufficient to characterize rovibrational coupling effects and corresponding isotope-specific bond lengths with correspondingly high confidence. This results in parameter uncertainties that are far greater than expected from error propagation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding support from the National Research Foundation of Korea under Grants No. NRF-2018R1D1A1A02042720 and Samsung Science and Technology Foundation under Grants No. SSTF-BA2001-08.Notes and references
- C. Schröter, J. C. Lee and T. Schultz, Proc. Natl. Acad. Sci., 2018, 115, 5072–5076 CrossRef PubMed.
- J. C. Lee, D. E. Lee and T. Schultz, Phys. Chem. Chem. Phys., 2019, 21, 2857–2860 RSC.
- S. Albert, K. K. Albert and M. Quack, in Handbook of High-resolution Spectroscopy, ed. M. Quack and F. Merkt, John Wiley & Sons, Ltd, 2011, vol. 2, pp. 965–1019 Search PubMed.
- H.-M. Frey, D. Kummli, S. Lobsiger and S. Leutwyler, in Handbook of High-resolution Spectroscopy, ed. M. Quack and F. Merkt, John Wiley & Sons, Ltd, 2011, vol. 2, pp. 1237–1265 Search PubMed.
- G. Herzberg, F. Patat and J. W. T. Spinks, Z. Phys., 1934, 92, 87–99 CrossRef CAS.
- J. Kraitchman, Am. J. Phys., 1953, 21, 17–24 CrossRef CAS.
- C. C. Costain, J. Chem. Phys., 1958, 29, 864–874 CrossRef CAS.
- D. R. Herschbach and V. W. Laurie, J. Chem. Phys., 1962, 37, 1668–1686 CrossRef CAS.
- V. W. Laurie and D. R. Herschbach, J. Chem. Phys., 1962, 37, 1687–1693 CrossRef CAS.
- J. K. Watson, J. Mol. Spectrosc., 1973, 45, 99–113 CrossRef CAS.
- H. D. Rudolph, Struct. Chem., 1991, 2, 581–588 CrossRef CAS.
- M. Harmony, V. Laurie, R. Kuczkowski, R. Schwendeman, D. Ramsay, F. Lovas, W. Lafferty and A. Maki, J. Phys. Chem. Ref. Data, 1979, 8, 619–721, DOI:10.1063/1.555605.
- J. K. Watson, A. Roytburg and W. Ulrich, J. Mol. Spectrosc., 1999, 196, 102–119 CrossRef CAS PubMed.
- Z. Kisiel, J. Mol. Spectrosc., 2003, 218, 58–67 CrossRef CAS.
- S. Kunishige, T. Katori, M. Baba, M. Nakajima and Y. Endo, J. Chem. Phys., 2015, 143, 244302 CrossRef PubMed.
- T. Hirano, U. Nagashima and M. Baba, J. Mol. Struct., 2021, 1243, 130537 CrossRef CAS.
- B. P. Stoicheff, J. Chem. Phys., 1953, 21, 1410–1411 CrossRef CAS.
- B. P. Stoicheff, Can. J. Phys., 1954, 32, 339–346 CrossRef CAS.
- R. C. Lord and T. K. McCubbin, J. Opt. Soc. Am., 1957, 47, 689–697 CrossRef CAS.
- A. Danti and R. Lord, Spectrochim. Acta, 1958, 13, 180–191 CrossRef CAS.
- R. Anttila, Z. Naturforsch. A, 1968, 23, 1089 Search PubMed.
- A. Cabana, J. Bachand and J. Giguére, Can. J. Phys., 1974, 52, 1949–1955 CrossRef CAS.
- H. B. Jensen and S. Brodersen, J. Raman Spectrosc., 1979, 8, 103–110 CrossRef CAS.
- J. Kauppinen, P. Jensen and S. Brodersen, J. Mol. Spectrosc., 1980, 83, 161–174 CrossRef CAS.
- J. Pliva and A. Pine, J. Mol. Spectrosc., 1982, 93, 209–236 CrossRef CAS.
- J. Pliva and J. W. C. Johns, Can. J. Phys., 1983, 61, 269–277 CrossRef CAS.
- J. Pliva and A. S. Pine, J. Mol. Spectrosc., 1987, 126, 82–98 CrossRef CAS.
- J. Pliva, J. Johns and L. Goodman, J. Mol. Spectrosc., 1990, 140, 214–225 CrossRef CAS.
- J. Lindenmayer, U. Magg and H. Jones, J. Mol. Spectrosc., 1988, 128, 172–175 CrossRef CAS.
- E. Riedle, T. Knittel, T. Weber and H. J. Neusser, J. Chem. Phys., 1989, 91, 4555–4563 CrossRef CAS.
- H. Hollenstein, S. Piccirillo, M. Quack and M. Snels, Mol. Phys., 1990, 71, 759–768 CrossRef CAS.
- M. Junttila, J. Domenech, G. T. Fraser and A. Pine, J. Mol. Spectrosc., 1991, 147, 513–520 CrossRef CAS.
- J. Domenech, M. Junttila and A. Pine, J. Mol. Spectrosc., 1991, 149, 391–398 CrossRef CAS.
- M. Okruss, R. Müller and A. Hese, J. Mol. Spectrosc., 1999, 193, 293–305 CrossRef CAS PubMed.
- C. Riehn, A. Weichert and B. Brutschy, J. Phys. Chem. A, 2001, 105, 5618–5621 CrossRef CAS.
- V. Matylitsky, W. Jarzeba, C. Riehn and B. Brutschy, J. Raman Spectrosc., 2002, 33, 877–883 CrossRef CAS.
- A. Doi, M. Baba, S. Kasahara and H. Katô, J. Mol. Spectrosc., 2004, 227, 180–186 CrossRef CAS.
- M. Baba, Y. Kowaka, U. Nagashima, T. Ishimoto, H. Goto and N. Nakayama, J. Chem. Phys., 2011, 135, 054305 CrossRef PubMed.
- J. Pliva, A. Valentin, J. Chazelas and L. Henry, J. Mol. Spectrosc., 1989, 134, 220–226 CrossRef CAS.
- M. Snels, H. Hollenstein, M. Quack, E. Cané, A. Miani and A. Trombetti, Mol. Phys., 2002, 100, 981–1001 CrossRef CAS.
- J. Pliva, J. Johns and L. Goodman, J. Mol. Spectrosc., 1991, 148, 427–435 CrossRef CAS.
- M. Oldani and A. Bauder, Chem. Phys. Lett., 1984, 108, 7–10 CrossRef CAS.
- M. Oldani, R. Widmer, G. Grassi and A. Bauder, J. Mol. Struct., 1988, 190, 31–40 CrossRef CAS.
- J. Coursey, D. Schwab, J. Tsai and R. Dragoset, in NIST Physical Measurement Laboratory, National Institute of Science and Technology [Online] February 16, 2001, https://www.nist.gov/pml/atomic-weights-and-isotopic-compositions-relative-atomic-masses, accessed July 20, 2021.
- W. Gordy and R. Cook, in Microwave Molecular Spectra, John Wiley & Sons, New York, 1984, ch. XIII Search PubMed.
- S. Rashev and D. C. Moule, J. Phys. Chem. A, 2004, 108, 1259–1267 CrossRef CAS.
- B. van Eijck, J. Mol. Spectrosc., 1982, 91, 348–362 CrossRef CAS.
- P. Nösberger, A. Bauder and H. Gunthard, Chem. Phys., 1973, 1, 418–425 CrossRef.
- R. H. Schwendeman, Critical evaluation of chemical and physical structural information, 1974 Search PubMed.
- V. Typke, J. Mol. Spectrosc., 1978, 69, 173–178 CrossRef CAS.
- J. Demaison and H. Rudolph, J. Mol. Spectrosc., 2002, 215, 78–84 CrossRef CAS.
- C. Schröter, K. Kosma and T. Schultz, Science, 2011, 333, 1011–1015 CrossRef PubMed.
- C. M. Western and B. E. Billinghurst, Phys. Chem. Chem. Phys., 2017, 19, 10222–10226 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision A.1, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- A. Doi, S. Kasahara, H. Katô and M. Baba, J. Chem. Phys., 2004, 120, 6439–6448 CrossRef CAS PubMed.
- NIST Computational Chemistry Comparison and Benchmark Database, ed. D. J. Russell, NIST, 2020 Search PubMed.
- W. Gordy and R. Cook, in Microwave Molecular Spectra, John Wiley & Sons, New York, 1984, ch. XIII, p. 709ff Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra03431j |
| ‡ These authors contributed equally to this work. |
| § The number of structural parameters required to characterize a particular molecule is equal to the number of totally symmetric vibrations.45 |
| ¶ The r(1)m terms are based on the approximate mass-dependence expected for harmonic vibration. |
|| 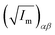 (α, β ∈ a, b, c) represent the tensor elements created by rotating the square root of the calculated principal inertial moments vector (α, β ∈ a, b, c) represent the tensor elements created by rotating the square root of the calculated principal inertial moments vector 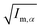 into the reference coordinate system. Off-diagonal parameters cαβ are treated as independent fit parameters. into the reference coordinate system. Off-diagonal parameters cαβ are treated as independent fit parameters. |
| ** Eijck's fit weights account for the fact that model errors are larger than the experimental uncertainty for high resolution data: for small values of σ, fit weights (σi2 + b2)−1 ≈ b−2 are constant. For low resolution data (σi ≫ b2), fit weights scale proportional to σi−2. |
| †† Note that the analysis, based on eqn (1), determines expectation values for 〈r2〉 and not 〈r〉2. Harmonic vibrations around re are symmetric and do not affect 〈r〉2 but increase 〈r2〉, i.e., lead to an apparent isotope-dependent displacement that does not correspond to a physical displacement of the corresponding atom. Anharmonic vibrations lead to an actual mass-dependent displacement of the nuclear position (re ≠ r0). Also note that we ignore the possible displacement of carbon atoms bonded to the substituted carbon, as this would break our underlying assumption of C6 rotational symmetry. |
| ‡‡ The small center-of-mass shift in asymmetrically deuterated isotopologues breaks the linear dependence to some degree. |
| §§ In the literature, first-order (r(1r)m) rovibrational correction terms were usually applied along the principal rotational axes of the main isotopologue. We see no reason why a particular set of axes should be preferred. Problems arise because the second-order correction terms in r(2r)m fits are only approximately aligned with these principal axes and the Laurie-correction is tied to the X–H bond axes. Corrections are therefore applied along different axes and these axes differ between isotopologues. A choice of coordinate system where many isotopologue principal axes coincide with the r(1r)m rovibrational correction axes, i.e., the default choice in the literature, is particularly problematic because it amplifies the weight of the remaining asymmetric isotopologues in determining r(2r)m and Laurie correction parameters. E.g., the unexpected negative Laurie correction term reported for H2O by Watson et al.13 is found only when the correction terms are calculated along the main isotopologue principal axes. In the ESI,† section 3.2.5, we describe Python code to systematically explore the angle-dependence of correction terms and fit parameters, using the Monte-Carlo formalism described above. |
| ¶¶ In particular, we considered excluding all Kunishige values for deuterated benzenes, because their rotational constants were determined with distortion constants DJ, DJK, and DK fixed to averaged values from C6H6 and C6D6, or excluding our own values for 13C isotopologues, because we determined rotational constants with distortion constants fixed to ab initio calculated values. |
| This journal is © The Royal Society of Chemistry 2022 |