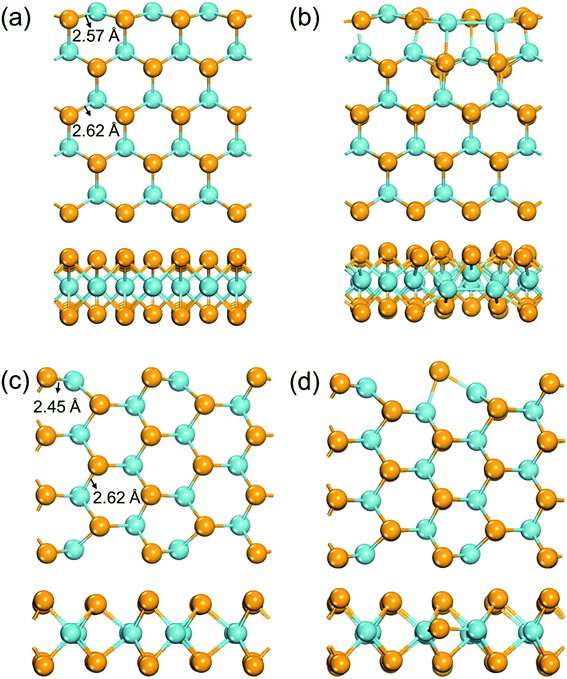Open Access Article
Open Access ArticleImproved nitrogen reduction activity of NbSe2 tuned by edge chirality†
Chen Zhou,
Saifei Yuan *,
Wen Zhao,
Wenyue Guo
*,
Wen Zhao,
Wenyue Guo * and
Hao Ren
* and
Hao Ren
School of Materials Science and Engineering, China University of Petroleum (East China), Qingdao 266580, Shandong, China. E-mail: ysaif1991@gmail.com; wyguo@upc.edu.cn
First published on 10th August 2022
Abstract
Efficient catalysts for the electroreduction of N2 to NH3 are of paramount importance for sustainable ammonia production. Recently, it was reported that NbSe2 nanosheets exhibit an excellent catalytic activity for nitrogen reduction under ambient conditions. However, existing theoretical calculations suggested an overpotential over 3.0 V, which is too high to interpret the experimental observations. To reveal the underlying mechanism of the high catalytic activity, in this work, we assessed NbSe2 edges with different chirality and Se vacancies by using first principles calculations. Our results show that N2 can be efficiently reduced to NH3 on a pristine zigzag edge via the enzymatic pathway with an overpotential of 0.45 V. Electronic structure analysis demonstrates that the N2 molecule is activated by the back-donation mechanism. The efficient tuning of the local chemical environments by edge chirality provides a promising approach for catalyst design.
Introduction
Ammonia (NH3) is one of the most essential chemical compounds, used widely as fertilizers, explosives, plastics, and clean hydrogen energy carriers.1,2 At present, the Haber–Bosch process is the main industrial technology to produce NH3, which requires iron-based catalysts and harsh conditions at high temperatures (400–600 °C) and high pressures (20–40 MPa).3 The hydrogen (H2) used in NH3 production usually comes from reforming natural gas, consuming approximately 1% of the global energy and releasing 1–2% of total CO2 emissions.4 Stimulated by the growing interest in exploring sustainable NH3 synthesis, electrochemical and photochemical approaches have emerged as promising alternatives to the Haber–Bosch process.5–9The past few years have witnessed remarkable progresses in the electrocatalytic and photocatalytic nitrogen reduction reaction (NRR) at mild conditions.8,10–13 The bottleneck of electrocatalytic and photocatalytic NRR is the lack of effective catalysts with high catalytic activity, high efficiency, high selectivity, and high stability.3 In this regard, intensive studies have focused on designing effective NRR catalysts, including transition metal-based catalysts10,14–16 and metal-free catalysts.8,17–19
Due to the versatile physical and chemical properties of transition metal dichalcogenides, this family of materials attracted tremendous interest in the catalysis community.18,20–23 For instance, Nb-based compounds have been considered as efficient NRR catalysts, where the partially occupied d-orbitals of Nb4+ cations provide empty states for strong N2 adsorption and activate the N2 triple bond with the back donation mechanism.24 Skúlason et al. predicted that the limiting potential of the (110) facet of NbO2 (−0.57 V) would be much lower than that of the Ru(0001) step surfaces (−1.08 V),25,26 where the latter has been widely adopted as a reference system for NRR. It has also been validated that NbO2 nanoparticles possess excellent electrochemical stability with an outstanding ammonia production rate of 11.6 μg h−1 mg−1 at −0.65 V versus the reversible hydrogen electrode (RHE).24,27 NbSe2 also exhibits its potential for nitrogen fixation catalysis.28–31 Wang et al. found that self-supported NbSe2 nanosheet arrays possess excellent NRR performance with a yield rate of 89.5 μg h−1 mg−1 at −0.45 V vs. RHE and a faradaic efficiency of 13.9%. However, the overpotential of NRR on the observed NbSe2(104) surface was predicted higher than 3.0 V by density functional theory (DFT) calculations,31 which is a quite large value and is not sufficient to interpret the experimental observations. This contradiction implies that the real active site might not be appropriately modeled in the calculations. Recently, Li et al. proposed that defect-rich MoS2 nanostructures boosted NH3 production rates more than two times compared to the pristine system, as well as lowering the energy barrier to 0.87 eV.32 The crystalline surface exposed to the reaction and the defects were crucial for the high performance. Both of the exposure of specific facets and the introduction of defects have been predicted to be effective to tune the catalytic activities via edge engineering of nanosheets.33,34 In this context, the observed high NRR catalytic performance of the NbSe2 nanosheets in ref. 31 would be rationalized by considering the probability that the active sites lie on crystalline surfaces other than the assessed (104) plane, or that the local chemical environments of the active sites been tuned by imperfect crystalline periodicity. The coordination number of the Nb ions varies significantly when they locate at surfaces or edges with different chirality and defects. Previous atomic-resolution annular dark-field scanning transmission electron microscope (ADF-STEM) imaging has revealed that the major defects in the monolayer NbSe2 are Se2 vacancy, Se vacancy, and anti-site defect where a Nb atom be substituted by two Se atoms.34 And the most frequently observed defect in monolayer NbSe2 is the Se vacancy.35 Furthermore, the exposed edges experience serious reconstruction,36–40 together with the probably existence of Se vacancies introduced during fabrication,41,42 there is a large set of freedoms to tune the electronic structures of the active center for efficient catalysis.
In this paper, we assessed the effects of edge engineering of NbSe2 monolayers on NRR catalytic performance based on first-principles calculations. As expected, both the zigzag and the armchair edges are capable of binding N2 strongly. Se vacancies would further significantly enhance the N2 affinity these edges. Our results indicate that the zigzag edge of the NbSe2 monolayer exhibits the overpotential as low as 0.45 V along the enzymatic pathway, which is even smaller than that on the well-established Re(111) surface (0.50 V),43 and explains the high NRR catalytic performance of the NbSe2 nanosheets. Our work explicitly indicates that edge engineering is a promising method to improve catalytic activities of nanomaterials.
Computational methods
All spin-polarized DFT calculations were performed by using the Vienna ab initio Simulation Package (VASP) with the projector-augmented wave (PAW) method and the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional.44–46 The dispersion interaction was described by the DFT-D3 scheme.47 The pseudo-wavefunctions were expanded by plane waves with kinetic energies up to 450 eV. All atoms were allowed to relax until the energy and force variation below 1 × 10−5 eV and 0.05 eV Å−1, respectively. The zigzag and armchair edges of NbSe2 were modeled with nanoribbon strips (Fig. 1). Vacuum layers of at least 10 Å were used to avoid unphysical interactions between neighboring images. The first Brillouin zone was sampled with a Γ centered 3 × 1 × 1 k-grid mesh in structure relaxation, and with a 5 × 1 × 1 mesh for electronic structure calculations. The projected crystal orbital Hamilton population (pCOHP) was calculated to reveal the nature of chemical bonding in LOBSTER package.48,49NRR is a multistep process involves N2 adsorption, six hydrogenation steps, and NH3 desorption. Each hydrogenation step is usually considered to take a coupled proton and electron transfer (CPET) mechanism, where a proton comes from the solution and an electron from the electrode. The free energy change in a hydrogenation step was calculated using the computational hydrogen electrode (CHE) model.50 The Gibbs free energy change of an elementary step was given by ΔG = ΔE + ΔEZPE − TΔS, where ΔE, ΔEZPE, and TΔS are the reaction energy of each elementary step, zero-point energy difference, and the entropy difference between the products and reactants, respectively. T is the absolute temperature set as 298.15 K in this work. Only the adsorbates and their nearest substrate atoms were allowed to move in the frequency calculations. Entropies of gas molecules, such as H2, N2, and NH3 were taken from the standard values obtained from the NIST database.51 The formation energies of Se vacancies were evaluated as Ef = E(VSe) + μ(Se) − E(edge), where E(VSe), μ(Se), and E(edge) are the energies of NbSe2 nanoribbon with a Se vacancy, the chemical potential of a Se atom in the bulk phase, and the energy of perfect NbSe2 nanoribbon.
Results and discussion
Structures of NbSe2 edges
A NbSe2 monolayer can be cut in two typical directions, i.e. the zigzag and the armchair directions, to form ribbons with typical edges. Previous studies have illustrated that the formation energies of both types of nanoribbons increases monotonically respect to the widths increase from ∼2 Å, and converged to −4.85 eV per atom at around 19 Å.52 This result implies that in a ribbon, atoms more than ∼10 Å from the edge would possess a similar chemical environment as in a 2D monolayer. Here we used nanoribbons with five zigzag chains (∼13 Å width) and seven armchair chains (∼10 Å width) to model chemical environments for the zigzag and armchair edges, respectively.The fully optimized structures of the edges are shown in Fig. 1. The formation energies of a Se vacancy on the zigzag (armchair) edge is 1.17 (0.40) eV, much lower than that on the NbSe2 monolayer (1.94 eV). The Nb–Se bonds have lengths of 2.62 Å in the extended monolayer, while as shown in Fig. 1a, these bonds are significantly shortened to 2.57 Å at the zigzag edge. The existence of a Se vacancy on the zigzag edge leads to severe reconstruction (Fig. 1b): the atoms near the Se vacancy move towards the vacancy, result to new Nb–Nb bonds and significant structural disorder. The Nb–Se bonds are shortened to 2.45 Å in the pristine armchair edge (Fig. 1c), while only exhibits slight reconstruction when a Se vacancy exists (Fig. 1d). The different structure relaxation behaviors of edges provide rich possibilities to tune the electronic structures of the edge Nb atoms, which would lead to distinct catalytic activities.
NRR pathways on NbSe2 edges
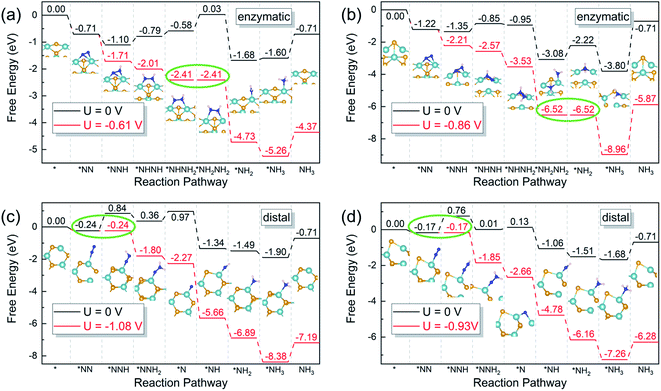
According to the sequence of the hydrogenation steps, the six-electron NRR processes can be categorized into 4 pathways, i.e. the distal, the alternating, the mixed, and the enzymatic pathways, as depicted in Scheme 1.1 The enzymatic pathway starts from the side-on adsorption configuration (insets in Fig. 2a and b), while the end-on adsorption configuration (insets in Fig. 2c and d) initializes the other pathways. The free energy diagrams of the most favorable pathway on different edges are shown in Fig. 2. During the nitrogen fixation catalytic cycle, the free N2 molecule firstly adsorbs on the Nb active sites with end-on or side-on pattern, then the *N2 (where * denotes the adsorption site) processes the six-electrons hydrogenation steps in the promising NRR mechanism in Scheme 1 to release two NH3 molecules in to aqueous solution. It is worth noting that the desorption of the second *NH3 does not relate to the electrons supplied from an external circuit and dose not change with the applied potential.53 To recovery the catalyst, the rapid desorption of the produced NH3 is crucial for nitrogen fixation, and the ΔG of the *NH3 desorption should be as low as possible.54 Once NH3 dissolved in the electrolyte, the NH3 can be further hydrogenated into NH4+, which requires much more detailed modeling of the solvated NH4+ in the liquid.26 In addition, the solvation of NH3 releases energy to stabilize the desorbed NH3, promoting the desorption produced NH3.55 Then the Nb sites recapture the N2 molecule to conduct the next NRR catalytic cycle.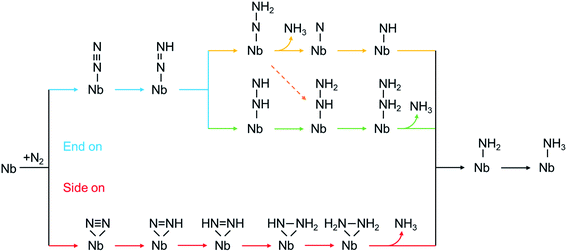 | ||
| Scheme 1 The mechanism of proton-coupled electron transfer for nitrogen reduction via a distal pathway (yellow), alternating (green), mixed (dashed orange), and enzymatic (red) pathways. | ||
On pristine zigzag edges, the N2 molecule prefers the side-on configuration on the edge Nb atom with an adsorption free energy of −0.71 eV, lower than that of the end-on pattern (−0.39 eV). Calculations suggest that the enzymatic pathway is favorable on this edge, of which the free energy diagram is shown in Fig. 2a. The first hydrogenation step (*N2 + H+ + e− = *NNH) and the first NH3 formation step (*NH2NH2 + H+ + e− = *NH2 + NH3) are exothermic, while the rest elementary steps are endothermic. The fourth hydrogenation step, i.e. *NHNH2 to *NH2NH2 is the potential-determining step requires an energy input of 0.61 eV. The existence of a Se vacancy on the zigzag edge lowers the N2 adsorption free energies to −0.55 eV and −1.22 eV, respectively, for the end-on and the side-on configurations.
The NRR on the defective zigzag edge also prefers the enzymatic mechanism, with the free energy diagram shown in Fig. 2b. It is intriguing that all the hydrogenation intermediates on the zigzag edge with a Se vacancy are lower than those on the pristine zigzag edge. The first NH3 formation step (*NH2NH2 + H+ + e = *NH2 + NH3) is the rate-limiting step with a free energy lifting of 0.86 eV.
Dinitrogen adsorption on both the pristine and the defective armchair edges prefer the end-on configuration, with adsorption Gibbs free energies of −0.24 and −0.17 eV, respectively. However, it is difficult to reduce the dinitrogen molecules on the armchair edges, due to the large free energy increase of the first hydrogenation steps. As shown in Fig. 2c, the first hydrogenation step on the pristine armchair edge requires an energy gain of 1.08 eV, indicating that NRR on this edge is not favorable. The introduction of a Se vacancy on the armchair edge lowers the energy requirement to 0.93 eV for the first hydrogenation step (Fig. 2d). But this value is still insufficient to interpret the observed high performance.31 The high limiting potential is the consequence of the insufficient activation of the dinitrogen molecules, of which only one of the nitrogen atoms is bonded to an edge Nb atom.
Both the differences in the free energy variations along the NRR pathways on NbSe2 edges with different chirality (zigzag vs. armchair), and the differences introduced by a Se vacancy, indicating that the NRR catalytic activity of the NbSe2 can be effectively tuned by edge engineering. This tunability stems from the rich possibilities in exposing an edge with specific chirality. The edge atoms at the resulted edges then possess various local chemical environments due to edge reconstruction or introduction of defects (Se vacancies in this case). The change in the local environment of the active site then tunes its electronic structure, which directly governs the catalytic activity.
The overpotential (η) is a good indicator of the electrochemical catalytic reactivity: a lower overpotential implies a more efficient NRR.10 Based on the CHE model, the η value is evaluated as η = Ueq − Ulim, where Ueq is the equilibrium potential of NRR with the value of −0.16 V.10 Ulim is the applied potential to eliminate the energy barrier of the potential-determining step, determined by Ulimiting = −ΔGmax/e, where ΔGmax is the free energy change of the potential-limiting step. The overpotentials of the most favorable NRR pathways of the pristine zigzag edge, the defective zigzag edge, the pristine armchair edge, and the defective armchair edge are 0.46 V, 0.70 V, 0.92 V, and 0.77 V, respectively. Therefore, NRR prefers to proceed on the pristine zigzag edge via the enzymatic mechanism with an overpotential of 0.46 V, which is even lower than the Re(111) surface (0.50 V).43 All these values are much lower than the previous predicted ∼3.0 V of the NbSe2 (104) surface,31 it would be more reasonable to ascribe the observed high catalytic performance of the NbSe2 nanosheets to the edges rather than the (104) surface.
Adsorption facilitated N2 activation
The intrinsic stability of the dinitrogen molecule provided by the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond is usually the main obstacle of NRR. Upon N2 adsorption on the catalyst, the interactions between the N atom(s) and the active site(s) is expected to activate the N
N triple bond is usually the main obstacle of NRR. Upon N2 adsorption on the catalyst, the interactions between the N atom(s) and the active site(s) is expected to activate the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond for ease hydrogenation.56 The stability of the N
N triple bond for ease hydrogenation.56 The stability of the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond can be understood by using the simple homonuclear diatomic molecular orbital theory,57 where all the six 2p electrons occupy the three bonding states (one σg and two πu) and left the antibonding states empty, resulting a bond order of 3. The N2 molecule can be activated by reducing the bond order, either by accommodating electrons in the antibonding states, or depleting electrons from the bonding states, or both. For example, an effective strategy is the back-donation mechanism: the active site possesses partially occupied states that are capable of accept and donate electrons simultaneously. Upon N2 adsorption, the bonding electrons transfers to the unoccupied states of the active site; in the meantime, the N2 antibonding states accept electrons from the occupied states of the active site.
N triple bond can be understood by using the simple homonuclear diatomic molecular orbital theory,57 where all the six 2p electrons occupy the three bonding states (one σg and two πu) and left the antibonding states empty, resulting a bond order of 3. The N2 molecule can be activated by reducing the bond order, either by accommodating electrons in the antibonding states, or depleting electrons from the bonding states, or both. For example, an effective strategy is the back-donation mechanism: the active site possesses partially occupied states that are capable of accept and donate electrons simultaneously. Upon N2 adsorption, the bonding electrons transfers to the unoccupied states of the active site; in the meantime, the N2 antibonding states accept electrons from the occupied states of the active site.
In the cases studied here, the electronic structure of the active site, i.e. the edge Nb atoms, varies significantly according to the change in their chemical environments.29 The coordination number of the Nb atoms on the edges is less than that of the internal ones, left dangling bonds that would facilitate adsorbate trapping.41 The energy gain of N2 adsorbed on the zigzag-edged Nb atoms are −0.89 and −1.19 eV, respectively, with the end-on and side-on configurations, indicating that the side-on configuration dominates the zigzag edge adsorption. As shown in Fig. 3a, the N2 molecule lies perpendicularly between two edge Nb atoms, with each N atoms bonded to both nearby Nb atoms. This strong bonding elongated the N–N bond length to 1.21 Å (from 1.11 Å in gas phase). A Se vacancy at the zigzag edge further stabilizes N2 side-on adsorption with an adsorption energy of −1.76 eV and a bond length of 1.20 Å. Although the adsorption energy on the defective edge is significantly higher than that on the pristine edge, the N–N bond length, another good indicator for activation, have similar values. That means the N2 molecule adsorbed on these two zigzag edges are at the similar degree of activation. The difference in adsorption energy can be ascribed to the saturation of the dangling bonds of the edge Nb atoms reside in different chemical environments. On the other hand, in the outmost chain of the armchair edges, the Nb and Se atoms are arranged alternatively, making it is difficult to accommodate the adsorbed N2 molecule in the side-on configuration to bonding to two nearby Nb atoms. In this case, N2 adsorbs on armchair edges prefer the end-on configuration, where only one N atom is bonded to an edge Nb atom, and leaving the other pointing outward. In consequence, the N2 molecule would only be weakly activated.
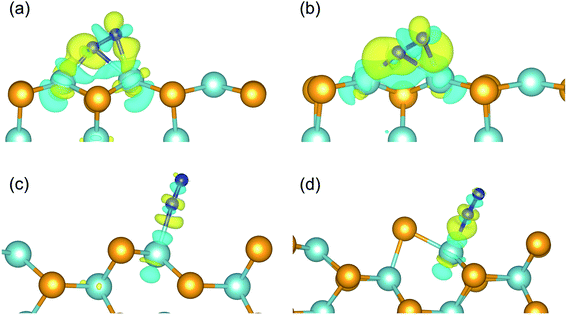
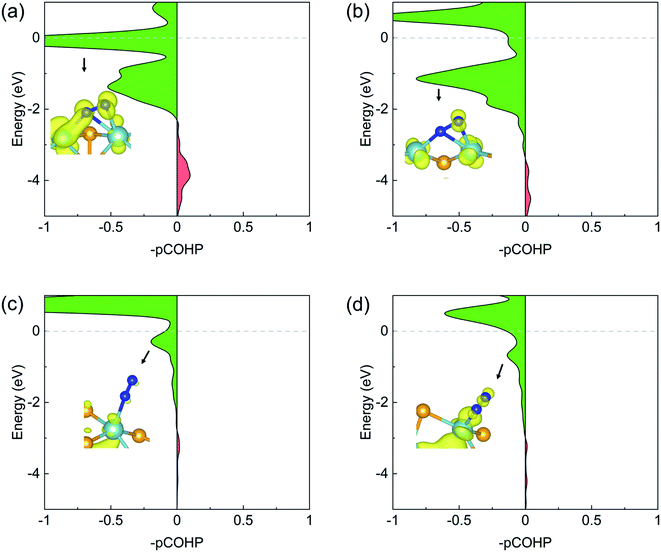
Fig. 3a depicts the charge density differences of the N2 adsorption on the pristine zigzag edge. Significant charge transfer can be observed between the edge Nb atom and the N2 molecule, according with the back donation mechanism.17 Specifically, electron depletion and accumulation occurs, respectively, inside and outside the internuclear region of the N2 molecule, corresponding to the spatial distribution of the bonding and the antibonding states. On the other hand, both electron accumulation and depletion occur around the two Nb atoms bonded to the N2 molecule. The case is similar for N2 adsorbed on the defective zigzag edge, as shown in Fig. 3b. As the consequence of the strong activation effect of the zigzag edges, the first hydrogenation step on the zigzag edges are thermodynamically favorable.
The N2 adsorption on the armchair edges are different. Due to the distinct edge structures than at the zigzag edges, the N2 molecule can not simultaneously bond to two edge Nb atoms. As shown in Fig. 3c and d, the N2 molecule adopt an end-on configuration. The charge transfer is much less than that at the zigzag edges. In consequence, the adsorbed N2 molecule would not be sufficiently activated, and the first hydrogenation steps are thermodynamically unfavorable. As shown in Fig. 3c and d, the free energy increases significantly upon the first hydrogenation steps making them the potential limiting steps.
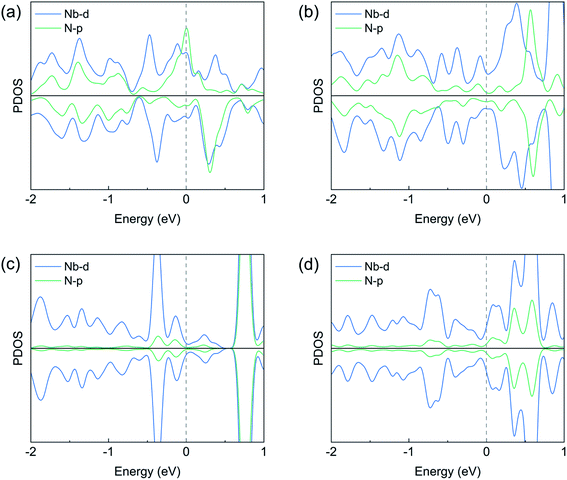
The above analysis can be validated by calculating the net charges of the atoms of interest. Bader charge analysis shows that, the net charge on the adsorbed N2 molecule is −0.86 (−0.83) e− on the pristine (defective) zigzag edge, indicating a considerable amount of electrons were transferred to N2 and the occupation of the antibonding states by these electrons weakens the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond effectively. The strong N–Nb bonding and significant charge transfer are in consistent with the projected density of states (PDOS) plots shown in Fig. 4a, b, S1a and b:† the Nb d states and the N p states overlaps considerably near the Fermi level, which is necessary for strong bonding. On the other hand, the net charge on the N2 molecule adsorbed on the pristine (defective) armchair edge is −0.11 (−0.17) e−. This much weaker charge transfer can be ascribed to the fact that only one N–Nb bond exists in the end-on configuration at armchair edges. The weak overlap between the N p states and Nb d states near the Fermi level (Fig. 4c, d, S1c and d†) is also an indication of much weaker N–Nb interactions.
N bond effectively. The strong N–Nb bonding and significant charge transfer are in consistent with the projected density of states (PDOS) plots shown in Fig. 4a, b, S1a and b:† the Nb d states and the N p states overlaps considerably near the Fermi level, which is necessary for strong bonding. On the other hand, the net charge on the N2 molecule adsorbed on the pristine (defective) armchair edge is −0.11 (−0.17) e−. This much weaker charge transfer can be ascribed to the fact that only one N–Nb bond exists in the end-on configuration at armchair edges. The weak overlap between the N p states and Nb d states near the Fermi level (Fig. 4c, d, S1c and d†) is also an indication of much weaker N–Nb interactions.
The N2 activation by the back-donation mechanism can also be illustrated by projected crystal orbital Hamilton population (pCOHP) analysis. As shown in Fig. 5, the positive (green) and the negative (red) shadings denote anti-bonding and bonding populations, respectively. In all cases of N2 adsorption, the anti-bonding character dominates the N–N interactions near the Fermi level, indicating significant occupation of the anti-bonding πg states. This anti-bonding population was schematically illustrated by the local density of states (LDOS) plots shown as the insets for each adsorption.
Conclusion
In summary, we performed systematical first principles analysis on the NRR catalytic activity of the typical edges of NbSe2 monolayer. We found that NRR on the pristine zigzag edge possesses quite low overpotential of 0.46 V through the enzymatic pathway. A Se vacancy on the zigzag edge would lift the overpotential to 0.70 V. Both values are significantly lower than the previously predicted ∼3.0 V, and thus be capable of interpreting the observed high performance of the NbSe2 nanosheets. Electronic structure analysis showed that the adsorbed N2 molecule were effectively activated by the strong Nb–N interactions via the back-donation mechanism, facilitating the first hydrogenation step. On the other hand, the armchair edges do not active the adsorbed N2 molecule sufficiently, resulting higher overpotentials at the first hydrogenation step. Our results illustrate that specific local chemical environments constructed by the chiral edges of TMD layers provide an effective approach to tune the catalytic activity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support from the National Key Research and Development Program of China (2019YFA0708703), the National Natural Science Foundation of China (NSFC, Grant No. 21773309), the Hefei National Research Center for Physical Sciences at the Microscale (KF2020004), and Taishan Scholars Program of Shandong Province (tsqn201909071).References
- G. Qing, R. Ghazfar, S. T. Jackowski, F. Habibzadeh, M. M. Ashtiani, C.-P. Chen, M. R. Smith and T. W. Hamann, Chem. Rev., 2020, 120, 5437–5516 CrossRef CAS PubMed.
- Y. Pang, C. Su, G. Jia, L. Xu and Z. Shao, Chem. Soc. Rev., 2021, 50, 12744–12787 RSC.
- W. Guo, K. Zhang, Z. Liang, R. Zou and Q. Xu, Chem. Soc. Rev., 2019, 48, 5658–5716 RSC.
- Y. Chen, H. Liu, N. Ha, S. Licht, S. Gu and W. Li, Nat. Catal., 2020, 3, 1055–1061 CrossRef CAS.
- S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Nat. Catal., 2018, 1, 490–500 CrossRef.
- B. H. R. Suryanto, H.-L. Du, D. Wang, J. Chen, A. N. Simonov and D. R. MacFarlane, Nat. Catal., 2019, 2, 290–296 CrossRef CAS.
- G. Soloveichik, Nat. Catal., 2019, 2, 377–380 CrossRef CAS.
- C. Ling, X. Niu, Q. Li, A. Du and J. Wang, J. Am. Chem. Soc., 2018, 140, 14161–14168 CrossRef CAS PubMed.
- P. Li, Z. Zhou, Q. Wang, M. Guo, S. Chen, J. Low, R. Long, W. Liu, P. Ding, Y. Wu and Y. Xiong, J. Am. Chem. Soc., 2020, 142, 12430–12439 CrossRef CAS PubMed.
- J. Zhao and Z. Chen, J. Am. Chem. Soc., 2017, 139, 12480–12487 CrossRef CAS PubMed.
- X. Niu, A. Shi, D. Sun, S. Xiao, T. Zhang, Z. Zhou, X. Li and J. Wang, ACS Catal., 2021, 14058–14066 CrossRef CAS.
- K. Hu, P. Qiu, L. Zeng, S. Hu, L. Mei, S. An, Z. Huang, X. Kong, J. Lan, J. Yu, Z. Zhang, Z. Xu, J. K. Gibson, Z. Chai, Y. Bu and W. Shi, Angew. Chem., Int. Ed., 2020, 59, 20666–20671 CrossRef CAS PubMed.
- Y. Li, J. Li, J. Huang, J. Chen, Y. Kong, B. Yang, Z. Li, L. Lei, G. Chai, Z. Wen, L. Dai and Y. Hou, Angew. Chem., 2021, 133, 9160–9167 CrossRef.
- L.-W. Chen, Y.-C. Hao, Y. Guo, Q. Zhang, J. Li, W.-Y. Gao, L. Ren, X. Su, L. Hu, N. Zhang, S. Li, X. Feng, L. Gu, Y.-W. Zhang, A.-X. Yin and B. Wang, J. Am. Chem. Soc., 2021, 143, 5727–5736 CrossRef CAS PubMed.
- S. Yuan, H. Ren, G. Meng, W. Zhao, H. Zhu and W. Guo, Appl. Surf. Sci., 2021, 555, 149682 CrossRef CAS.
- S. Yuan, B. Xu, S. Li, W. Zhu, S. Lei, W. Guo and H. Ren, Chin. Chem. Lett., 2022, 33, 399–403 CrossRef CAS.
- M.-A. Légaré, G. Bélanger-Chabot, R. D. Dewhurst, E. Welz, I. Krummenacher, B. Engels and H. Braunschweig, Science, 2018, 359, 896–900 CrossRef PubMed.
- C. Liu, Q. Li, C. Wu, J. Zhang, Y. Jin, D. R. MacFarlane and C. Sun, J. Am. Chem. Soc., 2019, 141, 2884–2888 CrossRef CAS PubMed.
- X. Liu, Y. Jiao, Y. Zheng and S.-Z. Qiao, ACS Catal., 2020, 10, 1847–1854 CrossRef CAS.
- R. Liu, T. Guo, H. Fei, Z. Wu, D. Wang and F. Liu, Adv. Sci., 2021, 2103583 Search PubMed.
- T. Yang, T. T. Song, J. Zhou, S. Wang, D. Chi, L. Shen, M. Yang and Y. P. Feng, Nano Energy, 2020, 68, 104304 CrossRef CAS.
- J. Li, S. Chen, F. Quan, G. Zhan, F. Jia, Z. Ai and L. Zhang, Chem, 2020, 6, 885–901 CAS.
- Y. Xie, H. Sun, Q. Zheng, J. Zhao, H. Ren and Z. Lan, J. Mater. Chem. A, 2019, 7, 27484–27492 RSC.
- L. Huang, J. Wu, P. Han, A. M. Al-Enizi, T. M. Almutairi, L. Zhang and G. Zheng, Small Methods, 2019, 3, 1800386 CrossRef.
- Á. B. Höskuldsson, Y. Abghoui, A. B. Gunnarsdóttir and E. Skúlason, ACS Sustainable Chem. Eng., 2017, 5, 10327–10333 CrossRef.
- E. Skúlason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2012, 14, 1235–1245 RSC.
- J. Han, Z. Liu, Y. Ma, G. Cui, F. Xie, F. Wang, Y. Wu, S. Gao, Y. Xu and X. Sun, Nano Energy, 2018, 52, 264–270 CrossRef CAS.
- A. Hamill, B. Heischmidt, E. Sohn, D. Shaffer, K.-T. Tsai, X. Zhang, X. Xi, A. Suslov, H. Berger, L. Forró, F. J. Burnell, J. Shan, K. F. Mak, R. M. Fernandes, K. Wang and V. S. Pribiag, Nat. Phys., 2021, 17, 949–954 Search PubMed.
- H. Yang, T. Zhang, Z. Huang, Y. Chen, X. Song, X. Hao, H. Yang, X. Wu, Y. Zhang, L. Liu, H.-J. Gao and Y. Wang, ACS Nano, 2022, 16, 1332–1338 CrossRef CAS PubMed.
- M. Liu, J. Leveillee, S. Lu, J. Yu, H. Kim, C. Tian, Y. Shi, K. Lai, C. Zhang, F. Giustino and C.-K. Shih, Sci. Adv., 2021, 7, eabi6339 CrossRef CAS PubMed.
- Y. Wang, A. Chen, S. Lai, X. Peng, S. Zhao, G. Hu, Y. Qiu, J. Ren, X. Liu and J. Luo, J. Catal., 2020, 381, 78–83 CrossRef CAS.
- X. Li, T. Li, Y. Ma, Q. Wei, W. Qiu, H. Guo, X. Shi, P. Zhang, A. M. Asiri, L. Chen, B. Tang and X. Sun, Adv. Energy Mater., 2018, 8, 1801357 CrossRef.
- F. Li, L. Chen, H. Liu, D. Wang, C. Shi and H. Pan, J. Phys. Chem. C, 2019, 123, 22221–22227 CrossRef CAS.
- H. Wang, X. Huang, J. Lin, J. Cui, Y. Chen, C. Zhu, F. Liu, Q. Zeng, J. Zhou, P. Yu, X. Wang, H. He, S. H. Tsang, W. Gao, K. Suenaga, F. Ma, C. Yang, L. Lu, T. Yu, E. H. T. Teo, G. Liu and Z. Liu, Nat. Commun., 2017, 8, 394 CrossRef PubMed.
- L. Nguyen, H.-P. Komsa, E. Khestanova, R. J. Kashtiban, J. J. P. Peters, S. Lawlor, A. M. Sanchez, J. Sloan, R. V. Gorbachev, I. V. Grigorieva, A. V. Krasheninnikov and S. J. Haigh, ACS Nano, 2017, 11, 2894–2904 CrossRef CAS PubMed.
- A. R. Kim, Y. Kim, J. Nam, H.-S. Chung, D. J. Kim, J.-D. Kwon, S. W. Park, J. Park, S. Y. Choi, B. H. Lee, J. H. Park, K. H. Lee, D.-H. Kim, S. M. Choi, P. M. Ajayan, M. G. Hahm and B. Cho, Nano Lett., 2016, 16, 1890–1895 CrossRef CAS PubMed.
- H. Ma, W. Zhao, S. Yuan, H. Ren, H. Zhu, H. Ma, F. Ding and W. Guo, Materials Today Physics, 2021, 19, 100411 CrossRef CAS.
- W. Zhao and F. Ding, Nanoscale, 2017, 9, 2301–2309 RSC.
- J. Sun, N. Lin, C. Tang, H. Wang, H. Ren and X. Zhao, Comput. Mater. Sci., 2017, 133, 137–144 CrossRef CAS.
- B. Tian, S. Li, S. Lei, L. Lin, W. Guo and H. Ren, Chin. Chem. Lett., 2021, 32, 2469–2473 CrossRef CAS.
- Y. Qu, L. Wang, Z. Li, P. Li, Q. Zhang, Y. Lin, F. Zhou, H. Wang, Z. Yang, Y. Hu, M. Zhu, X. Zhao, X. Han, C. Wang, Q. Xu, L. Gu, J. Luo, L. Zheng and Y. Wu, Adv. Mater., 2019, 31, 1904496 CrossRef CAS PubMed.
- D. Liu, H. Zhu, S. Yuan, N. Shi, J. Yu, T. Li, Q. Ma, W. Zhao, H. Ren and W. Guo, Appl. Surf. Sci., 2022, 576, 151803 CrossRef CAS.
- J. H. Montoya, C. Tsai, A. Vojvodic and J. K. Nørskov, ChemSusChem, 2015, 8, 2180–2186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, J. Chem. Phys., 1996, 6, 15–50 CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef.
- Computational Chemistry Comparison and Benchmark Database, https://cccbdb.nist.gov/.
- Y. Li, S. Tongay, Q. Yue, J. Kang, J. Wu and J. Li, J. Appl. Phys., 2013, 114, 174307 CrossRef.
- W. Zhao, L. Zhang, Q. Luo, Z. Hu, W. Zhang, S. Smith and J. Yang, ACS Catal., 2019, 9, 3419–3425 CrossRef CAS.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- X. Lv, W. Wei, F. Li, B. Huang and Y. Dai, Nano Lett., 2019, 19, 6391–6399 CrossRef CAS PubMed.
- H.-J. Himmel and M. Reiher, Angew. Chem., Int. Ed., 2006, 45, 6264–6288 CrossRef CAS PubMed.
- P. W. Atkins and J. De Paula, Physical chemistry: thermodynamics, structure, and change, W.H. Freeman, New York, tenth edn, 2014 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra03464f |
| This journal is © The Royal Society of Chemistry 2022 |