Open Access Article
Open Access ArticleInsights into the nonlinear optical (NLO) response of pure Aum (2 ≥ m ≤ 7) and copper-doped Aum–xCux clusters†
Fakhar Hussaina,
Riaz Hussain *a,
Muhammad Adnan
*a,
Muhammad Adnan b,
Shabbir Muhammad
b,
Shabbir Muhammad c,
Zobia Irshad
c,
Zobia Irshad d,
Muhammad Usman Khan
d,
Muhammad Usman Khan a,
Junaid Yaqooba and
Khurshid Ayub
a,
Junaid Yaqooba and
Khurshid Ayub e
e
aDepartment of Chemistry, University of Okara, 56300, Pakistan. E-mail: riazhussain@uo.edu.pk
bGraduate School of Energy Science and Technology, Chungnam National University, Daejeon, 34134, Republic of Korea
cDepartment of Chemistry, College of Science, King Khalid University, Abha 61413, P.O. Box 9004, Saudi Arabia
dDepartment of Chemistry, Chosun University, Gwangju, 61452, Republic of Korea
eDepartment of Chemistry, COMSAT University, Abbottabad, Pakistan
First published on 7th September 2022
Abstract
A series of small pure Aum (2 ≥ m ≤ 7) and copper-doped Aum−xCux clusters was evaluated by density functional theory (DFT) at the CAM-B3LYP/LANL2DZ level for their geometric, electronic, and nonlinear optical (NLO) properties. The charge transfer for the Au cluster significantly improved by reducing the HOMO–LUMO energy gap from 3.67 eV to 0.91 eV after doping with Cu atoms. The doping of Cu also showed noteworthy impacts on other optical and NLO properties, including a decrease in the excitation energy and increase in the dipole moment and oscillator strength. Furthermore, changes in the linear isotropic and anisotropic polarizabilities (αiso and αaniso) and first and second NLO hyperpolarizabilities (βstatic, γstatic) were also observed in the pure and Cu-doped clusters, which enhanced the NLO response. The nonlinear optical properties of the clusters were evaluated by calculating the static and frequency dependent second- and third-order NLO polarizabilities at 1064 nm wavelength. Among all the doped structures, the Au3Cu1 cluster showed the largest static first hyperpolarizability of β(total) = 4.73 × 103 au, while the Au1Cu6 cluster showed frequency dependent first hyperpolarizability of β(−2w;w,w) = 1.26 × 106 au. Besides this, large static and frequency-dependent second hyperpolarizability values of 6.30 × 105 au and 1.05 × 10 au were exhibited by Cu7 and Au1Cu6, respectively. This study offers an effective approach to design high-performance NLO materials utilizing mixed metal clusters which might have broad applications in the fields of optoelectronics and electronics.
Introduction
Nonlinear optics (NLO) is one of the sub-disciplines of modern optics, with an important academic status at par with laser physics. The study of nonlinear optics involves a variety of nonlinear effects that occur in the interaction between laser and matter.1,2 The purpose of nonlinear optics research, in particular, is for promoting new developments and new impacts on the co-operative process of powerful laser beams and materials, including gaining an in-depth understanding of the causes and common processes as well as evaluating potential applications in current or future fields. Laser interaction with a NLO material causes a modification in the optical properties of the material system, so that the next incoming photon sees something different.3 Generally, only laser light is strong enough to produce NLO phenomena; therefore, the beginning of this field of study is often regarded as the result of the discovery of second-generation harmonics by Franken et al. in 1961,4 one year after the first laser was constructed by Maiman.5 Although the observation of most NLO phenomena requires laser radiation, some classes of nonlinear optical effects were known long before the invention of laser. The most important examples of these phenomena include Pockels and Kerr electro-optic effects.6Inorganic NLO objects associated with nonlinear light distribution from the central region play an important role in optical science. Nowadays, NLO materials are used in many technological applications, including photonic devices, optoelectronics, second-harmonic generation (SHG), frequency doublers, fiber-optic telecommunication, and laser technology.7,8 The material requirement to reflect the NLO response is not centrosymmetric. In this regard, other non-centrosymmetric crystals exhibiting an indirect optical response are K3B6O10Cl ref. 9 and SrB5O7F3.10 Continuous efforts have been devoted to design and integrate new NLO materials due to rapid advances in the fields of nanoscience and nanotechnology.11 Materials used in the nano-scale have revealed an excellent NLO response that greatly enhances their growth in the current era.12 Gold nanoparticles (Au-NPs) play a vital role in the field of photonics.13,14
In addition, several design strategies for NLO materials have been proposed, including, the significant diradical character,15 designing octupolar molecules,16 the push–pull effect,17 and excess electron system.18 Among the above-mentioned approaches for designing NLO materials, the introduction of excess electrons is a well-known and widely used strategy.7 Gold copper bimetallic clusters are a good source of excess electrons and can be doped in many systems to generate excess electron compounds.19 Therefore, a number of theoretical studies and experiments have been presented evaluating the electronic stability and chemical application of transitional metal clusters.20
Metal clusters are obtained from the bonding of a few to hundreds of atoms and are called molecular entities.21 Gold clusters have declared as emerging materials in the 21st century due to their outstanding catalytic performances and their various NLO applications. Furthermore, gold clusters have proven to be key materials in electronics, optics22 and also in biomedical fields.23,24 Kokabi and Salehiyoun, studied the NLO and electronic properties of small neutral and singly charged iron-doped bismuth clusters.25 Recently, Knoppe et al. studied the NLO properties of thiolate-protected and phosphine-protected Au20 clusters.26,27
From the review of the valuable literature, it is evident that nano-scale materials possess excellent optical and nonlinear optical responses. Alloys of two clusters have also proved to be a better system with an excellent NLO response. Motivated by previous reports, we designed new alloys based on Cu and Au doping. The doping of two clusters can be an efficient approach for designing better NLO materials. In this report, we studied the changes produced in the electronic structure and geometry of Cu-doped Au-clusters by considering the dipole moment, HOMO–LUMO energy gap, NLO, average static β(0;0,0,0) and frequency-dependent β(−2w;w,w) second-order polarizability, and third-order static γ(0;0,0,0) and frequency-dependent γ(−2w;w,0,0) polarizability. The results of all the analyses suggested that our designed clusters are effective candidates as superb nonlinear optical materials.
Computational methodology
The Gaussian 09 program was used for all the computational calculations.28 The structures of all the studied gold and copper clusters were visualized and designed using the Gauss View 5.0 Program.29 Density functional theory (DFT) methods were used to compute the molecular geometries of the neutral gold clusters. This theoretical methodology was selected due to the presence of a great number of electrons in the metal clusters and required the introduction of electron correlation effects. The CAM-B3LYP functional was used with LANL2DZ (Los Alamos National Laboratory 2 Double-Zeta), which is a widely used ECP (effective core potentials) type basis set to model the metal atoms and can reduce the computational cost and energy required.30 The HOMO–LUMO energy gap and NLO properties were calculated by using the same method as used for the optimization.In our work, we focus on the comparison of the total electronic dipole moment μtot, static and the frequency-dependent linear isotropic αiso and anisotropic αaniso polarizabilities, total second-order polarizability β(total), average static β(0;0,0,0) and frequency-dependent β(−2w;w,w) first hyperpolarizabilities, and average static γ(0;0,0,0) and frequency-dependent γ(−2w;w,w,0) second hyperpolarizabilities [66, 67]. Mathematically, the anisotropic and isotropic polarizabilities can be stated as follows:31,32
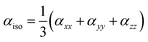 | (1) |
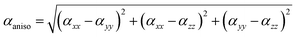 | (2) |
Estimation of the non-linearities, particularly the first hyperpolarizabilities, were calculated as follows.33,34
| βtotal = (βx2 + βy2 + βz2)1/2 | (3) |
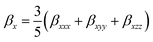 | (4) |
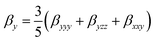 | (5) |
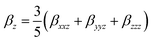 | (6) |
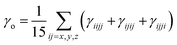 | (7) |
The following equation was used to calculate the H-L energy gap.35,36
| EH−L = EL−EH | (8) |
Results and discussion
Geometry of the pure and Cu-doped gold clusters
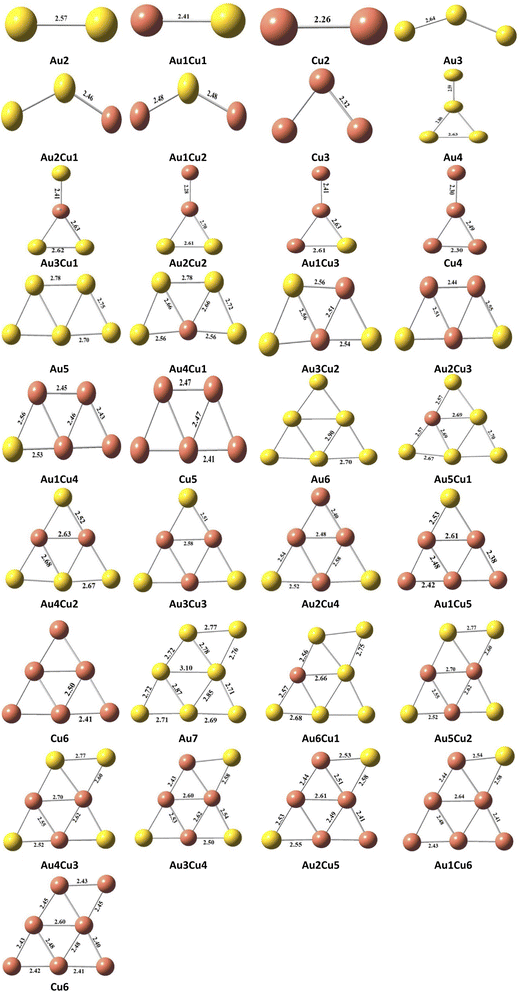
The structural geometry of the clusters plays an important role in modulating the NLO and optoelectronic properties of advanced functional materials. So, the effect of variations in the geometrical structures on their NLO properties by doping Cu atom in pure Au-clusters was investigated. In the present study, small Au-clusters Aum (2 ≥ m ≤ 7), namely Au2, Au3, Au4, Au5, Au6, and Au7, clusters were optimized through DFT calculations at the CAM-B3LYP/LANL2DZ level of theory, which is an efficient and frequently used method for doped clusters. In the literature, different reports effectively used the CAM-B3LYP/LanL2DZ level of theory for studying the electronic behavior of clusters.37 The average bond lengths and HOMO–LUMO energy gaps were calculated and compared with the reported Au-clusters, as it is very significant to relate the properties of the studied materials with others to ensure their uniqueness. As shown in Fig. 2, the reported bond lengths of the pure Au-clusters and our calculated values for pure Au-clusters were comparable.37 After careful analysis of all the designed clusters, the following lowest energy geometry structures of pure gold Aum (2 ≥ m ≤ 7) clusters were selected (based on stability), as shown in Fig. 1.Furthermore, by the replacement of both Au atoms of the Au2 cluster with a Cu atom the Au1Cu1, Cu2 lowest energy geometry structures were obtained. Similarly, for Au3(Au2Cu1, Au1Cu2, Cu3), Au4(Au3Cu1, Au2Cu2, Au1Cu3, Cu4), Au5(Au4Cu1, Au3Cu2, A2Cu3, A1Cu4, Cu5), Au6 (Au5Cu1, Au4Cu2, Au3Cu3, Au2Cu4, Au1Cu5, Cu6), and Au7 (Au6Cu1, Au5Cu2, Au4Cu3, Au3Cu4, Au2Cu5, Au1Cu6, Cu7) structures were obtained, as shown in Fig. 2.
Due to having applications in optoelectronics, gold clusters are considered as promising NLO materials. To enhance the conducting properties of pure gold clusters, these are doped with Cu atoms. The average bond length of the pure gold clusters Au2, Au3, Au4, Au5, Au6, and Au7 were 2.57, 2.64, 2.71, 2.77, 2.77, and 2.79 Å, respectively. While these lengths decreased by doping with Cu atom as Au1Cu1 2.57 Å 2.41, Cu2 2.26 Å. The average bond length for the pure Cu clusters Cu2, Cu3, Cu4, Cu5, Cu6, and Cu7 were 2.26, 2.33, 2.40, 2.44, 2.44, and 2.45 Å respectively. The average bond lengths were considerably decreased by doping Cu in the pure gold clusters, as shown in Table 1. The Eg values for the pure gold cluster structures Au2, Au3, Au4, Au5, Au6, and Au7 were 3.25, 3.14, 1.93, 2.49, 3.48, and 3.25 eV, respectively. A mixed trend for the energy bandgap was obtained for Cu2, Cu3, Cu4, Cu5, Cu6, and Cu7, as shown in Table 1. These results show that the HOMO–LUMO energy gap was altered upon doping with Cu atom. The band gap decreased from the pure to the doped system in the range of 3.67–0.91 eV. The lowest energy bandgap was observed for Au2Cu2, Au3Cu1, Cu3, Cu4, and Au4, as shown in Table 1.
| Molecule | First transition dipole (δμ) | fo | Transition (%C·I) | μ (D) | HOMO (ev) | LUMO (eV) | Eg (eV) | ΔE (eV) | ABL (Å) |
|---|---|---|---|---|---|---|---|---|---|
| Au2 | 0.0000 | 0.0000 | H−1 to L+1 (71) | 0.00 | −7.19 | −3.93 | 3.25 | 2.7346 | 2.57 |
| Au1Cu1 | 0.2152 | 0.0030 | H−1 to L+1 (70) | 2.63 | −6.40 | −3.02 | 3.38 | 2.6029 | 2.41 |
| Cu2 | 0.0000 | 0.0000 | H−1 to L+1 (70) | 0.00 | −5.59 | −2.34 | 3.25 | 2.5317 | 2.26 |
| Au3 | 0.0595 | 0.0001 | H+3 to L+1 (99) | 0.37 | −6.59 | −3.45 | 3.14 | 1.2269 | 2.64 |
| Au2Cu1 | 0.0740 | 0.0003 | H+2 to L−1 (73) | 3.27 | −5.72 | −2.96 | 2.75 | 1.4927 | 2.56 |
| Au1Cu2 | 0.4680 | 0.0085 | H to L+2 (47) | 1.40 | −4.97 | −2.53 | 2.44 | 1.5765 | 2.48 |
| Cu3 | 0.4958 | 0.0034 | H to L+1 (100) | 0.42 | −4.05 | −2.66 | 1.39 | 0.5600 | 2.33 |
| Au4 | 0.3176 | 0.0033 | H to L+1 (70) | 3.63 | −6.34 | −4.41 | 1.93 | 1.3526 | 2.71 |
| Au3Cu1 | 0.1746 | 0.0005 | H to L+1 (71) | 5.03 | −5.86 | −4.58 | 1.28 | 0.6436 | 2.58 |
| Au2Cu2 | 0.1961 | 0.0002 | H to L+1 (72) | 1.63 | −5.15 | −4.22 | 0.93 | 0.2505 | 2.56 |
| Au1Cu3 | 0.2813 | 0.0035 | H to L+1 (70) | 2.51 | −5.45 | −2.92 | 2.53 | 1.8158 | 2.58 |
| Cu4 | 0.2906 | 0.0025 | H to L+1 (71) | 3.02 | −4.76 | −2.91 | 1.85 | 1.2200 | 2.40 |
| Au5 | 0.2302 | 0.0001 | H to L+1 (97) | 0.02 | −5.91 | −3.42 | 2.49 | 1.2608 | 2.77 |
| Au4Cu1 | 0.1610 | 0.0008 | H to L−2 (91) | 0.22 | −5.80 | −3.32 | 2.48 | 1.2801 | 2.67 |
| Au3Cu2 | 0.4196 | 0.0066 | H to L−2 (96) | 1.19 | −5.66 | −2.70 | 2.95 | 1.4614 | 2.59 |
| Au2Cu3 | 0.3651 | 0.0054 | H to L−2 (91) | 1.71 | −5.29 | −2.57 | 2.72 | 1.6456 | 2.52 |
| Au1Cu4 | 0.2076 | 0.0025 | H to L−1 (24) | 2.47 | −4.88 | −2.42 | 2.46 | 1.5801 | 2.48 |
| Cu5 | 0.2558 | 0.0022 | H to L+1 (97) | 0.01 | −4.55 | −2.17 | 2.38 | 1.3774 | 2.44 |
| Au6 | 0.1572 | 0.0017 | H to L−1 (52) | 0.00 | −6.92 | −3.43 | 3.48 | 2.8508 | 2.77 |
| Au5Cu1 | 0.3057 | 0.0063 | H to L−2 (59) | 0.46 | −6.79 | −3.39 | 3.39 | 2.7549 | 2.69 |
| Au4Cu2 | 0.5691 | 0.0218 | H to L−1 (69) | 0.25 | −6.77 | −3.36 | 3.40 | 2.7487 | 2.60 |
| Au3Cu3 | 0.7955 | 0.0619 | H to L−1 (63) | 0.01 | −6.74 | −3.07 | 3.67 | 3.0298 | 2.54 |
| Au2Cu4 | 1.2070 | 0.1024 | H to L−1 (66) | 2.47 | −6.18 | −2.79 | 3.39 | 2.8677 | 2.50 |
| Au1Cu5 | 0.8135 | 0.0428 | H to L−1 (65) | 2.51 | −5.74 | −2.52 | 3.22 | 2.6353 | 2.47 |
| Cu6 | 0.0882 | 0.0489 | H to L−1 (61) | 0.00 | −5.50 | −2.25 | 3.25 | 2.6802 | 2.44 |
| Au7 | 0.0475 | 0.0001 | H to L−1 (87) | 0.39 | −5.82 | −3.58 | 2.24 | 1.3915 | 2.79 |
| Au6Cu1 | 0.2629 | 0.0023 | H to L−2 (95) | 1.17 | −5.61 | −3.60 | 2.01 | 1.2903 | 2.72 |
| Au5Cu2 | 0.2814 | 0.003 | H to L−2 (97) | 0.88 | −5.61 | −3.59 | 2.02 | 1.2706 | 2.65 |
| Au4Cu3 | 0.1160 | 0.0009 | H to L (91) | 0.81 | −5.70 | −3.22 | 2.49 | 1.4583 | 2.59 |
| Au3Cu4 | 0.1772 | 0.0016 | H to L (91) | 1.57 | −5.51 | −2.98 | 2.53 | 1.4386 | 2.54 |
| Au2Cu5 | 0.2171 | 0.0015 | H to L (98) | 0.90 | −5.34 | −2.61 | 2.68 | 1.1374 | 2.51 |
| Au1Cu6 | 0.2110 | 0.0021 | H to L (97) | 2.37 | −4.93 | −2.47 | 2.46 | 1.1618 | 2.48 |
| Cu7 | 0.2449 | 0.0021 | H to L−2 (92) | 0.17 | −4.40 | −2.34 | 2.06 | 1.2803 | 2.45 |
This decreases in bond length and energy gap were due to deformation in the electronic structures of the clusters and increases in the dipole moment and the conducting properties of the clusters. All the doped clusters had a small ABL (average bond length) and low energy gap, which showed that all the doped clusters were stable.
Dipole moment
The computed values of the dipole moment (μ) and change in the transition dipole moment (δμ) of the pure and Cu-doped gold clusters are given in Table 1. The doping of gold clusters significantly affected their electro-optical properties, such as the dipole moment and transition energy. The doping of metal unbalances the electron density of the pure clusters, which results in charge separation. The charge separation causes an increase in the dipole moment. A greater value of dipole moment in the doped system allows a higher NLO response. Therefore, the NLO polarizabilities were also calculated, which strongly depend on the dipole moment, oscillator strength, and orbital transition energy.The dipole moment was almost zero due to the centrosymmetric nature of the pure clusters. The doping of a transition metal (Cu) could significantly change the dipole moments as compared to pure clusters. The total and transition dipole moment for the pure gold and pure copper clusters Au2, Au3, Au4, Au5, Au6, and Au7 were almost 0.0 D. The doping of Cu into the pure Au-clusters imbalanced the electronic density, which resulted in charge separation. This charge separation caused an increase in the dipole moment. The calculated total dipole moment μD and transition dipole moment δμ for the optimized geometries of Au and Au–Cu doped clusters are presented in Table 1.
Large dipole moments μD for the Cu-doped clusters Au2Cu1, Au4, and Au3Cu1 were noted as 3.27, 3.63, and 5.03 D, respectively. The highest transition dipole moments δμ were 0.5691, 0.7955, 0.8135, and 1.2070 D for Au4Cu2, Au3Cu3, Au1Cu5, and Au2Cu4, respectively, due to the highly imbalanced structures of the molecules. The dipole moments of the pure Au and pure Cu clusters were less than the mixed Au–Cu clusters. Interestingly, the dipole moment of the pure clusters increased upon doping with Cu atoms. The Au2 clusters showed a lower value of dipole moment for pure Au and pure Cu cluster compared to the others. The doped clusters, like Au1–Cu1 clusters, exhibited a higher value of dipole moment, which was due to the change in charge separation. The dipole moment for a symmetric structure is always less than for nonsymmetric structures, like in the Au4 cluster, where the μD for the Au2Cu2 symmetric structure was less than for the Au3Cu1 nonsymmetric structure. The same trend of dipole moment was shown in Au6 (Au3Cu3) and Au7 (Au4Cu4) clusters. The dipole moment of the cluster structures containing a single Au atom was higher than the others with more than one Au atom clusters. The dipole moment of clusters containing a single Cu atom was also higher than the others with more than one Cu atom clusters, like in Au5(Au4Cu1), A6(Au5Cu1) and A7(Au6Cu1) clusters. Thus, one can expect better electronic and optoelectronic properties from these clusters.
Linear isotropic and anisotropic polarizabilities
In isotropic media, the polarizability αiso is defined as the ratio of the induced dipole moment of an atom to the electric field generating dipole moment, while in general, the polarizability cannot be expressed as a scalar quantity for anisotropic αaniso or non-spherical media. In scalar terms, the anisotropic polarizability αanisocan be referred to as the applied electric fields can only cause field parallel components to become polarized and as the x, y, z directions react in the same way to an applied electric field. The characterization of anisotropic media is done by the two tensor polarizability rank. Isotropic polarizability in scalar terms can be defined as the ratio of the induced atomic dipole moment to the dipole moment rising through an electric field.38 Here, we specifically investigated the static and frequency-dependent αiso and αaniso of pure and Cu-doped Au-clusters at the CAM-B3LYP/LANL2DZ level of DFT and their values are shown in Table 2. The doping of Cu in pure Au-clusters meaningfully affected the electro-optical characteristics, such as transition energy and dipole moment. The maximum dipole moment was seen in doped systems, which may be due to their high NLO response.| Molecule | α(0;0) (au) | α(−w;w) (au) | 2nd polarizability βo (au) | γo (au) | |||||
|---|---|---|---|---|---|---|---|---|---|
| (αiso) | (αaniso) | (αiso) | (αaniso) | β(0;0,0) | β(−2w;w,w) | βtotal | γo(0;0,0,0) | γo(−2w;w,w,0) | |
| Au2 | 78.86 | 69.91 | 60.16 | 84.03 | 0.00 × 101 | 0.00 × 10° | 1.15 × 101 | 6.01 × 103 | 8.03 × 103 |
| Au1Cu1 | 70.54 | 47.37 | 75.37 | 55.24 | 1.01 × 103 | 1.27 × 103 | 4.70 × 102 | 5.67 × 105 | 6.74 × 105 |
| Cu2 | 76.74 | 45.97 | 83.24 | 55.01 | 0.00 × 10° | 0.00 × 10° | 6.74 × 101 | 4.56 × 104 | 1.42 × 105 |
| Au3 | 142.89 | 177.24 | 186.02 | 285.96 | 2.41 × 102 | 1.26 × 103 | 1.26 × 103 | 1.42 × 103 | 1.45 × 105 |
| Au2Cu1 | 135.37 | 161.31 | 154.15 | 205.61 | 2.21 × 103 | 2.28 × 104 | 3.64 × 103 | 1.41 × 105 | 1.69 × 106 |
| Au1Cu2 | 146.45 | 189.12 | 175.11 | 262.17 | 1.08 × 103 | 3.26 × 103 | 1.79 × 103 | 1.08 × 105 | 5.03 × 105 |
| Cu3 | 131.57 | 106.17 | 133.82 | 943.76 | 1.43 × 103 | 6.21 × 102 | 2.39 × 103 | 2.47 × 105 | 9.80 × 105 |
| Au4 | 167.34 | 156.36 | 182.22 | 174.18 | 1.28 × 103 | 2.84 × 103 | 2.84 × 103 | 6.52 × 104 | 1.16 × 105 |
| Au3Cu1 | 152.36 | 121.33 | 162.80 | 143.06 | 2.73 × 103 | 4.46 × 103 | 4.73 × 103 | 1.44 × 105 | 2.99 × 105 |
| Au2Cu2 | 168.42 | 142.17 | 181.57 | 172.96 | 1.78 × 103 | 1.91 × 103 | 3.36 × 103 | 4.04 × 105 | 1.56 × 106 |
| Au1Cu3 | 138.90 | 119.24 | 148.71 | 134.41 | 1.19 × 103 | 2.62 × 103 | 1.98 × 103 | 1.79 × 105 | 3.83 × 105 |
| Cu4 | 145 | 147.35 | 132.26 | 139.74 | 3.78 × 102 | 5.21 × 102 | 3.66 × 102 | 3.17 × 105 | 9.83 × 105 |
| Au5 | 204.80 | 176.23 | 226.60 | 219.58 | 3.51 × 102 | 3.52 × 102 | 2.63 × 102 | 8.67 × 104 | 4.24 × 104 |
| Au4Cu1 | 194.87 | 160.67 | 217.13 | 205.13 | 9.10 × 101 | 1.28 × 104 | 7.07 × 101 | 2.02 × 105 | 1.52 × 107 |
| Au3Cu2 | 178.72 | 134.84 | 194.70 | 162.94 | 3.05 × 102 | 6.06 × 103 | 4.42 × 102 | 1.49 × 104 | 1.09 × 106 |
| Au2Cu3 | 177.16 | 136.25 | 192.44 | 159.26 | 4.17 × 102 | 1.82 × 104 | 7.15 × 102 | 2.15 × 105 | 4.26 × 107 |
| Au1Cu4 | 185.39 | 144.20 | 203.75 | 170.81 | 1.11 × 103 | 2.10 × 103 | 1.86 × 103 | 3.27 × 105 | 2.10 × 105 |
| Cu5 | 195.65 | 154.01 | 218.85 | 187.47 | 2.95 × 102 | 2.23 × 102 | 4.99 × 102 | 3.57 × 105 | 5.15 × 105 |
| Au6 | 234.61 | 170.68 | 247.08 | 186.02 | 1.74 × 10° | 4.35 × 101 | 1.94 × 101 | 9.84 × 104 | 2.10 × 105 |
| Au5Cu1 | 222.74 | 161.23 | 234.90 | 176.46 | 1.21 × 102 | 3.42 × 102 | 9.31 × 101 | 1.73 × 104 | 2.10 × 104 |
| Au4Cu2 | 209.73 | 146.72 | 221.02 | 160.91 | 1.92 × 102 | 7.56 × 102 | 3.97 × 102 | 1.19 × 105 | 2.65 × 105 |
| Au3Cu3 | 195.39 | 124.79 | 205.43 | 136.18 | 1.03 × 102 | 1.82 × 102 | 1.06 × 102 | 1.89 × 105 | 3.44 × 105 |
| Au2Cu4 | 201.60 | 132.80 | 213.71 | 146.69 | 1.08 × 103 | 2.31 × 103 | 1.79 × 103 | 9.13 × 104 | 1.84 × 105 |
| Au1Cu5 | 210.24 | 142.33 | 224.94 | 159.32 | 1.11 × 103 | 2.35 × 103 | 1.86 × 103 | 3.80 × 105 | 8.57 × 105 |
| Cu6 | 221.25 | 153.97 | 239.15 | 174.58 | 8.36 × 102 | 5.11 × 101 | 8.69 × 101 | 3.46 × 105 | 8.81 × 105 |
| Au7 | 298.49 | 270.15 | 322.77 | 311.97 | 3.95 × 102 | 6.20 × 103 | 6.60 × 102 | 1.83 × 105 | 1.15 × 106 |
| Au6Cu1 | 286.96 | 254.14 | 310.79 | 293.15 | 4.52 × 102 | 6.06 × 102 | 6.67 × 102 | 5.06 × 104 | 3.79 × 105 |
| Au5Cu2 | 269.18 | 220.05 | 295.90 | 254.51 | 3.89 × 102 | 1.13 × 104 | 6.55 × 102 | 3.53 × 105 | 2.42 × 107 |
| Au4Cu3 | 251.88 | 204.48 | 271.71 | 236.66 | 3.11 × 102 | 4.09 × 103 | 3.56 × 102 | 2.03 × 105 | 2.96 × 106 |
| Au3Cu4 | 251.05 | 205.78 | 272.79 | 238.00 | 2.94 × 102 | 2.80 × 103 | 4.98 × 102 | 2.00 × 105 | 2.88 × 105 |
| Au2Cu5 | 255.72 | 209.45 | 258.74 | 228.01 | 6.61 × 102 | 8.23 × 103 | 1.14 × 103 | 3.27 × 105 | 5.77 × 106 |
| Au1Cu6 | 267.89 | 226.57 | 287.96 | 438.78 | 1.61 × 103 | 1.26 × 106 | 2.68 × 103 | 4.22 × 105 | 1.05 × 108 |
| Cu7 | 281.49 | 248.24 | 316.76 | 303.68 | 5.35 × 102 | 1.31 × 104 | 9.00 × 102 | 6.30 × 105 | 5.15 × 106 |
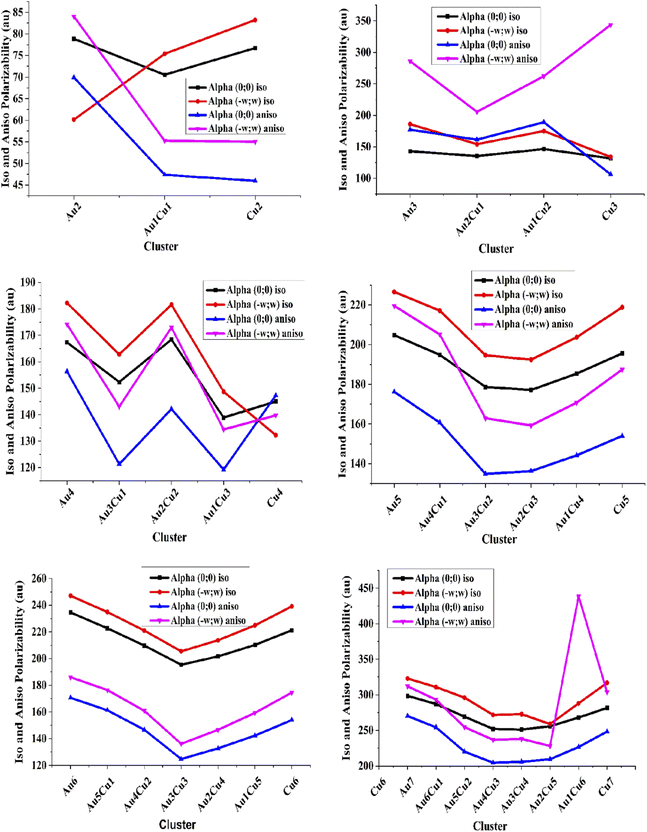
The linear static isotropic polarizabilities for the pure Au-clusters Au2, Au3, Au4, Au5, Au6, and Au7 were 78.86, 142.89, 167.34, 204.80, 234.61, and 298.49 au, respectively. The isotropic polarizabilities of pure Cu clusters were in the range of 76.74–281.49 au. The frequency-dependent isotropic polarizabilities for pure gold clusters were in the range of 60.16–322.77 au, and 45.97 = −248.24 au for pure Cu clusters. High values of static and frequency-dependent αiso were shown by Cu7 and Au7 clusters due to their large size and deformation structure.
The static anisotropic polarizabilities for pure Au-clusters were 69.91, 177.24, 156.36, 176.23, 170.68, and 270.15 au for Au2, Au3, Au4, Au5, Au6, and Au7, respectively. Frequency-dependent anisotropic polarizabilities for the pure Au (2–7) clusters were in the range of 69.91–311.97 au. These show that the frequency-dependent anisotropic polarizability is always higher than the static. Therefore, we can say that the anisotropic polarizabilities for the pure Au and Cu clusters were very close to each other. High values of αaniso static and frequency-dependent polarizabilities were also shown by the Cu-doped Au7(Au6Cu1, Au5Cu2, Au4Cu3, Au3Cu4, Au2Cu5, Au1Cu6, Cu7) clusters due to deformation in their structure by the doping of cupper and also due to their high dipole moment. A comparison of the linear and frequency-dependent isotropic and anisotropic polarizabilities is shown in Fig. 3.
Graphical comparison of the linear and frequency-dependent isotropic and anisotropic polarizabilities showed that the anisotropic polarizability was always less than isotropic polarizability. These results confirmed that the frequency-dependent isotropic and anisotropic polarizabilities were higher than the static one. The isotropic and anisotropic polarizability values were high for single Au and Cu containing cluster structures, like Au1Cu2 and Au1Cu3, Au1Cu4, Au1Cu5, Au1Cu6, Au6Cu1, Au5Cu1, Au4Cu1, Au3Cu1, Au2Cu. The graphical comparison showed that by the doping of Cu, the values of the αiso and αaniso first decreased, like in Au5 clusters, where the αiso and αaniso first decreased from Au5 to Au2Cu3 cluster and then increases by further doping up to the pure Cu5 cluster. The Au6 and Au7 clusters showed a similar trend for the isotropic and anisotropic polarizabilities. It could also be noted that the clusters containing equal numbers of gold and copper atoms showed low polarizability; for example, the αiso and αaniso for the Au1Cu1, Au2Cu2, and Au3Cu3 structures were less than for Au2Cu3, Au3Cu2, and Au4Cu5, etc. When the anisotropic polarizability αaniso values of the pure and Cu-doped clusters were compared, the values of the Cu-doped clusters were less than for the pure gold and pure copper clusters. The polarizability of the studied clusters gradually increased with increased size (atomic size) and the number of metals.
Second-order NLO polarizability
Density functional theory (DFT) at the CAM-B3LYP/LANL2DZ level was used to theoretically calculate the total second-order polarizability β(total), average static second-order polarizability β(0;0,0), and average frequency-dependent second-order polarizability β(−2w;w,w) of the pure and Cu-doped gold nano clusters. The computed values of β(0;0,0), β(−2w;w,w), and β(total) of the pure and doped Au–Cu clusters are shown in Table 2.A two-level model was applied to understand the factors affecting the hyperpolarizability.39–41 This model explains the dependency of the first hyperpolarizability on the oscillator strength (fo) and transition energy (ΔE) of the crucial excited state, and the difference in the dipole moment between the ground and crucial excited states (Δμ). The two-level model can be represented as follows:
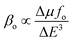 | (9) |
This equation shows that the first hyperpolarizability (βo) is directly related to the oscillator strength (fo) and transition dipole moment (Δμ), but inversely proportional to the third power of the transition energy (ΔE).
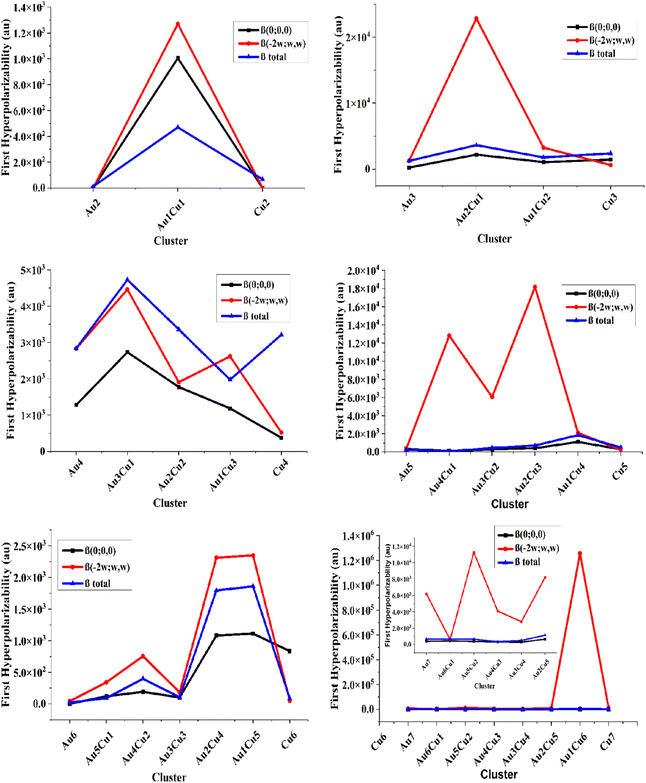
The first hyperpolarizabilities β(total) for the pure Au-clusters Au2, Au3, Au4, Au5, Au6, and Au7 were 1.15 × 101, 1.26 × 103, 2.84 × 103, 2.63 × 102, 1.94 × 101, and 6.60 × 102 au, respectively. The high first hyperpolarizabilities β(total) for the doped clusters Au1Cu6, Au4, Cu4, Au2Cu2, Au2Cu1, and Au3Cu1 were 2.68 × 103, 2.84 × 103, 3.21 × 103, 3.36 × 103, 3.64 × 103, and 4.73 × 103 au, respectively. The static second-order polarizabilities β(0;0,0) for the pure Au (2–7) clusters were in the range of 0–2.73 × 103 au. The highest static first hyperpolarizability for the doped clusters Au4, Cu3, Au1Cu6, Au2Cu2, Au2Cu1, and Au3Cu1 were 1.28 × 103, 1.43 × 103, 1.61 × 103, 1.78 × 103, 2.21 × 103 and 2.73 × 103 au, respectively.
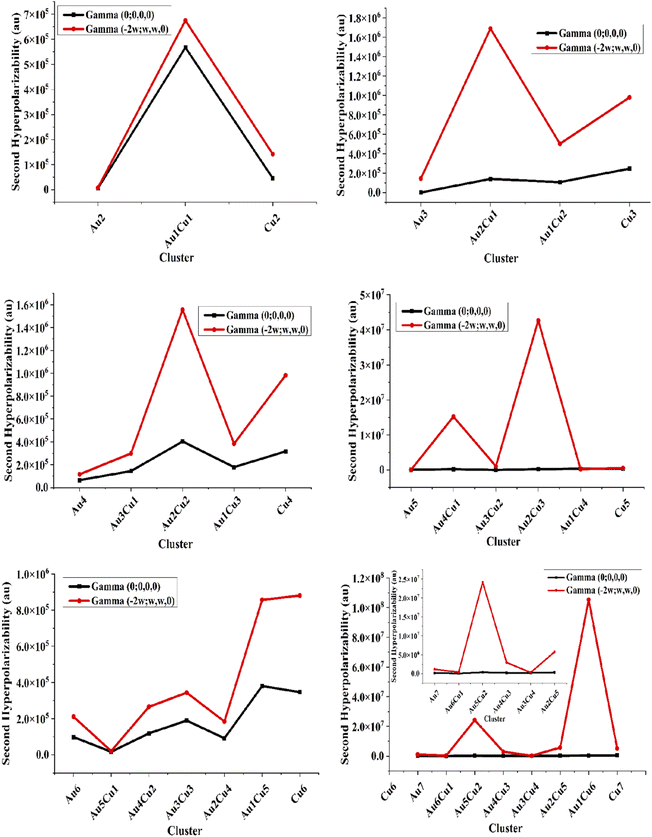
The frequency-dependent β(−2w;w,w) polarizabilities for the pure Aum (m = 2–7) clusters were in the range of 0–1.26 × 106 au. These showed that the frequency-dependent first hyperpolarizability β(−2w;w,w) was always higher than the static one. The first hyperpolarizability values of the pure Au and Cu clusters were very close to each other. While, the average frequency-dependent β(−2w;w,w) values were very high for the mixed Au–Cu clusters Au5Cu2, Au4Cu1, Cu7, Au2Cu3, Au2Cu1, and Au1Cu6 as 1.13 × 104, 1.28 × 104, 1.31 × 104, 1.82 × 104, 2.28 × 104, and 1.26 × 106, which were in accordance with the two-level model. These resulting values of the second hyperpolarizability for the doped clusters were higher than those of previously reported NLO materials, ranging from 2.55 × 104–3.63 × 104 au.42 For further investigation of the consistency of the different pure and Cu-doped Au-clusters, a graphical comparison was made for the first hyperpolarizability or second-order polarizability, as shown in Fig. 4.
The β values evaluated by the two-level model nicely correlated with the computed values of the static first hyperpolarizability. They increased with the increase in size of the clusters and thus followed a monotonic behavior. The doping of Cu resulted in the highest hyperpolarizability values in each cluster. It was observed that the frequency-dependent first hyperpolarizability β(−2w;w,w) was always higher than the static one and the pure Au-clusters showed the lowest values of the average first hyperpolarizability.
Comparing the pure Au and Cu-doped clusters, the β(0;0,0) for the pure cluster was always less than for the mixed Au–Cu clusters. Fascinatingly, the β(−2w;w,w) of the pure clusters was increased by doping with Cu atoms. For the 2A clusters, the value of the second-order polarizability for the pure Au and pure Cu clusters was less than for the mixed Au1–Cu1 clusters due to the large change in the electric dipole moment according to the two levels. The Au3Cu1 nonsymmetric structure showed notable values of hyperpolarizability, which signified their NLO behavior as compared to Cu2, Cu3, and Cu4 symmetric structures. The average first hyperpolarizability of clusters containing a single Au atom (Au1Cu4, Au1Cu5, and Au1Cu6) cluster was higher than the mixed doped clusters due to the deformation produced by doping, which enhances the dipole moment and changes the electronic structure of the clusters. The electronic dipole moment followed the same trend of variation as observed in the first and second hyperpolarizabilities.
Third-order NLO polarizability
To calculate the static and frequency-dependent second hyperpolarizability or third-order polarizability of the pure and Cu-doped gold clusters, DFT calculations at the CAM-B3LYP/LANL2DZ level were used, and the results for the average second hyperpolarizabilities are summarized in Table 2. The static third-order static polarizabilities γ(0;0,0) for pure Au-clusters Au2, Au3, Au4, Au5, Au6, and Au7 were 6.01 × 103, 1.42 × 103, 6.52 × 104, 8.67 × 104, 9.84 × 104, and 1.83 × 105 au, respectively. For the pure Cu (2–7) clusters, these were in the range of 4.56 × 104–6.30 × 105 au. The highest static second hyperpolarizabilities for the doped clusters Au2Cu2, Au1Cu6, Au1Cu1, and Cu7 were 4.04 × 105, 4.22 × 105, 5.67 × 105, and 6.30 × 105, respectively. The third-order frequency-dependent γ(−2w;w,w,0) polarizabilities for the pure gold clusters Au2, Au3, Au4, Au5, Au6, and Au7 were 8.03 × 103, 1.45 × 105, 1.16 × 105, 4.24 × 104, 2.10 × 105, and 1.15 × 106 au, respectively. The frequency-dependent γ(−2w;w,w,0) polarizabilities for the pure Cum (m = 2–7) clusters were in the range of 1.42 × 105–5.15 × 106 au. It was found that the second hyperpolarizability was much greater than the first hyperpolarizabilities and also that the frequency-dependent γ(−2w;w,w,0) polarizability was always higher than the static one. The average third-order frequency-dependent γ(−2w;w,w,0) polarizabilities were very high for the mixed Au–Cu doped Cu7, Au2Cu5, Au4Cu1, Au5Cu2, Au2Cu3, and Au1Cu6 clusters at 5.15 × 106, 5.67 × 106, 1.52 × 107, 2.42 × 107, 4.26 × 107, and 1.05 × 108 au, respectively. These computed first and second hyperpolarizabilities for the pure and Cu-doped gold clusters were larger than the already reported NLO materials, e.g., 51.99 × 104 to 138.25 × 104 au for superhalogen and superalkali doped phosphorenes,43 and 6.1 × 107 au for bimetallic superalkali clusters.44 To highlight the difference between the pure and Cu-doped Au-clusters, a graphical comparison was made for the third-order polarizability or second hyperpolarizability, as shown in Fig. 5.A graphical comparison between the static and frequency-dependent third-order polarizability is shown in Fig. 5. It was observed that the frequency-dependent second hyperpolarizability γ(−2w;w,w,0) was always higher than the static one. As we moved from Au2 to Au6 clusters, the second hyperpolarizability of the pure gold clusters was less than for the pure Cu clusters. Comparing between the Cu-doped clusters and pure clusters, the γ(0;0,0) of the pure clusters was less than for the mixed Au–Cu clusters. Interestingly, the γ(0;0,0) of the pure clusters was increased by doping with Cu atoms. For the Au2 clusters, the value of γ(0;0,0) and γ(−2w;w,w,0) for the Au1Cu1 cluster were higher than for the pure gold and copper clusters due to the change in the electronic structure. Also, it was found that the second hyperpolarizability for the symmetric structure was comparatively less than for the nonsymmetric structures, like the Au2 to Au7 clusters, where the second hyperpolarizability for the Au2Cu2, Au3Cu3, and Au4Cu4 symmetric structures was less than for the Au3Cu1 nonsymmetric structure. The γ(0;0,0) of clusters containing a single Au (Au1Cu4, Au1Cu5, Au1Cu6) cluster was higher than for the others with more than one Au-doped clusters due to the deformation produced by the doping, which enhanced the dipole moment. The Au4Cu2, Au5Cu1, and Au5Cu2 clusters showed very high γ(−2w;w,w,0) third-order polarizability due to their high dipole moment and complex structures. The excitation energy (ΔE in eV) and oscillator strength (fo) for all the doped and pure Au-clusters were also investigated. The excitation energies (ΔE) were 2.73, 1.23, 1.35, 1.26, 2.85, and 2.68 eV for the Au2, Au3, Au4, Au5, Au6, and Au7 pure Au-clusters, and decreased from 2.85–1.23 eV. These smaller values of ΔE for the doped complexes led to higher values of hyperpolarizability. The oscillator strength (fo) for the pure Au-cluster was 0 and it changed upon Cu-doping, whereby the values of fo were 0.0218, 0.0063, and 0.0030 for Au4Cu2, Au5Cu1, and Au5Cu2, respectively. All the calculated results for the excitation energy (ΔE) and oscillator strength (fo) were in accordance with the two-level model and related with their hyperpolarizability results. These computed first and second hyperpolarizabilities for the pure and Cu-doped gold clusters were much higher than those of the already reported NLO materials. Thus, the third-order NLO polarizability analysis showed that all the compounds in the present investigation are potential candidates for efficient third-order NLO applications.
Conclusions
The theoretical study of the current investigated Au–Cu clusters showed that the doping of Cu atoms did not largely affect the structural framework of the Au-clusters, while doping with Cu significantly enhanced the NLO properties of the clusters. A significant decrease in the HOMO–LUMO energy gap from 3.67 to 0.91 eV was observed, which was reduced by 74% by doping with Cu. Similarly, the optical properties, including the linear isotropic and anisotropic polarizabilities, increased by 4 to 5 times. Among all the structures, the Au3Cu1 and Au1Cu6 clusters showed the largest static β(total) = 4.73 × 103 au and frequency-dependent β (−2w; w, w) = 1.26 × 106 au first hyperpolarizabilities, respectively. The large static and frequency-dependent second hyperpolarizabilities of 6.30 × 105 au and 1.05 × 108 au were exhibited by Cu7 and Au1Cu6, respectively. Theoretically, it was shown that a single-doped system Aum (2 ≥ m ≤ 7) is a better choice to get a high NLO response as compared to other combinations. These computed values of the second and third-order polarizabilities are larger than some already reported clusters. This methodology can be extended to explore the NLO response of gold nanometallic structures having different shapes, such as stars, cage, rods, and core–shell.Author contributions
All authors contributed to the study conception and design. Materials designing, data collection and analysis were performed by F.·H, R. H, K. A, M. U. K. and J. Y. The initial draft was prepared by F.·H, R. H, Z. I and M. A. The final draft was edited by S. M, K. A and M. A. All authors read and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author from King Khalid University extends his appreciation to the Deanship of Scientific Research at King Khalid University for support through the research project (RGP.1/318/43). The authors also thankful for the computational facility support from the COMSAT University, Abbottabad, Pakistan.References
- Z. Chen, Q. Zhang, M. Zhu, H. Chen, X. Wang, S. Xiao, K. P. Loh, G. Eda, J. Meng and J. He, J. Phys. Chem. Lett., 2021, 12, 7010–7018 CrossRef CAS PubMed.
- S. R. Marder, J. E. Sohn and G. D. Stucky, Materials for nonlinear optics chemical perspectives, American Chemical Society Washington DC, 1991 Search PubMed.
- Z. S. Shanon and R. Sh, Int. J. Sci. Res., 2016, 1683 Search PubMed.
- P. Franken, A. E. Hill, C. e. Peters and G. Weinreich, Phys. Rev. Lett., 1961, 7, 118 CrossRef.
- T. Maiman, Optical and Microwave-Optical Experiments in Ruby, Phys. Rev. Lett., 1960, 4, 564 CrossRef.
- Y.-x. Zhang and Y.-h. Wang, RSC Adv., 2017, 7, 45129–45144 RSC.
- R.-L. Zhong, H.-L. Xu, Z.-R. Li and Z.-M. Su, J. Phys. Chem. Lett., 2015, 6, 612–619 CrossRef CAS.
- N. Hou, W.-M. Sun, F.-Y. Du and H.-S. Wu, Optik, 2019, 183, 455–462 CrossRef CAS.
- M. Böhm, J. Schulte and R. Schlögl, Phys. Status Solidi, 1996, 196, 131–144 CrossRef.
- M. Mutailipu, M. Zhang, B. Zhang, L. Wang, Z. Yang, X. Zhou and S. Pan, Angew. Chem., 2018, 130, 6203–6207 CrossRef.
- S. Sagadevan and M. Periasamy, Rev. Adv. Mater. Sci., 2014, 36, 62–69 CAS.
- X. Wang, Z. Li, J. Shi and Y. Yu, Chem. Rev, 2014, 114, 9346–9384 CrossRef CAS PubMed.
- S. B. Kolavekar, N. Ayachit, G. Jagannath, K. NagaKrishnakanth and S. V. Rao, Opt. Mater., 2018, 83, 34–42 CrossRef CAS.
- F.-K. Liu, J. Chromatogr. A, 2009, 1216, 9034–9047 CrossRef CAS PubMed.
- S. Muhammad, M. Nakano, A. G. Al-Sehemi, Y. Kitagawa, A. Irfan, A. R. Chaudhry, R. Kishi, S. Ito, K. Yoneda and K. Fukuda, Nanoscale, 2016, 8, 17998–18020 RSC.
- Z. Liu, S. Hua and G. Wu, J. Phys. Chem. C, 2018, 122, 21548–21556 CrossRef CAS.
- R. J. Durand, S. Gauthier, S. Achelle, S. Kahlal, J.-Y. Saillard, A. Barsella, L. Wojcik, N. Le Poul and F. Robin-Le Guen, Dalton Trans., 2017, 46, 3059–3069 RSC.
- H.-M. He, Y. Li, W.-M. Sun, J.-J. Wang, D. Wu, R.-L. Zhong, Z.-J. Zhou and Z.-R. Li, Dalton Trans., 2016, 45, 2656–2665 RSC.
- N. Kosar, T. Mahmood, K. Ayub, S. Tabassum, M. Arshad and M. A. Gilani, Opt. Laser Technol., 2019, 120, 105753 CrossRef CAS.
- W. M. Sun and D. Wu, Chem. - Eur. J., 2019, 25, 9568–9579 CrossRef CAS PubMed.
- M. Moskovits, Annu. Rev. Phys. Chem., 1991, 42, 465–499 CrossRef CAS.
- P. Schwerdtfeger, Angew. Chem., Int. Ed., 2003, 42, 1892–1895 CrossRef CAS PubMed.
- C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, Nature, 1996, 382, 607–609 CrossRef CAS.
- A. P. Alivisatos, K. P. Johnsson, X. Peng, T. E. Wilson, C. J. Loweth, M. P. Bruchez and P. G. Schultz, Nature, 1996, 382, 609–611 CrossRef CAS PubMed.
- A. Kokabi and M. Salehiyoun, J. Nanopart. Res., 2020, 22, 1–17 CrossRef.
- S. Knoppe, M. Vanbel, S. Van Cleuvenbergen, L. Vanpraet, T. Bürgi and T. Verbiest, J. Phys. Chem. C, 2015, 119, 6221–6226 CrossRef CAS.
- S. Knoppe, Q.-F. Zhang, X.-K. Wan, Q.-M. Wang, L.-S. Wang and T. Verbiest, Ind. Eng. Chem. Res., 2016, 55, 10500–10506 CrossRef CAS.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussian 16 (Revision A), Gaussian Inc., Pittsburgh, PA., 2016 Search PubMed.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView 6.0, 16., Semichem Inc., Shawnee Mission, KS, USA, 2016 Search PubMed.
- H. Paulsen, L. Duelund, H. Winkler, H. Toftlund and A. X. Trautwein, Inorg. Chem., 2001, 40, 2201–2203 CrossRef CAS PubMed.
- J. Iqbal and K. Ayub, J. Alloys Compd., 2016, 687, 976–983 CrossRef.
- L. Wang, W.-Y. Wang, Y.-Q. Qiu and H.-Z. Lu, J. Phys. Chem. C, 2015, 119, 24965–24975 CrossRef CAS.
- S. Muhammad, H. Xu, Z. Su, K. Fukuda, R. Kishi, Y. Shigeta and M. Nakano, Dalton Trans., 2013, 42, 15053–15062 RSC.
- S. Muhammad, R. A. Shehzad, J. Iqbal, A. G. Al-Sehemi, M. Saravanabhavan and M. Khalid, J. Theor. Comput. Chem., 2019, 18, 1950030 CrossRef CAS.
- T. Murakami, T. Nayak, W. Lynch, K. Swartz, Z. Chen, D. Fields, C. Gelbke, Y. Kim, M. Maier and J. Pochodzalla, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 1989, 275, 112–122 Search PubMed.
- A. Farhat, R. A. Khera, S. Iqbal and J. Iqbal, Opt. Mater., 2020, 107, 110154 CrossRef CAS.
- G. Zanti and D. Peeters, in Theoretical Chemistry in Belgium, Springer, 2014, pp. 261–275 Search PubMed.
- E. Wirnhier, M. Döblinger, D. Gunzelmann, J. Senker, B. V. Lotsch and W. Schnick, Chem. - Eur. J., 2011, 17, 3213–3221 CrossRef CAS PubMed.
- J.-L. Oudar and D. Chemla, J. Chem. Phys., 1977, 66, 2664–2668 CrossRef CAS.
- A. Datta and S. K. Pati, Chem. Soc. Rev., 2006, 35, 1305–1323 RSC.
- J. d. Oudar, J. Chem. Phys., 1977, 67, 446–457 CrossRef CAS.
- P. Khan, T. Mahmood, K. Ayub, S. Tabassum and M. A. Gilani, Opt. Laser Technol., 2021, 142, 107231 CrossRef CAS.
- R. Kiran, R. A. Khera, A. U. Khan, A. Ayoub, N. Iqbal, K. Ayub and J. Iqbal, J. Mol. Struct., 2021, 1236, 130348 CrossRef CAS.
- A. Ahsin and K. Ayub, J. Nanostruct. Chem., 2021, 1–17 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra03664a |
| This journal is © The Royal Society of Chemistry 2022 |