 Open Access Article
Open Access ArticleEcotoxicological prediction of organic chemicals toward Pseudokirchneriella subcapitata by Monte Carlo approach†
Shahram Lotfi *a,
Shahin Ahmadi
*a,
Shahin Ahmadi *b and
Parvin Kumar
*b and
Parvin Kumar c
c
aDepartment of Chemistry, Payame Noor University (PNU), 19395-4697 Tehran, Iran
bDepartment of Pharmaceutical Chemistry, Faculty of Pharmaceutical Chemistry, Tehran Medical Sciences, Islamic Azad University, Tehran, Iran. E-mail: Sh.lotfi@pnu.ac.ir
cDepartment of Chemistry, Kurukshetra University, Kurukshetra, Haryana 136119, India
First published on 1st September 2022
Abstract
In the ecotoxicological risk assessment, acute toxicity is one of the most significant criteria. Green alga Pseudokirchneriella subcapitata has been used for ecotoxicological studies to assess the toxicity of different toxic chemicals in freshwater. Quantitative Structure Activity Relationships (QSAR) are mathematical models to relate chemical structure and activity/physicochemical properties of chemicals quantitatively. Herein, Quantitative Structure Toxicity Relationship (QSTR) modeling is applied to assess the toxicity of a data set of 334 different chemicals on Pseudokirchneriella subcapitata, in terms of EC10 and EC50 values. The QSTR models are established using CORAL software by utilizing the target function (TF2) with the index of ideality of correlation (IIC). A hybrid optimal descriptor computed from SMILES and molecular hydrogen-suppressed graphs (HSG) is employed to construct QSTR models. The results of various statistical parameters of the QSTR model developed for pEC10 and pEC50 range from excellent to good and are in line with the standard parameters. The models prepared with IIC for Split 3 are chosen as the best model for both endpoints (pEC10 and pEC50). The numerical value of the determination coefficient of the validation set of split 3 for the endpoint pEC10 is 0.7849 and for the endpoint pEC50, it is 0.8150. The structural fractions accountable for the toxicity of chemicals are also extracted. The hydrophilic attributes like 1…n…(… and S…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) … exert positive contributions to controlling the aquatic toxicity and reducing algal toxicity, whereas attributes such as c…c…c…, C…C…C… enhance lipophilicity of the molecules and consequently enhance algal toxicity.
… exert positive contributions to controlling the aquatic toxicity and reducing algal toxicity, whereas attributes such as c…c…c…, C…C…C… enhance lipophilicity of the molecules and consequently enhance algal toxicity.
1. Introduction
The organic chemicals released into the environment by factories can be potentially toxic pollutants of the environment. Contamination of aquatic ecosystems with organic chemicals is a serious concern because these can affect multiple levels of biological organization, from the molecular to the ecosystem level. The goal of all global communities is to achieve the management of chemicals and hazardous wastes that minimizes notable harmful effects on human health and the environment. The eco-toxicities of chemicals at different endpoints are measured according to the test guidelines of the OECD (Organization for Economic Co-operation and Development) and are utilized for regulative purposes.1 Pseudokirchneriella subcapitata (P. subcapitata) is a microalga and it is frequently employed as a bioindicator species in freshwater habitats to measure nutrient or hazardous chemical levels. The OECD and US-EPA (United States Environmental Protection Agency) recommend P. subcapitata for ecotoxicological bioassays since this microalga exhibit faster growth rates and better susceptibility to diverse toxins than other algae.1–4 In the ecological risk assessment, the most commonly used measurement to summarize ecotoxicological effects is the ECx (effective concentration) where x can be 5–100.5,6However, the toxicological in vivo studies of all potential chemicals are practically impossible because these bioassays are expensive and time-consuming. Therefore, replacement approaches based on computational techniques are needed to mitigate these difficulties. In this regard, the Quantitative structure–activity/toxicity relationship (QSAR/QSTR), a significant computational technique, has been suggested to estimate the statistical relationship between the toxicity of a group of compounds with their molecular structure.7–10 A set of mathematical equations that equate the chemical structure to biological activity are designated as QSTR/QSAR models.
CORAL (CORrelation And Logic) software has been recommended for the construction of QSAR/QSTR models for various endpoints employing the inbuilt Monte Carlo algorithm.11–18 In the CORAL software, SMILES (Simplified Molecular Input Line Entry System) notations of the compound structures are employed as input to determine the descriptor of correlation weight (DCW). The DCW depends on the compound structure and the property under analysis but does not depend on the 3D geometry of the molecule. However, the QSAR/QSTR models of the CORAL software can be developed from three types of descriptors: SMILES-based, graph-based, and hybrid descriptors (a combination of SMILES and graphs). The models constructed based on the hybrid descriptors are statistically better than the models constructed by individually SMILES or graph descriptors.19–21
The index of ideality of correlation (IIC) has been implemented by the theoretical chemist to validate and improve the predictive potential constructed QSAR/QSTR models.14,22–25 The IIC is a parameter for assessing the predictive capability of QSPR/QSAR models that takes into account not only the coefficient of correlation, but also the organization of the group of dots images relative to the diagonal, in “observed-calculated” endpoint coordinates.26–28
The aim of the present work is to develop reliable QSTR models with the use of IIC to compute pEC10 and pEC50 of organic pollutants against P. subcapitata. A hybrid optimal descriptor is employed to design QSTR models for 334 diverse organic chemicals including pharmaceuticals, agrochemicals and personal care products using the Monte Carlo approach. Four random splits are implemented to assess the reliability and accuracy of the designed QSTR models.
2. Method
2.1. Data
In the present QSTR model development study, the prediction of effective concentration for 10% inhibition (EC10) and half-maximal effective concentration (EC50) was described for 334 diverse organic chemicals. Only those numerical values of EC10 and EC50 were taken into account for model development, which was calculated at the uniform exposure interval of 24 hours (EC10-24 h and EC50-24 h). The experimental acute toxicity of organic pollutants against P. subcapitata was taken from the article published by K. Khan & K. Roy.29 The functional group amines, esters, halohydrocarbons, aldehydes, isothiocyanates, organic acids, alcohols (or phenols), ketones, etc. were present in the dataset. The pEC10 (mol L−1) and pEC50 (mol L−1) of organic compounds against P. subcapitata were utilized as two separate endpoints. The range of pEC10 was from 0.54 to 9.3 mol L−1 whereas the range of pEC50 was from 0.3 to 9.1 mol L−1.30The BIOVIA Draw 2019 tool was used to sketch the molecular structures of all 334 organic chemicals and the SMILES notations. Three splits were made for the above-mentioned organic chemicals (n = 334) and each split was unselectively split into the training (≈35%), invisible training (≈25%), calibration (≈16%), and validation (≈25%) set.
The responsibility of each set was fixed and these were: (i) the active training set provided the information on which the model was built (correlation weights are calculated); (ii) the passive training set gave the information to check how well the correlation weights fitted for the molecular structures of the active set which were suitable for the structures not present in the active training set (“model quality inspector”); (iii) the calibration set should catch the moment when, despite the increase in the statistical quality of the model for the active and passive sets, the statistical quality for the calibration set begins to fall. In fact, this is the moment of the start of overtraining. (iv) The validation set was applied for the final assessment of the statistical quality of the model.
Table S1† represents the list of compounds IDs and SMILES code, as well as the corresponding experimental and estimated pEC50 and pEC10 values of chemicals.
2.2. Hybrid optimal descriptor
Herein, for designing the QSTR model of pEC10 and pEC50, the hybrid optimal descriptor was implemented and it was computed by the combination of molecular features extracted from SMILES and hydrogen suppressed molecular graph (HSG). In terms of statistical quality, the literature survey revealed that better models were generated by hybrid descriptors than the descriptors based only on SMILES or molecular graphs.31 The inbuilt Monte Carlo algorithm CORAL tool was employed to calculate the hybrid descriptors of correlation weights (DCW).According to the OECD second principle, the algorithm used at each start performs the same sequence of actions. However, since the algorithm performs a stochastic process of processing the presented (input) information, the numerical values of the model quality criteria used are not identical. But, in the case of comparing the results of several such processes (for example, with different partitions into training and testing sets), reproducible means and variances will be obtained for the statistical characteristics (correlation coefficient and RMSE).
The QSTR model to predict pEC10 and pEC50 of organic chemicals is computed using the following mathematical relationship:
| pEC10 or pEC50 = C0 + C1 × HybridDCW(T*, N*) | (1) |
| HybridDCW(T*, N*) = SMILESDCW(T, N*) + GraphDCW(T*, N*) | (2) |
| SMILESDCW(T*, N*) = ∑CW(SSSK) + CW(BOND) + CW(NOSP) + CW(PAIR) + CW(HARD) | (3) |
| GraphDCW(T*, N*) = ∑CW(e1k) + ∑CW(pt4k) + ∑CW(nnk) + ∑W(C5) + ∑(C6) | (4) |
In eqn (3) the code SSSk is the local SMILES attributes described as a combination of three SMILES-atoms; NOSP is global SMILES features and it denotes the absence or presence of N (nitrogen), O (oxygen), S (sulfur), and P (phosphorus); BOND displays the presence or absence of double (‘![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ’), triple (‘#’) and stereochemical (‘@’ or ‘@@)’ bonds; PAIR illustrates the combination of BOND and NOSP; HARD imply the existence or absence of NOSP, HALO (halogens), and BOND in the molecular structure.
’), triple (‘#’) and stereochemical (‘@’ or ‘@@)’ bonds; PAIR illustrates the combination of BOND and NOSP; HARD imply the existence or absence of NOSP, HALO (halogens), and BOND in the molecular structure.
In eqn (4), e1k, pt4k, and nnk are local graph attributes. The e1k is Morgan extended connectivity of first order; pt4k is the number of paths of length 4 beginning from a given vertex in HSG; nnk is the nearest neighbours code; C5 and C6 display the role of five- and six-member rings, respectively.
In CORAL software, two kinds of target functions (TF1 and TF2) can be applied to build the QSTR model with the Monte Carlo optimization. The balance of the correlation method was used to compute TF1 whereas the IIC was added to the TF1 to attain the modified target function TF2.32
| TF1 = RTRN + RITRN − |RTRN − RITRN| × 0.1 | (5) |
| TF2 = TF1 + IICCAL × C | (6) |
The IICCAL for the calibration (CAL) set is computed utilizing the following equation:
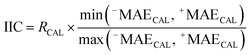 | (7) |
RCAL is the correlation coefficient between observed values and calculated values of pEC10 or pEC50 for the calibration set. The negative and positive mean absolute errors are indicated with −MAE and +MAE, which are computed by the subsequent equations:
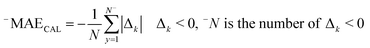 | (8) |
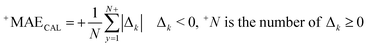 | (9) |
| Δk = Observedk − Calculatedk | (10) |
The ‘k’ is the index (1, 2, … N) and the observedk and calculatedk are related to the endpoint.
2.3. Applicability domain
According to the third principle of the OECD,33,34 a QSAR model should have a well-defined applicability domain (AD).The domain of applicability for the model obtained as a result of stochastic Monte Carlo optimization varies depending on the split into training and validation sets. The applicability domain is determined according to the prevalence of molecular features extracted from SMILES (e.g. nitrogen ‘N’, oxygen ‘O’, double bonds ‘![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ’, etc.) in the active training set. Thus, for several splits into training and validation sets, the domain of applicability may change, but not significantly. The corresponding calculations give only a qualitative picture in terms such as “this compound is suspicious, because its constituent molecular features are poorly represented in the active training set.” In CORAL software, AD is defined using the following relationship30
’, etc.) in the active training set. Thus, for several splits into training and validation sets, the domain of applicability may change, but not significantly. The corresponding calculations give only a qualitative picture in terms such as “this compound is suspicious, because its constituent molecular features are poorly represented in the active training set.” In CORAL software, AD is defined using the following relationship30
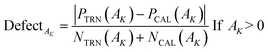 | (11) |
| DefectAK = 1 If AK = 0 |
PTRN(AK) and PTCAL(AK) are the probability of an attribute ‘AK’ in the training and the calibration sets; and are the number of times or frequency of ‘AK’ in the training and calibration sets, respectively.
The statistical defect can be defined as the sum of statistical defects of all attributes present in the SMILES notation.
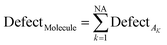 | (12) |
NA is the number of active SMILES attributes for the given compounds.
In CORAL, a substance is an outlier if inequality 13 is fulfilled:
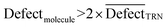 | (13) |
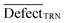 is an average of statistical defects for the dataset of the training set.
is an average of statistical defects for the dataset of the training set.
3. Results and discussion
3.1. QSAR modeling for pEC10 and pEC50
In order to build up the trustworthy QSAR model(s), the T* (optimal threshold) and the N* (number of epochs) for the calibration set was calculated by analyzing the best statistical characteristics. The optimum value of T* for models of pEC10 and pEC50 was 1 and N* was 10 for all splits. All QSTR models for pEC10 and pEC50 of organic compounds against P. subcapitata were constructed using the target function TF2 (WIIC = 0.2).The QSTR models obtained by the Monte Carlo optimization for both endpoints are the represented by the following relationship:
pEC10 model
| Split 1 pEC10 = 1.6154476 (±0.0136475) + 0.1917901 (±0.0006197) × DCW(1,10) | (14) |
| Split 2 pEC10 = 2.0134704 (±0.0124620) + 0.1346531 (±0.0005317) × DCW(1,10) | (15) |
| Split 3 pEC10 = 0.3932798 (±0.0145016) + 0.2487573 (±0.0007835) × DCW(1,10) | (16) |
pEC50 model
| Split 1 pEC50 = 1.2841679 (±0.0150488) + 0.1617599 (±0.0007597) × DCW(1,10) | (17) |
| Split 2 pEC50 = 1.2939204 (±0.0113965) + 0.1531264 (±0.0005331) × DCW(1,10) | (18) |
| Split 3 pEC50 = 1.1720502 (±0.0122202) + 0.1507783 (±0.0005351) × DCW(1,10) | (19) |
3.4. Model validation
Validation of the developed models is important in evaluating the reliability and robustness of the QSTR models. Validation of the model can be examined using the: (i) cross-validation (Q2) or internal validation (R2). The predictive ability of the QSTR model is acceptable if the numerical value of Q2 and R2 is greater than 0.7;35 (ii) external validation, CCC (concordance correlation coefficient), Q2F1, Q2F2, Q2F3, s (standard error of estimation), RMSE (root-mean-square error), MAE (mean absolute error), F (Fischer ratio), and metrics (R2m and MAE based metric). In terms of external validation, the model has good predictability if CCC is greater than 0.85.36 Also, if r2m values >0.5 and Δr2m < 0.2, the model can be interpreted as a reliable model; (iii) Y-scrambling or data randomization.Herein all these methods had been used for model validation. The IIC criterion was applied as a final statistical parameter to validate the developed QSTR models. The statistical characteristics calculated with eqn (14)–(19) are provided in Table 1. The mathematical equations of the applied statistical criteria are very well explained in the literature.32,37 All designed QSAR models were statistically reliable and the numerical values of statistical quantities were found in acceptable ranges as reported in the literature.33,34
| Split | Set | n | R2 | CCC | IIC | Q2 | QF12 | QF22 | QF32 | Rm2 | CRp2 | ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) m2 m2 |
Δrm2 | S | MAE | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pEC10 | ||||||||||||||||
| 1 | Training | 118 | 0.8550 | 0.9218 | 0.8072 | 0.8504 | 0.8522 | 0.651 | 0.496 | 684 | ||||||
| Invisible training | 79 | 0.8609 | 0.8856 | 0.5277 | 0.8535 | 0.8556 | 0.742 | 0.576 | 476 | |||||||
| Calibration | 54 | 0.7186 | 0.8349 | 0.8389 | 0.6883 | 0.7282 | 0.7045 | 0.8212 | 0.7154 | 0.7111 | 0.6049 | 0.1210 | 0.725 | 0.592 | 133 | |
| Validation | 83 | 0.7246 | 0.8435 | 0.6846 | 0.7149 | 0.7246 | 0.6174 | 0.143 | 0.8339 | 6291 | ||||||
| 2 | Training | 115 | 0.8855 | 0.9393 | 0.8932 | 0.8804 | 0.8793 | 0.533 | 0.408 | 874 | ||||||
| Invisible training | 73 | 0.8868 | 0.9022 | 0.4317 | 0.8802 | 0.8823 | 0.706 | 0.553 | 553 | |||||||
| Calibration | 63 | 0.8487 | 0.9146 | 0.9210 | 0.8391 | 0.8466 | 0.8460 | 0.8362 | 0.8160 | 0.8388 | 0.7468 | 0.1385 | 0.657 | 0.513 | 342 | |
| Validation | 83 | 0.7643 | 0.8716 | 0.7643 | 0.7731 | 0.7575 | 0.6965 | 0.1219 | 0.8779 | 0.7052 | ||||||
| 3 | Training | 113 | 0.8866 | 0.9399 | 0.7473 | 0.8826 | 0.8796 | 0.545 | 0.426 | 867 | ||||||
| Invisible training | 79 | 0.8775 | 0.9194 | 0.5672 | 0.8722 | 0.8742 | 0.691 | 0.517 | 551 | |||||||
| Calibration | 59 | 0.8106 | 0.8985 | 0.8632 | 0.7970 | 0.8002 | 0.7987 | 0.8465 | 0.7260 | 0.8049 | 0.7336 | 0.0152 | 0.679 | 0.537 | 244 | |
| Validation | 83 | 0.7892 | 0.8648 | 0.8831 | 0.7776 | 0.7612 | 0.6061 | 0.1010 | 0.6765 | 0.5691 | ||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||||||
| pEC50 | ||||||||||||||||
| 1 | Training | 114 | 0.8401 | 0.9131 | 0.7161 | 0.8331 | 0.8335 | 0.683 | 0.537 | 588 | ||||||
| Invisible training | 82 | 0.8395 | 0.9006 | 0.7660 | 0.8311 | 0.8278 | 0.733 | 0.587 | 418 | |||||||
| Calibration | 52 | 0.7915 | 0.8717 | 0.8839 | 0.7771 | 0.7853 | 0.7851 | 0.8433 | 0.7479 | 0.7792 | 0.6529 | 0.1900 | 0.681 | 0.533 | 190 | |
| Validation | 85 | 0.7924 | 0.8297 | 0.7490 | 0.7774 | 0.6276 | 0.5802 | 0.0949 | 0.7716 | 0.6247 | ||||||
| 2 | Training | 116 | 0.8341 | 0.9096 | 0.9133 | 0.8289 | 0.8297 | 0.655 | 0.517 | 573 | ||||||
| Invisible training | 76 | 0.8704 | 0.9186 | 0.8496 | 0.8626 | 0.8634 | 0.671 | 0.529 | 497 | |||||||
| Calibration | 59 | 0.7802 | 0.8795 | 0.8808 | 0.7623 | 0.7622 | 0.7435 | 0.7914 | 0.6309 | 0.7679 | 0.6918 | 0.1218 | 0.774 | 0.596 | 202 | |
| Validation | 83 | 0.7366 | 0.8517 | 0.8494 | 0.7231 | 0.5993 | 0.6371 | 0.0756 | 0.7696 | 0.6055 | ||||||
| 3 | Training | 116 | 0.8665 | 0.9285 | 0.7831 | 0.8617 | 0.8568 | 0.617 | 0.461 | 740 | ||||||
| Invisible training | 79 | 0.9130 | 0.9350 | 0.9123 | 0.9088 | 0.9065 | 0.512 | 0.409 | 808 | |||||||
| Calibration | 56 | 0.7270 | 0.8484 | 0.8525 | 0.7031 | 0.6898 | 0.6860 | 0.7888 | 0.5823 | 0.7205 | 0.6237 | 0.0829 | 0.756 | 0.606 | 144 | |
| Validation | 83 | 0.8150 | 0.9020 | 0.8320 | 0.8065 | 0.7743 | 0.7402 | 0.0683 | 0.7245 | 0.6110 | ||||||
In QSTR modelling of pEC10, the numerical values of R2Validation and Q2Validation were in the range of 0.7246–0.7849 and 0.7149–0.7776, respectively. Whereas, in the QSAR modelling of pEC50, the numerical values of R2Validation and Q2Validation were in the range of 0.7366–0.8150 and 0.7231–0.8065, respectively. The most reliable model was presented by Split 3 for pEC10 as the statistical result of the determination coefficient was the highest. The numerical values of various parameters for the validation set of split 3 were R2 = 0.7849, Q2 = 0.7776, CCC = 0.8648, r2m = 0.7612 and Δr2m = 0.1010 (Table 1). Similarly, for endpoint pEC50, the model developed for split 3 was assigned as a prominent model. The statistical results for benchmarks for the validation set were R2 = 0.8150; Q2 = 0.8065; CCC = 0.9020; r2m = 0.7743 and Δr2m = 0.0683. Thus, these statistical results confirmed that the models constructed were acceptable in terms of statistics. Fig. 1 shows the plots of experimental pEC10/pEC50 versus predicted pEC10/pEC50 for all splits and it displays that the predicted pEC10/pEC50 have a good correlation with its experimental data. Also, Fig. 1 indicates the uniform data distribution of pEC10/pEC50 for training, invisible training, calibration and validation sets across all runs. The plots of residual pEC10/pEC50 versus predicted pEC10/pEC50 for all QSTR models are represented in Fig. 2. Residual scattering of pEC10 and pEC50 was found near the horizontal line centred around zero, implying that all constructed QSTR models were well fitted. The Kolmogorov–Smirnov test for normality (at the 95% confidence level) was done by SPSS version 26. It confirmed a normal distribution of residuals for all proposed models for pIC10 and pIC50 (Table S2†).
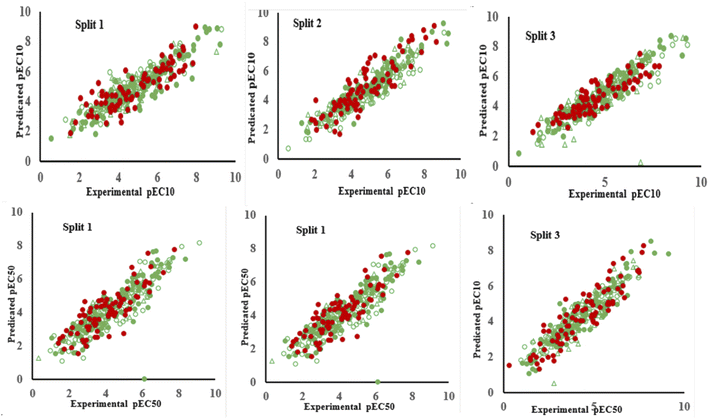 | ||
| Fig. 1 Graphical display of QSTR models for pEC10 and pEC50 of organic compounds obtained for three splits. | ||
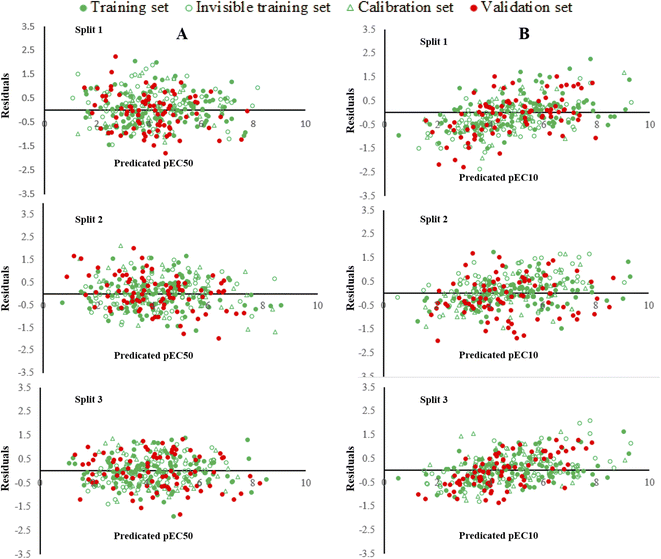 | ||
| Fig. 2 A graphical presentation of residual pEC10 versus predicted pEC10 (A) and residual pEC50 versus predicted pEC50 (B) for all constructed QSTR models. | ||
3.5. Mechanistic interpretation
“Mechanistic interpretation if possible” is the 5th principle of OECD. The objective of mechanistic interpretation is to explore a mechanistic relationship between the descriptors employed in a model and the endpoint being predicted.Monte Carlo optimization may be used numerous times to get a mechanistic explanation for CORAL models. If a molecular characteristic has acquired a positive correlation weight in all runs, its existence is likely to promote an increase in endpoint magnitude. If a molecular characteristic has a negative correlation weight in all of the preceding runs, its existence is more likely to decrease the intensity of the endpoint. The relevance of the molecular characteristic is unclear if the weights alternate (some positive, some negative). It is also necessary to consider the frequencies of molecular characteristics in the training and control sets.
In the present research, the structural attributes (SAk) extracted from SMILES and HSG attributes were employed to explore a relationship between the DCW and pEC10 or pEC50.
The SAk extracted from at last three or more independent runs of the Monte Carlo optimization were chosen for mechanistic interpretation. The SAk having the positive or negative CW values in all runs were kept in the category of a promoter of increase or decrease endpoint (pEC10 or pEC50). Table 2 illustrates the list of structural attributes of pEC10 and pEC50 with their CWs for three independent runs.
| Endpoint | SAk | Split | CWs run 1 | CWs run 2 | CWs run 3 | N1 | N2 | N3 | Defect | Comments |
|---|---|---|---|---|---|---|---|---|---|---|
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Promoter of increase | ||||||||||
| pEC10 | C5……0… | 1 | 0.0518 | 0.65382 | 0.39759 | 113 | 73 | 54 | 0.0003 | Absence of five-member rings |
| 2 | 0.65986 | 1.29285 | 0.5346 | 108 | 67 | 62 | 0.0003 | |||
| 3 | 1.07757 | 1.25744 | 0.48657 | 107 | 78 | 56 | 0 | |||
| c…c…c… | 1 | 0.60173 | 0.70843 | 0.06133 | 57 | 23 | 24 | 0.0005 | Presence of three consecutive aromatic carbons | |
| 2 | 0.05675 | 0.25722 | 0.44496 | 50 | 27 | 30 | 0.0005 | |||
| 3 | 0.12996 | 0.47028 | 0.75404 | 49 | 32 | 26 | 0.0001 | |||
| c…(…c… | 1 | 0.70809 | 0.0575 | 1.34021 | 56 | 22 | 25 | 0.0001 | Presence of two aromatic carbon with branching | |
| 2 | 0.38614 | 0.33907 | 0.1424 | 42 | 29 | 26 | 0.0007 | |||
| 3 | 0.11744 | 0.51584 | 1.00395 | 44 | 37 | 22 | 0.0002 | |||
| C…C…C… | 1 | 0.5463 | 1.04019 | 0.43998 | 27 | 22 | 18 | 0.0023 | Presence of three consecutive aliphatic carbons | |
| 2 | 1.06593 | 1.00475 | 0.65444 | 33 | 13 | 20 | 0.0006 | |||
| 3 | 0.6226 | 0.74328 | 0.93265 | 27 | 24 | 14 | 0 | |||
| N…(…C… | 1 | 0.40394 | 0.48781 | 1.00039 | 23 | 19 | 13 | 0.0013 | Presence of aliphatic nitrogen and aliphatic carbon with branching | |
| 2 | 1.07368 | 0.89617 | 0.01453 | 22 | 11 | 15 | 0.0013 | |||
| 3 | 0.3214 | 0.5839 | 0.59097 | 21 | 23 | 12 | 0.0005 | |||
| C…(…C… | 1 | 0.44453 | 0.59506 | 1.29729 | 43 | 45 | 31 | 0.0028 | Presence of two aliphatic carbon with branching | |
| 2 | 0.30408 | 0.72512 | 0.53272 | 55 | 36 | 29 | 0.0002 | |||
| 3 | 0.07648 | 0.49085 | 0.56336 | 52 | 40 | 31 | 0.0008 | |||
| Promoter of decrease | ||||||||||
| c…n…c… | 1 | −0.0287 | −0.44782 | −1.06545 | 3 | 5 | 2 | 0.0023 | Presence of aromatic nitrogen between two aromatic carbon | |
| 2 | −1.23621 | −0.75303 | −0.19895 | 4 | 3 | 2 | 0.0005 | |||
| 3 | −1.56359 | −1.69078 | −0.99982 | 4 | 2 | 2 | 0.0002 | |||
| S…(…C… | 1 | −0.49469 | −2.01565 | −0.11843 | 3 | 2 | 2 | 0.0023 | Presence of sulphur with branching with carbon | |
++++S⋯B2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
2 | −0.56135 | −0.0549 | −0.38003 | 13 | 9 | 7 | 0.0001 | Presence of sulphur with a double bond | |
S…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) … … |
3 | −1.33917 | −1.08063 | −1.01206 | 4 | 7 | 3 | 0.0022 | Presence of sulphur with branching and double bond | |
++++Cl⋯S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
1 | −0.57654 | −0.35935 | −0.62229 | 3 | 1 | 1 | 0.0017 | Presence of chlorine with sulphur | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Promoter of increase | ||||||||||
| pEC50 | C5……0… | 1 | 0.21385 | 0.49259 | 2.08764 | 111 | 77 | 46 | 0.0006 | Absence of five-member rings |
| 2 | 2.21049 | 0.704 | 1.70235 | 110 | 74 | 56 | 0 | |||
| 3 | 1.43226 | 1.5737 | 2.15936 | 110 | 75 | 54 | 0.0001 | |||
| C…(…C… | 1 | 0.25343 | 0.18014 | 0.42824 | 58 | 36 | 27 | 0.0001 | Presence of two aliphatic carbon with branching | |
| 2 | 1.24886 | 0.47209 | 1.01774 | 60 | 35 | 28 | 0.0005 | |||
| 3 | 1.25593 | 0.18762 | 1.24105 | 59 | 34 | 23 | 0.0012 | |||
| c…c…c… | 1 | 0.30441 | 0.73197 | 0.19607 | 47 | 38 | 17 | 0.0013 | Presence of three consecutive aromatic carbons | |
| 2 | 0.42912 | 0.29232 | 0.60473 | 46 | 31 | 27 | 0.0008 | |||
| 3 | 1.09812 | 0.29491 | 0.08848 | 45 | 36 | 24 | 0.0006 | |||
| C6…A…1… | 1 | 1.2658 | 0.05442 | 0.26358 | 38 | 21 | 15 | 0.0008 | Presence of one six-member aromatic ring | |
| 2 | 0.40875 | 0.26677 | 0.20824 | 32 | 22 | 21 | 0.0015 | |||
| 3 | 0.89128 | 1.05867 | 0.39511 | 30 | 28 | 21 | 0.0023 | |||
| C…C…C… | 1 | 0.91697 | 0.94405 | 0.63035 | 32 | 21 | 14 | 0.0002 | Presence of three consecutive aliphatic carbons | |
| 2 | 1.21722 | 1.07992 | 1.33949 | 29 | 24 | 16 | 0.0005 | |||
| 3 | 1.08398 | 1.16517 | 0.89018 | 29 | 17 | 15 | 0.0004 | |||
| Promoter of decrease | ||||||||||
| 1…n…(… | 1 | −0.82145 | −1.58394 | −0.45675 | 7 | 6 | 3 | 0.0004 | Presence of aromatic nitrogen on the first ring with branching | |
| 2 | −0.84679 | −1.04423 | −0.83943 | 6 | 3 | 4 | 0.0016 | |||
| 3 | −0.94912 | −0.6517 | −0.22174 | 6 | 5 | 1 | 0.0048 | |||
S…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) … … |
2 | −0.75816 | −0.71358 | −1.06783 | 8 | 3 | 2 | 0.0035 | Presence of sulphur with branching and double bond | |
++++O⋯S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
3 | −0.84696 | −0.5927 | −0.1503 | 14 | 2 | 5 | 0.0017 | Presence of oxygen with sulphur | |
| […–…Cl… | 2 | −0.95022 | −0.29786 | −0.57338 | 4 | 2 | 2 | 0.0001 | Presence of chloride ion | |
| 3 | −0.92707 | −0.72223 | −0.89901 | 5 | 3 | 0 | 1 | |||
Based on the results summarized in Table 2, the promoters of pEC10 increase were: C5…0…, c…c…c…, c…(…c…, C…C…C…, N…(…C…, C…(…C… and the promoters of pEC50 increase were: C5…0…, C…(…C…, c…c…c…, C6…A…1…, C…C…C…. On the other hand, the promoters of pEC10 decrease were: c…n…c…, S…(…C…, ++++S⋯B2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) , S…(…
, S…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …, and ++++Cl⋯S
…, and ++++Cl⋯S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ; whereas promoters of pEC50 decrease were: 1…n…(…, S…(…
; whereas promoters of pEC50 decrease were: 1…n…(…, S…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …, […–…Cl…, and++++O⋯S
…, […–…Cl…, and++++O⋯S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) . The results of mechanistic interpretation are illustrated in Fig. 3. Hence, The hydrophilic attributes like 1…n…(… and S…(…
. The results of mechanistic interpretation are illustrated in Fig. 3. Hence, The hydrophilic attributes like 1…n…(… and S…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) … exert positive contributions to controlling the aquatic toxicity and reducing algal toxicity, whereas attributes such as c…c…c…, C…C…C… enhance lipophilicity of the molecules and consequently enhance algal toxicity (see Fig. 3). The hydrophilic attributes like 1…n…(… and S…(…
… exert positive contributions to controlling the aquatic toxicity and reducing algal toxicity, whereas attributes such as c…c…c…, C…C…C… enhance lipophilicity of the molecules and consequently enhance algal toxicity (see Fig. 3). The hydrophilic attributes like 1…n…(… and S…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) … attributes and lipophilic attributes such as c…c…c…, C…C…C… influences the bioavailability of organic compounds and regulates their passage across biological membranes. A chemical with a greater lipophilicity may be more hazardous.
… attributes and lipophilic attributes such as c…c…c…, C…C…C… influences the bioavailability of organic compounds and regulates their passage across biological membranes. A chemical with a greater lipophilicity may be more hazardous.
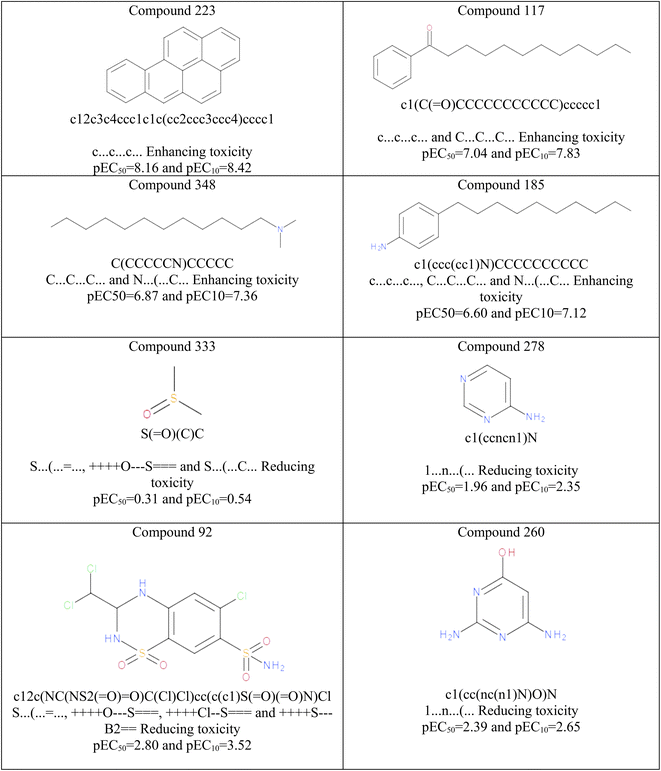 | ||
| Fig. 3 Some examples in organic chemicals responsible for enhancing and reducing algal toxicity based on model interpretation. | ||
3.6. Comparison with the previously reported models
Previously several QSARQSTR Models to predict pECx of organic chemicals against P. subcapitata have been reported and some statistical characteristics of the reported QSTR models are summarized in Table 3.| S. no. | X% effective concentrations | Chemical class | h (test duration in h) | No of descriptor | Total number of components | Data set size | R2 model | R2 | MAE | Ref. | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Training | Inv. train. | Cal | Test | Training | Test | Training | Test | ||||||||
| 1 | pEC50 | Benzoic acids | 48 | 2 | 20 | 20 | 0.965 and 0.921 | 38 | |||||||
| 2 | pEC50 | -Polar narcotic chemicals | 72 | 2 | 58 | 58 | 0.6 | — | 39 | ||||||
| 3 | pEC50 | Non-polar narcotic chemicals | 72 | 2 | 50 | 50 | 0.9469 | 40 | |||||||
| 4 | pEC50 | Polar and nonpolar narcotic chemicals | 72 | 3 | 108 | 87 | 21 | 0.9149 | |||||||
| 5 | pEC50 | Cosmetics | 96 | 4 | 30 | 20 | 10 | 0.885 | 0.712 | 0.328 | 41 | ||||
| 6 | pEC50 | Pharmaceuticals | 96 | 5 | 69 | 53 | 16 | 0.69 | 0.73 | 0.55 | 42 | ||||
| 7 | pEC50 | Pharmaceuticals | 96 | 5 | 69 | 53 | 16 | 0.71 | 0.64 | 0.57 | |||||
| 8 | pEC50 | Organic compounds | 24 | 6 | 334 | 251 | 83 | 0.72 | 0.7 | 0.69 | 0.67 | 29 | |||
| 9 | pEC10 | Organic compounds | 24 | 8 | 334 | 251 | 83 | 0.7 | 0.77 | 0.7 | 0.61 | ||||
| 10 | pEC10 | Organic chemicals | 24 | 6 | 334 | 167 | 167 | 0.76 | 0.75 | 0.60 | 0.61 | 43 | |||
| 11 | pEC50 | Organic chemicals | 24 | 6 | 334 | 167 | 167 | 0.75 | 0.74 | 0.6 | 0.61 | ||||
| 12 | pEC50 | Organic chemicals | 72 | 7 | 271 | 217 | 54 | 0.72 | 0.718 | 0.693 | 0.506 | 0.432 | 6 | ||
| 13 | pEC50 | Organic chemicals | 24 | 1 | 334 | 113 | 79 | 59 | 83 | 0.8150 | 0.8665 | 0.6110 | 0.461 | Present work | |
| 14 | pEC10 | Organic chemicals | 24 | 1 | 334 | 116 | 79 | 56 | 83 | 0.7892 | 0.8866 | 0.5691 | 0.426 | ||
Lee and Chen38 reported two QSAR models for the prediction of the pEC50 of 20 benzoic acids to P. subcapitata. The R2 of the models were 0.921 and 0.965. Aruoja et al.39,40 predicted the toxicity in terms of pEC50 of 58 polar narcotic chemicals (R2 = 0.6) and 50 non-polar narcotic chemicals (R2 = 0.9469) in two independent QSTR studies. They also built a combined model for 108 polar and nonpolar narcotic compounds based on three descriptors including log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow, molecular weight (MW) and ΔHf/#atoms (R2 of 0.9149).
Kow, molecular weight (MW) and ΔHf/#atoms (R2 of 0.9149).
Khan and Roy29,41,42 reported several QSTR models for the toxicity pEC50 of 30 cosmetics, 69 pharmaceuticals and 334 organic compounds (pEC10 and pEC50) against P. subcapitata in three independent studies. The dataset for the developed model of cosmetics was divided into 20 compounds of the training set and 10 compounds of the test set with R2 of 0.885 and 0.712, respectively. For QSTR modelling of 69 pharmaceutical compounds, the total data set was partitioned into sets of training (53 compounds) and test (16 compounds). The suggested models for pharmaceuticals, respectively, have R2 of 0.69 and 0.71 for the training and test sets. In the next study, they constructed several six descriptors-based QSTR models for pEC50 (24 h) and eight descriptors-based QSTR models for pEC10 using 334 organic chemicals against P. subcapitata. The dataset was divided into the training set (251 compounds, R2 = 0.72) and the test set (83 compounds, R2 = 0.70).
Later, Yu43 developed six descriptors QSTR models for 334 chemicals against P. subcapitata, by employing SVM (Support Vector Machine) and genetic algorithm. The dataset for the endpoint pEC10 was divided into training (n = 167 compounds, R2 = 0.76 and MAE = 0.60) and test sets (n = 167 compounds, R2 = 0.75 and MAE = 0.61) in the ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (training set and 167 compounds test set). Also, the QSTR models were developed for endpoint pEC50 with 167 compounds for training (R2 = 0.75 and MAE = 0.60) and 167 compounds for test sets (R2 = 0.74 and MAE = 0.61).
1 (training set and 167 compounds test set). Also, the QSTR models were developed for endpoint pEC50 with 167 compounds for training (R2 = 0.75 and MAE = 0.60) and 167 compounds for test sets (R2 = 0.74 and MAE = 0.61).
Recently, Masand et al.6 developed a QSTR model to estimate the EC50 for 72 h based assay for the microalga Pseudokirchneriella subcapitata utilising a data collection of 271 compounds from various chemical classes. The Genetic Algorithm Multi-linear regression (GA-MLR) was employed to develop models. The dataset was divided into two sets, i.e. a training set and a prediction set with a ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 (217
20 (217![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 compounds). The numerical values of R2, QLOO2 and MAE for the suggested QSTR model were 0.72, 0.70 and 0.524, respectively. Seven descriptors were employed to develop QSTR models.
54 compounds). The numerical values of R2, QLOO2 and MAE for the suggested QSTR model were 0.72, 0.70 and 0.524, respectively. Seven descriptors were employed to develop QSTR models.
If the QSTR models were judged based on the results of the MAE of the test or validation set, then the present QSTR modelling was also preferred over the reported QSTR models. The numerical value of MAE of the validation set for the pEC50 endpoint was 0.461 which was lower than the other reported results except for the work reported by Khan et al.41 and Masanad et al.6 But, only 69 chemicals were employed by Khan et al. to build the QSTR model. Whereas, 271 organic compounds were used by Masand et al. to develop the QSTR models.
However, In the earlier published work, two sets were applied to build up QSTR models (training and test set), but in the present research, the QSTR models were developed using four sets (training, invisible training, calibration and validation set). All previously reported models used a single split, but in the present research, 3 splits were used to generate three QSTR models using the target function TF2. Various validation parameters for the assessment of the model were employed in the earlier reported works, but, the index of ideality correlation (IIC) was never used and is employed in the present work. In the present study only one descriptor, DCW, was used to generate QSTR models, while previously reported methods were developed by utilizing more than one descriptor. The mechanistic interpretation in terms of SMILES fragment was reported first time in the present research. By using the results of mechanistic interpretation, one may predict the toxicity of unknown molecules. Hence, the QSTR models developed herein are more reliable and have better statistical quality and predictability.
4. Conclusion
Using a hybrid optimal descriptor, which was obtained by a combination of SMILES and HSG attributes, QSTR models were generated to predict the toxicity (EC10 and EC50) of 334 different organic chemicals against P. subcapitata based on the Monte Carlo optimization method. The balance of correlation method with IIC was used to establish QSTR models. The IIC was employed to construct the QSTR models which improve the robustness and predictability of the generated models, particularly for the validation set. Also, the developed QSTR models were monoparametric. To establish the reliability of QSTR models, three random splits and four sets of a single split (active training, invisible training, calibration, and validation sets) were employed. The reliability and predictability of the suggested QSTR models were evaluated using internal validation, external validation and data randomization including R2, CCC, IIC, Q2, Q2F1, Q2F2, Q2F3, s, MAE, F, RMSE, R2m, ΔR2m, CR2P, and Y test. The structural attributes responsible for the toxicity were also identified. The hydrophilic attributes like 1…n…(… and S…(…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) … exert positive contributions to controlling the aquatic toxicity and reducing algal toxicity, whereas attributes such as c…c…c…, C…C…C… enhance lipophilicity of the molecules and consequently enhance algal toxicity. However, all of the designed QSTR models were suitable to estimate the EC10 and EC50 of diverse chemicals.
… exert positive contributions to controlling the aquatic toxicity and reducing algal toxicity, whereas attributes such as c…c…c…, C…C…C… enhance lipophilicity of the molecules and consequently enhance algal toxicity. However, all of the designed QSTR models were suitable to estimate the EC10 and EC50 of diverse chemicals.
Conflicts of interest
The authors declare no conflicts of interest.References
- A. Furuhama, K. Hasunuma and Y. Aoki, SAR QSAR Environ. Res., 2015, 26, 809–830 CrossRef CAS PubMed.
- A. Furuhama, K. Hasunuma, T. Hayashi and N. Tatarazako, SAR QSAR Environ. Res., 2016, 27, 343–362 CrossRef CAS PubMed.
- OECD, 2011, 2, 25.
- O. G. No, 2004.
- T. N. OECD, OECD guidelines for the testing of chemicals, Section, 1992, 2 Search PubMed.
- V. H. Masand, M. E. Zaki, S. A. Al-Hussain, A. B. Ghorbal, S. Akasapu, I. Lewaa, A. Ghosh and R. D. Jawarkar, Aquat. Toxicol., 2021, 239, 105962 CrossRef CAS PubMed.
- U. EPA, Gammarid acute Toxic. test OPPTS, 1996, 850.
- O. A. G. I. Test, Paris, France: Organisation of Economic Cooperation and Development, 1984.
- V. Aruoja, H.-C. Dubourguier, K. Kasemets and A. Kahru, Sci. Total Environ., 2009, 407, 1461–1468 CrossRef CAS PubMed.
- L. Minguez, R. Bureau and M.-P. Halm-Lemeille, Aquat. Toxicol., 2018, 196, 117–123 CrossRef CAS PubMed.
- L. Musset, OCDE Series on testing and assessment, 2006, 54.
- S. Ahmadi, A. P. Toropova and A. A. Toropov, Nanotoxicology, 2020, 14, 1118–1126 CrossRef CAS PubMed.
- S. Ahmadi, S. Lotfi, S. Afshari, P. Kumar and E. Ghasemi, SAR QSAR Environ. Res., 2021, 32, 1013–1031 CrossRef CAS PubMed.
- S. Ahmadi, S. Lotfi and P. Kumar, Toxicol. Mech. Methods, 2021, 1–11 CAS.
- S. Lotfi, S. Ahmadi and P. Zohrabi, Struct. Chem., 2020, 31, 2257–2270 CrossRef CAS.
- A. Kumar, P. Kumar and D. Singh, Chemom. Intell. Lab. Syst., 2022, 224, 104552 CrossRef CAS.
- A. Kumar and P. Kumar, SAR QSAR Environ. Res., 2021, 32, 817–834 CrossRef CAS PubMed.
- A. Kumar and P. Kumar, J. Hazard. Mater., 2021, 402, 123777 CrossRef CAS PubMed.
- A. Kumar, J. Sindhu and P. Kumar, J. Biomol. Struct. Dyn., 2021, 39, 5014–5025 CrossRef CAS PubMed.
- S. Lotfi, S. Ahmadi and P. Kumar, RSC Adv., 2021, 11, 33849–33857 RSC.
- T. Ghiasi, S. Ahmadi, E. Ahmadi, M. Talei Bavil Olyai and Z. Khodadadi, SAR QSAR Environ. Res., 2021, 32, 495–520 CrossRef CAS PubMed.
- S. Ahmadi, Z. Moradi, A. Kumar and A. Almasirad, J. Recept. Signal Transduction, 2021, 1–12 CAS.
- P. Kumar and A. Kumar, Chemom. Intell. Lab. Syst., 2020, 200, 103982 CrossRef CAS.
- P. Kumar and A. Kumar, J. Biomol. Struct. Dyn., 2020, 38, 3296–3306 CrossRef CAS PubMed.
- P. Kumar and A. Kumar, SAR QSAR Environ. Res., 2020, 31, 697–715 CrossRef CAS PubMed.
- A. P. Toropova and A. A. Toropov, Nat. Prod. Res., 2019, 33, 2200–2207 CrossRef CAS PubMed.
- M. Duhan, J. Sindhu, P. Kumar, M. Devi, R. Singh, R. Kumar, S. Lal, A. Kumar, S. Kumar and K. Hussain, J. Biomol. Struct. Dyn., 2020, 1–22 Search PubMed.
- A. A. Toropov, R. Carbó-Dorca and A. P. Toropova, Struct. Chem., 2018, 29, 33–38 CrossRef CAS.
- K. Khan and K. Roy, SAR QSAR Environ. Res., 2019, 30, 665–681 CrossRef CAS PubMed.
- K. O. Kusk, A. M. Christensen and N. Nyholm, Chemosphere, 2018, 204, 405–412 CrossRef CAS PubMed.
- S. Ahmadi, S. Aghabeygi, M. Farahmandjou and N. Azimi, Struct. Chem., 2021, 32, 1893–1905 CrossRef CAS.
- S. Ahmadi, S. Ketabi and M. Qomi, New J. Chem., 2022, 46, 8827–8837 RSC.
- G. Gatidou, N. Vazaiou, N. S. Thomaidis and A. S. Stasinakis, Chemosphere, 2020, 241, 125071 CrossRef CAS PubMed.
- D. Yordanova, T. W. Schultz, C. Kuseva, K. Tankova, H. Ivanova, I. Dermen, T. Pavlov, S. Temelkov, A. Chapkanov and M. Georgiev, Comput. Toxicol., 2019, 10, 89–104 CrossRef.
- A. P. Toropova, A. A. Toropov, A. M. Veselinović, J. B. Veselinović, E. Benfenati, D. Leszczynska and J. Leszczynski, Ecotoxicol. Environ. Saf., 2016, 124, 32–36 CrossRef CAS PubMed.
- N. Chirico and P. Gramatica, J. Chem. Inf. Model., 2012, 52, 2044–2058 CrossRef CAS PubMed.
- S. Lotfi, S. Ahmadi and P. Kumar, J. Mol. Liq., 2021, 338, 116465 CrossRef CAS.
- P. Y. Lee and C. Y. Chen, J. Hazard. Mater., 2009, 165, 156–161 CrossRef CAS PubMed.
- V. Aruoja, M. Sihtmäe, H.-C. Dubourguier and A. Kahru, Chemosphere, 2011, 84, 1310–1320 CrossRef CAS PubMed.
- V. Aruoja, M. Moosus, A. Kahru, M. Sihtmäe and U. Maran, Chemosphere, 2014, 96, 23–32 CrossRef CAS PubMed.
- K. Khan and K. Roy, SAR QSAR Environ. Res., 2017, 28, 567–594 CrossRef CAS PubMed.
- K. Khan, E. Benfenati and K. Roy, Ecotoxicol. Environ. Saf., 2019, 168, 287–297 CrossRef CAS PubMed.
- X. Yu, Aquat. Toxicol., 2020, 224, 105496 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra03936b |
| This journal is © The Royal Society of Chemistry 2022 |
