Open Access Article
Open Access ArticleBond dissociation energies of X–H bonds in proteins†
Wojtek Treyde ab,
Kai Riedmiller
ab,
Kai Riedmiller a and
Frauke Gräter
a and
Frauke Gräter *abc
*abc
aHeidelberg Institute for Theoretical Studies, Heidelberg, Germany. E-mail: frauke.graeter@h-its.org
bMax Planck School Matter-to-Life (MtL), Heidelberg, Germany
cInterdisciplinary Center for Scientific Computing, Heidelberg University, Heidelberg, Germany
First published on 1st December 2022
Abstract
Knowledge of reliable X–H bond dissociation energies (X = C, N, O, S) for amino acids in proteins is key for studying the radical chemistry of proteins. X–H bond dissociation energies of model dipeptides were computed using the isodesmic reaction method at the BMK/6-31+G(2df,p) and G4(MP2)-6X levels of theory. The density functional theory values agree well with the composite-level calculations. By this high level of theory, combined with a careful choice of reference compounds and peptide model systems, our work provides a highly valuable data set of bond dissociation energies with unprecedented accuracy and comprehensiveness. It will likely prove useful to predict protein biochemistry involving radicals, e.g., by machine learning.
1 Introduction
The radical chemistry of proteins is of fundamental importance in biochemistry. Radicals are involved in many enzymatic reactions. Also, oxidative damage to proteins is generally initiated by radicals. For both, knowledge of reliable X–H bond dissociation energies (BDEs, X = C, N, O, S) for amino acids in proteins is important. X–H BDEs allow to predict which hydrogen atom abstractions will be thermodynamically possible, and which lesion sites can be repaired by cellular antioxidants. Preferred sites of radical attack and hydrogen atom abstraction are those associated with the lowest energy barriers, and, according to the Bell–Evans–Polanyi principle,1,2 these reactions are typically the most exothermic. Therefore, X–H BDEs can also provide a valuable input for machine learning models for the elucidation of the kinetics and mechanisms of radical reactions in proteins.The BDE is defined as the enthalpy required to homolytically cleave a given bond X–Y:3
| X–H → X˙ + H˙ BDE = H(X˙) + H(H˙) − H(X–H) | (1) |
Instead of computing BDEs directly using eqn (1), BDEs can also be calculated using the isodesmic reaction method.4 An isodesmic reaction is a reaction in which the number of bonds of each bond type is preserved. If an experimental BDE of a reference compound Y–H, BDE(Y–H)exp, is known, one can compute the enthalpy change associated with an isodesmic hydrogen atom transfer (HAT) from a compound of interest X–H to that reference compound Y˙, and use it together with BDE(Y–H)exp to obtain the BDE of the bond of interest, BDE(X–H):
| X–H + Y˙ → X˙ + Y–H | (2) |
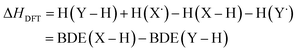 | (3) |
| BDE(X–H)isod = ΔHDFT + BDE(Y–H)exp | (4) |
The isodesmic reaction method is expected to give more accurate BDEs than if they were computed directly because systematic errors of the chosen functional should compensate to some extent if the reference compound is chosen to be electronically similar.
Previously, X–H BDEs for amino acids in proteins have been computed by Moore et al.5 using the isodesmic reaction method at the B3LYP/6-31G(d) level of theory. This study was an important step forward, as it was the first detailed catalogue of BDEs for proteins. However, while in the past often used, B3LYP is one of the less well performing functionals for radical reactions.6 Also, the set of references used previously5 lacks proper reference compounds for benzylic C–H, carboxylic O–H, and aromatic N–H bonds. Instead, tert-butyl amine was used as a reference compound for all side chain N–H bonds.
We report X–H BDEs of amino acids in proteins computed using the isodesmic reaction method at the BMK/6-31+G(2df,p)7 level of theory. We validate our BMK results by comparing the BDEs of smaller amino acids to results obtained at the G4(MP2)-6X8 level of theory. The BMK functional was chosen because it has been shown to perform well for both, thermodynamics and kinetics of radical reactions.9–11 G4(MP2)-6X is a composite method that uses BMK/6-31+G(2df,p) geometries and performs almost as well as G4 at lower computational cost. The G4(MP2)-6X energy is obtained as follows:
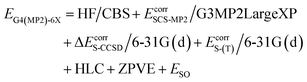 | (5) |
HF/CBS is a complete basis set (CBS) extrapolation of the Hartree–Fock (HF) energy. Ecorr are frozen-core correlation energies. EcorrS-CCSD and EcorrS-(T) are scaled CCSD and perturbative triples correlation energies beyond EcorrSCS-MP2/6-31G(d). SCS-MP2 is a modified MP2 method.12 HLC is a higher-level correction term and ESO is a spin–orbit correction from experiments or accurate calculations. The zero-point vibrational energy (ZPVE) is obtained using scaled BMK/6-31+G(2df,p) frequencies. In a benchmark study of reaction energies for Cα–H abstraction in amino acids by HO˙, G4(MP2)-6X showed the best performance out of the tested methods.13
This study builds upon and extends previous results in four aspects: (1) by choosing a level of theory that is very well suited for the treatment of radical reactions, (2) by using a set of reference compounds which correspond better to the local environment in proteins by including more neighbors of the radical center, (3) by using model peptides with C and N termini extended by the next two atoms in the protein backbone, thereby directly modeling the local environment of the amino acid in a protein, and (4) by including BDEs for aspartate, glutamate, dihydroxyphenylalanine (DOPA), hydroxyproline, hydroxylysine, an acetylated N terminus, and an anionic or amidated C terminus, as well as for the lowest-lying tautomer of arginine. The resulting data set, being both reliable and comprehensive, can provide the basis for computationally studying the rich radical chemistry of proteins.
2 Methods
BDEs in this work were mainly calculated using the hybrid BMK functional7 with the 6-31+G(2df,p) basis set. For smaller amino acids, BDEs were also computed at the G4(MP2)-6X8 level of theory. Additionally, calculations were performed using B3LYP/6-31G(d) to compare to previous literature results.Reference compounds and bonds used in the isodesmic reaction method are depicted in Fig. 1. Experimental BDEs were taken from Luo,14 except for alanine, for which no experimental BDE is available. Instead, the BDE was computed directly using G4(MP2)-6X. Including alanine as a reference compound seemed preferable to the use of another compound because Cα radicals are captodatively stabilized,15 and a reference compound should include this special electronic stabilization if compensation of systematic errors is desired. BDEs of reference bonds computed at the G4(MP2)-6X and BMK/6-31+G(2df,p) levels of theory agree well with experimental values14 (Table SI.1†). The mean absolute errors (MAEs) are 6.2 kJ mol−1 and 8.6 kJ mol−1, respectively.
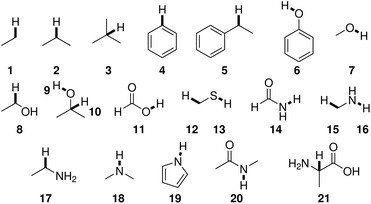 | ||
| Fig. 1 Reference compounds used to compute BDEs using the isodesmic reaction method. Reference bonds are highlighted and numbered. | ||
In addition to BDEs, for the sake of completeness, bond dissociation free energies (BDFEs) are reported as well. BDFEs were calculated directly, i.e., analogously to eqn (1).
Further experimental details are given in the ESI.† Optimized structures and results of the calculations are available.26
3 Results and discussion
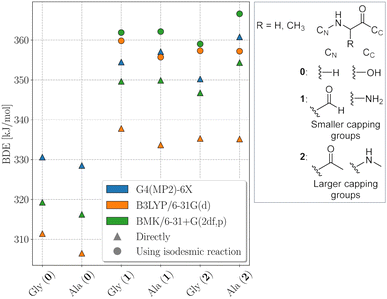
The electronic structure of the amino acids and thereby the BDEs are sensitive to their chemical surrounding. Hence, for proteins, adequate capping groups at the N and C termini that model the influence of the protein backbone must be used.To assess to what extent the way the protein backbone is modeled influences the computed BDEs, we compared BDEs of the Cα atom with varying capping groups. The way the protein backbone is modelled can be expected to have a particularly strong influence on the Cα–H BDEs, not only because of the close proximity of the Cα–H bond to the capping groups, but also because its radical is captodatively stabilized by the backbone amide groups. Cα–H BDEs of glycine and alanine were calculated with three different types of capping groups: without, with smaller capping groups corresponding to the next backbone atom, and with larger capping groups corresponding to the next two backbone atoms. Calculations were performed using BMK/6-31+G(2df,p) and G4(MP2)-6X, as well as using B3LYP/6-31G(d) for comparison to previous literature results.5 G4(MP2)-6X BDEs were computed directly, density functional theory (DFT) BDEs were obtained directly and using the isodesmic reaction method. The results are shown in Fig. 2.
Capping alanine with a formyl and an amino group raises the Cα–H BDE by around 30 kJ mol−1 compared to the free amino acid by lowering the captodative stabilization by the electron donating and withdrawing groups. This indicates a significant influence of the protein backbone on BDEs. Calculations at the G4(MP2)-6X level of theory further show that, although the Cα–H BDE of alanine as a free amino acid is lower than that of glycine as a free amino acid, already when considering the next atoms along the peptide backbone the relative order is reversed. The difference between the two BDEs becomes larger if one includes the next two atoms. This is in agreement with previous calculations at the G3(MP2)-RAD level of theory.16 The trend might be due to increased steric interactions for the Cα alanine dipeptide radical that outcompete the inductive stabilization (a trend that appears reversed for leucine, see Table 1).17 Therefore, both composite methods come to the conclusion that the Cα–H BDE of glycine in a protein should be lower than that of alanine. At the BMK/6-31+G(2df,p) level of theory, this is reproduced for the acetyl and N-methyl capping groups. Hence, all X–H BDEs in this work were computed using these capping groups. The resulting peptide models are shown in Fig. 3. At the B3LYP/6-31G(d) level of theory, the BDE of the alanine dipeptide remains higher than that of the glycine dipeptide even if acetyl and N-methyl capping groups are used, although the exact values are closer to the G4(MP2)-6X results than at the BMK/6-31+G(2df,p) level of theory. Consequently, if one were to use B3LYP, at least the next three atoms along the protein backbone would have to be included.
| AA | Pos. | BDE | BDFE | Bond | AA | Pos. | BDE | BDFE | Bond | AA | Pos. | BDE | BDFE | Bond |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Significant change in hydrogen bonding strength or pattern upon H abstraction.b Dipeptide exhibits extensive hydrogen bonding that distorts it from a fully extended geometry (ϕ ≈ 82°, ψ ≈ 66°).c Hydrogen bonding between the N–H bond of the C terminal N-methyl amino capping group and the central amide group. Dihedrals going from N to C terminus change from ϕ ≈ −159°, ψ ≈ 163°, ω ≈ 176°, ϕ′ ≈ −161°, ψ′ ≈ 162°, ω′ ≈ 178° to ϕ ≈ −158°, ψ ≈ 168°, ω ≈ 148°, ϕ′ ≈ −101°, ψ′ ≈ 65°, ω′ ≈ 178°.d Deviates from a fully extended geometry (ϕ ≈ −164°, ψ ≈ 91°).e Formyl capping group on N terminus. | ||||||||||||||
| Ala | α | 366.6 | 319.5 | 21 | His (N1–H) | αa | 339.5 | 297.7 | 21 | Phe | α | 368.1 | 318.9 | 21 |
| β | 429.2 | 396.5 | 1 | βe | 348.0 | 331.0 | 5 | β | 358.4 | 337.0 | 5 | |||
| Arg+ | αa | 326.9 | 288.5 | 21 | 1 | 394.3 | 349.9 | 19 | 1 | 473.5 | 437.7 | 4 | ||
| β | 360.0 | 333.2 | 2 | 2 | 492.1 | 455.0 | 4 | 2 | 472.1 | 432.1 | 4 | |||
| γ | 352.9 | 322.8 | 2 | 4 | 483.7 | 446.1 | 4 | 3 | 473.8 | 433.1 | 4 | |||
| δ | 391.0 | 358.4 | 17 | His (N3–H) | αa | 339.9 | 298.9 | 21 | cis Pro | α | 369.7 | 325.0 | 21 | |
| ε | 470.1 | 425.1 | 18 | β | 351.9 | 332.4 | 5 | 1 | 412.5 | 375.6 | 2 | |||
| η | 493.2 | 443.2 | 16 | 2 | 491.8 | 456.0 | 4 | 2 | 412.5 | 372.0 | 2 | |||
| Arg | α | 361.3 | 312.6 | 21 | 3 | 399.2 | 355.5 | 19 | 3 | 410.6 | 375.6 | 17 | ||
| β | 411.7 | 367.9 | 2 | 4 | 501.6 | 466.3 | 4 | trans Pro | α | 389.7 | 339.2 | 21 | ||
| γ | 410.1 | 375.4 | 2 | Hyl+ | α | 355.3 | 307.7 | 21 | 1 | 420.0 | 379.5 | 2 | ||
| δ | 410.2 | 374.0 | 17 | βa | 391.3 | 350.8 | 2 | 2 | 414.5 | 371.9 | 2 | |||
| ε | 370.0 | 319.3 | 18 | γ | 410.6 | 372.2 | 2 | 3 | 377.1 | 343.6 | 17 | |||
| η | 412.8 | 363.0 | 16 | δ | 390.0 | 342.0 | 10 | Ser | αa | 357.8 | 313.6 | 21 | ||
| Asn | α | 340.2 | 294.3 | 21 | δ′ | 490.3 | 433.0 | 9 | β | 436.4 | 384.4 | 7 | ||
| βa | 409.8 | 363.7 | 2 | ε | 431.7 | 397.2 | 17 | γ | 398.2 | 353.8 | 8 | |||
| δa | 459.4 | 440.1 | 14 | ζ | 423.0 | 369.2 | 16 | Thr | αa | 357.2 | 313.4 | 21 | ||
| Asp− | αa,b | 355.7 | 302.8 | 21 | Hyl | αa | 352.5 | 313.9 | 21 | β′ | 441.1 | 391.2 | 9 | |
| βa,b | 387.3 | 348.5 | 2 | βa | 395.7 | 366.7 | 2 | β | 390.4 | 345.2 | 10 | |||
| Asp | αa | 358.6 | 315.0 | 21 | γ | 411.6 | 371.8 | 2 | γ | 420.1 | 384.6 | 1 | ||
| β | 398.1 | 360.6 | 2 | δ | 402.3 | 356.2 | 10 | Trp | α | 372.6 | 331.9 | 21 | ||
| δ | 469.1 | 424.0 | 11 | δ′ | 438.7 | 390.6 | 9 | β | 361.4 | 344.4 | 5 | |||
| Backbone | 1a,c | 461.5 | 415.1 | 18 | ε | 372.4 | 339.4 | 17 | 1 | 500.1 | 465.8 | 4 | ||
| C term.− | α | 374.8 | 328.9 | 21 | ζ | 428.5 | 380.0 | 16 | 2 | 382.8 | 344.3 | 19 | ||
| C term. | α | 360.0 | 313.8 | 21 | cis Hyp | α | 371.2 | 324.7 | 21 | 4 | 475.1 | 438.2 | 4 | |
| Cys | α | 354.0 | 306.8 | 21 | 1 | 418.5 | 379.6 | 2 | 5 | 474.0 | 440.3 | 4 | ||
| β | 382.4 | 354.7 | 12 | 2 | 402.2 | 355.4 | 10 | 6 | 474.8 | 442.3 | 4 | |||
| γ | 346.7 | 310.7 | 12 | 2′ | 443.6 | 393.0 | 9 | 7 | 477.2 | 442.5 | 4 | |||
| DOPA | α | 368.0 | 320.1 | 21 | 3 | 384.1 | 342.8 | 2 | Tyr | α | 367.5 | 322.5 | 21 | |
| β | 354.3 | 331.8 | 5 | trans Hyp | α | 389.8 | 338.7 | 21 | β | 354.2 | 329.7 | 5 | ||
| 1 | 474.9 | 432.4 | 4 | 1 | 420.6 | 380.5 | 2 | 1 | 471.8 | 435.6 | 4 | |||
| 2 | 321.8 | 282.3 | 6 | 2 | 401.4 | 352.2 | 10 | 2 | 475.7 | 440.3 | 4 | |||
| 3 | 354.9 | 310.4 | 6 | 2′ | 436.2 | 385.6 | 9 | 3 | 359.6 | 318.8 | 6 | |||
| 4 | 482.2 | 440.8 | 4 | 3 | 375.3 | 337.7 | 2 | Val | α | 375.4 | 318.7 | 21 | ||
| 5 | 477.0 | 435.7 | 4 | Ile | α | 375.9 | 325.6 | 21 | β | 399.8 | 354.3 | 3 | ||
| DOPA− (1) | α | 368.6 | 322.4 | 21 | β | 396.2 | 355.8 | 3 | γ | 413.9 | 377.8 | 1 | ||
| β | 347.7 | 326.0 | 5 | γ′ | 421.1 | 386.1 | 1 | Ace-Ala-NMe | 1 | 409.2 | 376.8 | 1 | ||
| 1 | 472.4 | 431.9 | 4 | γ | 402.3 | 368.0 | 2 | 2 | 448.4 | 408.3 | 20 | |||
| 3 | 316.5 | 272.9 | 6 | δ | 419.3 | 385.7 | 1 | 3 | 450.1 | 412.4 | 20 | |||
| 4 | 465.1 | 426.2 | 4 | Leu | α | 355.9 | 312.5 | 21 | 4 | 398.7 | 355.6 | 15 | ||
| 5 | 471.8 | 430.1 | 4 | β | 412.4 | 375.3 | 2 | |||||||
| DOPA− (2) | α | 373.0 | 323.9 | 21 | γ | 398.1 | 354.6 | 3 | ||||||
| β | 318.4 | 297.8 | 5 | δ | 419.7 | 385.7 | 1 | |||||||
| 1 | 454.6 | 416.3 | 4 | Lys+ | αa | 289.1 | 247.9 | 21 | ||||||
| 2 | 260.4 | 218.9 | 6 | β | 332.5 | 302.2 | 2 | |||||||
| 4 | 472.6 | 434.0 | 4 | γ | 393.2 | 356.5 | 2 | |||||||
| 5 | 455.4 | 416.5 | 4 | δa | 337.3 | 306.1 | 2 | |||||||
| Gln | αa | 341.4 | 303.6 | 21 | ε | 430.6 | 394.5 | 17 | ||||||
| βa | 403.9 | 374.5 | 2 | ζ | 427.9 | 376.4 | 16 | |||||||
| γa | 379.2 | 353.5 | 2 | Lys | α | 360.9 | 313.1 | 21 | ||||||
| ε | 448.0 | 438.5 | 14 | β | 413.1 | 372.3 | 2 | |||||||
| Glu− | α | 355.7 | 305.5 | 21 | γ | 408.8 | 367.5 | 2 | ||||||
| β | 393.2 | 353.6 | 2 | δ | 411.9 | 370.0 | 2 | |||||||
| γ | 389.8 | 353.7 | 2 | ε | 377.6 | 342.6 | 17 | |||||||
| Glu | α | 356.2 | 313.5 | 21 | ζ | 423.1 | 371.6 | 16 | ||||||
| β | 404.5 | 374.9 | 2 | Met | α | 362.4 | 315.8 | 21 | ||||||
| γ | 388.1 | 356.2 | 2 | β | 410.5 | 373.9 | 2 | |||||||
| ε | 459.9 | 418.2 | 11 | γ | 375.1 | 347.6 | 12 | |||||||
| Gly | α | 359.0 | 315.1 | 21 | ε | 387.6 | 360.4 | 12 | ||||||
| His+ | α | 356.4 | 309.2 | 21 | N term.+ | α | 412.1 | 362.1 | 21 | |||||
| βa | 375.7 | 355.3 | 5 | N term. | α | 338.9 | 292.3 | 21 | ||||||
| 1a | 449.3 | 406.8 | 19 | 1 | 415.0 | 364.4 | 16 | |||||||
| 2 | 533.9 | 493.9 | 4 | |||||||||||
| 3a,d | 452.1 | 412.0 | 19 | |||||||||||
| 4a | 540.2 | 498.9 | 4 | |||||||||||
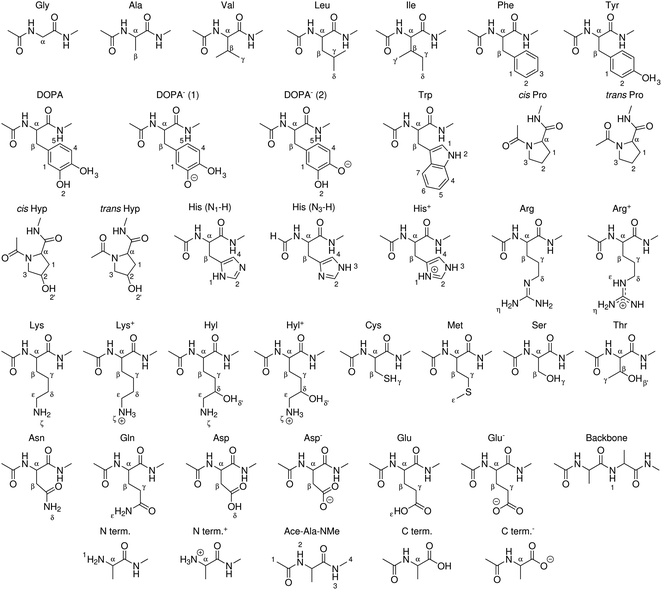 | ||
| Fig. 3 Peptide models of canonical amino acids, termini, and modified amino acids for which BDEs were computed in this work. X–H bonds are indexed. | ||
Compared to literature results computed with other composite methods using the isodesmic reaction method, G4(MP2)-6X seems to underestimate Cα–H BDEs, but BMK Cα–H BDEs computed using the isodesmic reaction method agree very well with composite level literature results (Table SI.2†). BMK BDEs are also closer to high-level composite methods than DSD-PBE-P86/aug′-cc-pVTZ+d BDEs reported by Chan et al.13 DFT, especially B3LYP, underestimates BDEs compared to G4(MP2)-6X if they are computed directly. Using the isodesmic reaction method, a large part of this deviation vanishes. This highlights the error-canceling power of the isodesmic reaction method.
We note that we were not able to reproduce the Cα–H BDEs of glycine and alanine dipeptides reported by Moore et al.,5 or the BDEs of their reference compounds, although our calculations agree well with previous literature results.18–20 Their reported BDEs also differ from previous literature results at the same level of theory and using the same reference compounds by as much as 9 kJ mol−1,19 and by over 30 kJ mol−1 compared to a study that uses glycine as a reference compound instead of alanine.20 Importantly, we and others,16 using composite methods or the BMK functional and the isodesmic reaction method, find the Cα–H BDE of the glycine dipeptide to be lower than that of the alanine dipeptide, in contrast to Moore et al., who also report overall much lower BDEs for these two radicals.
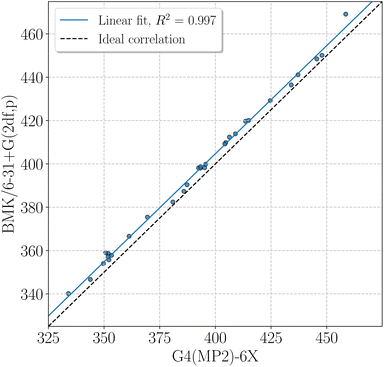
BMK BDEs are given in Table 1. G4(MP2)-6X BDEs of smaller amino acids can be found in Table 2. In general, BDEs at the BMK/6-31+G(2df,p) level of theory agree well with BDEs at G4(MP2)-6X level of theory (coefficient of determination of the linear fit, R2 = 0.997, mean absolute deviation, MAD = 4.7 kJ mol−1, Fig. 4). Some X–H BDEs were also computed for model peptides with formyl and amino capping groups. The BDEs for model peptides with larger and smaller capping groups correlate well with R2 = 0.981 (Fig. SI.1†), and just the Cα–H BDEs deviate unsystematically from the linear correlation, as also discussed above (see also Fig. 2). It is therefore sufficient to use Cα–H BDEs to determine adequate capping groups.
| Amino acid | Position | BDE [kJ mol−1] |
|---|---|---|
| Ala | α | 360.8 |
| β | 424.7 | |
| Asn | α | 334.0 |
| β | 404.7 | |
| Asp− | α | 352.2 |
| β | 385.9 | |
| Asp | α | 351.9 |
| β | 393.3 | |
| δ | 458.5 | |
| Cys | α | 349.7 |
| β | 380.9 | |
| γ | 343.8 | |
| Gly | α | 350.3 |
| Leu | β | 406.3 |
| γ | 392.4 | |
| δ | 413.6 | |
| Ser | α | 353.4 |
| β | 395.2 | |
| γ | 434.1 | |
| Thr | α | 351.8 |
| β′ | 437.1 | |
| β | 387.3 | |
| γ | 415.0 | |
| Val | α | 369.5 |
| β | 395.6 | |
| γ | 409.0 | |
| Ace-Ala-NMe | 1 | 404.2 |
| 2 | 445.5 | |
| 3 | 447.9 | |
| 4 | 393.4 |
For the BDEs given in Table 1, peptides were modeled in a fully extended trans geometry (ω ≈ 180°), except for proline and hydroxyproline, where both cis and trans conformers were modeled by setting ω, ϕ, ψ, and ω′ going from the N to the C terminus to approximately 0°, −75°, 160°, 180°, and 180°, −75°, 150°, 180°, respectively.21 Where applicable, amino acids were considered in their charged and neutral forms. For histidine, the neutral N1–H and N3–H tautomers were considered. In the gas phase, the N3–H tautomer is more stable by 4.9 kJ mol−1. For arginine, in agreement with previous investigations,22 out of the five possible neutral tautomers, the one in which the two terminal N atoms are doubly protonated was found to be most stable, and so this tautomer was considered.
In some cases, initial geometry optimizations resulted in hydrogen bonding between the amino acid side chain and backbone to different extent in radical and non-radical structures. This intramolecular hydrogen bonding is well known, and has also been found in a comprehensive study of the conformational landscape of amino acid dipeptides.23 For the computation of BDEs, this would lead to energetic artifacts. Intramolecular hydrogen bonding is unlikely to occur in proteins, since the backbone amide groups are involved in secondary structure formation. In aqueous solution, polar side chain groups will also be hydrogen-bonded to water molecules or coordinated to metal ions. Therefore, we aimed at minimizing intramolecular hydrogen bonding and changes in hydrogen bonding pattern. To this end, the same initial structure was used for geometry optimizations of both dipeptides and dipeptide radicals to reflect the potential structural constraints imposed by the protein that would make large conformational changes unlikely. Further efforts to this end are described in the ESI.† Yet, in some cases, significant changes in hydrogen bonding strength or pattern were observed, as specified in further detail in Table 1.
B3LYP BDEs by Moore et al.5 and BMK BDEs calculated in this work agree moderately (R2 = 0.851, MAD = 14.3 kJ mol−1, Fig. SI.2†), but better if BMK BDEs of model peptides with smaller capping groups are used (R2 = 0.910, MAD = 12.6 kJ mol−1, Fig. SI.3†). The difference between the BDEs at the two levels of theory is particularly pronounced for Cα–H BDEs. The poor performance of B3LYP becomes most noticeable if compared to the G4(MP2)-6X results (MAD = 10.6 kJ mol−1, Fig. SI.4†). The linear fit shows a reasonable R2 = 0.933, but a slope of 0.775 and an intercept of 86.4 kJ mol−1. For low BDEs, such as for Cα–H bonds and C–H bonds adjacent to O or S atoms, B3LYP values are too low. For higher BDEs, such as for O–H and secondary C–H bonds, B3LYP values are too high. The B3LYP BDE for the cysteine S–H bond is also much larger than at the G4(MP2)-6X level of theory.
BMK and G4(MP2)-6X BDEs overall agree well with other literature results for the same model peptides (Table SI.3†). Deviations from the BDEs reported by Zipse and colleagues17,24 can be attributed to the fact that they use Boltzmann averages. The resulting difference is small for the BDEs in tyrosine, proline, and phenylalanine, since these amino acids have less conformationally flexible side chains, but becomes apparent for the BDEs in cysteine, where the side chain is more flexible. Deviations from the BDEs reported by Chan et al.13 for amino acids with polar side chains come from the fact that they have used the lowest energy conformations of the peptides, which involve hydrogen bonding for those amino acids. In this work, hydrogen bonding in general and in particular changes in hydrogen bonding pattern between peptides and peptide radicals were avoided, and by design of our protocol the resulting conformers do not necessarily represent the most stable conformer.
Having a comprehensive data set of BDEs at hand, we analyzed trends in the BDEs across the chemical space covered by the amino acids. We grouped the X–H BDEs according to the reference compound used in the isodesmic reaction and show the distribution of the ten largest groups as well as an example radical for each group in Fig. 5. Since the reference compounds were chosen to correspond to the local chemical environment of the radical, Fig. 5 shows the influence of the local chemical environment on the BDEs. The observed stability trends agree with known chemical principles: captodative and resonance stabilization leads to low BDEs, as can be seen for Cα–H, as well as benzylic C–H and O–H bonds. Secondary C–H bonds and C–H bonds adjacent to a heteroatom have medium high BDEs. Primary C–H BDEs are higher. N–H, O–H, and aromatic C–H bonds are associated with the highest BDEs.
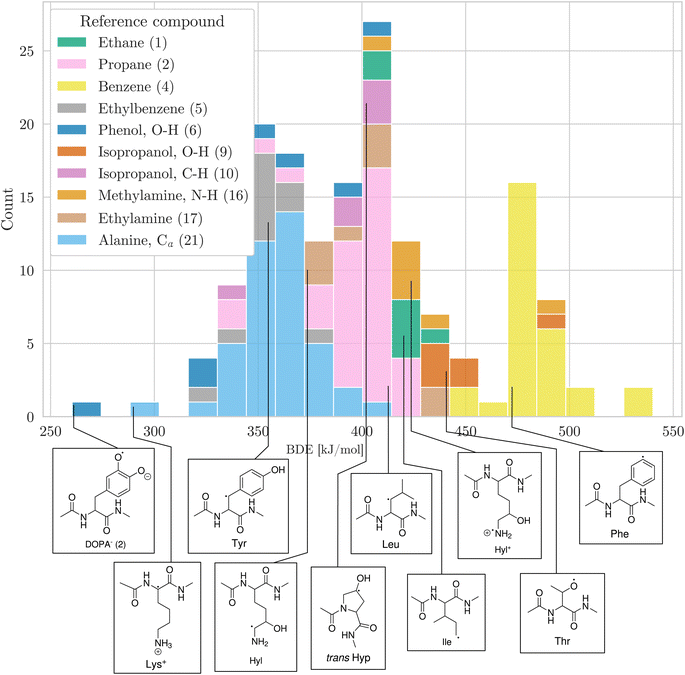 | ||
| Fig. 5 Distribution of BDEs calculated at the BMK/6-31+G(2df,p) level of theory. BDEs are grouped and colored according to the reference compound used in the isodesmic reaction method. In the legend, the numbers in parentheses refer to the numbering of reference bonds in Fig. 1. For each group, we show an arbitrary example molecule. For visual clarity, only the ten biggest groups are shown. | ||
Finally, we sought to evaluate the utility of our data set in the context of machine learning. To this end, we compared our data set to predictions made by ALFABET, a graph neural network for the prediction of BDEs trained on small organic molecules consisting of up to ten heavy atoms.25 Considering that most dipeptides in our data set consist of more than 10 heavy atoms, ALFABET predictions agree reasonably well with BMK BDEs (R2 = 0.918, MAD = 11.3 kJ mol−1, Fig. SI.5†). There is, however, considerable scatter for lower BDEs, suggesting that ALFABET does not fully capture the chemistry of amino acid radicals. Our data set could therefore prove useful in a transfer learning setting for the radical chemistry of proteins.
4 Conclusion
BDEs of all X–H bonds in amino acids were computed using the isodesmic reaction method at the BMK/6-31+G(2df,p) and G4(MP2)-6X levels of theory. The BDE values agree well with high-level calculations, and improve upon previous literature results by using a more appropriate level of theory, reference compounds, and peptide model systems.Data availability
Machine-readable BDEs, optimized structures and calculation output files are available at https://doi.org/10.11588/data/AA3UAQ.26Author contributions
Conceptualization: F. G., K. R.; methodology: K. R., W. T.; software: W. T.; validation: W. T.; formal analysis: K. R., W. T.; investigation: W. T.; resources: F. G.; data curation: W. T.; writing – original draft preparation: W. T.; writing – review & editing: F. G., K. R., W. T.; visualization: K. R., W. T.; supervision: F. G., K. R.; project administration: F. G.; funding acquisition: F. G.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for discussions with Robert Paton and Ganna Gryn'ova. We acknowledge financial support from the Klaus Tschira Foundation, the Max Planck School Matter to Life, and the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Programme (Grant agreement no. 101002812 RADICOL). This study was also supported by the HITS Lab.References
- R. P. Bell, Proc. R. Soc. London, Ser. A, 1936, 154, 414–429 Search PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1936, 32, 1333–1360 RSC.
- V. Gold, The IUPAC Compendium of Chemical Terminology, International Union of Pure and Applied Chemistry (IUPAC), Research Triangle Park, NC, 2019 Search PubMed.
- W. J. Hehre, R. Ditchfield, L. Radom and J. A. Pople, J. Am. Chem. Soc., 1970, 92, 4796–4801 CrossRef CAS.
- B. N. Moore and R. R. Julian, Phys. Chem. Chem. Phys., 2012, 14, 3148–3154 RSC.
- J. Hioe and H. Zipse, Encyclopedia of radicals in chemistry, biology and materials, Wiley-Blackwell, Oxford, 2012, vol. 1, pp. 449–476 Search PubMed.
- A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405–3416 CrossRef CAS PubMed.
- B. Chan, J. Deng and L. Radom, J. Chem. Theory Comput., 2011, 7, 112–120 CrossRef CAS PubMed.
- E. I. Izgorodina, D. R. B. Brittain, J. L. Hodgson, E. H. Krenske, C. Y. Lin, M. Namazian and M. L. Coote, J. Phys. Chem. A, 2007, 111, 10754–10768 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2008, 112, 1095–1099 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102 CrossRef CAS.
- B. Chan, A. Karton, C. J. Easton and L. Radom, J. Chem. Theory Comput., 2016, 12, 1606–1613 CrossRef CAS PubMed.
- Y.-R. Luo, Comprehensive Handbook of Chemical Bond Energies, CRC Press, 2007 Search PubMed.
- H. G. Viehe, Z. Janousek, R. Merenyi and L. Stella, Acc. Chem. Res., 1985, 18, 148–154 CrossRef CAS.
- J. Hioe, M. Mosch, D. M. Smith and H. Zipse, RSC Adv., 2013, 3, 12403–12408 RSC.
- J. Hioe, G. Savasci, H. Brand and H. Zipse, Chem.–Eur. J., 2011, 17, 3781–3789 CrossRef CAS PubMed.
- A. Rauk, D. Yu and D. A. Armstrong, J. Am. Chem. Soc., 1997, 119, 208–217 CrossRef CAS.
- A. Rauk, D. Yu and D. A. Armstrong, J. Am. Chem. Soc., 1998, 120, 8848–8855 CrossRef CAS.
- A. Rauk, D. Yu, J. Taylor, G. V. Shustov, D. A. Block and D. A. Armstrong, Biochemistry, 1999, 38, 9089–9096 CrossRef CAS PubMed.
- A. A. Morgan and E. Rubenstein, PLoS One, 2013, 8, e53785 CrossRef CAS PubMed.
- J. Norberg, N. Foloppe and L. Nilsson, J. Chem. Theory Comput., 2005, 1, 986–993 CrossRef CAS PubMed.
- Y. Yuan, M. J. L. Mills, P. L. A. Popelier and F. Jensen, J. Phys. Chem. A, 2014, 118, 7876–7891 CrossRef CAS PubMed.
- J. Hioe and H. Zipse, Faraday Discuss., 2010, 145, 301–313 RSC.
- P. C. St John, Y. Guan, Y. Kim, S. Kim and R. S. Paton, Nat. Commun., 2020, 11, 1–12 CrossRef.
- W. Treyde, K. Riedmiller and F. Gräter, Bond dissociation energies of X−H bonds in proteins [data], heiDATA, 2022 DOI:10.11588/data/AA3UAQ.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra04002f |
| This journal is © The Royal Society of Chemistry 2022 |