Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
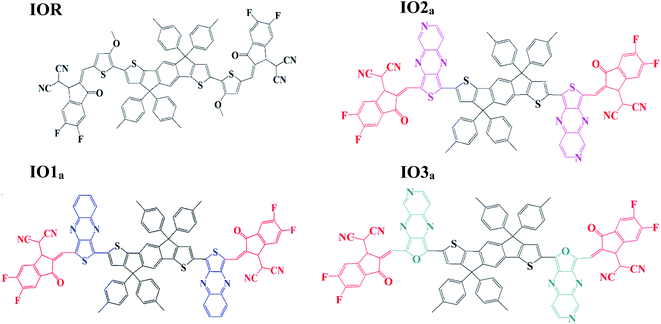
Impact of various heterocyclic π-linkers and their substitution position on the opto-electronic attributes of the A–π–D–π–A type IECIO-4F molecule: a comparative analysis†
Sahar Javaid Akrama,
N. M. A. Hadia *b,
Javed Iqbal
*b,
Javed Iqbal *a,
Rana Farhat Mehmoodc,
Saleem Iqbald,
Ahmed M. Shawkye,
Areeba Asifa,
H. H. Somailyfg,
Muhammad Raheelh and
Rasheed Ahmad Khera
*a,
Rana Farhat Mehmoodc,
Saleem Iqbald,
Ahmed M. Shawkye,
Areeba Asifa,
H. H. Somailyfg,
Muhammad Raheelh and
Rasheed Ahmad Khera *a
*a
aDepartment of Chemistry, University of Agriculture, 38000 Faisalabad, Pakistan. E-mail: javedkhattak79@gmail.com; javed.iqbal@uaf.edu.pk; rasheedahmadkhera@yahoo.com; rasheed.ahmad.khera@uaf.edu.pk
bPhysics Department, College of Science, Jouf University, P.O. Box 2014, Sakaka, Al-Jouf, Saudi Arabia. E-mail: nmhadia@ju.edu.sa
cDepartment of Chemistry, Division of Science and Technology, University of Education, Township, Lahore 54770, Pakistan
dDepartment of Chemical Engineering, Wah Engineering College, University of Wah, Quaid Avenue, 47040 Wah Cantt, Pakistan
eScience and Technology Unit (STU), Umm Al-Qura University, Makkah 21955, Saudi Arabia
fResearch Center for Advanced Materials Science (RCAMS), King Khalid University, Abha 61413, P.O. Box 9004, Saudi Arabia
gDepartment of Physics, Faculty of Science, King Khalid University, P.O. Box 9004, Abha, Saudi Arabia
hDepartment of Chemistry, Baluchistan University of Information Technology, Engineering and Management Sciences (BUITEMS), Quetta 87300, Pakistan
First published on 20th July 2022
Abstract
To investigate the consequence of different substitution positions of various π-linkers on the photovoltaic properties of an organic solar cell molecule, we have introduced two series of six three-donor molecules, by the substitution of some effective π-linkers on the A–π–D–π–A type reference molecule IECIO-4F (taken as IOR). In series “a” the thienyl or furyl bridge is directly linked between the donor and acceptor moieties, while in series “b” the phenyl ring of the same bridge is working as the direct point of attachment. The frontier molecular orbitals, density of states, transition density matrix, molecular electrostatic potential surfaces, exciton binding energy, excitation energy, wavelength of maximum absorption, open-circuit voltage, fill factor, and some other photovoltaic attributes of the proposed molecules were analyzed through density functional theory (DFT) and its time-dependent (TD) approach; the TD-DFT method. Though both series of newly derived molecules were a step up from the reference molecule in almost all of the studied characteristics, the “a” series (IO1a to IO3a) seemed to be better due to their desirable properties such as the highest maximum absorption wavelength (λmax), open-circuit voltage, and fill factor, along with the lowest excitation and exciton dissociation energy, etc. of its molecules. Also, the studied morphology, optical characteristics, and electronic attributes of this series of proposed molecules signified the fact that the molecules with thienyl or furyl ring working as the direct link between the acceptor and donor molecules showed enhanced charge transfer abilities, and could provide a maximum quantum yield of the solar energy supplied.
Introduction
Due to the increasing global energy crisis, the demand for renewable energy supplies has increased tremendously. Amongst the different sustainable energy sources, solar energy seems to be the most convenient and efficient.1 For decades, crystalline wafer-based silicon solar cells have been utilized to generate electricity from solar energy. These photovoltaic cells are expensive and brittle, and in addition, they have a low absorption range.2 In contrast, their counterparts, thin-film organic solar cells (OSCs), have proved themselves to be superior due to their facile and low-cost fabrication attained through different solution processing techniques. Moreover, they are light weight, mechanically flexible, semi-transparent, and have easily tunable energy gaps.3,4 However, their photo-conversion efficiency (PCE) is 18–20% lower than inorganic (silicon) solar cells. Thus numerous efforts have been made by scientists all around the globe in order to overcome this drawback.5,6The most recent of the many types of organic photovoltaic cells are the small molecule-based bulk-heterojunction (BHJ) OSCs. The molecules utilized in these solar cells have a definite weight and structure, high purity, and are also easily reproducible. The active layer of these significant OSCs is a blend of various donor and acceptor molecules, where donor molecules act as p-type, while acceptors act as n-type semiconductors.7,8 A necessary condition for efficient intramolecular charge transfer is proper differentiation of acceptor and donor regions. This way, the charge, after its generation in the donor region, can easily transfer within the molecule toward the acceptor region.9 Sometimes, the presence of a bridge between these donor and acceptor regions can significantly improve the intramolecular charge transfer. These bridges increase the conjugation in the molecule leading to a high fill factor and an increased photocurrent, owing to the reduced charge recombination in the molecule.10 In contrast to the molecules with no spacer, the molecules with a prominent spacer present, have significantly improved planarity and π–π interactions. In addition, upon stacking, they seem to suppress the aggression between them, owing to their increased conjugation length.11 Though various studies have been performed on the effect of different π-linkers on the photovoltaic performance of the OSCs, the data still seems to be lacking as compared to that present out there on the effect of different acceptor or donor regions.12
To increase the charge separation and ease of intramolecular charge transfer, various thiophene, furan, oligothiophene, polyenes, and other fused aromatic rings have been introduced into the otherwise donor–acceptor (D–A) type molecule. Photovoltaic molecules with thiophene derivatives as π-linkers have demonstrated efficient device performance in OSCs.13 For example, alkoxy-thiophene bridges were incorporated as π-spacers into IEIC molecule by Li Jianfeng et al., and a significant improvement in the optoelectronic properties of the resulting IEICO molecule was seen.14 In our research work, IEICO-4F was chosen as the reference molecule due to its promising optoelectronic and photovoltaic attributes cited in many literature. This molecule consists of an electron-rich indacenodithiophene (IDT) based donor core, which has four phenyl rings contributing to its electron-rich character. Attached to this donor core on both sides are the methoxy thiophene π-linkers that act as prominent charge transfer moieties for efficient charge transfer from the donor core to the peripheral acceptors. The acceptors attached at the peripheries of this molecule are the strongly electron withdrawing 2-(5,6-difluoro-2-methylene-3-oxo-indan-1-yl)-malononitrile groups. Accredited to these proficient fragments of this highly planar molecule, it shows significant absorption in the chloroform solvent with a range of 600–900 nm, locating close to the near-infrared region, and a narrow bandgap of only 1.73 eV.15 In addition, a blend of this molecule with PBDTTT-EFT donor molecule exhibited an impressive experimental power conversion efficiency of 10%, an open-circuit of voltage of 0.739 V with a notable short-circuit current of 22.8 mA cm−2 and an energy loss of only 0.501 eV.15 Furthermore, IEICO-4F, by promoting the crystallization of the film, reduces the charge recombination of the corresponding device.16 So, taking into account these remarkable attributes of IEICO-4F, this molecule was selected for our research in a quest to increase its already outstanding optoelectronic properties for prominent organic photovoltaic cells.
Liu et al. studied the effect of the substitution position of arylamine moieties on thiophene π-linkers. It was seen that the 2,5-position demonstrated a 40% increase in PCE as compared to the 3,4-position.17 It is generally seen that the point of attachment of the bridges between the donor and acceptor region of a molecule remarkably affects the hole mobility, electrochemical attributes, and photovoltaic performance of the molecule.18 Thus, two series (“a” and “b”) of donor molecules are designed here, to study the effect of the substitution position of various π-linkers on the device performance of the molecule under consideration. The spacers in the cited molecule IEICO-4F19 were replaced with three new bridges at different sites of attachment (either six-membered or five-membered rings). The bridges utilized for our research were thieno[3,4-b]quinoxaline (IO1), 2-thia-4,6,9-triaza-cyclopenta[b]naphthalene (IO2), and 2-oxa-4,6,9-triaza-cyclopenta[b]naphthalene (IO3). Fig. S1† illustrate the ChemDraw sketches of “b” series of designed molecules, while the rest of the molecules (reference and “a” series) are depicted in Fig. 1. Thus, six new molecules are reported, with two molecules (a and b) having only the difference in point of attachments. The bridges employed for the design of the newly proposed molecules were seen to give prominent results in the literature. These bridges have a slight difference with respect to the substitution of an atom or two, for example in IO2, the carbon of the second phenyl ring is replaced with a nitrogen, similarly, in IO3, the sulphur of the five membered ring is substituted with an oxygen atom.20
Computational details
All the investigated molecular structures were first sketched through ChemDraw 7.0.21 Then with the help of these sketches, the molecules were designed in GuassView 6.0 (ref. 22) program, the very same program through which the results obtained after quantum chemical simulations from Gaussian 09 (ref. 23) programs were visualized. After careful examination of the value of maximum absorption (λmax) of reference molecule IOR, the MPW1PW91 functional, in combination with the 6-31G(d,p) basis set, was selected for all the proceedings in this research work. Also, the spin was restricted for all the computations to avoid any spin contamination in the proposed molecules.Here, all the six newly designed structures were optimized at their ground state through the above-stated density functional theory (DFT)24 level of theory. Then, their molecular dynamics, such as frontier molecular orbitals (FMOs) and molecular electrostatic potential (MESP) surfaces, were assessed from the thus obtained geometrically optimized structures. The density of states (DOS) of these structures was also evaluated to authenticate the results of FMOs. These states were plotted in the form of graphs by the utilization of the PyMOlyze 1.1 (ref. 25) program. Moreover, the excited state properties (maximum absorption wavelength, excitation energy, oscillator strength, etc.) of these structures in the gas and solvent (chloroform) phase were also examined through time-dependent DFT (TD-DFT).26 The polarizable continuum model (PCM)27 model was employed to simulate the solvent environment, and the reason behind the selection of chloroform solvent was its utilization in the cited literature for the reference molecule.28 Moreover, the results of maximum absorption were envisioned with the help of graphs obtained from Origin 6.0 software.29
Reorganization energy (λh for the hole and λe for the electron) is an important parameter to determine the mobility of electrons or holes in the molecule after their separation. Thus, this characteristic of the molecules was also calculated according to eqn (1) and (2) from Marcus' theory, given below30,31
| λe = [E−0 − E−] + [E0− − E0] | (1) |
| λh = [E+0 − E+] + [E0+ − E0] | (2) |
The transition density matrices of the cited and newly designed molecules were procured through Multiwfn 3.6 application software.32 Some chemical descriptors like band gap, softness, and hardness of the newly derived structures at their ground state were also computed. Furthermore, the binding energy was assessed in order to estimate the minimum amount of energy required to separate the geminate (electron–hole pair) produced in the scrutinized structures after the absorption of radiations. Finally, the open-circuit voltage and fill factor of the studied molecules were calculated to give a direction about the photo-conversion efficiency (PCE) of these molecules, which is a significant parameter to determine the plausibility of the studied molecules in organic solar cells.
Results and discussion
Generally, alkyl chains have little to no effect on the spectral and optoelectronic properties of a molecule. Thus, for the sake of convention, the alkyl chains of the cited molecule IEICO-4F were substituted with methyl chains, and the molecule thus formed was named IOR. This reference molecule IOR was first examined theoretically through the density functional theory (DFT) method and its time-dependent approach in order to speculate the functional to be utilized for all the executed simulations in this research. For this purpose, firstly, the geometry optimization of the reference molecule IOR was performed at four extensively used and reliable functionals. The functionals utilized here were B3LYP,33 CAM-B3LYP,34 ωB97XD,35 and MPW1PW91.36 From there on, the values of bandgaps from all these functionals were compared to that of the experimental bandgap (1.73 eV) cited in the literature.28,37 The values of bandgaps attained from the afore-stated functionals are tabulated alongside the experimental one in Table 1.| Functionals | Computed bandgap | Cited bandgap |
|---|---|---|
| B3LYP | 1.46 | 1.73 |
| CAMB3LYP | 2.05 | — |
| ωB97XD | 2.16 | — |
| MPW1PW91 | 1.56 | — |
From the tabulated data, the bandgap from MPW1PW91 seems to be the closest one to the experimental value. Thus for ground state optimization of geometries, this functional was selected as the one. Furthermore, for the selection of the functional for the excited state properties, all the afore-stated functionals were evaluated for their wavelengths of maximum (λmax) absorption in the cited chloroform solvent. The values of maximum absorption (λmax) obtained from all these functionals, at split valence 6-31G(d,p) basis set, were compared with the experimental value (806 nm) of the IOR molecule cited in the literature.19 From the values of 847 nm, 606 nm, 573 nm, and 794 nm obtained for the afore-stated functionals, respectively, it is seen that the value from MPW1PW91 is the closest to the reference value (Fig. 2). Thus, from this point onwards, based on both these validations, MPW1PW91 functional was selected, for further computations in this investigation of the structural, photo-physical, and optoelectronic properties of the newly proposed series of donor molecules.
 | ||
| Fig. 2 Comparative bar graph illustrating λmax from different functionals and their closeness to the cited value of IOR. | ||
Structural design consideration
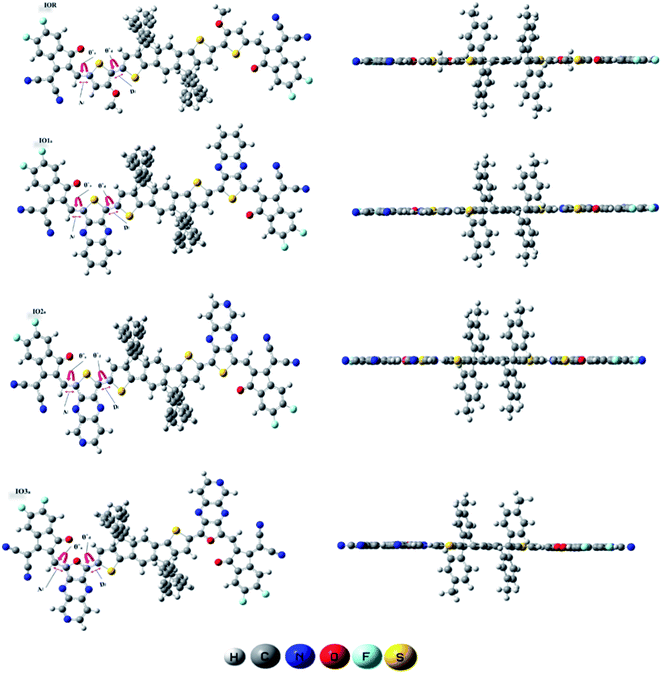
To examine the excited state properties of a molecule, it is crucial to first optimize the molecule at its ground state, so that a proper evaluation or comparison between the ground and excited state properties can be performed. Thus, all the investigated structures were first optimized at their ground state, and then their bond parameters (i.e., bond length and dihedral angle) were analyzed in order to study the variation in them caused due to the various bridges and their substitution positions.The bond parameters studied for the optimized molecular structures are enlisted in Table S1,† and they are also pictorially illustrated in Fig. 3 (for reference and “a” series of designed molecules) and Fig. S2† (for “b” series of newly formulated molecules). The bond length between the substituted π-linker and the attached acceptor moieties is demonstrated as Al, while the one between donor and π-linker is written as Dl. It was observed that the bond lengths between carbon atoms for all the studied point of attachments were within the range of the single bond length of 1.54 Å and double bond length of 1.34 Å. And it is commonly known that the closer a bond length is to the carbon–carbon double bond length, the more conjugated the corresponding molecule will be. This conjugation would help in better charge transfer and could significantly improve the opto-electronic properties of the evaluated molecules.38 Between our “a” and “b” series, all the three molecules of the “a” series established a decrease in their Al and Dl bond length, while a prominent increase in the studied bond lengths of molecules of the “b” series was seen. The decreased bond length in molecules of “a” series could contribute to their enhanced charge transfer attributes and absorption ranges due to their enhanced conjugation than that of their counterparts. Furthermore, in comparison to the reference molecule, the molecules of the “a” series seem to have lower values of evaluated bond lengths. While that of the “b” series have higher values and this illustrates the more enhanced conjugation in molecules of the “a” series than the reference IOR molecule and also hints toward the somewhat lowered conjugation in the molecules of the “b” series. The decreased conjugation in the studied bond length of molecules of the “b” series could be their twisted confirmation, as evaluated from their dihedral angles below.
The dihedral angle for the specified attachment sites in Fig. 3, (for reference and “a” series of designed molecules) and Fig. S2† (for “b” series of newly formulated molecules), was also examined in order to study the planarity in the molecules. The lower the dihedral angle a molecule has, the more planarity it will have. A general perspective is that planar molecules having bulky electron donor and acceptor segments are crucial in attaining effective separation and generation of charges. This planar geometry could also increase the conjugation length, as well as enhance the long-range π–π stacking in the molecule.39 In the studied molecules, the dihedral angle on the acceptor side, is represented through θa, and the one on the donor side, is written as θd. The θa and θd of all the molecules of the “a” series were lower than their counterparts in the “b” series. Moreover, these dihedral angles of all the molecules of the “a” series, except for θa of IO3a, were comparable to or lower than that of the reference molecule IOR, which shows the greater planarity in these molecules as compared to the reference molecules. This planarity could only be attributed to the fact that in the “a” series, all the acceptors and donors are attached through a thiophene/furan ring and not a bulky phenyl ring, as is the case in the “b” series. So, it could be supposed that molecules of “a” series, just like the reference molecule, due to the high level of planarity in their structures, could show better charge transfer attributes than that of the molecules of the “b” series.
Electronic properties
The highest occupied molecular orbitals (HOMO) and the lowest unoccupied molecular orbitals collectively constitute the frontier molecular orbitals (FMOs), and the difference between them is commonly known as the electronic band gap (Eg).40 Generally, for a high performing photovoltaic chromophore, the HOMO should be concentrated over the donor region of a molecule, while the LUMO should be more concentrated over the acceptor region. This way, the electron from the donor region could effectively be transferred over to the acceptor region.41 Also, the presence of charge density on the bridges show their contribution to the charge transfer from HOMO towards LUMO. Moreover, the lesser the band gap between the FMOs, the more efficient will be the active layer made from these molecules.42The orbital density analysis from Fig. S3† reveals that in the reference molecule IOR, the HOMO is spread over the donor, bridge, and a little bit on the acceptor region of the molecule. On the other hand, its LUMO is spread over the whole molecule except for the perpendicular phenyl rings in the central core. A similar trend of spread of charge density is followed by all the three molecules of the “a” series. This trend could be due to the similar planar topology of the reference and “a” series molecules. In the case of the “b” series, the HOMO charge density is highly concentrated over the central donor and π-linkers, and the LUMO is more densely spread over the π-linkers along with the acceptors. The lower charge density over the acceptors in the case of HOMO and donor in the case of LUMO could be due to the distorted configuration of the molecules in the “b” series.
So, here we could say that the molecules in the “b” series could act as better-performing photovoltaic molecules than the “a” series. But the spread of charge density over the whole molecule in “a” also signifies the presence of effective conjugation in them, which is an significant parameter in effective photovoltaic chromophores. The perpendicular orientation of the phenyl rings in the central core of the molecule could be the reason behind the no charge spread over them in both the HOMO and the LUMO. While comparing with the reference molecule, the trend of spread of charge density in bridges for FMOs of reference molecule was seen to be a bit different from all the newly proposed ones, as the HOMO charge density for all the newly reported molecules was minutely distributed over their bulky π-linkers, but this was not the case in IOR, where the charge density was actually significantly present on the alkoxy thiophene bridges.
The values of the evaluated FMOs and their calculated electronic band gap are tabulated in Table 2. It can be seen that the electronic band gap (Eg) for all the newly derived molecules is lower than the reference molecule. Also, from the values of FMOs, it was seen that the HOMO is lower-lying in the newly derived molecules than in the reference molecule, and this illustrates their better stability than IOR. This signifies the better performing capabilities of all our reported molecules than the IOR in the organic photovoltaic cells. Upon comparison between the Eg of both the series under consideration, the molecules in the “a” series exhibited a much lower band gap as compared to their counterparts in the “b” series. This lower Eg in the molecules of the “a” series could enhance the charge transfer between their FMOs.
| Molecules | EH (eV) | EL (eV) | Eg (eV) |
|---|---|---|---|
| IOR | −5.37 | −3.39 | 1.98 |
| IO1a | −5.50 | −3.85 | 1.65 |
| IO2a | −5.65 | −4.07 | 1.58 |
| IO3a | −5.70 | −4.10 | 1.60 |
| IO1b | −5.49 | −3.54 | 1.95 |
| IO2b | −5.50 | −3.72 | 1.78 |
| IO3b | −5.53 | −3.74 | 1.79 |
Specifically, the lowest bandgap amongst all the analyzed molecules of IO2 (both a and b). The reason behind this narrow bandgap could be due to the presence of its highly effective π-linkers, which though is quite similar to the bridges present in IO3, differing only in the presence of sulphur atom in place of oxygen, and this sulphur atom due to its lower ability to attract the electron towards itself as compared to the oxygen atom could effectively transfer charge from donor to terminal acceptor, instead of retaining it, thus lowering the bandgap. The highest bandgap within both the proposed series was of IO1a, which could be ascribed to the absence of one of the electron-withdrawing nitrogen atom at its π-linkers, as compared to the other two bridges. But overall, till now both the molecules in the “a” and the “b” series could act as better candidates for the active layer in the constructive organic solar cells due to their lower bandgaps than IOR.
Quantum chemical indices
In order to study the charge-transfer properties of any molecules, its softness, as well as hardness, could be analyzed.43 The chemical hardness is basically half of the difference between the ionization potential (IP) and electron affinity (EA) values. These values are also quite notable in determining the HOMO and LUMO energy levels of a molecule, as a low-lying HOMO exhibits high values of IP, and a higher value of EA proclaims a high LUMO.44 These values for the molecules under study calculated from eqn (3) and (4) are demonstrated in Table S2.†| IP = [E+0 − E0] | (3) |
| EA = [E0 − E−0] | (4) |
The relation of IP and EA with the chemical hardness and softness could be seen from the eqn (5) and (6).45
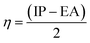 | (5) |
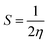 | (6) |
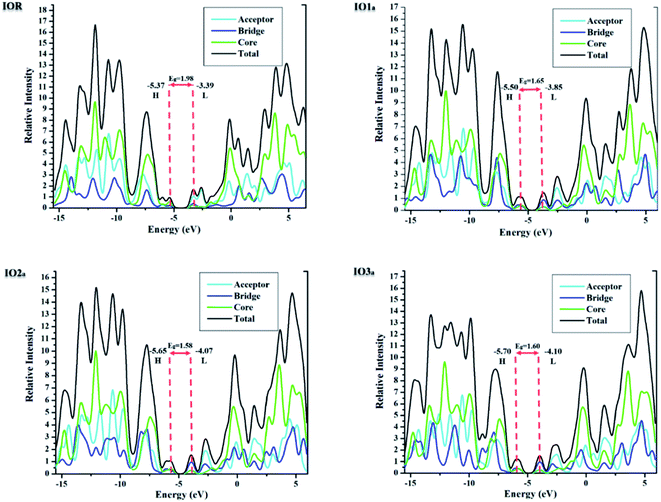
Density of states
The density of states (DOS) for all the scrutinized molecules was evaluated, in order to validate the results of the FMO analysis. These DOS are actually the number of states that an electron is allowed to occupy at a specific energy level, and they also represent the contribution of HOMO and LUMO orbitals in any electronic excitation.47 For the sake of ease of evaluation of the DOS, the molecules were fragmented into donor, acceptor, and bridges. In Fig. 4 and S4,† the partial density of states (PDOS) of acceptors is illustrated through the cyan line, bridges through blue, and that of the core is through the green line. These PDOS collectively formulate the black line, which is called the total DOS (TDOS). Moreover, the peaks to the left of the central planar zone represent the HOMO energy level, and those present towards its right illustrate the LUMO energy levels. While this planar “no peak zone” is actually the band gap between the analyzed energy levels and is in close collaboration with the findings of the value Eg from FMO analysis. A peak present more towards the LUMO region of the DOS plots illustrates the prominent conductive abilities of the corresponding fragment. In the plots of DOS, as compared to IOR, all the proposed molecules seem to have a high contribution of bridges in their LUMO region, with “a” series having the highest peaks of bridges in their DOS plots. This implies the higher involvement of the bridges in the “a” series to conduct charges.Table 3, obtained from Mulliken's calculations, helps in the quantitative assessment of the contribution of each fragment to a specific energy level. It is demonstrated that in IOR the contribution of the donor in elevating the HOMO value is higher than the molecules of the “a” series, while its contribution is lower than the molecules of the “b” series. Actually, the spread of charge density in the HOMO, as well as LUMO of the molecules in the “a” series, illustrates their somewhat better planar configuration than the reference molecule. An important point to note here is that the substituted bridges in both the “a” and “b” series have higher charge density than that of the cited molecule in both the studied FMOs, this signifies the contribution of the newly introduced bridges to transfer charges than that of the alkoxy thiophene bridges present in IOR. Furthermore, from the quantitative values of the percentage involvement of all the fragments of the molecules in DOS plots, it can be understood that the newly substituted bridges in the molecules have higher values of their involvement in the LUMO charge density than HOMO, which signifies their enhanced charge conductive abilities.
| Molecules | HOMO | LUMO | ||||
|---|---|---|---|---|---|---|
| Donor (%) | Linker (%) | Acceptors (%) | Donor (%) | Linker (%) | Acceptor (%) | |
| IOR | 58.1 | 22.7 | 19.2 | 17.5 | 24.4 | 58.1 |
| IO1a | 40.5 | 30.5 | 29.0 | 21.9 | 56.2 | 21.9 |
| IO2a | 42.6 | 29.8 | 27.6 | 19.4 | 60.0 | 20.7 |
| IO3a | 36.6 | 30.3 | 33.1 | 20.8 | 59.6 | 19.6 |
| IO1b | 65.6 | 24.6 | 9.80 | 11.3 | 51.2 | 37.5 |
| IO2b | 68.6 | 23.6 | 7.80 | 9.30 | 58.1 | 32.6 |
| IO3b | 68.7 | 23.9 | 7.40 | 9.20 | 56.5 | 34.3 |
Spectral absorption and other photovoltaic attributes
For the evaluation of the excited state photovoltaic properties of the scrutinized molecules in both the gas and solvent (chloroform) phase, the molecules were computed at the selected functional MPW1PW91 of the TD-DFT calculations. The wavelength of maximum absorption (λmax) of electromagnetic radiations between the HOMO and LUMO energy levels is pictorially illustrated with the graphs obtained from Origin 6.0 software in Fig. S5.† Moreover, for easy comparison between the λmax of the proposed molecules and the reference molecule, their bar graphs are represented in Fig. 5. Also, the values of optical band gap (Ex), oscillator strength (f), light-harvesting efficiency, and the percentage contribution of the FMOs in the studied excitation for both the gas and phase are enlisted in Tables 4 and 5, respectively.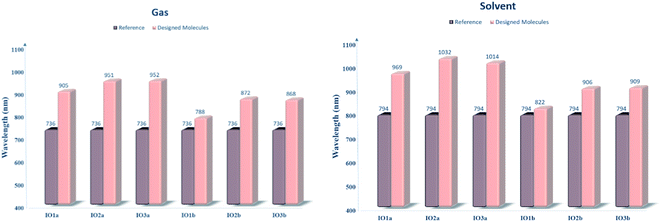 | ||
| Fig. 5 Bar graphs comparing the λmax of reference with that of the designed molecules in both the gas (left) and solvent (right) phase. | ||
| Molecules | Computed λmax (nm) | Experimental λmax (nm) | Ex (eV) | fos | LHE | Main configuration |
|---|---|---|---|---|---|---|
| IOR | 734 | 797 | 1.6848 | 2.8479 | 0.9986 | H to L (70%) |
| IO1a | 905 | 1.3716 | 2.2417 | 0.9943 | H to L (69%) | |
| IO2a | 951 | 1.3043 | 2.0534 | 0.9912 | H to L (69%) | |
| IO3a | 952 | 1.3018 | 1.6748 | 0.9789 | H to L (69%) | |
| IO1b | 788 | 1.5735 | 1.9338 | 0.9884 | H to L (69%) | |
| IO2b | 872 | 1.4218 | 1.6237 | 0.9762 | H to L (70%) | |
| IO3b | 868 | 1.4289 | 1.6295 | 0.9765 | H to L (70%) |
| Molecules | Computed λmax (nm) | Experimental λmax (nm) | Ex (eV) | fos | LHE | Main configuration |
|---|---|---|---|---|---|---|
| IOR | 794 | 806 | 1.5624 | 3.1403 | 0.9992 | H to L (69%) |
| IO1a | 969 | 1.2798 | 2.6178 | 0.9977 | H to L (69%) | |
| IO2a | 1032 | 1.2010 | 2.3839 | 0.9958 | H to L (69%) | |
| IO3a | 1014 | 1.2229 | 2.0187 | 0.9904 | H to L (69%) | |
| IO1b | 822 | 1.5075 | 2.2098 | 0.9938 | H to L (69%) | |
| IO2b | 906 | 1.3692 | 1.9186 | 0.9879 | H to L (69%) | |
| IO3b | 909 | 1.3635 | 1.8766 | 0.9867 | H to L (69%) |
The absorption spectra in Fig. S5† presents two peaks. Here the higher prominent peaks represent the maximum absorption (λmax), while the lower smaller peaks represent the presence of π–π stacking in the molecules. The smaller peaks are significantly enhanced in the designed molecules as compared to the IOR molecule, which shows the better π–π stacking in the newly reported molecules than the cited one.48 Also, the reference molecule IOR has the lowest λmax value amongst all, in both the evaluated phases. This λmax follows the ascending order of IOR < IO1b < IO2b < IO3b < IO1a < IO2a < IO3a in the gas phase, and a slightly different trend of IOR < IO1b < IO2b < IO3b < IO1a < IO3a < IO2a is followed in the solvent phase as well. The highest values of λmax in molecules of the “a” series signifies the presence of enhanced conjugation in their structures, which could lead to absorption of radiations in the higher wavelength. In addition, the IO2a molecule, due to its prominently charge transferring bulky π-bridges and their relative substitution position, displays the highest λmax amongst all in the solvent phase, also the reason behind the marginally higher λmax value of IO3a in the gas phase could illustrate the enhanced ability of this molecule to transfer charge than all others in the gaseous medium. Between the gas and the solvent phase, the high values of λmax in the latter phase exhibit the compatibility of the investigated molecules with the chloroform solvent.28 This way, we could assume that all the reported molecules can be easily used for effective solution manufacturing of OSCs, while IO3a could perform slightly better in the gas phase than in the solvent medium.
The optical band gap, commonly known as the excitation energy (Ex) of a molecule, is the minimum amount of energy required to excite an electron49 and is an important asset in determining the capability of the desired molecule to be utilized in the active layer of the OSCs. An effectively performing photovoltaic cell generally needs to have a low value of Ex.50 From Tables 4 and 5, it can be seen that the Ex of all the molecules in both the reported series is lower than the Ex of IOR, while between the “a” and “b” series, the former exhibits the lower values of Ex. Again, the lower Ex values of all the proposed molecules than reference could be due to their enhanced charge transferring bridges, as opposed to the ones in IOR, while the lowest value amongst all, of the molecules of “a” series, promotes our claim of this series being a better one due to the substitution position of its prominent bridges. In addition, the lowest Ex value amongst all the molecules in the evaluated solvent phase was seen for IO2a, which could also be the reason behind its highest λmax value in this solvent. Actually, all the molecules in both the analyzed phases follow the same trend as the one in the case of their λmax values, so it could be said that λmax has a direct relation to excitation energy in the case of our studied molecules.51
The oscillator strength (f) is a prominent dimensionless parameter, which has a direct relation with the light-harvesting efficiency (LHE) of a molecule. This LHE is the ability of a molecule to harvest the energy that falls upon its surface.52 Thus, the greater the value of f, the greater will be the LHE, and in return greater will be the photovoltaic abilities of the molecule.53 Between our newly reported series, the “a” series once again gave better results than its relative counterpart and thus could exhibit better charge transfer attributes than the “b” series. The values of LHE in Tables 4 and 5 were obtained from the formula written below.
| LHE = 1 − 10−f | (7) |
Solution processabilities
Dipole moment (μ) is a remarkable asset in the estimation of the solar efficiency of any photovoltaic cell. It has a direct association with the solubility of the molecule in the desired solvent. Molecules with high values of dipole moment are generally quite polar and thus are easily soluble in polar solvents.54 Though a symmetrical molecule should have a high μ, highly symmetrical molecules usually tend to have zero or close to zero dipole moment owing to the cancellation of opposite and antiparallel charges in them. A significant characteristic of dipole moment is that molecules with high values of dipole moment show better charge transfer between their FMOs.55 This should also be taken into account that molecules with low dipole moment, due to their highly symmetrical structure, have increased conjugation in them and thus could show better light absorption properties.56Between the two newly reported series of designed molecules, when compared to the reference IOR, the “a” series shows a slight decrease, while the “b” series exhibits a significant increase in its dipole moment values. The lowered values of μ in the “a” series could be attributed to their planar topology. And the increased μ values in the “b” series could be due to their more twisted conformation. This could be one of the reasons behind the increase in the photovoltaic attributes of the molecules in the “a” series, and the better separation of HOMO–LUMO charge density in the “b” series. Table 6 represents the values of μ computed for both the gas (μg) and the solvent (μs) phase, along with their difference. The increased values of μs as compared to μg illustrate the stability of our newly formulated molecules in the chloroform solvent. The difference of only 0.000016 in the IO2a molecule shows that this molecule could be effectively utilized in the active layer of OSCs irrespective of its medium. Overall, the highest dipole moment amongst all of IO2b could be due to the twisted conformation, as well as the prominent electron transferring bridges present in this molecule, and implies its superior charge transfer features to all others.
| Molecule | μg (Debye) | μs (Debye) | μs–μg (Debye) |
|---|---|---|---|
| IOR | 0.000616 | 0.000812 | 0.000196 |
| IO1a | 0.000510 | 0.000714 | 0.000204 |
| IO2a | 0.000316 | 0.000332 | 0.000016 |
| IO3a | 0.002500 | 0.003108 | 0.000608 |
| IO1b | 1.812156 | 2.379546 | 0.567390 |
| IO2b | 5.031879 | 6.825028 | 1.793149 |
| IO3b | 3.558277 | 4.845889 | 1.287612 |
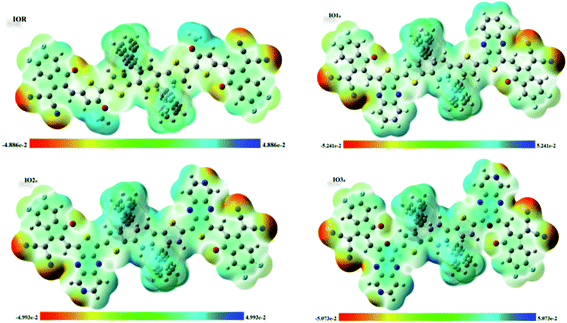
Molecular electrostatic potential (MESP) surfaces
MESPs are the hued contours around the molecules, which are attained through the selected functional and basis set at their ground state. These MESPs represent the potential a positive charge may experience when it is brought near the scrutinized molecule. These surfaces help to determine the effect of the structure on the reactivity, as well as the charge-density of the molecule.51 They also illustrate the sites of attack of the attacking reagent. These three-dimensional colored clouds around the molecules show a range of colors between two extremities of red and blue, where blue shows the maximum potential and red signifies the minimum potential.57 The red-colored areas are electron-deficient and thus are effective sites for the attack of an incoming nucleophile, while the blue-colored zones due to them being electron-rich acts as the sites of attack of an electrophile. The green-colored areas in the MESPs demonstrate the neutral or zero potential areas.58In the scrutinized molecules the red contours are seen all around the highly electronegative unsaturated oxygen and nitrogen atoms, while all the phenyl rings owing to them being electron-rich show blue-colored clouds around them (Fig. 6 (for reference and “a” series) and Fig. S6† (for “b” series)). The molecules of the “a” series show quite distinctive blue zones, while the red color is dispersed around the whole molecule in their counterparts of the “b” series. This provides us a shred of evidence towards our assumption that the molecules of the “a” series could act as better donor molecules and could have better charge transfer ability than that of the “b” series, accredited to the distinctive separation of charge density in these molecules.
Exciton dissociation energy
As the name indicates it is the amount of energy needed in order to dismantle the short-lived excitons (electron–hole pairs) generated after the absorption of electromagnetic radiations.59 It is also known as the binding energy (Eb), as it is the energy required to disintegrate the bound electron–hole pair. It has a direct relation with the coulombic interactions within the excitons. The reason behind the need to rapidly separate these charges is so that they can quickly and effectively move towards their respective electrodes and not recombine, and this way maximum photocurrent could be generated. So, the lower this binding energy is, the better will be the charge dissociation. Eb values in Table S3† are actually calculated through the difference between the values of optical and electronic band gap, as represented through the eqn (8) below60,61| Eb = Eg − Ex | (8) |
In the above equation, Eg is the electronic band gap, Ex demonstrates the optical band gap, while Eb shows the binding or exciton dissociation energy.
In gas phase, the newly reported molecules along with the reference IOR shows the decreasing order of IO1b > IO3b > IO2b > IO3a > IOR > IO1a > IO2a, and a different trend of IO1b > IO3b > IOR > IO2b > IO2a > IO3a > IO1a is followed by them in the solvent phase. It is clear from these trends that the binding energy is the lowest for molecules of “a” series amongst all, with the slight exception of IO3a in the gas phase. The lowest value of binding energy for IO2a in the gas phase illustrates the improved capability of this molecule to dissociate the excitons in the gas phase, amongst all other studied molecules. Similarly, in the solvent phase, the lowest value of binding energy of IO1a, amongst all, shows its notable ability to transfer charges towards the separated electrodes in the solvent phase. The highest value of binding energy in both the proposed series was seen to be of IO3 (a and b), which could be due to the presence of highly electron withdrawing oxygen atom present in the bridges of this molecule that instead of transfer the charges between the donor and acceptor must have shifted the charges towards themselves, thus raising the value of binding energy of the corresponding molecule. Overall, the lower values of binding energies for molecules of “a” series, signifies their ability to act as better light harvesting photovoltaic materials than the cited IOR molecule, as well as the molecules of the “b” series. Also, upon comparison between the binding energies in the gas phase and the solvent one, the high values of Eb in the solvent phase than the gas phase actually emphases' the notable association of the researched molecules with the solvent chloroform.
Transition density matrix
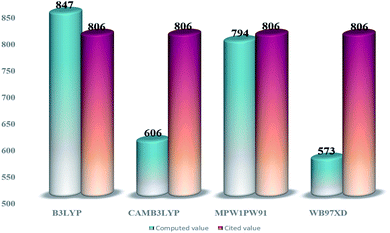
From the plots of transition density matrix (TDM), presence of electronic delocalization and localization in a molecule can be identified. From these plots, the excitation of electrons along with the position of excitons (electron–hole pair) can be estimated, as well.62 Moreover, the short-circuit current (JSC) in an organic photovoltaic cell can be evaluated through the analysis of charge density illustrated through the TDM plots. As the molecules having low electron–hole coupling (localization) tends to have high charge transfer rate, and thus high values of JSC.63The TDM plots in Fig. 7 (for reference and “a” series) and Fig. S7† (for “b” series), were formulated using the MPW1PW91 functional of TD-DFT computations, at the 6-31G(d,p) basis set. The two-dimensional plots of TDM thus generated, have on their left y- and lower x-axis, the number of atoms present in the molecule except for hydrogen atoms. The reason behind the exclusion of hydrogen atoms (by default) is their insignificant contribution in the migration of charge density in the molecule.64 Along the right y-axis of the TDM plots, the charge density is represented with the help of different colors ranging from blue at one extreme to red at the other. The blue color demonstrates zero charge density, while red shows the maximum charge density present in the transition of the specific molecule.65 For easier evaluation, the number of atoms in the TDMs were fragmented into donor core (C), bridges (π), and acceptor (A) of the molecule. Here, between IO1a and IO1b, the charge density is diagonally as well as off-diagonally spread over the bridges and acceptor components of the molecules, respectively, as represented by their brighter fringes in these areas as compared to others. But in case of all other designed molecules, the charge density is highly condensed over the π bridges. This spread of charge density signifies the contribution of the π-linkers in effective transfer of charges between acceptor and donor components of the molecules.
Charge transfer mobilities
Another notably prominent tool in determining the charge transfer attributes of a molecule is to analyze its reorganization energies (λ). This λ can be evaluated using the semi-classical Marcus theory. This theory leads to the conclusion that charge transfer mobilities and reorganization energies (λ) have an inverse association between them. This claim can be justified through the eqn (9) below66
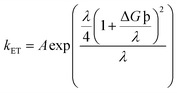 | (9) |
The kET in the above equation represents the rate of charge transfer and A directly depends on the type of charge transfer (whether intramolecular or intermolecular). The term ΔG° represents the standard free energy, which is close to zero in the self-exchange intramolecular transfer reaction studied for the newly derived molecules. Lastly, λ is the reorganization energy term and further consists of two parts; inner (λv) and outer (λs), as represented in eqn (10) below66
| λ = λv + λs | (10) |
The latter directly corresponds to the external solvent response, and its effect is neglected in this study, due to the constant external chloroform environment. The former term (λv) is related to the energy expenditure when a molecule switches its neutral geometry towards a charged geometry and vice versa.67 This λv further divides into electron (λe) and hole (λh) reorganization energies. Where λe is correlated to the energy utilized for the reorganization of the molecular geometry after the intramolecular transfer of electron, similar is the case for λh but with a hole instead of an electron transfer. The computed values for both the terms of λv, i.e., λe and λh, were calculated with the help of eqn (1) and (2), and are represented in Table 7.
| Molecules | λh (hole) | λe (electron) |
|---|---|---|
| IOR | 0.0077052 | 0.005041 |
| IO1a | 0.0060543 | 0.0067175 |
| IO2a | 0.0060808 | 0.0066025 |
| IO3a | 0.0063082 | 0.0065544 |
| IO1b | 0.0090177 | 0.0101874 |
| IO2b | 0.0090450 | 0.0106523 |
| IO3b | 0.0093598 | 0.0117805 |
Accredited to the lower number of electron withdrawing atoms (N and O) present in its bridges, the IO1a molecule seemed to have higher hole mobility than other studied ones, as seen from its lowest λh value amongst all. In case of the reference molecule IOR, its lowest λe implies the notable ability of this molecule to act as the fullerene-free acceptor, as cited in many literatures.68 But in case of our proposed molecule, all of them, due to their lower values of λh relative to the λe, could act as better donor molecules, as opposed to the reference molecule. Also, from the values of λh, it is demonstrated that all the molecules of “a” series have lower λh than the cited molecule (IOR), while reverse is the case for the molecules of the “b” series. So, it can be evaluated that all the molecules of “a” series would have better transfer of hole within their molecular structure than that of the IOR and the other series of designed molecules. The higher values of both the evaluated reorganization energies for molecules of “b” series could be credited to the twisted confirmation of the molecules, which upon transfer of charges would require greater energy to reorganize themselves. On another note, though the values of λe are higher than IOR for both the “a” as well as “b” series, still the “a” series could show better electron mobilities than the “b” series due to their low λe values. Contrary to their counterparts, the lowered values of λh in Fig. S8,† provides a significant evidence towards our claim of the newly designed molecules being donors in the active layer of effective OSCs.
Photo-conversion efficiency
The photo-conversion efficiency (η) of a molecule can be evaluated through the eqn (11) written below69
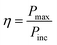 | (11) |
In the above equation, Pinc represents the intensity of radiant energy, which falls on the active layer of the organic photovoltaic cell, and Pmax in the numerator can be computed through the eqn (12).70
| Pmax = VOCFFJSC | (12) |
The first term in the eqn (10) above, i.e., the open-circuit voltage, is the maximum amount of voltage generated, when external supplied current is close to a minimum. This VOC can be calculated through the eqn (13).71
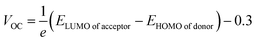 | (13) |
| Molecules | VOC (V) | Normalized VOC (voc) | Fill factor |
|---|---|---|---|
| IOR | 1.37 | 53.039 | 0.90776 |
| IO1a | 1.50 | 58.072 | 0.91410 |
| IO2a | 1.65 | 63.879 | 0.92161 |
| IO3a | 1.70 | 65.815 | 0.92220 |
| IO1b | 1.49 | 57.684 | 0.91365 |
| IO2b | 1.50 | 58.072 | 0.91410 |
| IO3b | 1.53 | 59.233 | 0.91544 |
Upon comparison with the reference molecule IOR, all the newly presented molecules exhibited higher VOC, which signifies their better voltage generating ability (Fig. 8). While, between the molecules of “a” and “b” series, the molecules of the “a” series once again suppressed their twisted counterparts, owing to their larger VOC than the “b” series molecules. While, within the “a” series, the highest open-circuit voltage was seen to be of IO3a, which could be accredited to its lowered and stabilized HOMO value.
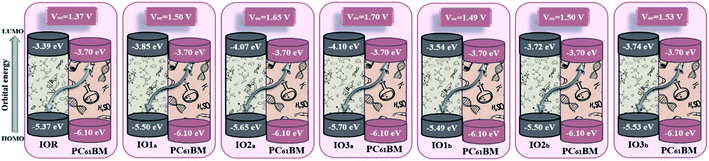 | ||
| Fig. 8 Open-circuit voltage of all the researched molecular donors attained with PC61BM acceptor molecule. | ||
The second evaluated factor for the PCE, the fill factor also has direct association with the photo-conversion efficiency of the molecule. This dimensionless value was determined through the eqn (14).
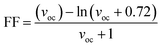 | (14) |
In the above equation, voc is the normalized VOC and is enlisted in Table 8 using the formula 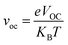 . Where, e is the charge of 1 on the molecule, KB is the Boltzmann constant in eV and T is the average room temperature of 300 K.61 From the values of FF in Table 8, it can be evaluated that all the newly reported molecules can have better PCE than the reference molecule IOR, with the molecules of the “a” series being better than their alternates. Here, the IO3a molecule, owing to its highest VOC, shows the maximum value of FF amongst all, and thus could be utilized in the active layer of organic solar cells with the aim of enhancing their solar efficiencies.
. Where, e is the charge of 1 on the molecule, KB is the Boltzmann constant in eV and T is the average room temperature of 300 K.61 From the values of FF in Table 8, it can be evaluated that all the newly reported molecules can have better PCE than the reference molecule IOR, with the molecules of the “a” series being better than their alternates. Here, the IO3a molecule, owing to its highest VOC, shows the maximum value of FF amongst all, and thus could be utilized in the active layer of organic solar cells with the aim of enhancing their solar efficiencies.
The last term in the numerator of eqn (12) is the short-circuit current (JSC) and can be theoretically calculated using the equation below72
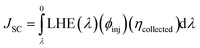 | (15) |
Conclusion
To the study the effect of different π-linkers and their substitution positions on the opto-electronic properties of IOR molecule, various π-linkers were attached at two sites of attachment, i.e., phenyl ring (b series) or thienyl/furyl ring (a series) of the same bridge. In this research work, three different bridges were substituted in the IOR molecule, and the thus formulated two series “a” and “b” were analyzed for their photo-physical and related photovoltaic attributes. It was seen that between these two series, the “a” series exhibited enhanced results in most of the studied properties. Such as, the maximum absorption values (λmax), excitons binding energy, electronic and optical band gap, open-circuit voltage, fill factor, chemical softness and hardness, and the hole reorganization energies, all gave outcomes in favor of utilizing the donor molecules of “a” series for the construction of effective organic photovoltaic cells. All these enhanced properties could be attributed to the extensively planar configuration of the molecules of the “a” series. The twisted molecules of the “b” series showed increased values of dipole moment along with better separation of charge densities in their FMOs. Though, the molecules of the “b” series were a step back from their superior counterparts, still they just like the molecules of the “a” series showed enhanced opto-electronic properties than the highly planar reference molecule IOR. This could be attributed to the presence of greater conjugation and enhanced charge transfer attributes in the newly substituted π-linkers in all the newly reported molecules than the ones in IOR. In addition, amongst all the proposed molecules of the “a” series, IO1a and IO2a seemed to show enhanced optoelectronic attributes, while IO3a showed the highest values of factors related to the PCE. But, the values of these factors was also quite high for the other two molecules. So overall, we can conclude that both the π-linker and their substitution position directly affects the opto-electronic attributes of different photovoltaic chromophores. Also, all the newly reported molecules would be proficient substitutes to IOR in order to construct superiorly effective active layers in OSCs, with the “a” series being the best one.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4331174DSR14). The authors also extend their appreciation to this work was supported by King Khalid University through a grant (KKU/RCAMS/22) under the Research Center for Advanced Materials Science (RCAMS) at King Khalid University, Saudi Arabia. Funding acquisition from Punjab Bio-energy Institute (PBI), University of Agriculture Faisalabad (UAF), Pakistan.References
- A. S. Jitender, A. Mahajan and S. Ahluwalia, Algal Biology and Biotechnology, 2009 Search PubMed.
- K. Jaffar, Z. M. Elqahtani, Q. Q. Afzal, M. Ans, S. Riaz, M. A. Tahir, J. Iqbal, Z. M. Mahmoud, Z. Alrowaili and M. Al-Buriahi, Polymer, 2022, 245, 124675 CrossRef CAS.
- J. Guo, B. Qiu, D. Yang, C. Zhu, L. Zhou, C. Su, U. S. Jeng, X. Xia, X. Lu and L. Meng, Adv. Funct. Mater., 2021, 2110159 Search PubMed.
- G. Chamberlain, Solar Cells, 1983, 8, 47–83 CrossRef CAS.
- A. Colsmann, H. Röhm and C. Sprau, Solar RRL, 2020, 4, 2000015 CrossRef.
- S. Zhao, X. Pi, C. Mercier, Z. Yuan, B. Sun and D. Yang, Nano Energy, 2016, 26, 305–312 CrossRef CAS.
- K. Sreedhar Ram, H. Mehdizadeh-Rad, D. Ompong, D. D. Y. Setsoafia and J. Singh, Nanomaterials, 2021, 11, 209 CrossRef PubMed.
- A. Tang, B. Xiao, F. Chen, J. Zhang, Z. Wei and E. Zhou, Adv. Energy Mater., 2018, 8, 1801582 CrossRef.
- L. Xu, Y. Ji, X. Shi, L. Wang and K. Gao, Org. Electron., 2020, 85, 105886 CrossRef CAS.
- X. Lu, Y. Shao, S. Wei, Z. Zhao, K. Li, C. Guo, W. Wang, M. Zhang and W. Guo, J. Mater. Chem. C, 2015, 3, 10129–10139 RSC.
- C.-K. Tai, Y.-J. Chen, H.-W. Chang, P.-L. Yeh and B.-C. Wang, Comput. Theor. Chem., 2011, 971, 42–50 CrossRef CAS.
- S. UrRehman, M. Anwer, S. BiBi, S. Jamil, M. Yasin, S. R. Khan, R. Nadeem, S. Ali and R. Jia, Mater. Sci. Semicond. Process., 2022, 140, 106381 CrossRef CAS.
- N. Prachumrak, T. Sudyoadsuk, A. Thangthong, P. Nalaoh, S. Jungsuttiwong, R. Daengngern, S. Namuangruk, P. Pattanasattayavong and V. Promarak, Mater. Chem. Front., 2017, 1, 1059–1072 RSC.
- J. Li, C. Sun, A. Tang, B. Zhang, Q. Guo, E. Zhou and Y. Li, J. Mater. Chem. C, 2020, 8, 15981–15984 RSC.
- H. Yao, Y. Cui, R. Yu, B. Gao, H. Zhang and J. Hou, Angew. Chem., 2017, 129, 3091–3095 CrossRef.
- T. An, Q. Wang, J. Xue and Y. Su, J. Mod. Opt., 2022, 69, 336–345 CrossRef CAS.
- X. Che, C. L. Chung, X. Liu, S. H. Chou, Y. H. Liu, K. T. Wong and S. R. Forrest, Adv. Mater., 2016, 28, 8248–8255 CrossRef CAS PubMed.
- X. Liu, F. Kong, R. Ghadari, S. Jin, W. Chen, T. Yu, T. Hayat, A. Alsaedi, F. Guo and Z. a. Tan, Energy Technol., 2017, 5, 1788–1794 CrossRef CAS.
- Y. Chang, X. Zhang, Y. Tang, M. Gupta, D. Su, J. Liang, D. Yan, K. Li, X. Guo and W. Ma, Nano Energy, 2019, 64, 103934 CrossRef CAS.
- A. Waqas, S. Bibi, S. u. Rehman, S. Afzal, M. Yaseen, M. Shoaib, U. Saeed and W. Da Ming, J. Phys. Org. Chem., 2019, 32, e4000 CrossRef CAS.
- R. E. Buntrock, J. Chem. Inf. Comput. Sci., 2002, 42, 1505–1506 CrossRef CAS PubMed.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView 6.0.16. Semichem Inc., Shawnee Mission, KS, USA, 2016 Search PubMed.
- A. Frisch, Gaussian 09W Reference, Wallingford, USA, 2009, p. 25 Search PubMed.
- J. Antony and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 5287–5293 RSC.
- N. M. O’boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- D. Jacquemin, J. Preat and E. A. Perpète, Chem. Phys. Lett., 2005, 410, 254–259 CrossRef CAS.
- A. C. Yüzer, G. Kurtay, T. İnce, S. Yurtdaş, E. Harputlu, K. Ocakoglu, M. Güllü, C. Tozlu and M. İnce, Mater. Sci. Semicond. Process., 2021, 129, 105777 CrossRef.
- W. Wang, B. Zhao, Z. Cong, Y. Xie, H. Wu, Q. Liang, S. Liu, F. Liu, C. Gao and H. Wu, ACS Energy Lett., 2018, 3, 1499–1507 CrossRef CAS.
- L. A. Deschenes and D. A. Vanden Bout, Origin 6.0, University of Texas, 2000 Search PubMed.
- C.-P. Hsu, Phys. Chem. Chem. Phys., 2020, 22, 21630–21641 RSC.
- S. Bibi, R. Jia, H.-X. Zhang and F.-Q. Bai, Solar Energy, 2019, 186, 311–322 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- H. Fang and Y. Kim, J. Chem. Theory Comput., 2011, 7, 642–657 CrossRef CAS PubMed.
- Y. Zhao, J. Pu, B. J. Lynch and D. G. Truhlar, Phys. Chem. Chem. Phys., 2004, 6, 673–676 RSC.
- Y. Liu, M. Li, X. Zhou, Q.-Q. Jia, S. Feng, P. Jiang, X. Xu, W. Ma, H.-B. Li and Z. Bo, ACS Energy Lett., 2018, 3, 1832–1839 CrossRef CAS.
- M. Ans, J. Iqbal, B. Eliasson and K. Ayub, Comput. Mater. Sci., 2019, 159, 150–159 CrossRef CAS.
- Y. Kim, H. Hwang, N. K. Kim, K. Hwang, J. J. Park, G. I. Shin and D. Y. Kim, Adv. Mater., 2018, 30, 1706557 CrossRef PubMed.
- S. J. Akram, J. Iqbal, M. Ans, Y. A. El-Badry, R. F. Mehmood and R. A. Khera, Solar Energy, 2022, 237, 108–121 CrossRef CAS.
- J. Bradley and G. Gerrans, J. Chem. Educ., 1973, 50, 463 CrossRef CAS.
- X. Wan, C. Li, M. Zhang and Y. Chen, Chem. Soc. Rev., 2020, 49, 2828–2842 RSC.
- Z. Liang, L. Yan, J. Si, P. Gong, X. Li, D. Liu, J. Li and X. Hou, Materials, 2021, 14, 6723 CrossRef CAS PubMed.
- C. Cárdenas, F. Heidar-Zadeh and P. W. Ayers, Phys. Chem. Chem. Phys., 2016, 18, 25721–25734 RSC.
- I. Zubair, R. A. Kher, S. J. Akram, Y. A. El-Badry, M. U. Saeed and J. Iqbal, Chem. Phys. Lett., 2022, 793, 139459 CrossRef CAS.
- J. L. Gázquez, Chemical Hardness, 1993, pp. 27–43 Search PubMed.
- M. U. Saeed, J. Iqbal, R. F. Mehmood, S. J. Akram, Y. A. El-Badry, S. Noor and R. A. Khera, Surf. Interfaces, 2022, 30, 101875 CrossRef CAS.
- H. Bin, J. Yao, Y. Yang, I. Angunawela, C. Sun, L. Gao, L. Ye, B. Qiu, L. Xue and C. Zhu, Adv. Mater., 2018, 30, 1706361 CrossRef PubMed.
- H.-Q. Peng, L.-Y. Niu, Y.-Z. Chen, L.-Z. Wu, C.-H. Tung and Q.-Z. Yang, Chem. Rev., 2015, 115, 7502–7542 CrossRef CAS PubMed.
- C. Yan, S. Barlow, Z. Wang, H. Yan, A. K.-Y. Jen, S. R. Marder and X. Zhan, Nat. Rev. Mater., 2018, 3, 1–19 CrossRef.
- S. Zahid, A. Rasool, M. Ans, M. Yaseen and J. Iqbal, Energy Fuels, 2021, 35, 15018–15032 CrossRef CAS.
- P. Li, Z. Wang, C. Song and H. Zhang, J. Mater. Chem. C, 2017, 5, 11454–11465 RSC.
- U. Yaqoob, A. R. Ayub, S. Rafiq, M. Khalid, Y. A. El-Badry, Z. M. El-Bahy and J. Iqbal, J. Mol. Liq., 2021, 341, 117428 CrossRef CAS.
- M. Salim, M. Rafiq, Y. A. El-Badry, R. A. Khera, M. Khalid and J. Iqbal, J. Mol. Model., 2021, 27, 1–14 CrossRef PubMed.
- C. Zhong, D. Bialas and F. C. Spano, J. Phys. Chem. C, 2020, 124, 2146–2159 CrossRef CAS.
- M. Rumi, J. E. Ehrlich, A. A. Heikal, J. W. Perry, S. Barlow, Z. Hu, D. McCord-Maughon, T. C. Parker, H. Röckel and S. Thayumanavan, J. Am. Chem. Soc., 2000, 122, 9500–9510 CrossRef CAS.
- M. Adnan, M. Y. Mehboob, R. Hussain and Z. Irshad, Energy Fuels, 2021, 35, 11496–11506 CrossRef CAS.
- H. Yao, D. Qian, H. Zhang, Y. Qin, B. Xu, Y. Cui, R. Yu, F. Gao and J. Hou, Chin. J. Chem., 2018, 36, 491–494 CrossRef CAS.
- Q.-Q. Pan, S.-B. Li, Y. Wu, G.-Y. Sun, Y. Geng and Z.-M. Su, RSC Adv., 2016, 6, 81164–81173 RSC.
- M. R. Narayan and J. Singh, Phys. Status Solidi C, 2012, 9, 2386–2389 CrossRef CAS.
- M. I. Khan, J. Iqbal, S. J. Akram, Y. A. El-Badry, M. Yaseen and R. A. Khera, J. Mol. Graphics Modell., 2022, 113, 108162 CrossRef CAS PubMed.
- Y. Li and C. Ullrich, Chem. Phys., 2011, 391, 157–163 CrossRef CAS.
- M. Ans, A. Ayub, N. Alwadai, A. Rasool, M. Zahid, J. Iqbal and M.S Al-Buriahi, J. Phys. D: Appl. Phys., 2022, 55, 235501 CrossRef.
- R. McWeeny, Rev. Mod. Phys., 1960, 32, 335 CrossRef.
- A. Tajammal, M. Ans, R. F. Mehmood, J. Iqbal, S. J. Akram, A. Murtaza and R. A. Khera, Comput. Theor. Chem., 2022, 1211, 113666 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599 CrossRef CAS.
- Y. Zhao and W. Liang, Chem. Soc. Rev., 2012, 41, 1075–1087 RSC.
- M. Chen, D. Liu, W. Li, R. S. Gurney, D. Li, J. Cai, E. L. Spooner, R. C. Kilbride, J. D. McGettrick and T. M. Watson, ACS Appl. Mater. Interfaces, 2019, 11, 26194–26203 CrossRef CAS PubMed.
- L. Kosyachenko and E. Grushko, Semiconductors, 2010, 44, 1375–1382 CrossRef CAS.
- J. Ajayan, D. Nirmal, P. Mohankumar, M. Saravanan, M. Jagadesh and L. Arivazhagan, Superlattices Microstruct., 2020, 143, 106549 CrossRef CAS.
- M. Rafiq, M. Salim, S. Noreen, R. A. Khera, S. Noor, U. Yaqoob and J. Iqbal, J. Mol. Liq., 2022, 345, 118138 CrossRef CAS.
- W. Li, J. Wang, J. Chen, F.-Q. Bai and H.-X. Zhang, Phys. Chem. Chem. Phys., 2014, 16, 9458–9468 RSC.
- M. Salim, M. Rafiq, R. A. Khera, M. Arshad and J. Iqbal, Solar Energy, 2022, 233, 31–45 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: S1 include Cartesian coordinates of internally optimized geometries of all molecules. See https://doi.org/10.1039/d2ra04097b |
| This journal is © The Royal Society of Chemistry 2022 |