3d Transition metal doping induced charge rearrangement and transfer to enhance overall water-splitting on Ni₃S₂ (101) facet: a first-principles calculation study

Abstract

Cost-efficient bifunctional electrocatalysts with good stability and high activity are in great demand to replace noble-metal-based catalysts for overall water-splitting. Ni₃S₂ has been considered a suitable electrocatalyst for either the hydrogen evolution reaction (HER) or the oxygen evolution reaction (OER) owing to its good conductivity and stability, but high performance remains a challenge. Based on density functional theory calculations, we propose a practical 3d-transition-metal (TM = Mn, Fe and Co) doping to enhance the catalytic performance for both HER and OER on the Ni₃S₂ (101) facet. The enhancement originates from TM-doping-induced charge rearrangement and charge transfer, which increases the surface activity and promotes catalytic behavior. In particular, Mn-doped Ni₃S₂ shows good bifunctional catalytic activity because it possesses more active sites, reduced hydrogen adsorption free energy (ΔG_H*) for HER and low overpotential for OER. Importantly, this work not only provides a feasible means to design efficient bifunctional electrocatalysts for overall water-splitting but also provides insights into the mechanism of improving catalytic behavior.

---

1. Introduction

Hydrogen production using electrochemical water-splitting has been considered one of the most attractive approaches to solving environmental problems and the energy crisis. Two half-reactions are involved in water-splitting: the hydrogen-evolution reaction (HER) and the oxygen-evolution reaction (OER).^1,2 Compared to HER, OER is more complex, because there are four sluggish proton-coupled electron-transfer processes. Chemisorption and dissociation of OH⁻ yielding intermediates (HO*, O* and HOO*) are critical to improving the activity of OER.^3,4 Pt is the most efficient HER electrocatalyst with near-zero hydrogen adsorption free energy (ΔG_H*), while Ir oxides are the most promising electrocatalysts for OER with very small overpotential, but they are far from practical application being subject to scarcity and high cost.^5,6 During the water-splitting process, ionized hydrogen ions are equivalent to hydroxide ions. Hydrogen and oxygen generation through overall water-splitting occur at the same time without adding sacrificial agents.^7,8 However, most research has focused on improving the catalytic efficiency for the half-reactions, and investigation into efficiently promoting the bifunctional electrocatalysis of both HER and OER has been ignored. Therefore, designing and constructing cost-efficient and bifunctional electrocatalysts with good activity toward overall water-splitting has become one of the most important tasks.

Recently, transition-metal dichalcogenides found in abundance in nature, with good surface to volume ratio and low charge carrier diffusion distance have been of wide interest as alternative non-noble-metal-based electrocatalysts, but their catalytic activities are always unsatisfactorily limited by their low electrical conductivity.^4,9–11 Ni₃S₂ naturally emerges as the mineral heazlewoodite and, unlike traditional transition-metal dichalcogenides, it exhibits an intrinsic metallic feature and possesses distinctive conductivity.¹² Many reports have shown that Ni₃S₂-based materials display high electrocatalytic performance for both HER and OER.^12–18 For instance, Feng et al. have shown that Ni₂S₃/NF could display ∼100% faradaic yield for either HER or OER and obtained a current density of 10 mA cm⁻² toward HER and OER under small overpotentials of 223 and 260 mV. In particular, Ni₃S₂ has different fractions of exposed facets, though high-index faced nanosheets possess more active catalytic behaviors but exhibit high surface energies.¹⁹ They are usually unstable. The low-index (101) facet is energetically stable, can be easily achieved experimentally, and displays plausible catalytic activity.^16,20,21 Doping with impurities is one practical strategy to improve the catalytic activity^22,23 Yuan et al. obtained Fe–Ni₃S₂/FeNi based on the one-step direct growth of metallic iron-nickel sulfide nanosheets on FeNi alloy foils, which exhibited high catalytic activity and long-term stability toward OER with a low overpotential of 282 mV at 10 mA cm⁻² and a small Tafel slope of 54 mV dec⁻¹.¹² Wang et al. prepared a series of self-supporting M–NiCo₂S₄/Ni₃S₂ (M = Mn, Fe, Cu, Zn) nanostructures grown on a nickel foam (NF) skeleton through a one-step hydrothermal strategy. The catalytic performance of Ni₃S₂-based catalysts could be improved by doping engineering.¹⁷ In this work, we find the incorporation of a 3d TM atom (TM = Mn, Fe) can enhance both HER and OER catalytic performance on the Ni₃S₂ (101) facet. The enhancement comes from TM-doping-induced charge rearrangement and charge transfer, which can be reflected in the following: (1) the systems display more metallic states, showing higher electronic conductivity; (2) the interaction between TM and the active atom becomes stronger, further activating surface activity; (3) the increased electrons concentrate on the active atom, accelerating catalytic behavior. As a result, the Mn-doped Ni₃S₂ (101) facet exhibits enhanced catalytic activity for overall water-spitting with increased active sites, reduced ΔG_H* for HER and overpotential for OER.

2. Computational model and methods

Based on density functional theory (DFT) calculations, generalized gradient approximation with the Perdew–Burke–Ernzerhof (PBE) exchange correlation functional is carried out in the Vienna ab initio simulation package (VASP).^24–26 The cutoff energy is 450 eV for the plane wave basis set. The electron–ion interactions are described by the projector-augmented plane wave. The Monkhorst–Pack k-point meshes are 7 × 7 × 1 and 11 × 11 × 1 for geometric optimization and electronic structure, respectively. The convergence thresholds in energy and in force are 1.0 × 10⁻⁵ eV and 0.01 eV Å⁻¹, respectively. The calculated lattice parameters are a = b = 5.754 Å, c = 7.063 Å, in good agreement with the experimental values (a = b = 5.745 Å, c = 7.135 Å).

Bulk Ni₃S₂ is a rhombohedral structure, belonging to the space group R32.²⁷ The Ni₃S₂ slab is cleaved from the (101) facet of bulk Ni₃S₂ with a vacuum > 15 Å incorporated to separate the interactions between adjacent images, as shown in Fig. 1. A bilayer 1 × 1 supercell containing 30 atoms is used, displaying a corrugated structure with three Ni atoms and three S atoms exposed to the surface. These six atoms are all considered possible adsorption sites to ensure the most active sites for HER and OER.^12,28 To investigate the effect of TM doping on the surface catalytic activity of Ni₃S₂, one TM atom (Mn, Fe or Co) substitutes an intrinsic Ni atom in the sub-surface, neighbouring a surface active site.

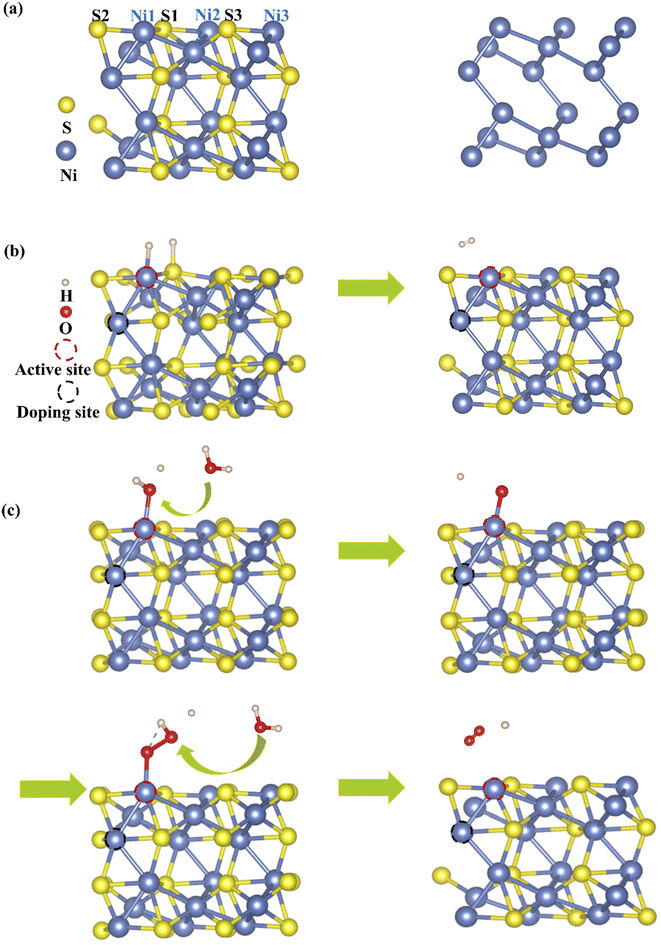Fig. 1 (a) Side views of the Ni₃S₂ (101) facet and the network of Ni–Ni bonds. Model diagrams of (b) HER and (c) OER on Ni₃S₂ (101) facets.

HER involves the adsorption of an H atom on the Ni₃S₂ surface and desorption of H₂ from the Ni₃S₂ surface, as shown in Fig. 1(b), so adsorption free energy of hydrogen (ΔG_H*) is a key indicator to evaluate HER activity, which can be defined as ΔG_H* = ΔE_H* + ΔE_ZPE − TΔS_H*, where ΔE_H*, ΔE_ZPE and ΔS_H* are the hydrogen chemisorption energy, zero-point energy change and the entropy of H* adsorption.^29,30 The closer ΔG_H* approaches zero, the higher the HER activity because atomic hydrogen is in a thermoneutral state, so proton/electron transfer and hydrogen release become more efficient. For the Ni₃S₂ (101) facet, the ΔG_H* are 0.733, 0.735, 0.737, 1.165, 1.249 and 1.287 on Ni1, Ni2, Ni3, S1, S2 and S3, respectively, as shown in Fig. S1 in the ESI.†³¹ Obviously, Ni atoms are more catalytically favorable than S atoms and Ni1 is the most active site for HER.

For OER, the reaction process is more complex than HER, involving four-electron-transfer steps, as shown in Fig. 1(c), with each step accompanied by proton-removal as follows:

H₂O + * → HO* + H⁺ + e⁻

HO* → O* + H⁺ + e⁻

O* + H₂O → HOO* + H⁺ + e⁻

HOO* → * + O₂ + H⁺ + e⁻

where * represents an adsorbed site of the surface. X* denotes the adsorbed X intermediate on the surface.^32,33 The free energy of OER can be defined as ΔG = ΔE + ΔZPE − TΔS, where ΔE, ΔZPE and ΔS respectively represent the energy of geometrical structures, the difference in zero point energy and the change in entropy contribution by employing the computed vibrational frequencies and standard tables for the reactants and products in the gas phase.^34,35 For the Ni₃S₂ (101) facet, an S atom is not suitable as the active site for OER because it is difficult to adsorb an H₂O molecule on surface S atoms. H₂O adsorption energies are −0.32, −0.29 and −0.26 eV on Ni1, Ni2 and Ni3, respectively. The lower E_ads (H₂O), the easier it is for H₂O adsorption. We further calculate the free energy of four steps with Ni1, Ni2 and Ni3, respectively, acting as the active site, as shown in Fig. S1 in the ESI.†³¹ As a result, Ni1 not only serves as an active site for HER but also for OER.

To verify the reliability of the GGA method, we compare the lattice constant, band structure, ΔG_H* and the free energy diagrams of OER on the Ni₃S₂ (101) facet with the GGA + U method, as shown in Table S1 and Fig. S2 in ESI.†³¹ The GGA-calculated lattice parameters are a = b = 5.754 Å, c = 7.063 Å, very similar to the GGA + U values (a = b = 5.781 Å, c = 7.135 Å), and very consistent with the experimental values (a = b = 5.745 Å, c = 7.063 Å). Additionally, the band structures, ΔG_H* and the free energy diagrams calculated using the two methods are almost the same. The Hubbard term can correct for the interaction of strongly-correlated electrons in the TM atom, but here we focus on electrocatalytic activity, so the Hubbard term has little influence on the results. Thus, we adopt the GGA method to investigate HER and OER activities on Ni₃S₂ (101) facets.

3. Results and discussion

3.1 Electronic structure of TM-doped Ni₃S₂ (101) facet

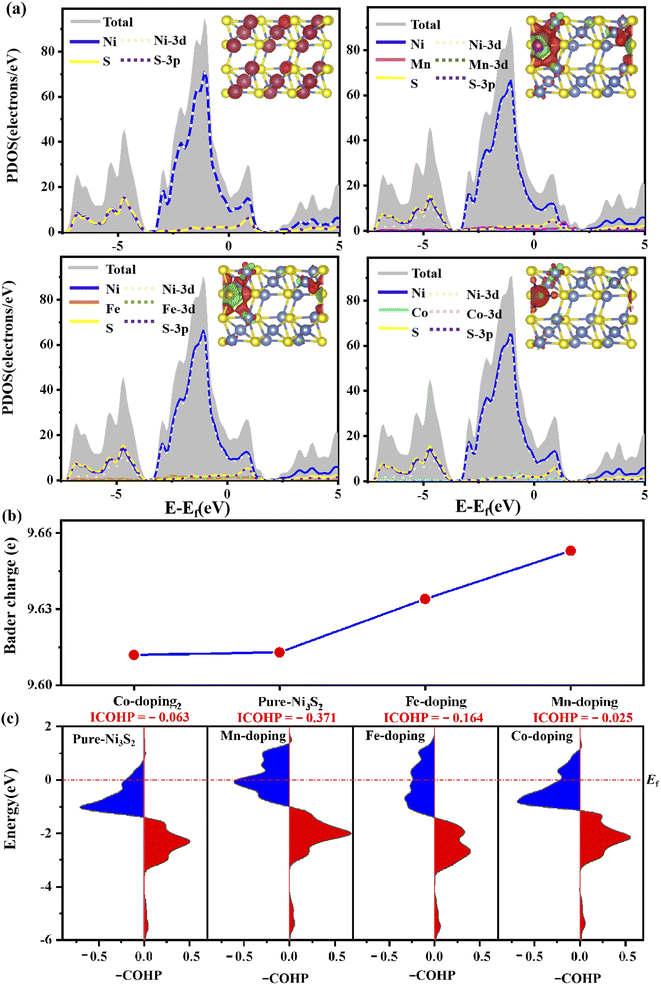
To further investigate the stability of TM-doped Ni₃S₂, we calculated the formation energy as follows: E_f = E_TM@X − E_X − (μ_TM − μ_Ni). The details of the calculation can be found in ref. 36 and 37, and the calculated results show that the formation energies are −0.56, −0.41 and 0.08 eV for Mn, Fe and Co doping, respectively. A more negative value indicates great stability. TM doping induces structural change, as shown in Table S2,† where bond lengths between dopant TM and active-site Ni1 atom are 2.459, 2.452 and 2.441 Å for Mn, Fe and Co doping, in which the Mn–Ni1 bond is close to the original Ni–Ni1 bond length of 2.457 Å. Meanwhile, the bond lengths of Ni–S also change. The structural change will generate an internal field and then induce charge transfer and charge recombination, so the electronic structure changes. Fig. 2(a) shows the electronic structure of (101) faceted Ni₃S₂, where the system displays metallic behavior as the electronic states come mainly from Ni-3d and S-3p orbitals spread across the Fermi level. This is a distinctive structure in which the Ni–Ni bond connects a continuous network, favoring electron-transfer and thus benefiting the catalytic reaction. For TM (TM = Mn, Fe, Co) doped Ni₃S₂, the systems continue to exhibit metallic features, and strong hybridization among the Ni-3d, S-3p and TM-3d states occurs near the Fermi level (E_f) [see Fig. 2(a)]. More DOS appears near the E_f especially for Mn-doping, meaning higher conductivity than for pure Ni₃S₂.¹² The change in electronic structure comes from TM-induced charge transfer and charge recombination. The inset in Fig. 2(a) shows the charge density difference of TM-doped Ni₃S₂, defined as Δρ = ρ(TM-Ni₃S₂) − ρ(Ni₃S₂) − ρ(TM), where ρ(TM-Ni₃S₂), ρ(Ni₃S₂) and ρ(TM) are the electronic charge densities of TM-doped Ni₃S₂, isolated Ni₃S₂ and TM atoms in frozen geometry. There is great electron transfer from dopant TM to neighbouring atoms. Bader charge analysis further verifies that there are 0.43, 0.24 and − 0.05e transfers from dopant Mn, Fe and Co to neighboring atoms and, as a result, there are 9.653, 9.635, 9.611e on the Ni atom for Mn-, Fe-, Co-doped Ni₃S₂, as shown in Fig. 2(b). The more electrons there are, the better it is to reduce H⁺ and promote OH⁻ oxidation.

Fig. 2 (a) Partial DOS, (b) the Bader charge on the active Ni atom and (c) –COHP of TM-Ni on the pure and TM-doped Ni₃S₂ (101) facet. The insets are charge density of pure Ni₃S₂ and charge density difference of TM-doped Ni₃S₂, respectively.

To investigate the effect of TM doping on the active site, we further calculate the bond strength of TM-Ni using Crystal Orbital Hamilton Population (COHP) and its integrated values (ICOHP). The positive and negative values in the –COHP curves correspond to the contributions of orbital interaction from bonding and antibonding states.³⁸ As shown in Fig. 2(c), the order of ICOHP is Mn-doping (−0.371) < Fe-doping (−0.164) < pure (−0.063) < Co-doping (−0.025). Based on ICOHP theory, a more negative ICOHP indicates stronger bonding strength. The stronger interaction between TM and the active site has a favorable influence on the catalytic performance.^39,40

3.2 Electrochemical overall-water-splitting performance of TM-doped Ni₃S₂ (101) facet

For HER, ΔG_H* is an important indicator. As shown in Fig. 3(a), ΔG_H* decreases to 0.565, 0.622 and 0.633 for Mn-, Fe- and Co-doping, respectively, lower than for pure Ni₃S₂ (ΔG_H* = 0.733 eV). TM doping improves HER catalytic activity, especially for Mn-doping. The improvement comes from TM-induced charge rearrangement and charge transfer. The Bader charge analysis in Fig. 3(b) shows that with hydrogen adsorption, there are 9.639, 9.609, 9.603, 9.601e on the active site for Mn-, Fe-, Co-doped and pure Ni₃S₂. –COHP of the active site Ni and H in Fig. 3(c) shows the ICOHP value order is Mn-doping (−3.543) < Fe-doping (−3.535) < Co-doping (−3.507) < pure Ni₃S₂ (−3.316). Obviously, the strength of the Ni–H bond in TM-doped Ni₃S₂ is stronger than that in pure Ni₃S₂, and Mn-doping is the strongest. Thus, the ΔG_H* of TM-doped Ni₃S₂ decreases, especially with Mn-doping.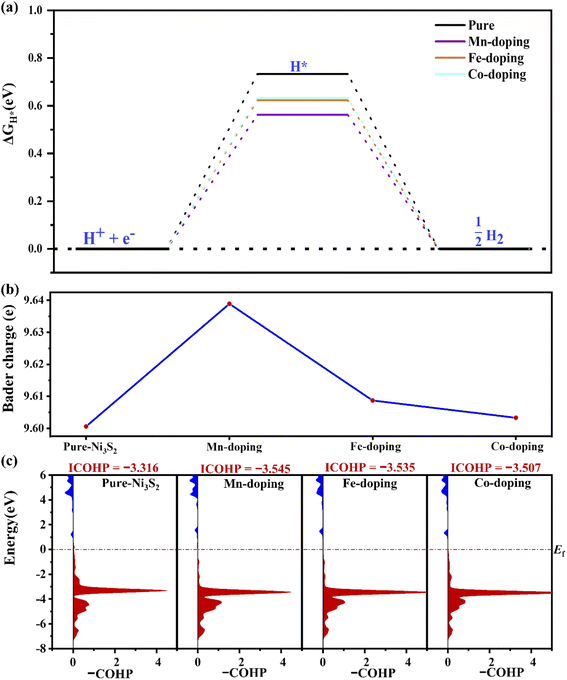

Fig. 3 (a) The ΔG_H*, (b) the Bader charge on the active-site Ni atom for hydrogen adsorption and (c) the –COHP of Ni–H in pure and TM-doped Ni₃S₂ (101) facets.

For OER, TM-doping-induced charge redistribution affects the interaction between adsorbate and Ni₃S₂, which plays an important role in OER efficiency. Fig. 4 shows the free energy diagram of OER on the TM-doped Ni₃S₂ (101) facet. The first step is H₂O adsorption on top of the surface Ni atom, losing one proton to form HO*. The energies rise steeply uphill to 0.96, 1.0, 0.96, 0.90 eV for pure, Mn-, Fe- and Co-doped Ni₃S₂. Secondly, the HO* loses another H_ad atom, generating O*, and the energies are 2.62, 2.61, 2.60, 2.61 eV for pure, Mn-, Fe- and Co-doped Ni₃S₂, respectively. Thirdly, another H₂O spontaneously adsorbs on top of the Ni₃S₂ surface, and a proton in this H₂O is removed, forming HOO*. The energies are 4.06, 4.07, 4.06, 3.96 eV for pure, Mn-, Fe- and Co-doped Ni₃S₂. Finally, O–O separates from the surface. The energy is 4.96 eV. All steps run uphill at U = 0 V, displaying an endothermic process. Though the first and the fourth steps become exothermic reactions, the intermediate steps remain uphill for an equilibrium potential of U = 1.23 V,⁴¹ until the applied potentials increase to U = 1.66, 1.61, 1.64, 1.71 V and therefore the overpotentials are 0.43 (= 1.66–1.23), 0.38, 0.41 and 0.48 V for pure, Mn-, Fe- and Co-doped Ni₃S₂. Though theoretically there is not much increase in overpotential, in fact, experimentally, Fe-doped Ni₃S₂ exhibits great enhancement in catalytic activity with low onset potential and overpotential, and a small Tafel slope.¹² For all Ni₃S₂ systems, the second step is the rate-determining step, indicating that proton release from the HO* adatom is difficult. For this key step, we compare the binding energy of HO* on the surface with E_b = E_HO + E_* − E_HO*, where E_HO, E_* and E_HO* represent the energy of adsorbate HO and the total energies of (101) facets without and with HO*, respectively. The binding energies are 3.05, 2.99, 3.01 and 3.10 eV for pure, Mn-, Fe- and Co-doped Ni₃S₂, respectively. Clearly, the binding energy of Mn-doped Ni₃S₂ is the smallest, indicating the interaction between HO* and the surface is weak, benefiting the conversion of HO* intermediate to O* intermediate.

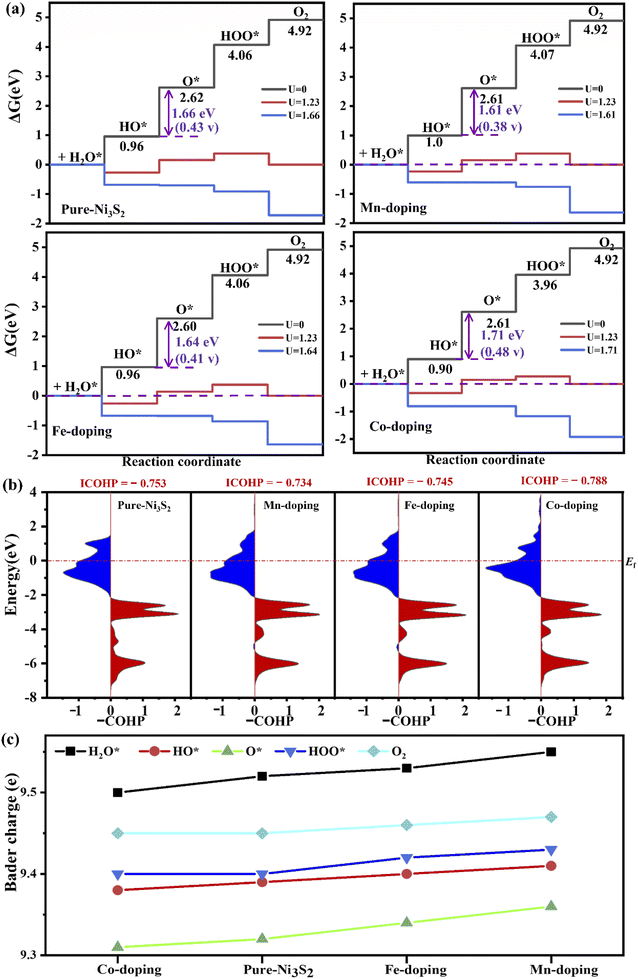Fig. 4 (a) The free energy of four steps at different applied potentials. (b) The –COHP of Ni–O at the second step and (c) the Bader charge on the active-site Ni in pure and TM-doped Ni₃S₂.

The –COHP curve in Fig. 4(b) shows the bonding strength between the active-site Ni and HO* intermediate. The ICOHP order is Co-doping (−0.788) < pure (−0.753) < Fe-doping (−0.745) < Mn-doping (−0.734). The Ni–O binding strengths of Fe- and Mn-doped Ni₃S₂ are weaker than those of pure and Co-doped Ni₃S₂, indicating that the dissociation of O* is easier in Fe- or Mn-doped Ni₃S₂. The reason can be found from the Bader charge analysis in Fig. 4(c). During the four steps, there are more electrons moving from TM to Ni, especially for Mn-doping. The electrons on the active Ni range from 9.37e to 9.57e. So there are more electrons on the Ni atom at each step for Mn-doped Ni₃S₂, and the electrons display the ordering: Mn-doping > Fe-doping > pure Ni₃S₂ > Co-doping. The more electrons accumulate, the higher surface activity. Thus, Mn-doped Ni₃S₂ possesses higher catalytic activities for both HER and OER.

Fig. 5 shows the high linear correlation between overpotential and ICOHP values. A small ICOHP indicates strong interaction between the active-site Ni and HO* intermediate, corresponding to a small overpotential. Additionally, overpotential and Bader charge also show high linear correlation, but the more electrons there are, the smaller overpotential it is.

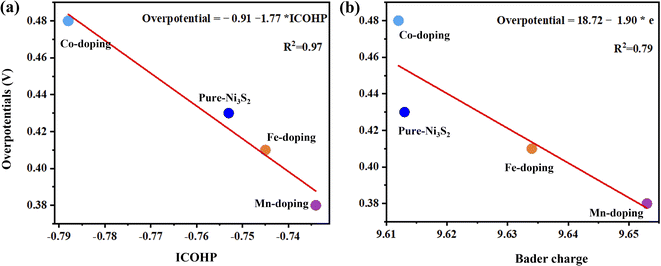Fig. 5 The overpotential as a function of (a) ICOHP values of the active site Ni and HO* intermediate and (b) bader charge of the active site for Ni₃S₂, and TM-doped Ni₃S₂ (TM = Mn, Fe, Co).

Here, we focus on the effect of dopant TM on the catalytic activity of Ni₃S₂ and take acid media as an example. The effect of solution pH values on catalytic activity will be discussed in detail in our subsequent work. In comparison with acid media, we briefly consider alkaline HER and OER, see the ESI.†³¹ Though HER and OER processes in alkaline media are different from those in acid media, the effect of dopant TM on catalytic activity is the same. During alkaline HER, the second step of H₂O dissociation is the rate-determining step for all Ni₃S₂ systems, Mn-doping decreases the H₂O dissociation barrier energy to 1.33 eV, lower than that of pure Ni₃S₂ at 1.36 eV, as shown in Fig. S3.† During alkaline OER, the second step of forming O* is the rate-determining step with overpotentials of 0.43 (= 0.83–0.4), 0.38, 0.41 and 0.48 V for pure, Mn-, Fe- and Co-doped Ni₃S₂, as shown in Fig. S4.† As a result, Mn-doped Ni₃S₂ possesses higher catalytic activities in both acid and alkaline media.

Additionally, we considered the Ni3 atom as the active site for OER activity because Ni3 is also neighboring to doped TM. As shown in Fig. 6, the overpotential is 0.47 V, and a notable reduction can be observed in Mn-doped Ni₃S₂ with an overpotential of 0.41 V, indicating Mn-doping effectively increases the number of active sites and further enhances OER activity. To investigate the effect of surface size on catalytic activity, we enlarge the supercell to twice as large as previously. The dopant concentration decreases from 5.5% to 2.7%, as shown in Fig. S3 in the ESI,†³¹ the active site remains the Ni1 atom, and the second step remains the rate-determining step. The free energy at each electric step and the overpotential change little at 0.44 and 0.36 V for 2 × 1 supercells of pure and Mn-doped Ni₃S₂, very similar to those of 1 × 1 supercells with 0.43 and 0.38 eV for pure and Mn-doped Ni₃S₂. Thus, the size of the supercell has little influence on the catalytic activity of the active sites. To compare the effect of different dopant positions on the active site, we consider four different dopant positions, as shown in Fig. S6,† and consider the TM atom as acting as the active site. When Mn is doped near active-site Ni1 (see Fig. S6(a) and (b)†), the overpotentials are clearly almost equal at 0.43 and 0.44 V because the distances between dopant Mn and active-site Ni1 are almost equal at 2.457 Å and 2.458 Å. When Mn is doped on the surface and acts as the active site (see Fig. S6(c)†), the overpotential increases greatly to 1.03 V, indicating that the catalytic activity of Ni is stronger than that of Mn and the Mn atom is unsuitable as the active site. Lastly, we doped Mn on the surface to investigate its effect on the active-site Ni1 (see Fig. S6(d)†). The overpotential is 0.81 V, larger than for Mn doped in the sub-surface because there is a competitive effect between Ni1 and Mn, so the adsorbate is adsorbed between them. This indicates that the dopant-TM position has a great influence on the catalytic activity.

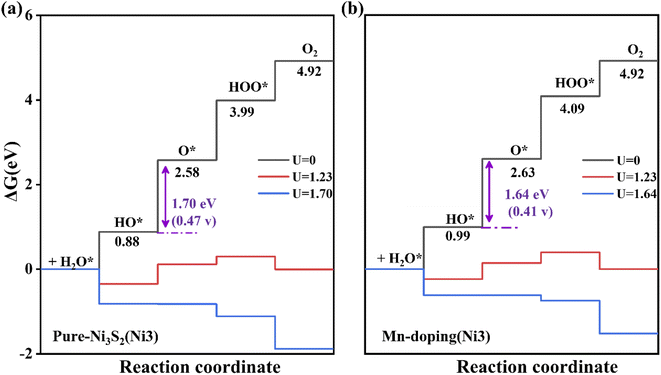Fig. 6 The free energy of four steps for OER on (a) pure and (b) Mn-doped Ni₃S₂ (101) facets. The Ni3 atom acts as the active site.

4. Conclusion

In summary, based on DFT calculations, we dope an Ni₃S₂ (101) facet with 3d-TM (TM = Mn, Fe and Co) to improve its bifunctional catalytic activity for either HER or OER. The improvement comes from TM-doping-induced charge rearrangement and charge transfer, which strengthens the interaction between doped TM and the active site because there are more electrons on the active site. In particular, Mn-doping greatly improves the catalytic performance of Ni₃S₂: (1) the metallic properties indicate good conductivity; (2) the lower ΔG_H* indicates enhanced HER activity; (3) the reduced overpotential indicates improvement in OER activity; (4) the increased active sites indicate more conducting paths for HER and OER.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the NSFC (12074332 and 21903014). The authors are grateful for access to the computational resources at YZU.

References

1. Y. K. Lu, Z. X. Li, Y. L. Xu, L. Q. Tang, S. J. Xu, D. Li, J. J. Zhu and D. L. Jiang, Chem. Eng. J., 2021, 411, 1385–8947.
2. Z. Wang, C. Li and K. Domen, Chem. Soc. Rev., 2019, 48, 2109–2125.
3. Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, Chem. Soc. Rev., 2015, 44, 2060–2086.
4. R. Gao and D. Yan, Adv. Energy Mater., 2020, 10, 1–19.
5. Y. Liu, X. Li, Q. Zhang, W. Li, Y. Xie, H. Liu, L. Shang, Z. Liu, Z. Chen, L. Gu, Z. Tang, T. Zhang and S. Lu, Angew. Chem., Int. Ed., 2020, 59, 1718–1726.
6. D. V. Esposito, S. T. Hunt, A. L. Stottlemyer, K. D. Dobson, B. E. McCandless, R. W. Birkmire and J. G. Chen, Angew. Chem., 2010, 122, 10055–10058.
7. Z. Xu, Y. Ying, G. Zhang, K. Li, Y. Liu, N. Fu, X. Guo, F. Yu and H. Huang, J. Mater. Chem. A, 2020, 8, 26130–26138.
8. E. Hu, Y. Feng, J. Nai, D. Zhao, Y. Hu and X. W. Lou, Energy Environ. Sci., 2018, 11, 872–880.
9. J. Zhang, T. Wang, D. Pohl, B. Rellinghaus, R. Dong, S. Liu, X. Zhuang and X. Feng, Angew. Chem., 2016, 128, 6814–6819.
10. J. Wang, W. Fang, Y. Hu, Y. Zhang, J. Dang, Y. Wu, B. Chen, H. Zhao and Z. Li, Appl. Catal., B, 2021, 298, 120490.
11. Y. Yang, H. Yao, Z. Yu, S. M. Islam, H. He, M. Yuan, Y. Yue, K. Xu, W. Hao, G. Sun, H. Li, S. Ma, P. Zapol and M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 10417–10430.
12. C. Z. Yuan, Z. T. Sun, Y. F. Jiang, Z. K. Yang, N. Jiang, Z. W. Zhao, U. Y. Qazi, W. H. Zhang and A. W. Xu, Small, 2017, 13, 1–8.
13. X. Li, X. Shang, Y. Rao, B. Dong, G. Q. Han, W. H. Hu, Y. R. Liu, K. L. Yan, J. Q. Chi, Y. M. Chai and C. G. Liu, Appl. Surf. Sci., 2017, 396, 1034–1043.
14. J. T. Ren, L. Chen, G. G. Yuan, C. C. Weng and Z. Y. Yuan, Electrochim. Acta, 2019, 295, 148–156.
15. X. Feng, Y. Shi, J. Shi, L. Hao and Z. Hu, Int. J. Hydrogen Energy, 2021, 46, 5169–5180.
16. Q. Liu, L. Xie, Z. Liu, G. Du, A. M. Asiri and X. Sun, Chem. Commun., 2017, 53, 12446–12449.
17. Y. Wang, N. Chen, X. Du, X. Han and X. Zhang, J. Alloys Compd., 2022, 893, 162269.
18. G. Li, X. Cui, B. Song, H. Ouyang, K. Wang, Y. Sun and Y. Wang, Chem. Eng. J., 2020, 388, 124319.
19. L. L. Feng, G. Yu, Y. Wu, G. D. Li, H. Li, Y. Sun, T. Asefa, W. Chen and X. Zou, J. Am. Chem. Soc., 2015, 137, 14023–14026.
20. L. Li, C. Sun, B. Shang, Q. Li, J. Lei, N. Li and F. Pan, J. Mater. Chem. A, 2019, 7, 18003–18011.
21. Z. Yu, H. Yao, Y. Yang, M. Yuan, C. Li, H. He, T. S. Chan, D. Yan, S. Ma, P. Zapol and M. G. Kanatzidis, Chem. Mater., 2022, 34, 798–808.
22. Z. Xing, D. Wang, T. Meng and X. Yang, ACS Appl. Mater. Interfaces, 2020, 12, 39163–39169.
23. A. C. Thenuwara, N. H. Attanayake, J. Yu, J. P. Perdew, E. J. Elzinga, Q. Yan and D. R. Strongin, J. Phys. Chem. B, 2018, 122, 847–854.
24. J. P. Perdew, A. Ruzsinszky, J. Tao, V. N. Staroverov, G. E. Scuseria and G. I. Csonka, J. Chem. Phys., 2005, 123, 9.
25. G. Kresse and J. Hafner, Phys. Rev. B, 1994, 49, 14251–14269.
26. P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979.
27. Y. Aray, D. Vega, J. Rodriguez, A. B. Vidal, M. E. Grillo and S. Coll, J. Phys. Chem. B, 2009, 113, 3058–3070.
28. J. Dong, F. Q. Zhang, Y. Yang, Y. B. Zhang, H. He, X. Huang, X. Fan and X. M. Zhang, Appl. Catal., B, 2019, 243, 693–702.
29. T. Liu, P. Diao, Z. Lin and H. Wang, Nano Energy, 2020, 74, 104787.
30. J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23.
31. ESI^†.
32. X. Cui, P. Ren, C. Ma, J. Zhao, R. Chen, S. Chen, N. P. Rajan, H. Li, L. Yu, Z. Tian and D. Deng, Adv. Mater., 2020, 32, 1–7.
33. Y. Sun, Z. Xue, Q. Liu, Y. Jia, Y. Li, K. Liu, Y. Lin, M. Liu, G. Li and C. Y. Su, Nat. Commun., 2021, 12, 1–8.
34. C. Liu, H. Dong, Y. Ji, T. Hou and Y. Li, Sci. Rep., 2018, 8, 1–9.
35. M. Wang, L. Zhang, J. Pan, M. Huang and H. Zhu, Nano Res., 2021, 14, 4740–4747.
36. Q. Wang, Y. Lin, P. Li, M. Ma, V. Maheskumar, Z. Jiang and R. Zhang, Int. J. Hydrogen Energy, 2021, 46, 247–261.
37. R. Zhao, L. Zhang, G. Fan, Y. Chen, G. Huang, H. Zhang, J. Zhu and X. Guan, Cem. Concr. Res., 2021, 144, 106420.
38. M. Ren, X. Guo and S. Huang, Appl. Surf. Sci., 2021, 556, 149801.
39. H. Niu, X. Wang, C. Shao, Z. Zhang and Y. Guo, ACS Sustainable Chem. Eng., 2020, 8, 13749–13758.
40. T. Zhang, J. Wu, J. Chen, Q. Pan, X. Wang, H. Zhong, R. Tao, J. Yan, Y. Hu, X. Ye, C. Chen and J. Chen, ACS Appl. Mater. Interfaces, 2021, 13, 24682–24691.
41. H. Dau, C. Limberg, T. Reier, M. Risch, S. Roggan and P. Strasser, ChemCatChem, 2010, 2, 724–761.

---

Footnotes

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra04252e

‡ These authors contributed equally.

---