On the formation of 2- and 3-cyanofurans and their protonated forms in interstellar medium conditions: quantum chemical evidence

Abstract

The literature is still poor in theoretical and experimental, including both spectroscopic and thermodynamic data for protonated furan and protonated 2-cyanofuran and 3-cyanofuran (FH⁺, 2CFH⁺ and 3CFH⁺). These data are, however, crucial for astrophysicists and astrochemists in the detection of new species in interstellar medium (ISM), the discovery of these molecular species being not yet reported. It is in this perspective that a computational study based on quantum chemistry on FH⁺, 2CFH⁺ and 3CFH⁺ was undertaken. A series of properties including the proton affinity (PA) of furan and the two cyanofurans, the variations of enthalpy (Δ_rH), entropy (Δ_rS), and Gibbs free energy (Δ_rG) for the reactions yielding cyanofurans (neutral and protonated forms), were studied at different temperatures (5 K, 10 K, 150 K and 298 K) and pressures (P = 1 atm and P = 10⁻⁵ atm) based on modern computational models (G2MP2, G3, G4MP2 and G4). While confirming that the protonation favors the α-position for furan, the PA values show that the protonation favors the nitrogen atom in cases of 2CFH⁺ and 3CFH⁺. The Δ_rH, Δ_rS and Δ_rG values revealed spontaneous reactions producing these species under ISM conditions of temperature and pressure. In addition quadrupole hyperfine structures and vibrational spectra which are essential tools for the characterization and the identification of interstellar molecular species are predicted, while the region where brightest lines fall for different temperatures is discussed. The results reported in this work are expected to assist astrophysicists and astrochemists, in the search for new chemical species in interstellar environments.

---

1 Introduction

Despite unfavourable conditions to the chemical formation in the interstellar medium (ISM),^1,2 more than a third of already detected molecules (more than 200 molecular species³) is made of complex organic molecules (COMs).⁴ In interstellar clouds and associated circumstellar envelopes of the asymptotic giant branch (AGB) stars, molecules with an order of magnitude of atom number ranging from 2 to 13 atoms in the gas phase have been discovered by high-resolution spectroscopy.⁵ Moreover, it has been argued that aromatic molecules and their protonated species as well as their substituted (heterocyclic) derivatives form an important component of the ISM.^6,7 Furthermore, the discovery of some five- and six-membered molecular species in the dark molecular cloud TMC-1 and other ISM environments constitute a good evidence that aromatic chemistry is likely widespread in the earliest stages of star formation. This is, for instance, the discoveries of the benzenitrile,⁸ of the two cyanocyclopentadienes,^9,10 that of the two cyanonapthlenes (1- and 2-cyanonaphthalenes),¹¹ but also that of the indene (C₉H₈),¹² the first pure polycyclic aromatic hydrocarbon (PAH) to be discovered in the ISM. The cyanobenzene has been also detected in pre-stellar regions,¹³ and tentatively in protostellar sources.¹² These discoveries are also an evidence that organic molecules of high complexity are readily synthesized in regions with high visual extinction at remarkably low temperatures and pressures.

Early studies on the ISM molecular formation have revealed that ion-neutral reactions induced by cosmic rays are the primary reaction mechanism to form molecules in ISM shells and dense cloudy regions where temperatures are as low as 10 K.^14,15 Moreover, the importance of grain surface formation is also reported in the literature.¹⁶ In general, among the three favorable environments to the molecular formation in space, i.e., the gas phase, the bare surface of dust and the mass of ice or its surface,^5,17,18 the latter is suspected of being the seat of the formation of complex molecules.¹⁹ Complex organic species have been detected in hot nuclei within stars of high masses but also in regions called corinos where their formation takes place by the phenomenon of heating.²⁰ Complex unsaturated molecular species are likely to be found in cold, dense regions such as the Taurus Molecular Cloud 1 (TMC-1, ∼10 K) where they, together with ions and radicals, are suggested to be formed on dust grains.^5,21 Unsaturated complex species are also present in the so called lukewarm corinos L1527 (T ≈ 30.00 K), which is known to contain significant abundances of complex molecules, including anionic forms.²²

Of the detected molecules, a big part is found via rotational emission spectra, obtained through the use of millimeter wave telescopes on the ground or in space.²³ A non-negligible part is also detected on the basis of vibrational transitions in the absorption infrared using background stars, whereas a small quantity is discovered by means of visible electron spectroscopy and UV rays against a star background through diffuse interstellar matter.⁵ Among the overall already detected molecules, only a very low proportion (≈2%) is of five- and six-membered types. They are, for instance, the four six-membered molecules, such as benzene (C₆H₆),²⁴ its nitrile substituted derivative (benzonitrile: c-C₆H₅CN),^8,13 and the two nitrile-group-functionalized PAHs (1- and 2-cyanonaphthalenes).¹¹ For five-membered heterocyclic molecules, two molecular species have been reported: the highly polar cyano derivative of cyclopentadiene (c-C₅H₅CN),⁹ and the 2-cyanocyclopentadiene (C₅H₅CN).¹⁰

The high symmetry, and consequently, the lack of a permanent electric dipole moment of key aromatic building blocks like benzene and naphthalene (c-C₁₀H₈) and also the five-membered heterocyclic compounds such as thiophene (C₄H₄S), furan (C₄H₄O)¹² and pyrrole (C₄H₄NH) prevent their radio and millimeter detections. Nonetheless, a hydrogen-substitution with a cyano group (–CN) dramatically increases a molecule's electric dipole moment relative to its non-substituted counterpart.

It has been found a high abundance of oxygen and other elements in B stars and pointed.^25,26 These authors have pointed out also that these young stars should most accurately model the abundance of oxygen. The literature search reveals that the atomic oxygen is depleted from interstellar gas at a rate that cannot even be explained.⁶ According to Lavoisier's law, it may be reasonably hypothesized that the quantity of depleted oxygen would bind with other atoms to form new chemical species, which are not detected yet. In the same way, it has argued that the depletion of sulfur in regions where it is expected to be abundant may be explained by the detection of gas-phase sulfur-bearing molecules in which the sulfur should be bind with other atoms.²⁷ Protonated species are known to play a key role in ion-molecule reactions in the gas phase interstellar chemistry.²⁸ In fact, the H₃⁺ ion plays a central role in interstellar chemistry, initiating chains of reactions which leads to the production of many complex molecular compounds observed in the interstellar medium (including protonated species) by neutral reactions.²⁹ This ion was found to exist abundantly in various ISM environmental regions, especially, in dense molecular clouds, but also in diffuse clouds. Its abundance in the latter environment was found to be of orders of magnitude higher than in the former.³⁰ Several protonated small molecules with a number of atoms ranging between 2 and 5 were found in the ISM. This is for instance the cases of H₂COH⁺,³¹ O₃H⁺,³² NCCNH⁺,³³ C₂H₃⁺,³⁴ etc. Up to know, only a few protonated complex organic molecules (COMs) have been detected in the ISM, even though it is established that they could evolve to the corresponding neutral species by dissociative recombination. For instance, the detections of CH₂CHCNH⁺,³⁵ HC₇NH⁺,³⁶ HCCNCH⁺, C₅NH⁺,³⁷ etc., have been reported. Beside being of astrophysical importance, aromatic heterocyclic molecules have astrobiological relevance as precursors of nucleobases.³⁸

A survey of the literature shows us very few reports on protonated heterocyclic compounds, especially, cyanofurans. Much effort has been focused on modelling the formation of small aromatic five- and six-membered rings and their subsequent reactions with smaller hydrocarbons and nitrogen species to produce PAHs and polycyclic aromatic nitrogen heterocycles.³⁹ A recent theoretical work by Simbizi and coworkers⁷ on the protonation of thiophene, 2-cyanothiophene (2CT) and 3-cyanothiophene (3CT) under ISM conditions of temperature and pressure was carried out. To the best of our knowledge the hydrogenation of furan, 2-cyanofuran and 3-cyanofuran (Fig. 1) under the same conditions is not reported yet.

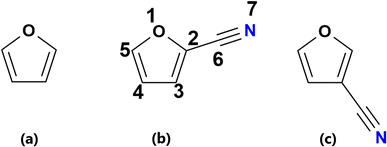Fig. 1 Chemical structures of (a) furan, (b) 2-cyanofuran (2CF) and (c) 3-cyanofuran (3CF): 1 to 7 are different positions of protonation.

The main objective of this investigation is to explore the formation of 2-cyanofuran (2CF) and 3-cyanofuran (3CF) and their protonated forms in the ISM conditions of temperature and pressure. The proton affinity (PA) of both 2CF and 3CF together with the enthalpy, entropy and Gibbs free energy changes (i.e., Δ_rH, Δ_rS and Δ_rG, respectively) of the reactions producing cyanofurans and the corresponding protonated forms are calculated at different conditions of temperature and pressure and with the aid of modern quantum chemical methods. The structures of protonated cyanofurans (C₄H₃O–CFNH⁺) are characterized through their vibrational and rotational spectra.

2 Computational details

Density functional theory (DFT) calculations were performed with the aid of Gaussian 09 package.⁴⁰ The Gabedit 2.5.0 ⁴¹ visualization program was used to build the starting molecular structures. Geometrical parameters for furan, 2CFH⁺, 3CFH⁺ and HCNH⁺ are determined using the method described and used in previous works.^42,43 This methodology includes geometry optimization followed by empirical corrections for systematic deficiencies of methods and basis sets and adjustments to some geometrical parameters. Based on this method, the B3LYP^44,45/6-31G(d,p) level of theory was chosen. This optimization scheme is first applied on furan which has experimental data and thereafter applied to 2CF, 3CF and their protonated forms (2CFH⁺, 3CFH⁺, respectively). Thermodynamic properties including the proton affinity, the entropy, enthalpy and Gibbs free energy changes (Δ_rS, Δ_rH and Δ_rG in kJ mol⁻¹) for reactions producing the cyanofurans and theirs protonated forms are calculated using at G2MP2 and G3. The calculations of these properties are done under different conditions of temperature (T = 298 K, T = 150 K, T = 10 K and T = 5 K) and pressure (P = 1 atm and P = 10⁻⁵ atm) prevailing in ISM environments where the present protonated species or COMs, in general, are expected to be found. These two levels were chosen because they give results which are close to the experimental value for existing furan. To improve the accuracy of the thermodynamic properties, these quantities were recomputed using the G4 and G4MP2 methods. The harmonic frequencies for RCNH⁺ were calculated at B3LYP/6-31G(d,p). In order to get reliable frequencies, the calculated frequencies were rescaled using MOLVIB.⁴⁶ For rotational spectra, the calculation of rotational transitions, as well as the analysis of quadrupole hyperfine splitting were done using the SPFIT/SPCAT package.⁴⁷

3 Results and discussion

3.1 Geometrical parameters

Experimental and calculated bond lengths (in Å), bond angles (in °) and rotational constants (in MHz), as well as deviations with respect to experimental rotational constants at different levels of theory are presented in Table S1 in the ESI† file. Table 1 contains root mean square deviations (RMSD) for bond length (in Å), bond angles (in °) and rotational constants (in MHz) for furan for the different assessed levels of theory with respect to experimental results.⁴⁸ As shown by the results in this table, for a given method, the larger is the basis set the higher is the accuracy for the geometrical structure. However, the accuracy of the rotational constants which are strongly linked to the molecular structure does not follow this increase of basis set. A careful analysis of the results in Table 1 reveals that B3LYP/6-31G(d) and B3LYP/6-31G(d,p) reproduce, relatively well the geometrical structure, but also very well the rotational constants for furan compared with other levels of theory. B3LYP/6-31G(d,p) was therefore chosen for the empirical correction as it combines the geometrical structure accuracy as well that of the rotational constants. The optimized geometric structures (including empirical corrections) at B3LYP/6-31G(d,p) for furan, 2CF, 3CF, 2CFH⁺ and 3CFH⁺ are presented in Tables 2 and S2.† For calibration of the method, the protonated form of cyanide (HCNH⁺ see Fig. S1†) for which experimental structure is known from the literature was considered. The results reveal a very good agreement between calculated and experimental structures for furan and HCNH⁺. Indeed, recalling that rotational constants are extremely linked to the molecular structure through the moment of inertia components, the comparison of calculated and experimental rotational constants in Table 2 for furan reveals a very good agreement between them. This agreement supports the accuracy of the used method and the reliability of the calculated results. Thus, applying the same methodology is reasonably to lead to accurate structures for both the neutral (2CF and 3CF) and the protonated (2CFH⁺ and 3CFH⁺) species forms for which no experimental data are reported yet. As expected, the comparison of calculated and experimental rotational constants in Table 2 for 2CF reveals also a very good agreement between them. This agreement is also an evidence that the calculated structures for all the molecular species are reliable and close to the experimental ones. The optimized 3D molecular geometries are displayed in Fig. 2 and S1.†

Table 1 RMSD bond length (in Å), bond angles (in °) and rotational constants (in MHz) for furan for at different assessed levels of theory with respect to experimental results

Level of theory	Bond lengths	Bond angles	Rotational constants
	RMSD/Exp^a	RMSD/Exp^a	RMSD/Exp^a
a Experimental data from Bak et al. (1962).^48b Calculated at B3LYP/6-31G(d,p) + empirical correction.
HF/6-31G(d)	0.0154	0.3817	246.4136
MP2/6-31G(d,p)	0.0034	0.2449	44.9147
MP3/6-311G(d)	0.0052	0.2204	39.9478
M06-2X/6-31G(d,p)	0.0051	0.1852	91.3475
M06-2X/6-311G(2d,2p)	0.0068	0.2449	134.6708
B3LYP/6-31G(d)	0.0036	0.3780	10.4848
B3LYP/6-31G(d,p)	0.0031	0.2976	11.6142
B3LYP/6-311G(2d,2p)	0.0033	0.2976	67.2463
B3LYP/6-311+G(2d,2p)	0.0031	0.2928	60.7535
B3LYP/6-31+G(d)	0.0043	0.3338	14.7672
B3LYP/6-311G(2df,2p)	0.0075	0.2070	147.9445
B3LYP/6-31G(d,p)^b	0.0078	0.6164	1.3454

---

Table 2 Experimental and B3LYP/6-31G(d,p) optimized geometrical parameters (including empirical corrections) for furan, 2CF, 3CF, 2CFH⁺ and 3CFH⁺ (bond lengths in Å, bond angles in °, rotational constants in MHz, principle moments of inertia and the inertial defects in amu Å^2a

	Furan		2CF		3CF	2CFH^+	3CFH^+
	Calc	Exp^b	Calc	Exp^c
a Numbering scheme used is that of Fig. 1 and Scheme S1.b Experimental data from Bak et al.^48c Experimental data from Engelbrecht & Sutter.^49
Bond length
O–C2	1.3584	1.362	1.3589	—	1.3422	1.3722	1.3212
O–C5	1.3584	1.362	1.350	—	1.3605	1.3503	1.3796
C2=C3	1.3622	1.361	1.3679	—	1.3746	1.3726	1.3909
C3–C4	1.4520	1.431	1.4462	—	1.44106	1.4423	1.4514
C4=C5	1.3622	1.361	1.3730	—	1.3478	1.3663	1.3519
C2/C3–C6	—	—	1.099	—	1.4163	1.4099	1.3856
C≡N	—	—	1.1717	—	1.1655	1.1716	1.1571
N–H	—	—	—	—	—	1.0113	1.0069
Bond angle
C5–O–C2	107.13	106.5	105.42	—	107.35	105.60	108.77
O–C2=C3	110.814	110.7	111.29	—	110.41	111.64	108.63
O–C5=C4	110.814	110.7	113.28	—	110.85	111.99	111.09
C5=C4–C3	105.622	106.0	103.52	—	105.96	105.89	104.04
C2=C3–C4	105.622	106.0	105.66	—	105.43	104.87	107.48
C2/C3–C6≡N	—	—	—		179.54	175.05	179.34
C6≡N–H	—	—		—		155.00	179.87
Constantes rotationnelles
A	9446.06	9446.9	9220.097	9220.106	9374.251	9070.367	9092.451
B	9246.25	9246.6	2028.751	2029.262	1936.447	1924.174	1875.140
C	4672.54	4670.8	1662.861	1662.640	1604.917	1588.967	1554.545
Principal moments of inertia and inertial defect
Iaa (amu Å^2)	191.051	—	195.727		53.911	55.715	55.717
Ibb (amu Å^2)	195.194	—	889.394		260.983	262.653	262.647
Icc (amu Å^2)	386.245	—	1085.120		314.895	318.062	318.055
ΔI (amu Å^2)	0.000	—	0.001		−0.001	0.306	0.309

---

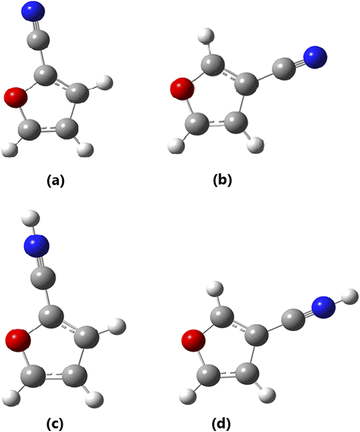Fig. 2 B3LYP/6-31G(d,p) optimized 3D geometries for: (a) 2CF, (b) 3CF, (c) 2CFH⁺ and (d) 3CFH⁺ (red = O, gray = C, blue = N and light gray = H).

It should be noted that HCNH⁺ is a linear molecule belonging to the C_∞V point group. While the inertial defect values (ΔI in Table 2) for furan, 2CF, 3CF and 3CFH⁺ are ≈0 (i.e., 0.000, 0.001 and −0.001 amu Ų, respectively), indicating that they are totally planar, those for 2CFH⁺ and 3CFH⁺ being high (≈0.306 and 0.309 amu Ų) indicating that these forms are distorted and non planar. The N–H is bent out of the plan containing the remain atoms; the hydrogen atom is thus out of this plan. The different molecular species are therefore asymmetric top molecules belonging to the C_s point group (for planar species) and C₁ point group for 2CFH⁺. This different structural behavior for 2CFH⁺ can be traced back to the ≈25° of difference in the C6–N–H bond angle 155.0° for 2CFH⁺ with respect to that of 3CFH⁺, i.e., 179.9°. This unexpected structural behavior will be discussed in another work.

3.2 Sites of protonation

The protonation (or hydrogenation) is the addition of a proton (H⁺) to an atom, or molecule, forming the conjugate acid according to eqn (1).⁵⁰

A + H⁺ ⇌ AH⁺ (1)

The proton affinity (PA) of a chemical species A is the negative of the change in enthalpy associated with the gas phase protonation of the reaction.⁵⁰ The PA is defined by enthalpy changes in eqn (2):

PA = ΔH(A) + ΔH(H⁺) − ΔH(AH⁺) (2)

where ΔH(A) and ΔH(AH⁺) are enthalpies of the unprotonated and protonated compound, respectively.

The PA of furan was calculated at different positions using G2MP2 and G3 at different temperatures (298 K, 150 K, 10 K and 5 K for P = 1 atm). The results are presented in Table 3. These temperatures are in the range of temperatures prevailing in molecular clouds where complex organic molecules (COMs) are expected to be found (10–300 K).^51,52

Table 3 G2MP2 and G3 proton affinity (PA in kJ mol⁻¹) of furan at different sites of protonation and temperatures (T = 298 K, T = 150 K, T = 10 K and T = 5 K)

Sites of protonation
Method	O	Cα^a	Cβ^b	O	Cα^a	Cβ^b
a Cαb Cβ are atoms number 2 (α-position) and 3 (β-position) on Fig. 1;c Experimental data from Van et al.^53 (NIST).
	298 K			150 K
G2MP2	701.41	815.91	771.73	698.92	813.46	769.54
G3	697.78	814.80	770.18	719.69	812.35	767.98
	10 K			5 K
G2MP2	696.07	810.72	766.83	695.97	810.62	766.73
G3	693.19	809.61	765.28	693.09	809.50	765.18
NIST	812^c

---

The protonation site for C₄H₄O and C₄H₅N has been investigated by resonant infrared multiphoton dissociation (IRMPD) spectroscopy in the 900–1700 cm⁻¹ range employing the free electron laser (FEL) at the Centre Laser Infrarouge Orsay (CLIO) by Ulrich and his coworkers.⁵⁴ B3LYP/6-311G(2df,2pd) level of theory has demonstrated that only the C_α protonated isomers are observed, and corresponds to the global minima on the potential energy surfaces. These results show that C_α is the preferred site of protonation. The National Institute of Science and Technology (NIST) provides also a value for the PA of furan, i.e., PA ≈ 812 kJ mol⁻¹.⁵³ This later value was calculated using Fourier transform ion cyclotron resonance (FT-ICR) mass spectrometry. Small discrepancies are observed then between this value and the results in Table 3: δ = 3.91 kJ mol⁻¹ for G2MP2 and δ = 2.80 kJ mol⁻¹ for G3 at 298 K; δ = 1.46 kJ mol⁻¹ for G2MP2 and δ = 0.35 kJ mol⁻¹ for G3 at 150 K; and δ = −1.28 kJ mol⁻¹ for G2MP2 and δ = 2.39 kJ mol⁻¹ for G3 at 10 K. The comparison of these results with the value of NIST shows a good agreement at 150 K, especially with G3 when the protonation is performed at the C_α. The calculated proton affinities for furan in the ascending order are such that PA(O) < PA(β) < PA(α). Considering that the site with high affinity for the proton corresponds to the site which has a high probability of attack by the proton,¹⁴ the results show that the α-position is the most favorable site for protonation of furan, confirming the existing literature.⁵⁵

The PA is also calculated for the nitrile substituted derivatives (2CF and 3CF) for the same temperatures (298 K, 150 K, 10 K and 5 K) for the pressure (P = 1 atm). The results calculated with G2MP2 and G3 at T = 298 K and T = 10 K are shown in Tables 4 and S3,† whereas those calculated at T = 150 K and T = 5 K are presented in Table S4.† According to the PA values, the favorable protonation site is the nitrogen atom for both the 2CF and 3CF at considerated temperatures (see Tables S3 and S4† for details). The results show us again that upon the protonation of the furan ring in the ISM conditions of temperature and pressure, the α-position is the most favorable site. A comparison between α and β protonation either for 2CF or 3CF shows that it occurs in α-position for both 2CF and 3CF. The PAs for these compounds in the decreasing order are such that PA(1) < PA(3) < PA(4) < PA(2) < PA(5) < PA(6) for 2CF and PA(1) < PA(3) < PA(4) < PA(5) < PA(2) < PA(6) for 3CF, where (6) is the nitrogen atom of the cyano group.

Table 4 G2MP2 and G3 proton affinity (PA in kJ mol⁻¹) of 2CF and 3CNF at different sites of protonation and temperatures (T = 298 K and T = 10 K)

Sites^a	2CF		3CF
	G2MP2	G3	G2MP2	G3
a Position numbering scheme is from Fig. 1 and Scheme S1.
1	643.39 (635.93)	642.18 (634.71)	636.48 (631.33)	635.54 (630.39)
2	732.07 (726.97)	727.39 (722.29)	753.58 (748.65)	751.89 (746.96)
3	702.78 (698.23)	701.18 (696.65)	677.78 (672.97)	672.71 (667.90)
4	709.78 (705.07)	707.45 (702.76)	709.00 (704.26)	706.34 (701.60)
5	747.83 (742.97)	746.38 (735.37)	747.75 (742.78)	745.32 (740.35)
N	795.14 (790.48)	796.35 (791.69)	801.47 (796.57)	802.75 (797.85)

---

3.3 Enthalpy (Δ_rH), Gibbs free energy (Δ_rG) and entropy (Δ_rS) changes of the reactions producing 2CF/3CF and their protonated forms

The reactions yielding R–CN/R–CNH⁺ and the corresponding enthalpy (Δ_rH), entropy (Δ_rS) and Gibbs free energy (Δ_rG) changes are explored using G2MP2 and G3 at different temperatures (298 K, 150 K, 10 K and 5 K) and low pressure (P = 10⁻⁵ atm). Calculations using G4MP2 and G4 were also performed at 298 K and 10 K) and low pressure (P = 10⁻⁵ atm). The results for G2MP2, G3, G4MP2 and G4 for T = 298 K and T = 10 K are shown in Table 5, whereas those for G2MP2 and G4 at T = 150 K and T = 5 K are presented in Table S5†).

Table 5 Gase phase G2MP2, G3, G4MP2 and G4 calculated enthalpy, entropy and Gibbs free energy variations (Δ_rH, Δ_rS and Δ_rG in kJ mol⁻¹) of reaction producing cyanofurans and their protonated forms (T = 298 K and T = 10 K for P = 10⁻⁵ atm)

Reactions	No	298 K			10 K
		ΔrH	ΔrG	ΔrS	ΔrH	ΔrG	ΔrS	Method
C4H4O^+ + CN^− → 2CF + H˙	(1)	−532.03	−517.07	−0.050	−532.98	−533.44	−0.045	G2MP2
		−567.58	−552.65	−0.050	−568.98	−568.54	−0.044	G3
		−556.02	−541.13	−0.050	−557.54	−557.09	−0.045	G4MP2
		−561.53	−546.64	−0.050	−563.05	−562.61	−0.045	G4
C4H4O^+ + CN^− → 3CF + H˙	(2)	−538.90	−523.98	−0.050	−539.84	−540.29	−0.044	G2MP2
		−573.73	−558.84	−0.049	−574.67	−575.11	−0.043	G3
		−563.38	−548.60	−0.050	−564.93	−564.49	−0.045	G4MP2
		−568.66	−553.88	−0.050	−570.21	−569.77	−0.045	G4
C4H3OCN + H3^+ → 2CFH^+ + H2	(3)	−374.98	−369.79	−0.017	−375.31	−373.49	−0.182	G2MP2
		−375.89	−370.63	−0.017	−376.00	−375.89	−0.010	G3
		−372.72	−365.70	−0.024	−371.85	−371.73	−0.011	G4MP2
		−373.42	−243.75	−0.435	−372.54	−372.43	−0.012	G4
C4H3OCN + H3^+ → 3CFH^+ + H2	(4)	−381.31	−375.59	−0.019	−381.49	−379.58	−0.190	G2MP2
		−382.28	−376.56	−0.019	−382.18	−382.07	−0.010	G3
		−377.74	−372.88	−0.024	−378.16	−378.04	−0.012	G4MP2
		−378.28	−373.42	−0.016	−378.69	−377.29	−0.139	G4

---

The results reveal that the Δ_rH, Δ_rS and Δ_rG are all negative, implying that the reactions leading to the formation of 2CF/3CF and their protonated forms are spontaneous.⁵⁶ It is worthy noting that these quantities are also negative regardless the used method. These results imply that all reactions are spontaneous at the considered conditions of temperature and pressure, conditions prevailing in ISM regions where COMs are mostly detected. They also imply that cyanofurans and their protonated forms are likely to be produced barrierlessly via the proposed reactions.

3.4 Vibrational parameters of 2CFH⁺ and 3CFH⁺

The use of IR spectroscopy is a reliable mean in the identification of chemical species in ISM.^51,52 However, the IR spectra are not reported yet for the 2CFH⁺ and 3CFH⁺ species. In this study, the simulation of vibrational spectra for the protonated cyanofurans, supported by the potential energy distribution (PED) is performed. The vibrational and rotational spectra for non protonated forms are dealt in an other works.

During the PED analysis, the contribution of each vibrational mode as well as the atoms involved for the 27 vibrational frequencies for each of these two compounds using MOLVIB.^46,57 The results are shown in Tables S6 and S7.† In addition, the 27 vibrational modes are distributed in the two representations of symmetry of the point group C_s: 3N − 6 = 20A′ (in-plan modes) + 7A′′ (out-of-plan modes) for 2CFH⁺ and C_s: 3N − 6 = 18A′ (in-plan modes) + 9A′′ (out-of-plan modes) for 3CFH⁺ as shown in the Tables S6 and S7.† The NH and CH stretching modes for the species studied are characterized in the region where they are supposed to appear, i.e., in the range 3000–3800 cm⁻¹.^58,59 In fact, the NH stretching modes appear at 3475 and 3486 cm⁻¹ for 2CFH⁺ and 3CFH⁺, respectively, with PED = 97% for both these compounds. Likewise, the CH stretching modes appear at 3176, 3130 and 3122 cm⁻¹ with contributions of 97, 98% and 98%, respectively, for 2CFH⁺. These modes of vibrations appear also at 3147, 3120 and 3120 cm⁻¹ with contributions of 98, 99% and 99%, respectively, for 3CFH⁺. The analysis of results in Table S8† shows that, whereas the lines corresponding to NH are very strong in IR for both compounds (≈1034 km mol⁻¹ for 2CFH⁺ and 1135 km mol⁻¹ for 3CFH⁺), those corresponding to CH are relatively weak (≈20 km mol⁻¹ for the most intense for 2CFH⁺ and ≈24 km mol⁻¹ for the most intense for 3CFH⁺). It is worthy stating that, from the results in this table, the Raman lines in this region are weak for both the two molecular species. Moreover, from the calculated frequencies and modes presented in Tables S6 and S7,† the in-planes and out-of-plane deformations characterizing the protonation, i.e., the one involving NH, have significant contributions below 650 cm⁻¹. Indeed, the in-plane deformations contribute at 590 cm⁻¹ (PED = 15%), 575 cm⁻¹ (PED = 20% and at 279 cm⁻¹ (PED = 62%) for 2CFH⁺. They contribute at 592 cm⁻¹ (PED = 59%) and at 168 cm⁻¹ (PED = 47%) for 3CFH⁺. Similarly, the out-of-plane deformation modes contribute at 630 cm⁻¹ (PED = 23%), 542 cm⁻¹ (PED = 78%) and at 179 cm⁻¹ (PED = 23%) for 2CFH⁺. They contribute also at 628 cm⁻¹ (PED = 35%), 627 cm⁻¹ (PED = 91%), 489 cm⁻¹ (PED = 21%) and at 209 cm⁻¹ (PED = 68%) for 3CFH⁺.

The in-plane CH deformations appear in the range 872–1546 cm⁻¹ with high contributions at 1190 cm⁻¹ (PED = 75%) for 2CFH⁺ and in the range 755–1591 cm⁻¹ with high contributions at 1222 cm⁻¹ (PED = 83%) and at 1099 cm⁻¹ (PED = 76%). In the same way, the out-of-plane CH deformations appear in the range 179–875 cm⁻¹ with main contributions at 875 cm⁻¹ (PED = 86%), at 839 cm⁻¹ and 875 cm⁻¹ with PED = 88% for 2CFH⁺. For 3CFH⁺, these vibrations modes appear in the range 209–887 cm⁻¹, contributing mainly at 889 cm⁻¹ (PED = 94%), 882 cm⁻¹ (PED = 88%), and at 808 cm⁻¹ (PED = 89%). IR and Raman intensities for protonated forms (2CFH⁺ and 3CFH⁺) are presented in Table S8† and plotted in Fig. S2 and S3.†

3.5 Rotational parameters of 2CFH⁺ and 3CFH⁺

The calculated rotational parameters for the two protonated species (in addition to those related to the molecular geometry presented in Table 2) are provided in Table 6. In general, protonation spectroscopic data are of great importance in unambiguously identifying the protonated species in the ISM.⁶⁰ In particular, hyperfine spectra, besides identifying the protonation site(s), also unravel the structural attribution of various isomers.⁶¹ The present work is the first study on the rotational spectroscopic properties of 2CFH⁺ and 3CFH⁺. The rotational parameters play an important role in the characterization of the spectra of molecules. A molecule has a spectrum if it has a permanent dipole moment. For the first times, rotational constants of protonated cyanofurans are provided. The results summarized in Table 6 show that 2CFH⁺ has a small dipole moment compared 3CFH⁺. Protonated hydrogen cyanide is a case of protonated simple molecular species which has drawn much attention because of its importance in the chemistry of interstellar clouds.⁶² It had been searched in many different environmental media and was, first, detected very early towards Sgr B2,⁶³ through three pure rotational transitions 1–0, 2–1 and 3–2 at 74, 148 and 222 GHz, respectively. It was, later, found in dark clouds towards TMC-1 (T ≈ 10 K),^64,65 through the quadrupole hyperfine structure of 1–0 and in the DR 21(OH) compact H II region.^64,66 It had even been detected in L1544 (T ≈ 7 K).^5,67 For non protonated forms, only 2CF has experimental rotational constants (Table 2). Results in this table show a very good agreement between experimental and calculated values for this molecule (ΔA = 0.009, ΔB = 0.5512 and ΔC = 0.221 MHz). We therefore expect the same accuracy for molecular species without experimental results, including protonated cyanofurans. Fig. 3 presents simulated rotational spectra (including ¹⁴N hyperfine quadrupole couplings) for 2CFH⁺ and 3CFH⁺ at T = 7, 10, 30, 100, 150 K and 300 K. The analysis of these spectra reveals that the most intense lines are observed for low temperatures. Indeed, temperatures (T ≈ 7 K and T ≈ 10 K), i.e., the temperature prevailing in TMC-1 or in many cold molecular clouds known to host COMs. The presence of the ¹⁴N quadrupole nucleus induces lines splittings. Indeed, Tables S9 and S10† present the B3LYP/6-31G(d,p) calculated strongest quadrupole hyperfine structures for 2CFH⁺ and 3CFH⁺, respectively, at T = 10 K. The results in these tables confirm, as it has been found from the Fig. 3, that the brightest lines are in the regions of frequencies around 45 GHz. For instance, Table S9† shows that the three strongest transition lines are 13_{1 12} ← 12_{1 11}, 12_{1 11} ← 11_{1 10} and 13_{0 13} ← 12_{0 12} centered at ≈46 479, ≈43 124.5 MHz and ≈43 054 MHz, respectively. Likewise, the analysis of results in Table S9† reveals also that the three strongest transition lines are 13_{1 12} ← 12_{1 11}, 12_{1 11} ← 11_{1 10} and 14_{0 14} ← 13_{0 13} centered in the regions around ≈45 438, ≈42 142 MHz and ≈45 216 MHz, respectively. A common analysis of results in these two tables reveals that the strongest component for a 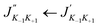transition correspond to the term for which F′′ = J′′ + 1 and F′ = J′ + 1. It is followed by the component corresponding to F′′ = J′′ ← F′ = J′ and then that corresponding to F′′ = (J′′ − 1) ← F′ = (J′ − 1). Terms corresponding to F′′ = (J′′ − 1) ← F′ = J′ and F′′ = J′′ ← F′ = (J′ + 1) are weak with equal intensities, whereas F′′ = (J′′ − 1) ← F′ = (J′ + 1) is the weakest one, with intensity nearly equal to zero. These observations are common either for 2CFH⁺ or 3CFH⁺. For both the two molecular species, strong lines correspond to the values of J in the range 11–15. Moreover, the analysis of Fig. 3 and Tables S9, S10† reveals also that transitions lines are stronger for 3CFH⁺ than for 2CFH⁺. Indeed, the 3CFH⁺ strongest line is about five times stronger than the 2CFH⁺ strongest line. For instance, the 3CFH⁺ line 13_{1 12}, 14 ← 12_{1 11}, 13 at 45 438.0092 MHz has intensity of 46.4430 × 10⁻³ nm² MHz, whereas, 13_{1 12}, 13 ← 12_{1 11}, 12 appearing at 46 479.2457 MHz has intensity of 8.7264 × 10⁻³ nm² MHz. In other words, one may find that the rotational spectrum for 2CFH⁺ is less intense than that for 3CFH⁺. The rotational line intensity being proportional to the square of the dipole moment,⁶⁸ this disparity in line intensity for the rotational spectra of these two species is ascribable to the difference in their dipole moments (see Table 6).

Table 6 Additional B3LYP/6-31G(d,p) calculated rotational parameters from optimized geometrical structures (including empirical corrections) of 2CFH⁺ and 3CFH⁺

Rotational parameters	2CFH^+	3CFH^+
Δj (kHz)	0.068	0.061
Δk (kHz)	1.002	12.379
Δkj (kHz)	2.185	1.901
Δj (kHz)	0.012	0.109
Δk (kHz)	1.276	1.107
μa (debye)	3.151	5.417
μb (debye)	1.118	−0.045
μc (debye)	1.126	0.380
μtot (debye)	3.970	5.430
χaa (MHz)	1.028	1.247
χbb (MHz)	0.955	0.347
χcc (MHz)	−1.983	−1.595
χab (MHz)	−0.023	0.019
κ	−0.910	−0.918

---

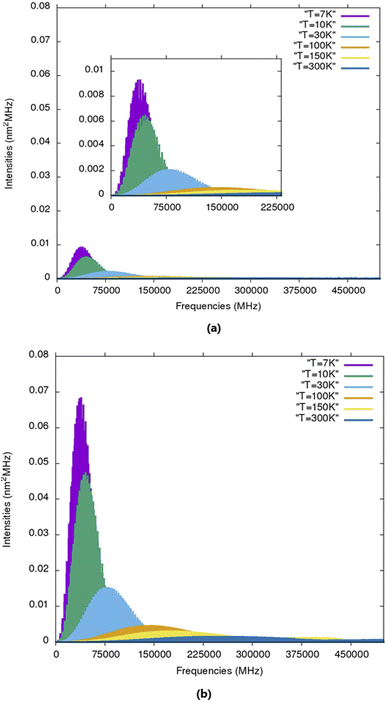Fig. 3 Simulated rotational spectra (including ¹⁴N hyperfine quadrupole couplings) for (a) 2CFH⁺ and (b) 3CFH⁺ at T = 7, 10, 30, 100, 150 K and 300 K.

4 Conclusions

For the first time, the thermodynamics of reactions leading to the formation of furan, 2-cyanofuran, 3-cyanofuran and their protonated forms under interstellar (ISM) conditions of pressure (1 atm and 10⁻⁵ atm) and temperature (5 K, 10 K, 150 K and 298 K) was conducted. The predicted enthalpy change (Δ_rH), the entropy change (Δ_rS) and the Gibbs free energy change (Δ_rG) of reactions, with the aid high performance methods (G3, G2MP2, G4 and G4MP2) has shown that all these thermodynamic properties have negative values under ISM conditions of pressure and temperature. Accordingly, it was concluded that these heterocyclic molecules emerge spontaneously in this medium. In addition, geometrical structures, vibrational an rotational spectra of the protonated species were investigated. IR lines corresponding to the NH stretching modes (characteristic of the protonation) were found to be very strong whereas, the Raman lines were found to be weak. From rotational analysis at temperature prevailing in molecular clouds where COMs are expected to be discovered (T ≈ 10 K, stronger lines are located in the regions around 45 GHz for both 2CFH⁺ and 3CFH⁺. Rotational lines (or strong hyperfine structure components) were found to be more intense in 3CFH⁺ than 2CFH⁺. In a context of gap in the scientific knowledge about these species, we believe that these data will serve for astrophysical and astrochemical purposes in detection of new entities in interstellar medium.

Conflicts of interest

No conflict of interest to declare.

Acknowledgements

This research was partially supported by VLIR-UOS cooperation (through the BI2017IUC022A102 Program). Prof GAHUNGU G. is grateful for the equipment donation by the Chinese Ministry of Sciences and Technology (MOST) through the China–Africa Sciences and Technology Partnership (CASTEP).

Notes and references

1. B. A. McGuire, Astrophys. J., Suppl. Ser., 2018, 239, 17.
2. L. Margulès, B. McGuire, R. Motiyenko, C. Brogan, T. Hunter, A. Remijan and J. Guillemin, Astron. Astrophys., 2020, 638, A3.
3. E. Herbst and R. T. Garrod, Frontiers in Astronomy and Space Sciences, 2022, 8, 209.
4. M. J. Abplanalp and R. I. Kaiser, Phys. Chem. Chem. Phys., 2019, 21, 16949–16980.
5. E. Herbst and E. F. Van Dishoeck, Annu. Rev. Astron. Astrophys., 2009, 47, 427–480.
6. A. G. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337.
7. R. Simbizi, G. Gahungu and M. T. Nguyen, Phys. Chem. Chem. Phys., 2020, 22, 24735–24743.
8. B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202–205.
9. M. C. McCarthy, K. L. K. Lee, R. A. Loomis, A. M. Burkhardt, C. N. Shingledecker, S. B. Charnley, M. A. Cordiner, E. Herbst, S. Kalenskii and E. R. Willis, et al., Nat. Astron., 2021, 5, 176–180.
10. K. L. K. Lee, P. B. Changala, R. A. Loomis, A. M. Burkhardt, C. Xue, M. A. Cordiner, S. B. Charnley, M. C. McCarthy and B. A. McGuire, Astrophys. J. Lett., 2021, 910, L2.
11. B. A. McGuire, R. A. Loomis, A. M. Burkhardt, K. L. K. Lee, C. N. Shingledecker, S. B. Charnley, I. R. Cooke, M. A. Cordiner, E. Herbst and S. Kalenskii, et al., Science, 2021, 371, 1265–1269.
12. A. M. Burkhardt, K. L. K. Lee, P. B. Changala, C. N. Shingledecker, I. R. Cooke, R. A. Loomis, H. Wei, S. B. Charnley, E. Herbst and M. C. McCarthy, et al., Astrophys. J. Lett., 2021, 913, L18.
13. U. Jacovella, J. A. Noble, A. Guliani, C. S. Hansen, A. J. Trevitt, J. Mouzay, I. Couturier-Tamburelli, N. Pietri and L. Nahon, Astron. Astrophys., 2022, 657, A85.
14. T. Oka, Faraday Discuss., 2011, 150, 9–22.
15. T. P. Snow and B. J. McCall, Annu. Rev. Astron. Astrophys., 2006, 44, 367–414.
16. C. R. Arumainayagam, R. T. Garrod, M. C. Boyer, A. K. Hay, S. T. Bao, J. S. Campbell, J. Wang, C. M. Nowak, M. R. Arumainayagam and P. J. Hodge, Chem. Soc. Rev., 2019, 48, 2293–2314.
17. E. Herbst, Int. Rev. Phys. Chem., 2017, 36, 287–331.
18. J. Chantzos, S. Spezzano, C. Endres, L. Bizzocchi, V. Lattanzi, J. Laas, A. Vasyunin and P. Caselli, Astron. Astrophys., 2019, 621, A111.
19. Y.-K. Li, Z.-C. Wang, S.-G. He and V. M. Bierbaum, Int. J. Mass Spectrom., 2018, 433, 1–6.
20. D. R. Gies and D. L. Lambert, Astrophys. J., 1992, 387, 673–700.
21. T. Soma, N. Sakai, Y. Watanabe and S. Yamamoto, Astrophys. J., 2018, 854, 116.
22. K. Cunha and D. L. Lambert, Astrophys. J., 1994, 426, 170–191.
23. C. Boersma, A. Mattioda, C. Bauschlicher, E. Peeters, A. Tielens and L. Allamandola, Astrophys. J., 2008, 690, 1208.
24. J. Cernicharo, A. M. Heras, A. Tielens, J. R. Pardo, F. Herpin, M. Guélin and L. Waters, Astrophys. J., 2001, 546, L123.
25. A. Penzias, Astrophys. J., 1981, 249, 518–523.
26. D. Whittet, Astrophys. J., 2010, 710, 1009.
27. B. A. McGuire, C. N. Shingledecker, E. R. Willis, K. L. K. Lee, M.-A. Martin-Drumel, G. A. Blake, C. L. Brogan, A. M. Burkhardt, P. Caselli, K.-J. Chuang, S. El-Abd, T. R. Hunter, S. Ioppolo, H. Linnartz, A. J. Remijan, C. Xue and M. C. McCarthy, Astrophys. J., 2019, 883, 201.
28. P. Boulet, F. Gilardoni, J. Weber, H. Chermette and Y. Ellinger, Chem. Phys., 1999, 244, 163–174.
29. D. Garcia-Hernandez, P. García-Lario, J. Cernicharo, D. Engels and J. Perea-Calderón, J. Phys.: Conf. Ser., 2016, 052003.
30. T. Oka, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12235–12242.
31. M. Ohishi, S.-i. Ishikawa, T. Amano, H. Oka, W. M. Irvine, J. E. Dickens, L. M. Ziurys and A. Apponi, Astrophys. J., 1996, 471, L61.
32. F. Cacace and M. Speranza, Science, 1994, 265, 208–209.
33. M. Agúndez, J. Cernicharo, P. De Vicente, N. Marcelino, E. Roueff, A. Fuente, M. Gerin, M. Guélin, C. Albo and A. Barcia, et al., Astron. Astrophys., 2015, 579, L10.
34. A. Glassgold, A. Omont and M. Guelin, Astrophys. J., 1992, 396, 115–119.
35. O. Martinez Jr, V. Lattanzi, S. Thorwirth and M. C. McCarthy, J. Chem. Phys., 2013, 138, 094316.
36. C. Cabezas, M. Agúndez, N. Marcelino, B. Tercero, R. Fuentetaja, P. de Vicente and J. Cernicharo, Astron. Astrophys., 2022, 659, L8.
37. N. Marcelino, M. Agúndez, B. Tercero, C. Cabezas, C. Bermúdez, J. Gallego, P. Devicente and J. Cernicharo, Astron. Astrophys., 2020, 643, L6.
38. V. M. Bierbaum, Proc. Int. Astron. Union, 2013, 9, 258–264.
39. G. Devi, M. Buragohain and A. Pathak, Planet. Space Sci., 2020, 183, 104593.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision A.02, Inc., Wallingford CT, 2009.
41. A. R. Allouche, Gabedit, 2017.
42. N. V. Riggs, L. Radom, M. Winnewisser, B. P. Winnewisser and M. Birk, et al., Chem. Phys., 1988, 122, 305–315.
43. R. Simbizi, G. Gahungu and M. T. Nguyen, Spectrochim. Acta, Part A, 2020, 239, 118393.
44. A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160.
45. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
46. T. Sundius, J. Mol. Struct., 1990, 218, 321–326.
47. H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377.
48. B. Bak, D. Christensen, W. B. Dixon, L. Hansen-Nygaard, J. R. Andersen and M. Schottländer, J. Mol. Spectrosc., 1962, 9, 124–129.
49. L. Engelbrecht and D. Sutter, Zeitschrift für Naturforschung A, 1976, 31, 670–672.
50. L. A. Curtiss, P. C. Redfern, K. Raghavachari, V. Rassolov and J. A. Pople, J. Chem. Phys., 1999, 110, 4703–4709.
51. A. Vasyunin and E. Herbst, Astrophys. J., 2013, 769, 34.
52. A. Bacmann, V. Taquet, A. Faure, C. Kahane and C. Ceccarelli, Astron. Astrophys., 2012, 541, L12.
53. E. S. Van Beelen, T. A. Koblenz, S. Ingemann and S. Hammerum, J. Phys. Chem. A, 2004, 108, 2787–2793.
54. U. J. Lorenz, J. Lemaire, P. Maitre, M.-E. Crestoni, S. Fornarini and O. Dopfer, Int. J. Mass Spectrom., 2007, 267, 43–53.
55. M. T. Nguyen and A. K. Chandra, et al., J. Chem. Soc., Faraday Trans., 1998, 94, 1277–1280.
56. T. L. Brown, H. E. LeMay Jr and B. E. Bursten, Chemical Thermodynamics of Zirconium, NEA OECD, Elsevier, 2005, ISBN-13978–980.
57. a. T. Sundius, Vib. Spectrosc., 2002, 29, 89–95.
58. K. Chatterjee and O. Dopfer, J. Chem. Phys., 2018, 149, 174315.
59. P. Ehrenfreund and S. B. Charnley, Annu. Rev. Astron. Astrophys., 2000, 38, 427–483.
60. J. Palotás, J. Martens, G. Berden and J. Oomens, J. Mol. Spectrosc., 2021, 378, 111474.
61. V. Barone, M. Biczysko and C. Puzzarini, Acc. Chem. Res., 2015, 48, 1413–1422.
62. M. Araki, H. Ozeki and S. Saito, Astrophys. J., 1998, 496, L53.
63. L. M. Ziurys and B. Turner, Astrophys. J., 1986, 302, L31–L36.
64. P. Schilke, C. Walmsley, T. Millar and C. Henkel, Astron. Astrophys., 1991, 247, 487–496.
65. L. Ziurys, A. Apponi and J. Yoder, Astrophys. J., 1992, 397, L123–L126.
66. T. Hezareh, M. Houde, C. McCoey, C. Vastel and R. Peng, Astrophys. J., 2008, 684, 1221.
67. D. Quénard, C. Vastel, C. Ceccarelli, P. Hily-Blant, B. Lefloch and R. Bachiller, Mon. Not. R. Astron. Soc., 2017, 470, 3194–3205.
68. L. Daumont, J. Vander Auwera, J.-L. Teffo, V. I. Perevalov and S. A. Tashkun, J. Quant. Spectrosc. Radiat. Transfer, 2007, 104, 342–356.

---

Footnote

† Electronic supplementary information (ESI) available: Table S1 for details about optimized geometrical parameters at different levels of theory; Table S2 for details about experimental and optimized geometrical parameters (including empirical corrections); Tables S3 and S4 for details about proton affinity (PA); Table S5 for details about enthalpy, entropy and Gibbs free energy variations of reactions; Tables S6 and S7 for details about potential energy distribution (PED); Table S8 for details about frequencies, IR intensities, Raman activities and Raman intensities; Tables S9 and S10 for details about selected strongest rotational line transitions and the corresponding hyperfine splitting components for T = 10 K; Scheme S1 for details about chemical structures and atomic numbering; Fig. S1 for details about optimized 3D geometries; Fig. S2 for details about IR spectra; Fig. S3 for details about Raman spectra. See https://doi.org/10.1039/d2ra04351c

---