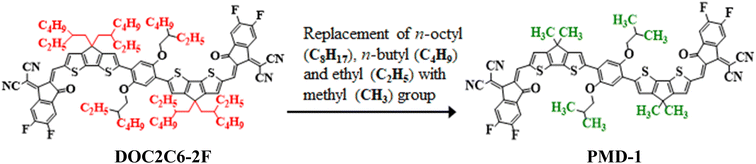Open Access Article
Open Access ArticleFirst theoretical probe for efficient enhancement of optical nonlinearity via structural modifications into phenylene based D–π–A configured molecules†
Muhammad Khalid *ab,
Salma Nazab,
Khalid Mahmood
*ab,
Salma Nazab,
Khalid Mahmood c,
Shabbir Hussaina,
Ataualpa Albert Carmo Braga
c,
Shabbir Hussaina,
Ataualpa Albert Carmo Braga d,
Riaz Hussain
d,
Riaz Hussain e,
Ahmed H. Ragabf and
Saedah R. Al-Mhyawig
e,
Ahmed H. Ragabf and
Saedah R. Al-Mhyawig
aInstitute of Chemistry, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan. E-mail: muhammad.khalid@kfueit.edu.pk; Khalid@iq.usp.br
bCentre for Theoretical and Computational Research, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan
cInstitute of Chemical Sciences, Bahauddin Zakariya University, Multan 60800, Pakistan
dDepartamento de Química Fundamental, Instituto de Química, Universidade de São Paulo, Av. Prof. Lineu Prestes, 748, São Paulo, 05508-000, Brazil
eDepartment of Chemistry, Division of Science and Technology, University of Education Lahore, Pakistan
fDepartment of Chemistry, Faculty of Science, King Khalid University, Abha 62224, Saudi Arabia
gDepartment of Chemistry, College of Science, University of Jeddah, Jeddah 21419, Saudi Arabia
First published on 1st November 2022
Abstract
The design of nonlinear optical (NLO) materials using conjugated molecules via different techniques is reported in the literature to boost the use of these systems in NLO. Therefore, in the current study, designed phenylene based non-fullerene organic compounds with a D–π–A framework were selected for NLO investigation. The initial compound (PMD-1) was taken as a reference and its seven derivatives (PMDC2–PMDC8) were made by introducing different acceptor moieties into the chemical structure of PMD-1. To explain the NLO findings, frontier molecular orbital (FMO), transition density matrix (TDM), density of states (DOS), natural bond orbital (NBO) and UV-Vis study of the title compounds was executed by applying the PBE1PBE functional with the 6-311G(d,p) basis set. The descending order of band gaps (Egap) was reported as PMDC7 (2.656) > PMDC8 (2.485) > PMD-1 (2.131) > PMDC3 (2.103) > PMDC2 (2.079) > PMDC4 (2.065) > PMDC5 (2.059) > PMDC6 (2.004), in eV. Global reactivity parameters (GRPs) were associated with Egap values as PMDC6 with the lowest band gap showed less hardness (0.0368 Eh) and high softness (13.5785 Eh). The UV-Vis investigation revealed that the maximum λmax (739.542 nm) was exhibited by PMDC6 in dichloromethane (DCM) as compared to other derivatives. Additionally, natural bond orbital (NBO) based findings revealed that PMDC6 exhibited the highest stability value (34.98 kcal mol−1) because of prolonged hyper-conjugation. The dipole moment (μ), average linear polarizability 〈α〉, first hyperpolarizability (βtot) and second hyperpolarizability (γtot) were evaluated for the reference and its derivatives. Consequently, among the designed compounds, the highest βtot (4.469 × 10−27 esu) and γtot (5.600 × 10−32 esu) values were shown by PMDC6. Hence, it's concluded from said results that these structural modifications proved PMDC6 as the best second and third order NLO candidate for various applications like fiber optics, signal processing and data storage.
Introduction
Nonlinear optical (NLO) materials appeared in the 1960's for the first time1 and have been studied by the researchers owing to their advanced high-tech applications in optical data storage,2 optics, optoelectronic tools and the telecommunication sector.3,4 Massive scientific efforts have been accomplished in the past few years to disclose the remarkable NLO materials including molecular dyes, synthetic resins, inorganic and organic semiconductor diodes.5 Organic NLO compounds are preferred over other NLO molecules due to their extended π-electrons framework and versatile formulation.6 NLO properties depend on intramolecular charge transfer (ICT) which is the fundamental process. In the organic compounds, the ICT system can be implied through donor–π–acceptor arrangement with excellent polarization, showing substantial NLO properties.7,8 Generally, the compound is designed through the combination of electron donating (D) and accepting groups (A) through the conjugated π-linker.9 The aromatic π-spacer is main component that influences the intramolecular charge transfer process.10,11 The ICT properties are responsible for the variation of molecular organizations and could be prolonged by altering the basic D–π–A frameworks inside the system. The first hyperpolarizability (βtot) unfolds from the NLO study, also correlates with ICT that takes place from the donor with the help of π-conjugated spacers to the acceptor.7 A variety of donor–π–acceptor organic compounds tuned with different acceptors has been revealed earlier.12 The electron density moves smoothly via π-linker from donor towards the acceptor moiety creating large dipole moment (μ), attaining average linear polarizability 〈α〉 or first hyperpolarizability (βtot).13–15 Molecules containing excessive free electrons i.e., fullerenes (C60) also possess notable NLO properties.16,17 Though, fullerene-based systems are reported to have some drawbacks like poor photostability and less absorption in the visible region.18,19 In recent years, non-fullerene (NF) based compounds have received a lot of attention owing to their potential to adopt different chemical structures, extensive range of electron affinities, tunable energy levels and facile synthesis.20,21 The NF-based organic acceptors, which replaced the classic fullerene acceptors have many advantages including; (i) light absorption, (ii) variety of D–A blending, (iii) higher dipole moment and (iv) balanced charge transfer.22 Hence, a lot of non-fullerene based molecules are reported in the previous era to investigate the electronic and photo-chemical properties owing to their strong electron transference potential.23 Moreover, NLO behavior of organic compounds can also be boosted by applying appropriate tailoring approaches. Literature survey has reported the compounds with various configurations, i.e., D–A, D–π–A, A–π–D–π–A, D–π–A–π–D, D–π–π–A, D–A–π–A, and D–D–π–A, where “D” represents the donor unit, “π” shows the π-spacer, and “A” indicates the acceptor moiety.24 These schemes promote good agreement between the donor, π-spacer and acceptor moieties to construct a significant push–pull mechanism and results in reduction of HOMO–LUMO Egap,9,25,26 increase asymmetric charge scattering and bathochromic shift, hence, producing a well-known NLO response. However, extended π-conjugation, by the insertion of several electron with-drawing (EWD) end-capped moieties (–NO2, –CN, –Cl and –F substituents) in NFAs enhances the NLO response. Upon introducing cyano group in A creates positive molecular electrostatic potential (MEP), uprights the electron affinity and reduces the energy (eV) of the lowest unoccupied molecular orbitals (LUMOs).27 Therefore, keeping in view the aforesaid aspects, herein, we have selected an organic non-fullerene based synthesized parent molecule 2,2′-((2Z,2′Z)-((6,6′-(2,5-bis((2-ethylhexyl)oxy)-1,4-phenylene)bis(4,4-bis(2-ethylhexyl)4H-cyclopenta[1,2-b:5,4-b′]dithiophene-6,2-diyl))bis(methanylylidene))bis(5,6-difluoro-3-oxo-2,3-dihydro-1H-indene-2,1-diylidene))dimalononitrile (DOC2C6-2F)28,29 consisting A–π–A configuration. In the DOC2C6-2F, n-octyl (–C8H17), n-butyl (–C4H9) and ethyl (–C2H5) groups present on the donor unit are replaced with methyl (–CH3) group to minimize the effect of steric hindrance caused by long alkyl chains as well as to reduce the computational cost. After these minor structural modifications, the compound is renamed from “DOC2C6-2F” to “PMD-1” (Fig. 1). The NLO research of the entitled phenylene based NF reference molecule (PMD-1) and its derivatives (PMDC2–PMDC8) might not been reported yet. Hence, to fulfill the research gap, DFT and TD-DFT based computations are carried out to execute their NLO properties. This paper would be a new addition in the advancement of NLO compounds and will surely serves as descriptive model for second and third-order NLO properties due to their suitable D–π–A framework in the future applications.Computational study
The entire l computations of this work were done with the help of Gaussian 09 (ref. 30) program. The DFT based computations and input files of the studied systems were developed by using the GaussView 6.0 (ref. 31) software. DFT analysis was performed for the optimization of parent compound (DOC2C6-2F) by employing various functionals such as: TPSS,32 PBE1PBE,33 M06-2X34 and ωB97XD35 of DFT with 6-311G(d,p) basis set in dichloromethane (DCM) solvent. The computed absorption maxima of DOC2C6-2F at aforesaid functionals were compared with the experimental results reported in literature for selection of suitable theoretical method. The λmax values of DOC2C6-2F obtained at various levels were noted as: 1039.438, 734.243, 582.715 and 543.171 nm, respectively, while the experimental value of DOC2C6-2F was 743 nm.29 Functional PBE1PBE/6-311G(d,p) showed a good agreement with experimental UV-Vis results of reference as displayed in Fig. S1† thus, PBE1PBE was selected for further computational analyses. Moreover, in order to visualize the optoelectronic and photovoltaic properties, the frontier molecular orbitals (FMOs), UV-Vis, density of states (DOS), natural bond orbitals (NBOs) and NLO analyses were executed at said level of DFT. The results were obtained by employing Avogadro,36 Chemcraft,37 GaussSum,38 PyMOlyze 2.0 (ref. 38) and Multiwfn 3.7 (ref. 39) softwares from the output files. The FMOs examination was used to compute the global reactivity parameters (GRPs) of studied compounds. The transition density matrix (TDM) analysis was computed to investigate charge dissociation patterns in enlisted compounds. The dipole moment (μ),40 average linear polarizability 〈α〉,41 first hyperpolarizability (βtot),42 and second hyperpolarizability (γtot)43 values were calculated by using eqn (S1)–(S4).†Results and discussion
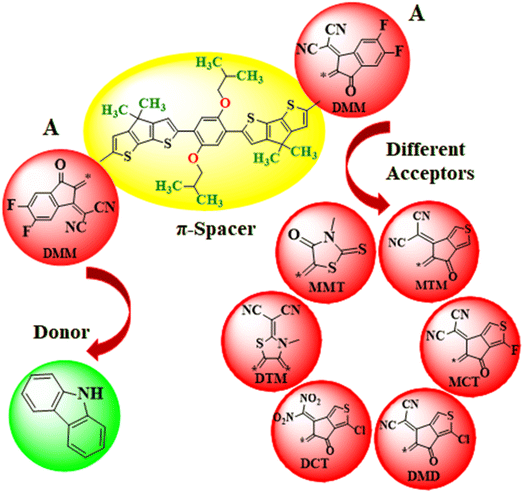
The current work focuses on the computational study of NLO responses of phenylene based organic non-fullerene compounds. In our present study, PMD-1 is taken as a reference molecule after minor changes in the already reported parent compound (DOC2C6-2F) as shown in Fig. 1.In this work, the different acceptors are used in chemical structure of designed systems (PMDC2–PMDC8) to comprehend their effect for NLO response. First of all, the one end-capped acceptor group i.e., [2-(2-ethylidene-5,6-difluoro-3-oxo-indan-1-ylidene)-malononitrile] of the PMD-1 is replaced with donor moiety (9H-carbazole) to design PMDC2. Further modifications are done in PMDC2 by the replacement of the other acceptor group with different acceptor groups 2-(5,6-difluoro-2-methylene-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile (DMM), 2-(5-methylene-6-oxo-5,6-dihydro-4H-cyclopenta[c]thiophene-4-ylidene)malononitrile (MTM), 2-(1-fluoro-5-methylene-6-oxo-5,6-dihydro-4H-cyclopenta[c]thiophene-4-ylidene)malononitrile (MCT), 2-(1-chloro-5-methylene-6-oxo-5,6-dihydro-4H-cyclopenta[c]thiophene-4-ylidene)malononitrile (MDM), 3-chloro-6-(dinitromethylene)-5-methylene-5,6-dihydro-4H-cyclopenta[c]thiophene-4-one (DCT), 2-(3-methyl-4,5-dimethylenethiazolidin-2-ylidene)malononitrile (DTM) and 3-methyl-5-methylene-2-thioxothiazolidin-4-one (MMT), to achieve simple and efficient D–π–A configuration for boosting the electronic and optical effects44–46 of all the derivatives. Further, by executing these alterations in PMD-1, seven derivatives PMDC2–PMDC8 are designed with D–π–A framework as shown in Scheme 1 and Fig. S2 (ESI). The IUPAC names of the newly designed compounds are provided in Table S24.† The influence of different acceptor moieties on NLO response, ELUMO − EHOMO, absorption spectra, average linear polarizability 〈α〉, first hyperpolarizability (βtot) and second hyperpolarizability (γtot) are investigated. The current work will be a remarkable addition to the field of NLO and will also provoke researchers in this field. The optimized structures of the PMD-1 and PMDC2–PMDC8 are displayed in Fig. S4.†
Electronic properties
Frontier molecular orbitals (FMOs) investigation is an efficient method to explore electronic properties of the studied compounds.11,47 FMOs are mainly comprised of two main orbitals i.e., LUMO with capability to accept electrons and HOMO having electron donation ability.48 Various quantum chemical parameters like molecular interactions, chemical reactivity, chemical stability, charge transfer, UV-Vis spectra and optical properties are elucidated by FMOs.49 Furthermore, Egap (ELUMO − EHOMO) obtained from FMOs analysis is a key parameter to compute the global reactivity information possessing dynamic stability, reactivity, chemical hardness and softness of investigated systems.50 DFT calculations have been made using above mentioned level of theory and basis set. Their results for EHOMO, ELUMO and ELUMO − EHOMO are displayed in Table 1.| Compounds | EHOMO | ELUMO | ΔE |
|---|---|---|---|
| PMD-1 | −5.575 | −3.444 | 2.131 |
| PMDC2 | −5.408 | −3.329 | 2.079 |
| PMDC3 | −5.396 | −3.293 | 2.103 |
| PMDC4 | −5.410 | −3.345 | 2.065 |
| PMDC5 | −5.413 | −3.354 | 2.059 |
| PMDC6 | −5.430 | −3.426 | 2.004 |
| PMDC7 | −5.192 | −2.536 | 2.656 |
| PMDC8 | −5.307 | −2.822 | 2.485 |
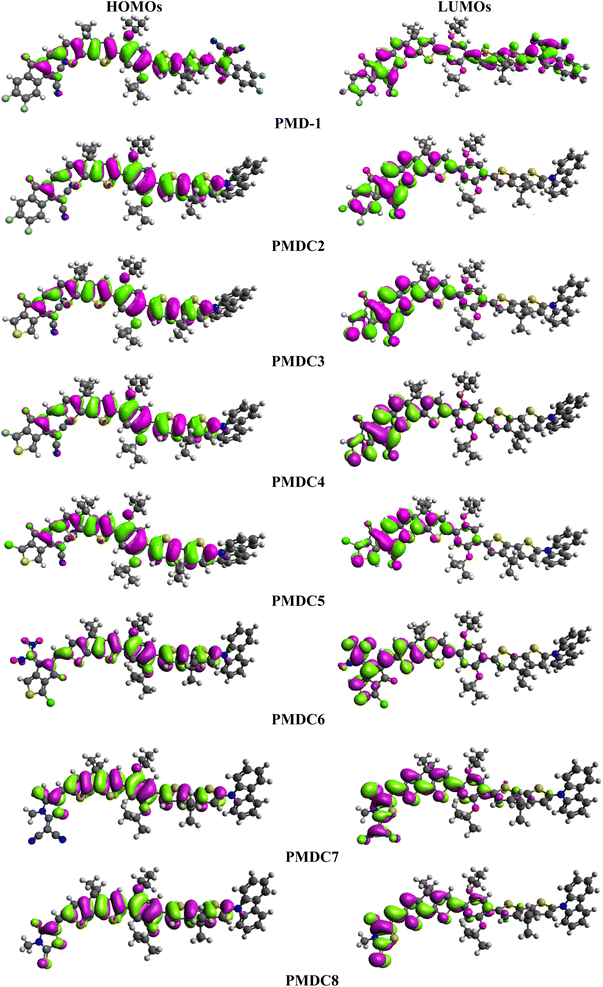
Table 1 shows that the EHOMO/ELUMO values for PMD-1 and PMDC2–PMDC8 are obtained as −5.575/−3.444, −5.408/−3.329, −5.396/−3.293, −5.410/−3.345, −5.413/−3.354, −5.430/−3.426, −5.192/−2.536 and −5.307/−2.822 eV, respectively. The ELUMO − EHOMO (ΔE) values of reference and derivatives are calculated as 2.131, 2.079, 2.103, 2.065, 2.059, 2.004, 2.656 and 2.485 eV, respectively. The simulated HOMO/LUMO (−5.575/−3.444 eV) energies and band gap (ΔE = 2.131 eV) of reference molecule showed a good agreement with its experimental values (HOMO/LUMO = −5.52/−3.84 and ΔE = 1.43 eV).29 A reduction in Egap is noticed in PMDC2–PMDC6 which might be due the presence of electron capturing nature of substituents (cyano, fluoro and chloro) positioned at the acceptor moiety in contrast to reference. However, PMDC7 (2.656 eV) and PMDC8 (2.485 eV) shows slightly larger ΔE value than PMD-1 due to the presence of DTM and MMT acceptors, respectively. The movement of electrons towards acceptor region enhances with the increase in electronegativity of the moieties due to the inductive effect of –F and –Cl.51 The PMDC2 exhibited 2.079 eV band gap which is lesser than the PMD-1 (2.131 eV), which may be due to the electron capturing nature of the fluoro and cyano substituents at the end-capped acceptor (DMM). The smallest value of ΔE is shown by PMDC6 with 2.004 eV due to the existence of two nitro groups at the terminal (DCT) acceptor. These nitro groups exert strong EWD effect both inductively and mesomerically thus, efficiently pull electronic charge towards acceptor.52 Moreover, depending upon the type of moiety to which it is attached, the electron accepting tendency of nitro group varies substantially.53 The overall decreasing order for the Egap in eV is as: PMDC7 (2.656) > PMDC8 (2.485) > PMD-1 (2.131) > PMDC3 (2.103) > PMDC2 (2.079) > PMDC4 (2.065) > PMDC5 (2.059) > PMDC6 (2.004). The energy band gap is an essential for charge transfer process, lesser the bandgap higher will be the charge transference. The contour surface diagrams of HOMOs and LUMOs provided in Fig. 2 depicts that HOMOs are mainly located over the π-spacer and partially across the acceptor. While, in LUMOs the charge density is majorly concentrated on acceptors and minutely on the π-spacer among all the investigated compounds. This indicates that the electron donor moiety is interconnected to the electron acceptor unit via π-linker, which facilitates the ICT between D and A units. Hence, the molecular systems under study have shown efficient ICT from donor to acceptor through π-linker thus, demonstrating them as potential NLO materials. The other values of HOMO−1, LUMO+1, HOMO−2 and LUMO+2 are displayed in Table S9† whereas, the counter surface diagrams of HOMO−1, LUMO+1, HOMO−2 and LUMO+2 are provided in Fig. S3.†
Density of states (DOS) analysis
The results of DOS are utilized to estimate the electronic properties to reinforce the FMOs analysis of all the investigated compounds. The electronic charge density is delocalized in different pattern all over HOMOs and LUMOs upon replacing the end-capped acceptor groups as shown in Fig. 2. The DOS discloses the electron distribution from the HOMOs with great tendency to give electron to the LUMOs which have great tendency to gain electron.54 The charge distribution pattern on molecular orbitals (MOs) based on the various acceptor groups, validated by computing the DOS percentages on HOMOs and LUMOs.55 The negative values in DOS pictographs show the HOMOs whereas, positive values denote LUMOs along x-axis and distance between HOMOs and LUMOs expresses the Egap.39 For the DOS computation, we have splitted the entitled molecules into separate fragments. PMD-1 is divided into two segments i.e., donor (D) and acceptor (A) while, PMDC2–PMDC8 are divided into three portions as: D, π-spacer and A. The electronic cloud of HOMOs in the PMD-1 is only arranged on the π-spacer while, acceptor terminal has major charge concentration of LUMOs (Fig. S6†). In the PMDC2–PMDC8, a different pattern of HOMOs and LUMOs concentration is detected i.e., major electronic cloud on the π-spacer region and minor distribution over the donor. In nutshell, it is inspected from DOS spectra that highest charge density of HOMOs is positioned over the π-spacer as blue high peak traced at nearly −7.5 eV, while the electronic charge distribution for LUMOs is found to be near 2 to 3 eV on the acceptor group. It is observed that π-spacer contributes 82.6% to HOMOs and 56.5% to LUMOs in PMD-1 while, contribution of acceptor is 17.4 and 43.5% to HOMOs and LUMOs, respectively. However, 92.1, 98.6, 91.7, 91.7, 92.4, 86.6 and 90.3% contribution to HOMOs while, 52.6, 89.7, 57.3, 57.4, 45.7, 59.7 and 61.1% to LUMOs is shown by π-spacer in PMDC2–PMDC8, respectively. Whereas, 7.2, 0.7, 6.9, 7.5, 6.9, 13.0, 9.1 and 47.4, 10.3, 32.6, 42.6, 54.3, 40.2, 38.9% contributions to HOMO and LUMO are shown by acceptor moieties, respectively. Similarly, donor contributes 0.7, 0.7, 1.4, 0.7, 0.7, 0.4 and 0.6% to HOMOs and 0.0, 0.0, 10.1, 0.0, 0.0, 0.1 and 0.0% to LUMOs in PMDC2–PMDC8. From previous discussion, it is cleared that the HOMOs of all the derivatives are chiefly located on the π-spacer while, the LUMOs are considerably resided on the acceptor units (see Fig. 2 and S6†). Overall, DOS study displays substantial charge transferal from π-spacer to acceptor moieties in all the investigated compounds.UV-Vis analysis
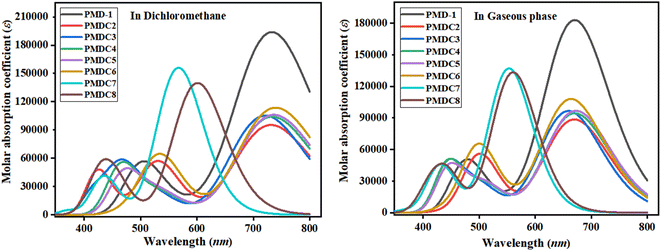
The valuable electronic information proposed by the UV-Vis study is linked to the nature of electronic transition, transitions contributing configurations and charge transfer ability in the molecules.56 Absorption spectra of the reference and its derivatives have been intended to acknowledge the effects of different acceptor groups on spectral properties using TD-DFT.57 Tables S10 and S11† shows the computed λmax, energy of transition (E), oscillation strength (fos) and transitions effect of the PMD-1 and PMDC2–PMDC8 at same functional. The UV-Vis analysis of the said compounds is performed in both dichloromethane solvent and gaseous phase and their absorption spectra is shown in Fig. 3. Tables S10 and S11† reveals that the computed λmax for PMD-1 is 734.243 nm, which is in good agreement to its experimental absorption peak at 743 nm. The simulated λmax of PMDC2–PMDC6 existed in the range of 721.174–739.542 nm, with transition energies 1.684–2.186 eV and oscillation strength of 1.314–2.644 in the dichloromethane (DCM) solvent. Transitions in the studied compounds were emerged from H → L, conferred by the principle of D–π–A configuration in NF based organic compounds.45 NLO active compounds require this type of ICT which is responsible for the NLO behavior in the investigated compounds.9 The increasing order of the λmax (nm) noticed in DCM is: PMDC6 (739.542) > PMDC5 (736.292) > PMD-1 (734.243) > PMDC4 (733.461) > PMDC2 (731.298) > PMDC3 (721.174) > PMDC8 (600.902) > PMDC7 (567.200). It is also cleared that among all the derivatives, the highest λmax (739.542 nm) with transition energy of 1.677 eV and 1.568 oscillator strength is observed in PMDC6 due to H → L (98%) electronic transitions, complete ICT and solvent polarity. Moreover, in PMDC6 the intramolecular H-bonding occurs between the –O atom of –NO2 group substituted at end capped acceptor (DCT) and neighboring H-atom, as a result π → π* transitions are red shifted due to DCM polarity. Further, PMDC7 showed lowest absorption properties in comparison to rest of designed molecules due to poor charge withdrawing ability, hence, charge delocalization is hindered in acceptor (DTM) region. Moreover, when analysis is done in gaseous phase, the values are found to be in the range of 553.205 to 672.840 nm. The decreasing order of the designed molecules on the basis of λmax in gaseous phase is: PMDC7 < PMDC8 < PMDC3 < PMDC6 < PMDC2 < PMDC4 < PMD-1 < PMDC5. Among all the derivatives gaseous phase prominent wavelength is observed in PMDC5 (672.840 nm). Different contribution of various orbitals in electronic transitions is due to structural tailoring of PMD-1 via different acceptor groups. In studied compounds, the vital excited states are formed due to the shifting of electrons from HOMO towards LUMO. However, regular decrease in λmax values in DCM solvent and gaseous phase is noticed in all the derivatives. This might be due to different acceptor groups and position of various electron withdrawing substituents attached with acceptor moieties. Concisely, the blue shifted absorption spectra for almost every molecule is observed in gaseous phase. Literature survey, revealed that the absorption maxima is greatly affected by the polarity and nature of solvent which can be confirmed through prominent bathochromic shift (red shift), which is highest in dichloromethane solvent in all the D–π–A configured compounds58 except PMDC7 and PMDC8.Global reactivity parameters (GRPs)
The global reactivity parameters (GRPs) are computed by using the energy gap (Egap) between HOMOs and LUMOs to investigate stability and reactivity of PMD-1 and PMDC2–PMDC8. The Egap is a dynamic aspect to determine the GRPs like ionization potential, electron affinity, hardness, electronegativity, chemical potential, softness and electrophilicity index.59 The ionization potential (IP = −EHOMO) and electron affinity (EA = −ELUMO) are computed by using the given formulae.60,61 The chemical hardness [η = (IP − EA)/2],40 electronegativity [X = (IP + EA)/2]62 and chemical potential [μ = (EHOMO + ELUMO)/2] are calculated by the help of Koopman's theorem.60 The global softness (σ = 1/2η) is calculated with the help of given formula.60 Parr et al.62 presented an electrophilicity index that is determined by using the given equation (ω = μ2/2η).63 The IP and EA describe the electron-donating and electron-capturing tendency and are equivalent to the energy required to eliminate an electron from the valence band (HOMOs). The chemical reactivity and stability of the molecules are also correlated to its chemical potential. The band gap, chemical potential, hardness and stability of the molecule are directly associated to each other while, in case of reactivity the relation is inverse.9 Therefore, the compound with larger band gap is considered as harder and possesses less reactivity with high stability. The molecular stability depends upon electronegativity of the substituent as well as their position to E.N. atom. Electronegativity explains the efficiency of representative molecules to absorb the upcoming electrons. The molecule with higher Egap exhibits more stability, less reactivity and high value of hardness.64 However, IP and EA are the other parameters that reveal reactivity of compounds due to direct relation with polarizability. PMD-1 and PMDC2–PMDC8 demonstrate high ionization potential with low electron affinity as represented in Table S25.† The IP of PMDC6 is found to be highest at 0.1995 Eh than other derivatives. The descending order of IP is: PMD-1 > PMDC6 > PMDC5 > PMDC4 > PMDC2 > PMDC3 > PMDC8 > PMDC7 with values as: 0.2049 > 0.1995 > 0.1989 > 0.1988 > 0.1987 > 0.1983 > 0.1950 > 0.1908 Eh, respectively. The hardness (η) and softness (σ) of the compound are correlated to the band gap and provide details about reactivity of the system. The hardness of the compound is directly associated to ΔE and inversely with reactivity. Higher the value of ΔE greater will be hardness, which results in lower ICT and less reactivity. Lower the Egap, higher will be the softness and polarizability of the compound which yields high reactivity.65 Table S25† reveals that among all derivatives, PMDC7 exhibits highest (0.0488 Eh) value of hardness while, PMDC6 shows lowest value (0.0368 Eh). The decreasing order of hardness is: PMDC7 > PMDC8 > PMD-1 > PMDC3 > PMDC2 > PMDC4 > PMDC5 > PMDC6. Furthermore, μ is also used to estimate the reactivity and stability of the compounds which was further verified by a direct and inverse relation of chemical potential with stability and reactivity of the molecule, respectively. Among all the derivatives PMDC6 exhibited highest value (−0.1627) of chemical potential. The descending order of μ across the inspected compounds is: PMD-1 > PMDC6 > PMDC5 > PMDC4 > PMDC2 > PMDC3 > PMDC8 > PMDC7. Finally, all GRPs data of the enlisted molecules is associated with the ELUMO − EHOMO, the chemical species with lesser Egap disclose less hardness and chemical potential with higher softness. Interestingly, PMDC6 demonstrated the highest softness value (13.5785 Eh) and it is considered as the most polarizable specie among all the investigated molecules and holds promising NLO properties.Natural bond orbitals (NBOs) analysis
The molecular stability, charge delocalization, hybridization and electronic structure can be adequately accomplished by NBOs investigation. Several second-order interfaces between the occupied and unoccupied orbitals and intramolecular and intermolecular hydrogen bonding can be efficiently explained by NBOs investigation.66,67 Therefore, the NBOs examination was accomplished for the PMD-1 and its derivative compounds (PMDC2–PMDC8) at same functional and the characteristics transitions are recorded in Tables S12–S19.† Second-order perturbation method along with eqn (1) is used to compute the stabilization energies E(2) in NBOs analysis.68
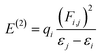 | (1) |
The donor and acceptor parts are denoted by i, j subscripts, E(2) is the stabilization energy, qi, εi, εj and Fi,j characterize the orbital occupancy, diagonal and off-diagonal NBO Fock matrix components.69 NBOs analysis shows that four types of transitions are noticed for reference PMD-1 and PMDC2–PMDC8, which are: σ → σ*, π → π*, LP → σ* and LP → π* (Tables S12–S19†). These transitions particularly π → π* are essential for the ICT and play role in system stabilization. In PMD-1, the π(C9–C10) → π*(C51–C61) and π(C85–N86) → π*(C83–N84) transitions provide strongest and lowest stabilization values of 30.03 and 0.64 kcal mol−1, accordingly. Moreover, σ → σ* transitions such as σ(C53–H54) → σ*(C78–C81) have 9.24 kcal mol−1 as highest energy and σ(C51–C61) → σ*(C9–H10) with 0.50 kcal mol−1 are the lowest energy value. The other transitions as LP → π* and LP → σ* have the highest values as 32.44 and 22.00 kcal mol−1 for LP2(O89) → π*(C1–C2) and LP2(O88) → σ*(C78–C87), respectively. For compounds, PMDC2 and PMDC3 π → π* electronic transitions such as π(C27–C28) → π*(C51–C59) and π(C27–C28) → π*(C51–C55) display maximum stabilization energies as 29.56 and 29.15 kcal mol−1, correspondingly. Similarly, π(C66–N65) → π*(C66–N67) and π(C56–C57) → π*(C60–N61) transitions show minimum energies as 0.66 and 0.50 kcal mol−1, respectively. In addition, σ → σ* transitions like σ(C51–H52) → σ*(C59–C62) and σ(C51–H52) → σ*(C55–C56) have 9.14 and 9.16 kcal mol−1 as highest stabilization energies for PMDC2–PMDC3, respectively. LP1(N94) → π*(C108–C109) and LP1(N86) → π*(C87–C88) transitions have highest values as 35.62 and 35.63 kcal mol−1, respectively. While, LP2(O69) → σ*(C59–C68) and LP2(O63) → σ*(C55–C62) have highest energies as 21.87 and 22.28 kcal mol−1, respectively. In PMDC4 and PMDC5 the prominent π → π* transitions like π(C27–C28) → π*(C51–C55) showed the vital stabilization energies as 29.86 and 29.88 kcal mol−1, respectively. Similarly, π(C60–N61) → π*(C58–N59) transitions exhibited lowest stabilization energies as 0.55 kcal mol−1, respectively. Besides, maximum and minimum σ → σ* transitions energies are 9.09, and 0.50 kcal mol−1 obtained in σ(C51–H52) → σ*(C55–C56), σ(C22–S34) → σ*(C25–C33) and σ(C68–H69) → σ*(O68–C68) transitions, respectively. Furthermore, in PMDC4–PMDC5 the highest stabilization energies like 35.62, 35.62, 22.02 and 22.84 kcal mol−1 are noticed for LP1(N86) → π*(C100–C101), LP1(N86) → π*(C100–C101), LP2(O63) → σ*(C55–C62) and LP2(O63) → σ*(C53–C62) transitions, respectively. For PMDC6 and PMDC7 the dominant π → π* transitions like π(C27–C28) → π*(C51–C55), π(C27–C28) → π*(C51–C56), π(C56–O105) → π*(C51–C55) and π(C102–N103) → π*(C53–C54) are found with highest and lowest energy values of 34.98, 24.95, 3.58 and 1.42 kcal mol−1, respectively. In parallel way, the σ → σ* transitions such as σ(C51–H52) → σ*(C27–S31) and σ(C51–H52) → σ*(C56–S101) possessed maximum energies of stabilization as 11.12 and 10.3 kcal mol−1. While σ(C22–S34) → σ*(C25–C33) and σ(C86–H90) → σ*(N80–C81) with lowest values of 0.50 and 0.51 kcal mol−1 are obtained for PMDC6 and PMDC7, respectively. The additional LP1(N80) → π*(C81–C86) and LP2(O105) → σ*(C54–C56) transitions have greatest transition energies as 40.40 and 22.61 kcal mol−1, respectively, for PMDC6. The stabilization energy values 70.27 and 14.62 kcal mol−1 are found to be highest due to resonance are shown in LP1(N106) → π*(C53–C54) and LP1(N80) → σ*(C9–S21), respectively, in PMDC7. In PMDC8, the most prominent π → π* transitions like π(C27–C28) → π*(C51–C55) and π(C104–O106) → π*(C51–C55) transitions are detected to have maximum and minimum energies as 28.50 and 3.14 kcal mol−1, respectively. Moreover, the σ(C51–H52) → σ*(C55–S100) transition exhibited the maximum energy of stabilization which is 10.86 kcal mol−1 while, σ(C95–H99) → σ*(N79–C94) have the minimum value (0.51 kcal mol−1) of stabilization energy. However, the highest 84.27 and the lowest 29.74 kcal mol−1 stabilization energies due to the phenomena of resonance are LP1(N101) → π*(C53–S105) and LP2(O106) → σ*(N101–C104) transitions, respectively. The aforementioned results revealed that among all the entitled compounds, the PMDC6 exhibits the extra stability (34.98 kcal mol−1) due to the prolonged hyper-conjugation. Therefore, NBOs study of aforementioned compounds entails that the strong ICT and the extended hyper-conjugation play a remarkable role in stabilization of these systems and giving them exclusive NLO features.
Electron–hole analysis
Hole–electron analysis is very effective and extensively utilized tool to understand the movement of electron cloud in a molecule.70,71 Herein, we performed the hole–electron analysis in order to understand the movement of charge in our studied compounds with the aid of Multiwfn 3.7.39 Fig. S5† reveals that in reference compound, hole is created at a carbon atom of thiophene ring of the π-spacer, while electron intensity is found intense over carbon atoms present in highly electron withdrawing vinylene region of the acceptor part, further attached with cyano (–CN) group. This may occurs due to the presence of strongly EWD nature of cyano groups over the acceptor part. Interestingly, in all the designed derivatives, it is found that hole is created in different atoms of the π-spacer part, successively moving towards the acceptor part, indicating an efficient charge transfer from π-linker towards the acceptor moiety, under the influence of donor group. From Fig. S5,† it is clear that hole intensity is found high at various atoms of the π-spacer part, whereas, electron intensity is shifted at acceptor region and found intense over the carbon atoms of vinylene group further attached to two strong cyano groups imparting excellent electrons withdrawal and resulting in excellent ICT in all designed derivatives (PMD-1–PMDC8). Exceptionally, in compound PMDC6, where cyano group is replaced with strong nitro (–NO2) groups, the electron intensity is found greater at nitrogen atoms of –NO2 group and most efficient charge transfer was found PMDC6, which might be due to resonance and strong negative inductive effect (−I). Overall, the investigated designed derivatives, PMD-1–PMDC7, including the reference compound, seems to be electron type materials, as electron intensity is found high at electronic band as compared to hole intensity at hole band (Fig. S5†). Only the compound PMDC8 is found having intensity ratio higher at hole band and thus is a hole type material.Transition density matrix (TDM) analysis
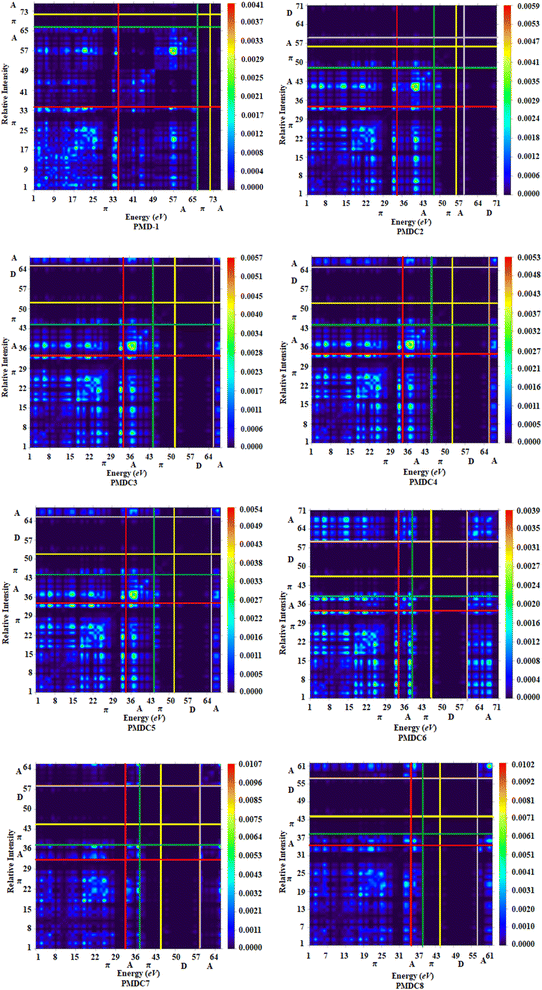
TDM is an effective method for the evaluation and interpreting electronic excitation processes in molecular systems. In a many body system, for any transition between two eigen states the TDM study offers a characteristic spatial heat map which shows the scattering of associated electron–hole pairs and allows one to identify their delocalization and coherence lengths.72 For TDM analysis, we have divided our reference compound (PMD-1) in two segments; terminal acceptor (A) moieties and central π-spacer while, the derivatives (PMDC2–PMDC8) into three fragments; donor (D), central π-spacer and end capped acceptor (A). In this study, the hydrogen atoms minutely involved in the transitions, hence, their impact has been ignored. The TDM findings of PMD-1 and PMDC2–PMDC8 are obtained at said level of DFT and their pictographs are displayed in Fig. 4.From FMOs analysis it is observed that the charge density mainly executed over the π-spacer and LUMOs which yield significant variation in TDM pictographs. Fig. 4 reveals that the electron density has been effectively transmitted diagonally from π-bridge to acceptor segment in all derivatives, allowing for good charge transfer without any trapping. Findings of TDM snapshots entail effortless and higher charge separation from ground state (S0) to an excited state (S1). Remarkably, in TDM map of PMDC6, efficient diagonal charge transfer coherence is observed only at the acceptor portion and this response is different from other compounds. On the other hand, calculations of TDM heat maps of PMDC2–PMDC8 suggest schematic, easier and developed exciton separation in the excited state which would be helpful in future applications.
Exciton binding energy (Eb) analysis
It is the difference of HOMO–LUMO band gap (EL–H) and the smallest quantity of energy which is useful for first excitation (Eopt).73 It is an important method for the assessment of optoelectronic qualities of the examined molecules. The Eb of investigated molecules (PMD-1 and PMDC2–PMDC8) is inspected using eqn (2).| Eb = ELH − Eopt | (2) |
| Compounds | EL–H | Eopt | Eb |
|---|---|---|---|
| PMD-1 | 2.131 | 1.689 | 0.442 |
| PMDC2 | 2.079 | 1.695 | 0.384 |
| PMDC3 | 2.103 | 1.719 | 0.384 |
| PMDC4 | 2.065 | 1.690 | 0.375 |
| PMDC5 | 2.059 | 1.684 | 0.375 |
| PMDC6 | 2.004 | 1.677 | 0.327 |
| PMDC7 | 2.656 | 2.186 | 0.470 |
| PMDC8 | 2.485 | 2.063 | 0.422 |
Where EL is the energy of lowest unoccupied molecular orbitals (LUMOs) and EH is the energy of the highest occupied molecular orbitals (HOMOs). All the designed compounds show greater charge separation ability with low value of binding energy. The descending order of Eb values is: PMDC7 (0.470) > PMD-1 (0.442) > PMDC8 (0.422) > PMDC3 (0.384) = PMDC2 (0.384) > PMDC4 (0.375) = PMDC5 (0.375) > PMDC6 (0.327) in eV. Among all the designed compounds, PMDC6 exhibit reduced value (0.327 eV) of binding energy elucidating greater optoelectronic properties with high magnitude of exciton dissociation in excited state (S1). The compounds with 1.9 eV value of binding energy are investigated to be suitable candidate for optical activity. Interestingly, our all studied compounds have Eb value lower than 1.9 eV and found as fit for optical activity and variety of NLO applications. The trend of change in binding energies is displayed in Fig. S7.†
Nonlinear optical (NLO) properties
In recent years, NLO materials are emerging as the matter of great interest owing to their novel applications in optoelectronic devices, signal manipulation and nuclear sciences.75 A lot of work has been done to explore new organic molecules with enhanced NLO properties. Organic NLO compounds are preferably used because of structural diversity, polarity and extensive conjugation.76 The electronic properties of the material are correlated to the average linear polarizability 〈α〉, first hyperpolarizability (βtot) and second hyperpolarizability (γtot) responses and are also responsible for optical activity. Moreover, these NLO properties can be improved by using various π-bridge and acceptor moieties.77 By orienting the non-centrosymmetric qualities of the system, the second-order NLO substances are produced.78 The experimental and computational fields are providing multidisciplinary endeavors for the growth of NLO materials due to their superior data rates, optical signal processing, electro-optical modulation, frequency and potential harmonic generation in optical communication technology.4 In compounds PMD-1–PMDC8, the movement of the π-electrons sandwiched between the aromatic rings is boosted and the C–C π-bond is not static. Consequently, it plays role in prolonged conjugation of two or more aromatic rings.79 Thus, the charge transfer is increased between investigated compounds by introducing chloro (–Cl), fluoro (–F), nitro (–NO2) and cyano (–CN) groups as substituents, which pulls electrons impressively. So, by linking the various acceptor groups through π-spacer is an effective approach to reduce the band gap and to enhance polarizabilities.80 NLO characteristics are related to the relationship between structural properties and can be explained by quantum chemical methods, after understanding the concepts of 〈α〉, βtot and γtot.81 The linear and nonlinear optical polarizabilities are determined by applying the PBE1PBE/6-311G(d,p) level in DCM solvent. To assess the effect of various acceptors on NLO properties of PMD-1–PMDC8, the dipole moment (μ), 〈α〉, βtot and γtot values of aforementioned molecules are determined in esu and listed in Tables S20–S23.† Dipole moments (μ) are produced because of the electronegativity (E.N.) differences, greater the difference in E.N., larger the dipole moment.82 Furthermore, the polarity plays a substantial role in dipole moment by raising their nonlinear values.83 The dipole moments of the reference and derivatives are determined and the outcomes are mentioned in Table 3.| Compounds | μtot | 〈α〉 × 10−22 | βtot × 10−27 | γtot × 10−32 |
|---|---|---|---|---|
| a Unit for μtot (D) and 〈α〉, βtot and γtot are in esu. | ||||
| PMD-1 | 11.467 | 2.860 | 0.817 | 7.295 |
| PMDC2 | 11.459 | 2.292 | 3.205 | 3.819 |
| PMDC3 | 10.002 | 2.284 | 3.224 | 3.818 |
| PMDC4 | 10.640 | 2.306 | 3.475 | 4.119 |
| PMDC5 | 10.776 | 2.350 | 3.628 | 4.328 |
| PMDC6 | 12.265 | 2.451 | 4.469 | 5.600 |
| PMDC7 | 11.748 | 2.022 | 0.772 | 1.460 |
| PMDC8 | 7.742 | 2.012 | 1.476 | 1.900 |
Table 3 indicates that the PMDC6 among all the derivatives shows the largest dipole moment (μtot) at 12.265 D. In PMDC7, the dipole moment is increased due to the presence of nitrogen atom which is more E.N. than carbon atom. Thus, it will pull the bonded electrons towards itself and creates the polarity in the molecule. Overall the μtot decreases in the given manner: PMDC6 > PMDC7 > PMD-1 > PMDC2 > PMDC5 > PMDC4 > PMDC3 > PMDC8.
The linear response is described by average linear polarizability 〈α〉. Hence, it is fascinating to observe the effects of different acceptor moieties on the 〈α〉 and to recognize their structural NLO properties associated to functional electric field.84 The 〈α〉 with its respective tensor components are computed and values in esu are recorded in Table S21.† Table S21† shows that αxx tensor reveals greater values indicating that polarization occurred along x-axis (Fig. S2†). Among all the derivatives, PMDC6 shows highest (2.451 × 10−22 esu) value of 〈α〉, which may be due to the presence of nitro and chloro substituent at acceptor (DCT) moiety which made it more electron-withdrawing with extended conjugation. The decreasing order of 〈α〉 value of entitled molecules is: PMD-1 > PMDC6 > PMDC5 > PMDC4 > PMDC2 > PMDC3 > PMDC7 > PMDC8. The first hyperpolarizability (βtot) describes the NLO responses of the molecules. The βtot along with its contributing tensors is calculated at the said functional and basis set and respective values are recorded in the Table S22.† Among all the designed compounds, PMDC6 shows the highest (4.469 × 10−27 esu) βtot amplitude with 3-chloro-6-(dinitromethylene)-5-methylene-5,6-dihydro-4H-cyclopenta[c]thiophene-4-one (DCT) acceptor. There is a proficient association acquired among the molecular organizations and βtot values. The βtot factor generally enhances with the EWD tendency of the groups linked with acceptor moieties, like the fluoro (–F), chloro (–Cl), sulphur (–S) and cyano (–CN) which takes part in the molecular nonlinearity. Furthermore, the impact of the extended conjugation to βtot is also prevailed by the substitution.85 The decreasing trend of βtot for all designed compounds is as: PMDC6 > PMDC5 > PMDC4 > PMDC3 > PMDC2 > PMDC8 > PMD-1 > PMDC7. Among the individual tensor components, βxxx exhibits highest values which entail better ICT along x-axis (Fig. S2†). Second hyperpolarizability (γtot) is a key factor for the estimation of NLO response.86 Among all the derivatives the highest value of γtot is also observed in PMDC6 (5.600 × 10−32 esu). The decreasing order of γtot is: PMD-1 > PMDC6 > PMDC5 > PMDC4 > PMDC2 > PMDC3 > PMDC8 > PMDC7. Among the individual tensor components, γx is dominant and displays remarkably greater values than other tensors (Table S23†). It can be seen that PMDC6 exhibits the largest γx value of 5.555 × 10−32 esu among all the studied molecules, which described the more charge shifting process along x-axis and symbolizes the prominent diagonal tensor. It is concluded from the above results that the electron accepting tendency of compounds plays a dynamic role in producing a remarkable nonlinear response.
Conclusion
To explore the nonlinear optical (NLO) properties, non-fullerene based organic compounds (PMD-1 and PMDC2–PMDC8) are designed via structural modulation by using efficient end-capped electron accepting groups. The effect of different acceptors in all the designed compounds has been carefully observed for NLO response. These findings exposed that the acceptors have promising influence over D–π–A framework and changed all the properties of theoretically designed molecules as compared to PMD-1. Larger red shifted spectrum value of λmax = 739.542 nm with low transitional energy (1.677 eV) has been recorded in DCM solvent for PMDC6. FMOs analysis has shown that HOMOs are majorly occupied over π-spacer, whereas, the LUMOs are located on the acceptor moieties in all the titled molecules. The ELUMO − EHOMO of reference and its derivatives has reported in the range of 2.004–2.656 eV. Interestingly, the NBOs study has shown that the most prominent electronic transitions with greater stabilization energy (34.98 kcal mol−1) have been examined for PMDC6. The NBOs and FMOs response in PMDC6 are elevated as a result of the delocalization of π-system. Moreover, NLO study has revealed that among all the derivatives, PMDC6 has shown the highest value of βtot (4.469 × 10−27 esu) and γtot (5.600 × 10−32 esu). Therefore, it can be concluded that PMDC6 exhibits promising second and third-order NLO properties in the non-fullerene based optoelectronic compounds and might prove best NLO material for future applications.Data availability
Cartesian co-ordinates, HOMO−1, HOMO, LUMO and LUMO+1 energies and their band gap, UV-Vis data (wave lengths, excitation energies and oscillator strengths), NBOs analysis, structures and IUPAC names of derivatives, dipole moments, linear polarizabilities with major contributing tensors, the first hyperpolarizabilities (βtot) and second hyperpolarizabilities (γtot) with their contributing tensors of the reported compounds were calculated using PBE1PBE/6-311G(d,p) and represented in ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Dr Muhammad Khalid gratefully acknowledges the financial support of HEC Pakistan (project no. 20-14703/NRPU/R&D/HEC/2021). Authors are also thankful for cooperation and collaboration of A. A. C. B. from IQ-USP, Brazil especially for his continuous support and providing computational lab facilities. This research was assisted and funded by the Dean of Science and Research at King Khalid University via the General Research Project: grant no. (R.G.P.2/114/43).References
- T. H. Maiman, Nature, 1960, 187, 493–494 CrossRef.
- S. Taboukhat, N. Kichou, J.-L. Fillaut, O. Alévêque, K. Waszkowska, A. Zawadzka, A. El-Ghayoury, A. Migalska-Zalas and B. Sahraoui, Sci. Rep., 2020, 10, 15292 CrossRef CAS.
- N. Tsutsumi, M. Morishima and W. Sakai, Macromolecules, 1998, 31, 7764–7769 CrossRef CAS.
- E. M. Breitung, C.-F. Shu and R. J. McMahon, J. Am. Chem. Soc., 2000, 122, 1154–1160 CrossRef CAS.
- Z. Yang, A. Tudi, B.-H. Lei and S. Pan, Sci. China Mater., 2020, 63, 1480–1488 CrossRef CAS.
- M. Shkir, S. Muhammad, S. AlFaify, A. R. Chaudhry and A. G. Al-Sehemi, Arabian J. Chem., 2019, 12, 4612–4626 CrossRef CAS.
- J. Rotzler, D. Vonlanthen, A. Barsella, A. Boeglin, A. Fort and M. Mayor, Eur. J. Org. Chem., 2010, 2010, 1096–1110 CrossRef.
- M. U. Khan, M. Khalid, S. Asim, R. Hussain, K. Mahmood, J. Iqbal, M. N. Akhtar, A. Hussain, M. Imran and A. Irfan, Front. Mater., 2021, 8, 287 Search PubMed.
- M. Khalid, A. Ali, R. Jawaria, M. A. Asghar, S. Asim, M. U. Khan, R. Hussain, M. F. ur Rehman, C. J. Ennis and M. S. Akram, RSC Adv., 2020, 10, 22273–22283 RSC.
- B. S. Arslan, S. N. Ülüş, M. Gezgin, B. Arkan, E. Güzel, D. Avcı, M. Nebioğlu and İ. Şişman, Opt. Mater., 2020, 106, 109974 CrossRef.
- F. C. Asogwa, H. Louis, U. S. Ameuru, T. O. Unimuke, K. A. Adegoke, T. O. Magu and E. C. Agwamba, J. Mol. Model., 2022, 28, 245 CrossRef PubMed.
- A. Al-Yasari, N. Van Steerteghem, H. El Moll, K. Clays and J. Fielden, Dalton Trans., 2016, 45, 2818–2822 RSC.
- S. R. Maidur, P. S. Patil, S. V. Rao, M. Shkir and S. M. Dharmaprakash, Opt. Laser Technol., 2017, 97, 219–228 CrossRef.
- P. N. Prasad and D. J. Williams, Introduction to nonlinear optical effects in molecules and polymers, Wiley, New York, 1991, vol. 1 Search PubMed.
- M. R. S. A. Janjua, Mol. Simul., 2017, 43, 1539–1545 CrossRef.
- A. Ahsin and K. Ayub, J. Mol. Graphics Modell., 2021, 109, 108031 CrossRef.
- A. Ahsan and K. Ayub, Opt. Laser Technol., 2020, 129, 106298 CrossRef.
- A. Wadsworth, M. Moser, A. Marks, M. S. Little, N. Gasparini, C. J. Brabec, D. Baran and I. McCulloch, Chem. Soc. Rev., 2019, 48, 1596–1625 RSC.
- D. M. Guldi, Chem. Commun., 2000, 321–327 RSC.
- M. N. Arshad, I. Shafiq, M. Khalid and A. M. Asiri, ACS Omega, 2022, 7, 11606–11617 CrossRef.
- Y. Lin and X. Zhan, Mater. Horiz., 2014, 1, 470–488 RSC.
- H. Wu, B. Zhao, H. Zhao, L. Wang, W. Wang, Z. Cong, J. Liu, W. Ma and C. Gao, ACS Appl. Mater. Interfaces, 2019, 12, 789–797 CrossRef PubMed.
- D. M. Guldi, M. Maggini, G. Scorrano and M. Prato, J. Am. Chem. Soc., 1997, 119, 974–980 CrossRef.
- M. Panneerselvam, A. Kathiravan, R. V. Solomon and M. Jaccob, Phys. Chem. Chem. Phys., 2017, 19, 6153–6163 RSC.
- E. A. Eno, H. Louis, T. O. Unimuke, E. C. Agwamba, A. T. Etim, J. I. Mbonu, H. O. Edet, T. Egemoye, K. A. Adegoke and U. S. Ameuru, Phys. Sci. Rev., 2022 Search PubMed.
- U. J. Undiandeye, H. Louis, T. E. Gber, T. C. Egemonye, E. C. Agwamba, I. A. Undiandeye, A. S. Adeyinka and B. I. Ita, J. Indian Chem. Soc., 2022, 99, 100500 CrossRef.
- C. Yao, Y. Yang, L. Li, M. Bo, J. Zhang, C. Peng, Z. Huang and J. Wang, J. Phys. Chem. C, 2020, 124, 23059–23068 CrossRef.
- S. Pang, X. Zhou, S. Zhang, H. Tang, S. Dhakal, X. Gu, C. Duan, F. Huang and Y. Cao, ACS Appl. Mater. Interfaces, 2020, 12, 16531–16540 CrossRef.
- H. Huang, Q. Guo, S. Feng, C. Zhang, Z. Bi, W. Xue, J. Yang, J. Song, C. Li and X. Xu, Nat. Commun., 2019, 10, 1–10 CrossRef.
- M. J. Frisch, F. R. Clemente, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino and G. Zhe, Gaussian 16, Gaussian Inc., Wallingford, CT, 2009, pp. 20–44 Search PubMed.
- R. D. Dennington, T. A. Keith and J. M. Millam, GaussView 6.0, Gaussian Inc., Wallingford, 2008 Search PubMed.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef.
- W. An, Y. Gao, S. Bulusu and X. C. Zeng, J. Chem. Phys., 2005, 122, 204109 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17 Search PubMed.
- G. A. Zhurko and D. A. Zhurko, http://www.chemcraftprog.com.
- N. M. O’boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef PubMed.
- L. Kara Zaitri and S. M. Mekelleche, Mol. Phys., 2020, 118, 1618508 CrossRef.
- A. Alparone, Chem. Phys., 2013, 410, 90–98 CrossRef.
- A. Plaquet, M. Guillaume, B. Champagne, F. Castet, L. Ducasse, J.-L. Pozzo and V. Rodriguez, Phys. Chem. Chem. Phys., 2008, 10, 6223–6232 RSC.
- K. B. Lipkowitz and D. B. Boyd, Reviews in Computational Chemistry, John Wiley & Sons, 2009, vol. 12 Search PubMed.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5004 CrossRef.
- M. Khalid, M. U. Khan, I. Shafiq, R. Hussain, K. Mahmood, A. Hussain, R. Jawaria, A. Hussain, M. Imran and M. A. Assiri, Arabian J. Chem., 2021, 14, 103295 CrossRef.
- A. Ayadi, A. Szukalski, A. El-Ghayoury, K. Haupa, N. Zouari, J. Myśliwiec, F. Kajzar, B. Kulyk and B. Sahraoui, Dyes Pigm., 2017, 138, 255–266 CrossRef.
- M. Srnec and E. I. Solomon, J. Am. Chem. Soc., 2017, 139, 2396–2407 CrossRef PubMed.
- M. Wielopolski, J.-H. Kim, Y.-S. Jung, Y.-J. Yu, K.-Y. Kay, T. W. Holcombe, S. M. Zakeeruddin, M. Grätzel and J.-E. Moser, J. Phys. Chem. C, 2013, 117, 13805–13815 CrossRef.
- F. Kandemirli and S. Sagdinc, Corros. Sci., 2007, 49, 2118–2130 CrossRef CAS.
- M. Khalid, M. Ali, M. Aslam, S. H. Sumrra, M. U. Khan, N. Raza, N. Kumar and M. Imran, Int. J. Pharma Sci. Res., 2017, 8, 13040 Search PubMed.
- S. Namuangruk, R. Fukuda, M. Ehara, J. Meeprasert, T. Khanasa, S. Morada, T. Kaewin, S. Jungsuttiwong, T. Sudyoadsuk and V. Promarak, J. Phys. Chem. C, 2012, 116, 25653–25663 CrossRef.
- J. E. Huheey, J. Phys. Chem., 1966, 70, 2086–2092 CrossRef.
- O. A. Stasyuk, H. Szatylowicz, C. Fonseca Guerra and T. M. Krygowski, Struct. Chem., 2015, 26, 905–913 CrossRef.
- P. Goszczycki, K. Stadnicka, M. Z. Brela, J. Grolik and K. Ostrowska, J. Mol. Struct., 2017, 1146, 337–346 CrossRef CAS.
- M. Ans, J. Iqbal, Z. Ahmad, S. Muhammad, R. Hussain, B. Eliasson and K. Ayub, ChemistrySelect, 2018, 3, 12797–12804 CrossRef CAS.
- M. U. Khan, M. Ibrahim, M. Khalid, S. Jamil, A. A. Al-Saadi and M. R. S. A. Janjua, Chem. Phys. Lett., 2019, 719, 59–66 CrossRef CAS.
- M. Khalid, A. Ali, R. Jawaria, M. A. Asghar, S. Asim, M. U. Khan, R. Hussain, M. F. ur Rehman, C. J. Ennis and M. S. Akram, RSC Adv., 2020, 10, 22273–22283 RSC.
- C. Sissa, V. Parthasarathy, D. Drouin-Kucma, M. H. Werts, M. Blanchard-Desce and F. Terenziani, Phys. Chem. Chem. Phys., 2010, 12, 11715–11727 RSC.
- N. R. Sheela, S. Muthu and S. Sampathkrishnan, Spectrochim. Acta, Part A, 2014, 120, 237–251 CrossRef CAS.
- T. Koopmans, Physica, 1933, 1, 104–113 CrossRef CAS.
- R. G. Pearson, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 8440–8441 CrossRef CAS.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- P. K. Chattaraj and D. R. Roy, Chem. Rev., 2007, 107, PR46–PR74 CrossRef CAS.
- S. He, Y. Tan, X. Xiao, L. Zhu, Y. Guo, M. Li, A. Tian, X. Pu and N.-B. Wong, J. Mol. Struct.: THEOCHEM, 2010, 951, 7–13 CrossRef CAS.
- N. Maqsood, A. Asif, K. Ayub, J. Iqbal, A. Y. Elnaggar, G. A. Mersal, M. M. Ibrahim and S. M. El-Bahy, RSC Adv., 2022, 12, 16029–16045 RSC.
- E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42 Search PubMed.
- M. Imran, M. Khalid, R. Jawaria, A. Ali, M. A. Asghar, Z. Shafiq, M. A. Assiri, H. M. Lodhi and A. A. C. Braga, ACS Omega, 2021, 6, 33914–33922 CrossRef PubMed.
- A. J. Pounds, J. Chem. Educ., 2007, 84, 43 CrossRef.
- R. Hussain, M. U. Khan, M. Y. Mehboob, M. Khalid, J. Iqbal, K. Ayub, M. Adnan, M. Ahmed, K. Atiq and K. Mahmood, ChemistrySelect, 2020, 5, 5022–5034 CrossRef.
- T. Hassan, R. Hussain, M. U. Khan, U. Habiba, Z. Irshad, M. Adnan and J. Lim, Mater. Sci. Semicond. Process., 2022, 151, 107010 CrossRef CAS.
- Z. Liu, T. Lu and Q. Chen, Carbon, 2020, 165, 461–467 CrossRef CAS.
- Y. Li and C. A. Ullrich, Chem. Phys., 2011, 391, 157–163 CrossRef CAS.
- A. Dkhissi, Synth. Met., 2011, 161, 1441–1443 CrossRef CAS.
- A. Lesar and I. Milošev, Chem. Phys. Lett., 2009, 483, 198–203 CrossRef CAS.
- S. M. B. Dhas and S. Natarajan, Opt. Commun., 2007, 278, 434–438 CrossRef CAS.
- M. Shkir, S. Muhammad, S. AlFaify, A. R. Chaudhry and A. G. Al-Sehemi, Arabian J. Chem., 2019, 12, 4612–4626 CrossRef CAS.
- T. Zhang, X. Wei, Y. Zuo and J. Chao, Optik, 2019, 182, 295–302 CrossRef CAS.
- C. Bosshard, M. S. Wong, F. Pan, P. Günter and V. Gramlich, Adv. Mater., 1997, 9, 554–557 CrossRef.
- A. Dulcic, C. Flytzanis, C. L. Tang, D. Pepin, M. Fetizon and Y. Hoppilliard, J. Chem. Phys., 1981, 74, 1559–1563 CrossRef.
- Z. Peng and L. Yu, Macromolecules, 1994, 27, 2638–2640 CrossRef.
- H. S. Nalwa, T. Watanabe and S. Miyata, Photochem. Photophys., 1992, 5, 103–185 Search PubMed.
- K. Fukui, Science, 1982, 218, 747–754 CrossRef PubMed.
- A. Saeed, S. Muhammad, S. Rehman, S. Bibi, A. G. Al-Sehemi and M. Khalid, J. Mol. Graphics Modell., 2020, 100, 107665 CrossRef CAS PubMed.
- M. Khalid, H. M. Lodhi, M. U. Khan and M. Imran, RSC Adv., 2021, 11, 14237–14250 RSC.
- D. R. Kanis, M. A. Ratner and T. J. Marks, Chem. Rev., 1994, 94, 195–242 CrossRef CAS.
- T. J. Marks and M. A. Ratner, Angew. Chem., Int. Ed. Engl., 1995, 34, 155–173 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra04844b |
| This journal is © The Royal Society of Chemistry 2022 |