Open Access Article
Open Access ArticleCombining enhanced sampling and deep learning dimensionality reduction for the study of the heat shock protein B8 and its pathological mutant K141E†
Daniele Montepietraab,
Ciro Cecconiab and
Giorgia Brancolini *b
*b
aDepartment of Physics, Computer Science and Mathematics, University of Modena and Reggio Emilia, Via Campi 213/A, 41100 Modena, Italy
bIstituto Nanoscienze – CNR-NANO, Center S3, Via G. Campi 213/A, 41100 Modena, Italy. E-mail: giorgia.brancolini@nano.cnr.it
First published on 8th November 2022
Abstract
The biological functions of proteins closely depend on their conformational dynamics. This aspect is especially relevant for intrinsically disordered proteins (IDP) for which structural ensembles often offer more useful representations than individual conformations. Here we employ extensive enhanced sampling temperature replica-exchange atomistic simulations (TREMD) and deep learning dimensionality reduction to study the conformational ensembles of the human heat shock protein B8 and its pathological mutant K141E, for which no experimental 3D structures are available. First, we combined homology modelling with TREMD to generate high-dimensional data sets of 3D structures. Then, we employed a recently developed machine learning based post-processing algorithm, EncoderMap, to project the large conformational data sets into meaningful two-dimensional maps that helped us interpret the data and extract the most significant conformations adopted by both proteins during TREMD. These studies provide the first 3D structural characterization of HSPB8 and reveal the effects of the pathogenic K141E mutation on its conformational ensembles. In particular, this missense mutation appears to increase the compactness of the protein and its structural variability, at the same time rearranging the hydrophobic patches exposed on the protein surface. These results offer the possibility of rationalizing the pathogenic effects of the K141E mutation in terms of conformational changes.
1 Introduction
Small heat shock proteins (sHsps) are the most ubiquitous family of ATP-independent chaperones, being present in all kingdoms of life.1–4 The three-dimensional structure of these chaperones comprises a conserved structured α-crystallin domain (ACD), which represents their signature motif, a flexible N-terminal region (NTR) of variable length and sequence, and a short C-terminal region (CTR).3,5,6 The terminal regions are often intrinsically disordered (IDR),7 with a high number of charged residues and a low number of hydrophobic residues, and therefore are capable of non-specific interactions with a wide variety of substrates, from small peptides to large proteins.8–11 This capability helps explain the cellular function of the sHsps. Their general role appears to be the trapping and holding of non-native proteins in a state from which they can refold to the native state assisted by ATP-dependent chaperones.2,12 To this end, in humans several tissues (mainly muscle) constitutively express the heat shock protein B8 (HSPB8), also called Hsp22, which is a sHSP that limits the levels of aberrant proteins escaping degradation.13,14HSPB8 acts as a limiting factor in a larger chaperone complex targeting misfolded proteins to autophagy called the Chaperone-Assisted Selective Autophagy (CASA) complex, which is composed by HSPB8, BAG3, HSP70, and CHIP/STUB1.15 This complex is part of the autophagic degradation pathway that, along with the Ubiquitin Proteasome System (UPS), maintains proteostatic equilibrium in humans.16 The imbalance of these degradation pathways, finely controlled by specific chaperones and co-chaperones, can lead to several neurodegenerative diseases (ND).15 In particular, the single point mutation K141E in HSPB8 causes hereditary distal motor neuropathy of type II, while other mutations lead to motor neuron and muscle cell pathologies such as the Charcot–Marie–Tooth type 2L disease and distal myopathy.17–20 The consequences of these mutations reveal the crucial role that this chaperone plays in preserving motoneuron function and viability.
While the functional role of HSPB8 is becoming clearer, the atomistic details of its structure are not. At present, no experimental 3D structure of HSPB8 has been resolved. The technical difficulties in resolving the structure of the intrinsically disordered N and C terminal segments play a crucial role, as most experimental and analytical techniques have been created to investigate structured proteins. Computational simulations are increasingly used as a complementary method to experiments to gain insights into the conformational ensembles of IDPs and IDRs. In HSPB8 and sHsps in general, highly flexible IDRs shape the free energy landscape of the protein into having many shallow minima, which determine the presence of multiple protein conformations at physiological conditions.21–23 Earlier computational studies by Sehgal et al. tried to provide information on HSPB8 structure and its interaction with drugs through classical MD simulations.24 However, the protein conformational landscape accessible to classical MD simulations is very limited in most cases, even when force fields and water models specifically designed to reproduce experimental IDP conformations are used. To overcome some of these limitations, including the numerous energy barriers between conformational basins of an IDP, enhanced sampling methods and high-performance computational resources can be employed.25,26
When analyzing large volumes of simulation data, extracting useful information about relevant states and major conformational transitions requires the use of dimensionality reduction techniques that project high-dimensional data (protein conformations) into low-dimensional representations. These low-dimensional maps can be more easily interpreted and can form a basis for clustering the simulation data into conformational states.27,28
Artificial neural networks are increasingly being applied to study proteins and IDPs,29–34 as they are able to extract complex non-linear patterns and highly non-trivial relationships from a large amount of data. In particular, autoencoders (AE) are artificial neural networks trained to learn the encoding–decoding scheme that best reproduces the high-dimensional data provided to the encoder part (input) into the output of its decoder part. A narrow bottleneck layer divides the encoder from the decoder, which is fundamental to retain the essential features of the input data, as the autoencoder has to find a low-dimensional representation (encoding) for the high-dimensional training data.
EncoderMap is a dimensionality reduction algorithm that combines an autoencoder with multidimensional scaling, through a pairwise distance-based cost function,35–37 ensuring that the map arising from the projection of all high-dimensional points into 2D retains information about distances. The map can thus be interpreted as a landscape of the conformational space in which the point density is related to the free energy of the corresponding conformations. High point density regions in the 2D map separated by low-population regions can be considered (meta-)stable states that the system frequently visits. By selecting the highest population densities on the 2D map (i.e. low-dimension representation of the trajectory) it is possible to backmap the structures by reconstructing the coordinates using only the information encoded in the trajectory. EncoderMap has been successfully deployed to analyze large volumes of simulation data from different proteins.28,35,36 In this work we apply for the first time EncoderMap to the study of the conformational ensembles of IDPs.
In this work, by means of a workflow combining homology modeling, TREMD simulations and a deep learning algorithm, we analyzed the wt and K141E variants of HSPB8. The methodology is potentially applicable to the study of other IDRs-containing proteins. A schematic representation of the workflow is reported in Fig. S1.† From the homology model servers ROSETTA,38 I-TASSER,39 and MODELLER,40 we obtained different starting structures for HSPB8 that were then simulated with the temperature replica exchange (TREMD) enhanced sampling method using the state-of-the-art force field for IDPs CHARMM36m,41 with TIP3P as water model. Eventually, the resulting trajectories were used to train EncoderMap. The structures most frequently visited obtained from the dimensionality reduction of the simulation data of the wt and K141E variants were then extrapolated.
We developed a 4-step protocol for the computational generation of relevant structure ensembles for IDP and proteins containing IDR and applied it to the study of wt HSPB8 and its pathologically relevant mutant K141E. The analysis of the EncoderMap low-dimensional mapping suggests that the K141E mutation causes an increase in the conformational variability of the protein, making it less stable than the wt variant. We hypothesize that this mutation effectively increases the level of disorder of the protein that, together with the increased compactness of the three-dimensional structure, could eventually lead to the loss of chaperone function.
2 Results and discussion
In this section we outline the general computational workflow (Fig. S1†) and the analysis performed on the resulting simulation data, relying on new machine leaning algorithm, EncoderMap, that can handle large data sets of molecular conformations allowing simultaneous processing and comparison between them.2.1 Homology modeling and MD refinements
The homology models (HMs) are initially built by iterative threading and then subjected to 500 ns MD simulations to determine the individual thermodynamic stability and the possible structural configurations. Three homology models were obtained for HSPB8 sequence with different algorithms, namely I-TASSER,39 ROSETTA38 and MODELLER40 as reported in Fig. 1 (for K141E the same models were used). The root mean square deviation (RMSD) is used to measure how much a given protein model type deviates from the others. The backbone RMSD calculated between I-TASSER HM and ROSETTA HM is 2.521 Å, between I-TASSER and MODELLER HMs is 2.469 Å, between ROSETTA and MODELLER HMs is 1.584, indicating the I-TASSER model to deviate the most from ROSETTA and MODELLER. The radius of gyration (Rg) is computed to compare the degree of compactness of the different HMs: Rg for ROSETTA is 2.126 Å, for I-TASSER is 2.189 Å, and for MODELLER is 2.229 Å, indicating that ROSETTA and I-TASSER models are slightly less packed with respect to the MODELLER model.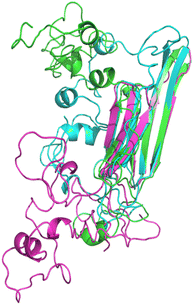 | ||
| Fig. 1 Pymol cartoon visualization of the structural superposition of the homology models obtained for wt HSPB8 with ROSETTA (cyan), I-TASSER (green), and MODELLER (magenta) algorithms. | ||
The obtained HMs were also compared with a recently published 3D structure of HSPB8 that was predicted with AlphaFold2. The AlphaFold2 predicted HM is available at the UNIPROT page (entry Q9UJY1) and is reported in Fig. S1.† The tendency of AlfaFold2 algorithm to predict the 3D structures of non-disordered proteins42 better than the 3D structures of disordered proteins43 is confirmed in the case of HSPB8. As can be seen in Fig. S2,† ACD is predicted with very high model confidence, while NTD and CTD with low or very low model confidence. Furthermore, the IUPRED3 web server,44 a disorder prediction method based on energy estimation, was applied to evaluate the disorder of the wt HSPB8's IDRs (Fig. S3†), where the protein residues' disorder propensity is reported in a scale from 0 (complete order) to 1 (complete disorder). We observed that HSPB8's IDRs (residues 1–96 corresponding to NTD and 170–196 to CTD, as well as a loop connecting two β-sheets in the ACD between residues 122–138) have disorder propensities mainly between 0.3 and 0.65, with peaks between 0.6 and 0.8 for residues 77–86, 122–124, 130, 132, 182, 193–194. Moreover, most HSPB8 residues have a disorder propensity below 0.5, IUPRED's threshold for distinguishing ordered from disordered regions.45 In contrast, for the human microtubule-associated tau protein (UNIPROT entry P10636), the disorder propensities for the first 600 amino acids are all above 0.6. These findings indicate that HSPB8's NTD and CTD are only low to moderately disordered, rather than extremely disordered such as the human tau protein. Consequently, the prediction of AlphaFold2, although a priori as reliable as those of the other homology modeling servers, was discarded because the IDRs were not consistent with the low disorder of HSPB8. Only I-TASSER, MODELLER, and ROSETTA were employed to obtain the structures used as the starting points for subsequent simulations.
Once collected, all HMs underwent 500 ns MD simulations and root mean square deviations were evaluated to measure how much each protein configuration deviated from its initial conformation. The RMSD plots for the 500 ns MD refinements for each HM and protein variant are reported in Fig. S4.† During the MD simulation, ROSETTA structures were observed to largely change conformation over the first 50 ns, while I-TASSER and MODELLER structures were undergoing smaller changes, as is evident from the respective RMSDs. During the MD simulations, the MODELLER and ROSETTA wt Rg were stable at 2.5 nm, while the I-TASSER wt HM increases from 2.0 nm to around 2.5 nm. For the K141E variants, we observed for all three HMs a steady decrease in Rg from 2.4 nm to 2.2 nm over the course of the simulation.
MD refinement simulations were able to provide insights into properties of proteins, like the relative thermodynamic stability of distinct conformations in solution, but as expected it was not possible to obtain converged equilibrated ensembles for our systems due to the large amount of degrees of freedom involved. For this reason, as described in the following section, we adopted parallel temperature replica exchange (TREMD) as an efficient method for enhanced conformational sampling.
2.2 Enhanced sampling simulations
To examine the conformational equilibrium of the wt and K141E HSPB8, we used six parallel 500 ns TREMD runs with 32 replica temperatures between 298 K and 323 K, each one starting from a different obtained HM, three for wt and three for the K141E, resulting in large data sets on the systems.Analysis of the simulations were initially performed by measuring various parameters including the radius of gyration (Rg) (Fig. 2 and S5†), backbone RMSD (Fig. S6†), backbone RMSF (Fig. S7†), ratio between hydrophobic solvent accessible surface area (hSASA) and solvent accessible surface area (SASA) (Fig. S8†) and salt bridges analysis (Fig. 3). For these analyses, replicas at 298 K were considered as they correspond to temperatures at which experiments testing sHSP chaperone activity are normally performed.
To assess the convergence of the TREMD simulations, we used the replica exchange statistics (Fig. S9†) and the RMSD and Rg autocorrelation function (Fig. S10 and S11†), as explained in the Methods section. It appears from Fig. S9† that the temperature exchanges of replica 1 are uniform, so all simulations were able to sample all accessible temperatures homogeneously. Furthermore, the autocorrelation times obtained from the graphs in Fig. S10 and S11† are all less than 50 ns. Given that each TREMD is 500 ns long (10 times the autocorrelation time), it is reasonable to assume that the simulations have reached equilibrium.
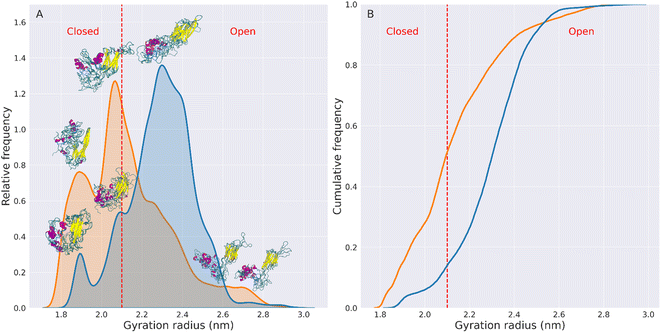
These graphs show that the mutated variant of HSPB8 preferentially assumes structures with a Rg smaller than the Rg of the wt structures, indicative of a greater compactness for K141E.
The increased compactness of K141E can be more precisely analyzed by defining the types of conformations assumed by HSPB8. More specifically, representative structures are classified as open or closed based on the distance between IDRs and ACD, which also relates with the Rg and hSASA values. Namely, the closed structures of HSPB8 have IDRs close to the ACD, whereas the IDRs of open structures are further away from the ACD. Given that residues involved in the chaperone action of HSPB8 are located in the ACD,46–49 it is possible that IDRs in the more closed conformations prevent interaction with misfolded proteins and therefore interfere with the chaperone activity of HSPB8. We also identified a dihedral angle formed by the Cα of residues 91–92–93–94, which is mainly attributable to an hinge between NTD and ACD (Fig. S13†), which regulates the transition between closed or open structures of the protein. As shown in Fig. S14,† the preferred value of the dihedral hinge of the closed structures of the protein is around 64°, while for the open structures is either 9° or 114°. Based on these considerations we have empirically chosen 2.1 nm as the Rg threshold below which HSPB8 conformations are classified as closed structures and above which are classified as open structures. The open/closed Rg threshold for HSPB8 conformations is shown in Fig. 2 and S12† as a dashed red line. The conformations displayed above each peak of the Rg distributions (Fig. 2) clearly show how the distance between IDRs and ACDs tends to be greater in open structures than in closed structures.
Using the open/closed conformation definition described above, we observed that for the wt, the percentage of conformations with Rg > 2.1 nm (open structures) was 86%, while conformations with Rg < 2.1 nm (closed structures) were 14%.
In contrast, for the mutated protein, open conformations account for 49% of the total conformations, while closed conformations account for 51%. This implies a 154% increase in the fraction of closed structures in the HSPB8 K141E ensemble compared to the wt variant.
The increase in compactness of the mutated protein relative to wt does not seem to affect significantly the flexibility or conformational variability of the protein. In fact, the RMSF plots reported in Fig. S7† show a reduction in the RMSFs only for the residues of the CTD of the mutated protein. The residues of the NTD and ACD instead undergo larger fluctuations in the mutated structure than in the wt structure, indicating that the K141E mutation does not restrict the motion of these protein regions. Our analysis in Fig. S12† demonstrates that the differences between the distinct open and closed ensembles are difficult to be fully characterized using only traditional shape parameters, such as the distribution of radius of gyration values. For this reason we have further employed a deep learning algorithm, to determine an optimal two-dimensional representation for viewing the ensemble of conformations, in a more effective way.
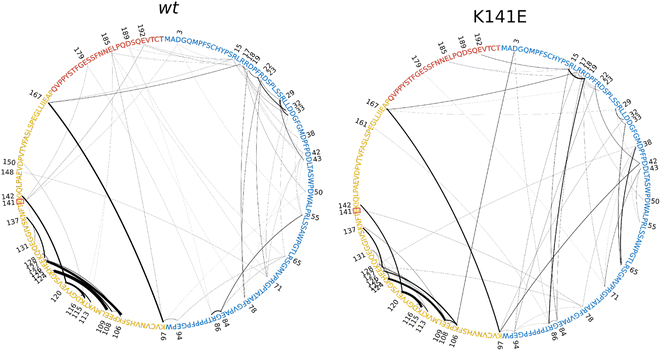
Results show a marked difference between the two variants. The wt IDR displays a larger number of salt bridges (44 intra- and inter-IDR salt bridges), but a relative low mean frequency (4.49%). The mutated IDR, instead, presents only 33 intra- and inter-IDR salt bridges but a higher mean frequency (6.11%).
On the other hand, in the K141E mutant the 23 intra-ACD salt bridges are of lower frequency compared to the 20 wt intra-ACD salt bridges (16.77% compared to 22.89%). Because the K141E mutation occurs within the ACD and involves the replacement of a positively charged Lys residue with a negatively charged Glu residue, we can attribute to the mutation the breaking of certain salt bridges and the formation of others with different frequency. Indeed, as a result of the mutation, residue 141 goes from forming salt bridges with residues 3, 179, and 192 in the wt variant to forming a salt bridge only with residue 78 in the mutated variant. The number of ACD-IDR salt bridges is maintained between wt and K141E, but in the latter, their frequency is stronger, being 4.18% instead of 2.84%. Fig. S10† reports a visual recap of the salt bridges' number and frequency between the three domains of the protein.
Overall, the K141E missense mutation disrupts the salt bridge network of HSPB8, rearranging and weakening the electrostatic interactions within the ACD and strengthening those within the IDR.
Results point to a more frustrated dynamic flexibility of the wt protein with respect to mutated protein which is reflected in the less efficient conformational shift from open to closed (86% open and 14% closed). Conversely, both the wide range of frequency and the multiplicity in the choice of ionic-bond pairs in the salt-bridges of K141E appear to be beneficial for the conformational shift from closed to open (45% open and 51% closed).
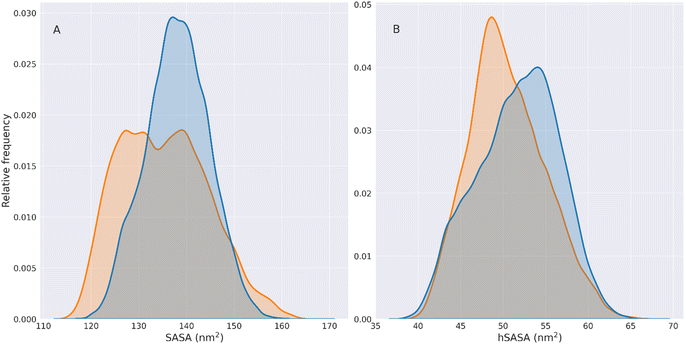
We can observe that the wt hSASA has generally higher values than its mutated counterpart, indicating that the wt hydrophobic residues are more exposed. However, HSPB8 K141E generally exposes less surface. Therefore the overall density of hydrophobic residues exposed per unit of the exposed area (the overall hSASA/SASA distribution) does not change significantly between the two variants of HSPB8. This is observable from the hSASA/SASA distributions and cumulative plots in Fig. S8.†
Although the overall distributions are not significantly different, the hSASA/SASA peak values for the wt and K141E distributions are different. Indeed, it can be seen that in the wt distribution the peaks of hSASA/SASA are found at values 0.361 and 0.378, while for K141E at 0.364.
This shows that in the set of K141E conformations there is a rearrangement of the hydrophobic residues exposed on the surface of the protein relative to wt structures, which does not change the overall value of hSASA/SASA but generates a local rearrangement of the solvent-exposed hydrophobic patches.
As a result, effects on global distributions do not necessarily reflect local changes at the level of individual hydrophobic residues.
This aspect is illustrated by the solvent-accessible surface changes of hydrophobic residues in the ACD and tryptophan residues of HSPB8. The highly conserved ACD hydrophobic residues (at positions 96, 98, 100, 102, 105, 107, 110, 111, 112, 119, and 121) function as binding sites for denatured substrates and thus play a crucial role in the chaperone activity of HSPB8 and other sHsps.46 As can be seen in Fig. S16† the hSASA/SASA median value of the ACD hydrophobic residues is systematically higher in the K141E variant than in the wt. Our results indicate that while the SASA of these hydrophobic residues is similar in the wt and mutated variants (Fig. S16,† bottom panel), the overall SASA of K141E is instead generally lower because the mutated protein is preferably more compact than the wt. Consequently, the relative contribution of these residues to the overall SASA of the protein increases in the K141E variant, with possible consequences for the chaperone activity of the protein. Our analysis of the four HSPB8 Trp residues' SASA, carried out to compare it with the experimental Trp fluorescence,50 is shown in Fig. S17.† The SASA TRP/SASA distributions indicate that the four Trp residues are exposed to the solvent differently, with residues 48, 60, and 51 being more exposed than residue Trp 96. In addition, the median SASA TRP/SASA value of Trp residues located in the NTD increases in the K141E case compared to wt.
From our results, we can formulate the following hypothesis regarding the structural changes induced by the K141E mutation in HSPB8: the mutation from lysine to glutamate at residue 141, which changes a positively charged residue into a negatively charged residue and the overall charge of the protein, causes the rearrangement of charges within the mutant HSPB8 and a reorganization of the salt bridge network, making it stronger towards the IDR and keeping the NTD and CTD closer to the ACD. This new rearrangement causes greater compactness in the mutant with respect to the wt and an overall lower radius of gyration by moving the ensemble equilibrium towards closed conformations, with less surface area exposed to the solvent. As a side effect, the electrostatic driving force of this change rearranges the hydrophobic residues exposed to the surface of the protein.
2.3 Overall conformations by dimensionality reduction with EncoderMap
TREMD trajectories of wt and mutant HSPB8 posed challenges to comparative analysis since conventional metrics poorly captures subtle differences between proteins structures, including transient structures. Machine learning (ML) algorithms are especially effective at discriminating among high-dimensional inputs whose differences are extremely subtle, making them well suited to the study of IDPs in general.To reduce the dimensionality of the input trajectories and get an understanding of the behavior of the investigated proteins, a dimensionality reduction algorithm called EncoderMap was applied to our data sets. This algorithm provides a powerful platform to process, understand, and compare the massive amounts of data that arose during 500 ns TREMD simulations of 32 replicas of our systems and makes the analysis of large and complex molecular systems computationally tractable.
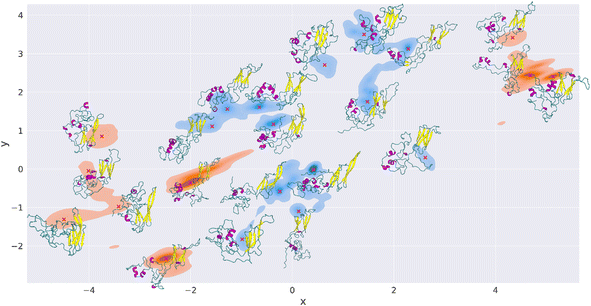
The plot in Fig. 5 shows the combined TREMD trajectories of wt (blue) and K141E (orange) after the dimensionality reduction with EncoderMap. The most frequently visited conformations during the simulation correspond to darker colors.
The EncoderMap plot shows that the K141E variant has visited 6 major conformational basins, which correspond to “islands” of conformations in the EncoderMap plot. The wt variant has instead visited 8 major conformational basins. Each of these basins possesses multiple high-frequency regions and the lower energy points are identified and marked with red crosses, Fig. 5. Next to each red cross is shown the corresponding HSPB8 structure. Nine structures were extracted for K141E and thirteen structures for wt. We observe that in the EncoderMap representation, the K141E conformational basins are more distant from each other than those of wt, thus the wt conformational basins appear to be more localized than those of the mutant. In Fig. S18† we inspect the basins explored by different HMs showing that they are not overlapping, being unrealistic to think to be able to achieve exhaustive sampling with a protein with such a large IDR part. Our results, being robust with respect to the uncertainty on the conformations, suggest that EncoderMap learn a low-dimensional representation of different protein structures that separates them based on their features.
Since the distance between points in the 2D plot of EncoderMap is proportional to the difference between the corresponding protein conformations in 3D (multidimensional scaling), we infer that the wt protein visited a more similar set of structures during the simulations than K141E.
Furthermore, calculating the Rg of each of the structures extracted with EncoderMap, we note that the Rg of the most frequented structures of K141E (5, 6, 21, 22 in Fig. S19†) is highly variable going from 2.04 nm (close structure) to 2.71 nm (open structure). In contrast, the Rg values of the most frequented wt structures (8, 9, 13, 14) are less variable, from 2.21 nm to 2.41 nm, and they all correspond to Rg of open structures.
If we compare the structures obtained from EncoderMap with those reported in the Rg peaks in Fig. 2, we see the correspondence between the structures obtained by the two different methods. The Rg peaks of K141E correspond to structures 1, 20, and 5–6–21 of EncoderMap, respectively, while the structures in the Rg peaks of HSPB8 wt correspond to structures 15, 18, and 8–9–14–17 generated with EncoderMap.
A summary of the Rg, SASA, hSASA, hSASA/SASA values for each generated EncoderMap structure is reported in Fig. S20.†
These results emphasize that the effect of the K141E mutation is to increase the conformational variability of HSPB8 relative to wt.
With EncoderMap we can represent the large data set of structures obtained with extensive TREMD simulations in a simplified but meaningful 2D plot, and we can identify and extract the most representative structures that the wt and K141E HSPB8 variants adopt during the simulations. In fact, if we look at the right panel in Fig. 4, for the structures generated by EncoderMap the trend of a given secondary structure element (e.g. the increase or decrease of a specific value going from wt to K141E) exactly mirrors the trend observed for the overall simulations on TREMD trajectories, with differences in absolute value ranging from 0.1% up to a maximum of 1.9%.
The dimensionality reduction provided by EncoderMap is therefore an effective technique to complement classical structural analyses of protein trajectories. While the latter is able to detect changes at the structural level between variants of the same protein, EncoderMap allows us to have a broader view and observe changes between wt and K141E not at the level of individual structures but at the ensemble level.
2.4 Comparison of simulations with available experimental data
The secondary structure of the molecular conformations generated by our simulations was compared with that estimated through circular dichroism experiments (CD)50 that, to the best of our knowledge, represent the only experimental data published so far on the structures of HSPB8 wt and K141E. Fig. 6 displays the percentages of various secondary structural elements estimated through CD experiments50 (panel (A)), and through DSSP calculations applied either to all TREMD trajectories (panel (B)) or to a restricted set of representative configurations selected through the EncoderMap algorithm (panel (C)). Experimental and computational data i.e. the relative values of the secondary structural elements within each secondary structure compare well, with the “unordered”, “strand” and “turn” elements being the most represented ones, in decreasing order. Also the effect of the K141E mutation on the different secondary structure elements of the experimentally and simulated structures is similar, with the sole exception of the “turn” elements on which the effect is opposite. This means that EncoderMap was able to extract the most representative structures from the large ensemble of conformations obtained, validating the EncoderMap algorithm.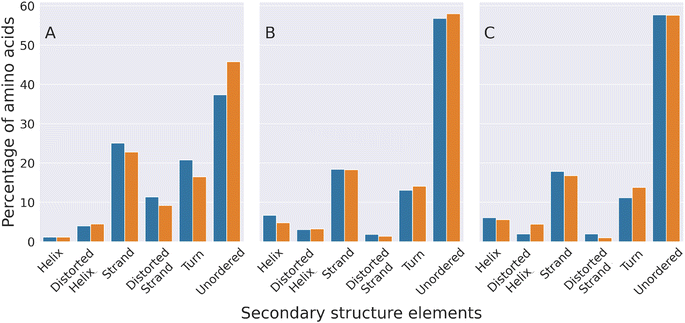 | ||
| Fig. 6 Experimental and computational characterization of the secondary structure of HSPB8 and its disease-linked mutant K141E. The percentage of amino acids forming different secondary structure elements is shown with blue (wt) and orange (K141E mutant) bars. The percentages shown in panel (A) were estimated through circular dichroism (CD) spectroscopy experiments,50 while those of panel (B) were calculated by analyzing the molecular structures adopted by HSPB8 wt and K141E during all TREMD trajectories. Panel (C) displays percentages calculated by analyzing the representative molecular structures obtained from the EncoderMap plot of Fig. 5. | ||
Finally, in order to compare our simulated data with the decrease of internal fluorescence detected experimentally for the K141E mutant,50 in Fig. S21† we show the heatmap representation of the median distances across the TREMD simulations between the four Trp residues of HSPB8 wt and K141E and the other protein residues. The lighter the color is, the smaller the distance between Trp and the protein residues is. We observe a marked difference between wt and K141E. Because the structures of K141E tend to be more compact than those of wt, the distances between the Trp residues present in NTD (48, 51, 60) and the residues in ACD are smaller (lighter colors between 97 and 169). These results, together with the SASA TRP/SASA distributions described above (Fig. S17†), indicate that the K141E mutation changes the microenvironment of the Trp residues of HSPB8, in accord with fluorescence experimental data.
3 Methodology
The proposed computational workflow consists of four steps. Starting from the wt protein sequence of HSPB8, we obtained three different initial 3D structures of the protein using distinct homology modeling software. The homology models (HM) were then refined with 500 ns MDs, giving the proteins enough time to reach an equilibrium state (Fig. S4†). The final MD protein structures were subjected to 500 ns temperature replica exchange molecular dynamics simulations (TREMD). The TREMD trajectories were then combined, according to the protein variant (wt or K141E), and structurally analyzed. Finally, the aggregated wt and K141E simulation data were encoded into a 2D map using EncoderMap in order to analyze patterns in the simulated conformations of the protein variants and recover their highest populated conformations. In what follows, we explain in detail the different steps of the workflow.3.1 Homology modelling
Although some homology modeling algorithms such as AlphaFold2 today are able to predict the native structure of structured proteins with astounding accuracy,42 their reliability plummets dramatically if IDP or IDR structures are being predicted.43 Moreover, the most likely prediction of an HM by a single homology modeling server and the following molecular dynamics simulations are usually not sufficient to characterize the incredible variety of conformations accessible to disordered protein fragments under physiological conditions. The relative shallowness of IDP and IDR free energy minima allows disordered fragments to assume ensembles of possible conformations instead of single native stable structures as structured proteins.51 In response to these considerations, starting from the 196 amino acid sequence of wt HSPB8 found in UNIPROT52 (entry Q9UJY1) we obtained 3 different HMs from as many algorithms: ROSETTA,38 I-TASSER,39 and MODELLER40 (Fig. 1 and S22†).For the ROSETTA algorithm, we employed the Robetta server https://robetta.bakerlab.org/ with the RoseTTAFold method.53 We chose model 1, which had a confidence value of 0.63.
We used the online I-TASSER server (https://zhanggroup.org/I-TASSER/) and we again used model 1, with the highest C-score (−0.69), and expected TM-score of 0.63 ± 0.14. The PDB templates used by the I-TASSER algorithm are 1ikqA, 1wleB, 2q5tA, 2x4bA, 2ygdA, 2z8sA, 2zuyA, 4ql6A, 4uniA, 5wqlC.
The MODELLER homology model was obtained from the MPI Bioinformatics Toolkit server (https://toolkit.tuebingen.mpg.de/tools/hhpred), first by running an HHPred search to find the homology templates selecting PDB_mmCIF70 as structural database and restricting the proteome to Homo sapiens (Euk_Homo_sapiens_04_Jul_2017) with standard parameters. The obtained PDB templates from HHPred selected for the following MODELLER run (https://toolkit.tuebingen.mpg.de/tools/modeller) were the first five hits, with the lowest E-score (from 10−21 to 10−17): UNKP1, 6DV5_J, 5LTW_G, 2YGD_F, 6F2R_N. The K141E mutated structure of each HM was obtained by replacing the amino acid Lys 141 with Glu using the PyMol mutagenesis tool.54 This left us with three HMs for the wt variant and three HMs for the K141E variant of HSPB8. The Root Mean Square Deviations (RMSD) between the different pairs of HM have been calculated using the GROMACS rms command, while the radius of gyration (Rg) of the whole protein for every HM has been computed with the GROMACS gyrate command. Throughout our simulations and analysis, we employed GROMACS 2020.1.
3.2 MD refinement
All the obtained wt and mutated HSPB8 HM structures were refined by 500 ns classical MD simulations in explicit water solvent using GROMACS 2020.1 as simulation software,55 with CHARMM36m + TIP3P as force field and water model.41,56 Force field comparison studies have shown that CHARMM36m possesses an improved accuracy in generating polypeptide backbone conformational ensembles for IDP and IDR, while at the same time maintaining folded regions' structure.57 All MD simulations were carried out using periodic boundary conditions in cubic boxes centered on the protein center of mass, with side lengths equal to the protein diameter plus 1.3 nm (with the flag -d in GROMACS command editconf), to avoid protein self-interactions during the simulation. After solvation, ions were added to obtain neutral systems, considering a neutral protonation state for histidine residues. 6 Na+ ions were added for the wt and 8 for the K141E mutant. The I-TASSER, MODELLER, and ROSETTA wt systems contained 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 673, 120
673, 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919, and 75
919, and 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 484 atoms respectively. The K141E mutated systems contained 62
484 atoms respectively. The K141E mutated systems contained 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780, 120
780, 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 914, and 75
914, and 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482 atoms. Initially, the entire system is minimized using the steepest descent algorithm to remove van der Waals contacts of high potential energy, with the maximum force threshold value was set at 1000 kJ mol−1 nm−1. Minimization was followed by a 100 ps relaxation of the solvent around the position-restrained protein and a 100 ps NPT equilibration with isotropic Berendsen pressure coupling at 1 bar.58 The temperature was kept at 298.15 K using a velocity rescaling thermostat.59 The 500 ns full MD simulation of the systems were performed using the leap-frog algorithm with a 2 fs time step, the Verlet cutoff scheme for van der Waals interactions, and the Particle Mesh Ewald (PME) method for the treatment of electrostatic interactions with 1.0 nm cutoff was adopted. The temperature coupling method used was velocity rescale, with 0.1 ps of time coupling constant. We used an isotropic Berendsen barostat with 1 bar of reference pressure and 1 ps of time constant. Covalent bonds involving hydrogen atoms were constrained using the LINCS algorithm. Positions and coordinates were saved every 20 ps. Standard structural analysis on the MD trajectories as RMSD, RMSF, and Rg was performed using GROMACS. Trajectories and structures were visualized using VMD60 and PyMol.54
482 atoms. Initially, the entire system is minimized using the steepest descent algorithm to remove van der Waals contacts of high potential energy, with the maximum force threshold value was set at 1000 kJ mol−1 nm−1. Minimization was followed by a 100 ps relaxation of the solvent around the position-restrained protein and a 100 ps NPT equilibration with isotropic Berendsen pressure coupling at 1 bar.58 The temperature was kept at 298.15 K using a velocity rescaling thermostat.59 The 500 ns full MD simulation of the systems were performed using the leap-frog algorithm with a 2 fs time step, the Verlet cutoff scheme for van der Waals interactions, and the Particle Mesh Ewald (PME) method for the treatment of electrostatic interactions with 1.0 nm cutoff was adopted. The temperature coupling method used was velocity rescale, with 0.1 ps of time coupling constant. We used an isotropic Berendsen barostat with 1 bar of reference pressure and 1 ps of time constant. Covalent bonds involving hydrogen atoms were constrained using the LINCS algorithm. Positions and coordinates were saved every 20 ps. Standard structural analysis on the MD trajectories as RMSD, RMSF, and Rg was performed using GROMACS. Trajectories and structures were visualized using VMD60 and PyMol.54
3.3 Enhanced sampling simulations
We used TREMD simulations61–63 as the enhanced sampling method of choice to generate our conformational ensembles for their well-documented suitability in studying IDP and IDR dynamics.64–71 During TREMD simulations, the free energy barrier is effectively lowered by enhancing the probability of sampling high-energy configurations at elevated temperatures, thus allowing efficient conformational sampling.72 This is achieved by creating several copies of the same starting structure, called replicas, each of which is assigned a different simulation temperature. The replicas are then run in parallel, and at regular intervals, neighboring replicas perform a temperature exchange attempt with a Boltzmann-weighted probability using a Monte Carlo criterion.59 When this condition is satisfied, an exchange attempt is considered successful, the conformations in neighboring replica temperatures are swapped, and the corresponding replicas' velocities are rescaled to the new replica temperatures. The process is repeated iteratively throughout the simulation, so that each replica has the opportunity to evolve by uniformly exploring the entire temperature range, thus expanding the conformational sampling of the protein.In our work, all TREMD simulations were run at the CINECA MARCONI100 cluster, in Bologna (Italy), using 32 replicas with temperatures spanning from 298 K to 323 K. The temperature of each replica was assigned using the virtualchemistry web server for generating temperatures for REMD calculations (https://virtualchemistry.org/remd-temperature-generator/) and extracted from an exponential distribution.62 The temperatures of each replica were the following: 298.00 K, 298.80 K, 299.61 K, 300.42 K, 301.23 K, 302.04 K, 302.85 K, 303.67 K, 304.48 K, 305.30 K, 306.12 K, 306.94 K, 307.77 K, 308.59 K, 309.42 K, 310.25 K, 311.08 K, 311.91 K, 312.75 K, 313.58 K, 314.42 K, 315.26 K, 316.10 K, 316.94 K, 317.79 K, 318.64 K, 319.48 K, 320.34 K, 321.19 K, 322.04 K, 322.90 K, and 323.00 K.
The structure of the system (protein + solvent) present in the final frame of each of the six different MD relaxations (I-TASSER wt and K141E, MODELLER wt and K141E, ROSETTA wt and K141E) was used as the starting structure for a TREMD. For each of these structures, 32 copies were created, one for each replica of the corresponding TREMD. The systems in the replicas of each different simulation underwent an independent 500 ps NPT equilibration with a 2 fs time step, during which the replica temperature was increased from 0 to the target replica temperature using a velocity rescaling thermostat, with an initial random velocity seed.
The six solvated protein equilibrated systems thereby obtained (I-TASSER wt and K141E, MODELLER wt and K141E, ROSETTA wt and K141E) were composed of 32 replicas each, with temperatures ranging from 298 K to 323 K assigned as explained above and initial random velocities. Each of these systems finally underwent 500 ns TREMD simulations, with replica exchanges attempted every 1 ps. Newton's equation of motion is solved using the leap-frog algorithm with an integration step of 2 fs. The Verlet cutoff scheme is applied for van der Waals interactions, and the Particle Mesh Ewald (PME) method for the treatment of electrostatic interactions, both with 1.0 nm cutoff. The temperature coupling method used was velocity-rescale, with coupling frequency of 10 steps and 0.1 ps of time coupling constant. The box size was kept fixed by using no pressure coupling. Covalent bonds involving hydrogen atoms were constrained using the LINCS algorithm. The output and coordinate files were saved every 1 ps. The force field was CHARMM36m with TIP3P as water model.41 The resulting simulation time for each of the six TREMD was 16 μs, yielding a total combined time per protein variant of 48 μs (three TREMD for the wt, and three for K141E, corresponding to the three different starting HM). All trajectories were processed with the GROMACS demux.pl script to filter the trajectory corresponding to a given temperature. Analysis was performed on the replica 1 trajectories for each TREMD. The analyses of the protein variants as a whole were performed by combining the replica 1 trajectories of the corresponding protein variant with the trjcat tool of GROMACS, i.e., replica 1 of the TREMDs of I-TASSER, MODELLER, and ROSETTA wt were concatenated into a single trajectory that was then used for the wt variant analyses, and the same was done for the K141E variant.
RMSD and RMSF analysis on the obtained TREMD trajectories were performed using GROMACS rms and rmsf tools respectively. The results of these analyses are reported in Fig. S4–S6 and S7.†
3.4 Convergence assessment
Two methods were used to verify the convergence of the TREMD trajectories, the first based on the temperature sampling uniformity, the other on the RMSD and the radius of gyration autocorrelation. In the first method, for each frame, the replica index with the temperature assumed by replica 1 was retrieved from the replica_index.xvg file obtained from the demux.pl script. In Fig. S9† are plotted the histograms of the indices thus obtained for each TREMD simulation. Autocorrelation can be defined as the similarity between observations of a random variable as a function of the time interval between them. In this paper, the observed variables were RMSD and radius of gyration. The method by which these variables were calculated from the trajectories is described in the paragraphs below. The plots in Fig. S10 and S11† were obtained with the plot_acf function of the Python package statsmodels.73 The autocorrelation value was calculated for each lag value from 1 to the total length of the simulation. Autocorrelation time is defined as the time distance (lag) between two observations for their values to be uncorrelated with 95% confidence. For each simulation, autocorrelation times were extrapolated from the intersection between the autocorrelation curve and the shaded area representing 95% confidence (right panels in Fig. S10 and S11†) and plotted as vertical dashed lines. Throughout the analysis, we employed Python version 3.8.10.3.5 Salt bridges
A salt bridge is an electrostatic interaction between two closely spaced residues of opposite charge. In this work, a salt bridge connecting two oppositely charged residues (among Asp, Glu, Arg, and Lys) was considered present if the distance between their oxygen and nitrogen atoms was less than 4.5 Å. Salt bridges were computed using the VMD salt bridges tool and represented in Fig. 3 and S15† using the Inkscape software. The salt bridge frequency between two protein residues is computed as the percentage of the number of trajectory frames in which the salt bridge is present.3.6 Radius of gyration
The radius of gyration (Rg) of a protein about its axis of rotation is defined as the radial distance to a point that would have a moment of inertia the same as the protein's actual distribution of mass if the total mass of the protein were concentrated there. We compute the Rg distributions for every considered trajectory using the GROMACS gyrate tool and represent them using in-house Python codes (Fig. S5 and the left panels of Fig. S11†). The Kernel Density Estimation (KDE) distribution in Fig. 2 and S12 † (on the left side) were represented using Python package seaborn kdeplot74 with bw_adjust parameter set to 0.8, and the right side cumulative plots in Fig. 2 and S12† using the ecdfplot function from seaborn Python package. The KDE distributions are normalized so that the total area under the curve is equal to one. Peak values of Rg distributions with a frequency greater than 0.05 were extracted using the find_peaks function of Python's scipy.signal package.75 The protein conformations represented above the peaks of the Rg distributions were obtained by first extracting the frames of the trajectories corresponding to the structures with Rg included in a 0.001 nm interval centered on the Rg value of the peak, then by clustering the resulting structures with the GROMACS cluster tool and keeping the centroid structures of the three most populated clusters.3.7 Solvent accessible surface area (SASA)
SASA, or solvent accessible surface area, is the area of the protein surface that is accessible to the solvent. The portion of SASA belonging to the hydrophobic residues Ala, Val, Leu, Ile, Pro, Phe, Met, and Trp (87 in total in HSPB8) is called hydrophobic SASA (hSASA). To obtain a normalized value hSASA/SASA representing the hydrophobic exposed surface per unit of the exposed surface (or the density of hydrophobic surface on the protein surface) we divide the hSASA value in each trajectory frame for the SASA value in the same frame. In the same way, when calculating the SASA of individual Trp residues present in HSPB8 (4 in total), the SASA TRP/SASA value represents the fraction of total SASA in the protein due to the SASA of a single Trp residue. The different SASA indicators have been calculated using the GROMACS tool sasa with the flags -surface and -output. The KDE and cumulative plots for the SASA, hSASA, and hSASA/SASA distributions in Fig. 4 and S8,† have been drawn using in-house Python scripts with the same procedure described above for the Rg distributions. The boxplots in Fig. S16 and S17† have been created with the boxplot function of the Python package seaborn.743.8 Secondary structure
We computed the percentage of different secondary structures categories using the DSSP version 2.2.0,76 as implemented in the Python package MDTraj version 1.9.4 (ref. 77) (mdtraj.compute_dssp). We used the 8-category scheme, where the DSSP assignment codes are: ‘H’ for alpha helix; ‘B’ for residue in isolated beta-bridge; ‘E’ for extended strand (participates in β-ladder); ‘G’ for 3-helix (3/10 helix); ‘I’ for 5 helix (π-helix); ‘T’ for hydrogen-bonded turn; ‘S’ for bend; ‘ ’ (blank space) for loops and irregular elements. To compare the results from our simulations with the experimental circular dichroism (CD) data in Kim et al.,50 we assigned category ‘H’ to ‘regular α-helix’ (‘helix’ in Fig. 6), categories ‘G’ and ‘I’ to ‘distorted α-helix’, category ‘E’ to ‘regular β-strand’ (‘strand’ in Fig. 6), category ‘B’ to ‘distorted β-strand’, category ‘T’ to ‘turns’, and categories ‘S’ and ‘ ’ (blank space) to ‘unordered’. To calculate the percentage of each secondary structure category for the wt and K141E variant of HSPB8, we calculated the occurrences of each secondary structure category among all residues of the protein for each frame of the concatenated wt and K141E simulations and summed the occurrences of the same category among all frames. Then we divided the resulting number by the number of frames and the number of residues in the protein. The results of the DSSP analysis reported in Fig. 6 have been represented with the catplot function of the Python package seaborn.743.9 Distance matrix
We computed the distance between the four Trp residues naturally present in the HSPB8 sequence (in positions 48, 51, 60, 96) and the other residues of the protein for each trajectory frame using the compute_contacts function of the Python package MDTraj version 1.9.4.77 The median value on all the trajectory frames is represented using the heatmap function of the Python package seaborn74 (Fig. S21†).3.10 Dimensionality reduction with EncoderMap
EncoderMap is a dimensionality reduction algorithm combining multidimensional scaling with the versatility of a variational autoencoder via a cost function based on pairwise distances and dihedral angles between the atoms of the protein backbone.35,36 Being based on neural networks, EncoderMap autonomously extracted and optimized the essential features from our large trajectory dataset and represented them with a minimum loss of information. The EncoderMap algorithm maintained similar protein structures in the high-dimensional space close in the generated 2D map, graphically providing global information about the conformational ensembles visited during a trajectory in a simplified but accurate manner. The map is interpreted as a landscape of the conformational space in which the point density is related to the free energy of the corresponding conformations. High point density regions in the 2D map separated by low-population regions are considered (meta-)stable states that the system frequently visits. Also, by selecting these high-density regions plotted into the low-dimensional map, we were able to back map the most stable structures obtained during the simulation. The EncoderMap code was retrieved from its GitHub repository (AG-Peter/EncoderMap). EncoderMap cost function is a weighted sum of three contributions: the dihedral cost, the Cα cost, and the distance cost. The dihedral cost is the mean absolute deviation between the dihedrals of the input conformations and the generated conformations (ensuring accurate short-range order). The Cα cost is the mean absolute deviation between all Cα-atom pairwise distances of the input conformations and the generated conformations (ensuring accurate long-range order). The distance cost compares distances between data points in the high-dimensional space with the corresponding distances of these points in the map. The distance cost uses the multidimensional scaling variant of SketchMap,37 which transforms the pairwise distances with sigmoid functions. The sigmoid functions for the high dimensional and the low dimensional space are described by three parameters each: σH, aH, bH, σL, aL, and bL. The σ parameters define the location of the inflection point of the sigmoid while a and b determine how quickly the function approaches 0 and 1, respectively. In this work, the EncoderMap training set comprised all wt and K141E replica 1 TREMD trajectories concatenated with the GROMACS tool trjcat (for a total of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 002 frames), using the initial frame as the reference structure for the pairwise distance calculations. The pairwise distances were calculated for every 200 input frames, with Sketchmap Cartesian sigmoid parameters σH = 1100, aH = 10, bH = 5, σL = 1, aL = 2, bL = 5, selected according to the Sketch-map literature.37 The total number of training steps was set at 50
002 frames), using the initial frame as the reference structure for the pairwise distance calculations. The pairwise distances were calculated for every 200 input frames, with Sketchmap Cartesian sigmoid parameters σH = 1100, aH = 10, bH = 5, σL = 1, aL = 2, bL = 5, selected according to the Sketch-map literature.37 The total number of training steps was set at 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, with the first 45
000, with the first 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps without the Cα cost and the last 5000 steps with the Cα cost. According to the EncoderMap literature,36 an earlier activation of the Cα cost interferes with the finding of correct short-range order, as the dihedrals are required to adjust accordingly to the long-range spatial arrangement and not independently. The EncoderMap neural network is composed of 7 fully connected layers: an input layer with 1170 neurons, 2 hidden layers with 128 neurons each, a bottleneck layer with 2 neurons, again 2 hidden layers with 128 neurons each, and an output layer with 1170 neurons, the activation function is tanh for all hidden layers and the identity function for all other layers. The network was optimized with batches of 256 points using the Adam optimizer78 with a learning rate of 0.001 and exponential decay rates β1 = 0.9 and β2 = 0.999 as implemented in TensorFlow 1.9.79 Weights were regularized using L2-regularization with a regularization constant of 0.001 (Table 1).
000 steps without the Cα cost and the last 5000 steps with the Cα cost. According to the EncoderMap literature,36 an earlier activation of the Cα cost interferes with the finding of correct short-range order, as the dihedrals are required to adjust accordingly to the long-range spatial arrangement and not independently. The EncoderMap neural network is composed of 7 fully connected layers: an input layer with 1170 neurons, 2 hidden layers with 128 neurons each, a bottleneck layer with 2 neurons, again 2 hidden layers with 128 neurons each, and an output layer with 1170 neurons, the activation function is tanh for all hidden layers and the identity function for all other layers. The network was optimized with batches of 256 points using the Adam optimizer78 with a learning rate of 0.001 and exponential decay rates β1 = 0.9 and β2 = 0.999 as implemented in TensorFlow 1.9.79 Weights were regularized using L2-regularization with a regularization constant of 0.001 (Table 1).
| Parameter | HSPB8 (wt + K141E) |
|---|---|
| Nsteps | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| σH | 1100 |
| aH | 10 |
| bH | 5 |
| σL | 1 |
| aL | 2 |
| bL | 5 |
| Nlayers | 7 |
| Nneurons | 1170 |
| Batch size | 256 |
| L | 0.001 |
| β1 | 0.9 |
| β2 | 0.999 |
| L2 | 0.001 |
Nsteps is the total number of training steps, with the first 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps without the Cα cost and the last 5000 steps with the Cα cost. The Sketchmap Cartesian sigmoid parameters σH, aH, bH, σL, aL, bL. The EncoderMap neural network is composed of 7 fully connected layers (Nlayers): an input layer with 1170 neurons (Nneurons), 2 hidden layers with 128 neurons each, a bottleneck layer with 2 neurons, again 2 hidden layers with 128 neurons each, and an output layer with 1170 neurons.
000 steps without the Cα cost and the last 5000 steps with the Cα cost. The Sketchmap Cartesian sigmoid parameters σH, aH, bH, σL, aL, bL. The EncoderMap neural network is composed of 7 fully connected layers (Nlayers): an input layer with 1170 neurons (Nneurons), 2 hidden layers with 128 neurons each, a bottleneck layer with 2 neurons, again 2 hidden layers with 128 neurons each, and an output layer with 1170 neurons.
The activation function is tanh for all hidden layers and the identity function for all other layers. The network was optimized with batches of 256 points using the Adam optimizer with a learning rate L and exponential decay rates β1 and β2, as implemented in TensorFlow 1.9.79 Weights were regularized using L2-regularization with a regularization constant L2.
The EncoderMap 2D plot in Fig. 5 has been realized with the kdeplot function of the Python package seaborn,74 with the bw_adjust parameter set to 0.2. The protein structures reported on the plot have been extracted using the generator function in EncoderMap, which employs the decoder part of the algorithm.
We extracted 13 structures for wt HSPB8 and 9 structures for K141E HSPB8. For each structure, we computed the Rg, SASA and hSASA with the tools described above, and the percentage of the secondary structure of each conformation using the DSSP algorithm. The median value among all conformations, for each type of secondary structure, is reported in the right panel of Fig. 6.
4 Conclusions
In this paper we have generated high-dimensional data sets of 3D structures of the human heat shock protein B8 and its pathological mutant K141E by means of extensive enhanced sampling TREMD simulations (48 μs per protein variant). Resulting trajectories were compared using a dimensionality reduction algorithm, EncoderMap, for simplifying the complex ensemble of structures adopted by each variant and rationalizing the pathogenic effects of the K141E mutation in terms of differences between distinct disordered ensembles. A detailed structural analysis on the observed ensembles revealed a substantial change in the structural features of the K141E variant compared to wt. In particular, the missense mutation converting Lys to Glu at position 141, present in the conserved ACD, appears to disrupt the neighboring salt bridges network, making the electrostatic interactions between ACD and the N- and C-terminal IDRs stronger. The salt bridge rearrangement is accompanied by an overall decrease in the gyration radius in the K141E mutant, with the corresponding percentage increase in closed structures (identified as those protein conformations with gyration radius < 2.1 nm). The structural reorganization of the IDRs results in a rearrangement of the hydrophobic residue patches exposed on the surface of the mutated protein.Using EncoderMap,36 a neural network-based dimensionality decreasing algorithm, we were able to generate meaningful two-dimensional maps of high dimensional data sets obtained for both protein variants. Due to the efficiency of the method, very large data sets of long-time scale simulations of multiple proteins models could be processed and projected in the same map. From these low-dimensional representations we obtained a very detailed picture of the overall effect of the K141E mutation, especially its capability to increase the conformational variability of K141E relative to wt. We also extracted the most significant protein structures from the EncoderMap plot, that is the structures that are most frequently populated during TREMDs.
The proposed methodology presented here offers a powerful platform to understand IDPs/IDRs protein ensembles. The results represent the first structural insights into the conformational ensembles of HSPB8 wt and K141E, providing the basis for rationalizing the physiological effect of this pathogenic mutation.
Data availability
The obtained TREMD simulations of wt and K141E HSPB8 are freely available on Zenodo (10.1234/HSPB8) under Creative Commons Attribution 4.0 International license, and the in-house Python scripts used for the analyses reported above have been uploaded to GitHub (https://github.com/Monte95/HSPB8).Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We wish to thank Prof. Serena Carra for fruitful discussions. Funding from the PRIN2020 (under the grant 2020LW7XWH) are gratefully acknowledged. We acknowledge the CINECA award under the ISCRAB initiative (code HP10BR6DPT) for the availability of high-performance computing resources (MARCONI 100) and support. GB acknowledges Oak Ridge National Laboratory by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy is acknowledged for the supercomputing project CNMS2020-B-00433. GB acknowledges facilities of the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the U.S. Department of Energy under contract no. DE-AC02-05CH11231, are also acknowledged.References
- I. Obuchowski and K. Liberek, Small but Mighty: A Functional Look at Bacterial SHSPs, Cell Stress Chaperones, 2020, 25(4), 593–600, DOI:10.1007/s12192-020-01094-0.
- M. Haslbeck, S. Weinkauf and J. Buchner, Small Heat Shock Proteins: Simplicity Meets Complexity, J. Biol. Chem., 2019, 294(6), 2121–2132, DOI:10.1074/jbc.REV118.002809.
- W. W. de Jong, J. A. Leunissen and C. E. Voorter, Evolution of the Alpha-Crystallin/Small Heat-Shock Protein Family, Mol. Biol. Evol., 1993, 10(1), 103–126, DOI:10.1093/oxfordjournals.molbev.a039992.
- F. Narberhaus, Alpha-Crystallin-Type Heat Shock Proteins: Socializing Minichaperones in the Context of a Multichaperone Network, Microbiol. Mol. Biol. Rev., 2002, 66(1), 64–93, DOI:10.1128/MMBR.66.1.64-93.2002.
- E. Basha, H. O'Neill and E. Vierling, Small Heat Shock Proteins and α-Crystallins: Dynamic Proteins with Flexible Functions, Trends Biochem. Sci., 2012, 37(3), 106–117, DOI:10.1016/j.tibs.2011.11.005.
- T. Kriehuber, T. Rattei, T. Weinmaier, A. Bepperling, M. Haslbeck and J. Buchner, Independent Evolution of the Core Domain and Its Flanking Sequences in Small Heat Shock Proteins, FASEB J., 2010, 24(10), 3633–3642, DOI:10.1096/fj.10-156992.
- M. V. Sudnitsyna, E. V. Mymrikov, A. S. Seit-Nebi and N. B. Gusev, The Role of Intrinsically Disordered Regions in the Structure and Functioning of Small Heat Shock Proteins, Curr. Protein Pept. Sci., 2012, 13(1), 76–85, DOI:10.2174/138920312799277875.
- V. N. Uversky, J. R. Gillespie and A. L. Fink, Why Are “Natively Unfolded” Proteins Unstructured under Physiologic Conditions?, Proteins, 2000, 41(3), 415–427, DOI:10.1002/1097-0134(20001115)41:3<415::aid-prot130>3.0.co;2-7.
- G. Bianchi, S. Longhi, R. Grandori and S. Brocca, Relevance of Electrostatic Charges in Compactness, Aggregation, and Phase Separation of Intrinsically Disordered Proteins, Int. J. Mol. Sci., 2020, 21(17) DOI:10.3390/ijms21176208.
- A. Dabbaghizadeh and R. M. Tanguay, Structural and Functional Properties of Proteins Interacting with Small Heat Shock Proteins, Cell Stress Chaperones, 2020, 25(4), 629–637, DOI:10.1007/s12192-020-01097-x.
- V. N. Uversky, Intrinsic Disorder-Based Protein Interactions and Their Modulators, Curr. Pharm. Des., 2013, 19(23), 4191–4213, DOI:10.2174/1381612811319230005.
- T. Stromer, M. Ehrnsperger, M. Gaestel and J. Buchner, Analysis of the Interaction of Small Heat Shock Proteins with Unfolding Proteins, J. Biol. Chem., 2003, 278(20), 18015–18021, DOI:10.1074/jbc.M301640200.
- V. Crippa, D. Sau, P. Rusmini, A. Boncoraglio, E. Onesto, E. Bolzoni, M. Galbiati, E. Fontana, M. Marino, S. Carra, C. Bendotti, S. De Biasi and A. Poletti, The Small Heat Shock Protein B8 (HspB8) Promotes Autophagic Removal of Misfolded Proteins Involved in Amyotrophic Lateral Sclerosis (ALS), Hum. Mol. Genet., 2010, 19(17), 3440–3456, DOI:10.1093/hmg/ddq257.
- R. Cristofani, V. Crippa, P. Rusmini, M. E. Cicardi, M. Meroni, N. V. Licata, G. Sala, E. Giorgetti, C. Grunseich, M. Galbiati, M. Piccolella, E. Messi, C. Ferrarese, S. Carra and A. Poletti, Inhibition of Retrograde Transport Modulates Misfolded Protein Accumulation and Clearance in Motoneuron Diseases, Autophagy, 2017, 13(8), 1280–1303, DOI:10.1080/15548627.2017.1308985.
- P. Rusmini, R. Cristofani, M. Galbiati, M. E. Cicardi, M. Meroni, V. Ferrari, G. Vezzoli, B. Tedesco, E. Messi, M. Piccolella, S. Carra, V. Crippa and A. Poletti, The Role of the Heat Shock Protein B8 (HSPB8) in Motoneuron Diseases, Front. Mol. Neurosci., 2017, 10, 176, DOI:10.3389/fnmol.2017.00176.
- I. Korovila, M. Hugo, J. P. Castro, D. Weber, A. Höhn, T. Grune and T. Jung, Proteostasis Oxidative Stress and Aging, Redox Biol., 2017, 13, 550–567, DOI:10.1016/j.redox.2017.07.008.
- J.-M. Fontaine, X. Sun, A. D. Hoppe, S. Simon, P. Vicart, M. J. Welsh and R. Benndorf, Abnormal Small Heat Shock Protein Interactions Involving Neuropathy-Associated HSP22 (HSPB8) Mutants, FASEB J., 2006, 20(12), 2168–2170, DOI:10.1096/fj.06-5911fje.
- J. Irobi, L. Almeida-Souza, B. Asselbergh, V. De Winter, S. Goethals, I. Dierick, J. Krishnan, J.-P. Timmermans, W. Robberecht, P. De Jonghe, L. Van Den Bosch, S. Janssens and V. Timmerman, Mutant HSPB8 Causes Motor Neuron-Specific Neurite Degeneration, Hum. Mol. Genet., 2010, 19(16), 3254–3265, DOI:10.1093/hmg/ddq234.
- R. Ghaoui, J. Palmio, J. Brewer, M. Lek, M. Needham, A. Evilä, P. Hackman, P.-H. Jonson, S. Penttilä, A. Vihola, S. Huovinen, M. Lindfors, R. L. Davis, L. Waddell, S. Kaur, C. Yiannikas, K. North, N. Clarke, D. G. MacArthur, C. M. Sue and B. Udd, Mutations in HSPB8 Causing a New Phenotype of Distal Myopathy and Motor Neuropathy, Neurology, 2016, 86(4), 391–398, DOI:10.1212/WNL.0000000000002324.
- A. S. Kwok, K. Phadwal, B. J. Turner, P. L. Oliver, A. Raw, A. K. Simon, K. Talbot and V. R. Agashe, HspB8 Mutation Causing Hereditary Distal Motor Neuropathy Impairs Lysosomal Delivery of Autophagosomes, J. Neurochem., 2011, 119(6), 1155–1161, DOI:10.1111/j.1471-4159.2011.07521.x.
- G. Mahmoudabadi, K. Rajagopalan, R. H. Getzenberg, S. Hannenhalli, G. Rangarajan and P. Kulkarni, Intrinsically Disordered Proteins and Conformational Noise: Implications in Cancer, Cell Cycle, 2013, 12(1), 26–31, DOI:10.4161/cc.23178.
- U. B. Choi, H. Sanabria, T. Smirnova, M. E. Bowen and K. R. Weninger, Spontaneous Switching among Conformational Ensembles in Intrinsically Disordered Proteins, Biomolecules, 2019, 9(3) DOI:10.3390/biom9030114.
- V. Perovic, N. Sumonja, L. A. Marsh, S. Radovanovic, M. Vukicevic, S. G. E. Roberts and N. Veljkovic, IDPpi: Protein-Protein Interaction Analyses of Human Intrinsically Disordered Proteins, Sci. Rep., 2018, 8(1), 10563, DOI:10.1038/s41598-018-28815-x.
- S. A. Sehgal, S. Mannan and S. Ali, Pharmacoinformatic and Molecular Docking Studies Reveal Potential Novel Antidepressants against Neurodegenerative Disorders by Targeting HSPB8, Drug Des., Dev. Ther., 2016, 2016(10), 1605–1618, DOI:10.2147/DDDT.S101929.
- S. Bhattacharya and X. Lin, Recent Advances in Computational Protocols Addressing Intrinsically Disordered Proteins, Biomolecules, 2019, 9 DOI:10.3390/biom9040146.
- S.-H. Chong, P. Chatterjee and S. Ham, Computer Simulations of Intrinsically Disordered Proteins, Annu. Rev. Phys. Chem., 2017, 68, 117–134, DOI:10.1146/annurev-physchem-052516-050843.
- O. Kukharenko, K. Sawade, J. Steuer and C. Peter, Using Dimensionality Reduction to Systematically Expand Conformational Sampling of Intrinsically Disordered Peptides, J. Chem. Theory Comput., 2016, 12(10), 4726–4734, DOI:10.1021/acs.jctc.6b00503.
- A. Berg, L. Franke, M. Scheffner and C. Peter, Machine Learning Driven Analysis of Large Scale Simulations Reveals Conformational Characteristics of Ubiquitin Chains, J. Chem. Theory Comput., 2020, 16(5), 3205–3220, DOI:10.1021/acs.jctc.0c00045.
- G. Grazioli, R. W. Martin and C. T. Butts, Comparative Exploratory Analysis of Intrinsically Disordered Protein Dynamics Using Machine Learning and Network Analytic Methods, Front. Mol. Biosci., 2019, 6, 42, DOI:10.3389/fmolb.2019.00042.
- A. Ramanathan, H. Ma, A. Parvatikar and S. C. Chennubhotla, Artificial Intelligence Techniques for Integrative Structural Biology of Intrinsically Disordered Proteins, Curr. Opin. Struct. Biol., 2021, 66, 216–224, DOI:10.1016/j.sbi.2020.12.001.
- Y. Jin, L. O. Johannissen and S. Hay, Predicting New Protein Conformations from Molecular Dynamics Simulation Conformational Landscapes and Machine Learning, Proteins: Struct., Funct., Bioinf., 2021, 89(8), 915–921, DOI:10.1002/prot.26068.
- F. Noé, G. De Fabritiis and C. Clementi, Machine Learning for Protein Folding and Dynamics, Curr. Opin. Struct. Biol., 2020, 60, 77–84, DOI:10.1016/j.sbi.2019.12.005.
- F. F. Alam, T. Rahman and A. Shehu, Learning Reduced Latent Representations of Protein Structure Data, in Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics; BCB '19, Association for Computing Machinery, New York, NY, USA, 2019, pp. 592–597, DOI:10.1145/3307339.3343866.
- Y. Wang, J. M. Lamim Ribeiro and P. Tiwary, Machine Learning Approaches for Analyzing and Enhancing Molecular Dynamics Simulations, Curr. Opin. Struct. Biol., 2020, 61, 139–145, DOI:10.1016/j.sbi.2019.12.016.
- T. Lemke and C. Peter, EncoderMap: Dimensionality Reduction and Generation of Molecule Conformations, J. Chem. Theory Comput., 2019, 15(2), 1209–1215, DOI:10.1021/acs.jctc.8b00975.
- T. Lemke, A. Berg, A. Jain and C. Peter, EncoderMap(II): Visualizing Important Molecular Motions with Improved Generation of Protein Conformations, J. Chem. Inf. Model., 2019, 59(11), 4550–4560, DOI:10.1021/acs.jcim.9b00675.
- M. Ceriotti, G. A. Tribello and M. Parrinello, Simplifying the Representation of Complex Free-Energy Landscapes Using Sketch-Map, Proc. Natl. Acad. Sci., 2011, 108(32), 13023–13028, DOI:10.1073/pnas.1108486108.
- Y. Song, F. Dimaio, R. Y. R. Wang, D. Kim, C. Miles, T. Brunette, J. Thompson and D. Baker, High-Resolution Comparative Modeling with RosettaCM, Structure, 2013, 21(10), 1735–1742, DOI:10.1016/j.str.2013.08.005.
- J. Yang, R. Yan, A. Roy, D. Xu, J. Poisson and Y. Zhang, The I-TASSER Suite: Protein Structure and Function Prediction, Nat. Methods, 2015, 7–8, DOI:10.1038/nmeth.3213.
- B. Webb and A. Sali, Comparative Protein Structure Modeling Using MODELLER, Curr. Protoc. Bioinf., 2016, 54(1), 5.6.1–5.6.37, DOI:10.1002/cpbi.3.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. J. MacKerell, CHARMM36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins, Nat. Methods, 2017, 14(1), 71–73, DOI:10.1038/nmeth.4067.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Highly Accurate Protein Structure Prediction with AlphaFold, Nature, 2021, 596(7873), 583–589, DOI:10.1038/s41586-021-03819-2.
- K. M. Ruff and R. V. Pappu, AlphaFold and Implications for Intrinsically Disordered Proteins, J. Mol. Biol., 2021, 433(20), 167208, DOI:10.1016/j.jmb.2021.167208.
- G. Erdős, M. Pajkos and Z. Dosztányi, IUPred3: Prediction of Protein Disorder Enhanced with Unambiguous Experimental Annotation and Visualization of Evolutionary Conservation, Nucleic Acids Res., 2021, 49(W1), W297–W303, DOI:10.1093/nar/gkab408.
- Z. Dosztányi, V. Csizmok, P. Tompa and I. Simon, IUPred: Web Server for the Prediction of Intrinsically Unstructured Regions of Proteins Based on Estimated Energy Content, Bioinformatics, 2005, 21(16), 3433–3434, DOI:10.1093/bioinformatics/bti541.
- S. Carra, M. Sivilotti, A. T. Chávez Zobel, H. Lambert and J. Landry, HspB8, a Small Heat Shock Protein Mutated in Human Neuromuscular Disorders, Has In Vivo Chaperone Activity in Cultured Cells, Hum. Mol. Genet., 2005, 14(12), 1659–1669, DOI:10.1093/hmg/ddi174.
- R. C. Augusteyn, α-Crystallin: A Review of Its Structure and Function, Aust. J. Optom., 2004, 87(6), 356–366, DOI:10.1111/j.1444-0938.2004.tb03095.x.
- R. Van Montfort, C. Slingsby and E. Vierling, Structure and Function of the Small Heat Shock Protein/Alpha-Crystallin Family of Molecular Chaperones, Adv. Protein Chem., 2001, 59, 105–156, DOI:10.1016/s0065-3233(01)59004-x.
- K. K. Sharma, R. S. Kumar, G. S. Kumar and P. T. Quinn, Synthesis and Characterization of a Peptide Identified as a Functional Element in AlphaA-Crystallin, J. Biol. Chem., 2000, 275(6), 3767–3771, DOI:10.1074/jbc.275.6.3767.
- M. V. Kim, A. S. Kasakov, A. S. Seit-Nebi, S. B. Marston and N. B. Gusev, Structure and Properties of K141E Mutant of Small Heat Shock Protein HSP22 (HspB8, H11) That Is Expressed in Human Neuromuscular Disorders, Arch. Biochem. Biophys., 2006, 454(1), 32–41, DOI:10.1016/j.abb.2006.07.014.
- B. Strodel, Energy Landscapes of Protein Aggregation and Conformation Switching in Intrinsically Disordered Proteins, J. Mol. Biol., 2021, 433(20), 167182, DOI:10.1016/j.jmb.2021.167182.
- A. Bateman, UniProt: A Worldwide Hub of Protein Knowledge, Nucleic Acids Res., 2019, 47(D1), D506–D515, DOI:10.1093/nar/gky1049.
- N. Hiranuma, H. Park, M. Baek, I. Anishchenko, J. Dauparas and D. Baker, Improved Protein Structure Refinement Guided by Deep Learning Based Accuracy Estimation, Nat. Commun., 2021, 12(1), 1340, DOI:10.1038/s41467-021-21511-x.
- Schrödinger LLC and W. DeLano, PyMOL Search PubMed.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, GROMACS: A Message-Passing Parallel Molecular Dynamics Implementation, Comput. Phys. Commun., 1995, 91(1–3), 43–56, DOI:10.1016/0010-4655(95)00042-E.
- L. A. Abriata and M. Dal Peraro, Assessment of Transferable Forcefields for Protein Simulations Attests Improved Description of Disordered States and Secondary Structure Propensities, and Hints at Multi-Protein Systems as the next Challenge for Optimization, Comput. Struct. Biotechnol. J., 2021, 19, 2626–2636, DOI:10.1016/j.csbj.2021.04.050.
- M. U. Rahman, A. U. Rehman, H. Liu and H.-F. Chen, Comparison and Evaluation of Force Fields for Intrinsically Disordered Proteins, J. Chem. Inf. Model., 2020, 60(10), 4912–4923, DOI:10.1021/acs.jcim.0c00762.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular Dynamics with Coupling to an External Bath, J. Chem. Phys., 1984, 81(8), 3684–3690, DOI:10.1063/1.448118.
- G. Bussi, D. Donadio and M. Parrinello, Canonical Sampling through Velocity Rescaling, J. Chem. Phys., 2007, 126(1), 14101, DOI:10.1063/1.2408420.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14(1), 33–38, DOI:10.1016/0263-7855(96)00018-5.
- R. H. Swendsen and J. S. Wang, Replica Monte Carlo Simulation of Spin Glasses, Phys. Rev. Lett., 1986, 57(21), 2607–2609, DOI:10.1103/PhysRevLett.57.2607.
- D. J. Earl and M. W. Deem, Parallel Tempering: Theory, Applications, and New Perspectives, Phys. Chem. Chem. Phys., 2005, 7(23), 3910–3916, 10.1039/b509983h.
- A. Patriksson and D. Van Der Spoel, A Temperature Predictor for Parallel Tempering Simulations, Phys. Chem. Chem. Phys., 2008, 10(15), 2073–2077, 10.1039/b716554d.
- S. Patel, E. Vierling and F. Tama, Replica Exchange Molecular Dynamics Simulations Provide Insight into Substrate Recognition by Small Heat Shock Proteins, Biophys. J., 2014, 106(12), 2644–2655, DOI:10.1016/j.bpj.2014.04.048.
- T. Nishimoto, Y. Takahashi, S. Miyama, T. Furuta and M. Sakurai, Replica Exchange Molecular Dynamics Simulation Study on the Mechanism of Desiccation-Induced Structuralization of an Intrinsically Disordered Peptide as a Model of LEA Proteins, Biophys. Physicobiol., 2019, 16, 196–204, DOI:10.2142/biophysico.16.0_196.
- N. G. Sgourakis, M. Merced-Serrano, C. Boutsidis, P. Drineas, Z. Du, C. Wang and A. E. Garcia, Atomic-Level Characterization of the Ensemble of the Aβ(1-42) Monomer in Water Using Unbiased Molecular Dynamics Simulations and Spectral Algorithms, J. Mol. Biol., 2011, 405(2), 570–583, DOI:10.1016/j.jmb.2010.10.015.
- W. Zhang, D. Ganguly and J. Chen, Residual Structures, Conformational Fluctuations, and Electrostatic Interactions in the Synergistic Folding of Two Intrinsically Disordered Proteins, PLoS Comput. Biol., 2012, 8(1), e1002353, DOI:10.1371/journal.pcbi.1002353.
- M. Knott and R. B. Best, A Preformed Binding Interface in the Unbound Ensemble of an Intrinsically Disordered Protein: Evidence from Molecular Simulations, PLoS Comput. Biol., 2012, 8(7), e1002605, DOI:10.1371/journal.pcbi.1002605.
- J. Mittal, T. H. Yoo, G. Georgiou and T. M. Truskett, Structural Ensemble of an Intrinsically Disordered Polypeptide, J. Phys. Chem. B, 2013, 117(1), 118–124, DOI:10.1021/jp308984e.
- C. Miller, G. H. Zerze and J. Mittal, Molecular Simulations Indicate Marked Differences in the Structure of Amylin Mutants, Correlated with Known Aggregation Propensity, J. Phys. Chem. B, 2013, 117(50), 16066–16075, DOI:10.1021/jp409755y.
- O. Coskuner and O. Wise-Scira, Structures and Free Energy Landscapes of the A53T Mutant-Type α-Synuclein Protein and Impact of A53T Mutation on the Structures of the Wild-Type α-Synuclein Protein with Dynamics, ACS Chem. Neurosci., 2013, 4(7), 1101–1113, DOI:10.1021/cn400041j.
- M. Han, J. Xu and Y. Ren, Sampling Conformational Space of Intrinsically Disordered Proteins in Explicit Solvent: Comparison between Well-Tempered Ensemble Approach and Solute Tempering Method, J. Mol. Graphics Modell., 2017, 72, 136–147, DOI:10.1016/j.jmgm.2016.12.014.
- S. Seabold and J. Perktold, Statsmodels: Econometric and Statistical Modeling with Python, in Proceedings of the 9th Python in Science Conference, SciPy, 2010 Search PubMed.
- M. L. Waskom, Seaborn: Statistical Data Visualization, J. Open Source Softw, 2021, 6(60), 3021, DOI:10.21105/joss.03021.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt, A. Vijaykumar, A. P. Bardelli, A. Rothberg, A. Hilboll, A. Kloeckner, A. Scopatz, A. Lee, A. Rokem, C. N. Woods, C. Fulton, C. Masson, C. Häggström, C. Fitzgerald, D. A. Nicholson, D. R. Hagen, D. V. Pasechnik, E. Olivetti, E. Martin, E. Wieser, F. Silva, F. Lenders, F. Wilhelm, G. Young, G. A. Price, G.-L. Ingold, G. E. Allen, G. R. Lee, H. Audren, I. Probst, J. P. Dietrich, J. Silterra, J. T. Webber, J. Slavič, J. Nothman, J. Buchner, J. Kulick, J. L. Schönberger, J. V. de Miranda Cardoso, J. Reimer, J. Harrington, J. L. C. Rodríguez, J. Nunez-Iglesias, J. Kuczynski, K. Tritz, M. Thoma, M. Newville, M. Kümmerer, M. Bolingbroke, M. Tartre, M. Pak, N. J. Smith, N. Nowaczyk, N. Shebanov, O. Pavlyk, P. A. Brodtkorb, P. Lee, R. T. McGibbon, R. Feldbauer, S. Lewis, S. Tygier, S. Sievert, S. Vigna, S. Peterson, S. More, T. Pudlik, T. Oshima, T. J. Pingel, T. P. Robitaille, T. Spura, T. R. Jones, T. Cera, T. Leslie, T. Zito, T. Krauss, U. Upadhyay, Y. O. Halchenko and Y. Vázquez-Baeza, SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 2020, 17(3), 261–272, DOI:10.1038/s41592-019-0686-2.
- W. Kabsch and C. Sander, Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-Bonded and Geometrical Features, Biopolymers, 1983, 22(12), 2577–2637, DOI:10.1002/bip.360221211.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernández, C. R. Schwantes, L.-P. Wang, T. J. Lane and V. S. Pande, MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories, Biophys. J., 2015, 109(8), 1528–1532, DOI:10.1016/j.bpj.2015.08.015.
- D. P. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, 3rd International Conference on Learning Representations, ICLR 2015, Conference Track Proceedings, San Diego, CA, USA, May 7–9, 2015, DOI:10.48550/ARXIV.1412.6980.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mane, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viegas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems, In Proceedings of the 12th USENIX conference on Operating Systems Design and Implementation (OSDI'16), USENIX Association, USA, pp. 265–283, DOI:10.48550/ARXIV.1603.04467.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra04913a |
| This journal is © The Royal Society of Chemistry 2022 |