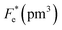DOI:
10.1039/D2RA04914G
(Paper)
RSC Adv., 2022,
12, 30771-30784
Enhanced electrocaloric effect, energy storage density and pyroelectric response from a domain-engineered lead-free BaTi0.91Sn0.08Zr0.01O3 ferroelectric ceramic
Received
6th August 2022
, Accepted 5th October 2022
First published on 27th October 2022
Abstract
A BaTi0.91Sn0.08Zr0.01O3 (BTSZ) ceramic was prepared by a conventional solid-state reaction method. Its structural, dielectric, ferroelectric, and pyroelectric properties were carefully studied. The Rietveld refinement was used to characterize the structural proprieties of the synthesized ceramic. The microstructure was observed by scanning electron microscopy. Phase transitions observed in the temperature dependent dielectric permittivity (εr–T and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T) showed a transition close to room temperature, resulting in improved piezoelectric, pyroelectric and electrocaloric performance. In addition, it was found that an electric field poling process changed the character of εr–T and tan
δ–T) showed a transition close to room temperature, resulting in improved piezoelectric, pyroelectric and electrocaloric performance. In addition, it was found that an electric field poling process changed the character of εr–T and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T plots. Resonance modes in the polarized state, where maximum power transmission was achieved, were observed in the impedance spectrum. The extra-slim hysteresis loops revealed a relatively low coercive field and hysteresis loss related to the diffuse phase transition, which can significantly improve energy storage efficiency up to 75% at 100 °C. To characterize the electrocaloric effect (ECE), indirect and direct methods based on the thermodynamic approach were used. Both methods results showed good consistency and revealed a large ECE peak evolving along the phase diagram. Furthermore, pyroelectric figures of merit (FOMs) for voltage responsivity (Fv), current responsivity (Fi), energy harvesting (FE), new energy harvesting
δ–T plots. Resonance modes in the polarized state, where maximum power transmission was achieved, were observed in the impedance spectrum. The extra-slim hysteresis loops revealed a relatively low coercive field and hysteresis loss related to the diffuse phase transition, which can significantly improve energy storage efficiency up to 75% at 100 °C. To characterize the electrocaloric effect (ECE), indirect and direct methods based on the thermodynamic approach were used. Both methods results showed good consistency and revealed a large ECE peak evolving along the phase diagram. Furthermore, pyroelectric figures of merit (FOMs) for voltage responsivity (Fv), current responsivity (Fi), energy harvesting (FE), new energy harvesting 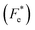 and detectivity (Fd) were calculated. Finally, thermal energy harvesting (ND) was determined by using the Olsen cycle. The obtained maximum ND was 233.7 kJ m−3 when the Olsen cycle operated at 25–100 °C and 0–30 kV cm−1. This study introduces not only a technique to produce a high performance ceramic for refrigeration devices, but also broadens the range of applications for BT-based lead-free ferroelectrics beyond actuators, sensors, and energy harvesting to solid-state cooling.
and detectivity (Fd) were calculated. Finally, thermal energy harvesting (ND) was determined by using the Olsen cycle. The obtained maximum ND was 233.7 kJ m−3 when the Olsen cycle operated at 25–100 °C and 0–30 kV cm−1. This study introduces not only a technique to produce a high performance ceramic for refrigeration devices, but also broadens the range of applications for BT-based lead-free ferroelectrics beyond actuators, sensors, and energy harvesting to solid-state cooling.
1. Introduction
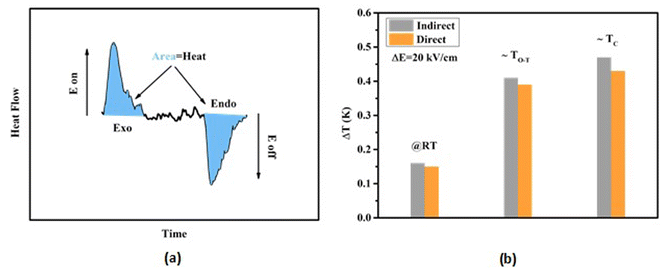
The world's power consumption is increasing with the increasing demand for air-conditioning and cooling machines. Furthermore, the majority of these devices use vapor-compression technology, which produces greenhouse gases such as freon. As a result, scientists and environmentalists are working hard to develop new eco-friendly refrigeration technology. The electrocaloric effect (ECE) is a novel alternative technology that involves the change of entropy (ΔS) and temperature (ΔT) in polar materials in the presence of an external electric field (E).1 After attaining a great ECE in P(VDF–TrFE) copolymer and Pb(Zr,Ti)O3 thin films, ECE has gained more and more popularity among scientists.1,2 Since then, ferroelectric materials have been the focus of much research, with the goal of making the solid-state refrigeration system a reality. Many studies on bulk materials, thin films, and polymer materials have been conducted.3–5 Scientists have noticed that the ECE of thin films and polymeric materials are great due to their high dielectric strength. By increasing the dielectric strength of the materials, the ECE can be improved. Scientists have established a new parameter, electrocaloric strength, which is denoted as ΔT/ΔE,6 to further research the EC performance of materials with varying thicknesses. Using this parameter in bulk materials has clear benefits. Thin films have a high ECE but a limited cooling capacity. Thus, they can not be employed in medium or large-scale refrigeration equipment. Because the bulk materials have a big volume and a high cooling capacity, they are suitable for use in medium and large-scale refrigeration equipment.7,8 As a result, studying the ECE of ceramic materials is extremely useful.
Ferroelectric ceramics are now widely used in many applications other than solid-state refrigeration, such as transducers, sensors, medical devices and microelectronics.9,10 A number of these applications are founded on their superior piezoelectric and pyroelectric properties, which allow them to be used for multiphysics applications.11 In this regard, lead-based materials have been extensively studied thanks to their robust properties, but are subject to major global restrictions because of the serious health and environmental problems associated with lead toxicity. For this reason, it is necessary to develop new eco-friendly ceramics such as BiFeO3 (BF), (Bi1/2Na1/2)TiO3 (BNT), (K,Na)NbO3 (KNN) and BaTiO3 (BT)-based ceramics.12,13
In this field, BT is one of the prospective contenders among lead-free ceramics. It shows three distinct phase transitions, i.e., the rhombohedral–orthorhombic phase transition (TR–O = −90 °C), the orthorhombic–tetragonal phase transition (TO–T = 0 °C) and the tetragonal–cubic phase transition (TC = 120 °C).14,15 However, it shows a low dielectric constant and poor energy storage properties that require strategies carried out by site engineering involving the substitution of Ba2+ sites by Sr2+, Ca2+, Bi3+… and/or Ti4+ sites by Hf4+, Zr4+, Sn4+…,16–18 to improve these characteristics. Therefore, the substitution of BT can significantly increase their energy storage density.19 Bi, Zn, and Sn doping were used by M. Zhou et al.20 to create a BT-based ceramic with an energy storage density of 2.21 J cm−3, while Gang Liu et al.21 used Ca and Sn to produce a ceramic with an energy storage density of 1.57 J cm−3. As a result, co-doping in one or both sites can cause the morphotropic phase boundary (MPB) to occur at room temperature (RT), resulting in improved piezoelectric, dielectric and electrocaloric characteristics.22,23 The most prominent discovery in BT-based systems over the past decade was the discovery of MPB24 and multi-phase co-existence that can significantly enhance properties of BT-based ceramics.25 Low energy barriers in the MPB region make the extension process and polarization rotation easier.23 To achieve a two- or multi-phase coexistence close to RT, electrical properties should be improved. Previous theoretical work26 has shown that the four-phase C–T–O–R point is a critical point where the energy barrier between different phases disappears. The results of their work could help future designs of high-performance ferroelectric materials, such as those with high-permittivity, high-piezoelectricity, high-electrostrain and large-electrocaloric. Also, the presence of MPB could enhance the electrocaloric effect due to the strong polarization variations in the system.27,28 In (Ba0.92Ca0.08)(Zr0.05Ti0.95)O3, Singh et al.29 observed a relatively high electrocaloric sensitivity of 0.25 K mm kV−1 near TC. Thus, it is necessary to understand the influence of doping on phase transition temperatures in order to create a multi-phase coexistence phase structure at RT. Sn4+ and/or Zr4+ have been shown to lower TC and increase TR–O and TO–T temperatures.30 When 0.09 mol of Sn4+ is introduced to a Ba(Ti1−xSnx)O3 (BTSx) ceramic,31 all phase transitions of BT change to 40 °C, whereas when 0.10 mol of Zr4+ is added to a Ba(Ti1−xZrx)O3 (BTZx) system,30 phase transitions shift, respectively, to 60 °C, 75 °C and 90 °C. TR–O and TO–T show a clearly faster drop in TC and a slower increase in BTSx than in BTZx. There are records in BTSx of a slower increase in TR–O and TO–T and a significantly faster decay in TC than in BTZx. To date, the mechanism by which Sn4+ and Zr4+ influences phase transition temperatures is unclear.
Therefore, the current study aims to investigate the Ba(Ti,Sn,Zr)O3-based system as a viable material for a variety of applications. BaTi0.91Sn0.08Zr0.01O3 (BTSZ) was chosen because (i) it is lead-free, and (ii) it allows to design phase transitions (both TR–O and TO–T) around RT, which could improve pyroelectric performance. All of the findings in this study could point to a new way to create pyroelectric devices with better performance and a potential replacement for lead-based ceramics.
2. Experimental procedure
In our research, a solid-state reaction was used to prepare a BTSZ polycrystalline sample. In this process, the appropriate molar ratios of BaCO3, SnO2, ZrO2, and TiO2 precursors were used to achieve stoichiometry. The mixture was immersed in ethanol and ground for 2 h in an agate mortar to create the initial powder. The resulting powder was calcined in two stages: at 900 °C for 24 h and then at 1200 °C for 12 h. The powder was thoroughly ground in the interim between the two phases, and for the second stage, it was compacted into a pellet with a 12 mm diameter. The resultant powder was then re-ground for 2 h and pressed into pellets with an 8 mm diameter. These pellets were sintered at 1400 °C for 2 h to produce dense ceramic. By using X-ray diffraction (XRD) analysis, which was recorded on a Philips diffractometer in the angle range 20° ≤ 2° ≤ 90°, the formation and quality of our ceramic were examined. The microstructures of the prepared ceramic was observed utilizing a scanning electron microscopy (SEM) TS QUATA 250 model.
For electrical characterizations, the prepared pellets were polished to 1 mm thickness. To make electrical connections, silver paste was blasted on opposite sides of pellets. BTSZ pellets were crushed and then annealed at 500 °C for 2 h. Temperature-dependent dielectric permittivity (εr) and loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of the ceramic specimens were recorded by HP4194A impedance analyzer under different frequencies with a heating/cooling rate of 2 °C min−1. After being submerged in silicon oil, the ceramic pellets were exposed to the field. On sintered pellets, the temperature-dependent P–E loop studies at a frequency of 1 Hz were performed using a Keithley 428 current amplifier and a TREK Model 20/20C high voltage amplifier operating. The piezoelectric coefficient d33 was displayed for poled pellet at RT with a d33-meter (YE2730A). After that, the electromechanical factors (kp) and (Qm) were calculated from the resonance and antiresonance frequencies measured with an impedance analyzer (HP4194A). When the sample was exposed to an applied E at isothermal conditions, the heat-flow was measured using a modified differential scanning calorimetry (MHTC96 Setaram, France).
δ) of the ceramic specimens were recorded by HP4194A impedance analyzer under different frequencies with a heating/cooling rate of 2 °C min−1. After being submerged in silicon oil, the ceramic pellets were exposed to the field. On sintered pellets, the temperature-dependent P–E loop studies at a frequency of 1 Hz were performed using a Keithley 428 current amplifier and a TREK Model 20/20C high voltage amplifier operating. The piezoelectric coefficient d33 was displayed for poled pellet at RT with a d33-meter (YE2730A). After that, the electromechanical factors (kp) and (Qm) were calculated from the resonance and antiresonance frequencies measured with an impedance analyzer (HP4194A). When the sample was exposed to an applied E at isothermal conditions, the heat-flow was measured using a modified differential scanning calorimetry (MHTC96 Setaram, France).
3. Results and discussions
3.1 Structural and microstructural properties
3.1.1 Phase structure. An XRD investigation was done at RT to evaluate the structural properties of our ceramic (Fig. 1). All of the reflections in the model corresponded to a BTSZ perovskite without any impurities, indicating that the perovskite structure was completely formed. Rietveld refinement showed the formation of BTSZ ceramic at MPB, with the coexistence of two-phases: the rhombohedral phase (R3m) and the orthorhombic phase (Amm2) providing a good agreement between the experimental and theoretical data. The lattice parameters obtained by the Rietveld refinement are illustrated in Fig. 1. Furthermore, generally, the temperature-dependent dielectric permittivity can be used to identify phase structures of BT-based materials,32–34 particularly the relationship between tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and temperature, which can be used to detect the R–O phase transition more easily, as mentioned by ref. 32.
δ and temperature, which can be used to detect the R–O phase transition more easily, as mentioned by ref. 32.
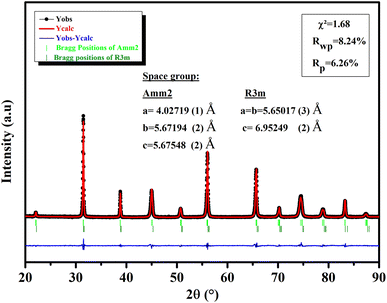 |
| | Fig. 1 XRD of BTSZ ceramic measured at RT fitted by Rietveld structural refinement. | |
3.1.2 Microstructure. The SEM images of the BTSZ ceramic as shown in Fig. 2 exhibited a good densification, with well interconnected grains and no notable voids or anomalies, as well as a bimodal grain size distribution (bigger grains coexist with smaller grains). The introduction of Zr into BTS resulted in the increase of the grain size from 0.6 μm for pure BTS31 to 18.56 μm for BTSZ.
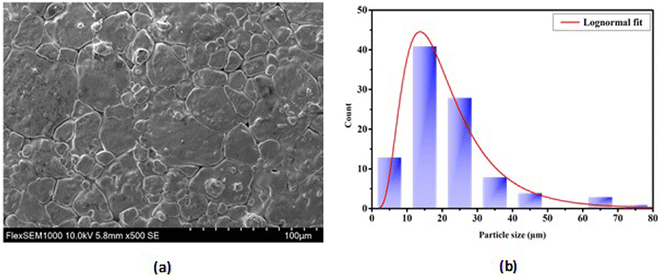 |
| | Fig. 2 (a) Micrographs of the BTSZ surface taken using a scanning electron microscope (SEM). (b) Distribution of grain size. | |
3.2 Dielectric properties
As shown in Fig. 3(a), the dielectric spectra upon heating and cooling processes of unpoled BTSZ ceramic exhibited an obvious dielectric thermal hysteresis with a ΔTm of 19 °C. The transition's continuous behavior is confirmed by the narrow thermal hysteresis loop. At 1 kHz, the maximal dielectric constant equal to 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 386.53 during the cooling run was higher than our previously reported result on BTS.31 The εr–T variation showed three dielectric anomalies: the first anomaly was small bump near RT, but was much more pronounced and appeared as a clear broad peak in the tan
386.53 during the cooling run was higher than our previously reported result on BTS.31 The εr–T variation showed three dielectric anomalies: the first anomaly was small bump near RT, but was much more pronounced and appeared as a clear broad peak in the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T curve (inset Fig. 4), which is related to TR–O phase transition. The second anomaly at ∼50 °C is related to TO–T phase transition and the third anomaly at ∼75 °C related to TC. In addition, TC decreased with frequency increase but remained unchanged for all frequencies. This anomalous behavior of the εr–T–f is known as the phenomenon of non-relaxation with nano polar regions (NRPs).
δ–T curve (inset Fig. 4), which is related to TR–O phase transition. The second anomaly at ∼50 °C is related to TO–T phase transition and the third anomaly at ∼75 °C related to TC. In addition, TC decreased with frequency increase but remained unchanged for all frequencies. This anomalous behavior of the εr–T–f is known as the phenomenon of non-relaxation with nano polar regions (NRPs).
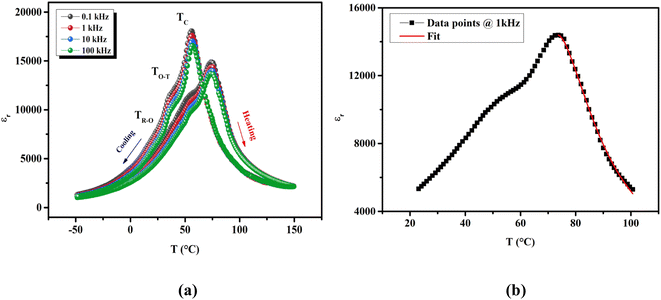 |
| | Fig. 3 (a) The thermal hysteresis of the εr during the cooling and heating runs at different frequency. (b) The measured εr and adjusted data as a function of temperature at 1 kHz of BTSZ ceramic. | |
 |
| | Fig. 4 (a) Dielectric constant versus temperature and the inset show tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ variation as a function of temperature for unpoled and poled sample. (b) Frequency-dependent impedance variations for unpoled and poled BTSZ sample. δ variation as a function of temperature for unpoled and poled sample. (b) Frequency-dependent impedance variations for unpoled and poled BTSZ sample. | |
To better understand the nature of phase transition and to deduce its diffusive character, we have adjusted the εr–T variation by the Santos–Eiras law:35
| |
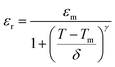 | (1) |
where
γ the empirical coefficient that describes the diffuse character of the transition (=1 for normal' ferroelectric and =2 for relaxor) and
δ defines the degree of diffusivity of the transition. As shown in
Fig. 3(b), fitting this law to 1 kHz, shows that
γ gave a value of 1.72, suggesting an incomplete diffuse phase transition (DPT) character with
δ = 18.02 °C. The size of the ceramic's grain and its chemical heterogeneity are used to explain this phenomena.
36–38 BTSZ ceramics' incomplete DPT promotes material stability and applicability across a wide temperature range. In a more interesting way, the apparent increase in
εr during cooling around
TC can be attributed to the formation of NRPs.
35
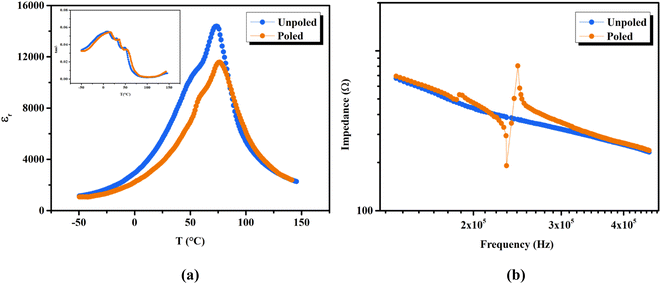
The phase transition temperatures of unpoled and poled BTSZ ceramic were studied by measuring temperature-dependent εr, and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at a fixed frequency (1 kHz) in the temperature range −50 to 150 °C as shown in Fig. 4(a). After poling, TC shifted towards higher temperature along with slight broadening, which can see the same character in the tan
δ at a fixed frequency (1 kHz) in the temperature range −50 to 150 °C as shown in Fig. 4(a). After poling, TC shifted towards higher temperature along with slight broadening, which can see the same character in the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T shown in the inset of Fig. 4(a). Additionally, εr also showed a significant decrease in value after poling. According to general principles, when E is applied to ferroelectric domains, the sample becomes less sensitive to smaller ac fields as polarization coherence rises along the field direction, and as a result, εr falls.39,40
δ–T shown in the inset of Fig. 4(a). Additionally, εr also showed a significant decrease in value after poling. According to general principles, when E is applied to ferroelectric domains, the sample becomes less sensitive to smaller ac fields as polarization coherence rises along the field direction, and as a result, εr falls.39,40
The use of piezoceramics in piezomechanical systems ensures that energy is transferred efficiently. When the device is implemented at piezomechanical resonant frequencies, the highest energy transfer is expected.41 Consequently, it is necessary to excite the system and extract these frequencies. The examination of the sample's piezoelectric impedance as a function of frequency response is one of the most effective ways to determine its resonant properties. The piezoelectric impedance spectrum vs. frequency for unpoled and poled BTSZ ceramic is presented in Fig. 4(b). Resonance around 230 kHz can be found in the poled sample, which is the result of the piezoceramics' natural vibration frequency with the applied ac frequency.41,42 Indeed, the piezoelectric devices transform electrical energy into mechanical energy when they are in resonance. The piezoelectric (d33) and piezomechanical parameters: planar electromechanical coupling coefficient (kp)43 and mechanical quality factor (Qm) are calculated from the impedance spectrum by the following equations:
| |
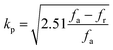 | (2) |
| |
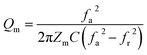 | (3) |
where
C,
Zm,
fr and
fa are, respectively, the capacitance, the minimum impedance, the resonance and anti-resonance frequencies. The measured
d33 is 310 pC N
−1 and the calculated
kp is 0.36 and
Qm is 44. To achieve better piezoelectric characteristics, density, homogeneity of grain size and average grain size may be crucial factors.
44 The relation between the domain size and the grain size can be given as follows:
45,46| | |
(Domain size) ∝ (grain size)q
| (4) |
where
q is a constant. According to
eqn (4), a small domain size correlated with a fine grain size. In effect, the domain boundary occupies a large percentage of the grain, thus preventing domain reversal.
47 In this way, piezoelectric and polarization switching are reduced due to extrinsic effects. Large-grained ceramics, on the other hand, offer better piezoelectric characteristics
48 because the domain walls may move about more easily.
3.3 Ferroelectric properties
3.3.1 Effect of electric field on the polarization. The ferroelectric nature of our ceramic was investigated. Fig. 5(a) depicts, at RT, the hysteresis loops (P–E) of the BTSZ ceramic under different E applied. An increase in E lead to an increase in the maximum and remnant polarization (Pmax, Pr) because a higher E gives a higher amount of driving force for ferroelectric domain switching. The domain volume and, as a result, total polarization, including hysteresis parameters, increase with the increase of the driving force.49 At E = 30 kV cm−1, the Pmax = 18.35 C cm−2 and Pr = 7.93 C cm−2 were noted, with a lower coercive field of Ec = 2.65 kV cm−1. Ec's low value indicates a low energy loss during E passage and a low energy barrier for polarization rotation, both of which boost piezoelectric characteristics.50
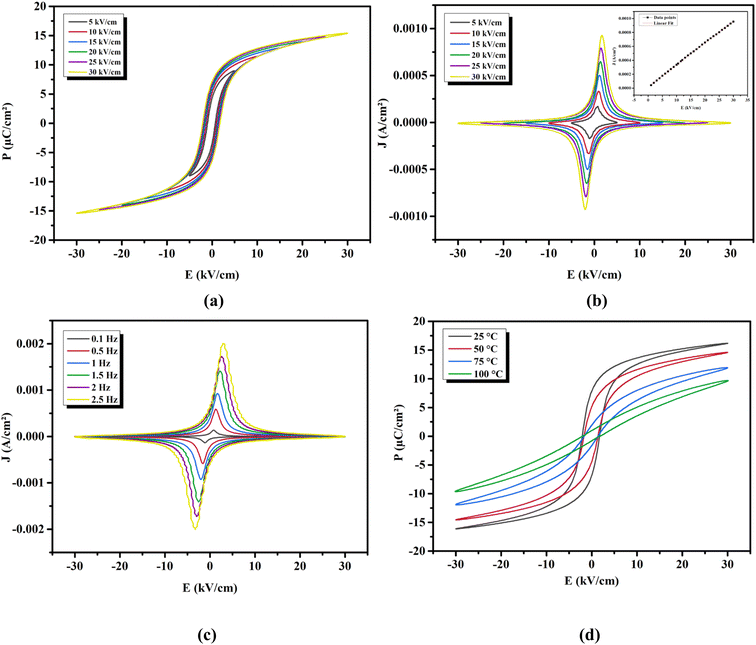 |
| | Fig. 5 (a) P–E hysteresis and (b) J–E loops at different applied electric field at RT and 1 Hz of BTSZ ceramic. (c) J–E loops at different frequency at RT and 30 kV cm−1. (d) The temperature-dependent P–E hysteresis loops. | |
Fig. 5(b) depicts the polarization current density (J–E) under various applied E at 1 Hz. The current density peak was observed for both positive and negative cycles of the applied E, which is a characteristic of good ferroelectric ceramic with saturation polarization.51 As a result, we obtained high-quality BTSZ ceramic with saturated polarization. The field dependence of the current density (inset Fig. 5(b)) can be represented by the power law function J ∝ Em. The slope (m) of this plot was close to 1, which indicates that the BTSZ ceramic exhibited an ohmic conduction behavior between the measurement conditions.
3.3.2 Effect of frequency on the polarization. Fig. 5(c) illustrates the effect of another key factor, the hysteresis frequency, on the J–E loops. The peak polarization current value rose with the increase of the hysteresis frequency from 0.1 to 2.5 Hz. It should also be noted that when the frequency in the measured range increases, the corresponding amount of E for a certain peak value of polarization current, an indication of Ec, increased. According to Chong et al.,52 the higher polarization current at higher frequencies, may be ascribed to the larger rate of change of E and the related switching rate, as illustrated below.The production of new domain nuclei is thought to cause domain switching when E is applied. In the direction of E, the rate of change of polarization (jE) will have the following definition:52
| |
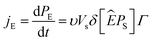 | (5) |
where d
PE,
PS,
υ,
Γ and
δ are, respectively, the associated change in polarization along the applied
E direction, the spontaneous polarization, the number of nucleation sites per unit volume, the rate of formation of nuclei and the angle between
PS and
Ê before and after the switching.
Fig. 5(c) shows that, based on
eqn (5), increasing
Γ at high frequencies yields an increase in polarization current. The occurrence of a cyclic and uniform
Pr in both directions, a common characteristic of ferroelectric materials, is indicated by the peak value of current recorded in both positive and negative cycles.
3.3.3 Effect of temperature on the polarization. Fig. 5(d) shows the P–E loops measured at various temperatures under an applied E = 30 kV cm−1 at 1 Hz. The ferroelectric nature of BTSZ ceramic is described by significantly saturated hysteresis loops below TC. The P–E loops grew increasingly slanted and narrow as they heated up, which is better for energy storage applications.53 On the other hand, due to DPT behavior, the P–E loops did not disappear at TC, which is consistent with dielectric data. The polarization behaved linearly above TC, suggesting the appearance of the paraelectric phase.
3.4 Energy storage performances
Due to their consistent and unchanging limited charge response to dynamic thermal oscillations, ferroelectric materials make a significant contribution to waste thermal energy harvesting. This effect is obtainable in ferroelectric materials as a result of the strong dependence of polarization on temperature because of the maintenance of polarization/charge and depolarization/discharge phenomena upon exposure to a thermal wave. Fundamentally, several physical factors of the specimen, including doping, nature of polar, crystal structure, developed domains and ordering and range of involved dipolar interaction affect the degree of polarization. The total energy density (Wtot), the recoverable energy density (Wrec) and the efficiency of energy storage (η) of the ferroelectric material are estimated from the following equations:31,54| |
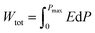 | (6) |
| |
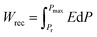 | (7) |
| |
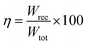 | (8) |
Fig. 6 shows the thermal evolution of Wrec, and η found to be 65.16 mJ cm−3 and 57.26% at RT, respectively. The values of Wrec and η showed an increasing trend with increasing temperature. The observed increase in Wrec may be due to the enhancement of domain wall mobility with increasing temperature.55 On another hand, with the increase of temperature, η increases slightly and Wrec increase significantly, which indicated that suggests a poor thermal stability for energy storage properties. Our studied is comparable to the works of Wei Cai et al.56 Table 1 lists some lead-free ceramic materials' reported literature energy storage capabilities.31,57–61 Thus, these results suggest that BTSZ ceramic is a potential candidate for capacitor operations such as filtering, voltage smoothing, coupling, decoupling, DC blocking and power conditioning etc.62 In a ferroelectric system, maximizing the difference between Pmax and Pr and increasing the material's capacity to withstand the strongest electric field without breaking down are two ways to improve energy storage density.
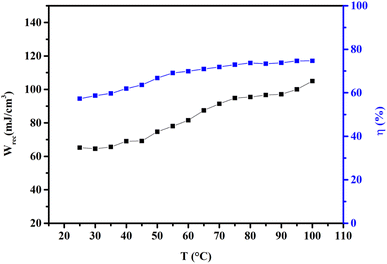 |
| | Fig. 6 Temperature dependence of Wrec, and η for the BTSZ ceramic. | |
Table 1 Comparison of the energy storage properties of BTSZ ceramic with other lead-free ceramics reported in literature
| Ceramic |
T (°C) |
E (kV cm−1) |
Wrec (mJ cm−3) |
η (%) |
Ref. |
| BTSZ |
25 |
30 |
65.16 |
57.26 |
This work |
| BTSZ |
100 |
30 |
105 |
75 |
This work |
| BT |
— |
110 |
450 |
28.23 |
57 |
| BaTi0.89Sn0.11O3 |
30 |
25 |
72.4 |
85.07 |
58 |
| BaTi0.895Sn0.105O3 |
— |
10 |
31 |
— |
59 |
| BaTi0.91Sn0.09O3 |
110 |
30 |
48.18 |
41 |
31 |
| BaTi0.96Zr0.4O3 |
25 |
60 |
240 |
62.3 |
60 |
| BaTi0.9Ce0.1O3 |
— |
24 |
77 |
39 |
61 |
3.5 Electrocaloric properties
3.5.1 Indirect electrocaloric measurements. Due to its reported diffused dielectric behavior and notable shifting of phase transition temperatures close to RT, the BTSZ ceramic's electrocaloric activity was investigated. The results of P–E–T (see Fig. 7) are used to evaluate ECE's indirect experimental method. The 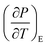 data were interpolated from 5th order polynomial fits of P–T values. Maxwell's relation was used to calculate the adiabatic change in temperature (ΔT) and the corresponding entropy change (ΔS) of the prepared ceramic, which are given in ref. 16 and 63:
data were interpolated from 5th order polynomial fits of P–T values. Maxwell's relation was used to calculate the adiabatic change in temperature (ΔT) and the corresponding entropy change (ΔS) of the prepared ceramic, which are given in ref. 16 and 63:| |
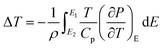 | (9) |
| |
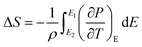 | (10) |
where ρ and Cp are, respectively, the density of our prepared ceramic (5.3 g cm−3) and the specific heat of the sample.64 Fig. 8(a and b) illustrates the thermal evolution of ΔT and ΔS, for the BTSZ ceramic, at various electric fields. Both ΔT and ΔS showed two large peaks corresponding, respectively, to the O–T and T–C phase transitions, which deviated to high temperatures in comparison to the dielectric data. These deviations can be related to the different thermometers employed in each approach. Chunlin Zhao et al. and Ming-Ding Li et al. reported the same behavior, respectively, in x(Ba0.7–Ca0.3)TiO3(1 − x) Ba(Sn0.11Ti0.89)O3 (with x = 0, 0.1, 0.2, and 0.3) and Ba(HfxTi1−x)O3 (with x = 0.03, 0.05, 0.08 and 0.11).65,66 At 30 kV cm−1, the prepared ceramic has a high EC response and ΔT and ΔS reached a maximum of 0.74 K and 0.83 J kg−1 K−1 around TC, respectively. The thermal evolution of electrocaloric responsivity ξ = ΔT/ΔE at 30 kV cm−1 is depicted in Fig. 8(c). The evolution of ξ was similar to that of ΔT and ΔS, and reached a maximum of 0.246 K mm kV−1. The obtained results (ΔT, ΔS and ξ) under 30 kV cm−1 are compared with other BT-based ceramics B-site substituted which are presented in Table 2.3,16,59,66–72 The BTSZ ceramic exhibited an exceptional EC response due to the appearance the coexistence of multiple phases in this composition. The contribution of F–F transitions (TR–O or TO–T) actually led to an important ferroelectric intrinsic polarization, which can improve the ΔS due to the disordered/ordered polar dipoles. As a result, a single F–P transition might be used to generate a high T in comparison to other doped BT.65,73,74 As a result, including multiphase coexistence into EC material systems can improve their EC properties.64,75,76 EC results are also influenced by a number of parameters, including synthesis conditions, the applied electric field and grain size.
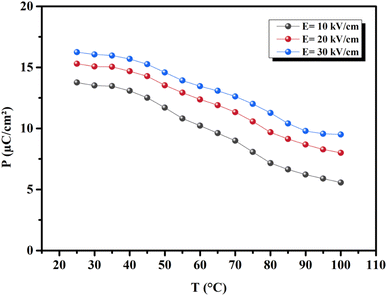 |
| | Fig. 7 Temperature-dependent polarization evolution (extracted from the maximum polarization in each P–E loop). | |
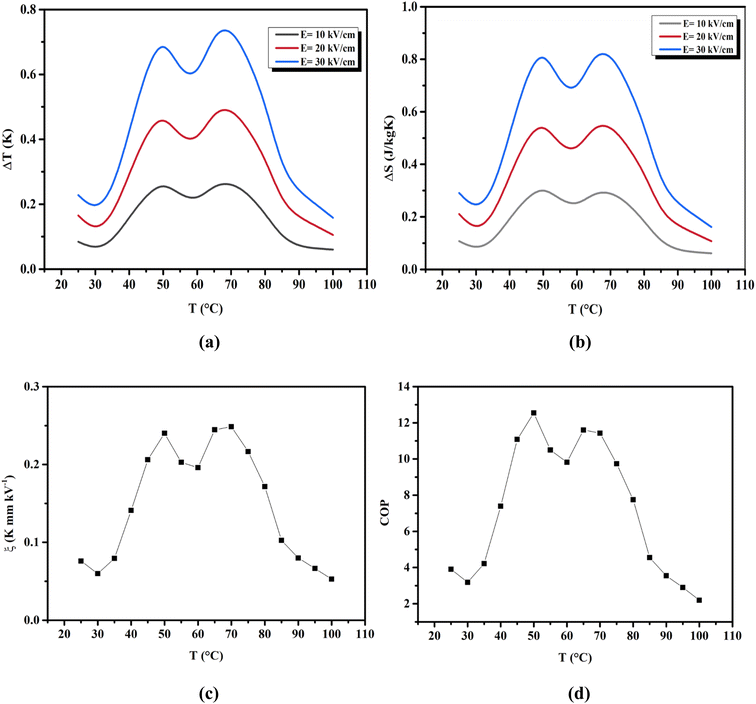 |
| | Fig. 8 Temperature dependence of (a) ΔT, (b) ΔS and (c) ξ for the BTSZ ceramic at different applied electric fields. (d) Temperature dependence of the COP. | |
Table 2 Comparison of ΔT and the maximum electrocaloric strength for BTSZ ceramic with other ceramics
| Ceramic |
T (°C) |
ΔT (K) |
ΔE (kV cm−1) |
ξ (K mm kV−1) |
Ref. |
| BTSZ |
TO–T |
0.68 |
30 |
0.226 |
This work |
| BTSZ |
TC |
0.74 |
30 |
0.246 |
This work |
| BT |
130 |
0.78 |
55 |
0.142 |
3 |
| BaTi0.82Sn0.18O3 |
0 |
0.187 |
10 |
0.187 |
67 |
| BaTi0.89Sn0.11O3 |
52 |
0.71 |
25 |
0.284 |
59 |
| BaTi0.9Sn0.1O3 |
70 |
0.4 |
20 |
0.2 |
67 |
| BaTi0.91Sn0.09O3 |
54.33 |
0.47 |
30 |
0.158 |
15 |
| BaTi0.8Zr0.2O3 |
39 |
4.5 |
145 |
0.31 |
68 |
| BaTi0.85Zr0.15O3 |
69 |
4.2 |
150 |
0.28 |
68 |
| BaTi0.9Zr0.1O3 |
90 |
0.2 |
8.7 |
0.23 |
69 |
| BaTi0.823Sn0.075Zr0.029O3 |
30 |
0.19 |
8.7 |
0.22 |
69 |
| BaTi0.944Y0.056O2.972 |
75 |
0.4 |
45 |
0.089 |
70 |
| BaTi0.97Hf0.03O3 |
42 |
0.33 |
30 |
0.11 |
66 |
| BaTi0.97Hf0.03O3 |
108 |
0.83 |
30 |
0.27 |
66 |
| BaTi0.9Ce0.1O3 |
105 |
0.41 |
45 |
0.09 |
71 |
| BaTi0.875(Nb0.5Y0.5)0.125O3 |
9 |
0.053 |
5 |
0.106 |
71 |
The efficiency of the ECE of the BTSZ ceramic was investigated for industrial applications using the coefficient of performance COP, as stated by eqn (11):77
| |
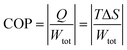 | (11) |
where
Q represents the isothermal heat.
Fig. 8(d) displays the evolution of the estimated COP at 30 kV cm
−1, which increased with temperature, reaching a maximum of 11.5, before decreasing below
TC. The COP value of the prepared ceramic was higher than that of 0.97K
0.5Na
0.5NbO
3–0.03LaNbO
3 ceramic (COP = 4.16) under 50 kV cm
−1,
77 and in Ba
0.85Ca
0.15Zr
0.10Ti
0.90O
3 ceramic upon 55 kV cm
−1 (COP = 6.29 at 365 K).
78 The ECE of the BTSZ ceramic was equivalent to practically all bulk materials already examined. This suggests that our research provides excellent EC materials with important EC values and coefficients.
3.6 Pyroelectric properties
The capacity of ferroelectric materials to convert pyroelectric energy is well recognized.81 This characteristic feature renders them popular for a wide range of applications like infrared detectors, sensors, energy harvesting and thermal imaging applications.82,83 These processes exhibit a high pyroelectric coefficient as well as specific heat capacity, low εr, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and conductivity. Fig. 10(a) shows the pyroelectric coefficient (p) of BTSZ as a function of temperature. Representative parameters such as Pr are taken from the P–E hysteresis loops produced upon heating to determine p using a static method:
δ and conductivity. Fig. 10(a) shows the pyroelectric coefficient (p) of BTSZ as a function of temperature. Representative parameters such as Pr are taken from the P–E hysteresis loops produced upon heating to determine p using a static method:| |
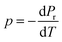 | (14) |
where p and T are, respectively, the pyroelectric coefficient and the temperature. Fig. 10(a) displays two peaks for the BTSZ ceramic, which are related to TO–T and TC, respectively. Various material criteria should be addressed when characterizing a certain pyroelectric property due to the diverse needs in real-world applications. In order to evaluate the reactivity of pyroelectric sensing performance between different materials, five important types of figure of merit (FOM) have been established from p, which are listed below :84–86| |
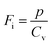 | (15) |
| |
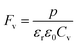 | (16) |
| |
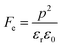 | (17) |
| |
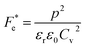 | (18) |
| |
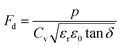 | (19) |
where Cv, Fi, Fv, Fe, 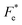 and Fd are, respectively, the specific heat capacity which is borrowed from the literature,87 the potential current responsivity performance, the voltage responsivity, pyroelectric energy harvesting figure of merit, the modified figure of merit and the detection capability. The development of improved pyroelectric sensitivity, more effective cost, fabrication feasibility and a higher TC are critical parameters to be taken into account. Fig. 10(b) shows the variation of FOMs with temperature, which have a similar trend to the pyroelectric coefficient. The BTSZ ceramic exhibited the highest FOMs of Fi = 803 pm V−1, Fv = 9.7 m2 C−1, Fe = 39.5 J m−3 K−2,
and Fd are, respectively, the specific heat capacity which is borrowed from the literature,87 the potential current responsivity performance, the voltage responsivity, pyroelectric energy harvesting figure of merit, the modified figure of merit and the detection capability. The development of improved pyroelectric sensitivity, more effective cost, fabrication feasibility and a higher TC are critical parameters to be taken into account. Fig. 10(b) shows the variation of FOMs with temperature, which have a similar trend to the pyroelectric coefficient. The BTSZ ceramic exhibited the highest FOMs of Fi = 803 pm V−1, Fv = 9.7 m2 C−1, Fe = 39.5 J m−3 K−2, 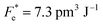 and Fd = 19.6 Pa0.5 around TC. Table 3 shows a few chosen materials with their pyroelectric properties in order to compare the performance of the BTSZ ceramic with that of other well-known polymers, lead-based and lead-free pyroelectric materials.61,82,83,87–91 According to these findings, the BTSZ ceramic could be a viable replacement for lead-based pyroelectric materials in pyroelectric applications.
and Fd = 19.6 Pa0.5 around TC. Table 3 shows a few chosen materials with their pyroelectric properties in order to compare the performance of the BTSZ ceramic with that of other well-known polymers, lead-based and lead-free pyroelectric materials.61,82,83,87–91 According to these findings, the BTSZ ceramic could be a viable replacement for lead-based pyroelectric materials in pyroelectric applications.
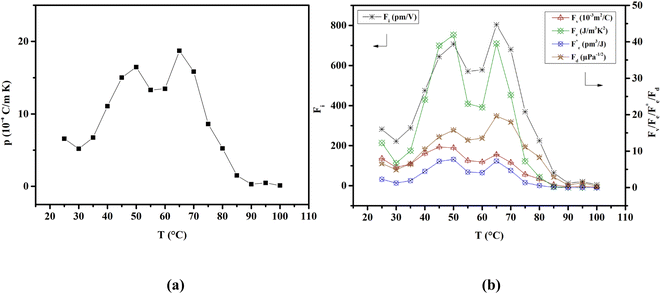 |
| | Fig. 10 Temperature-dependent of (a) pyroelectric coefficient and (b) FOMs for the BTSZ ceramic. | |
Table 3 Comparison of some important pyroelectric materials FOMs of lead-based and lead-free ceramics at room temperature
| Ceramic |
Fi (pm V−1) |
Fv (m2 C−1) |
Fd (Pa0.5) |
Fe (J m−3 K−2) |
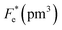
|
Ref. |
| BTSZ |
282.2 |
7.9 |
6.6 |
12.2 |
2.3 |
This work |
| BaTiO3 |
80 |
8 |
— |
4.2 |
0.6 |
87 |
| BaTi0.95Sn0.05O3 |
320 |
6.3 |
|
17.1 |
2 |
88 |
| BaTi0.9Sn0.1O3 |
149 |
1.5 |
|
2.3 |
0.2 |
88 |
| BaTi0.9Ce0.1O3 |
171 |
9 |
3.85 |
6.8 |
1.5 |
61 |
| BaTi0.85Ce0.15O3 |
23 |
13 |
|
0.1 |
0.02 |
61 |
| Ba0.85Sr0.15Ti0.9Zr0.1O3 |
125 |
5 |
4.01 |
|
|
89 |
| [Bi0.5(Na0.94K0.05Li0.016)0.5]0.95Ba0.05TiO3 |
127 |
17 |
— |
19 |
2.1 |
82 |
| [Bi0.5(Na0.95K0.05)0.5]0.95Ba0.05TiO3 |
112 |
21 |
— |
— |
— |
82 |
| LiTaO3 |
55 |
132 |
— |
— |
— |
83 |
| Ca0.15Sr0.5Ba0.5Nb2O6 |
172 |
20 |
11.5 |
17 |
3.4 |
90 |
| PZT |
142 |
8 |
— |
9 |
9.7 |
82 |
| PVDF |
100 |
147 |
— |
10 |
1.7 |
91 |
| P(VDF–TrFE)50/50 |
17 |
109 |
— |
12 |
1.9 |
91 |
3.7 Pyroelectric energy harvesting properties
In pyroelectric materials, a significant temperature fluctuation with a small tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and εr is a critical condition for a successful of conversion of waste heat into electric energy. Furthermore, when compared to the conventional pyroelectric effect, the Olsen cycle can enhance energy harvesting capacity by three orders of magnitude or more. In this way, numerous pyroelectric energy harvesting systems based on the Olsen cycle have been created over the past three decades.92 Therefore, the Olsen cycle is employed in this study to calculate the pyroelectric energy harvesting potential of the produced sample. For further explanation, the following ref. 31 can be consulted. Thus, the following equation can be used to define the energy harvesting density (ND)
δ and εr is a critical condition for a successful of conversion of waste heat into electric energy. Furthermore, when compared to the conventional pyroelectric effect, the Olsen cycle can enhance energy harvesting capacity by three orders of magnitude or more. In this way, numerous pyroelectric energy harvesting systems based on the Olsen cycle have been created over the past three decades.92 Therefore, the Olsen cycle is employed in this study to calculate the pyroelectric energy harvesting potential of the produced sample. For further explanation, the following ref. 31 can be consulted. Thus, the following equation can be used to define the energy harvesting density (ND)
Fig. 11 shows the variation of ND as a function of ΔT (TH − TL) and ΔE (EH − EL). For the present work, TL and EL are taken to be 25 °C and 0 kV cm−1, respectively. The value of ND is shown to improve with temperature and electric field increase. The maximum ND (233.7 kJ m−3) was obtained when the Olsen cycle was operated at 25–100 °C and 0–30 kV cm−1. The potential energy harvesting based on the Olsen cycle in various BT-based ceramics is presented in Table 4.31,71,93–95 It can be seen that ND of the prepared BTSZ ceramic is comparable to those of other BT-based bulk ceramics. The normalized energy harvest per unit of temperature change 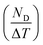 as well as the normalized energy harvest per unit of electric field change
as well as the normalized energy harvest per unit of electric field change 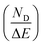 were calculated to evaluate the significance of our ceramic in the field of energy recovery. According to these results, our ceramic ranks among the most effective non-toxic materials for energy harvesting applications.
were calculated to evaluate the significance of our ceramic in the field of energy recovery. According to these results, our ceramic ranks among the most effective non-toxic materials for energy harvesting applications.
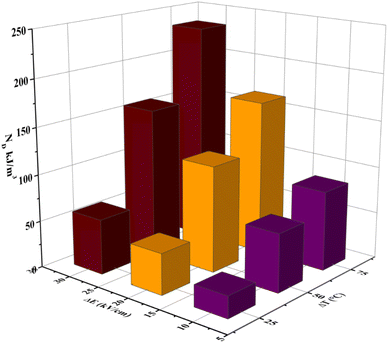 |
| | Fig. 11 ΔT (TL = 25 °C) and EH-dependent (EL = 0 kV cm−1) pyroelectric energy harvesting density per cycle for the BTSZ ceramic. | |
Table 4 Comparison of the energy conversion performance and corresponding conditions of different ferroelectric materials
| Ceramic |
ND (kJ m−3) |
TL (°C) |
TH (°C) |
ND/ΔT (kJ m−3 K−1) |
EL (kV cm−1) |
EH (kV cm−1) |
(ND/ΔE) × 10−2 (J m−2 V−1) |
Ref. |
| BTSZ |
233.7 |
25 |
100 |
3.12 |
0 |
30 |
7.79 |
This work |
| BaTiO3 |
12 |
20 |
80 |
0.2 |
10 |
20 |
1.2 |
93 |
| BaTi0.91S0.09O3 |
210 |
20 |
120 |
2.1 |
0 |
30 |
7 |
31 |
| BaTi0.95Zr0.05O3 |
425 |
30 |
125 |
4.47 |
3.25 |
7.42 |
1.01 |
94 |
| BaTi0.8 Zr0.2O3 |
63 |
20 |
80 |
1.05 |
20 |
30 |
6.3 |
93 |
| BaTi0.95Hf0.05O3 |
491.3 |
20 |
140 |
4.10 |
0 |
50 |
98.3 |
95 |
| BaTi0.9Ce0.1O3 |
140 |
100 |
170 |
2 |
0 |
45 |
3.5 |
71 |
4. Conclusion
BaTi0.91Sn0.08Zr0.01O3 (BTSZ) ceramic was synthesized using the conventional solid-state reaction method. Good dielectric, piezoelectric, pyroelectric and ferroelectric characteristics were obtained in the BTSZ ceramic. The evolution of the phase structure was revealed by XRD and was confirmed by dielectric spectroscopy. The SEM images demonstrated a dense microstructure. The dielectric spectrum showed a slight rise in TC and a significant fall in εr after poling, which might be attributed to field-induced orientational dipoles aligning in a direction other than the applied field. The measured resonance modes in the impedance spectrum, where the greatest possible piezomechanical energy transfer is possible, support the effective dipole alignment by poling. In addition, we have studied the evolution of energy storage performance as function of temperature. It was found that our synthesized ceramic achieved a maximum efficacy of 75% at 100 °C. The ECE of the BTSZ ceramic was studied by two different methods. Results showed good agreement between both methods and that the BTSZ ceramic has higher ECE (0.74 K) with larger electrocaloric strength (0.246 × 10−6 K m V−1). Further, the temperature dependence of figure of merits (FOMs) for current responsivity (Fi), voltage responsivity (Fv), energy harvesting (Fe and 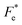 ) and detectivity (Fd) were calculated. The findings suggest that the produced ceramic could be an excellent technological candidate for pyroelectric devices. Moreover, the Olsen cycle was used to determine thermal energy harvesting (ND), which is equal to 233.7 kJ m−3 when operated at 25–100 °C and 0–30 kV cm−1. According to these results, high ECE material can be synthesized with important pyroelectric and energy storage properties in Sn and Zr substituted BT ceramic.
) and detectivity (Fd) were calculated. The findings suggest that the produced ceramic could be an excellent technological candidate for pyroelectric devices. Moreover, the Olsen cycle was used to determine thermal energy harvesting (ND), which is equal to 233.7 kJ m−3 when operated at 25–100 °C and 0–30 kV cm−1. According to these results, high ECE material can be synthesized with important pyroelectric and energy storage properties in Sn and Zr substituted BT ceramic.
Conflicts of interest
All authors have declared no conflicts of interest.
Acknowledgements
The authors express their gratitude to Princess Nourah Bint Abdulrahman University Researchers Supporting Project (Grant No. PNURSP2022R46), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.
References
- A. S. Mischenko, Q. Zhang, J. F. Scott, R. W. Whatmore and N. D. Mathur, Science, 2006, 311(5765), 1270–1271, DOI:10.1126/science.1123811.
- B. Neese, B. Chu, S. G. Lu, Y. Wang, E. Furman and Q. M. Zhang, Science, 2008, 321(5890), 821–823, DOI:10.1126/science.1159655.
- M. D. Li, X. G. Tang, S. M. Zeng, Q. X. Liu, Y. P. Jiang and W. H. Li, J. Alloys Compd., 2018, 747, 1053–1061, DOI:10.1016/j.jallcom.2018.03.102.
- X. Moya, S. Kar-Narayan and N. D. Mathur, Caloric materials near ferroic phase transitions, Nat. Mater., 2014, 13(5), 439–450, DOI:10.1038/nmat3951.
- S. G. Lu and Q. Zhang, Adv. Mater., 2009, 21(19), 1983–1987, DOI:10.1002/adma.200802902.
- X. Moya, E. Stern-Taulats, S. Crossley, D. González-Alonso, S. Kar-Narayan, A. Planes and N. D. Mathur, Adv. Mater., 2013, 25(9), 1360–1365, DOI:10.1002/adma.201203823.
- S. Patel, A. Chauhan and R. Vaish, Int. J. Appl. Ceram. Technol., 2015, 12(4), 899–907, DOI:10.1111/ijac.12418.
- S. Patel, A. Chauhan and R. Vaish, Energy Technol., 2015, 3(1), 70–76, DOI:10.1002/ente.201402118.
- Y. Zhang, E. Wang, H. Li, Y. Cai and J. Zhang, J. Mater. Sci.: Mater. Electron., 2015, 26(1), 37–41, DOI:10.1007/s10854-014-2359-3.
- H. Khanbareh, S. van Der Zwaag and W. A. Groen, Smart Mater. Struct., 2014, 23(10), 105030, DOI:10.1088/0964-1726/23/10/105030.
- S. Yao, W. Ren, H. Ji, X. Wu, P. Shi, D. Xue and Z. G. Ye, J. Phys. D: Appl. Phys., 2012, 45(19), 195301, DOI:10.1088/0022-3727/45/19/195301.
- C. H. Hong, H. P. Kim, B. Y. Choi, H. S. Han, J. S. Son, C. W. Ahn and W. Jo, J. Materiomics, 2016, 2(1), 1–24, DOI:10.1016/j.jmat.2015.12.002.
- Y. Saito, H. Takao, T. Tani, T. Nonoyama, K. Takatori, T. Homma and M. Nakamura, Nature, 2004, 432(7013), 84–87, DOI:10.1038/nature03028.
- D. Fu and M. Itoh, Ferroelectric materials—synthesis and characterization, 2015 Search PubMed.
- H. Kacem, Z. Sassi, M. A. Gdaiem, A. Dhahri, L. Seveyrat, L. Lebrun and J. Dhahri, Inorg. Chem. Commun., 2022, 144, 109771, DOI:10.1016/j.inoche.2022.109771.
- H. Kacem, A. Dhahri, M. A. Gdaiem, Z. Sassi, L. Seveyrat, L. Lebrun and J. Dhahri, Appl. Phys. A: Mater. Sci. Process., 2021, 127(6), 1–10, DOI:10.1007/s00339-021-04604-8.
- G. Liu, Y. Li, M. Shi, L. Yu, P. Chen, K. Yu and J. Gao, Ceram. Int., 2019, 45(15), 19189–19196, DOI:10.1016/j.ceramint.2019.06.166.
- Y. H. Huang, J. J. Wang, T. N. Yang, Y. J. Wu, X. M. Chen and L. Q. Chen, Appl. Phys. Lett., 2018, 112(10), 102901, DOI:10.1063/1.5020515.
- Y. Li, Y. Liu, M. Tang, J. Lv, F. Chen, Q. Li and G. Liu, Chem. Eng. J., 2021, 419, 129673, DOI:10.1016/j.cej.2021.129673.
- M. Zhou, R. Liang, Z. Zhou and X. Dong, J. Mater. Chem. C, 2018, 6(31), 8528–8537, 10.1039/C8TC03003K.
- G. Liu, Y. Li, J. Gao, D. Li, L. Yu, J. Dong and L. Jin, J. Alloys Compd., 2020, 826, 154160, DOI:10.1016/j.jallcom.2020.154160.
- H. Zaitouni, L. Hajji, D. Mezzane, E. Choukri, A. Alimoussa, S. B. Moumen and Z. Kutnjak, Phys. B, 2019, 566, 55–62, DOI:10.1016/j.physb.2019.04.026.
- D. Damjanovic, Appl. Phys. Lett., 2010, 97(6), 062906, DOI:10.1063/1.3479479.
- W. Liu and X. Ren, Phys. Rev. Lett., 2009, 103(25), 257602, DOI:10.1103/PhysRevLett.103.257602.
- Y. Yao, C. Zhou, D. Lv, D. Wang, H. Wu, Y. Yang and X. Ren, EPL, 2012, 98(2), 27008, DOI:10.1209/0295-5075/98/27008.
- X. Ke, S. Yang, Y. Wang, D. Wang, L. Zhao, J. Gao and X. Ren, Phys. Rev. B, 2021, 103(8), 085132, DOI:10.1103/PhysRevB.103.085132.
- S. K. Upadhyay, V. R. Reddy, P. Bag, R. Rawat, S. M. Gupta and A. Gupta, Appl. Phys. Lett., 2014, 105(11), 112907, DOI:10.1063/1.4896044.
- B. A. Tuttle and D. A. Payne, Ferroelectrics, 1981, 37(1), 603–606, DOI:10.1080/00150198108223496.
- G. Singh, V. S. Tiwari and P. K. Gupta, Appl. Phys. Lett., 2013, 103(20), 202903, DOI:10.1063/1.4829635.
- A. K. Kalyani, K. Brajesh, A. Senyshyn and R. Ranjan, Appl. Phys. Lett., 2014, 104(25), 252906, DOI:10.1063/1.4885516.
- H. Kacem, A. Dhahri, Z. Sassi, L. Seveyrat, L. Lebrun, V. Perrin and J. Dhahri, J. Alloys Compd., 2021, 872, 159699, DOI:10.1016/j.jallcom.2021.159699.
- H. Kaddoussi, A. Lahmar, Y. Gagou, B. Manoun, J. N. Chotard, J. L. Dellis and M. El Marssi, J. Alloys Compd., 2017, 713, 164–179, DOI:10.1016/j.jallcom.2017.04.148.
- W. Y. Pan, Y. C. Tang, Y. Yin, A. Z. Song, J. R. Yu, S. Ye and J. F. Li, Ceram. Int., 2021, 47(16), 23453–23462, DOI:10.1016/j.ceramint.2021.05.061.
- K. Dey, A. Ahad, K. Gautam, A. Tripathy, S. S. Majid, S. Francoual and D. K. Shukla, Phys. Rev. B, 2021, 103(10), L100205, DOI:10.1103/PhysRevB.103.L100205.
- I. D. Santos and J. A. Eiras, J. Phys.: Condens. Matter, 2001, 13(50), 11733, DOI:10.1088/0953-8984/13/50/333.
- C. Zhao, H. Wu, F. Li, Y. Cai, Y. Zhang, D. Song and S. J. Pennycook, J. Am. Chem. Soc., 2018, 140(45), 15252–15260, DOI:10.1021/jacs.8b07844.
- F. Li, S. Zhang, D. Damjanovic, L. Q. Chen and T. R. Shrout, Adv. Funct. Mater., 2018, 28(37), 1870262, DOI:10.1002/adfm.201870262.
- X. G. Tang and H. L. W. Chan, J. Appl. Phys., 2005, 97(3), 034109, DOI:10.1063/1.1849817.
- P. Yadav, S. Sharma and N. P. Lalla, J. Appl. Phys., 2017, 121(18), 184101, DOI:10.1063/1.4983073.
- K. C. Koa, Dielectric Phenomena in Solids with Emphasis of Physical Concepts of Electronic Processes, 2004 Search PubMed.
- N. Guo, P. Cawley and D. Hitchings, J. Sound Vib., 1992, 159(1), 115–138, DOI:10.1016/0022-460X(92)90454-6.
- S. D. Kumar, J. Magesh and V. Subramanian, Mater. Des., 2017, 122, 315–321, DOI:10.1016/j.matdes.2017.03.019.
- A. Kumar, V. B. Prasad, K. J. Raju and A. R. James, J. Alloys Compd., 2014, 599, 53–59, DOI:10.1016/j.jallcom.2014.02.037.
- L. Zhao, B. P. Zhang, P. F. Zhou, X. K. Zhao and L. F. Zhu, Phys. Status Solidi A, 2014, 211(3), 611–617, DOI:10.1002/pssa.201329379.
- W. Cao and C. A. Randall, J. Phys. Chem. Solids, 1996, 57(10), 1499–1505, DOI:10.1016/0022-3697(96)00019-4.
- C. A. Randall, N. Kim, J. P. Kucera, W. Cao and T. R. Shrout, J. Am. Ceram. Soc., 1998, 81(3), 677–688, DOI:10.1111/j.1151-2916.1998.tb02389.x.
- I. P. Bykov, M. D. Glinchuk, V. V. Laguta, Y. L. Maximenko, L. Jastrabik, V. A. Trepakov and M. Hrabovský, J. Phys. Chem. Solids, 1995, 56(7), 919–923, DOI:10.1016/0022-3697(95)00024-0.
- J. Hao, W. Bai, W. Li and J. Zhai, J. Am. Ceram. Soc., 2012, 95(6), 1998–2006, DOI:10.1111/j.1551-2916.2012.05146.x.
- N. Wongdamnern, N. Triamnak, M. Unruan, K. Kanchiang, A. Ngamjarurojana, S. Ananta and R. Yimnirun, Phys. Lett. A, 2010, 374(3), 391–395, DOI:10.1016/j.physleta.2009.11.019.
- M. Acosta, N. Novak, V. Rojas, S. Patel, R. Vaish, J. Koruza and J. J. A. P. Rödel, Appl. Phys. Rev., 2017, 4(4), 041305, DOI:10.1063/1.4990046.
- B. G. Baraskar, S. G. Kakade, A. R. James, R. C. Kambale and Y. D. Kolekar, AIP Conf. Proc., 2016, 1731(1), 140066, DOI:10.1063/1.4948232.
- K. B. Chong, F. Guiu and M. J. Reece, Thermal activation of ferroelectric switching, J. Appl. Phys., 2008, 103(1), 014101, DOI:10.1063/1.2822179.
- V. S. Puli, D. K. Pradhan, I. Coondoo, N. Panwar, S. Adireddy, S. Luo and D. B. Chrisey, J. Phys. D: Appl. Phys., 2019, 52(25), 255304, DOI:10.1088/1361-6463/ab161a.
- H. Palneedi, M. Peddigari, G. T. Hwang, D. Y. Jeong and J. Ryu, Adv. Funct. Mater., 2018, 28(42), 1803665, DOI:10.1002/adfm.201803665.
- K. R. Kandula, K. Banerjee, S. S. K. Raavi and S. Asthana, Phys. Status Solidi A, 2018, 215(7), 1700915, DOI:10.1002/pssa.201700915.
- W. Cai, Q. Zhang, C. Zhou, R. Gao, S. Zhang, Z. Li and C. Fu, J. Mater. Sci.: Mater. Electron., 2020, 31(12), 9167–9175, DOI:10.1007/s10854-020-03446-z.
- Y. Lin, D. Li, M. Zhang, S. Zhan, Y. Yang, H. Yang and Q. Yuan, ACS Appl. Mater. Interfaces, 2019, 11(40), 36824–36830, DOI:10.1021/acsami.9b10819.
- S. Merselmiz, Z. Hanani, D. Mezzane, M. Spreitzer, A. Bradeško, D. Fabijan and Z. Kutnjak, Ceram. Int., 2020, 46(15), 23867–23876, DOI:10.1016/j.ceramint.2020.06.163.
- J. Gao, Y. Wang, Y. Liu, X. Hu, X. Ke, L. Zhong and X. Ren, Sci. Rep., 2017, 7(1), 1–10, DOI:10.1038/srep40916.
- Y. Fang, Y. Zhang, C. Wu, C. Liu, W. Ge, H. Zhao and H. Yuan, J. Mater. Sci.: Mater. Electron., 2021, 32(10), 13972–13984, DOI:10.1007/s10854-021-05973-9.
- K. S. Srikanth and R. Vaish, J. Eur. Ceram. Soc., 2017, 37(13), 3927–3933, DOI:10.1016/j.jeurceramsoc.2017.04.058.
- M. Zannen, A. Lahmar, Z. Kutnjak, J. Belhadi, H. Khemakhem and M. El Marssi, Solid State Sci., 2017, 66, 31–37, DOI:10.1016/j.solidstatesciences.2017.02.007.
- J. F. Scott, Annu. Rev. Mater. Res., 2011, 41, 229–240, DOI:10.1146/annurev-matsci-062910-100341.
- Z. Luo, D. Zhang, Y. Liu, D. Zhou, Y. Yao, C. Liu and X. Lou, Appl. Phys. Lett., 2014, 105(10), 102904, DOI:10.1063/1.4895615.
- C. Zhao, J. Yang, Y. Huang, X. Hao and J. Wu, J. Mater. Chem. A, 2019, 7(44), 25526–25536, 10.1039/C9TA10164K.
- M. D. Li, X. G. Tang, S. M. Zeng, Q. X. Liu, Y. P. Jiang, T. F. Zhang and W. H. Li, ACS Sustainable Chem. Eng., 2018, 6(7), 8920–8925, DOI:10.1021/acssuschemeng.8b01277.
- X. Zhang, L. Wu, S. Gao, J. Q. Liu, B. Xu, Y. D. Xia and Z. G. Liu, AIP Adv., 2015, 5(4), 047134, DOI:10.1063/1.4919096.
- X. S. Qian, H. J. Ye, Y. T. Zhang, H. Gu, X. Li, C. A. Randall and Q. M. Zhang, Adv. Funct. Mater., 2014, 24(9), 1300–1305, DOI:10.1002/adfm.201302386.
- H. Kaddoussi, Y. Gagou, A. Lahmar, J. Belhadi, B. Allouche, J. L. Dellis and M. El Marssi, Solid State Commun., 2015, 201, 64–67, DOI:10.1016/j.ssc.2014.10.003.
- Y. Zhao, X. Q. Liu, J. W. Wu, S. Y. Wu and X. M. Chen, J. Alloys Compd., 2017, 729, 57–63, DOI:10.1016/j.jallcom.2017.09.161.
- Y. Zhao, X. Q. Liu, S. Y. Wu and X. M. Chen, J. Electroceram., 2019, 43(1), 106–116, DOI:10.1007/s10832-019-00183-6.
- Z. Abdelkafi and I. Kriaa, Ceram. Int., 2018, 44(4), 4413–4418, DOI:10.1016/j.ceramint.2017.12.041.
- M. Sanlialp, C. Molin, V. V. Shvartsman, S. Gebhardt and D. C. Lupascu, IEEE Trans. Ultrason. Eng., 2016, 63(10), 1690–1696, DOI:10.1109/TUFFC.2016.2592542.
- A. Pramanick, W. Dmowski, T. Egami, A. S. Budisuharto, F. Weyland, N. Novak and M. R. V. Jørgensen, Phys. Rev. Lett., 2018, 120(20), 207603, DOI:10.1103/PhysRevLett.120.207603.
- M. Sanlialp, Z. Luo, V. V. Shvartsman, X. Wei, Y. Liu, B. Dkhil and D. C. Lupascu, Appl. Phys. Lett., 2017, 111(17), 173903, DOI:10.1063/1.5001196.
- Y. Liu, J. F. Scott and B. Dkhil, Some strategies for improving caloric responses with ferroelectrics, APL Mater., 2016, 4(6), 064109, DOI:10.1063/1.4954056.
- R. Kumar, A. Kumar and S. Singh, Sustain. Energy Fuels, 2018, 2(12), 2698–2704, 10.1039/C8SE00276B.
- Z. Hanani, S. Merselmiz, D. Mezzane, A. Bradeško, B. Rožič, M. Lahcini and M. Gouné, RSC Adv., 2020, 10(51), 30746–30755, 10.1039/D0RA06116F.
- N. Zhang, T. Zheng, C. Zhao, X. Wei and J. Wu, J. Mater. Res., 2021, 36(5), 1142–1152, DOI:10.1557/s43578-020-00081-6.
- J. Yang, Y. Zhao, X. Lou, J. Wu and X. Hao, J. Mater. Chem. C, 2020, 8(12), 4030–4039, 10.1039/C9TC06443E.
- C. R. Bowen, J. Taylor, E. Le Boulbar, D. Zabek and V. Y. Topolov, Mater. Lett., 2015, 138, 243–246, DOI:10.1016/j.matlet.2014.10.004.
- S. T. Lau, C. H. Cheng, S. H. Choy, D. M. Lin, K. W. Kwok and H. L. W. Chan, J. Appl. Phys., 2008, 103(10), 104105, DOI:10.1063/1.2927252.
- R. W. Whatmore, Rep. Prog. Phys., 1986, 49(12), 1335, DOI:10.1088/0034-4885/49/12/002.
- W. L. Zhang, Y. C. Yu, W. B. Luo, Y. Shuai, X. Q. Pan, Q. Q. Wu and C. G. Wu, Infrared Phys. Technol., 2017, 80, 100–104, DOI:10.1016/j.infrared.2016.09.005.
- P. Yu, Y. Ji, N. Neumann, S. G. Lee, H. Luo and M. Es-Souni, IEEE Trans. Ultrason. Eng., 2012, 59(9), 1983–1989, DOI:10.1109/TUFFC.2012.2417.
- C. R. Bowen, J. Taylor, E. LeBoulbar, D. Zabek, A. Chauhan and R. Vaish, Energy Environ. Sci., 2014, 7(12), 3836–3856, 10.1039/C4EE01759E.
- S. B. Lang, Phys. Today, 2005, 58(8), 31 CrossRef CAS.
- K. Srikanth, S. Patel and R. Vaish, Int. J. Appl. Ceram. Technol., 2018, 15(2), 546–553, DOI:10.1111/ijac.12814.
- S. Patel, K. S. Srikanth, S. Steiner, R. Vaish and T. Froemling, Ceram. Int., 2018, 44(17), 21976–21981, DOI:10.1016/j.ceramint.2018.08.312.
- J. Zhang, X. Dong, F. Cao, S. Guo and G. Wang, Appl. Phys. Lett., 2013, 102(10), 102908, DOI:10.1063/1.4795795.
- S. B. Lang and D. K. Das-Gupta, in Handbook of advanced electronic and photonic materials and devices, Academic Press, 2001, pp. 1–55, DOI:10.1016/B978-012513745-4/50036-6.
- R. B. Olsen and D. Evans, Pyroelectric energy conversion: hysteresis loss and temperature sensitivity of a ferroelectric material, J. Appl. Phys., 1983, 54(10), 5941–5944, DOI:10.1063/1.331769.
- H. Maiwa, in Nanoscale Ferroelectric-Multiferroic Materials for Energy Harvesting Applications, Elsevier, 2019, pp. 217–229, DOI:10.1016/B978-0-12-814499-2.00012-8.
- G. N. Bhargavi, A. Khare, T. Badapanda, M. S. Anwar and N. Brahme, J. Mater. Sci.: Mater. Electron., 2018, 29(13), 11439–11448, DOI:10.1007/s10854-018-9236-4.
- M. D. Li, X. G. Tang, S. M. Zeng, Q. X. Liu, Y. P. Jiang, T. F. Zhang and W. H. Li, J. Am. Ceram. Soc., 2019, 102(6), 3623–3629, DOI:10.1111/jace.16237.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Ah. Dhahricd,
F. Aouainie,
Z. Sassib,
L. Seveyrat
*a,
Ah. Dhahricd,
F. Aouainie,
Z. Sassib,
L. Seveyrat b,
L. Lebrunb and
J. Dhahri
b,
L. Lebrunb and
J. Dhahri a
a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T) showed a transition close to room temperature, resulting in improved piezoelectric, pyroelectric and electrocaloric performance. In addition, it was found that an electric field poling process changed the character of εr–T and tan
δ–T) showed a transition close to room temperature, resulting in improved piezoelectric, pyroelectric and electrocaloric performance. In addition, it was found that an electric field poling process changed the character of εr–T and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T plots. Resonance modes in the polarized state, where maximum power transmission was achieved, were observed in the impedance spectrum. The extra-slim hysteresis loops revealed a relatively low coercive field and hysteresis loss related to the diffuse phase transition, which can significantly improve energy storage efficiency up to 75% at 100 °C. To characterize the electrocaloric effect (ECE), indirect and direct methods based on the thermodynamic approach were used. Both methods results showed good consistency and revealed a large ECE peak evolving along the phase diagram. Furthermore, pyroelectric figures of merit (FOMs) for voltage responsivity (Fv), current responsivity (Fi), energy harvesting (FE), new energy harvesting
δ–T plots. Resonance modes in the polarized state, where maximum power transmission was achieved, were observed in the impedance spectrum. The extra-slim hysteresis loops revealed a relatively low coercive field and hysteresis loss related to the diffuse phase transition, which can significantly improve energy storage efficiency up to 75% at 100 °C. To characterize the electrocaloric effect (ECE), indirect and direct methods based on the thermodynamic approach were used. Both methods results showed good consistency and revealed a large ECE peak evolving along the phase diagram. Furthermore, pyroelectric figures of merit (FOMs) for voltage responsivity (Fv), current responsivity (Fi), energy harvesting (FE), new energy harvesting 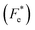 and detectivity (Fd) were calculated. Finally, thermal energy harvesting (ND) was determined by using the Olsen cycle. The obtained maximum ND was 233.7 kJ m−3 when the Olsen cycle operated at 25–100 °C and 0–30 kV cm−1. This study introduces not only a technique to produce a high performance ceramic for refrigeration devices, but also broadens the range of applications for BT-based lead-free ferroelectrics beyond actuators, sensors, and energy harvesting to solid-state cooling.
and detectivity (Fd) were calculated. Finally, thermal energy harvesting (ND) was determined by using the Olsen cycle. The obtained maximum ND was 233.7 kJ m−3 when the Olsen cycle operated at 25–100 °C and 0–30 kV cm−1. This study introduces not only a technique to produce a high performance ceramic for refrigeration devices, but also broadens the range of applications for BT-based lead-free ferroelectrics beyond actuators, sensors, and energy harvesting to solid-state cooling.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of the ceramic specimens were recorded by HP4194A impedance analyzer under different frequencies with a heating/cooling rate of 2 °C min−1. After being submerged in silicon oil, the ceramic pellets were exposed to the field. On sintered pellets, the temperature-dependent P–E loop studies at a frequency of 1 Hz were performed using a Keithley 428 current amplifier and a TREK Model 20/20C high voltage amplifier operating. The piezoelectric coefficient d33 was displayed for poled pellet at RT with a d33-meter (YE2730A). After that, the electromechanical factors (kp) and (Qm) were calculated from the resonance and antiresonance frequencies measured with an impedance analyzer (HP4194A). When the sample was exposed to an applied E at isothermal conditions, the heat-flow was measured using a modified differential scanning calorimetry (MHTC96 Setaram, France).
δ) of the ceramic specimens were recorded by HP4194A impedance analyzer under different frequencies with a heating/cooling rate of 2 °C min−1. After being submerged in silicon oil, the ceramic pellets were exposed to the field. On sintered pellets, the temperature-dependent P–E loop studies at a frequency of 1 Hz were performed using a Keithley 428 current amplifier and a TREK Model 20/20C high voltage amplifier operating. The piezoelectric coefficient d33 was displayed for poled pellet at RT with a d33-meter (YE2730A). After that, the electromechanical factors (kp) and (Qm) were calculated from the resonance and antiresonance frequencies measured with an impedance analyzer (HP4194A). When the sample was exposed to an applied E at isothermal conditions, the heat-flow was measured using a modified differential scanning calorimetry (MHTC96 Setaram, France).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and temperature, which can be used to detect the R–O phase transition more easily, as mentioned by ref. 32.
δ and temperature, which can be used to detect the R–O phase transition more easily, as mentioned by ref. 32.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 386.53 during the cooling run was higher than our previously reported result on BTS.31 The εr–T variation showed three dielectric anomalies: the first anomaly was small bump near RT, but was much more pronounced and appeared as a clear broad peak in the tan
386.53 during the cooling run was higher than our previously reported result on BTS.31 The εr–T variation showed three dielectric anomalies: the first anomaly was small bump near RT, but was much more pronounced and appeared as a clear broad peak in the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T curve (inset Fig. 4), which is related to TR–O phase transition. The second anomaly at ∼50 °C is related to TO–T phase transition and the third anomaly at ∼75 °C related to TC. In addition, TC decreased with frequency increase but remained unchanged for all frequencies. This anomalous behavior of the εr–T–f is known as the phenomenon of non-relaxation with nano polar regions (NRPs).
δ–T curve (inset Fig. 4), which is related to TR–O phase transition. The second anomaly at ∼50 °C is related to TO–T phase transition and the third anomaly at ∼75 °C related to TC. In addition, TC decreased with frequency increase but remained unchanged for all frequencies. This anomalous behavior of the εr–T–f is known as the phenomenon of non-relaxation with nano polar regions (NRPs).

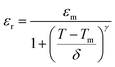
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at a fixed frequency (1 kHz) in the temperature range −50 to 150 °C as shown in Fig. 4(a). After poling, TC shifted towards higher temperature along with slight broadening, which can see the same character in the tan
δ at a fixed frequency (1 kHz) in the temperature range −50 to 150 °C as shown in Fig. 4(a). After poling, TC shifted towards higher temperature along with slight broadening, which can see the same character in the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T shown in the inset of Fig. 4(a). Additionally, εr also showed a significant decrease in value after poling. According to general principles, when E is applied to ferroelectric domains, the sample becomes less sensitive to smaller ac fields as polarization coherence rises along the field direction, and as a result, εr falls.39,40
δ–T shown in the inset of Fig. 4(a). Additionally, εr also showed a significant decrease in value after poling. According to general principles, when E is applied to ferroelectric domains, the sample becomes less sensitive to smaller ac fields as polarization coherence rises along the field direction, and as a result, εr falls.39,40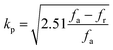
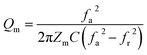
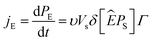
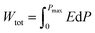
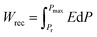
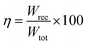
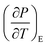 data were interpolated from 5th order polynomial fits of P–T values. Maxwell's relation was used to calculate the adiabatic change in temperature (ΔT) and the corresponding entropy change (ΔS) of the prepared ceramic, which are given in ref. 16 and 63:
data were interpolated from 5th order polynomial fits of P–T values. Maxwell's relation was used to calculate the adiabatic change in temperature (ΔT) and the corresponding entropy change (ΔS) of the prepared ceramic, which are given in ref. 16 and 63: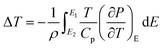
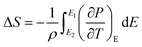


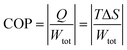
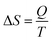
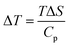
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and conductivity. Fig. 10(a) shows the pyroelectric coefficient (p) of BTSZ as a function of temperature. Representative parameters such as Pr are taken from the P–E hysteresis loops produced upon heating to determine p using a static method:
δ and conductivity. Fig. 10(a) shows the pyroelectric coefficient (p) of BTSZ as a function of temperature. Representative parameters such as Pr are taken from the P–E hysteresis loops produced upon heating to determine p using a static method: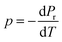
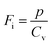
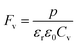
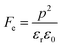
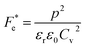
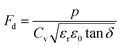
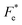 and Fd are, respectively, the specific heat capacity which is borrowed from the literature,87 the potential current responsivity performance, the voltage responsivity, pyroelectric energy harvesting figure of merit, the modified figure of merit and the detection capability. The development of improved pyroelectric sensitivity, more effective cost, fabrication feasibility and a higher TC are critical parameters to be taken into account. Fig. 10(b) shows the variation of FOMs with temperature, which have a similar trend to the pyroelectric coefficient. The BTSZ ceramic exhibited the highest FOMs of Fi = 803 pm V−1, Fv = 9.7 m2 C−1, Fe = 39.5 J m−3 K−2,
and Fd are, respectively, the specific heat capacity which is borrowed from the literature,87 the potential current responsivity performance, the voltage responsivity, pyroelectric energy harvesting figure of merit, the modified figure of merit and the detection capability. The development of improved pyroelectric sensitivity, more effective cost, fabrication feasibility and a higher TC are critical parameters to be taken into account. Fig. 10(b) shows the variation of FOMs with temperature, which have a similar trend to the pyroelectric coefficient. The BTSZ ceramic exhibited the highest FOMs of Fi = 803 pm V−1, Fv = 9.7 m2 C−1, Fe = 39.5 J m−3 K−2, 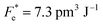 and Fd = 19.6 Pa0.5 around TC. Table 3 shows a few chosen materials with their pyroelectric properties in order to compare the performance of the BTSZ ceramic with that of other well-known polymers, lead-based and lead-free pyroelectric materials.61,82,83,87–91 According to these findings, the BTSZ ceramic could be a viable replacement for lead-based pyroelectric materials in pyroelectric applications.
and Fd = 19.6 Pa0.5 around TC. Table 3 shows a few chosen materials with their pyroelectric properties in order to compare the performance of the BTSZ ceramic with that of other well-known polymers, lead-based and lead-free pyroelectric materials.61,82,83,87–91 According to these findings, the BTSZ ceramic could be a viable replacement for lead-based pyroelectric materials in pyroelectric applications.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and εr is a critical condition for a successful of conversion of waste heat into electric energy. Furthermore, when compared to the conventional pyroelectric effect, the Olsen cycle can enhance energy harvesting capacity by three orders of magnitude or more. In this way, numerous pyroelectric energy harvesting systems based on the Olsen cycle have been created over the past three decades.92 Therefore, the Olsen cycle is employed in this study to calculate the pyroelectric energy harvesting potential of the produced sample. For further explanation, the following ref. 31 can be consulted. Thus, the following equation can be used to define the energy harvesting density (ND)
δ and εr is a critical condition for a successful of conversion of waste heat into electric energy. Furthermore, when compared to the conventional pyroelectric effect, the Olsen cycle can enhance energy harvesting capacity by three orders of magnitude or more. In this way, numerous pyroelectric energy harvesting systems based on the Olsen cycle have been created over the past three decades.92 Therefore, the Olsen cycle is employed in this study to calculate the pyroelectric energy harvesting potential of the produced sample. For further explanation, the following ref. 31 can be consulted. Thus, the following equation can be used to define the energy harvesting density (ND)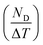 as well as the normalized energy harvest per unit of electric field change
as well as the normalized energy harvest per unit of electric field change 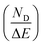 were calculated to evaluate the significance of our ceramic in the field of energy recovery. According to these results, our ceramic ranks among the most effective non-toxic materials for energy harvesting applications.
were calculated to evaluate the significance of our ceramic in the field of energy recovery. According to these results, our ceramic ranks among the most effective non-toxic materials for energy harvesting applications.
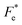 ) and detectivity (Fd) were calculated. The findings suggest that the produced ceramic could be an excellent technological candidate for pyroelectric devices. Moreover, the Olsen cycle was used to determine thermal energy harvesting (ND), which is equal to 233.7 kJ m−3 when operated at 25–100 °C and 0–30 kV cm−1. According to these results, high ECE material can be synthesized with important pyroelectric and energy storage properties in Sn and Zr substituted BT ceramic.
) and detectivity (Fd) were calculated. The findings suggest that the produced ceramic could be an excellent technological candidate for pyroelectric devices. Moreover, the Olsen cycle was used to determine thermal energy harvesting (ND), which is equal to 233.7 kJ m−3 when operated at 25–100 °C and 0–30 kV cm−1. According to these results, high ECE material can be synthesized with important pyroelectric and energy storage properties in Sn and Zr substituted BT ceramic.