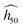Open Access Article
Open Access ArticleCan a shock-induced phonon up-pumping model relate to impact sensitivity of molecular crystals, polymorphs and cocrystals?†
X. Bidault *a and
S. Chaudhuri*ab
*a and
S. Chaudhuri*ab
aDepartment of Civil, Materials and Environmental Engineering, University of Illinois at Chicago, Chicago, Illinois 60607, USA. E-mail: xavbdlt@uic.edu
bApplied Materials Division, Argonne National Laboratory, Lemont, IL 60439, USA. E-mail: santc@uic.edu
First published on 1st November 2022
Abstract
Impact sensitivity engineering of high-energy molecular crystals requires accurate predictive models. For this purpose, the promising multi-phonon based approach is selected, assessing a bit more its strengths and weaknesses. Presently used with high-quality phonon calculations of 22 molecular crystals, using a physics-based criterion to determine the phonon bath extent, the resulting intrinsic shock sensitivity index (SSI) is compared to the most common marker of impact sensitivity, h50, as determined from drop-weight impact tests. Selecting a data subset from experiments performed under very similar conditions (2.5 kg hammer with grit and 30–40 mg samples), the model can predict h50 values for mono-molecular crystals with very good accuracy, including the ability to discriminate the polymorphs of HMX and CL20. This very good agreement validates an initial indirect up-pumping mechanism occurring under these conditions, where the doorway modes also interact with the phonon bath. However, the phonon bath criterion for mono-molecular crystals does not transfer well to cocrystals. Owing to the vibrational coupling of the co-molecules, it seems a broader phonon bath should be considered. Additionally recalling experimental uncertainty and various experimental factors affecting h50 values for a given compounds, we recommend that the density of the sample, granularity and morphology be systematically considered and reported along with measurements, which will in turn allow for more systematic data and predictive capabilities for sensitivity models.
I. Introduction
Tailoring the impact sensitivity of high-energy molecular crystals is important for developing a quantitative perspective on use and safety protocols across different applications. In general, an ideal balance between maximum power1 and acceptable sensitivity2–4 is hard to achieve without a multiscale approach to control key molecular and mesoscale drivers. Controlling the explosive sensitivity can be achieved in many ways, including using nanograins,5–10 a coating of micrograins11–13 for desensitization, or changing the molecular blocks and their packing using co-crystallization.2,14–18 Currently, a common route to create cocrystals is through an experimental trial-and-error process. Then, further experiments can be performed to rank their sensitivity with respect to their pure compounds. But with the increasing trend of computational design,19 it is tempting to predict such cocrystals alongside their full properties. The thermomechanical properties and shock properties can be well-predicted from ab initio methods using energy and dispersion corrected DFT-D,20 but predicting shock sensitivity remains challenging.The most common marker of impact sensitivity is the height, denoted h50, at which a dropped weight ignites a sample with 50% probability (or the related energy E50). The large database of experimental h50, covering hundreds of molecular crystals, has helped in devising many data-centric models. These models give insights about some trends with various factors pertaining to molecular formula or to physical properties of the crystal. But scarce are the ones outperforming 80% accuracy. A few most recent models are shortly described hereafter. Jensen et al.21 have calculated bond dissociation energy, heat and temperature of detonation of 70 isolated, nitroaromatic molecules to come up with a model with a correlation coefficient R2 between 0.81 and 0.85. Mathieu et al.22,23 have retrieved numerous data for 308 energetic molecules to devise a model based on both thermodynamic and kinetic descriptors, with a correlation coefficient R2 of 0.8. Xiong et al.24 have a similar but less accurate model, incorporating the self-sustaining ignition ability of 150 energetic molecules, and reaching a Pearson correlation coefficient of 0.67 (meaning an R2 value around 0.45). Nevertheless, Mathieu et al. hypothesize in their papers many sources of discrepancy from experimental h50, and propose to add a crystal packing coefficient for a possible improvement. In an attempt to go beyond mere molecular properties, Bondarchuk25 has considered solid-state properties of 24 energetic crystals, calculated the pressure at which the electronic band gap is lower than 1 meV, and ended up with a shock sensitivity model with a correlation coefficient R2 of 0.83. The method is a bit expensive, and considering the bulk modulus instead may be more efficient, as done by Deng et al.26 for 240 nitroaromatics. They achieve a correlation coefficient R2 of 0.91. However, our application of their model to nitramines – see Section 1 in our ESI – is acceptable only for nitroaromatics, like TATB and TNT, but deeply erroneous for the non-aromatic nitramines: for instance, β-HMX is predicted with an h50 higher than 800 cm, which is much less sensitive than even TATB. Considering polymorphs, this model erroneously predicts β- and δ-HMX similarly insensitive, whereas both are actually sensitive, with δ-HMX even more so.27 Then, β- and ε-CL20 are predicted with sensitivity similar to TNT, whereas both are actually more sensitive than that, and β-CL20 more than ε-CL20.28 This model lacks transferability and it would need a parameterization for nitramines. Alternatively, extending it to a broader range of energetic crystals than initially intended will likely result in a decreased correlation coefficient R2, probably around 0.8, like the other models.
Using vibrational properties of the molecular crystals, an approach based on phonon interactions and up-pumping,29–31 and improved by Michalchuk et al.32,33 looks promising. In their studies, they recall the theoretical approach to up-pumping with the following assumptions. The shock energy is first transferred to the phonon bath, the low frequency modes within the range [0, ωmax] related to intermolecular or lattice vibrations and some amalgamated intramolecular modes. Then, this energy is transferred to the “doorway” modes, whose frequencies are within the range [ωmax, 2ωmax], and they can be subsequently up-pumped to higher frequencies related to intramolecular vibrations until bond rupture. In their model, ωmax depends on the distribution of low-frequency modes in a given material, generally around 200 cm−1. A few approximations, such as ab initio calculation of the vibrational density of states (vDOS) restricted to the Gamma point and, from it, the derivation of multiphonon spectra, make this method affordable. Overall, their model was applied to less than 20 energetic materials and the sensitivity prediction aligns well with experimental h50, albeit without explicitly quantifying a correlation coefficient. Their model succeeds in ranking δ-HMX as more sensitive than β-HMX.34 Ab initio calculations restricted to the Gamma point can be motivated by high throughput considerations, but this approximation may not be suitable to discriminate other molecular crystals, co-crystals and their polymorphs. Indeed, we show in Section 2 of the ESI† that the vDOS of β-HMX (Fig. S1†) obtained using this approximation strongly differs from the ones using a larger number of k-points or supercells, and especially in the low-frequency range. A good description of this range associated with lattice/intermolecular vibrations is crucial for molecular crystals,35 both in frequencies and relative amplitudes. It has been shown that paying attention to this critical range can resolve large discrepancies between theory and experiments.20
Dlott and Fayer30 posited that a vibrational up-pumping scheme describing the internal energy flow in shocked organic materials occurs within a few tens of picoseconds after the shock front. This approach cannot a priori relate to impact experiments, where the deformations or compressions do not always generate a shockwave. The shock-less impact is thus commonly accepted. Storm et al.36 recall the large differences in time scale and pressure between shock and impact experiments (0.05–2 μs and 3–20 GPa versus 200–250 μs and 0.7–1.5 GPa). The thermalization of the phonon bath is extremely fast, around 1 ps (ref. 37) or less,38 which is significantly faster than internal-mode lifetime of a few nanoseconds.37,38 Analyzing 21 explosives, their h50 from impact experiments and their P90 (pressure to initiate an explosive pressed to 90% of its theoretical maximum density) from shock experiments, Storm et al.36 actually find an excellent correlation (R2 = 0.99, excluding 3 outliers). This high correlation supports the approach for predicting impact sensitivity from shock-induced phonon up-pumping.
From the high-quality phonon spectra of 20 mono-molecular (molecules of one type) crystals, including some polymorphs and 2 cocrystals, this paper explores the capabilities of the multi-phonon based approach to predict their impact sensitivity from a shock sensitivity index (SSI), with a thorough comparison to experimental h50 and observations. One difficulty in the up-pumping scheme is the selection of the phonon bath extent ωmax.32 The criterion of a frequency gap to define the upper limit of the phonon bath was found not fully satisfactory, and we presently use a more physics-based criterion. The model and its capabilities to discriminate polymorphs and cocrystals are discussed, acknowledging sources of discrepancy in theory and on the experimental side.
II. Methods
A. DFT-D and variable-cell relaxation
First principle calculations are carried out using the Density Functional Theory (DFT) as implemented in Quantum Espresso 6.7 (QE),39 the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) functional, the Grimme D2 correction for a proper description of the van der Waals interactions (denoted hereafter PBE-D2) and the ultrasoft plane-wave pseudopotential (PP) from PSlibrary 1.0.0 (ref. 40) with non-linear core correction (NLCC). The energy cutoff for wave functions is set at 90 Ry for all molecular crystals and the cutoff for charge density is set at 900 Ry. A convergence threshold of 10−8 Ry is used for Self-Consistent Field (SCF) calculations. The Brillouin zone is sampled using a Monkhorst–Pack off-grid k-point mesh adapted to every crystal and cocrystal reported in the ESI, Table S3.† Performing variable-cell relaxation at zero pressure, the convergence is monitored using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm for both lattice parameters and atom positions, using thresholds of 10−5 Ry for the system energy, 10−4 Ry bohr−1 for the forces and 0.1 kbar for the pressure tensor. The resulting lattice parameters, reported in Table S4 of the ESI,† are in excellent agreement with ambient experimental data. The ability of PBE-D2 and PP to reproduce ambient structures of explosive molecular crystals is known,20,41 as well as the suitability for accurate determination of their phonon density of state.20B. Vibrational density of state
Phonon properties are determined using atomic finite displacements and the supercell method as implemented in Phonopy 2.9.1,42 with supercells as specified in Table S3.† For every optimized structure, Phonopy generates supercell configurations where the atoms of a given vibrational mode are displaced by 0.02 bohr. Using the molecule symmetry and the group symmetry of each crystal (Table S4†), these modes are reduced to the number of irreducible representations reported in Table S3.† The force constants are then calculated by QE (a single off-grid k-point is enough, due to supercell replication), and post-processed by Phonopy to obtain the vDOS, also denoted g(ω), using a dense 16 × 16 × 16 q-point mesh grid and a Gaussian broadening of 2 cm−1. The vDOS bin size is 1 cm−1, and vDOS values below a threshold of 10−4 states per cm−1 are considered zero. Note that, as expected, the vDOS integration correctly yields three times the number of atoms per unit cell (3N). Fig. S2 in the ESI† compares the vDOS of β-HMX, α-NTO, TATB and α-FOX-7 to experimental spectra of inelastic neutron scattering (INS) performed at 20 K.32,43 Peak positions are in very good agreement (see Section 4 of the ESI†). In addition, to visualize the phonon modes and to quickly assign them to their corresponding frequencies, vDOS at the Γ q-point are calculated for every molecular crystal and for the extracted molecules in gas phase. For the latter, the extracted molecules are not geometrically re-optimized, but kept in the conformation they had in the crystal, and placed in a box of at least twice the molecule size. An example for β-HMX is provided in Fig. 1(a). It can be seen that, as expected, the frequencies of the extracted molecule in gas phase are lower than in the crystal, and especially for the phonon bath. Also, some molecular modes can degenerate in the crystal,44 and some others can synchronize.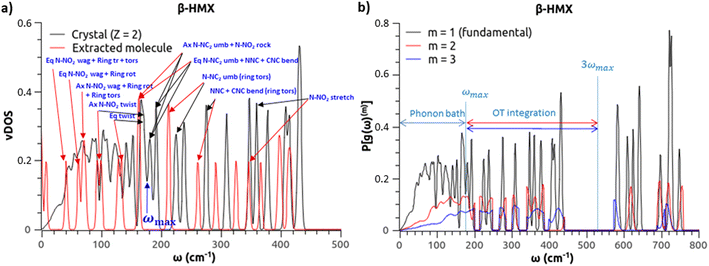 | ||
| Fig. 1 (a) vDOS of the β-HMX molecular crystal (2 molecules per unit cell) and of the extracted HMX molecule in gas phase. The axial (Ax) and equatorial (Eq) N-NC2 umbrella modes of the isolated molecule degenerate in the crystal. On the contrary, the N-NO2 twisting modes of the Ax and Eq nitro groups of the isolated molecule synchronize in the crystal (large peak between 159 and 176 cm−1). Since there is no N-NO2 twisting modes beyond 176 cm−1, this value defines ωmax. (b) Fundamental vDOS (black) and projected OTs for m = 2 and m = 3 (red and blue, respectively), and integration domain. Using eqn (1) and (2), the resulting SSI for β-HMX is 0.9020. | ||
C. Sensitivity prediction from the overtone-based model
Following our effort to obtain accurate vDOS for molecular crystals, especially in the low-frequency range, it makes sense to use methods based on a multi-phonon approach to model their shock sensitivity. As described by Michalchuk et al.,32 the lattice phonon bath (frequency ω < ωmax, where ωmax depends on the given molecular crystal) is excited and stores the initial energy of the shock. This amount of energy is then rapidly up-pumped to intra-molecular modes, quicker than dissipation, and some of these vibrational modes are responsible for bond breaking. In the doorway mode approach, the initial stage of up-pumping is dominated by processes involving two “bath” phonons converting into one intra-molecular phonon (the doorway modes are thus defined by ωmax < ω < 2ωmax). The excited doorway modes can subsequently interact with the phonon bath again, building an indirect thermal mechanism, and up-pumping is thus considered up to 3ωmax.33 Direct interactions between three “bath” phonons are also considered within the same limit of 3ωmax.Michalchuk et al.32 have proposed more sophisticated variants of their own method. This study focuses on the simplest version: the overtone (OT) based model. Its advantage is that it requires only one empirically adjusted parameter: the extent ωmax of the phonon bath. In an attempt to minimize the human factor, ωmax is adjusted the same way for all molecular crystals. From our observation of the calculated vDOS and the assigned vibrational modes, we have noticed that the best correlation and consistency across the board is achieved when ωmax corresponds to the X-NO2 twisting modes (see example in Fig. 1(a)). The present work thus focuses on this physics-based criterion applied to all the crystals hereafter. Note that a comparative study with ωmax assigned to some other modes is out of the scope of the present work.
Then, the phonon density of the mth OT (m = 2, 3…) has the form g(ω)(m) = g(ω)/m, using stretched frequencies ω(m) = mω. The projection onto the fundamental vDOS yields the quantity P[g(ω)(m)], which is integrated from ωmax to 3ωmax and normalized by the number of states in the phonon bath (Nphonon bath). The resulting shock sensitivity index is hereafter denoted SSI (eqn (1)). An example is provided for β-HMX in Fig. 1(b). Eqn (1a) yields the number of states in the phonon bath, which is Nphonon bath = 30 states. The contributions to eqn (1b) are 0.4707 and 0.4313 for m = 2 and m = 3, respectively, yielding a total SSI of 0.9020 for β-HMX. Michalchuk et al.32 have shown that only considering OTs m = 2 and m = 3 and adding up their contributions is enough to relate fairly well to h50 as obtained from mass drop experiments. This corroborates Bondarchuck's recent choice44 to use a damping factor which attenuates the contribution of higher overtones.
Experimental h50 values can be found in Table 1. All of them but α-FOX-7's are from experiments using a hammer with grit, which enables significantly less uncertainty than a bare hammer, as statistically observed by Marrs et al.45. They also observed that ignition and burning with a bare hammer are more inhomogeneous. For these reasons, tests with a gritted hammer are a better proxy to relate experimental h50 values to the present theoretical model, i.e., to relate actual initiation to an initial vibrational up-pumping scheme.
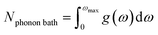 | (1a) |
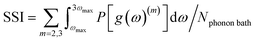 | (1b) |
 from eqn (2) and experimental h50 values of various molecular crystals
from eqn (2) and experimental h50 values of various molecular crystals
| (cm) | h50 (cm) | Ref. | Hammer (kg) | Tool typea | Sample mass (mg) | Remarks | |
|---|---|---|---|---|---|---|---|
| a Tool types 12 and 12B: hammer with and without sandpaper, respectively. | |||||||
| PETN | 12.6 | 13.8 | 45 | 2.5 | 12 | 40 | Average of many h50 from only LANL |
| β-CL20 | 11.8 | 14 | 46 | 2.5 | 12 | 35 | |
| ε-CL20 | 21.9 | 17.7 | 46 | 2.5 | 12 | 35 | Average of the reported values |
| BTF | 29.6 | 21 | 47 | 2.5 | 12 | — | Non-recryst, highest dens. sample |
| β-HMX | 32.6 | 32 | 48 | 2.5 | 12 | 35 | 33 cm with 12B and 2.0 kg (ref. 49) |
| δ-HMX | 19.7 | 18 | 50 | 2.5 | 12 | 40 | Av. of pure δ and δ with β traces |
| α-NTO | 141 | 291 | 51 | — | 12 | — | 293 cm with tool 12B |
| HNB | 21.5 | 15.6 | 52 | 2.5 | 12 | 30–40 | |
| Tetryl | 83.0 | 38.5 | 52 | 2.5 | 12 | 30–40 | |
| HNAB | 26.1 | 32 | 36 | 2.5 | 12 | 40 | |
| HNS | 48.8 | 39 | 36 | 2.5 | 12 | 40 | HNS-II (denser than HNS-I) |
| DIPAM | 44.0 | 85.1 | 36 | 2.5 | 12 | 40 | |
| TNB | 81.8 | 100 | 36 | 2.5 | 12 | 40 | |
| MATB | 119 | 177 | 36 | 2.5 | 12 | 40 | |
| DATB | 434 | 320 | 36 | 2.5 | 12 | 40 | |
| TATB | 585 | 490 | 36 | 2.5 | 12 | 40 | >320 cm. Value extrapolated from TNB, MATB and DATB |
| α-FOX-7 | 126 | 53 | 2.0 | BAM | — | Recrystallized sample, bare hammer | |
| 54 | |||||||
| α-CL20 | 20.7 | 55 | 5.0 | 12 | 50 | ||
| β-CL20 | 24.2 | 55 | 5.0 | 12 | 50 | ||
| γ-CL20 | 24.9 | 55 | 5.0 | 12 | 50 | ||
| ε-CL20 | 26.8 | 55 | 5.0 | 12 | 50 | ||
III. Results and discussions
A. Prediction of h50 for various molecular crystals
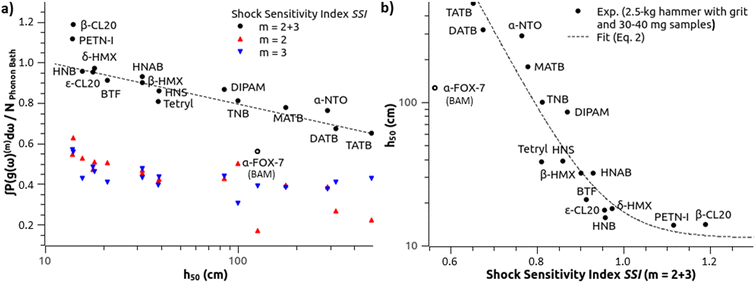 | ||
Fig. 2 SSI from the OT-based method to predict impact sensitivity of (a) various molecular crystals (Table 1), (b) the same with swapped axis. Red, blue and black color code is for OTs m = 2, m = 3, and total contributions, respectively. The dashed line in (a) is a visual guide from which two high-sensitive explosives and α-FOX7 deviate. The dashed curve in (b) displays the estimate 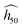 determined as in eqn (2) (excluding α-FOX-7 – see Section III.A.1). determined as in eqn (2) (excluding α-FOX-7 – see Section III.A.1). | ||
Discarding α-FOX-7, a fit with an exponential decay function succeeds in modeling the trend, and all the SSI data align well along the black dashed curve representing the estimate 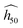 in Fig. 2(b) (eqn (2) with y0 = 11.27 cm, a1 = 509.58 cm, b1 = 0.0761141, and SSI0 = 0.660437). The theoretical
in Fig. 2(b) (eqn (2) with y0 = 11.27 cm, a1 = 509.58 cm, b1 = 0.0761141, and SSI0 = 0.660437). The theoretical 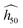 for the molecular crystals of interest are reported in Table 1. Using a log scale, the correlation coefficient R2 of the OT-based model is 90%.
for the molecular crystals of interest are reported in Table 1. Using a log scale, the correlation coefficient R2 of the OT-based model is 90%.
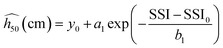 | (2) |
(a) HMX. β-HMX is one of the most investigated molecular explosives and experimental values of h50 are available.48,49,52 A few values for δ-HMX have also been reported, for instance for a pure sample and for some samples with traces of β-HMX.50 Averaging them, the resulting value of 18 cm compares well with the 19.7 cm from the OT-based model (eqn (2)). The sensitivity of δ-HMX appears thus similar to that of ε-CL20.
However, there is still no consensus whether the observed higher sensitivity of δ-HMX comes from the molecular conformation or from the cracks generated by the β-to-δ phase transformation. Decorrelating the effects of porosity, because the particles were confined in a polymer matrix, δ-HMX was experimentally found to be intrinsically more sensitive than β-HMX and comparable to PETN.27 Under different conditions, using a BAM apparatus and 10 mg samples, a recent experimental study57 contradictorily claims that the molecular conformation of HMX has little to no relevance. Their figures show very similar pore/crack distributions in “small” particles of both pristine β-HMX and δ-HMX, which represents an opportunity to compare their intrinsic sensitivity. But the authors strangely deem that δ more sensitive than β by 2.6 cm is statistically not meaningful. Yet, this value corroborates the previous experimental finding as well as our theoretical observation. To emphasize the importance of molecular conformation and packing, quantum molecular dynamics simulations show that the onset of shock chemistry occurs at 2200 K for β-HMX and 2000 K for δ-HMX, and involving different decomposition mechanisms.58
Pristine β-HMX was transformed to δ-HMX and then reverted. Concatenating the recent results57 with previous studies,27,59 a trend rather appears, as shown in Table 2. The smaller the initial particle size of pristine β, the less sensitive reverted-β is. But the “small” and “large” particle regimes involve different phenomena. In the “small” particle regime, the reverted-β particles look smoother than in pristine β, which is likely at the origin of their reduced sensitivity. In the “large” particle regime, reverted-β has crack porosity larger than in pristine β, explaining their higher sensitivity.
Some other factors affecting the sensitivity are addressed in Section III.B. Therefore, eqn (2) should be understood as a transfer function between the SSI and experimental h50, for samples with the “standard” granulometry and porosity of the compounds displayed in Table 1.
(b) CL-20. At the impact and shock timescales, all CL-20 phase transformations but one (γ ↔ ζ) are too slow to occur, and there is no liquid phase.60 This makes the discussion for CL-20 more straightforward than for HMX. An experiment using a standard protocol and a hammer of 2.5 kg (ref. 46) ranks β-CL20 as more sensitive than ε-CL20, and our theoretical determination in Fig. 2(b) agrees well with the reported h50 values. Using another standard protocol and a hammer of 5.0 kg,55 these values for α-, β-, γ- and ε-CL20 are measured at 20.7 cm, 24.2 cm, 24.9 cm and 26.8 cm, respectively. Fig. 3 compares these determinations with the SSI, showing that the OT-based model agrees with the experimental ranking. Indeed, β-, γ- and ε-CL20 are visually well aligned along the black dashed line, which supports once more the effect of molecular conformation and packing on sensitivity. α-CL20 appears a bit under, but it always naturally contains small molecules like H2O,61 CO or CO2,60 which could affect its effective sensitivity. Using eqn (2), our estimates for 35 mg samples tested with a 2.5 kg grit hammer would be 11.3 cm, 11.8 cm, 12.3 cm and 21.9 cm, respectively. It may be difficult to experimentally discriminate α-, β-, and γ-CL20 with this standard protocol, due to overdriven sensitivity, as mentioned in Section III.A.1.
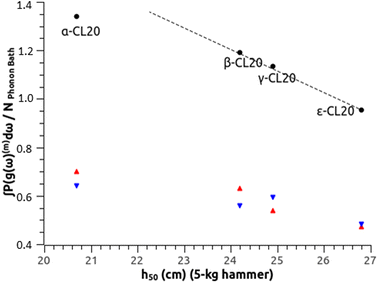 | ||
| Fig. 3 SSI from the OT-based method to predict impact sensitivity of CL20 polymorphs (Table 1). The dashed line is a visual guide, which shows the alignment between β-, γ- and ε-CL20. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystal of CL20
1 cocrystal of CL20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
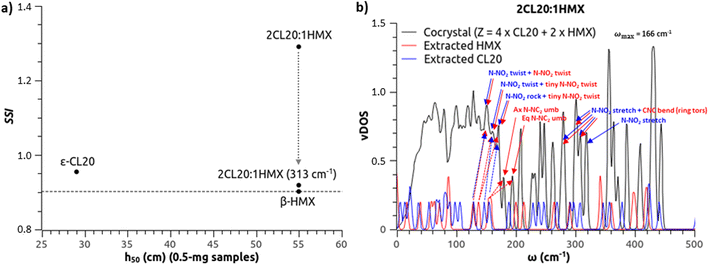
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MTNP,62 yielding h50 values of 20.4 cm, 125 cm and 30.6 cm, respectively. The sensitivity of the cocrystal is expected to be similar to that of β-HMX. From eqn (2), our estimates for 35 mg samples tested with a 2.5 kg grit hammer are 21.9 cm, 444 cm and 11.8 cm, respectively. If MTNP is successfully predicted as insensitive, the cocrystal is wrongly predicted as highly sensitive. We have checked for configurational issues in the cocrystal structure. In the cocrystal, the CL20 molecules are in the γ conformation as expected. When only considering the number of doorway modes, a recent study found the right ranking.63 But Michalchuk et al.32 have demonstrated that this simple approach is more qualitative than quantitative, and lacks transferability over a more complete set of molecular crystals.
MTNP,62 yielding h50 values of 20.4 cm, 125 cm and 30.6 cm, respectively. The sensitivity of the cocrystal is expected to be similar to that of β-HMX. From eqn (2), our estimates for 35 mg samples tested with a 2.5 kg grit hammer are 21.9 cm, 444 cm and 11.8 cm, respectively. If MTNP is successfully predicted as insensitive, the cocrystal is wrongly predicted as highly sensitive. We have checked for configurational issues in the cocrystal structure. In the cocrystal, the CL20 molecules are in the γ conformation as expected. When only considering the number of doorway modes, a recent study found the right ranking.63 But Michalchuk et al.32 have demonstrated that this simple approach is more qualitative than quantitative, and lacks transferability over a more complete set of molecular crystals.Fig. 4(a) compares the theoretical SSI to experimental h50 of ε-CL20, β-HMX and the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystal, as measured by Bolton et al.,14 using very small amounts of explosive (0.5 mg) and a hammer of 2.5 kg. Here again, the cocrystal is wrongly predicted as very sensitive. Note that instead of a random spatial distribution of the CL20 molecules in β or γ conformations in the cocrystal at ambient conditions, our optimized cell only contains CL20 molecules in γ conformation. Starting the optimization from CL20 molecules all in β conformation ends up with all in γ conformation. Even though it is not certain how the presence of CL20 molecules in β conformation would affect the sensitivity, the model fails to rank the sensitivity of the cocrystals with respects to their counterparts.
1 cocrystal, as measured by Bolton et al.,14 using very small amounts of explosive (0.5 mg) and a hammer of 2.5 kg. Here again, the cocrystal is wrongly predicted as very sensitive. Note that instead of a random spatial distribution of the CL20 molecules in β or γ conformations in the cocrystal at ambient conditions, our optimized cell only contains CL20 molecules in γ conformation. Starting the optimization from CL20 molecules all in β conformation ends up with all in γ conformation. Even though it is not certain how the presence of CL20 molecules in β conformation would affect the sensitivity, the model fails to rank the sensitivity of the cocrystals with respects to their counterparts.
The model needs a correction for cocrystals. Long range and local couplings between modes are presumably more complex due to a higher number of possible combinations involving van der Waals interactions, hydrogen bonds of various intensities, or some weaker intermolecular O⋯O, O⋯N and N⋯N interactions.64–70 Note that despite individually weaker than hydrogen bonds, the cumulative population of O⋯O and O⋯N interactions makes them the prevailing intermolecular contribution in ε-CL20.69 Some of these easily breakable O⋯O bonds could be advantageously replaced in the vicinity of a co-molecule like HMX, involving a coupling of the pertaining moieties. While co-crystals are expected to be of lower sensitivity if the most sensitive component is mixed with a lower sensitivity molecular partner, the up-pumping mechanisms can be significantly different. The co-molecules are probably more coupled than expected (see a few mode assignments in Fig. 4(b)) and a broader phonon bath could make sense. For instance, considering the highest non-coupled N-NO2 stretching mode and selecting the coupled N-NO2 stretching modes before (CL20 vibrations synchronized to HMX ring torsion (Fig. 4(b)) or to MTNP ring twisting, respectively) and amalgamating them to the phonon bath, we find ωmax = 313 cm−1 for 2CL20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1HMX and ωmax = 311 cm−1 for 1CL20
1HMX and ωmax = 311 cm−1 for 1CL20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1MTNP. This yields SSI = 0.9189 for 2CL20
1MTNP. This yields SSI = 0.9189 for 2CL20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1HMX and SSI = 0.9739 for 1CL20
1HMX and SSI = 0.9739 for 1CL20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1MTNP. This ranks 2CL20
1MTNP. This ranks 2CL20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1HMX slightly more sensitive than β-HMX, as expected, and 1CL20
1HMX slightly more sensitive than β-HMX, as expected, and 1CL20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1MTNP similar to ε-CL20, which is better but still a bit high.
1MTNP similar to ε-CL20, which is better but still a bit high.
Sensitivity prediction for cocrystals seems more subtle and complex than for mono-molecular crystals. Up-pumping schemes for cocrystals should also probably include energy transfer rates. Looking at N-NO2 stretching modes (Fig. 4(b)), which could trigger bond rupture, the corresponding lowest frequencies are the peaks at 280, 301 and 308 cm−1. Dividing these values by 2, the resulting frequencies fall in the part of the phonon bath involving N-NO2 twisting in both CL20 and HMX molecules. Therefore, a vibrational cooling of the N-NO2 stretching modes by the phonon bath is very likely, depending on the specific mode-to-mode scattering rates, in turn reducing the sensitivity. This vibrational cooling was recently demonstrated to theoretically happen in α-RDX.38
B. Experimental uncertainty and factors affecting the relationship with the SSI
The relationship between the SSI and the estimate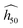 (eqn (2)) relies on experimental data. For consistency, we used data measured from similar tool type, hammer weight and sample mass (Table 1). But even for this consistent set, we must keep in mind that experimental errors can be as large as 20%. For instance, 435 tests on PETN performed at LANL over the past decades have been recently analyzed by Marrs et al.45 to investigate various sources of sensitivity variations. They were able to discard factors like when was and who performed the measurements, because of no substantial effect. All tests were performed using a 2.5 kg hammer. The resulting mean h50 value and 95% confidence interval are 13.8+3.2−2.5 cm with grit (hammer with sandpaper, like tool type 12 in Table 1) and 23.0+5.3−4.7 cm without it (bare hammer, like tool type 12B). This represents around 20% of maximum experimental uncertainty (7% on a log scale). Moreover, the difference with/without grit is as large as 9.2 cm, which is very significant. Discrepancies between laboratories also exist, with −4.4 cm on average (more sensitive) in the cumulated labs other than LANL. The various “Go/No go” methods have less effects, although the discrepancies are within 2.9 cm. Nevertheless, they demonstrate that this latter factor has significant effects on variability of TNT sensitivity. Uncertainty is expected to increase with less sensitive materials, supporting the use of a log scale. They conclude that, while ranking explosives in the range 8–12 cm is not reliable, relative observations performed in the same lab under the same conditions remain true.
(eqn (2)) relies on experimental data. For consistency, we used data measured from similar tool type, hammer weight and sample mass (Table 1). But even for this consistent set, we must keep in mind that experimental errors can be as large as 20%. For instance, 435 tests on PETN performed at LANL over the past decades have been recently analyzed by Marrs et al.45 to investigate various sources of sensitivity variations. They were able to discard factors like when was and who performed the measurements, because of no substantial effect. All tests were performed using a 2.5 kg hammer. The resulting mean h50 value and 95% confidence interval are 13.8+3.2−2.5 cm with grit (hammer with sandpaper, like tool type 12 in Table 1) and 23.0+5.3−4.7 cm without it (bare hammer, like tool type 12B). This represents around 20% of maximum experimental uncertainty (7% on a log scale). Moreover, the difference with/without grit is as large as 9.2 cm, which is very significant. Discrepancies between laboratories also exist, with −4.4 cm on average (more sensitive) in the cumulated labs other than LANL. The various “Go/No go” methods have less effects, although the discrepancies are within 2.9 cm. Nevertheless, they demonstrate that this latter factor has significant effects on variability of TNT sensitivity. Uncertainty is expected to increase with less sensitive materials, supporting the use of a log scale. They conclude that, while ranking explosives in the range 8–12 cm is not reliable, relative observations performed in the same lab under the same conditions remain true.
Considering the granulometry of the samples, sensitivity predictions can become less intuitive. In the same paper,45 the h50 values of PETN comprised of small (≈26.08 μm) or large (≈331.7 μm) particles are measured. With a bare hammer, small particles are found less sensitive than large ones (by roughly 3 cm) as expected,71,72 but it is counterintuitively the opposite with grit (by roughly 3 cm). A similar apparent inconsistency between impact sensitivity and grain size of HNS pressed to a single density was shown to depend on the shock amplitude and duration,73 and the author mentioned a similar behavior for RDX and TATB. The non-monotonic sensitivity with median micrograin size of 10%-porous RDX was also shown.74 This non-monotonic behavior was theoretically confirmed for HMX, TATB and TNT.75 At a given porosity, the voids must be sufficiently small, depending on the considered explosive, for the sensitivity to decrease and ignition to eventually fail. From reactive molecular dynamics, decreasing the size of nanoparticles in nanostructured RDX have been found to inhibit the shock-induced chemistry.5
The crystal morphology also affects its sensitivity. The behavior of “single” (S) or “multiple” (M) crystals, as named by Cole in his study49 (the latter can be understood as powders), is different. His h50 values are reported in Table 3. Without grit, it seems that the cyclic nitramines (HMX and RDX) are barely affected by the crystal morphology, whereas the nitramine PETN behaves as expected ((M) more sensitive than (S)), and in an opposite way for nitroaromatic TNT. With grit, the sensitivity variations with the sample mass make the trends less clear: the sensitivity decreases as the sample mass increases, except for the single crystal of TNT and the powder of HMX. The exception is confirmed for the latter with an h50 value as low as 55 cm for a tiny 0.5 mg sample of β-HMX powder.14 Extrapolating, there must be for HMX a sample mass threshold for which (S) becomes more sensitive than (M), and the opposite for TNT.
| h50 (cm) | Without grit | Sensitivity (S) vs. (M) | With grit | Sensitivity (S) vs. (M) | ||
|---|---|---|---|---|---|---|
| (S) | (M) | (S) | (M) | |||
| a Sensitivity increases (h50 decreases) when sample mass decreases.b Sensitivity decreases (h50 increases) when sample mass decreases. | ||||||
| PETN | 33 | 15 | − | 10a | 10a | = |
| HMX | 33 | 33 | = | 16a | 20b | + |
| RDX | 43 | 46 | ≈ | 18a | 30a | + |
| TNT | 53 | 102 | + | 56b | 25a | − |
To complete the picture, shock-induced polymorphic transitions are likely to occur more than anticipated. This is the case for γ-FOX-7, which reverts to α-FOX-7 during drop-weight experiments.43
In the light of all these experimental variabilities, we can understand why the sensitivity models presented in the introduction, fitted on raw and patchy h50 data, barely outperform the 80% accuracy. Gathering h50 data of dozens or hundreds of explosive compounds and, whether using machine learning or not, connecting these data to simple molecular, thermodynamic or kinetic descriptors can help understand the molecular origins of trends. But to take a step further in impact sensitivity engineering, it is recommended to thoroughly take into account the factors addressed above, which are often overlooked. Improved experiments may systematically report the sample granulometry/porosity and morphology, or define standards for these factors as well, which could help machine-learned models sort out the role of these factors.
Providing more than trends, the OT-based model can discriminate the sensitivity of the polymorphs of the same molecule. This feature is made possible due to the use of the phonon spectrum, which intrinsically contains more information than molecular descriptors. The vDOS is like a fingerprint of both the molecule and the crystal. Additionally, the smart post-processing proposed by Michalchuk et al.32,33 in their method gives an insight of the underlying physics. The present agreement of 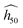 validates the indirect up-pumping mechanism occurring under these conditions, with the doorway modes also interacting with the phonon bath during the shock initiation stage (Section II.C). A more detailed approach of the mechanism and straight overtone relationships have been used by Bondarchuk44 in his recently revisited impact theory. Of course, once the hotspots are initiated or melting begins, further activation may not follow the doorway mode ordering.76
validates the indirect up-pumping mechanism occurring under these conditions, with the doorway modes also interacting with the phonon bath during the shock initiation stage (Section II.C). A more detailed approach of the mechanism and straight overtone relationships have been used by Bondarchuk44 in his recently revisited impact theory. Of course, once the hotspots are initiated or melting begins, further activation may not follow the doorway mode ordering.76
The estimate 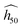 is fitted on a subset of experimental data whose maximum uncertainty is evaluated at 7% on a log scale.45 The accuracy of the OT-based model is very good (R2 ≈ 90% on a log scale), and we believe that this great achievement is due to the use of high-quality DFT-D to perform the phonon calculations. Nonetheless, we want to emphasize that the predicted
is fitted on a subset of experimental data whose maximum uncertainty is evaluated at 7% on a log scale.45 The accuracy of the OT-based model is very good (R2 ≈ 90% on a log scale), and we believe that this great achievement is due to the use of high-quality DFT-D to perform the phonon calculations. Nonetheless, we want to emphasize that the predicted 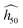 (eqn (2)) is valid only for experiments performed under conditions similar to that of Fig. 1(b).
(eqn (2)) is valid only for experiments performed under conditions similar to that of Fig. 1(b).
The theoretical SSI is determined for bulk crystals. Its relationship with the derived 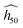 may change, depending on the subset of h50 data it is adjusted on. For instance with a subset of h50 data pertaining to the bare hammer only, it is likely that the phonon bath extent ωmax should be adjusted with a less stringent criteria for amalgamated intramolecular modes. This will be the subject of further investigations in future to drive studies on shock-resilient energetic crystals.
may change, depending on the subset of h50 data it is adjusted on. For instance with a subset of h50 data pertaining to the bare hammer only, it is likely that the phonon bath extent ωmax should be adjusted with a less stringent criteria for amalgamated intramolecular modes. This will be the subject of further investigations in future to drive studies on shock-resilient energetic crystals.
IV. Conclusion
In order to devise an accurate predictive model for impact sensitivity of molecular crystals, we used the promising overtone (OT) based approach by Michalchuk et al.32 in conjunction with high-quality phonon calculations. For the determination of the phonon bath extent, we systematically amalgamated the highest X-NO2 twisting modes. The resulting intrinsic shock sensitivity index (SSI) was compared to the most common marker of impact sensitivity, h50, as determined from drop weight impact tests. When the data subset is selected from experiments performed under very similar conditions (2.5 kg grit hammer and 30–40 mg samples), the model can predict h50 values with very good accuracy. Eqn (2) acts like a transfer function between the theoretical SSI and experimental h50. The parameters of eqn (2) do not explicitly account for overlooked aspects like sample granulometry or porosity. Eqn (2) thus applies to the “standard” granulometry and porosity of the compounds reported in Table 1.This model has the ability to discriminate polymorphs, ranking δ-HMX as more sensitive than β-HMX, and correctly ranking the four polymorphs of CL20 as well. This very good agreement for mono-molecular crystals validates the initial indirect up-pumping mechanism occurring under these conditions, where the doorway modes also interact with the phonon bath.
However, the case of the cocrystals is more subtle and the phonon bath criterion used for mono-molecular crystals does not transfer well. Owing to the vibrational coupling of the co-molecules, it seems a broader phonon bath can be more appropriate. This also renders the choice of ωmax less straightforward and intuitive, although our physics-based approach showed that frequencies of about 310 cm−1 could be considered.
Recalling experimental uncertainty and how various experimental factors affect h50 values for a given molecular crystal, we suggest the sample granularity, porosity, mass and morphology be systematically considered and reported with measurements. This will in turn allow sharpening the predictive capabilities of sensitivity models.
The OT-based model has a calculation cost. Accelerating phonon calculations without compromising accuracy in the low-frequency range pertaining to lattice and intermolecular vibrations becomes essential. This may be achieved using machine learning techniques, as successfully done for inorganic materials.77–79 These techniques have shown promising progress for molecular crystals.80,81 Meanwhile, the OT-based model could predict the h50 value of computationally-designed mono-molecular crystals with engineered sensitivity, as if they were tested with a 2.5 kg hammer with grit and using 30–40 mg samples.
Data availability
The data that support the findings of this study are available within the article and its ESI.†Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
We are thankful to Dr Adam Michalchuk for the useful discussions about his OT-based model and for providing experimental INS spectra. This work was supported by the Air Force Office of Scientific Research (AFOSR) under grant number FA9550-18-1-0236, by the Army Research Office (ARO) through EXEED center with grant number W911NF2110275, by high-performance computer time and resources from the DoD High Performance Computing Modernization Program (HPCMP) and from the Advanced Cyberinfrastructure for Education and Research (ACER) of the University of Illinois at Chicago (UIC).References
- S. V. Bondarchuk, Magic of Numbers: A Guide for Preliminary Estimation of the Detonation Performance of C–H–N–O Explosives Based on Empirical Formulas, Ind. Eng. Chem. Res., 2021, 60(4), 1952–1961, DOI:10.1021/acs.iecr.0c05607.
- W. Pang, K. Wang, W. Zhang, L. T. D. Luca, X. Fan and J. Li, CL-20-Based Cocrystal Energetic Materials: Simulation, Preparation and Performance, Molecules, 2020, 25(18), 18, DOI:10.3390/molecules25184311.
- Y. Ma, A. Zhang, C. Zhang, D. Jiang, Y. Zhu and C. Zhang, Crystal Packing of Low-Sensitivity and High-Energy Explosives, Cryst. Growth Des., 2014, 14(9), 4703–4713, DOI:10.1021/cg501048v.
- C. Zhang, et al., Toward low-sensitive and high-energetic co-crystal II: structural, electronic and energetic features of CL-20 polymorphs and the observed CL-20-based energetic–energetic co-crystals, CrystEngComm, 2014, 16(26), 5905–5916, 10.1039/C4CE00584H.
- X. Bidault and N. Pineau, Granularity impact on hotspot formation and local chemistry in shocked nanostructured RDX, J. Chem. Phys., 2018, 149(22), 224703, DOI:10.1063/1.5049474.
- B. Risse, F. Schnell and D. Spitzer, Synthesis and Desensitization of Nano-β-HMX, Propellants, Explos., Pyrotech., 2014, 39(3), 397–401, DOI:10.1002/prep.201300161.
- X. Song, Y. Wang and C. An, Thermochemical properties of nanometer CL-20 and PETN fabricated using a mechanical milling method, AIP Adv., 2018, 8(6), 065009, DOI:10.1063/1.5030155.
- Y. Bayat and V. Zeynali, Preparation and Characterization of Nano-CL-20 Explosive, J. Energ. Mater., 2011, 29(4), 281–291, DOI:10.1080/07370652.2010.527897.
- H. Qiu, R. B. Patel, R. S. Damavarapu and V. Stepanov, Nanoscale 2CL-20·HMX high explosive cocrystal synthesized by bead milling, CrystEngComm, 2015, 17(22), 4080–4083, 10.1039/C5CE00489F.
- A. Shokrolahi, A. Zali, A. Mousaviazar, M. H. Keshavarz and H. Hajhashemi, Preparation of Nano-K-6 (Nano-Keto RDX) and Determination of Its Characterization and Thermolysis, J. Energ. Mater., 2011, 29(2), 115–126, DOI:10.1080/07370652.2010.507237.
- C. Hou, C. Li, X. Jia, Y. Zhang and S. Zhang, Facile Preparation and Properties Study of CL-20/TATB/VitonA Composite Microspheres by a Spray-Drying Process, J. Nanomater., 2020, 2020, e8324398, DOI:10.1155/2020/8324398.
- B. Huang, et al., Ultrasonic approach to the synthesis of HMX@TATB core–shell microparticles with improved mechanical sensitivity, Ultrason. Sonochem., 2014, 21(4), 1349–1357, DOI:10.1016/j.ultsonch.2014.02.010.
- S. Wang, C. An, J. Wang and B. Ye, Reduce the Sensitivity of CL-20 by Improving Thermal Conductivity Through Carbon Nanomaterials, Nanoscale Res. Lett., 2018, 13(1), 85, DOI:10.1186/s11671-018-2496-3.
- O. Bolton, L. R. Simke, P. F. Pagoria and A. J. Matzger, High Power Explosive with Good Sensitivity: A 2:1 Cocrystal of CL-20:HMX, Cryst. Growth Des., 2012, 12(9), 4311–4314, DOI:10.1021/cg3010882.
- Y. Liu, C. An, J. Luo and J. Wang, High-density HNIW/TNT cocrystal synthesized using a green chemical method, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 74(4), 4, DOI:10.1107/S2052520618008442.
- Y. Tan, et al., High Energy Explosive with Low Sensitivity: A New Energetic Cocrystal Based on CL-20 and 1,4-DNI, Cryst. Growth Des., 2019, 19(8), 4476–4482, DOI:10.1021/acs.cgd.9b00250.
- C. An, H. Li, B. Ye and J. Wang, Nano-CL-20/HMX Cocrystal Explosive for Significantly Reduced Mechanical Sensitivity, J. Nanomater., 2017, 2017, e3791320, DOI:10.1155/2017/3791320.
- D. Guo, Q. An, S. V. Zybin, W. A. G. Iii, F. Huang and B. Tang, The co-crystal of TNT/CL-20 leads to decreased sensitivity toward thermal decomposition from first principles based reactive molecular dynamics, J. Mater. Chem. A, 2015, 3(10), 5409–5419, 10.1039/C4TA06858K.
- M. Pakhnova, I. Kruglov, A. Yanilkin and A. R. Oganov, Search for stable cocrystals of energetic materials using the evolutionary algorithm USPEX, Phys. Chem. Chem. Phys., 2020, 22(29), 16822–16830, 10.1039/D0CP03042B.
- X. Bidault and S. Chaudhuri, Improved predictions of thermomechanical properties of molecular crystals from energy and dispersion corrected DFT, J. Chem. Phys., 2021, 154(16), 164105, DOI:10.1063/5.0041511.
- T. L. Jensen, J. F. Moxnes, E. Unneberg and D. Christensen, Models for predicting impact sensitivity of energetic materials based on the trigger linkage hypothesis and Arrhenius kinetics, J. Mol. Model., 2020, 26(4), 65, DOI:10.1007/s00894-019-4269-z.
- D. Mathieu and T. Alaime, Impact sensitivities of energetic materials: Exploring the limitations of a model based only on structural formulas, J. Mol. Graphics Modell., 2015, 62, 81–86, DOI:10.1016/j.jmgm.2015.09.001.
- D. Mathieu, Sensitivity of Energetic Materials: Theoretical Relationships to Detonation Performance and Molecular Structure, Ind. Eng. Chem. Res., 2017, 56(29), 8191–8201, DOI:10.1021/acs.iecr.7b02021.
- X. Xiong, X. He, Y. Xiong, X. Xue, H. Yang and C. Zhang, Correlation between the self-sustaining ignition ability and the impact sensitivity of energetic materials, Energ. Mater. Front., 2020, 1(1), 40–49, DOI:10.1016/j.enmf.2020.06.002.
- S. V. Bondarchuk, Quantification of Impact Sensitivity Based on Solid-State Derived Criteria, J. Phys. Chem. A, 2018, 122(24), 5455–5463, DOI:10.1021/acs.jpca.8b01743.
- Q. Deng, et al., Probing impact of molecular structure on mechanical property and sensitivity of energetic materials by machine learning methods, Chemom. Intell. Lab. Syst., 2021, 104331, DOI:10.1016/j.chemolab.2021.104331.
- B. W. Asay, B. F. Henson, L. B. Smilowitz and P. M. Dickson, On the Difference in Impact Sensitivity of Beta and Delta HMX, Energ. Mater., 2003, 21(4), 223–235, DOI:10.1080/713770434.
- S. Zeman, M. Jungová and Q.-L. Yan, Impact Sensitivity in Respect of the Crystal Lattice Free Volume and the Characteristics of Plasticity of Some Nitramine Explosives, Chin. J. Energ. Mater., 2015, 23(12), 1186–1191, DOI:10.11943/j.issn.1006-9941.2015.12.007.
- C. S. Coffey and E. T. Toton, A microscopic theory of compressive wave-induced reactions in solid explosives, J. Chem. Phys., 1982, 76(2), 949–954, DOI:10.1063/1.443065.
- D. D. Dlott and M. D. Fayer, Shocked molecular solids: Vibrational up pumping, defect hot spot formation, and the onset of chemistry, J. Chem. Phys., 1990, 92(6), 3798–3812, DOI:10.1063/1.457838.
- J. Bernstein, Ab initio study of energy transfer rates and impact sensitivities of crystalline explosives, J. Chem. Phys., 2018, 148(8), 084502, DOI:10.1063/1.5012989.
- A. A. L. Michalchuk, et al., Predicting the reactivity of energetic materials: an ab initio multi-phonon approach, J. Mater. Chem. A, 2019, 7(33), 19539–19553, 10.1039/C9TA06209B.
- A. A. L. Michalchuk, J. Hemingway and C. A. Morrison, Predicting the impact sensitivities of energetic materials through zone-center phonon up-pumping, J. Chem. Phys., 2021, 154(6), 064105, DOI:10.1063/5.0036927.
- A. A. L. Michalchuk, Mechanochemical Processes in Energetic Materials: A Computational and Experimental Investigation. Springer Nature, 2020 Search PubMed.
- P. A. Banks, Z. Song and M. T. Ruggiero, Assessing the Performance of Density Functional Theory Methods on the Prediction of Low-Frequency Vibrational Spectra, J. Infrared, Millimeter, Terahertz Waves, 2020, 41, 1411–1429, DOI:10.1007/s10762-020-00700-7.
- C. B. Storm, J. R. Stine, and J. F. Kramer, Sensitivity Relationships in Energetic Materials, in Chemistry and Physics of Energetic Materials, ed. S. N. Bulusu, Springer Netherlands, Dordrecht, 1990, pp. 605–639, DOI:10.1007/978-94-009-2035-4_27.
- F. J. Zerilli and E. T. Toton, Shock-induced molecular excitation in solids, Phys. Rev. B, 1984, 29(10), 5891–5902, DOI:10.1103/PhysRevB.29.5891.
- G. Kumar, F. G. VanGessel, L. B. Munday and P. W. Chung, 3-Phonon Scattering Pathways for Vibrational Energy Transfer in Crystalline RDX, J. Phys. Chem. A, 2021, 125(35), 7723–7734, DOI:10.1021/acs.jpca.1c03225.
- P. Giannozzi, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502, DOI:10.1088/0953-8984/21/39/395502.
- A. Dal Corso, Pseudopotentials periodic table: From H to Pu, Comput. Mater. Sci., 2014, 95, 337–350, DOI:10.1016/j.commatsci.2014.07.043.
- D. C. Sorescu, B. M. Rice and D. L. Thompson, Theoretical Studies of the Hydrostatic Compression of RDX, HMX, HNIW, and PETN Crystals, J. Phys. Chem. B, 1999, 103(32), 6783–6790, DOI:10.1021/jp991202o.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5, DOI:10.1016/j.scriptamat.2015.07.021.
- A. A. L. Michalchuk, S. Rudić, C. R. Pulham and C. A. Morrison, Predicting the impact sensitivity of a polymorphic high explosive: the curious case of FOX-7, Chem. Commun., 2021, 57(85), 11213–11216, 10.1039/D1CC03906G.
- S. V. Bondarchuk, Theory of impact sensitivity revisited: mechanical-to-vibrational energy transfer phenomenon, FirePhysChem, 2021 DOI:10.1016/j.fpc.2021.10.001.
- F. W. Marrs, et al., Sources of Variation in Drop-Weight Impact Sensitivity Testing of the Explosive Pentaerythritol Tetranitrate, Ind. Eng. Chem. Res., 2021, 60(13), 5024–5033, DOI:10.1021/acs.iecr.0c06294.
- R. L. Simpson, P. A. Urtiew, D. L. Ornellas, G. L. Moody, K. J. Scribner and D. M. Hoffman, CL-20 performance exceeds that of HMX and its sensitivity is moderate, Propellants, Explos., Pyrotech., 1997, 22(5), 249–255, DOI:10.1002/prep.19970220502.
- R. R. McGuire, Properties of benzotrifuroxan, California Univ., Lawrence Livermore Lab., Livermore (USA), UCRL-52353(Rev.1), Mar. 1978. Accessed: Nov. 27, 2021. [Online]. Available: https://www.osti.gov/biblio/5117236 Search PubMed.
- B. M. Dobratz and P. C. Crawford, LLNL Explosives Handbook: Properties of Chemical Explosives and Explosive Simulants. 1985 Search PubMed.
- J. E. Cole, HMX, RDX, PETN, and TNT Revisited for Single Crystal and Vacuum Drop Weight Sensitivity, Army Ballistic Research Lab Aberdeen Proving Ground Md, Feb. 1979. Accessed: Aug. 02, 2020. [Online]. Available: https://apps.dtic.mil/sti/citations/ADA069122 Search PubMed.
- H. H. Cady, Studies on the Polymorphs of HMX, Los Alamos Scientific Laboratory of the University of California, 1962 Search PubMed.
- K. Y. Lee and M. D. Coburn, 3-nitro-1,2,4-triazol-5-one, a less sensitive explosive, Los Alamos National Lab., NM (USA), LA-10302-MS, Feb. 1985. Accessed: Nov. 25, 2021. [Online]. Available: https://www.osti.gov/biblio/5716279 Search PubMed.
- T. R. Gibbs and A. Popolato, LASL explosive property data, Univ of California Press, 1980, vol. 4, [Online]. Available: https://www.ucpress.edu/op.php?isbn=9780520040120 Search PubMed.
- H. Ostmark, A. Langlet, H. Bergman, U. Wellmar, and U. Bemm, FOX-7—A New Explosive with Low Sensitivity and High Performance, Proceedings of the 11th International Detonation Symposium, 1998, vol. 11, pp. 807–813 Search PubMed.
- I. J. Löchert, FOX-7 – A New Insensitive Explosive, DTSO – Aeronautical and Maritime Research Laboratory, DTSO-TR-1238, 2001 Search PubMed.
- Y. Ou, C. Wang, Z. Pan and B. Chen, Sensitivity of Hexanitrohexaazaisowurtzitane, Energ. Mater., 1999, 7(3), 100–102 CAS.
- P. Politzer and J. S. Murray, Impact sensitivity and crystal lattice compressibility/free space, J. Mol. Model., 2014, 20(5), 2223, DOI:10.1007/s00894-014-2223-7.
- N. R. Cummock, J. R. Lawrence, M. Örnek and S. F. Son, The influence of microstructure and conformational polymorph on the drop-weight impact sensitivity of δ-phase HMX, J. Energ. Mater., 2021, 1–26, DOI:10.1080/07370652.2021.1895915.
- C.-C. Ye, Q. An, W.-Q. Zhang and W. A. Goddard, Initial Decomposition of HMX Energetic Material from Quantum Molecular Dynamics and the Molecular Structure Transition of β-HMX to δ-HMX, J. Phys. Chem. C, 2019, 123(14), 9231–9236, DOI:10.1021/acs.jpcc.9b01169.
- P. D. Peterson, K. -Y. Lee, D. S. Moore, R. J. Scharff and G. R. Avilucea, The evolution of sensitivity in hmx-based explosives during the reversion from delta to beta phase, AIP Conf. Proc., 2007, 955(1), 987–990, DOI:10.1063/1.2833297.
- T. P. Russell, P. J. Miller, G. J. Piermarini and S. Block, Pressure/temperature phase diagram of hexanitrohexaazaisowurtzitane, J. Phys. Chem., 1993, 97(9), 1993–1997, DOI:10.1021/j100111a043.
- A. T. Nielsen, et al., Synthesis of polyazapolycyclic caged polynitramines, Tetrahedron, 1998, 54(39), 11793–11812, DOI:10.1016/S0040-4020(98)83040-8.
- Q. Ma, et al., A novel multi-nitrogen 2,4,6,8,10,12-hexanitrohexaazaisowurtzitane-based energetic co-crystal with 1-methyl-3,4,5-trinitropyrazole as a donor: experimental and theoretical investigations of intermolecular interactions, New J. Chem., 2017, 41(10), 4165–4172, 10.1039/C6NJ03976F.
- R. Guo, J. Tao, X.-H. Duan, C. Wu and H.-Z. Li, Study on phonon spectra and heat capacities of CL-20/MTNP cocrystal and co-formers by density functional theory method, J. Mol. Model., 2020, 26(6), 148, DOI:10.1007/s00894-020-04415-3.
- E. A. Zhurova, V. V. Zhurov and A. A. Pinkerton, Structure and Bonding in β-HMX-Characterization of a Trans-Annular N···N Interaction, J. Am. Chem. Soc., 2007, 129(45), 13887–13893, DOI:10.1021/ja073801b.
- F. Chen, H. Zhang, F. Zhao, C. Meng and X. Cheng, A first-principles investigation into the hydrogen bond interaction in β-HMX, Sci. China: Phys., Mech. Astron., 2010, 53(6), 1080–1085, DOI:10.1007/s11433-010-4002-5.
- V. V. Zhurov, E. A. Zhurova, A. I. Stash and A. A. Pinkerton, Importance of the consideration of anharmonic motion in charge-density studies: a comparison of variable-temperature studies on two explosives, RDX and HMX, Acta Crystallogr. A, 2011, 67(2), 2, DOI:10.1107/S0108767310052219.
- J. Evers, T. M. Klapötke, P. Mayer, G. Oehlinger and J. Welch, α- and β-FOX-7, Polymorphs of a High Energy Density Material, Studied by X-ray Single Crystal and Powder Investigations in the Temperature Range from 200 to 423 K, Inorg. Chem., 2006, 45(13), 4996–5007, DOI:10.1021/ic052150m.
- Z. Chua, C. G. Gianopoulos, B. Zarychta, E. A. Zhurova, V. V. Zhurov and A. A. Pinkerton, Inter- and Intramolecular Bonding in 1,3,5-Triamino-2,4,6-trinitrobenzene: An Experimental and Theoretical Quantum Theory of Atoms in Molecules (QTAIM) Analysis, Cryst. Growth Des., 2017, 17(10), 5200–5207, DOI:10.1021/acs.cgd.7b00674.
- Y. Ma, A. Zhang, X. Xue, D. Jiang, Y. Zhu and C. Zhang, Crystal Packing of Impact-Sensitive High-Energy Explosives, Cryst. Growth Des., 2014, 14(11), 6101–6114, DOI:10.1021/cg501267f.
- E. A. Zhurova, et al., Atoms-in-Molecules Study of Intra- and Intermolecular Bonding in the Pentaerythritol Tetranitrate Crystal, J. Am. Chem. Soc., 2006, 128(45), 14728–14734, DOI:10.1021/ja0658620.
- C. M. Tarver, S. K. Chidester and A. L. Nichols, Critical Conditions for Impact- and Shock-Induced Hot Spots in Solid Explosives, J. Phys. Chem., 1996, 100(14), 5794–5799, DOI:10.1021/jp953123s.
- H. Qiu, V. Stepanov, A. R. Di Stasio, T. Chou and W. Y. Lee, RDX-based nanocomposite microparticles for significantly reduced shock sensitivity, J. Hazard. Mater., 2011, 185(1), 489–493, DOI:10.1016/j.jhazmat.2010.09.058.
- R. E. Setchell, Grain-size effects on the shock sensitivity of hexanitrostilbene (HNS) explosive, Combust. Flame, 1984, 56(3), 343–345, DOI:10.1016/0010-2180(84)90068-3.
- R. J. Spear and V. Nanut, Reversal of particle size/shock sensitivity relationship at small particle size for pressed heterogeneous explosives under sustained shock loading, J. Energ. Mater., 1989, 7(1–2), 77–114, DOI:10.1080/07370658908012561.
- C. L. Mader and J. D. Kershner, Numerical modeling of the effect of temperature and particle size on shock initiation properties of HMX and TATB, J. Energ. Mater., 1992, 10(2–3), 69–95, DOI:10.1080/07370659208018230.
- K. Joshi, M. Losada and S. Chaudhuri, Intermolecular Energy Transfer Dynamics at a Hot-Spot Interface in RDX Crystals, J. Phys. Chem. A, 2016, 120(4), 477–489, DOI:10.1021/acs.jpca.5b06359.
- Z. Chen, et al., Direct Prediction of Phonon Density of States With Euclidean Neural Networks, Adv. Sci., 2021, 8(12), 2004214, DOI:10.1002/advs.202004214.
- T. C. Duong, N. H. Paulson, M. Stan and S. Chaudhuri, An efficient approximation of the supercell approach to the calculation of the full phonon spectrum, Calphad, 2021, 72, 102215, DOI:10.1016/j.calphad.2020.102215.
- S. Kong, F. Ricci, D. Guevarra, J. B. Neaton, C. P. Gomes, and J. M. Gregoire, Density of States Prediction for Materials Discovery via Contrastive Learning from Probabilistic Embeddings, arXiv, 2021, preprint, arXiv:211011444 [Cond-Mat Physicsphysics], Accessed: Dec. 14, 2021. [Online]. Available: http://arxiv.org/abs/2110.11444.
- Y. Han, et al., Machine learning accelerates quantum mechanics predictions of molecular crystals, Phys. Rep., 2021, 934, 1–71, DOI:10.1016/j.physrep.2021.08.002.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine learning for molecular and materials science, Nature, 2018, 559(7715), 7715, DOI:10.1038/s41586-018-0337-2.
Footnote |
| † Electronic supplementary information (ESI) available: (1) Evaluation of the “nitroaromatics” model for nitramines; (2) phonon density of states of β-HMX from DFT-D – issues when using only the Gamma point; (3) optimized lattice parameters from DFT-D. vDOS of the molecular crystals and of the extracted molecules in gas phase, and some mode frequency assignments. Zip file of the vDOS data for the molecular crystals. See DOI: https://doi.org/10.1039/d2ra05062e |
| This journal is © The Royal Society of Chemistry 2022 |