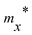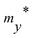Open Access Article
Open Access ArticleFirst-principles study on the structural properties of 2D MXene SnSiGeN4 and its electronic properties under the effects of strain and an external electric field†
Vo D. Dat ab,
Tuan V. Vu
ab,
Tuan V. Vu ab,
A. A. Lavrentyevc,
O. Y. Khyzhun
ab,
A. A. Lavrentyevc,
O. Y. Khyzhun d,
Nguyen N. Hieu
d,
Nguyen N. Hieu *ef and
Hien D. Tong*g
*ef and
Hien D. Tong*g
aLaboratory for Computational Physics, Institute for Computational Science and Artificial Intelligence, Van Lang University, Ho Chi Minh City, Vietnam. E-mail: dat.vd@vlu.edu.vn
bFaculty of Mechanical – Electrical and Computer Engineering, Van Lang University, Ho Chi Minh City, Vietnam
cDepartment of Electrical Engineering and Electronics, Don State Technical University, 1 Gagarin Square, 344010 Rostov-on-Don, Russian Federation
dFrantsevych Institute for Problems of Materials Science, National Academy of Sciences of Ukraine, 3 Krzhyzhanovsky Street, UA-03142 Kyiv, Ukraine
eInstitute of Research and Development, Duy Tan University, Da Nang 550000, Vietnam. E-mail: hieunn@duytan.edu.vn
fFaculty of Natural Sciences, Duy Tan University, Da Nang 550000, Vietnam
gFaculty of Engineering, Vietnamese-German University, Binh Duong, Vietnam. E-mail: hien.td@vgu.edu.vn
First published on 12th October 2022
Abstract
The MXene SnSiGeN4 monolayer as a new member of the MoSi2N4 family was proposed for the first time, and its structural and electronic properties were explored by applying first-principles calculations with both PBE and hybrid HSE06 approaches. The layered hexagonal honeycomb structure of SnSiGeN4 was determined to be stable under dynamical effects or at room temperature of 300 K, with a rather high cohesive energy of 7.0 eV. The layered SnSiGeN4 has a Young's modulus of 365.699 N m−1 and a Poisson's ratio of 0.295. The HSE06 approach predicted an indirect band gap of around 2.4 eV for the layered SnSiGeN4. While the major donation from the N-p orbitals to the band structure makes SnSiGeN4's band gap close to those of similar 2D MXenes, the smaller distributions from the other orbitals of Sn, Si, and Ge slightly vary this band gap. The work functions of the GeN and SiN surfaces are 6.367 eV and 5.903 eV, respectively. The band gap of the layered SnSiGeN4 can be easily tuned by strain and an external electric field. A semiconductor–metal transition can occur at certain values of strain, and with an electric field higher than 5 V nm−1. The electron mobility of the layered SnSiGeN4 can reach up to 677.4 cm2 V−1 s−1, which is much higher than the hole mobility of about 52 cm2 V−1 s−1. The mentioned characteristics make the layered SnSiGeN4 a very promising material for use in electronic and photoelectronic devices, and for solar energy conversion.
1 Introduction
After important achievements in the study and isolation of graphene, more and more 2D materials have become interesting subjects of scientific research, where the common target is to overcome modern problems, such as excessive energy consumption, environmental pollution, and the need for higher-efficiency electronic devices. The advantages of these 2D materials come from their unique properties, including high charge-carrier mobility and thermal conductivity, tunable band gaps and electronic features, good mechanical characteristics, and the ability to be well-integrated in electronic devices.1–6 Recently, the application of 2D materials has gone from theoretical prediction to practical uses. Monolayer graphene has been used in gamma and beta radiation sensors, and 2D Bi2Se3 has been applied in photodetectors.7,8 Both InSe and MoTe2 have been shown to be very effective when used in field-effect transistors.9,10 Moreover, hexagonal boron nitride has been applied in light-emitting diodes, and 2D WS2 can improve the photocatalytic activity of mesoporous titania films.11 Therefore, more and more 2D materials have been experimentally realized, including silicene, phosphorene, germanene, stanene, borophene, antimonene, arsenene, tellurene, selenene, bismuthene, aluminene, and gallenene.12–22In addition, transition metal chalcogenides (TMDs) are also very popular 2D materials consisting of transition metal elements and chalcogens. Monolayer TMDs are usually characterized as having strong spin–orbit coupling effects leading to a spin-valley phenomenon that, in combination with the buckled hexagonal structure, results in an enhancement of the quantum spin/anomalous Hall effects.23,24 TMDs, depending on their geometric structure and the d electrons of the transition metals, can be semiconducting, metallic, superconducting, and possess a charge density wave.25–35 Janus 2D materials are a sub-branch of TMDs whose electronic properties are asymmetric, which may lead to strong Rashba spin splitting, piezoelectric polarization, and second-harmonic generation.36
MXenes are another branch of TMDs where one of the chalcogens is either an N or C element. Recently, 2D MoSiN4 and WSiN4 have been successfully synthesized and are considered to be another family of MXenes, whose structures are in the form of septuple-atomic-layers.37 This study has inspired many other studies that predict the existence of many other compounds having the general formula MA2N4, where M represents transition metals W, V, Nb, Ta, Cr, Mo, Zr and Hf, and A represents chalcogens Si and Ge.38–40 MXenes are very promising 2D materials as they have been shown to have great practical applications, including in electrode designs that allow new batteries to be charged much faster,41 triboelectric nanogenerators,42 conductive coatings with great flexibility,43 and gas sensors.44
Theoretical studies predict that there are many more MXenes yet to be synthesized and with interesting properties to discover.45 Therefore, the aim of the current study is to expand the family of MXenes with a septuple-atomic-layer structure by proposing and studying the properties of a SnSiGeN4 monolayer. The mechanical and thermal stabilities of this material are justified based on the cohesive energy, phonon dispersion, elastic properties, including the Young's modulus and Poisson's ratio, and AIMD simulation. As mentioned above, MXenes can be applied in many devices where elasticity is sometimes highly required.46 Meanwhile, it is well-known that the electronic properties of 2D materials can be greatly affected by strain and even an external electric field.47–51 As a consequence, the effect of strain and an electric field on the properties of SnSiGeN4 are also considered in this study.
2 Methodology
Based on the stable configurations of most compounds in the MoSi2N4 family, the initial atomic structure of SnSiGeN4 was simulated with space group P3m1, where the in-plane lattice parameters a = b = 3.083 Å, and the normal lattice parameter c = 40 Å, were used to prevent interaction between the atoms of neighboring unit cells. The Vienna Ab initio Simulation Package (VASP) was used to perform the structural optimization of SnSiGeN4, where the generalized gradient approximation parameterized by Perdew–Burke–Ernzerhof (PBE)52 and the Heyd–Scuseria–Ernzerhof (HSE06)53 hybrid functional were applied within the DFT framework. The buckling in the SnSiGeN4 structure originates from the connection of the SnN2, SiN, and GeN planes. Therefore, the DFT-D3 (ref. 54) semi-empirical function was included in the calculation to account for the van der Waals interlayer interactions. The pseudopotentials used to describe the Sn, Si, Ge, and N atoms were generated by Kresse based on the projector-augmented wave (PAW) method55 with an energy cut-off of 500 eV. The partial occupancies of the orbitals were described by the Gaussian smearing method with a smearing width of 0.05 eV. The Monkhorst–Pack method was used to sample a 16 × 16 × 1 k-point mesh of the Brillouin zone. The structural optimization was converged when the difference in total energy of the atomic structure was smaller than 10−4 eV, the force acting on the ions was about 0.01 eV Å−1, and the electron energy was 1 meV.3 Results and discussion
3.1 Structural properties of the layered SnSiGeN4
The optimized structure of SnSiGeN4, shown in Fig. 1(a), is a layered structure whose xy-projection has a hexagonal shape with lattice parameters a = b = 3.083 Å. This in-plane lattice parameter is very close to the values of 3.0282 Å and 3.143 Å of monolayers SnSi2N4 and SnGe2N4, respectively,56,57 and it is also comparable to those of MX2N4 compounds (M = Hf, Zr, Ti, Cr, Mo, W, or Sn; X = Si or Ge), which range from 2.91 Å to 3.0282 Å.37,56,58,59 The bond lengths d2 and d3 between Sn and the two nearest N atoms are about 2.18 Å, which is close to the range of 2.10–2.18 Å for the M–N bond lengths in MSiN4 compounds (M = Mo, W, Cr, Ti, Zr, or Hf),60 and it is also close to the Sn–N bond lengths of 2.166 Å and 2.2 Å in the two similar monolayers of SnSi2N4 and SnGe2N4.56,57 The side view of SnSiGeN4 is depicted in Fig. 1(b), where the middle SnN2 layer is stacked between the SiN and GeN layers via bonding with N atoms. The bond lengths between the N and Si atoms, and between the N and Ge atoms, are denoted as d1 and d4, respectively. The Si–N, Ge–N, and Sn–N bond lengths are also very close to those in the SiN2, GeN2, and SnN2 compounds that were obtained in previous theoretical and experimental studies.61,62 As shown in Table 1, the bond lengths increase down group 14 from Si to Ge and Sn. This finding is consistent with an earlier experimental study on the pyrite forms of group 14 elements.62 In comparison to Si3N4,63 whose Si–N bond length is 1.89 Å, the bonding between Si and N atoms in SnSiGeN4 is more covalent due to a shorter bond length of about 1.837 Å. The strength of the bonding in SnSiGeN4 is also estimated by the cohesive energy Ecoh of the layered SnSiGeN4 in one unit cell by the following formula:
 | (1) |
| a (Å) | d1 (Å) | d2 (Å) | d3 (Å) | d4 (Å) | θ1 (deg) | θ2 (deg) | θ3 (deg) | Ecoh (eV per atom) |
|---|---|---|---|---|---|---|---|---|
| 3.083 | 1.837 | 2.185 | 2.180 | 1.882 | 104.30 | 70.72 | 109.15 | −7.004 |
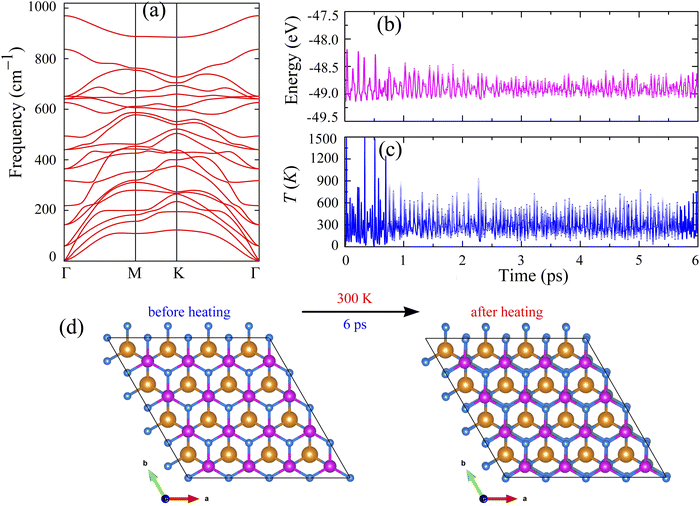
The calculated cohesive energy of SnSiGeN4 is −7.004 eV per atom. It is higher than those of phosphorene (−3.3 eV per atom), MoSi2P4 (−5.5 eV per atom), and MoSi2As4 (−6.1 eV per atom).64–66 At the same time, this value is slightly smaller than those of graphene (−7.7 eV per atom) and MoSi2N4 (−8.46 eV per atom).67,68 As a result, the mechanical strength of the layered SnSiGeN4 is predicted to be higher than that of phosphorene and some other members of the MoSi2N4 family, but comparable to graphene and slightly lower than that of MoSi2N4. Furthermore, the mechanical stability of the layered SnSiGeN4 can be estimated by its phonon dispersion, which was calculated and presented in Fig. 2(a).
As with other hexagonal structures, the highly symmetric path of the layered SnSiGeN4 is Γ–M–K–Γ, along which the phonon dispersion was calculated. All 21 vibrational modes originating from Sn, Si, Ge, and 4 N atoms are positive, confirming the layered SnSiGeN4's dynamic stability. Because the acoustic branches have a low slope, the elastic modulus and melting temperature of SnSiGeN4 are expected to be moderate. It can also be seen in Fig. 2(a) that the gap between the optical and acoustic branches is very narrow, implying that heat transfer in the layered SnSiGeN4 can be affected by optical effects. The thermal stability of the layered SnSiGeN4 was also estimated by applying ab initio molecular dynamics (AIMD) to study the changes in total energy and temperature of this material when heated to 300 K for 6 ps. The total energy of the layered SnSiGeN4 changes slightly in response to the extreme temperature fluctuation at the beginning of the heating process, as seen in Fig. 2(b and c). However, because the structure of the layered SnSiGeN4 quickly returns to near-equilibrium states, both the total energy and temperature of the system fluctuate gradually. These findings support the thermal stability of the layered SnSiGeN4, as shown in Fig. 2(d), where the atomic structure of this semiconductor changes slightly during the heating process.
In the case of the SnSiGeN4 monolayer, its mechanical stability can be investigated using Born–Huang's criteria69 with elastic constants Cij, shown in Table 2, where only C11 and C12 are required to be determined because C22 = C11, and C66 is half the difference between C11 and C12. These elastic constants can be calculated by fitting the values of elastic energy to different strains.70 Both Born–Huang's criteria, C11 > 0 and C112 − C122 > 0, are satisfied in the case of the SnSiGeN4 monolayer, confirming the mechanical stability of this material.71 Moreover, the Young's modulus Y2D and Poisson's ratio ν of the SnSiGeN4 monolayer were also calculated as follows:
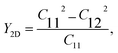 | (2) |
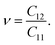 | (3) |
| C11 | C12 | C66 | Y2D | υ |
|---|---|---|---|---|
| 400.657 | 118.347 | 141.155 | 365.699 | 0.295 |
The values of Y2D and ν are listed in Table 2. With a Young's modulus of 365.699 N m−1, the ability of the layered SnSiGeN4 to withstand deformation under compression or tension is medium in comparison with other members of the MoSi2N4 family, such as MoSi2As4, MoSi2P4, WSi2N4, and MoSi2N4, whose Young's modulus values are in the range of 118–600 N m−1.72,73 The Poisson's ratio of 0.295 is generally considered to be low, therefore the layered SnSiGeN4 is expected to be easily fractured. The Poisson's ratio of SnSiGeN4 is very close to that of MoSiGeN4 and WSiGeN4 (ν = 0.290–0.296) in the MoSi2N4 family.58 Generally, the SnSiGeN4 monolayer is less mechanically stable than SnSi2N4 and SnGe2N4 due to its lower Young's modulus and Poisson's ratio in comparison with these two similar compounds.56,57 The existence of the SnSiGeN4 monolayer can also be verified by comparing with experimental data, therefore, the theoretical X-ray diffraction pattern for SnSiGeN4 was also calculated and is presented in Fig. S1 of the ESI.†
3.2 Electronic properties of the SnSiGeN4 monolayer
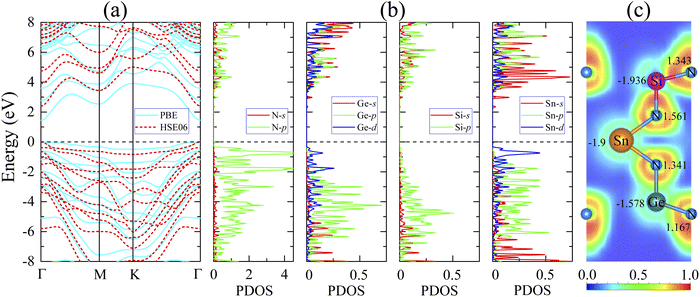
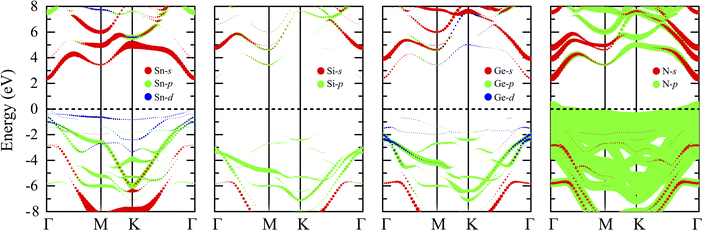
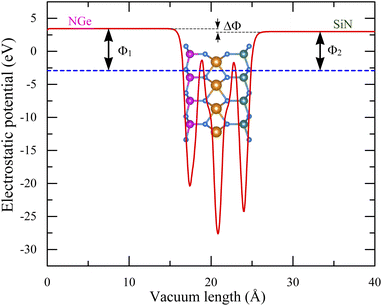
Most members of the MoSi2N4 family have been shown to be suitable for applications in optoelectronics and photocatalytic devices,38,73 which usually require specific electronic structures. Therefore, it is interesting to study the electronic properties of the newly proposed SnSiGeN4 compound. Since the layered SnSiGeN4 has a symmetric hexagonal structure in the x–y plane, its band structure was calculated along the Γ–M–K–Γ path. In Fig. 3(a), both the PBE and HSE06 methods reveal a direct band gap of the layered SnSiGeN4 compound, where both the highest valence band and the lowest conduction band are located at the Γ-point. However, the band gaps of the SnSiGeN4 monolayer reproduced by the two calculation methods differ by around 0.9 eV, with the PBE band gap being 1.446 eV and the HSE06 band gap being 2.396 eV. A similar difference in the band gaps calculated by the PBE and HSE06 methods is also found for SnSi2N4 and SnGe2N4 monolayers.56,57 Furthermore, the HSE06 band gap of SnSiGeN4 is located between those of SnSi2N4 and SnGe2N4, which are 3.19 eV and 1.832 eV, respectively. Comparing the PBE band gap of the layered SnSiGeN4 to those of its analogous 2D MXenes MoSiGeN4 and WSiGeN4, which are 1.35 eV and 1.63 eV, respectively,58 it is evident that the band gap changes moderately with the variation of Mo, W, and Sn metals. It is widely known that the poor handling of the exchange-correlation in PBE calculations leads to an underestimation of the band gap in semiconductors and insulators.74 Therefore, the accuracy of the band gap can be increased by including a small portion of the accurate Hartree–Fock exchange in hybrid functionals, like HSE, B3LYP, and PBE0.75–77 The band gap of the SnSiGeN4 monolayer reproduced by the HSE06 method is 2.396 eV, which is in good agreement with the PBE band gap values (2.396–2.70 eV)60,78 of similar 2D compounds MSi2N4 (M = Mo, W, Ti, Zr, or Hf). The PBE and HSE06 band structures of the SnSiGeN4 monolayer (shown in Fig. 3(a) as blue solid lines and red dashed lines, respectively) were found to be comparable to one another. However, in the HSE06 calculations, the valence bands are moved to lower energy levels, while the conduction bands' energy levels are raised, resulting in widening of the band gap with HSE06. The four elements Sn, Si, Ge and N are close to one another in the SnSiGeN4 monolayer resulting in substantial orbital splitting, which is depicted in Fig. 3(b), with many peaks in both the valence and conduction bands. This advantage allows the SnSiGeN4 monolayer to absorb a wide range of solar wavelengths and be a promising material for solar energy conversion. The characteristics of the SnSiGeN4 monolayer band structure, Fig. 4, are well reflected by the weighted band structure. It can be seen that the band gap of SnSiGeN4 is largely established by the N-p orbitals, which contribute major portions to both the highest valence bands (HVBs) and the lowest conduction bands (LCBs), as in other 2D MXenes where the N element is the main component in the layered structures.58,60,78 Meanwhile, the small deviation in the band gap of SnSiGeN4 from those of other 2D MXenes is caused by the minor contributions of the d orbitals of Sn and Ge atoms to the HVBs, as well as the s orbitals of Ge, Si, and Sn atoms to the LCBs. The bonding characteristics of the SnSiGeN4 monolayer are reflected by the electron localization function (ELF) in Fig. 3(c), where the regions with fully localized electrons, fully delocalized electrons, and extremely low electron density are denoted by red (1.0), green (0.5), and blue (0.0) colors, respectively. Most localized electrons are observed to concentrate around the N atoms, whereas the regions between all atoms are fully occupied by delocalized electrons, demonstrating the covalent nature of the bonding in the SnSiGeN4 monolayer.Many 2D MXenes similar to SnSiGeN4 have been discovered to be promising materials for photoelectric applications,57,79 where the work function plays one of the most important roles.80–82 Therefore, modification of the work function of 2D materials has long been an interesting research subject.83 The work functions of the SnSiGeN4 monolayer were calculated by eqn (4), as shown below, and are shown in Fig. 5 as Φ1 (6.367 eV) and Φ2 (5.903 eV) for the NGe and NSi surfaces, respectively. These work functions are comparable to those of a MoGe2N4 monolayer (5.44 eV) and SnSi2N4 (6.20 eV).56,84 It is interesting to note that the work function of SnGe2N4 (6.216 eV)57 is a little bit higher than that of SnSi2N4 (6.20 eV).56 Meanwhile, the work function of the SnSi2N4 surface can be enhanced by about 0.2 eV by substituting one Si by one Ge atom to form a SnSiGeN4 monolayer. Because pz orbitals are important in determining the magnitude of the work function in 2D materials,85 the occupation of Ge-p and Sn-p orbitals at different energy levels in the HVBs, as seen in Fig. 4, is expected to account for a potential drop of around ΔΦ = 0.464 eV. This anisotropy is favorable for the separation of photo-driven electron–hole pairs. Another advantage of the SnSiGeN4 monolayer is that its work function values are in the range of 4–7 eV, which have been shown to be suitable for optoelectronics and photoelectric applications.86,87
| Φ = Φvac − ΦF | (4) |
The band structure of most 2D materials can be easily tuned by strain88,89 because the decrease of symmetry can greatly affect the Hamiltonian function.90 Moreover, an external electric field has also been reported to influence the band structure of some special semiconductors, such as phosphorene/graphene-like GaN, a SnS2/PbI2 heterostructure, and two-dimensional transition metal dichalcogenides.91–93 2D materials whose band gap is tunable play an important role in electrical and optoelectronic devices.93 In order to investigate the potential of the SnSiGeN4 monolayer for application in the mentioned areas, its band structure under the effect of strains ranging from −10% to 10%, and an electric field whose magnitude is −5 V nm−1 to 5 V nm−1 is explored. The primary effect of compressive strains on the band structure is a redistribution in the band edges. As illustrated in Fig. 6(a and b), the higher the strain rate, the more the valence bands are concave up and the conduction bands are concave down, indicating that the mobility of electrons and holes would rise. Tensile strains, on the other hand, tend to flatten the valence and conduction bands, therefore, these strains are expected to reduce the charge-carrier mobility in the layered SnSiGeN4. Compressive and tensile strains have a considerable influence on the energy levels of the band edges, with some minor redistribution of the extrema of the valence and conduction bands. As a result, the nature and amplitude of the band gap in the layered SnSiGeN4 are likely to be modified. To further comprehend this problem, the change in band gap of the layered SnSiGeN4 as a discrete function of strain is shown in Fig. 6(c). The band gap increases to its maximum value of about 2 eV at −6% compression. As the compressive strain increases, the band gap decreases significantly, and the direct band gap transforms into an indirect band gap. All tensile strains generate a fast reduction in the band gap, during which the indirect band gap becomes direct at roughly 1% tensile strain and returns to being indirect at greater tensile rates. The electronic structure of the SnSiGeN4 monolayer changes in a similar way to the SnGe2N4 monolayer, where compressive strains tend to enlarge the band gap and tensile strains cause the band gap to narrow.57 External electric fields have a negligible effect on the form of the valence and conduction bands, as seen in Fig. 6(d and e), while the band gap remains constant. An external electric field with a magnitude of 4 V nm−1 was discovered to be the critical point affecting SnSiGeN4's band structure, as illustrated in Fig. 6(f), where the band gap begins to decrease dramatically. The layered SnSiGeN4 was also observed to turn into a metal under a tensile strain of 10%, as shown in Fig. 6(c). However, this is a theoretical prediction where the stability of the SnSiGeN4 structure under very high strains must be carefully verified. Actually, there are many 2D structures that have been proven, both experimentally and theoretically, to be stable at strains higher than 6–10%,94 therefore, this phenomenon of the layered SnSiGeN4 is an interesting subject for further studies.
The variation of SnSiGeN4's band structure under strain, as shown in Fig. 8, is very interesting and it can cause a change in the mobility of the charge carrier. In order to uncover the mechanism causing these effects and how it can affect the transport properties of the SnSiGeN4 monolayer, it is necessary to analyze the redistribution of electrons in the structures under some representative strain rates of 4% and 8%. Therefore, the electron localization function and Bader charges were calculated for both biaxial and uniaxial strains. The ELF shown in Fig. 7 and the Bader charges (see Tables S1 and S2 of the ESI†) of the compressively strained, unstrained, and tensile-strained SnSiGeN4 monolayer are depicted from left to right. Similar to Fig. 3(c), the green area represents fully delocalized electrons, the red regions correspond to fully localized electrons and the regions with low electron density are blue. The changes in the band gap of SnSiGeN4 as a function of biaxial and uniaxial strains are presented in Fig. S2 of the ESI.†
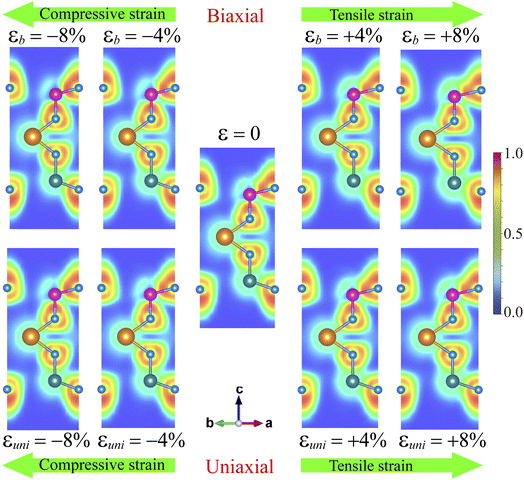 | ||
| Fig. 7 Electron localization function of SnSiGeN4 under biaxial/uniaxial compressive strains, at equilibrium, and under biaxial/uniaxial tensile strains. | ||
Both biaxial and uniaxial strains cause similar effects. Under increasing compressive strain, the green regions spread out more between the atoms, indicating a higher level of covalent bonding. Meanwhile, the tensile strains cause wider spaces between the green regions, reflecting a decrease in the overlap between the valence electrons of neighboring atoms in the SnSiGeN4 monolayer. The Bader charge data show that, under compressive strains, more electrons are transferred from the metals to the N atoms. Consequently, the partly empty 2p orbital of N receives more electrons, lowering the conduction bands at the M-point in Fig. 4. At the same time, the Sn atoms lose their electrons from the 5s2 and 5p2 orbitals; this raises the conduction bands at the Γ-points. Considering Fig. 3, it is obvious that the Sn-s orbitals mainly donate to the lowest conduction bands, and the N-p orbitals dominate the highest valence bands. As long as the conduction bands at the Γ-point are higher than those at the M-point, the band gap of SnSiGeN4 still widens under compressive strains. When the conduction bands at the M-point are lower than those at the Γ-points, SnSiGeN4 has an indirect band gap, which is also narrowed. Under tensile strains, charge transfer happens in the reverse direction when more electrons stay in the 5s2 and 5p2 orbitals of the Sn atoms, causing a narrower gap between the valence and conduction bands at the Γ-points, which leads to the decreasing of the SnSiGeN4's band gap at low tensile rates. At higher tensile rates, the valence and conduction bands at the Γ-point overlap each other, making the SnSiGeN4 monolayer a metal. The highest valence band also fluctuates strongly due to fewer electrons being concentrated on the N atoms.
Generally, both compressive and tensile strains cause the redistribution of charge density, which can be observed from the ELF and Bader charge plots. This change affects the occupation of electrons in the valence bands (mainly constructed by N-p orbitals) and conduction bands (largely donated to by Sn-s orbitals) causing some fluctuations in the extrema of these bands. As a result, the band gap is tuned. Because the effective mass is proportional to the derivative of the band-edge curves, a change in the shape of the conduction and valence band edges can cause a change in the mobility of electrons and holes. As shown in Fig. 8, the tensile strains tend to flatten the valence bands, therefore, it is expected that the effective mass of the hole is decreased. Meanwhile, the hole's effective mass may increase as the valence bands are more concave down under compressive strains. Analogously, the effective mass of the electron is expected to be higher as the peaks in the lowest conduction bands are sharper under strain.
3.3 Transport properties of the SnSiGeN4 monolayer
The charge-carrier mobility μ2D for the layered SnSiGeN4 was calculated based on deformation potential theory.95 Firstly, the total energy E, and band-edge alignment ΔEedge were calculated and constructed as functions of uniaxial strain εuni along the x-axis and y-axis. The E(εu) and ΔEedge(εuni) functions are presented in Fig. 9(a and b), respectively. Moreover, the dependence of total energy E(k) on the k-points was also constructed. Then, the effective mass m*, the elastic modulus C2D, and the deformation energy constant Ed, were as follows:
 | (5) |
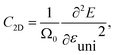 | (6) |
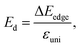 | (7) |
Finally, the charge-carrier mobility μ2D was calculated as follows:
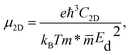 | (8) |
 | ||
| Fig. 9 (a) Strain-dependent total energy and (b) the band-edge positions of the SnSiGeN4 structures along the two transport directions x and y. | ||
The layered SnSiGeN4 has a symmetric hexagonal structure in the x–y plane, therefore, its charge-carrier mobilities and related quantities, as shown in Table 3, are independent of the direction along which they were determined. They are, however, dependent on the energy functions of the k-point, as given in eqn (5)–(7). The effective masses are inversely proportional to the second derivatives of the energy functions, according to eqn (5). As a result, the layered SnSiGeN4 with sharply curved conduction bands and relatively flat valence bands, as shown in Fig. 4, has a lower electron effective mass than hole effective mass. These characteristics cause the electron mobility to be greater than the hole mobility, which are 670.83–677.4 cm2 V−1 s−1 and 50.2–51.9 cm2 V−1 s−1, respectively. Considering the charge-carrier mobilities of SnSi2N4 and SnGe2N4 (electron mobilities of 2735.97 and 1061.66 cm2 V−1 s−1, respectively),56,57 it is obvious that the substitution of one Si atom in SnSi2N4 by one Ge atom to form SnSiGeN4 causes a significant decrease of the electron mobility. The layered SnSiGeN4 has greater electron mobility than other similar 2D compounds, MX2N4 (M = Mo or W; X = Ge or Si).38 It's worth noticing that the post-transition metal Sn produces an opposite charge-carrier mobility pattern compared to other compounds in the MoSi2N4 family, MX2Y4 (M = V, Cr, Mo, or W; X = Si or C; Y= N, P, or As),66,96 where the electron mobility is substantially lower than the hole mobility. A similar phenomenon has been reported in monolayers of SnGe2N4 and SnSi2N4.56,57
4 Conclusions
In conclusion, the atomic, electronic, and transport characteristics of a SnSiGeN4 monolayer were investigated by first-principles calculations. The theoretical results show that the SnSiGeN4 monolayer is dynamically, mechanically, and thermally stable. The band gap of the layered SnSiGeN4 was estimated to be about 2.4 eV, which is easily tuned by strain. Both strain and an external electric field at some specific values can cause the SnSiGeN4 monolayer to change from a semiconductor to a metal. Being an indirect semiconductor with a suitable band gap to absorb visible light and a high electron mobility of 677.4 cm2 V−1 s−1, SnSiGeN4 monolayers are very promising materials for application in nanoelectronics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully appreciate the useful discussion of O. V. Marchuk (Department of Chemistry and Technology, Lesya Ukrainka Volyn National University, Lutsk, Ukraine).References
- M. C. Lemme, D. Akinwande, C. Huyghebaert and C. Stampfer, Nat. Commun., 2022, 13, 1392 CrossRef CAS PubMed.
- E. Singh, P. Singh, K. S. Kim, G. Y. Yeom and H. S. Nalwa, ACS Appl. Mater. Interfaces, 2019, 11, 11061–11105 CrossRef CAS PubMed.
- S. Yang, C. Jiang and S.-h. Wei, Appl. Phys. Rev., 2017, 4, 021304 Search PubMed.
- X. Wang, S. Kajiyama, H. Iinuma, E. Hosono, S. Oro, I. Moriguchi, M. Okubo and A. Yamada, Nat. Commun., 2015, 6, 6544 CrossRef CAS PubMed.
- X. Xi, Z. Wang, W. Zhao, J.-H. Park, K. T. Law, H. Berger, L. Forró, J. Shan and K. F. Mak, Nat. Phys., 2016, 12, 139–143 Search PubMed.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699–712 CrossRef CAS.
- M. W. Tawfik, A. Sharaf and M. Serry, Nanomaterials, 2022, 12, 305 CrossRef CAS PubMed.
- C.-C. Wang, P.-T. Lin, F.-S. Shieu and H.-C. Shih, Nanomaterials, 2021, 11, 3353 CrossRef CAS PubMed.
- Y. Zhang, X. Sun, K. Jia, H. Yin, K. Luo, J. Yu and Z. Wu, Nanomaterials, 2021, 11, 3311 CrossRef CAS PubMed.
- G. Y. Bae, J. Kim, J. Kim, S. Lee and E. Lee, Nanomaterials, 2021, 11, 2805 CrossRef CAS PubMed.
- J. Ren, L. Stagi, L. Malfatti, V. Paolucci, C. Cantalini, S. Garroni, M. Mureddu and P. Innocenzi, Nanomaterials, 2022, 12, 1074 CrossRef CAS PubMed.
- B. Aufray, A. Kara, S. Vizzini, H. Oughaddou, C. Léandri, B. Ealet and G. Le Lay, Appl. Phys. Lett., 2010, 96, 183102 CrossRef.
- W. Li, M. Li, J. Li, J. Liang, K. R. Adair, Y. Hu, Q. Xiao, X. Cui, R. Li and F. Brandys, et al., ACS Appl. Nano Mater., 2020, 3, 7508–7515 CrossRef CAS.
- E. Bianco, S. Butler, S. Jiang, O. D. Restrepo, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 4414–4421 CrossRef CAS PubMed.
- J. Ouyang, L. Zhang, L. Li, W. Chen, Z. Tang, X. Ji, C. Feng, N. Tao, N. Kong and T. Chen, et al., Nano-Micro Lett., 2021, 13, 90 CrossRef CAS PubMed.
- V. Kochat, A. Samanta, Y. Zhang, S. Bhowmick, P. Manimunda, S. A. S. Asif, A. S. Stender, R. Vajtai, A. K. Singh and C. S. Tiwary, et al., Sci. Adv., 2018, 4, e1701373 CrossRef PubMed.
- M. O. Valappil, A. Ganguly, J. Benson, V. K. Pillai, S. Alwarappan and P. Papakonstantinou, RSC Adv., 2020, 10, 43585–43591 RSC.
- C. Gibaja, M. Assebban, I. Torres, M. Fickert, R. Sanchis-Gual, I. Brotons, W. S. Paz, J. J. Palacios, E. G. Michel and G. Abellán, et al., J. Mater. Chem. A, 2019, 7, 22475–22486 RSC.
- S. Chahal, P. Ranjan, M. Motlag, S. S. Yamijala, D. J. Late, E. H. S. Sadki, G. J. Cheng and P. Kumar, Adv. Mater., 2021, 33, 2102039 CrossRef CAS PubMed.
- Z. Xie, C. Xing, W. Huang, T. Fan, Z. Li, J. Zhao, Y. Xiang, Z. Guo, J. Li and Z. Yang, et al., Adv. Funct. Mater., 2018, 28, 1705833 CrossRef.
- S. M. Beladi-Mousavi, A. M. Pourrahimi, Z. Sofer and M. Pumera, Adv. Funct. Mater., 2019, 29, 1807004 Search PubMed.
- P.-Y. Liao, J.-K. Qin, G. Qiu, Y. Wang, W. Wu and D. Y. Peide, Xenes, Elsevier, 2022, pp. 197–224 Search PubMed.
- C. Liu, Y. Wang, H. Li, Y. Wu, Y. Li, J. Li, K. He, Y. Xu, J. Zhang and Y. Wang, Nat. Mater., 2020, 19, 522–527 CrossRef CAS PubMed.
- G.-B. Liu, W.-Y. Shan, Y. Yao, W. Yao and D. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085433 CrossRef.
- M. Chhowalla, H. S. Shin, G. Eda, L.-J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263–275 CrossRef PubMed.
- G. Eda, H. Yamaguchi, D. Voiry, T. Fujita, M. Chen and M. Chhowalla, Nano Lett., 2011, 11, 5111–5116 CrossRef CAS PubMed.
- Y. Venkata Subbaiah, K. Saji and A. Tiwari, Adv. Funct. Mater., 2016, 26, 2046–2069 CrossRef CAS.
- K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805 CrossRef PubMed.
- A. A. Soluyanov, D. Gresch, Z. Wang, Q. Wu, M. Troyer, X. Dai and B. A. Bernevig, Nature, 2015, 527, 495–498 CrossRef CAS PubMed.
- D. H. Keum, S. Cho, J. H. Kim, D.-H. Choe, H.-J. Sung, M. Kan, H. Kang, J.-Y. Hwang, S. W. Kim and H. Yang, et al., Nat. Phys., 2015, 11, 482–486 Search PubMed.
- N. E. Staley, J. Wu, P. Eklund, Y. Liu, L. Li and Z. Xu, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 184505 CrossRef.
- A. F. Kusmartseva, B. Sipos, H. Berger, L. Forro and E. Tutiš, Phys. Rev. Lett., 2009, 103, 236401 CrossRef CAS PubMed.
- B. Sipos, A. F. Kusmartseva, A. Akrap, H. Berger, L. Forró and E. Tutiš, Nat. Mater., 2008, 7, 960–965 CrossRef CAS PubMed.
- T. Kidd, T. Miller, M. Chou and T.-C. Chiang, Phys. Rev. Lett., 2002, 88, 226402 CrossRef CAS PubMed.
- G. Li, W. Hu, D. Qian, D. Hsieh, M. Hasan, E. Morosan, R. J. Cava and N. Wang, Phys. Rev. Lett., 2007, 99, 027404 CrossRef CAS PubMed.
- L. Zhang, Z. Yang, T. Gong, R. Pan, H. Wang, Z. Guo, H. Zhang and X. Fu, J. Mater. Chem. A, 2020, 8, 8813–8830 RSC.
- Y.-L. Hong, Z. Liu, L. Wang, T. Zhou, W. Ma, C. Xu, S. Feng, L. Chen, M.-L. Chen and D.-M. Sun, et al., Science, 2020, 369, 670–674 CrossRef CAS.
- B. Mortazavi, B. Javvaji, F. Shojaei, T. Rabczuk, A. V. Shapeev and X. Zhuang, Nano Energy, 2021, 82, 105716 CrossRef CAS.
- A. Priydarshi, Y. S. Chauhan, S. Bhowmick and A. Agarwal, Nanoscale, 2022, 14, 11988–11997 RSC.
- Y. Chen, S. Tian and Q. Tang, J. Phys. Chem. C, 2021, 125, 22581–22590 CrossRef CAS.
- M. R. Lukatskaya, S. Kota, Z. Lin, M.-Q. Zhao, N. Shpigel, M. D. Levi, J. Halim, P.-L. Taberna, M. W. Barsoum and P. Simon, et al., Nat. Energy, 2017, 2, 17105 CrossRef CAS.
- Y. Dong, S. S. K. Mallineni, K. Maleski, H. Behlow, V. N. Mochalin, A. M. Rao, Y. Gogotsi and R. Podila, Nano Energy, 2018, 44, 103–110 CrossRef CAS.
- H. An, T. Habib, S. Shah, H. Gao, M. Radovic, M. J. Green and J. L. Lutkenhaus, Sci. Adv., 2018, 4, eaaq0118 CrossRef PubMed.
- S. J. Kim, H.-J. Koh, C. E. Ren, O. Kwon, K. Maleski, S.-Y. Cho, B. Anasori, C.-K. Kim, Y.-K. Choi and J. Kim, et al., ACS Nano, 2018, 12, 986–993 CrossRef CAS.
- T. L. Tan, H. M. Jin, M. B. Sullivan, B. Anasori and Y. Gogotsi, ACS Nano, 2017, 11, 4407–4418 CrossRef CAS.
- W. Lu, B. Mustafa, Z. Wang, F. Lian and G. Yu, Nanomaterials, 2022, 12, 871 CrossRef CAS PubMed.
- G. J. Kraberger, D. A. Egger and E. Zojer, Adv. Mater. Interfaces, 2015, 2, 1500323 CrossRef.
- G. G. Naumis, S. Barraza-Lopez, M. Oliva-Leyva and H. Terrones, Rep. Prog. Phys., 2017, 80, 096501 CrossRef.
- H. Jiang, L. Zheng, Z. Liu and X. Wang, InfoMat, 2020, 2, 1077–1094 CrossRef CAS.
- M. A. Bissett, M. Tsuji and H. Ago, Phys. Chem. Chem. Phys., 2014, 16, 11124–11138 RSC.
- W. Chen, X. Gui, L. Yang, H. Zhu and Z. Tang, Nanoscale Horiz., 2019, 4, 291–320 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- M. Tian, C. Wei, J. Zhang, J. Wang and R. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 103, 195305 CrossRef CAS.
- V. D. Dat and T. V. Vu, RSC Adv., 2022, 12, 10249–10257 RSC.
- S.-D. Guo, W.-Q. Mu, Y.-T. Zhu, R.-Y. Han and W.-C. Ren, J. Mater. Chem. C, 2021, 9, 2464–2473 RSC.
- S.-D. Guo, Y.-T. Zhu, W.-Q. Mu and W.-C. Ren, Europhys. Lett., 2020, 132, 57002 CrossRef CAS.
- Y. Yin, M. Yi and W. Guo, ACS Appl. Mater. Interfaces, 2021, 13, 45907–45915 CrossRef CAS PubMed.
- R. Weihrich, V. Eyert and S. F. Matar, Chem.Phys. Lett., 2003, 373, 636–641 CrossRef CAS.
- K. Niwa, H. Ogasawara and M. Hasegawa, Dalton Trans., 2017, 46, 9750–9754 RSC.
- B. Xu, J. Dong, P. F. McMillan, O. Shebanova and A. Salamat, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 014113 CrossRef.
- J. Guan, Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 113, 226801 CrossRef PubMed.
- P.-J. Chen and H.-T. Jeng, Sci. Rep., 2016, 6, 23151 CrossRef CAS PubMed.
- H. Yao, C. Zhang, Q. Wang, J. Li, Y. Yu, F. Xu, B. Wang and Y. Wei, Nanomaterials, 2021, 11, 559 CrossRef CAS PubMed.
- V. Ivanovskaya, A. Zobelli, D. Teillet-Billy, N. Rougeau, V. Sidis and P. Briddon, Eur. Phys. J. B, 2010, 76, 481–486 CrossRef CAS.
- A. Bafekry, M. Faraji, A. A. Ziabari, M. Fadlallah, C. V. Nguyen, M. Ghergherehchi and S. Feghhi, New J. Chem., 2021, 45, 8291–8296 RSC.
- M. Born, K. Huang and M. Lax, Am. J. Phys., 1955, 23, 474 CrossRef.
- Y. Guo, S. Zhou, Y. Bai and J. Zhao, Appl. Phys. Lett., 2017, 110, 163102 CrossRef.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- C. Shen, L. Wang, D. Wei, Y. Zhang, G. Qin, X.-Q. Chen and H. Zhang, arXiv preprint arXiv:2108.03671, 2021.
- A. Bafekry, M. Faraji, D. M. Hoat, M. Shahrokhi, M. Fadlallah, F. Shojaei, S. Feghhi, M. Ghergherehchi and D. Gogova, J. Phys. D: Appl. Phys., 2021, 54, 155303 CrossRef CAS.
- E. L. Shirley, X. Zhu and S. G. Louie, Phys. Rev. Lett., 1992, 69, 2955 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, 174101 CrossRef PubMed.
- J. Muscat, A. Wander and N. Harrison, Chem. Phys. Lett., 2001, 342, 397–401 CrossRef CAS.
- Q. Wu, L. Cao, Y. S. Ang and L. K. Ang, Appl. Phys. Lett., 2021, 118, 113102 CrossRef CAS.
- C.-c. Jian, X. Ma, J. Zhang and X. Yong, J. Phys. Chem. C, 2021, 125, 15185–15193 CrossRef CAS.
- C. Peng, T. Zhou, P. Wei, W. Xu, H. Pan, F. Peng, J. Jia, K. Zhang and H. Yu, APL Mater., 2021, 9, 070703 CrossRef CAS.
- M. Jakhar, A. Kumar, P. K. Ahluwalia, K. Tankeshwar and R. Pandey, Materials, 2022, 15, 2221 CrossRef CAS PubMed.
- Y. Wang, Z. Ding, N. Arif, W.-C. Jiang and Y.-J. Zeng, Mater. Adv., 2022, 3, 3389–3417 RSC.
- M. Kwan, R. Winter, P. H. Mutin, M. Eizenberg and G. Ramanath, Appl. Phys. Lett., 2017, 111, 121602 CrossRef.
- C. Nguyen, N. V. Hoang, H. V. Phuc, A. Y. Sin and C. V. Nguyen, J. Phys. Chem. Lett., 2021, 12, 5076–5084 CrossRef CAS PubMed.
- J. T. Robinson, J. Culbertson, M. Berg and T. Ohta, Sci. Rep., 2018, 8, 2006 CrossRef PubMed.
- N. Bhalla, S. Taneja, P. Thakur, P. K. Sharma, D. Mariotti, C. Maddi, O. Ivanova, D. Petrov, A. Sukhachev and I. S. Edelman, et al., Nano Lett., 2021, 21, 9780–9788 CrossRef CAS PubMed.
- Z. Yu, W. Feng, W. Lu, B. Li, H. Yao, K. Zeng and J. Ouyang, J. Mater. Chem. A, 2019, 7, 11160–11169 RSC.
- A. Chaves, J. G. Azadani, H. Alsalman, D. Da Costa, R. Frisenda, A. Chaves, S. H. Song, Y. D. Kim, D. He and J. Zhou, et al., npj 2D Mater. Appl., 2020, 4, 29 CrossRef CAS.
- S. Yang, Y. Chen and C. Jiang, InfoMat, 2021, 3, 397–420 CrossRef.
- Y. Sun, S. Thompson and T. Nishida, J. Appl. Phys., 2007, 101, 104503 CrossRef.
- J. Guo, Z. Zhou, H. Li, H. Wang and C. Liu, Nanoscale Res. Lett., 2019, 14, 174 CrossRef PubMed.
- Y. Ma, X. Zhao, M. Niu, X. Dai, W. Li, Y. Li, M. Zhao, T. Wang and Y. Tang, RSC Adv., 2017, 7, 25582–25588 RSC.
- F. Liu, J. Zhou, C. Zhu and Z. Liu, Adv. Funct. Mater., 2017, 27, 1602404 CrossRef.
- F. Motazedian, J. Zhang, Z. Wu, D. Jiang, S. Sarkar, M. Martyniuk, C. Yan, Y. Liu and H. Yang, Mater. Des., 2021, 197, 109257 CrossRef CAS.
- S. Bruzzone and G. Fiori, Appl. Phys. Lett., 2011, 99, 222108 CrossRef.
- B. Mortazavi, F. Shojaei, B. Javvaji, T. Rabczuk and X. Zhuang, Mater. Today Energy, 2021, 22, 100839 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra05265b |
| This journal is © The Royal Society of Chemistry 2022 |