Open Access Article
Open Access ArticleTransformer-based multitask learning for reaction prediction under low-resource circumstances†
Haoran Qiaoa,
Yejian Wu b,
Yun Zhang
b,
Yun Zhang b,
Chengyun Zhang
b,
Chengyun Zhang b,
Xinyi Wu
b,
Xinyi Wu b,
Zhipeng Wu
b,
Zhipeng Wu b,
Qingjie Zhao
b,
Qingjie Zhao c,
Xinqiao Wangb,
Huiyu Li
c,
Xinqiao Wangb,
Huiyu Li *a and
Hongliang Duan*bd
*a and
Hongliang Duan*bd
aCollege of Mathematics and Physics, Shanghai University of Electric Power, Shanghai 200090, China. E-mail: huiyuli@shiep.edu.cn
bArtificial Intelligence Aided Drug Discovery Institute, College of Pharmaceutical Sciences, Zhejiang University of Technology, Hangzhou 310014, China. E-mail: hduan@zjut.edu.cn
cInnovation Research Institute of Traditional Chinese Medicine, Shanghai University of Traditional Chinese Medicine, Shanghai 201203, China
dState Key Laboratory of Drug Research, Shanghai Institute of Materia Medica (SIMM), Chinese Academy of Sciences, Shanghai 201203, China
First published on 8th November 2022
Abstract
Recently, effective and rapid deep-learning methods for predicting chemical reactions have significantly aided the research and development of organic chemistry and drug discovery. Owing to the insufficiency of related chemical reaction data, computer-assisted predictions based on low-resource chemical datasets generally have low accuracy despite the exceptional ability of deep learning in retrosynthesis and synthesis. To address this issue, we introduce two types of multitask models: retro-forward reaction prediction transformer (RFRPT) and multiforward reaction prediction transformer (MFRPT). These models integrate multitask learning with the transformer model to predict low-resource reactions in forward reaction prediction and retrosynthesis. Our results demonstrate that introducing multitask learning significantly improves the average top-1 accuracy, and the RFRPT (76.9%) and MFRPT (79.8%) outperform the transformer baseline model (69.9%). These results also demonstrate that a multitask framework can capture sufficient chemical knowledge and effectively mitigate the impact of the deficiency of low-resource data in processing reaction prediction tasks. Both RFRPT and MFRPT methods significantly improve the predictive performance of transformer models, which are powerful methods for eliminating the restriction of limited training data.
1 Introduction
With the growth of technology, deep learning for chemistry research has made significant contributions to various aspects, such as chemical reaction generation, yield prediction, retrosynthesis analysis, absorption, distribution, metabolism, excretion, and toxicity prediction, prediction of drug–target interaction, drug–target binding affinity, and compound–protein interaction.1–10 For example, the Zhavoronkov group discovered effective inhibitors using an artificial intelligence method in 21 days, which is of significance to human life science.11 Among these, deep learning methods that combine deep learning and reaction prediction have recently drawn much attention. Reaction prediction is typically regarded as a machine translation task from the viewpoint of natural language processing.9 One of the popular machine translation models is the transformer, which is a fully-attention-based architecture.12 This model provides strong support for chemical reaction scenarios. In previous studies, reaction prediction has achieved remarkable generalization ability.13 Coley et al. refer to reaction centers as the minimum set of graph editors needed to convert reactant graphs to product graphs and treat reaction prediction as a graph transformation problem. They use a graph convolutional neural network to predict the set of atoms/bonds in the reaction center and then generate candidate products by enumerating all possible bond conformation changes within the set. Their model achieved a top-1 accuracy of 85.6% in the USPTO_MIT dataset.14 However, their model did not consider the stereo structure, which is important for chemical reactions. Schwaller et al. treated chemical reaction prediction as a translation problem from reactants to products and applied the transformer model to it for the first time. In their study, the transformer model achieved a top-1 accuracy of 90.4% in the USPTO_MIT dataset.12 The USPTO_MIT dataset used in these studies contained 480k chemical reactions, which is a huge amount of data. In real life, data for specific reaction types are often scarce. For example, Wang et al. focused on the Heck reaction prediction and relied on a transformer model. The datasets they obtained, however, only total 9000, which was not enough for a data-driven model. Therefore, the top-1 accuracy of the model was only 66.3%.15 This phenomenon suggests that the size of the training dataset significantly influences the performance of deep-learning algorithms. To address the issue caused by low-resource datasets, our study used reaction prediction as a vehicle to implement a multitasking fully data-driven model for a low-resource dataset problem.Multitask learning is an approach to inductive transfer that improves generalization by using the domain data in the training signals of related tasks as an inductive bias. This is accomplished by learning multiple tasks simultaneously while using a shared representation; what is learned for one task can aid the learning of other tasks more effectively.16 A multitask model is a combinational model with a capacity for multiple task prediction that can be simultaneously trained with data from various datasets and ultimately produce an enhanced multitask prediction.17 There are many scenarios for multitask learning applications, such as pixel prediction, sentiment analysis, hotspot detection, and audio pattern recognition.18–22
This study implements a multiforward reaction prediction transformer (MFRPT) and retro-forward reaction prediction transformer (RFRPT) to demonstrate the feasibility of multitasking in chemical reaction prediction. Several classical low-resource datasets involving Baeyer–Villiger, Heck, and Chan–Lam reactions are used. Our models are trained without the aid of any reaction data from outside the dataset. Under the same conditions, our model outperformed all previous seq2seq models. Additionally, our models can estimate their uncertainty. We hope our study provides new insights into the application of the natural language processing model in chemical reactions and ease its dilemma under low-resource datasets.
2 Materials and methods
2.1 Problem description
The reaction prediction problem is a procedure of predicting precursor products resulting in the input reactants. Given the token sequence of the source product, x, the template-free reaction prediction model finds the most probable product token sequence, y, as follows:
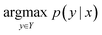 | (1) |
2.2 Baseline model
The baseline model used in this study is based on the transformer architecture.12 The model was originally constructed for neural machine translation tasks. The primary feature of this architecture is the complete removal of the recurrent neural network component, which is entirely dependent on the attention mechanism.The transformer is a stepwise autoregressive encoder–decoder model, which consists of a combination of multi-head attention layers and a positional feed-forward layer. The multi-head attention layers in the encoder attend to the input sequence and encode it into a hidden representation. The decoder has two types of multi-head attention layers. The first is masked and only attends to the preceding outputs of the decoder. The second multi-head attention layer attends to the encoder and outputs of the initial decoder attention layer.
A multi-head attention layer has several scaled-dot attention layers running in parallel that are then concatenated. The scaled-dot attention uses three inputs: the keys, K; the values, V; and the queries, Q and computes the attention as follows:
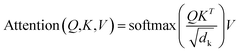 | (2) |
The dot product of the queries and keys compute how closely these two are aligned. If the query and key are aligned, their dot product will be large and vice versa. Each key has a corresponding value vector, which is multiplied by the output of softmax to normalize the dot products and emphasize their largest components. The scaling factor dk depends on the layer size. Based on its preceding outputs, the decoder queries the computed interesting features of the encoder from the input sequence.
2.3 Multitask-transformer model
Our model serves as a general framework for translating from one source language to many targets. Fig. 1 illustrates our multitask-transformer model. The model is a transformer-based encoder–decoder architecture with multiple target tasks, each of which has a specific translation direction. Different tasks share the same translation encoder across various reaction datasets. The objective function of our multitask model is set as the sum of multiple task likelihoods, which is the sum of several conditional probability terms conditioned on representations generated from the same encoder.
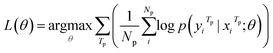 | (3) |
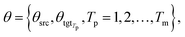 θsrc is a collection of parameters for the source encoder, and
θsrc is a collection of parameters for the source encoder, and 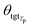 is the parameter set of the Tp th target language. Then, Np is the size of the parallel training corpus of the pth language pair. The target encoder parameters for different target languages are divided, allowing for the optimization of Tm.
is the parameter set of the Tp th target language. Then, Np is the size of the parallel training corpus of the pth language pair. The target encoder parameters for different target languages are divided, allowing for the optimization of Tm.
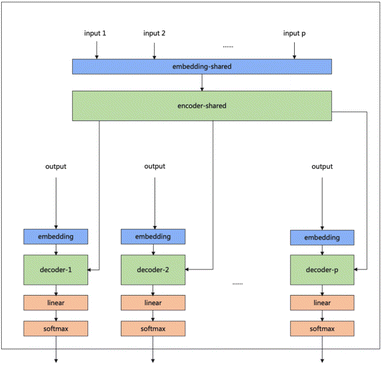 | ||
| Fig. 1 Multitask transformer model architecture. Each task has a decoder and decoder-embedding. The encoder and encoder-embedding for all tasks are shared. | ||
In this study, we designed two models for different purposes according to the multitasking architecture.
(1) In the multitasking architecture, the number of tasks determines the number of decoders. MFRPT has n decoders and decoder embeddings and one encoder. For the input of n datasets, the data of the same dataset will be entered in a batch during training. During training, the data of the same dataset will be entered in one batch, and each batch will be entered into the decoder embedding to the task for the output and derive the loss to update parameter weights, while the other decoders do not update parameter weights. The test is required to specify the type of prediction reaction so that the input data into the encoder to derive the context will be input to the specified decoder. As a result, in our experiment, there are three different reaction datasets, so we trained the MFRPT with three decoders and their decoder-embedding and one encoder.
(2) We treat the reaction prediction and retrosynthesis prediction of one reaction dataset as two different tasks, with two decoders and their decoder embeddings and an encoder. We term it RFRPT. From the input point of view, only one reaction dataset is input, and the dataset is processed as forward prediction and retrosynthesis prediction (by swapping the source language and the target language) to do both tasks. In our experiments, there are three different reaction datasets, so we trained three different RFRPTs.
2.4 Datasets
In this study, we used name and structure searches from the “Reaxys” database to export Chan–Lam, Heck, and Baeyer–Villiger reaction datasets. Each dataset was preprocessed using the following procedures. First, irrelevant data (for example, pressure, temperature, and yield) were deleted from these datasets, and only reaction entries were maintained. Second, the reaction simplified molecular input line entry system (SMILES) was canonized and all duplicate reaction entries are removed. The three reaction datasets were then filtered using template screening that adheres to the respective reaction rules and the dataset was split into training, validation, and test datasets at a ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
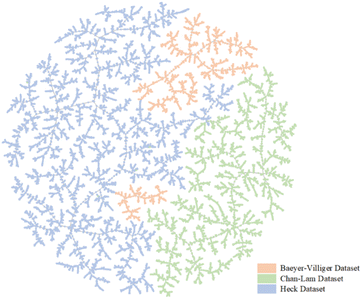
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (further details are shown in Sections S1–S3 of the ESI†). To further demonstrate the differences between the three datasets, a dimensionality reduction algorithm called locality-sensitive hashing (LSH) forest was used to show our datasets by using TMAP. TMAP is a data visualization module designed for the visualization of molecular datasets. Schwaller et al. designed a reaction fingerprint and extended it to interpret chemical reactions.28 In TMAP, reactions of the same type form a cluster and are separated from other types of reactions. Different colors are used to illustrate different reaction clusters. As shown in Fig. 2, TMAP distinguishes the three reaction types applied in our study. The three colors show the regional distribution in Fig. 2. The TMAP result demonstrates that the reaction fingerprints of the three datasets are not correlated.
1 (further details are shown in Sections S1–S3 of the ESI†). To further demonstrate the differences between the three datasets, a dimensionality reduction algorithm called locality-sensitive hashing (LSH) forest was used to show our datasets by using TMAP. TMAP is a data visualization module designed for the visualization of molecular datasets. Schwaller et al. designed a reaction fingerprint and extended it to interpret chemical reactions.28 In TMAP, reactions of the same type form a cluster and are separated from other types of reactions. Different colors are used to illustrate different reaction clusters. As shown in Fig. 2, TMAP distinguishes the three reaction types applied in our study. The three colors show the regional distribution in Fig. 2. The TMAP result demonstrates that the reaction fingerprints of the three datasets are not correlated.
2.5 Experimental details
Our models were developed using Python (version 3.8.10). A transformer model was constructed using Pytorch29 (version 1.11) and fairseq30 (version 0.12.2). Additionally, we used RDKit (version 2020.09.01) for reaction preprocessing and SMILES standardization. The number of encoder layers was 6, the number of decoder layers was 6, the hidden size of the positional feed-forward layers was 2048, the number of attention heads was 4. The total parameters of the baseline model were 30 million, the total parameters of RFPRT were 50 million, the total parameters of MFPRT were 70 million. A dropout probability of 0.3 was also adopted to avoid overfitting. The initial learning rate of the model was 1 × 10−3. The Adam optimizer was used to update the learning rate, and its parameter for optimization started at 1 × 10−7.31 We trained for 1500 epochs using an NVIDIA RTX 3090 GPU. The source code is available online at https://github.com/qiaohaoran/MFRPT-and-RFRPT.After training, each model was evaluated on the test set. The transformer is an autoregressive model. According to the vocabulary, each token in the sentence received its corresponding score. This study used a beam search to find the best results. Fig. 3 describes the time for the beam search results with a beam size of 10. Each time step of the beam search produces candidate sequences based on the first N. We set the maximum decoding length to 200. If sentence decoding exceeds this length or decodes to <end> token, decoding stops. After decoding, we receive the decoded sentence, which is the output and the softmax score for each token. To calculate the top-n accuracy of each dataset, we use the decoded sentence. The top-n accuracy represents the ratio of the total number of correct outcomes predicted by the model. In “top-n,” the “n” is a variable and can be all positive integers. Top-1 denotes that once the first prediction is found, the prediction results of the model scan stops. Similarly, top-2 denotes that once the first and second predictions are found, the prediction results of the model scan stops.
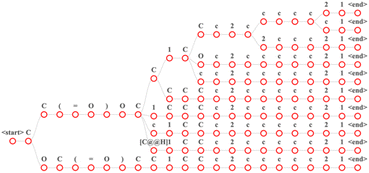 | ||
Fig. 3 Input the “CC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) CC1CCc2ccccc21” in the MFRPT model of beam search with a beam size of 10. In this figure, each path from the root node to the leaf node is a result. O) CC1CCc2ccccc21” in the MFRPT model of beam search with a beam size of 10. In this figure, each path from the root node to the leaf node is a result. | ||
3 Results and discussion
3.1 Comparisons with baseline models
To discuss the performance of the MFRPT model in predicting reactions on different datasets, we show the top-n accuracies of the MFRPT model and their corresponding baseline models in Table 1. The top-1 accuracy on the Baeyer–Villiger dataset increased from 71.2% to 75.7%. For the reaction prediction on the Heck dataset, the top-1 accuracy increased from 73.3% to 81.0%, and the top-1 accuracy of reaction prediction on Chan–Lam dataset increased from 65.2% to 83.0%. After using the multitask model, the top-n accuracy of the MFRPT model in reaction prediction was significantly higher than the baseline in any top-n accuracy situation. This demonstrates that the shared encoder parameters can help the model learn the deeper logic contained in the SMILES, enhancing the generalization ability of the model.| Model | Dataset | Top-n accuracy (%) | |||
|---|---|---|---|---|---|
| Top-1 | Top-2 | Top-5 | Top-10 | ||
| Baseline | Baeyer–Villiger | 71.2 | 77.9 | 80.5 | 81.4 |
| Heck | 73.3 | 77.5 | 79.4 | 79.7 | |
| Chan–Lam | 65.2 | 71.0 | 72.9 | 74.1 | |
| MFRPT | Baeyer–Villiger | 75.7 | 80.5 | 81.9 | 82.3 |
| Heck | 81.0 | 84.4 | 86.4 | 87.0 | |
| Chan–Lam | 83.0 | 86.0 | 86.7 | 87.5 | |
Similarly, to verify the reaction prediction effect of the RFRPT model under different datasets, we show the top-1 accuracy of the three RFRPT models on three datasets and their corresponding baseline models in Fig. 4 (more detailed top-n accuracies are shown in Section S4 of the ESI†). On the Baeyer–Villiger dataset, the RFRPT model's forward reaction prediction task top-1 accuracy is 72.1% which is higher than the baseline model's 71.2%. In the retrosynthesis prediction task, the RFRPT model is 81.6% which is higher than the baseline model's 77.9%. The RFRPT's forward and retrosynthesis prediction tasks on the Heck dataset are 80.4% and 55.2%, respectively, which are higher than the baseline models' 73.3% and 37.6%, respectively. The top-1 accuracies of the Chan–Lam dataset are 78.2% and 66.5%, respectively, which are higher than the baseline models' 65.2% and 57.4%, respectively. Regarding top-1 accuracy, the RFRPT model performs better than the baseline model. In the same dataset, the RFRPT model's top-n accuracy is also higher than the baseline model. This demonstrates that the baseline model does not fully extract the chemical reaction rules from the data. Because the RFRPT model can learn from the source and target molecules, it has a good generalization ability. Despite having a lower top-n accuracy than MFRPT, RFRPT fully uses the data within a single dataset. This is a powerful way to enhance model generalization ability in low-resource situations and when there are no available data alternatives.
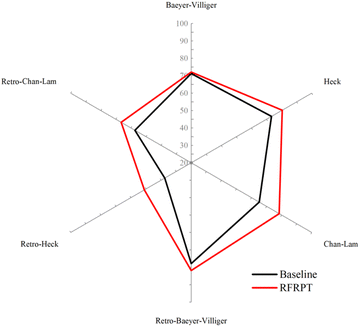 | ||
| Fig. 4 Accuracies of the baseline model and retro-forward reaction prediction transformer (RFRPT) model for different reactions. | ||
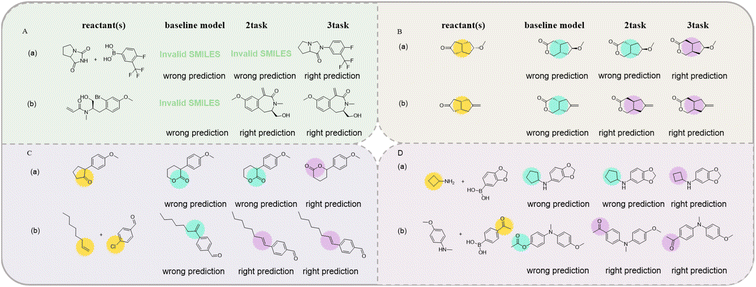
3.2 Error analysis
3.3 Uncertainty estimation of the model
It is necessary to estimate the uncertainty of the model to verify its validity. We use the logarithmic average of the probability of the model-predicted token as the confidence score to eliminate the issue of low probability caused by sentence length. We count the predictions that match the reported products and take the confidence scores above the threshold as true-positives (TPs), predictions that do not match the reported products and are below the threshold as true-negatives (TNs), predictions that match the reported products but are below the threshold as false-negatives (FNs), and finally, predictions that do not match the reported products but are above the threshold as false-positives (FPs). Further metric details are shown in Section S6 of the ESI.† Table 2 shows the results of our proposed MFRPT, RFRPT, and transformer baseline model on a full forward reaction prediction dataset. As shown in Table 2 and Fig. 6, the MFRPT model achieved the highest accuracy (0.883) and precision (0.931), but the RFRPT had the highest specificity (0.669), Matthews correlation coefficient (MCC) (0.594), and area under the receiver operating characteristic (ROC) curve (AUC) (0.834).| Model | Accuracy | Specificity | Precision | MCC | AUC |
|---|---|---|---|---|---|
| Baseline | 0.803 | 0.667 | 0.860 | 0.527 | 0.774 |
| RFRPT | 0.877 | 0.669 | 0.925 | 0.594 | 0.834 |
| MFRPT | 0.883 | 0.620 | 0.931 | 0.551 | 0.818 |
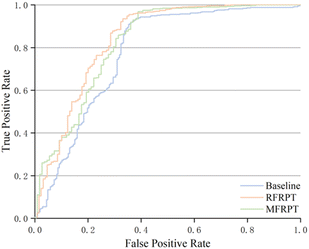 | ||
| Fig. 6 ROC curve for baseline, RFRPT, and MFRPT models on full datasets when evaluated on the test set. | ||
Fig. 6 shows the comparison results based on the ROC curves of the various models. The AUCs of RFRPT and MFRPT were 0.834 and 0.818. Compared with the baseline, the RFRPT increased the AUC by 7%.
Table 2 and Fig. 6 show that RFRPT and MFRPT are generally superior to the transformer baseline model. The RFRPT model has a better effect, and the AUC value further suggests that combining the forward reaction prediction and retrosynthesis can help the model comprehend the reaction more thoroughly, which enhances the ability of the model to discriminate. Simultaneously, the combination of various reaction datasets also enhances the reaction knowledge and qualifies the model for SMILES.
4 Conclusions
This study presents two methods: RFRPT and MFRPT for reaction prediction and retrosynthesis reaction prediction tasks based on Baeyer–Villiger, Heck, and Chan–Lam reaction datasets. Compared with the baseline model, MFRPT and RFRPT increased accuracy by 9.9% and 7%, respectively. This indicates that sharing the encoder and embedding parameters between various tasks can significantly boost the prediction performance. It also implies that the multitask framework can capture sufficient chemical knowledge and effectively address the scarcity of data in processing reaction prediction tasks. Additionally, we conducted a deeper analysis of errors like SMILES, chirality, and regioselective that appeared in the baseline, RFRPT, and MFRPT models. Comparisons of these errors show the success of multitask framework in chemical reaction prediction. Furthermore, the uncertainty of the model is evaluated, showing that the RFRPT and MFRPT models have higher AUC than the baseline model in several indicators. The results show the efficacy of the multitask learning and transformer model and offer a useful tool for the chemical reaction prediction of small datasets. This method could be used for similar reactions and combined with other algorithms to further accelerate artificial intelligence development in reaction prediction fields.Author contributions
All authors contributed to the study conception and design. Conceptualization, H. D.; methodology, H. Q., Y. W.; investigation, H. Q., Y. W., Y. Z.; data curation, Y. Z., X. W., X. W., Q. Z.; writing—original draft preparation, H. Q., C. Z.; writing—review and editing, H. L., Y. Z., Y. W., Z. W.; visualization, X. W., H. Q.; supervision, H. D., H. L.; funding acquisition, H. D., and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was supported by the National Natural Science Foundation of China, (No. 81903438) and Natural Science Foundation of Zhejiang Province (LD22H300004).Notes and references
- S. Moon, W. Zhung, S. Yang, J. Lim and W. Y. Kim, Chem. Sci., 2022, 13, 3661–3673 RSC.
- S. Hu, D. Xia, B. Su, P. Chen, B. Wang and J. A. Li, IEEE/ACM Trans. Comput. Biol. Bioinf., 2021, 18, 1315–1324 CAS.
- I. Lee and H. Nam, J. Cheminf., 2022, 14, 5 CAS.
- H. Stark, O.-E. Ganea, L. Pattanaik, R. Barzilay and T. Jaakkola, Presented in Part at 39th International Conference on Machine Learning (ICML 2022), Baltimore MD, USA, July, 2022 Search PubMed.
- K. Wang, R. Zhou, Y. Li and M. Li, DeepDTAF: a deep learning method to predict protein-ligand binding affinity, Briefings Bioinf., 2021, 22, bbab072 CrossRef PubMed.
- S. Li, F. Wan, H. Shu, T. Jiang, D. Zhao and J. Zeng, Cell Syst., 2020, 10, 308–322.e11 CrossRef CAS.
- X. Wang, D. Liu, J. Zhu, A. Rodriguez-Paton and T. Song, Biomolecules, 2021, 11, 643 CrossRef CAS PubMed.
- R. K. Bijral, I. Singh, J. Manhas and V. Sharma, Arch. Comput. Methods Eng., 2022, 29, 2513–2529 CrossRef.
- V. H. Nair, P. Schwaller and T. Laino, Chimia, 2019, 73, 997–1000 CrossRef CAS PubMed.
- J. Dong, M. Zhao, Y. Liu, Y. Su and X. Zeng, Briefings Bioinf., 2022, 23, bbab391 CrossRef PubMed.
- A. Zhavoronkov, Y. A. Ivanenkov, A. Aliper, M. S. Veselov, V. A. Aladinskiy, A. V. Aladinskaya, V. A. Terentiev, D. A. Polykovskiy, M. D. Kuznetsov, A. Asadulaev, Y. Volkov, A. Zholus, R. R. Shayakhmetov, A. Zhebrak, L. I. Minaeva, B. A. Zagribelnyy, L. H. Lee, R. Soll, D. Madge, L. Xing, T. Guo and A. Aspuru-Guzik, Nat. Biotechnol., 2019, 37, 1038–1040 CrossRef CAS PubMed.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, in Advances in Neural Information Processing Systems 30 (NIPS 2017), 2017, vol. 30 Search PubMed.
- P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. A. Hunter, C. Bekas and A. A. Lee, ACS Cent. Sci., 2019, 5, 1572–1583 CrossRef CAS PubMed.
- C. W. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola, W. H. Green, R. Barzilay and K. F. Jensen, Chem. Sci., 2019, 10, 370–377 RSC.
- L. Wang, C. Zhang, R. Bai, J. Li and H. Duan, Chem. Commun., 2020, 56, 9368–9371 RSC.
- R. Caruana, Mach. Learn., 1997, 28, 41–75 CrossRef.
- C. Cai, S. Wang, Y. Xu, W. Zhang, K. Tang, Q. Ouyang, L. Lai and J. Pei, J. Med. Chem., 2020, 63, 8683–8694 CrossRef CAS PubMed.
- F. Rahimi, E. E. Milios and S. Matwin, in Proceedings of the 21st ACM Symposium on Document Engineering (DocEng 2021), vol. 8, pp. 1–4, DOI:10.1145/3469096.3474926.
- L. Ilias and D. Askounis, IEEE J. Biomed. Health Inform., 2022, 26, 4153–4164 Search PubMed.
- X. Zhang, S. Zhang, Z. Cui, Z. Li, J. Xie and J. Yang, IEEE Trans. Multimed., 2022 DOI:10.1109/TMM.2022.3147664.
- T. Zhang, X. Gong and C. L. P. Chen, IEEE Trans. Cybern., 2021, 52, 6232–6243 Search PubMed.
- S. Kataria, J. Villalba and N. Dehak, in Proceedings of the 2021 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2021), pp. 7118–7122 Search PubMed.
- P. Schwaller, T. Gaudin, D. Lanyi, C. Bekas and T. Laino, Chem. Sci., 2018, 9, 6091–6098 RSC.
- X. Wang, Y. Li, J. Qiu, G. Chen, H. Liu, B. Liao, C.-Y. Hsieh and X. Yao, Chem. Eng. J., 2021, 420, 129845 CrossRef CAS.
- E. Kim, D. Lee, Y. Kwon, M. S. Park and Y. S. Choi, J. Chem. Inf. Model., 2021, 61, 123–133 CrossRef CAS PubMed.
- I. V. Tetko, P. Karpov, R. Van Deursen and G. Godin, Nat. Commun., 2020, 11, 5575 CrossRef CAS.
- K. Mao, X. Xiao, T. Xu, Y. Rong, J. Huang and P. Zhao, Neurocomput, 2021, 457, 193–202 CrossRef.
- P. Schwaller, D. Probst, A. C. Vaucher, V. H. Nair, D. Kreutter, T. Laino and J.-L. Reymond, Nat. Mach. Intell., 2021, 3, 144–152 CrossRef.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, in Advances in Neural Information Processing Systems 32 (NIPS 2019), 2019, vol. 32 Search PubMed.
- M. Ott, S. Edunov, A. Baevski, A. Fan, S. Gross, N. Ng, D. Grangier and M. Auli, arXiv, 2019, preprint, arXiv:1904.01038, DOI:10.48550/arXiv.1904.01038.
- B. Cortiñas-Lorenzo and F. Pérez-González, Entropy, 2020, 22, 1379 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra05349g |
| This journal is © The Royal Society of Chemistry 2022 |