Open Access Article
Open Access ArticleVisible optical nonlinearity of vanadium dioxide dispersions
Longlong Chen,
Jing Huang,
Qian Yi,
Dongyang Liu,
Yuan He,
Ning Li,
Yi Feng,
Lili Miao and
Chujun Zhao *
*
Key Laboratory for Micro-/Nano-Optoelectronic Devices of Ministry of Education, Hunan Provincial Key Laboratory of Low-Dimensional Structural Physics and Devices, School of Physics and Electronics, Hunan University, Changsha 410082, China. E-mail: cjzhao@hnu.edu.cn
First published on 24th October 2022
Abstract
Vanadium dioxide (VO2), a correlated oxide compound, is one of the functional materials extensively studied in solid state physics due to its attractive physical properties. However, the nonlinear optical response of VO2 and related all-optical applications have been paid less attention. Here, the nonlinear refractive index (n2) and third-order nonlinear susceptibility (χ(3)) of VO2 dispersions have been acquired to be 3.06 × 10−6 cm2 W−1 and 1.68 × 10−4 esu at a wavelength of 671 nm, and 5.17 × 10−6 cm2 W−1 and 2.83 × 10−4 esu at a wavelength of 532 nm via the spatial self-phase modulation (SSPM) and spatial cross-phase modulation (SXPM) effects in the visible regime, respectively. Based on the excellent nonlinear optical properties of VO2 dispersions, the proof-of-principle functions such as optical logic or-gates, all-optical switches, and inter-channel information transfer are implemented in the visible wavelength. The experimental results on the response time of VO2 to light indicate that the formation of diffraction rings is mainly an electronically coherent third-order nonlinear optical process. The experimental results show that the VO2 dispersions exhibit an excellent nonlinear optical response and may lay the foundation for the application of VO2-based all-optical devices.
1. Introduction
All-optical modulation, a light-control-light scheme analogous to its counterpart of electronic modulation, plays an important role in signal processing, such as multiplexing and demultiplexing, signal regeneration, and optical logic gates.1,2 Usually, all-optical modulation can be achieved by utilizing the third-order nonlinear response of optical material or the thermo-optic effect via waveguide or free-space configurations.3–5 By comparison with the waveguide-based optical modulation, the free-space ones can realize broadband, high-power and high efficiency optical modulation, not limited by the availability of the low-loss waveguides.6The all-optical modulation can be demonstrated by the SSPM and SXPM effects in free space.7,8 The SSPM effect is a coherent third-order nonlinear optical process observed in liquid crystals in 1981.9 Subsequently, the phenomenon was also noticed in other materials, such as ferrofluid,10 SrxBa1−xNb2O6 and BaTiO3 crystal,11 and carbon nanotube.12 In 2011, Wu et al. studied the SSPM effect of two-dimensional graphene.13 Then, the SSPM effect was also discovered for many two-dimensional materials.4,8,14–16 In 2015, Wu et al. studied the SXPM effect of two-dimensional MoS2 for the first time and achieved an all-optical switch, showing that the SXPM effect is a typical all-optical modulation or all-optical control technique that enables light-to-light control.17 Subsequently, the SXPM effect of various two-dimensional materials has been studied successively, demonstrating the modulation and processing of optical signals.18–21 However, the performance of the all-optical device is limited by the physiochemical properties of the optical material, such as the stability and the optical nonlinearity. Two-dimensional materials have some common problems, such as poor stability, easy oxidation, and low threshold of optical damage, which can weaken the optical performance of materials. To avoid these drawbacks, it is necessary to find optical materials with excellent performance in other dimensions.
VO2 is one of the most widely explored functional materials in solid state physics given its attractive physical properties.22–24 Based on the characteristics of VO2, researchers have implemented devices that can actively modulate the performance by external excitation, such as cloaking device25,26 and active metasurface.27,28 In addition, the refractive index of VO2 changes by orders of magnitude during the structural change, which provides the possibility of dynamic adjustment of the optical system.29 The ultrafast response of VO2 to light is accompanied by a considerable number of photoexcited carriers, which makes it a candidate material for photodetector and phototransistor applications.30 The excellent properties of VO2 have made it widely used in the field of optics and optoelectronics, such as reversible all-optical switch,31 memorizer,32 adjustable optical polarization state system,33 memory metamaterial34 and optical driver.35 However, the nonlinear optical response of VO2 and related applications, especially in the visible spectrum range, have been paid less attention.
Here, we studied the nonlinear optical response of VO2 dispersions using the SSPM and SXPM effects and demonstrated their all-optical applications in the visible range. The n2 and χ(3) of the VO2 dispersions have been extracted at the incident wavelengths of 671 nm and 532 nm, respectively. It is found that the nonlinear optical response of VO2 dispersions can be modulated by the SXPM effect, which is beneficial to meet the needs of different optical applications. In addition, VO2-based all-optical applications in the visible spectral have been experimentally demonstrated, including the optical logic or-gate, all-optical switch, and inter-channel information transfer device. Furthermore, the response time of the SXPM effect suggests that the formation of diffraction rings of VO2 dispersions is mainly an electronically coherent third-order nonlinear optical process.
2. Material preparation and characterization
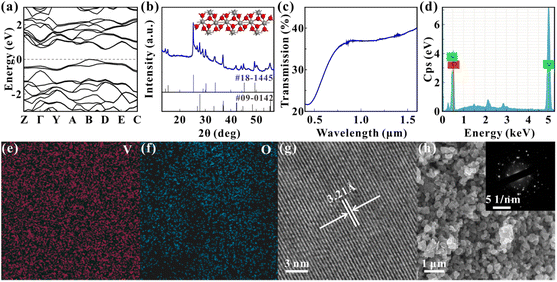
The VO2 particles are obtained from Macklin Biochemical Technology Co. The particles are ground and dissolved in N-methylpyrrolidone (NMP), and the concentration of the solution is 0.6 mg mL−1. Fig. 1(a) shows the energy band diagram of VO2 calculated with the first principle. The figure indicates that the bandgap of VO2 is about 0.57 eV, which means that the VO2 can respond to the visible light. Fig. 1(b) shows the X-ray diffraction (XRD) pattern of the samples with the peak positions corresponding to JCPDS codes 18-1445 (VO2·xH2O) and 09-0142 (VO2), indicating that the composition of the samples is VO2, and the inset shows the molecular structure of VO2. Fig. 1(c) shows the linear transmission spectra of the samples, and the curve follows the same trend as the VO2 thin films.28,36 Fig. 1(d), (e) and (f) show the energy dispersive spectroscopy (EDS) characterization of the samples, indicating that only V and O elements are present in the samples and that both elements are uniformly distributed in the samples. The atomic ratio of V to O is 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64, which is about 1
64, which is about 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and is consistent with the atomic ratio of VO2. The transmission electron microscopy (TEM) characterization of samples is shown in Fig. 1(g). The photograph clearly displays the lattice fringes of samples, indicating the crystalline nature of the samples. The lattice spacing is measured to be about 3.21 Å, which is consistent with the reported results.37 Fig. 1(h) shows the scanning electron microscope (SEM) photograph of samples, which shows that the grain size of particles is about several hundred nanometers. The inset of Fig. 1(h) displays the selected area electron diffraction (SAED) characterization of samples, which indicates that the samples are polycrystalline.
2 and is consistent with the atomic ratio of VO2. The transmission electron microscopy (TEM) characterization of samples is shown in Fig. 1(g). The photograph clearly displays the lattice fringes of samples, indicating the crystalline nature of the samples. The lattice spacing is measured to be about 3.21 Å, which is consistent with the reported results.37 Fig. 1(h) shows the scanning electron microscope (SEM) photograph of samples, which shows that the grain size of particles is about several hundred nanometers. The inset of Fig. 1(h) displays the selected area electron diffraction (SAED) characterization of samples, which indicates that the samples are polycrystalline.
3. Results and discussion
3.1 Nonlinear optical response of vanadium dioxide dispersions
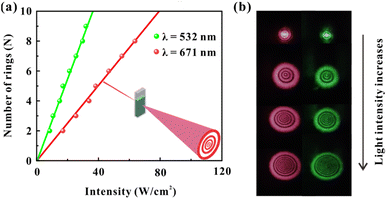
The interaction between light and VO2 dispersions can excite diffraction rings. When the Gaussian light passes through the samples, the phase shift Δψ of the light is expressed as,38
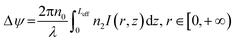 | (1) |
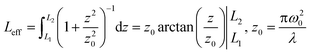 | (2) |
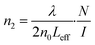 | (3) |
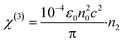 | (4) |
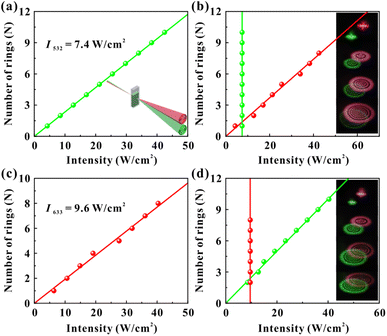
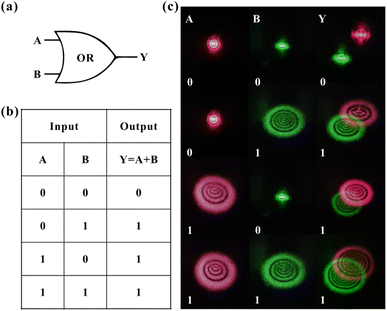
The light-control-light experimental results are shown in Fig. 3. Fig. 3(a) and (b) show the results of red light (control light) control of green light (probe light). The intensity of two monochromatic lights is low at the beginning (red: 4.3 W cm−2, green: 7.4 W cm−2), and lasers show only Gaussian spots when passing through the dispersions. Then, by only gradually increasing the intensity of the red beam (the intensity of the green beam is always 7.4 W cm−2 and remains constant), two colors of diffraction rings can be observed in the far field due to the SXPM effect. Fig. 3(a) shows the correspondence between the intensity of red light and the number of green diffraction rings, and Fig. 3(b) shows the correspondence between the number of rings for two beams and their incident intensity. The figures show that the ring number of green light is linearly related to the intensity of red light. Moreover, the ring number of red light still shows a linear relationship with the intensity of the red light. The inset in Fig. 3(b) shows the diffraction rings for two beams, which correspond to the gradual increase in intensity of red light from top to bottom. It can be seen from the figures that both the diameter and the ring number of two beams increase as the intensity of red light (control light) increases. Fig. 3(c) and (d) show the experimental results of the green light control of red light. The intensity of red light remains constant (9.6 W cm−2), and only the intensity of green light gradually increases. The figures show that the diffraction ring number of two beams is linearly related to the intensity of green light, which is similar as the experimental results in Fig. 3(a) and (b).
With the above experimental results, the modulation of nonlinear optical response of dispersions can be achieved by taking advantage of the interaction between red and green light in the SXPM effect. Here, the nonlinear optical response of red light to the samples is modulated from an initial 0.13 cm2 W−1 to 0.18 cm2 W−1 and 0.20 cm2 W−1, while the nonlinear optical response of green light to the samples is modulated from an initial 0.28 cm2 W−1 to 0.24 cm2 W−1 and 0.26 cm2 W−1. The method of modulating the nonlinear optical response of the VO2 dispersions by SXPM effect may enable on-demand modulation of the nonlinear optical response of materials.
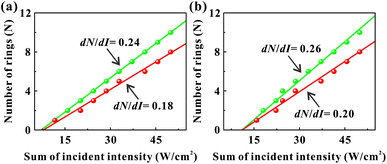
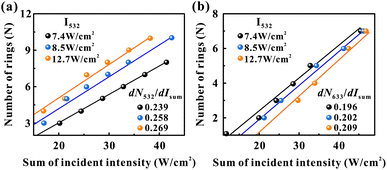
In the SXPM effect, we keep the intensity of the green light constant at 7.4 W cm−2 and vary the intensity of the red light (see Fig. 3(a) and (b)). Here, we vary the intensity of the green light and study the variation of dN/dI. As shown in Fig. 5, the black data, blue data, and orange data represent the green light intensity as 7.4 W cm−2, 8.5 W cm−2 and 12.7 W cm−2, respectively. Fig. 5(a) represents the variation pattern of dN532/dIsum, from which it can be seen that dN532/dIsum increases slightly as the green light intensity increases. Fig. 5(b) represents the variation pattern of dN633/dIsum, from which it can be seen that dN633/dIsum also increases slightly as the light intensity of green light increases. This can also be explained by the fact that the absorption of green light is stronger than that of red light, and an increase in the intensity of green light will also modulate red light more strongly.
3.2 All-optical applications based on vanadium dioxide dispersions
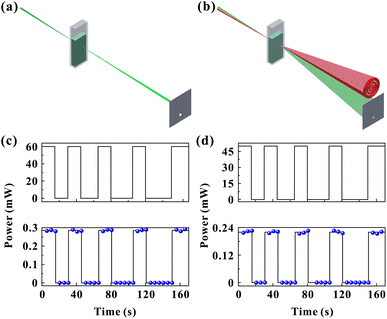
Fig. 8(c) and (d) show the experimental results of inter-channel information transmission. Firstly, the power of red light (control light) is kept at 60 mW and the green light (probe light) power at 7 mW (the green beam cannot excite diffraction rings at such a power). The red light is closed for 15, 20, 25, and 30 s all at 15 s intervals. Fig. 8(c) shows the power corresponding to time for red light and the power corresponding to time for green light passing through the aperture, respectively. As can be seen from the figure, the information curve of the green light (green channel) is the same as the red light (red channel), which means that the information transmitted by control light can be obtained by detecting the probe light.
Then, the power of the green beam is kept at 55 mW and the power of the red beam at 9 mW (red light at such a power cannot excite the diffraction rings). A similar experimental operation is performed, intermittently close the green light (input) while recording the power of red light (output) passing through the aperture, as shown in Fig. 8(d). The figure shows that the information curves of the green channel and the red channel are essentially the same, indicating the inter-channel information transmission function.
3.3 Diffraction rings formation as an electronically coherent nonlinear optical processes: a study of the response time
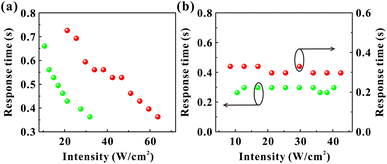
There are two prevailing views on the formation mechanism of diffraction rings: mainly thermal nonlinear effects11,45,46 or mainly electronic coherence nonlinear effects.13,17,20,47 Here, we experimentally verify by the response time that electronic coherence should play a major role in the VO2 dispersions. During the experiment of SSPM effect, the response time is defined as the time required from the appearance of diffraction rings to their maximum diameter.48,49 Fig. 9(a) represents the incident intensity corresponding to the response time for two monochromatic lights irradiating the dispersions (SSPM effect). The shortest response time in the experiment is about 0.36 s, as shown in Fig. 9(a), which is shorter than the response time of most two-dimensional materials.16,19,43 The response time T is expressed as,17
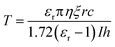 | (5) |
As the incident intensity increases, the temperature of the dispersions also increases. However, the experimental results in Fig. 9(b) show that the response time does not vary with the increase of the incident intensity. Thus, our results suggest that the formation of diffraction rings should be mainly attributed to electronically coherence nonlinear effects in VO2 dispersions. According to the “wind-bell” model,17 the suspended particles are polarized when the laser irradiates the dispersions, then the suspended particles tend to reorient from the disordered orientation to the electric field direction, as shown in Fig. 10. Thus, the response time of the SSPM effect is the time required from disordered orientation of the suspended particles under electric field to the completion of orientation, which can be shown as “Step one” in Fig. 10.
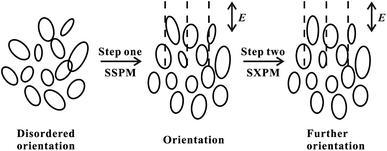 | ||
| Fig. 10 The orientation process of the suspended particles. Step one: the response process of the SSPM effect. Step two: the response process of the SXPM effect. E: the direction of electric field. | ||
In the study of the SXPM effect, it is necessary to implement the control light (strong light) to modulate the probe light (weak light). The SSPM effect has a short response time of a few hundred milliseconds, so that the orientation (Step one) of the suspended particles due to the probe light is actually completed before the control light irradiation to the VO2 dispersions. When the control light is irradiated to the dispersions, the suspended particles need to complete further orientation under the stronger field. That is, the response time of the SXPM effect is the time required from control light irradiation to the dispersions to the completion of further orientation of the suspended particles, which can be shown as “Step two” in Fig. 10. In the SSPM effect, the large orientation angle between the disorderly oriented particles and the electric field, together with the viscous force of the solution, requires a certain amount of time to complete the orientation of the suspended particles. In the case of the SXPM effect, the orientation of the suspended particles is already quite close to the direction of the electric field, because the irradiation of the probe light causes the suspended particles tend to the direction of the electric field (Step one in Fig. 10). Therefore, a small orientation angle and viscous forces need to be overcome under stronger control light irradiation in order to complete further orientation for the suspended particles (Step two in Fig. 10), and thus the time required for this process is relatively short.
4. Conclusions
In conclusion, the interaction between light and VO2 dispersions has been studied utilizing the SSPM and SXPM effects in the visible light regime. The dispersions exhibit excellent optical properties and promising nonlinear optical response. The n2 and χ(3) of VO2 dispersions are measured to be 3.06 × 10−6 cm2 W−1 and 1.68 × 10−4 esu at λ = 671 nm, and 5.17 × 10−6 cm2 W−1 and 2.83 × 10−4 esu at λ = 532 nm, respectively. Due to the excellent nonlinear optical response of VO2 dispersions, optical logic or-gate, optical switch, and inter-channel information transmission in visible regime have been implemented. The band gap of VO2 is about 0.6 eV, indicating the broadband response of the VO2-based optical modulators. In addition, the VO2 dispersion can be used to realize the broadband, high-power and high efficiency all-optical modulation with simple experimental configuration. The response time indicates that the diffraction rings are mainly formed by an electronically coherent third-order nonlinear optical process. The findings contribute to a better understanding of the nonlinear optical response of VO2 and may lay the foundation for their applications in all-optical devices. All-optical devices require low loss, high efficiency, miniaturization and high integration for practical applications, and thus our all-optical devices need to be designed and optimized in such direction.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (NSFC) (61975055).Notes and references
- M. Hochberg, T. Baehr-Jones, G. Wang, M. Shearn, K. Harvard, J. Luo, B. Chen, Z. Shi, R. Lawson and P. Sullivan, Nat. Mater., 2006, 5, 703–709 CrossRef CAS PubMed.
- Z. Shi, L. Gan, T. Xiao, H. Guo and Z. Li, ACS Photonics, 2015, 2, 1513–1518 CrossRef CAS.
- P. B. Deotare, I. Bulu, I. W. Frank, Q. Quan, Y. Zhang, R. Ilic and M. Loncar, Nat. Commun., 2012, 3, 846 CrossRef PubMed.
- J. Yi, J. Li, S. Huang, L. Hu, L. Miao, C. Zhao, S. Wen, V. N. Mochalin and A. M. Rao, InfoMat, 2020, 2, 601–609 CrossRef CAS.
- Z. Shi, J. Gong, J. Zhang, P. Xu, N. Yao, W. Fang, P. Wang, X. Guo and L. Tong, ACS Photonics, 2020, 7, 2571–2577 CrossRef CAS.
- S. Yu, X. Wu, Y. Wang, X. Guo and L. Tong, Adv. Mater., 2017, 29, 1606128 CrossRef PubMed.
- Y. Dong, S. Chertopalov, K. Maleski, B. Anasori, L. Hu, S. Bhattacharya, A. M. Rao, Y. Gogotsi, V. N. Mochalin and R. Podila, Adv. Mater., 2018, 30, 1705714 CrossRef PubMed.
- G. Wang, S. Zhang, X. Zhang, L. Zhang, Y. Cheng, D. Fox, H. Zhang, J. N. Coleman, W. J. Blau and J. Wang, Photonics Res., 2015, 3, A51–A55 CrossRef.
- S. D. Durbin, S. M. Arakelian and Y. R. Shen, Opt. Lett., 1981, 6, 411–413 CrossRef CAS.
- S. Pu, X. Chen, L. Chen, W. Liao, Y. Chen and Y. Xia, Appl. Phys. Lett., 2005, 87, 021905 CrossRef.
- M. Horowitz, R. Daisy, O. Werner and B. Fischer, Opt. Lett., 1992, 17, 475–477 CrossRef CAS PubMed.
- W. Ji, W. Chen, S. Lim, J. Lin and Z. Guo, Opt. Express, 2006, 14, 8958–8966 CrossRef CAS.
- R. Wu, Y. Zhang, S. Yan, F. Bian, W. Wang, X. Bai, X. Lu, J. Zhao and E. Wang, Nano Lett., 2011, 11, 5159–5164 CrossRef CAS PubMed.
- J. Li, K. Yang, L. Du, J. Yi, J. Huang, J. Zhang, Y. He, B. Huang, L. Miao, C. Zhao and S. Wen, Adv. Opt. Mater., 2020, 8, 2000382 CrossRef CAS.
- S. Xiao, Y. Ma, Y. He, Y. Wang, H. Xin, Q. Fan, J. Zhang, X. Li, Y. Zhang, J. He and Y. Wang, Photonics Res., 2020, 8, 1725–1733 CrossRef CAS.
- L. Wu, X. Jiang, J. Zhao, W. Liang, Z. Li, W. Huang, Z. Lin, Y. Wang, F. Zhang, S. Lu, Y. Xiang, S. Xu, J. Li and H. Zhang, Laser Photonics Rev., 2018, 12, 1800215 CrossRef.
- Y. Wu, Q. Wu, F. Sun, C. Cheng, S. Meng and J. Zhao, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11800–11805 CrossRef CAS.
- L. Wu, Y. Dong, J. Zhao, D. Ma, W. Huang, Y. Zhang, Y. Wang, X. Jiang, Y. Xiang, J. Li, Y. Feng, J. Xu and H. Zhang, Adv. Mater., 2019, 31, 1807981 CrossRef.
- Y. Jia, Y. Shan, L. Wu, X. Dai, D. Fan and Y. Xiang, Photonics Res., 2018, 6, 1040–1047 CrossRef CAS.
- L. Lu, W. Wang, L. Wu, X. Jiang, Y. Xiang, J. Li, D. Fan and H. Zhang, ACS Photonics, 2017, 4, 2852–2861 CrossRef CAS.
- L. Wu, S. Wei, Y. Zhang, Y. Zhang, Y. Xiang, H. Zhang and Y. Qin, Adv. Opt. Mater., 2022, 10, 2102537 CrossRef CAS.
- F. J. Morin, Phys. Rev. Lett., 1959, 3, 34–36 CrossRef CAS.
- A. Zylbersztejn and N. F. Mott, Phys. Rev. B, 1975, 11, 4383–4395 CrossRef CAS.
- A. Cavalleri, C. Tóth, C. W. Siders, J. A. Squier, F. Ráksi, P. Forget and J. C. Kieffer, Phys. Rev. Lett., 2001, 87, 237401 CrossRef CAS PubMed.
- L. Xiao, H. Ma, J. Liu, W. Zhao, Y. Jia, Q. Zhao, K. Liu, Y. Wu, Y. Wei, S. Fan and K. Jiang, Nano Lett., 2015, 15, 8365–8370 CrossRef CAS.
- S. Chandra, D. Franklin, J. Cozart, A. Safaei and D. Chanda, ACS Photonics, 2018, 5, 4513–4519 CrossRef CAS.
- J. Rensberg, S. Zhang, Y. Zhou, A. S. McLeod, C. Schwarz, M. Goldflam, M. Liu, J. Kerbusch, R. Nawrodt, S. Ramanathan, D. N. Basov, F. Capasso, C. Ronning and M. A. Kats, Nano Lett., 2016, 16, 1050–1055 CrossRef CAS.
- T. Kang, Z. Ma, J. Qin, Z. Peng, W. Yang, T. Huang, S. Xian, S. Xia, W. Yan, Y. Yang, Z. Sheng, J. Shen, C. Li, L. Deng and L. Bi, Nanophotonics, 2021, 10, 909–918 CrossRef CAS.
- M. Li, S. Magdassi, Y. Gao and Y. Long, Small, 2017, 13, 1701147 CrossRef PubMed.
- J. Lu, H. Liu, S. Deng, M. Zheng, Y. Wang, J. A. van Kan, S. Tang, X. Zhang, C. H. Sow and S. G. Mhaisalkar, Nanoscale, 2014, 6, 7619–7627 RSC.
- O. L. Muskens, L. Bergamini, Y. Wang, J. M. Gaskell, N. Zabala, C. H. de Groot, D. W. Sheel and J. Aizpurua, Light: Sci. Appl., 2016, 5, e16173 CrossRef CAS PubMed.
- D. Lei, K. Appavoo, F. Ligmajer, Y. Sonnefraud, R. F. Haglund and S. A. Maier, ACS Photonics, 2015, 2, 1306–1313 CrossRef CAS.
- Z. Jia, F. Shu, Y. Gao, F. Cheng, R. Peng, R. Fan, Y. Liu and M. Wang, Phys. Rev. Appl., 2018, 9, 034009 CrossRef.
- T. Driscoll, H. T. Kim, B. G. Chae, B. J. Kim, Y. W. Lee, N. M. Jokerst, S. Palit, D. R. Smith, M. Di Ventra and D. N. Basov, Science, 2009, 325, 1518–1521 CrossRef CAS PubMed.
- T. Wang, D. Torres, F. E. Fernandez, A. J. Green, C. Wang and N. Sepulveda, ACS Nano, 2015, 9, 4371–4378 CrossRef CAS.
- J. H. Yu, S. H. Nam, J. W. Lee, D. I. Kim and J. H. Boo, Appl. Surf. Sci., 2019, 477, 22–26 CrossRef CAS.
- K. L. Gurunatha, S. Sathasivam, J. Li, M. Portnoi, I. P. Parkin and I. Papakonstantinou, Adv. Funct. Mater., 2020, 30, 2005311 CrossRef CAS.
- L. Wu, W. Huang, Y. Wang, J. Zhao, D. Ma, Y. Xiang, J. Li, J. S. Ponraj, S. C. Dhanabalan and H. Zhang, Adv. Funct. Mater., 2019, 29, 1806346 CrossRef.
- L. Wu, T. Fan, S. Wei, Y. Xu, Y. Zhang, D. Ma, Y. Shu, Y. Xiang, J. Liu, J. Li, K. Panajotov, Y. Qin and H. Zhang, Opto-Electron. Adv., 2022, 5, 200046 CAS.
- L. Wu, X. Yuan, D. Ma, Y. Zhang, W. Huang, Y. Ge, Y. Song, Y. Xiang, J. Li and H. Zhang, Small, 2020, 16, 2002252 CrossRef CAS PubMed.
- C. Song, Y. Liao, Y. Xiang and X. Dai, Sci. Bull., 2020, 65, 1030–1038 CrossRef CAS.
- X. Li, R. Liu, H. Xie, Y. Zhang, B. Lyu, P. Wang, J. Wang, Q. Fan, Y. Ma, S. Tao, S. Xiao, X. Yu, Y. Gao and J. He, Opt. Express, 2017, 25, 18346–18354 CrossRef CAS.
- L. Wu, Z. Xie, L. Lu, J. Zhao, Y. Wang, X. Jiang, Y. Ge, F. Zhang, S. Lu, Z. Guo, J. Liu, Y. Xiang, S. Xu, J. Li, D. Fan and H. Zhang, Adv. Opt. Mater., 2018, 6, 1700985 CrossRef.
- Y. Liao, Y. Shan, L. Wu, Y. Xiang and X. Dai, Adv. Opt. Mater., 2020, 8, 1901862 CrossRef CAS.
- S. Radha, S. Mohan and C. Pai, Physica B, 2014, 448, 341–345 CrossRef CAS.
- S. Xiao, B. Lv, L. Wu, M. Zhu, J. He and S. Tao, Opt. Express, 2015, 23, 5875–5887 CrossRef CAS PubMed.
- B. Shi, L. Miao, Q. Wang, J. Du, P. Tang, J. Liu, C. Zhao and S. Wen, Appl. Phys. Lett., 2015, 107, 151101 CrossRef.
- S. Xiao, Y. Zhang, Y. Ma, Y. Wang, Y. He, J. Zhang, Y. Jiang, X. Li, R. Yang, J. He and Y. Wang, Opt. Lett., 2020, 45, 2850–2853 CrossRef.
- L. Wu, Y. Zhang, X. Yuan, F. Zhang, W. Huang, D. Ma, J. Zhao, Y. Wang, Y. Ge, H. Huang, N. Xu, J. Kang, Y. Xiang, Y. Zhang, J. Li and H. Zhang, Appl. Mater. Today, 2020, 19, 100589 CrossRef.
- L. Lu, Z. Liang, L. Wu, Y. Chen, Y. Song, S. C. Dhanabalan, J. S. Ponraj, B. Dong, Y. Xiang, F. Xing, D. Fan and H. Zhang, Laser Photonics Rev., 2018, 12, 1700221 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |