Open Access Article
Open Access ArticleSpectral filtering method for improvement of detection accuracy of Mg, Cu, Mn and Cr elements in aluminum alloys using femtosecond LIBS
Jieqi Yao a,
Qi Yang
a,
Qi Yang ab,
Xiaoyong He
ab,
Xiaoyong He *a,
Jiale Li
*a,
Jiale Li a,
Dongxiong Linga,
Dongshan Wei
a,
Dongxiong Linga,
Dongshan Wei a and
Yipeng Liaoc
a and
Yipeng Liaoc
aSchool of Electrical Engineering and Intelligentization, Dongguan University of Technology, Dongguan, 523808, China. E-mail: hxy@dgut.edu.cn
bGuangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices, South China Normal University, Guangzhou, 510631, China
cSchool of Microelectronics, Shenzhen Institute of Information Technology, Shenzhen, 518172, China
First published on 10th November 2022
Abstract
In this work, magnesium (Mg), copper (Cu), manganese (Mn) and chromium (Cr) in aluminum alloy samples were quantified by femtosecond laser-induced breakdown spectroscopy (fs-LIBS). The different parameters affecting the experimental results, including the laser pulse energy, moving speed of the 2D platform and spectral average number were optimized. The background signal preprocessing methods of median filtering (MF corrected) and Savitzky–Golay filtering (SG corrected) algorithms were used and the effect of the LIBS spectral analysis in the experiment investigated. The calibration curves of Mg, Cu, Mn and Cr elements were established separately and their corresponding detection limits (LODs) were calculated. After background correction, the LODs of Mg, Cu, Mn and Cr elements in MF corrected were 54.52, 11.69, 7.33 and 27.72 ppm, and in SG corrected were 59.15, 17.48, 14.75 and 31.97 ppm. The LODs of these elements in MF corrected and SG corrected have 1.4–5.2 and 1.2–2.5 improvement factors compared to those obtained using the fs-LIBS technique. This work demonstrates that background signal preprocessing methods are very helpful for improving analytical sensitivity and accuracy in quantitative analyses of aluminum alloys.
1. Introduction
Laser-induced breakdown spectroscopy (LIBS) is also known as laser-induced plasma spectroscopy and laser spark spectroscopy. It is a highly accurate elemental analysis technique based on atomic emission spectroscopy. Its advantage of enabling microdestructive testing and multi-element analysis have made it popular in recent decades. The elemental analysis technology of LIBS has been widely used for applications in food safety,1,2 industrial testing,3–5 geological correlation analysis,6,7 environmental quality monitoring,8–10 cultural heritage,11,12 materials science,13 biomedicine14 and many other fields. Related basic research in LIBS has been continuously advancing.Femtosecond lasers have some important characteristics such as low thermal effect, high peak power and stability. LIBS using a femtosecond laser source is usually termed fs-LIBS. Fs-LIBS produces very little damage to samples with, absence of fractional evaporation, even can realize micron- and nanometer-scale precision detection. In light of the many advantages of the femtosecond laser and fs-LIBS described above, they are widely used by researchers. Carvalho et al.15 compared surface elemental mapping analysis of spinach leaves after the action of ns-LIBS and fs-LIBS and found that established higher accuracy and less uncertainty on mass fractions quantification from fs-LIBS, regardless of using the classical least squares regression model or multivariate partial least squares (PLS) regression models. Scaffidi et al.16 observed minor reductions in atomic emission and as much as 15 fold improvements in mass removal for fs single-pulse LIBS of heated brass and aluminum samples. Finney et al.17 statistically analyzed the uranium detection efficiency based on several characteristic features in the plasma emission spectrum. They found that nearly 100% detection probability can be reached with 1% false-alarm probability in ≲1 second when using an 80 Hz laser and data acquisition system. Shaik et al.18 used LIBS for the long- and close-range detection of explosive molecules (nitroimidazoles and nitropyrazoles). Different aspects influencing the LIBS signal strength at far distances such as fluence at target, the efficiency of collection system etc. are discussed. This demonstrates that any improvement to the LIBS signal will benefit the application.
Despite the many advantages of fs-LIBS, it is subject to multiple sources of interference during experiments. Most LIBS systems are exposed to air and subjected to ambient noise (water cooling, etc.) and atmospheric pressure during measurements. Current noise in the internal components of the instrument, noise in the photoelectric conversion process and dark currents in the detector can all interfere with the accuracy of elemental analyses. Therefore, to obtain reliable results, it is essential to use preprocessing methods to reduce the noise in spectral data. Sun et al.19 achieved the automatic deduction of a continuous background by removing the minimum points in the spectral line that are larger than the set threshold and accurately estimated varying continuum backgrounds over a wide range of wavelengths. Body et al.20 showed that normalization of the overall plasma intensity could be effective, i.e., normalization of the spectral intensity could reduce the interference of abnormal data. Schlenke et al.21 utilized adaptive variable threshold denoising for spectral data using signal smoothing degree and mean square error analysis, with good denoising results. Yang et al.22 studied LIBS spectra of lead-contaminated cabbage in the wavelength range of 400.45–410.98 nm, pre-treated by Savitzky–Golay (SG), which was experimentally shown to have good smoothing effects. To date, wavelet analysis techniques have been widely studied in spectral denoising processing, and good application results have also been achieved.23–26
In this study, the effect of the median filtering (MF corrected) and Savitzky–Golay (SG corrected) filtering algorithms on the denoising effect of the LIBS spectrum were compared. A femtosecond laser was used as the sample ablation source, and some standard aluminum alloy samples were used as the test samples. The effect of different experimental parameters on signal intensity were investigated in the experiment. After optimizing the experimental conditions, quantitative analysis of Mg, Cu, Mn and Cr in aluminum alloys was conducted, and two signal processing methods were analyzed. Compared with the original data, calibration curves were prepared, and their corresponding detection limits were calculated. The analytical performance of the two noise processing methods is evaluated and discussed in this paper.
2 The experimental setup diagram and background treatment methods
2.1 The experimental setup
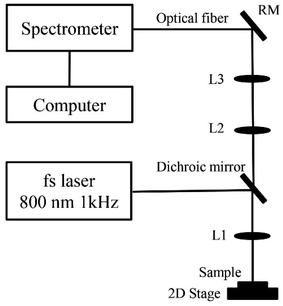
The experimental setup of fs-LIBS is shown in Fig. 1. An ultrafast Ti: sapphire femtosecond laser (model Astrella) is used for the studies, with the pulse width of approximately 35 fs, laser center wavelength of 800 nm, and an output laser beam diameter of 10 mm. The repeated frequency was 1 kHz, and the maximum pulse energy output was 7.5 mJ. For the sample we used the aluminium alloy discs of 40 mm diameter and 3 mm thickness. We used a programmable X–Y mobile platform and fixed the aluminum alloy sample to be tested on it.The coated mirrors were used to guide the femtosecond laser beam and focused on the sample surface through a quartz lens L1 (f = 50 mm). Transmitting a specific wavelength beam to L2 using a dichroic mirror. The plasma spectrum was collimated by shaping the beam into parallel light through a quartz lens L2 (f = 150 mm) and converging the beam through a quartz lens L3 (f = 100 mm). The converged plasma spectrum was then collected using an optical probe. Here, plasma spectra were recorded and processed by using a small portable three-channel fiber spectrometer (Avantes, Netherland, model 12012156U3, 1202157U3 and 1202158U3). Finally, the spectral data were analysed by a computer. The optimum experimental conditions were selected for the different experimental variables, the relative intensities of the different elements of the samples were analysed and their relative standard deviations were calculated. In turn, comparing with the original data, calibration curves were prepared, and their corresponding detection limits were calculated.
Six verified standard aluminum alloy samples were GBW(E)020095, 020097, 020100, 020093, 020094, and 020101, purchased from Jinan Zhongbiao Technology Co., Ltd. The concentrations of Mg, Cu, Cr, and Mn elements in these standard samples are listed in Table 1. These samples were used to investigate parameter optimization, calibration curves preparation, detection limit calculations and evaluation of technical analysis.
| Samples | Mg | Cu | Cr | Mn |
|---|---|---|---|---|
| GBW020093 | 0.544 | 2.850 | 0.000 | 0.292 |
| GBW020094 | 0.341 | 2.080 | 0.001 | 0.521 |
| GBW020095 | 5.910 | 0.019 | 0.050 | 0.642 |
| GBW020097 | 4.180 | 0.057 | 0.260 | 0.471 |
| GBW020100 | 2.210 | 0.144 | 0.214 | 0.292 |
| GBW020101 | 1.620 | 0.174 | 0.117 | 0.216 |
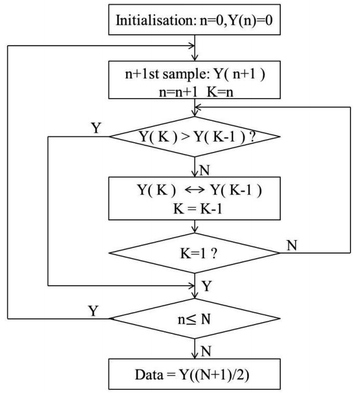
2.2 Background processing methods
The spectral data obtained contains more random noise signals due to multiple interferences, which reduces the quality of the data. But then we need to get the type and content of the target element based on the qualitative and quantitative analysis of the signal. Therefore, the spectral information needs to be smoothed to reduce noise and improve the accuracy of the analysis. In this experiment, two methods of background noise signal processing were proposed.The Savitzky–Golay algorithm can be derived as follows. Consider a set of 2 M + 1 data centered on n = 0, fit it with the following polynomial:
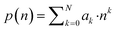 | (1) |
The residuals of its least significant fit are:
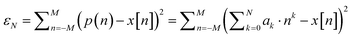 | (2) |
Convolution is used to obtain the constant term of the fitted polynomial, i.e., a weighted average of the input data as follows:
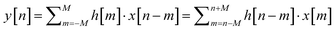 | (3) |
The partial differentiator of the above equation, when simplified, is as follows:
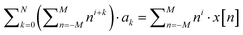 | (4) |
Let A = {ani}, ani = ni, M ≤ n ≤ M, 0 ≤ i ≤ N, B = AT·A, then
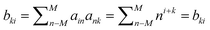 | (5) |
Thus,
| Ba = AT·Aa = ATx | (6) |
The estimated value of a is obtained by fitting with least-squares.
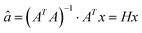 | (7) |
3. Results and discussion
Experimental parameters, such as the speed of the 2D platform, the pulse of the fs laser and the spectra average number acquisitions, play a crucial role in the evaluation of the analytical performance of the technique. Therefore, in the fs-LIBS experiment, we analyzed the speed of the 2D stage, the pulse of the fs laser and the spectra average number acquisitions using a rigorously controlled variables approach and obtained optimized experimental parameters. Four atomic net signal spectral lines, including Mg I (285.21 nm), Cu I (324.75 nm), Mn I (403.44 nm) and Cr I (428.97 nm), were selected to test the experimental results under different parametric conditions, and the optimum experimental parameters were determined.3.1 Influence of platform speed on spectral signal intensity
As the repetition rate of femtosecond laser is 1 kHz, and the overlapping focus of the laser pulse on the aluminum alloy sample affects the signal intensity, the aluminum alloy sample detection signal has a great relationship with the sample speed. To prevent signal weakening caused by overlapping focus positions and improve detection sensitivity, we set up a series of experiments to investigate the effect of the speed of the sample on the 2D platform on the signal intensity. In the experiments, we kept the LIBS laser single pulse energy at 1.5 mJ and the integration time at 5 ms. The spectra were obtained by averaging over 500 repeated measurements and adjusting the moving speed of the stepper motor driving the 2D motion stage to 1–6 mm s−1. Fig. 3 below shows the experimental results of the signal intensity at Mg I 285.21 nm, Cu I 324.75 nm, Mn I 403.44 nm, and Cr I 428.97 nm and the moving speed of the aluminum alloy sample. Fig. 3 shows that as the sample movement speed increased, the relative intensities of the four elements also increased. The diameter of the ablated crater on the sample surface was observed by the LIBS laser pulse through an optical microscope, which can explain the relationship between the reaction of four elements and the sample moving speed reflected in Fig. 3 above. When the moving speed of the sample is small, the positions of the pits ablated by two adjacent LIBS pulses overlap each other, and the previous pits will affect the LIBS laser pulse to break down and strip the sample to form plasma, thereby affecting the relative intensities of the four elements. When the sample travel speed is increased to 5 mm s−1, the positions of the pits ablated by the two adjacent LIBS laser pulses no longer overlap. The location of the sample ablated with each LIBS laser pulse was new, resulting in the formation of the highest-intensity signal. At this time, the increase in the speed of the sample does not have a substantial effect, so the plasma signal tends to be stable.28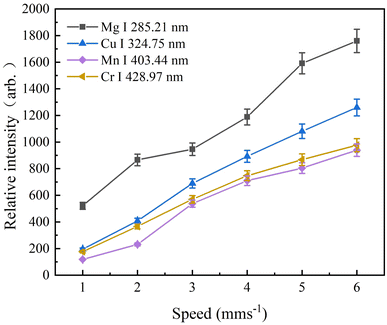 | ||
| Fig. 3 Plots of signal intensities of Mg, Cu, Mn and Cr elements versus 2D mobile platform speed. Error bar shows the signal deviation of the multiple repeated measurements. | ||
When it exceeded 6 mm s−1, the motor of the 2D mobile platform became hot and instability. To protect the stability of the atomic signal intensity and durability of the 2D mobile platform, the speed was selected as 5 mm s−1 in the following experiments.
3.2 Influence of laser pulse energy on spectral signal intensity
If the selected laser pulse energy is too small, then the laser pulse energy density at the focus point cannot reach the breakdown threshold of the element to be measured. Even if a very sensitive detector is used or the frequency of the laser pulse is increased, the atom cannot be excited, resulting in a weak signal intensity, which makes it impossible to analyze the spectral information of the element. When the selected laser pulse energy is too large, although the intensity of the plasma emission signal is enhanced, it easily leads to saturation of some atomic or ion spectral lines due to the strong self-absorption effect, thereby reducing the sensitivity of the elemental analysis. Therefore, the selection of the appropriate laser single pulse energy is of great importance for improving the sensitivity of elemental analysis.In this experiment, four atomic lines for Mg I (285.21 nm), Cu I (324.75 nm), Mn I (403.44 nm), and Cr I (428.97 nm) were studied with laser pulse energy of 0.3, 0.5, 0.8, 1.0 and 1.5 mJ. The speed of the 2D platform was fixed at 5 mm s−1, the CCD integration time of the Avantes multichannel fiber optic spectrometer was 5 ms, and the spectrum was obtained by averaging 500 repeated measurements. The experimental results are shown in Fig. 4, where we find that the signal intensities of several elements increase with increasing laser single pulse energy. The signal strength here adopts the peak strength of the spectral line.
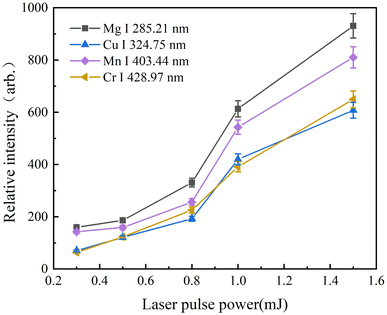 | ||
| Fig. 4 Plots of signal intensities of Mg, Cu, Mn and Cr elements versus pulse energy of the femtosecond. | ||
3.3 The advantage of the average number of spectra on the detection limit
The most common method to improve the measurement precision is to use the average of multiple spectral data in fiber spectrometer measurements, but this approach also increases the measurement time and is not conducive for industrial applications. To analyze the influence of the average number of spectra on the precision of the fs-LIBS measurements, four atomic lines, Mg I (285.21 nm), Cu I (324.75 nm), Mn I (403.44 nm) and Cr I (428.97 nm), were still chosen for the study. At a laser single pulse energy of 1.5 mJ and an integration time of 5 ms, the average number of spectra were 1, 10, 50, 100, 200, 300, 500 and 1000, followed by 10 repeated measurements, and the precision was evaluated by the relative standard deviation values of these 10 repeated measurements. Fig. 5 shows the variation curve of the relative standard deviation of the spectral line intensities with increasing spectral averaging number. The standard deviations were high at the initial stage when the number of averages increased and fell rapidly as the number of spectra averaged increased, after which the behavior worsened. When the average number of spectra was 500, the relative standard deviation was clearly reduced, which indicated that the effect of increasing the average number of times to improve the measurement precision was not very obvious. The graphs below also show that the relative standard deviation values for the different spectral lines follow essentially the same pattern of variation with the number of spectral averages.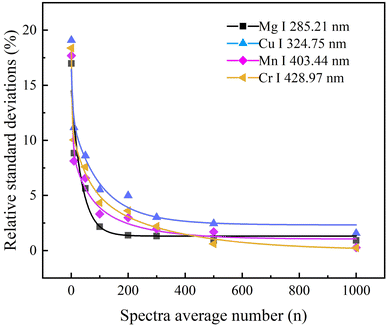 | ||
| Fig. 5 Plots of signal intensities of Mg, Cu, Mn and Cr elements versus number of spectral averages. | ||
From the present experiment, it can be concluded that the multiple averaging methods of the spectral signal can effectively improve the precision of the measurement. According to the variation in the relative standard deviation of the intensity of the spectral lines with the number of spectral averages in Fig. 5, the more stable data point after the turn of the curve, and the data taken too large is not conducive to practical industrial applications. So here we choose the number of spectral averages of 500 as measurements.
3.4 Quantitative analysis
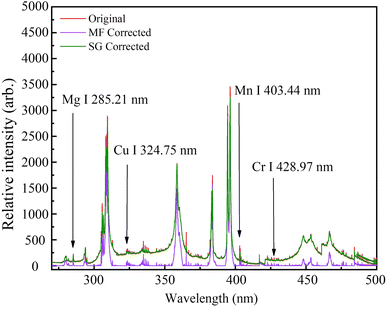
As can be seen from Fig. 6, the original LIBS spectrum has more noise signals and the spectrum is noisy; the smoothing of the spectrum after the MF correction improved significantly, retaining the main information of the original spectrum and reducing the overall intensity; SG corrected smoothing reduces the spectral noise, but not as much as MF corrected, and is almost identical to the original spectrum in terms of main information and maximum fidelity.
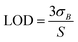 | (8) |
To obtain the detection limits for different trace elements, it is necessary to obtain the slopes of the calibration curves and the standard deviations of the background signals corresponding to the different analytical lines. Here, the standard deviation of the background in a range of wavelengths where no distinct atomic lines are observed near each analytical line was approximated as the standard deviation of the background defined in the formula. The rationality of this is that there are no observable atomic or ionic lines in these two bands, and the background of the plasma is approximately continuous. Therefore, the standard deviation of the signal near the analysis line should be approximately equal to the standard deviation of the background on the analysis line. The slope of the calibration curve was obtained directly by fitting the data points in the calibration curve.
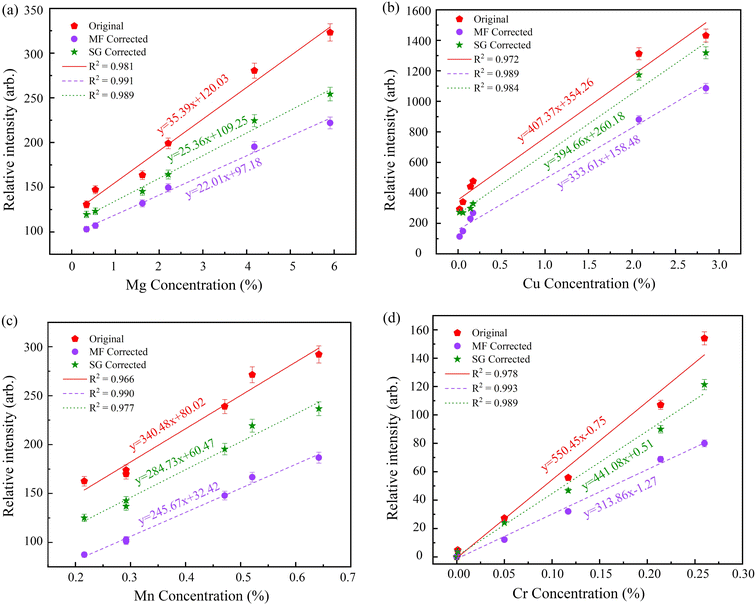
In this set of experiments, to improve the sensitivity of trace element detection, the laser single pulse energy was chosen to be 1.5 mJ, the average number of spectral samples of the fiber optic spectrometer was 500, and the speed of the 2D platform was chosen to be 5 mm s−1. The four elements Mg, Cu, Mn and Cr were quantified in aluminum alloy samples under the current experimental conditions. The analytical lines of Mg I 285.21 nm, Cu l 324.75 nm, Mn I 403.44 nm and Cr I 428.97 nm were selected for the calibration curves with the original data, MF corrected and SG corrected methods, and they are shown in Fig. 7(a)–(d), respectively. The coefficient of determination (R2) and LOD of the calibration curve were calculated and are listed in Table 2. Table 2 and Fig. 7 show that the R2 coefficient can reach 0.977–0.993 after background correction using both denoising algorithms. The LODs obtained with the MF correction improved by a factor of 1.4–5.2 compared to the LODs of the original data, while the LODs obtained with the SG corrected improved by a factor of 1.2–2.5 compared to the LODs of the original data.
| Element | Line (nm) | Σ | S | R2 | LOD (ppm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Original | MF corrected | SG corrected | Original | MF corrected | SG corrected | Original | MF corrected | SG corrected | Original | MF corrected | SG corrected | ||
| Mg | 285.21 | 0.11 | 0.04 | 0.05 | 35.39 | 22.01 | 25.36 | 0.981 | 0.991 | 0.988 | 93.24 | 54.52 | 59.15 |
| Cu | 324.75 | 0.33 | 0.13 | 0.23 | 407.37 | 333.61 | 394.66 | 0.972 | 0.989 | 0.984 | 24.30 | 11.69 | 17.48 |
| Mn | 403.44 | 0.43 | 0.06 | 0.14 | 340.48 | 245.67 | 284.73 | 0.966 | 0.990 | 0.977 | 37.89 | 7.33 | 14.75 |
| Cr | 428.97 | 0.72 | 0.29 | 0.47 | 550.45 | 313.86 | 441.08 | 0.978 | 0.993 | 0.989 | 39.24 | 27.72 | 31.97 |
4. Conclusions
In this paper, femtosecond laser-induced breakdown spectra was used for quantitative analysis of four trace elements, Mg, Cu, Mn and Cr, in aluminum alloys. At the same time, we optimized and compared the spectral data using different filtering algorithms. The research shows that the R2 and LOD calculated by different denoising methods are improved under fs-LIBS. The R2 values of the linaer fit on the data after MF and SF filtering are 0.990 and 0.977, respectively. The LODs obtained using the MF algorithm and SG filtering method were 1.4–5.2 and 1.2–2.5 times better than the LODs of the original data, respectively. Therefore, the results presented in this paper showed the advantages of noise reduction of fs-LIBS data and the good prospects for signal denoising when concentrations of elements are low and features in spectra are weak. Currently, the evaluation work is being extended to a wider range of alloy materials and soil samples. Furthermore, studies on precision and more experimental variables are in progress.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by Dongguan Social Development Science and Technology Funds (20211800904632), Guangdong Basic and Applied Basic Research Foundation (2019A1515110978 & 2021B1515140018), Guangdong Province for Science and Technology Innovative Young Talents (2021KQNCX097).Notes and references
- R. A. Multari, D. A. Cremers, J. A. M. Dupre and J. E. Gustafson, J. Agric. Food Chem., 2013, 61, 8687–8694 CrossRef CAS PubMed.
- R. Hedwig, K. Lahna, Z. S. Lie, M. Pardede, K. H. Kurniawan, M. O. Tjia and K. Kagawa, Appl. Opt., 2016, 55, 8986–8992 CrossRef CAS PubMed.
- A. D. Giacomo, C. Koral, G. Valenza, R. Gaudiuso and M. Dell' Aglio, J. Anal. Chem., 2016, 88, 9869–9870 Search PubMed.
- T. B. Yuan, Z. Wang, S. L. Lui, Y. T. Fu, Z. Li, J. M. Liu and W. D. Ni, J. Anal. At. Spectrom., 2013, 28, 1045–1053 RSC.
- S. A. Davari, S. Hu, R. Pamu and D. Mukherjee, J. Anal. At. Spectrom., 2017, 32, 1378–1387 RSC.
- J. Rakovsky, O. Musset, J. F. Buoncristiani, V. Bichet, F. Monna, P. Neige and P. Veis, Spectrochim. Acta, Part B, 2012, 74–75, 57–65 CrossRef CAS.
- J. J. Choi, S. J. Choi and J. J. Yoh, Appl. Spectrosc., 2016, 70, 1411–1419 CrossRef CAS PubMed.
- H. M. Hou, L. Cheng, T. Richardson, G. Y. Chen, M. Doeff, R. E. Zheng, R. E. Russo and V. Zorba, J. Anal. At. Spectrom., 2015, 30, 2295–2302 RSC.
- E. C. Ferreira, J. A. G. Neto, D. M. B. P. Milori, E. J. Ferreirab and J. M. Anzanoc, Spectrochim. Acta, Part B, 2015, 110, 96–99 CrossRef CAS.
- M. Wall, Z. Sun and Z. T. Alwahabi, Opt. Express, 2016, 24, 1507–1517 CrossRef CAS PubMed.
- S. Tzortzakis, D. Anglos and D. Gray, Opt. Lett., 2006, 31, 1139–1141 CrossRef PubMed.
- A. Botto, B. Campanella, S. Legnaioli, M. Lezzerini, G. Lorenzetti, S. Pagnotta, F. Poggialinibd and V. Palleschi, J. Anal. At. Spectrom., 2019, 34, 81–103 RSC.
- S. Acquaviva, E. D. Anna, M. L. De Giorgi and F. Moro, Spectrochim. Acta, Part B, 2006, 61, 810–816 CrossRef.
- G. D. Christian, J. Anal. Chem., 1969, 41, 24A–40A CAS.
- G. G. A. Carvalho, J. Moros, D. Santos, F. J. Krug and J. J. Laserna, Anal. Chim. Acta, 2015, 876, 26–38 CrossRef PubMed.
- J. Scaffidi, W. Pearman, J. C. Carter, B. W. Colston and S. M. Angel, Appl. Opt., 2004, 43, 2786–2791 CrossRef PubMed.
- L. A. Finney, P. J. Skrodzki, M. Burger, J. Nees, S. S. Harilal and I. Jovanovic, Opt. Lett., 2019, 44, 2783–2786 CrossRef CAS.
- A. K. Shaik, N. R. Epuru, H. Syed, C. Byram and V. R. Soma, Opt. Express, 2018, 26, 8069–8083 CrossRef CAS PubMed.
- L. Sun and H. Yu, Spectrochim. Acta, Part B, 2009, 64, 278–287 CrossRef.
- D. Body and B. L. Chadwick, Spectrochim. Acta, Part B, 2001, 56, 725–736 CrossRef.
- J. Schlenke, L. Hildebrand, J. Moros and J. J. Laserna, Anal. Chim. Acta, 2012, 754, 8–19 CrossRef CAS PubMed.
- H. Yang, L. Huang, T. B. Chen, G. F. Rao, M. H. Liu, J. Y. Chen and M. Y. Yao, Chin. J. Anal. Chem., 2017, 45, 1123–1128 CAS.
- W. Yang, B. Li, J. Zhou, Y. Han and Q. Wang, Appl. Opt., 2018, 57, 7526–7532 CrossRef CAS PubMed.
- B. Zhang, H. Yu, L. Sun, Y. Xin and Z. Cong, J. Appl. Spectrosc., 2013, 67, 1087–1097 CrossRef CAS PubMed.
- B. Zhang, L. Sun, H. Yu, Y. Xin and Z. Cong, Spectrochim. Acta, Part B, 2015, 107, 32–44 CrossRef CAS.
- K. R. Coombes, S. Tsavachidis, J. S. Morris, K. A. Baggerly, M. C. Hung and H. M. Kuerer, Proteomics, 2005, 5, 4107–4117 CrossRef CAS PubMed.
- H. G. Schulze, R. B. Foist, A. Ivanov and R. F. B. Turner, J. Appl. Spectrosc., 2008, 62, 1160–1166 CrossRef CAS PubMed.
- J. Kang, R. H. Li, Y. R. Wang, Y. Q. Chen and Y. X. Yang, J. Anal. At. Spectrom., 2017, 32, 2292 RSC.
| This journal is © The Royal Society of Chemistry 2022 |