Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Decomposition analysis on the excitation behaviors of thiazolothiazole (TTz)-based dyes via the time-dependent dielectric density functional theory approach†
Takumi Naito,
Yukiumi Kita,
Tomomi Shimazaki and
Masanori Tachikawa
and
Masanori Tachikawa
Graduate School of Nanobioscience, Yokohama City University, 22-2 Seto, Kanazawa-ku, Yokohama 236-0026, Japan. E-mail: tshima@yokohama-cu.ac.jp
First published on 2nd December 2022
Abstract
Thiazolothiazole (TTz)-based materials have been attracting much attention because of their widespread applications. In this paper, we discuss the excited electronic behaviors of asymmetric TTz dyes in solvents based on the time-dependent dielectric density functional theory method. Based on dipole moment and charge distribution (population) analyses, we discuss large intramolecular electron transfers, which are triggered by photon excitations, toward the acceptor part of dyes. In addition, we explore the contributions of geometrical changes and solvent reorientations (reorganizations) to the solvatofluorochromic phenomena based on a decomposition technique. The decomposition analysis shows that the solvent reorientation effect mainly contributes to changes in the fluorescent spectra in response to solvents.
1. Introduction
Organic materials with the thiazolothiazole (TTz) molecular backbone have been widely employed in various applications, such as organic electronics, displays, photonics, and fluorescent sensors.1–9 The rigid and coplanar structure of TTz is suitable for extending π-conjugated systems of organic materials with high carrier mobility. For example, organic photocells employ TTz units in polymer materials, which are effective for not only developing highly efficient devices but also improving device stability and manufacturing reproducibility.10,11 In such devices, TTz is used as rigid π-bridge blocks to control the crystallinity and morphology of organic compounds. In addition to applications as a polymer building block, TTz-based (small) molecules were recently proposed as acceptor materials to replace fullerene derivatives.12 The non-fullerene organic photocell devices have been actively studied because of their superior advances in power conversion efficiency.13–16 The TTz molecular framework is promising to develop non-fullerene acceptor materials for organic photocells. TTz-based dyes are intensively studied for bioimaging applications. For example, Kumar et al. reported a fluorescent imaging technique for cells by using a TTz-based dye with pyrene and pyridine moieties serving as donor and acceptor parts, respectively.17 Sayresmith et al. developed TTz-bridged dye sensors, which have an electron-donor part (N,N-dibutylaniline or N,N-diphenylaniline) and an electron-acceptor part (pyridine, benzoic acid, or carboxaldehyde) by using a simple one-pot and single-step synthesis techniques, and they reported that the strong solvatofluorochromic characteristics of these dyes can be effectively utilized for imaging cell membranes.18To develop fluorescent dyes, the molecular design based on donor–π–acceptor, with TTz as the π-bridge, is frequently employed. The electron-donating and -withdrawing (push–pull) functional groups are introduced at the ends of the TTz-bridge, and they serve as the donor and acceptor parts, respectively, in the dye. Such an asymmetric molecular design from the viewpoint of TTz is essential to control intermolecular electron transfers toward the acceptor part in excited dyes. In this paper, we discuss the intermolecular electron transfer process of excited asymmetric TTz dyes. We focus on the solvatofluorochromic phenomena because of its important applications such as cellular imaging to investigate the response of dyes to dielectric environments.
During photon absorption, a dye is vertically excited from the stable molecular conformation in the ground state. In contrast, in the fluorescent state (emission), the conformation of the dye is relaxed under the excited state to emit a photon. In addition to the structural (conformational) relaxation, the reorientation (reorganization) of solvent molecules in response to the excited dye should be taken into account to consider the fluorescent spectra.19,20 To discuss these effects, we performed a decomposition analysis, where the contributions from the conformational changes of the dye and solvent reorientations were distinguished by using density functional theory (DFT) calculation techniques.
In this study, we employed the dielectric-dependent approach21 in the time-dependent DFT framework22–27 to examine the excitation behaviors of dyes. The basic concept of the dielectric DFT approach was derived from the simplified dielectric function model,21 which is closely related to the GW method.28 Thus, the dielectric-dependent approach has been verified mainly for inorganic bulk materials and used to investigate their material properties.21,29–46 In addition, applications of the dielectric DFT method toward molecular systems are also developing in recent years. We previously reported that the dielectric-dependent DFT method can give good descriptions of the electronic structures of molecules in the ground and excited states.47–49 Conversely, this paper will focus more on TTz excitation behaviors with the structural change and solvent reorientation effects.
In the next section, we briefly explain the dielectric DFT approach. In Section 3, we present the calculation results and discussions, including the intermolecular electron (charge) transfer process of asymmetric TTz dyes, with emphasis on the structural change and solvent reorientation effects. The summary is provided in Section 4.
2. Calculation method
The dielectric exchange screening term can be derived from the simplified semiconductor dielectric function of ε(k) = 1 + [(εs − 1)−1 + β(k2/kTF2)]−1 with dielectric constant εs.21 Here, k is the wavenumber; kTF is the Thomas–Fermi wavenumber; β is a constant parameter introduced by Bechstedt et al.50 In this study, we applied β = 2.5 for all the molecules.49 From the model dielectric function, we can obtain the following screened exchange potential.
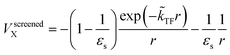 | (1) |
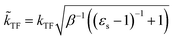 . The inverse Fourier transformation of V screenedX = −(2π)−3∫4πk−2ε−1(k)exp(ik·r)dk is employed to derive the equation. The second term in eqn (1) describes the incomplete screening in a semiconductor, which is proportional to the inverse of the dielectric constant εs. For ε = 1, the screened exchange potential represents a bare interaction between an electron and exchange hole in the Hartree–Fock (HF) approximation. Conversely, it reduces to a Thomas–Fermi (Yukawa)-type screened potential in the case of metals (ε → ∞), and complete screening is achieved. To efficiently handle the short-range term in the Gaussian basis set framework, we can employ erfc(2
. The inverse Fourier transformation of V screenedX = −(2π)−3∫4πk−2ε−1(k)exp(ik·r)dk is employed to derive the equation. The second term in eqn (1) describes the incomplete screening in a semiconductor, which is proportional to the inverse of the dielectric constant εs. For ε = 1, the screened exchange potential represents a bare interaction between an electron and exchange hole in the Hartree–Fock (HF) approximation. Conversely, it reduces to a Thomas–Fermi (Yukawa)-type screened potential in the case of metals (ε → ∞), and complete screening is achieved. To efficiently handle the short-range term in the Gaussian basis set framework, we can employ erfc(2![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) TFr/3)/r instead of exp(−
TFr/3)/r instead of exp(−![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) TFr)/r because of their similar behaviors.21 The Coulomb hole (COH) interactions in the COHSEX approximation of the GW method can be considered by using the simplified model dielectric function.31 The concept of the dielectric-screening potential can then be incorporated into the conventional hybrid DFT framework as follows:
TFr)/r because of their similar behaviors.21 The Coulomb hole (COH) interactions in the COHSEX approximation of the GW method can be considered by using the simplified model dielectric function.31 The concept of the dielectric-screening potential can then be incorporated into the conventional hybrid DFT framework as follows:
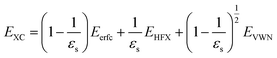 | (2) |
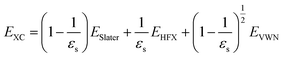 | (3) |
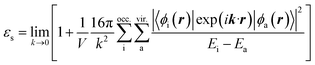 | (4) |
We discuss the absorption and emission spectra of asymmetric TTz dyes obtained by the dielectric-dependent approach, and we compare our results with those obtained using B3LYP and HandH methods with the nonlocal exchange ratios of 20% and 50%, respectively.55,56 In this study, we used Gaussian16 program for geometry optimization and excited electronic structure calculations with the 6-31+g* basis set.57 We estimated the dielectric constants of dyes by the self-consistent technique based on eqn (4) using a dynamic-language-based quantum chemistry tool.58,59 This study focused on asymmetric TTz dyes synthesized by Sayresmith et al., which are shown in Fig. 1.18 The self-consistent method using eqn (2) provides the constants as 2.80, 3.13, 3.20, and 3.14 are calculated for Bu2N-TTz-Py, Py2N-TTz-Py, Py2N-TTz-CHO, and Py2N-TTz-COOH, respectively, whereas eqn (3) gives slightly different values of 2.78, 3.11, 3.18, and 3.11, respectively, for these dyes. We used these dielectric constants for excitation energy calculations. In this study, the polarizable continuum model using the integral equation formalism was adopted to handle the solvent effects.60 The same calculation procedures based on the time-dependent DFT method were employed in previous studies.49
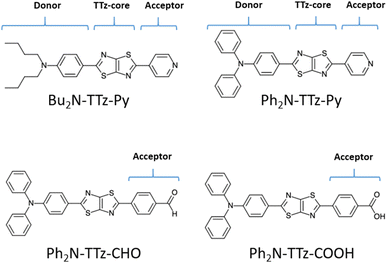 | ||
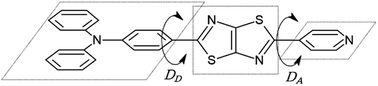
| Fig. 1 Chemical structure of asymmetric TTz dyes. The definitions of the donor, TTz-core, and acceptor parts used in the charge (electron) distribution analysis are also provided. | ||
3. Results and discussions
3.1 Absorption and emission spectra calculations
The absorption energies obtained from first-principles quantum chemistry methods are summarized in Table 1, where experimental results are also presented for comparison.18 Previous studies have shown that the absorption energies of TTz dyes are not strongly affected by the solvent effect unlike the emission spectra.18 This tendency can be reproduced in the quantum chemistry calculations. In contrast, the B3LYP (HandH) method tends to underestimate (overestimate) the experimental absorption energies of TTz dyes, though the dielectric-dependent approach yields better results. For example, the B3LYP (HandH) method gives absorption spectra of 2.55 (3.27) eV for Bu2N-TTz-Py in dichloromethane (DCM), whereas the corresponding experimental result is 2.89 eV. The dielectric-dependent method using eqn (2) provides an absorption energy of 2.92 eV. In the ESI,† we showed calculation results when basis sets are changed. We summarized calculation results using the CAM-B3LYP61 and M06-2X62 methods, which tend to slightly overestimate absorption energies for these TTz dyes. The HF exchange ratio is automatically tuned by using the self-consistent scheme based on eqn (4) in the dielectric-dependent approach. This characteristic behavior may be useful to describe the electronic structure of dyes in the excited state.| B3LYP | HandH | B3LYP-CAM | M06-2X | Eqn (2) | Eqn (3) | Exp. | |
|---|---|---|---|---|---|---|---|
| Bu2N-TTz-Py | |||||||
| Toluene | 2.61 | 3.30 | 3.25 | 3.25 | 2.94 | 3.01 | — |
| Chloroform | 2.57 | 3.28 | 3.24 | 3.23 | 2.92 | 2.99 | 2.88 |
| DCM | 2.55 | 3.27 | 3.23 | 3.22 | 2.92 | 2.98 | 2.89 |
| Methanol | 2.55 | 3.28 | 3.23 | 3.22 | 2.93 | 2.98 | 2.93 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Ph2N-TTz-Py | |||||||
| Toluene | 2.50 | 3.24 | 3.24 | 3.20 | 2.85 | 2.83 | 2.96 |
| Chloroform | 2.49 | 3.23 | 3.23 | 3.20 | 2.85 | 2.82 | 2.93 |
| DCM | 2.48 | 3.23 | 3.23 | 3.20 | 2.88 | 2.82 | 2.94 |
| Methanol | 2.48 | 3.24 | 3.24 | 3.21 | 2.91 | 2.83 | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Ph2N-TTz-CHO | |||||||
| Toluene | 2.30 | 3.13 | 3.15 | 3.12 | 2.75 | 2.66 | 2.92 |
| Chloroform | 2.28 | 3.12 | 3.15 | 3.12 | 2.76 | 2.64 | — |
| DCM | 2.27 | 3.12 | 3.15 | 3.12 | 2.77 | 2.64 | 2.86 |
| Methanol | 2.27 | 3.13 | 3.16 | 3.13 | 2.79 | 2.64 | — |
The theoretical and experimental emission energies of asymmetric TTz molecules are listed in Table 2. To obtain the emission (fluorescence) spectra, the geometrical optimization calculations under the excited electronic state were performed by considering the solvent effect by adopting the time-dependent DFT method. Unlike the absorption spectra, the theoretical and experimental emission energies are strongly affected by solvents. For example, eqn (3) yields energy values of 2.48 and 2.35 eV for Ph2N-TTz-Py in toluene and DCM, respectively, while the corresponding experimental results are 2.57 and 2.31 eV, respectively. The dielectric-dependent approach can describe well the electronic structure of asymmetric TTz dyes in the excited state. Hence, we focus on calculations and discussions based on the dielectric-dependent method in the following sections.
| B3LYP | HandH | CAM-B3LYP | M06-2X | Eqn (2) | Eqn (3) | Exp. | |
|---|---|---|---|---|---|---|---|
| Bu2N-TTz-Py | |||||||
| Toluene | 2.40 | 2.75 | 2.66 | 2.67 | 2.38 | 2.64 | — |
| Chloroform | 2.29 | 2.64 | 2.55 | 2.56 | 2.27 | 2.52 | 2.33 |
| DCM | 2.23 | 2.58 | 2.48 | 2.49 | 2.20 | 2.46 | 2.41 |
| Methanol | 2.17 | 2.51 | 2.42 | 2.43 | 2.14 | 2.40 | 2.20 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Ph2N-TTz-Py | |||||||
| Toluene | 2.12 | 2.70 | 2.64 | 2.64 | 2.31 | 2.48 | 2.57 |
| Chloroform | 2.11 | 2.60 | 2.54 | 2.55 | 2.22 | 2.40 | 2.39 |
| DCM | 2.09 | 2.55 | 2.49 | 2.49 | 2.16 | 2.35 | 2.31 |
| Methanol | 2.06 | 2.50 | 2.43 | 2.44 | 2.11 | 2.30 | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Ph2N-TTz-CHO | |||||||
| Toluene | 2.00 | 2.57 | 2.52 | 2.52 | 2.19 | 2.33 | 2.48 |
| Chloroform | 1.96 | 2.47 | 2.42 | 2.43 | 2.09 | 2.24 | — |
| DCM | 1.92 | 2.41 | 2.36 | 2.37 | 2.03 | 2.18 | 2.21 |
| Methanol | 1.89 | 2.35 | 2.30 | 2.32 | 1.98 | 2.13 | — |
3.2 Ph2N-TTz-COOH monomers and dimers in solvents
This section provides the calculation results of Ph2N-TTz-COOH considering both monomers and dimers. Ph2N-TTz-COOH with carboxyl group may take a dimmer structure in low-polarity solvents. Fig. 2 shows the ground state Py2N-TTz-COOH dimer structure in DCM obtained from the optimization calculation using the dielectric-dependent DFT method with eqn (2). The absorption and emission excitation energies of monomers and dimers in solvents are summarized in Table 3. From these calculations, we can confirm that small differences exist between monomer and dimer spectra. For example, the absorption excitation energies of monomer and dimer TTz dyes in toluene were evaluated as 2.82 and 2.81 eV, respectively, using eqn (2), and the experimental result was 2.93 eV. Further, the emission spectra of monomer and dimer TTz dyes in toluene were calculated as 2.23 and 2.22 eV, respectively, and the experimentally measured value was 2.55 eV. Thus, we will discuss monomers for Ph2N-TTz-COOH in the subsequent sections. | ||
| Fig. 2 Optimized dimer structure of Ph2N-TTz-COOH obtained from the dielectric-dependent density functional theory (DFT) method with eqn (2). | ||
| Toluene | Chloroform | Dichloromethane | Methanol | |
|---|---|---|---|---|
| Absorption | ||||
| Exp. | 2.93 | 2.92 | 2.93 | 3.00 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Monomer | ||||
| Eqn (2) | 2.82 | 2.84 | 2.84 | 2.86 |
| Eqn (3) | 2.78 | 2.75 | 2.74 | 2.75 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Dimer | ||||
| Eqn (2) | 2.81 | 2.81 | 2.82 | 2.83 |
| Eqn (3) | 2.73 | 2.71 | 2.70 | 2.70 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Emission | ||||
| Exp. | 2.55 | 2.26 | 2.37 | 2.32 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Monomer | ||||
| Eqn (2) | 2.23 | 2.13 | 2.08 | 2.03 |
| Eqn (3) | 2.39 | 2.31 | 2.26 | 2.21 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Dimer | ||||
| Eqn (2) | 2.22 | 2.13 | 2.07 | 2.02 |
| Eqn (3) | 2.37 | 2.13 | 2.07 | 2.02 |
3.3 Dipole moment and charge (electron) distribution analyses
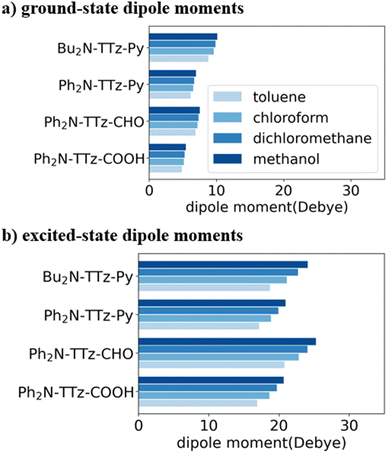
To investigate the excited-state behaviors of asymmetric TTz dyes, we first focused on their dipole moments in the ground and excited states in solvents, as shown in Fig. 3, based on the dielectric DFT method using eqn (2). These calculation results show that molecular excitations can induce significant modifications in the dipole moments. The dipole moments in the excited state are several times those in the ground state. For example, the dipole moments of Ph2N-TTz-CHO in the ground and excited states in toluene are obtained as 6.88 and 20.77 debye, respectively. We summarized the detailed data in the ESI.† In addition, the dipole moments in the excited state are largely affected by surrounding solvents; for example, the dipole moments of Ph2N-TTz-Py in the excited state in toluene, chloroform, and methanol are 17.14, 18.86, and 20.91 debye, respectively. Thus, the dipole moment analysis suggests that electronic structures of dyes are modified by molecular excitations and solvents.Next, we discuss the charge (electron) distributions in the dyes in the ground and excited states. For this purpose, we considered molecules to be composed of three parts, namely, the donor, TTz-core, and acceptor regions, as shown in Fig. 1. Fig. 4 summarizes the charge (electron) distributions aggregated in these parts (moieties) in the ground and excited states. We employed the Mulliken-based population analysis to obtain the charge distributions in the dyes. From these calculations, we observe that molecular excitations can also induce large changes on the charge (electron) distributions; each part in the excited state has larger negative or positive partial charges compared with those in the ground state. For example, the donor part of Bu2N-TTz-Py has a positive charge of about 0.1 a.u. in methanol under the ground state, and the charge increases greatly to around 0.4 a.u. in the excited state. The acceptor part has almost no charge in the ground sate, but it is negatively charged (about −0.2 a.u.) in the excited state. The partial charge on the TTz-core part increases to about −0.2 from −0.1 a.u. in the response to changes in charge distribution. In particular, the behavior of the acceptor part may be interesting; the polarization of the dye in the ground state occurs only in the donor and TTz-core regions, but it spreads throughout the molecule, including the acceptor region, in the excited state. These behaviors can be observed in the case of other asymmetric TTz dyes. These phenomena may be explained based on the shapes of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO). Fig. 5 shows the molecular orbitals of Ph2N-TTz-Py, where HOMO has a small participation with regard to the acceptor part, but LUMO has a much larger contribution. In asymmetric TTz dyes, an excited electron mainly transitions from the HOMO to the LUMO. For example, the largest configurational interaction (CI) coefficient of 0.67 is calculated for the transition from the HOMO to the LUMO for Bu2N-TTz-Py in toluene for photon absorption. Other cases are summarized in the ESI.† Such an electron transition drives a large intermolecular electron transfer toward the acceptor part in dyes. In addition, the solvent effect influences electron distributions in the excited state. Thus, solvent molecules can affect the electron transfer process between acceptor and donor parts. In the next section, we discuss the solvent effect on asymmetric TTz dyes with focus on the geometrical changes and solvent reorientations (reorganizations) induced by molecular excitations.
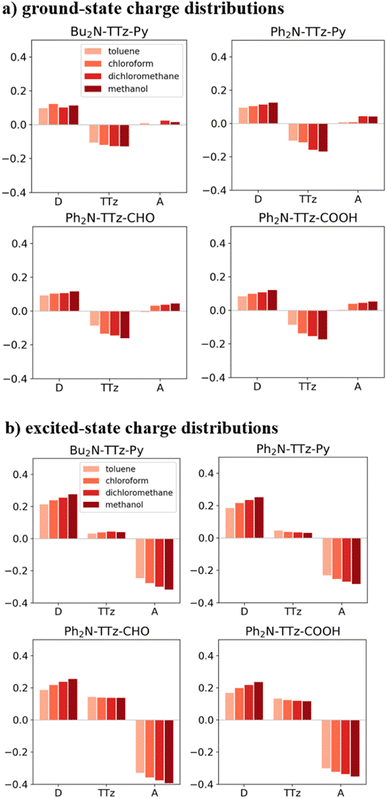 | ||
| Fig. 4 Charge distributions of the TTz dyes in the (a) ground and (b) excited states. The definitions of acceptor (A), TTz, and donor (D) regions are depicted in Fig. 1. Here, the optimized structures of the excited state are employed to obtain the charge distributions in the excited state. The intermolecular electron transfers toward the acceptor region, which are induced by molecular excitations, drive large changes in the charge distributions in the dyes. | ||
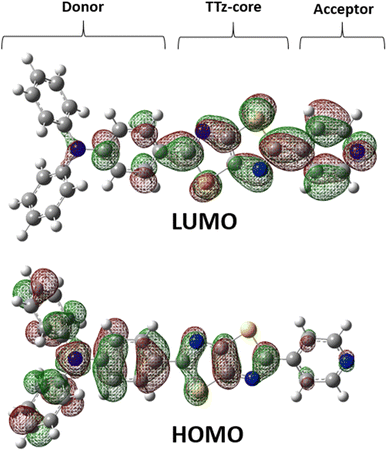 | ||
| Fig. 5 Highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) molecular orbitals of Ph2N-TTz-Py in dichloromethane. | ||
3.4 Decomposition analysis on the solvatofluorochromism
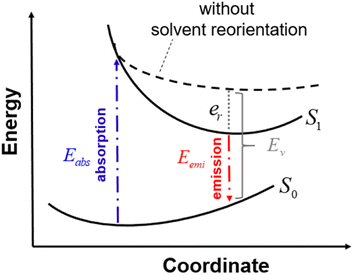
In this section, we discuss the Stokes shift property, which can be evaluated from the difference between the absorption and emission excitation energies of the dye. When asymmetric TTz dyes absorb photons, their electronic structures are greatly modified by the intermolecular electron (charge) transfer process, as discussed in the previous sections. Consequently, the geometric conformation of the excited dye relaxes toward a more energetically stable one under the excited state. Such conformational (geometrical structure) changes can strongly influence the Stokes shift. On the other hand, it is essential to consider the interactions between dyes and solvents when dealing with molecular emissions. Solvent molecules change their orientations depending on the excited electronic structure of dyes; this phenomenon is known as the solvent reorientation (reorganization) effect. The Stokes shifts of dyes are also affected by the solvent reorientation effect. In this section, we divide the Stokes shift into parts contributed by the geometrical change in the dye and solvent reorientation. Fig. 6 explains the decomposition technique, where Eabs and Eemi are the absorption and emission energies of asymmetric TTz dyes in solvents, respectively. Eemi is obtained from the time-dependent DFT method by executing geometric optimization in the excited state with the solvent reorientation effect. Conversely, the value of Ev is the vertical excitation energy without the solvent reorientation effect, though the optimized molecular coordinate in the excited state is employed. Ev is usually difficult to observe experimentally, and therefore, it may be a virtual computed quantity. However, we can estimate the solvent reorientation effect of er from the difference between Ev and Eemi. From these relationships, the following decomposition analysis can be employed to investigate the solvatofluorochromic phenomena of asymmetric TTz dyes.| Stokes shift = Eabs − Eemi = Eabs − (Ev − er) = (Eabs − Ev) + er |
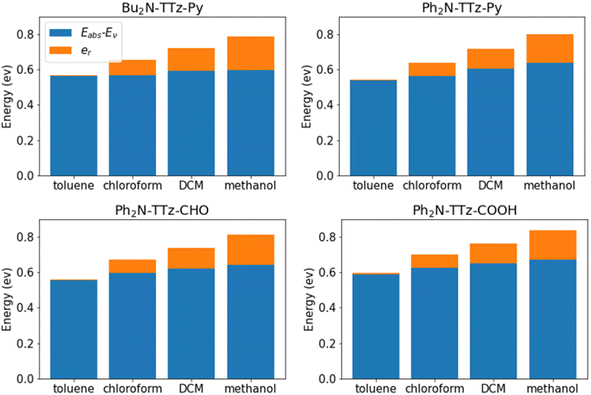
We analyzed the excited state behaviors of asymmetric TTz dyes based on the decomposition approach. Fig. 7 presents the contributions of the change in molecular geometry (Eabs − Ev) and solvent reorientation (er), which are depicted in blue and orange, respectively. We also summarized these details in the ESI.† These results show that the changes in the molecular geometry have a greater influence on the Stokes shift, especially for low-polarity solvents such as toluene. For example, the conformational change contribution of Bu2N-TTz-Py in toluene is 0.56 eV for a Stokes shift of 0.57 eV. For Ph2N-TTz-Py in methanol, the contribution of conformational change is 0.64 eV for a Stokes shift of 0.80 eV. In these cases, the conformational change contributions have high ratios of 98.2% and 80.0%. Thus, the conformational changes induced by the excitations of dyes have the largest impact on the Stokes shift. Conversely, the conformational change contributions of dyes themselves undergo little modifications even if the solvents are changed. From the viewpoint of response to solvents, the solvent reorientation contribution is more important. For Bu2N-TTz-Py in toluene, the reorientation effect is 0.01 eV, but it changes to 0.09, 0.13, and 0.19 eV when the solvents used are chloroform, dichloromethane, and methanol, respectively. These tendencies can be observed in the case of other dyes as well. The solvatofluorochromism is considered as changes in the emission spectra of dye in response to changes in solvents. Thus, we can conclude that the reorientation (reorganization) effect mainly contributes to solvatofluorochromic phenomena of asymmetric TTz dyes.
Finally, we discuss structural changes induced by the excitation of dyes in solvents. In the ground state, the molecular structures of asymmetric TTz dyes are slightly twisted. To analyze the twists in the molecules, we focused on the (dihedral) angle DA (DD) between the TTz-core part and the acceptor (donor) part, as shown in Fig. 8. In this paper, we simply discuss only the absolute values of the dihedral angles because of the high molecular symmetries. The dihedral angles of TTz molecules in the ground and excited states are summarized in Table 4. For example, the twisted angle DA (DD) is 15.31° (18.17°) for the ground state Ph2N-TTz-Py in toluene. The DA angles are 15.96°, 20.05°, and 21.06° in chloroform, dichloromethane, and methanol, respectively. The twists in asymmetric TTz molecules change depending on the solvents. In contrast, these twists are released in the excited dyes. That is, asymmetric TTz dyes contain more planar structures because of molecular excitations. For example, DA angles in the excited state Ph2N-TTz-Py in toluene and methanol are 0.22° and 0.13°, respectively. Changes from twisted structures to planar structures in the excited state have been confirmed for other TTz dyes. These phenomena may be explained by the molecular orbitals depicted in Fig. 5. Although the HOMO mainly participates in the TTz core and acceptor regions, the LUMO is more widely spread throughout the molecule, and therefore, the planar structures of dyes in the excited state may become more stable because of extended conjugated systems. We also observe that the planar structures of excited dyes are influenced when solvents are changed, but these influences are not very large. The TTz-based dyes have a rigid molecular skeleton (structure), and therefore, large conformational (geometrical) changes may be prevented in the excited state. Thus, the solvent reorientation effect may mainly contribute to the solvatofluorochromic phenomena because of the small conformational changes in asymmetric TTz dyes.
| Ground-state | Excited-state | |||
|---|---|---|---|---|
| DA | DD | DA | DD | |
| Bu2N-TTz-Py | ||||
| Hexane | 15.50 | 14.61 | 0.04 | 0.45 |
| Chloroform | 15.24 | 13.99 | 0.31 | 0.61 |
| Dichloromethane | 18.26 | 14.65 | 0.74 | 0.36 |
| Methanol | 18.19 | 16.14 | 0.08 | 0.13 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Ph2N-TTz-Py | ||||
| Toluene | 15.31 | 18.17 | 0.22 | 0.27 |
| Chloroform | 15.96 | 18.84 | 0.26 | 0.43 |
| Dichloromethane | 20.05 | 18.89 | 0.18 | 0.67 |
| Methanol | 21.06 | 20.90 | 0.13 | 0.88 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Ph2N-TTz-CHO | ||||
| Toluene | 17.83 | 17.77 | 0.05 | 0.69 |
| Chloroform | 20.85 | 18.52 | 0.06 | 0.99 |
| Dichloromethane | 21.91 | 19.09 | 0.11 | 1.07 |
| Methanol | 22.94 | 20.04 | 0.19 | 1.18 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Ph2N-TTz-COOH | ||||
| Toluene | 19.52 | 18.50 | 0.47 | 0.37 |
| Chloroform | 21.70 | 18.85 | 0.41 | 0.70 |
| Dichloromethane | 22.62 | 19.60 | 0.47 | 0.78 |
| Methanol | 23.52 | 20.91 | 0.43 | 0.93 |
4. Summary
In this paper, we discussed the excited state of asymmetric TTz dyes based on the time-dependent dielectric DFT approach, focusing on the solvatofluorochromic effect. We showed that the results obtained by the dielectric-dependent approach are in good agreement with experimental results related to the absorption and emission (fluorescence) spectra. The dipole moment analysis was performed to investigate the behaviors of the excited dyes, where the dipole moments in the excited state are much larger than those in the ground state. In addition, we evaluated the charge distributions in the ground and excited states of the dyes. In the ground state, the TTz core and donor parts have positive and negative charges, respectively, and there are few charges on the acceptor parts. In contrast, in the excited states of dyes, the acceptor parts can have large negative charges because of intramolecular electron transfers. Thus, the electron transfer process drives large electronic structure changes in excited asymmetric dyes.To more precisely investigate the solvatofluorochromism of TTz dyes, we performed the decomposition analysis where the Stokes shifts are divided into the contributions arising from geometrical changes and solvent reorientation. The decomposition analysis showed that geometrical changes induced by photon absorptions have the largest impact on the Stokes shifts of asymmetric TTz dyes. Conversely, we also showed that the solvent reorientation effect can have a larger influence on spectral changes in response to solvents. The solvatofluorochromic phenomenon is observed as changes in the emission spectra in response to solvents. Thus, the strong solvatofluorochromic phenomena of asymmetric TTz dyes are caused by the solvent reorientation effect. The rigid molecular structures of TTz-based dyes may prevent large geometrical changes in the excited state, and therefore, the contribution of geometrical changes may become less important.
Several fluorescent dyes have been developed for visualizing intracellular membranes and β-amyloid aggregations.63,64 In order to design novel dyes for bioimaging, TTz will play important roles as a molecular backboned. On the other hand, TTz-containing materials and molecules are actively studied especially for dye-sensitized solar cells (DSSCs) and organic photocells.65,66 Those studies show strong potential of TTz for applications on DSSCs. In this paper, we discussed the excited electronic structure of functional dyes using several analysis techniques. These analysis results will be useful to develop various types of dye-based materials.
Conflicts of interest
There are no conflicts to declare.References
- A. Dessi, M. Calamante, A. Mordini, M. Peruzzini, A. Sinicropi, R. Basosi, F. F. de Biani, M. Taddei, D. Colonna, A. Di Carlo, G. Reginato and L. Zani, Chem. Commun., 2014, 50, 13952–13955 RSC.
- S. Subramaniyan, H. Xin, F. S. Kim, N. M. Murari, B. A. E. Courtright and S. A. Jenekhe, Macromolecules, 2014, 47, 4199–4209 CrossRef CAS.
- J. Luo, B. Hu, C. Debruler and T. L. Liu, Angew. Chem., Int. Ed., 2018, 57, 231–235 CrossRef CAS PubMed.
- I. Roy, S. Bobbala, J. Zhou, M. T. Nguyen, S. K. M. Nalluri, Y. Wu, D. P. Ferris, E. A. Scott, M. R. Wasielewski and J. F. Stoddart, J. Am. Chem. Soc., 2018, 140, 7206–7212 CrossRef CAS PubMed.
- A. Khatun, D. K. Panda, N. Sayresmith, M. G. Walter and S. Saha, Inorg. Chem., 2019, 58, 12707–12715 CrossRef CAS PubMed.
- T. J. Adams, A. R. Brotherton, J. A. Molai, N. Parmar, J. R. Palmer, K. A. Sandor and M. G. Walter, Adv. Funct. Mater., 2021, 31, 2103408 CrossRef CAS.
- Y. Dou, R. Yang, Y. Xiao, J. Wu, L. B. Qu, Y. Q. Sun and Z. H. Li, Sens. Actuators, B, 2022, 354, 131226 CrossRef CAS.
- A. Fitri, A. T. Benjelloun, M. Benzakour, M. McHarfi, M. Hamidi and M. Bouachrine, Spectrochim. Acta, Part A, 2014, 132, 232–238 CrossRef CAS PubMed.
- A. Irfan and A. Mahmood, J. Cluster Sci., 2018, 29, 359–365 CrossRef CAS.
- J. N. Wu, G. W. Li, J. Fang, X. Guo, L. Zhu, B. Guo, Y. L. Wang, G. Y. Zhang, L. Arunagiri, F. Liu, H. Yan, M. J. Zhang and Y. F. Li, Nat. Commun., 2020, 11, 4612 CrossRef CAS PubMed.
- A. V. Akkuratov, S. L. Nikitenko, A. S. Kozlov, P. M. Kuznetsov, I. V. Martynov, N. V. Tukachev, A. Zhugayevych, I. Visoly-Fisher, E. A. Katz and P. A. Troshin, Sol. Energy, 2020, 198, 605–611 CrossRef CAS.
- W. H. Peng, G. J. Zhang, L. Shao, C. Ma, B. Zhang, W. J. Chi, Q. Peng and W. G. Zhu, J. Mater. Chem. A, 2018, 6, 24267–24276 RSC.
- H. B. Naveed and W. Ma, Joule, 2018, 2, 621 CrossRef CAS.
- L. C. Chang, M. Sheng, L. P. Duan and A. Uddin, Org. Electron., 2021, 90, 106063 CrossRef CAS.
- Y. Firdaus, V. M. Le Corre, J. I. Khan, Z. P. Kan, F. Laquai, P. M. Beaujuge and T. D. Anthopoulos, Adv. Sci., 2019, 6, 1802028 CrossRef PubMed.
- T. Umeyama, K. Igarashi, D. Sasada, Y. Tamai, K. Ishida, T. Koganezawa, S. Ohtani, K. Tanaka, H. Ohkita and H. Imahori, Chem. Sci., 2020, 11, 3250–3257 RSC.
- V. Kumar, S. Sony, N. Kaur, S. M. M. Mobin, P. Kaur and K. Singh, Anal. Chim. Acta, 2022, 1206, 339776 CrossRef CAS PubMed.
- N. A. Sayresmith, A. Saminathan, J. K. Sailer, S. M. Patberg, K. Sandor, Y. Krishnan and M. G. Walter, J. Am. Chem. Soc., 2019, 141, 18780–18790 CrossRef CAS PubMed.
- Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899–4032 CrossRef PubMed.
- A. Y. Freidzon, A. A. Safonov, A. A. Bagaturyants and M. V. Alfimov, Int. J. Quantum Chem., 2012, 112, 3059–3067 CrossRef CAS.
- T. Shimazaki and Y. Asai, Chem. Phys. Lett., 2008, 466, 91 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
- M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449 CrossRef CAS.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447 CrossRef CAS.
- G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 094107 CrossRef PubMed.
- C. Adamo and D. Jacquemin, Chem. Soc. Rev., 2013, 42, 845–856 RSC.
- A. D. Laurent, C. Adamo and D. Jacquemin, Phys. Chem. Chem. Phys., 2014, 16, 14334–14356 RSC.
- L. Hedin, Phys. Rev., 1965, 139, A796 CrossRef.
- T. Shimazaki and Y. Asai, J. Chem. Phys., 2009, 130, 164702 CrossRef PubMed.
- T. Shimazaki and Y. Asai, J. Chem. Phys., 2010, 132, 224105 CrossRef PubMed.
- T. Shimazaki and T. Nakajima, J. Chem. Phys., 2014, 141, 114109 CrossRef PubMed.
- T. Shimazaki and T. Nakajima, J. Chem. Phys., 2015, 142, 074109 CrossRef PubMed.
- T. Shimazaki and T. Nakajima, Chem. Phys. Lett., 2015, 634, 83–87 CrossRef CAS.
- A. Alkauskas, P. Broqvist, F. Devynck and A. Pasquarello, Phys. Rev. Lett., 2008, 101, 106802 CrossRef PubMed.
- A. Alkauskas, P. Broqvist and A. Pasquarello, Phys. Status Solidi B, 2011, 248, 775–789 CrossRef CAS.
- H. Wang, V. Eyert and U. Schwingenschlogl, J. Phys.: Condens. Matter, 2011, 23, 116003 CrossRef CAS PubMed.
- D. Koller, P. Blaha and F. Tran, J. Phys.: Condens. Matter, 2013, 25, 435503 CrossRef PubMed.
- S. Refaely-Abramson, S. Sharifzadeh, M. Jain, R. Baer, J. B. Neaton and L. Kronik, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 081204 CrossRef.
- J. H. Skone, M. Govoni and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195112 CrossRef.
- M. Gerosa, C. E. Bottani, L. Caramella, G. Onida, C. Di Valentin and G. Pacchioni, J. Chem. Phys., 2015, 143, 134702 CrossRef PubMed.
- A. M. Ferrari, R. Orlando and M. Rerat, J. Chem. Theory Comput., 2015, 11, 3245–3258 CrossRef CAS PubMed.
- J. H. Skone, M. Govoni and G. Galli, Phys. Rev. B, 2016, 93, 235106 CrossRef.
- L. Kronik and S. Kummel, Adv. Mater., 2018, 30, 1706560 CrossRef PubMed.
- A. K. Manna, S. Refaely-Abramson, A. M. Reilly, A. Tkatchenko, J. B. Neato and L. Kronik, J. Chem. Theory Comput., 2018, 14, 2919–2929 CrossRef CAS PubMed.
- L. A. Cipriano, G. Di Liberto, S. Tosoni and G. Pacchioni, J. Chem. Theory Comput., 2020, 16, 3786–3798 CrossRef CAS PubMed.
- D. Wing, G. Ohad, J. B. Haber, M. R. Filip, S. E. Gant, J. B. Neaton and L. Kronik, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104556118 CrossRef CAS PubMed.
- T. Shimazaki and T. Nakajima, Phys. Chem. Chem. Phys., 2016, 18, 27554–27563 RSC.
- T. Shimazaki and M. Tachikawa, Phys. Chem. Chem. Phys., 2021, 23, 21078–21086 RSC.
- T. Shimazaki and M. Tachikawa, Chem. Phys. Lett., 2022, 802, 139740 CrossRef CAS.
- F. Bechstedt, R. Delsole, G. Cappellini and L. Reining, Solid State Commun., 1992, 84, 765–770 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- J. C. Slater, The Self-Consistent Field for Molecules and Solids, Quantum Theory of Molecules and Solids, McGraw-Hill, New York, 1974 Search PubMed.
- J. M. Ziman, Principles of the Theory of Solids, Cambridge University Press, Cambridge, 1979 Search PubMed.
- G. Grosso and G. P. Parravicini, Solid State Physics, Academic Press, Orlando, 2000 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- T. Shimazaki, M. Hashimoto and T. Maeda, Proceedings of the 3rd International Workshop on Software Engineering for High Performance Computing in Computational Science and Engineering, 2015, p. 9, DOI:10.1145/2830168.2830170.
- T. Shimazaki, in Recent Advances of the Fragment Molecular Orbital Method, ed. Y. Mochizuki, S. Tanaka and K. Fukuzawa, Springer, Singapore, 2021, pp. 589–600 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- Y. Niko, P. Didier, Y. Mely, G. Konishi and A. S. Klymchenko, Sci. Rep., 2016, 6, 18870 Search PubMed.
- L. Espinar-Barranco, J. M. Paredes, A. Orte, L. Crovetto and E. Garcia-Fernandez, Dyes Pigm., 2022, 202, 110274 CrossRef CAS.
- G. Reginato, A. Mordini, L. Zani, M. Calamante and A. Dessi, Eur. J. Org. Chem., 2016, 2016, 233–251 CrossRef CAS.
- A. Dessi, M. Calamante, A. Sinicropi, M. L. Parisi, L. Vesce, P. Mariani, B. Taheri, M. Ciocca, A. Di Carlo, L. Zani, A. Mordini and G. Reginato, Sustainable Energy Fuels, 2020, 4, 2309–2321 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta07200a |
| This journal is © The Royal Society of Chemistry 2022 |