Introduction of plumbole to f-element chemistry

Abstract

Herein, we present the synthesis and characterization of heteroleptic lanthanide complexes bearing a dianionic η⁵-plumbole ligand in their coordination sphere. The reaction proceeds via a salt elimination reaction between the dilithioplumbole ([Li(thf)]₂[1,4-bis-tert-butyl-dimethylsilyl-2,3-bis-phenyl-plumbolyl] = [Li₂(thf)₂(η⁵-L^Pb)]) and specifically designed [Ln(η⁸-COT^TIPS)BH₄] precursors (Ln = lanthanide, La, Ce, Sm, Er; COT^TIPS = 1,4-bis-triisopropylsilyl-cyclooctatetraenyl), that are capable of stabilizing a planar plumbole moiety in the coordination sphere of different trivalent lanthanide ions. In-depth ab initio calculations show that the aromaticity of the dianionic plumbole is retained upon coordination. Electron delocalization occurs from the plumbole HOMO to an orbital of mainly d-character at the lanthanide ion. The magnetic properties of the erbium congener were investigated in detail, leading to the observation of magnetic hysteresis up to 5 K (200 Oe s⁻¹), an unequivocal proof for single molecule magnet behavior in this system. The magnetic behavior of the erbium species can be modulated by manipulating the position of the lithium cation in the complex, which directly influences the bonding metrics in the central [(η⁵-L^Pb)Er(η⁸-COT^TIPS)]⁻ fragment. This allowed us to assess a fundamental magneto-structural correlation in an otherwise identical inner coordination sphere.

---

Introduction

Sandwich complexes have been among the most important compound classes since the early days of modern organometallic chemistry. In fact, ferrocene [(η⁵-Cp)₂Fe] (Cp = C₅H₅), which was discovered by Kealy and Pauson,¹ is one of the archetypes for organometallic compounds. Its structural analysis took place in the course of a famous competition between Fischer and Wilkinson.² In a sandwich complex or metallocene, the central metal is exclusively coordinated by two planar, cyclic, and π-bonded ligands. In this context, as for example in ferrocene, the ligand of choice, in most metallocenes, is the five membered cyclopentadienyl ring. Besides their historic role in modern organometallics, sandwich complexes remain an indispensable part of fundamental and applied chemistry, e.g., ferrocene, has been widely used in a variety of applications, such as synthesis, catalysis, electrochemistry, medicine and even as fuel additive.³ Since the early days, chemists have been modifying classical sandwich complexes to tailor their structures and properties. Mostly peripherally substituted ring systems are employed for this purpose. Here, the substituents may not only influence the steric demand and the electronic properties, but also hinder ligand rotation, e.g., in ansa-metallocenes, or induce chirality. Another approach is the use of heterocyclic rings as ligands, e.g., cyclopentadienyl-like systems where one or more carbon atoms have been replaced with heteroatoms, e.g., carboranes.⁴

While there is a rich variety of sandwich complexes of the d-metals, the number of sandwich complexes of f-metals, especially of lanthanides, is still limited and mostly based on ηⁿ-carbocyclic ligands. In their typical trivalent oxidation state, tris-cyclopentadienyl complexes [(η⁵-C₅H₅)₃Ln], which have no sandwich structure, are formed.⁵ Typical sandwich structures are formed in the trivalent state by the dianionic cyclooctatetraenyl (COT) ligand,⁶e.g., [(η⁸-COT)₂Ln^III]⁻ and [(η⁵-Cp)Ln^III(η⁸-COT)] and also mixed valent species as [Sm^III/II/III₃(COT^TIPS)₄] (COT^TIPS = 1,4-bis-triisopropylsilyl-cyclooctatetraenyl).^7,8 In the divalent oxidation state, bis-cyclopentadienyl complexes, e.g., [(η⁵-C₅Me₅)₂Sm^II], form bent metallocene structures,⁹ while cyclooctatetraenyl ligands give dianionic linear metallocenes [(η⁸-COT)₂Ln^II]²⁻.¹⁰

Recently, new developments in the area of single molecule magnets (SMMs) initiated a renaissance in the investigation of lanthanide sandwich complexes. Some design principles were developed, in which the local electron density is tailored around the central lanthanide ion, to enhance its anisotropic properties.¹¹ In the wake of this approach, charged, aromatic π-ligands have become a popular tool for manipulating the coordination and electronic environment of lanthanide ions.¹²

However, some of the organometallic compounds used to develop these concepts are among afore-mentioned examples dating back to the 1970s and 1980s, e.g. [(η⁸-COT)₂Ln^III]⁻ and [(η⁵-Cp)Ln^III(η⁸-COT)].^8a,b In contrast, recently reported Dy SMMs, with very high relaxation times and blocking temperatures, used a newly developed synthetic approach based on established ligand systems.^12c,d,17 This peaked in a series of dysprosocenium cations exhibiting magnetic hysteresis up to T_h = 80 K, an important milestone towards the implementation of SMMs in technical devices.^12f However, limitations due to the sole application of carbon-based ligand moieties might catch up with this fast-developing field. A straightforward approach to further increase the accessible design space is replacing one or more skeletal carbon atoms in the metallocene ligands by heteroatoms.¹⁸ Surprisingly, only a few heterocyclic lanthanide sandwich complexes are known. Most of them are based on phosphole (A, B, C),^13,14,16 and arsole (C),¹⁹ while only the phosphole derivatives were investigated in terms of their magnetic properties (Fig. 1).^13,14 Aside from these so called five membered metalloles, the six membered boratabenzene ligand was successfully established as part of a lanthanide SMM (D).¹⁶ Especially the metalloles, which are five membered Cp-like systems where one carbon has been replaced by a heteroatom, represent a widely explored field for themselves with the possibility to introduce a vast variety of elements all over the periodic table into neutral and charged systems.²⁰ For example, all of the group-14 metallole dianions [EC₄R₄]²⁻ (E = Si, Ge, Sn, Pb) have been synthesized and studied in terms of their coordination behaviour towards different main group- and transition-metals.²¹ Nevertheless, their coordination chemistry with lanthanides is severely underdeveloped. Hence, introducing different metallole anions into the coordination sphere of lanthanides might give rise to novel lanthanide sandwich complexes with intriguing structures and properties. Dianionic metalloles are of special interest, as they could be used to prepare multimetallic lanthanide species, of the type [(η⁸-COT)Ln(L^Pb)Ln(η⁸-COT)] or [Ln₂(L^Pb)₃] (L^Pb = 1,4-bis-tert-butyl-dimethylsilyl-2,3-bis-phenyl-plumbolyl), to name two possible motifs, where the anionic metallole moiety acts as a bridging unit between two lanthanide ions.^21d,22 Arrangements like these might promote magnetic through ligand exchange coupling between the metal ions if the molecular orbitals of the charged dianionic ligand units are capable of interacting with the lanthanide 4f orbitals.²³ We therefore directed our interest towards the heaviest group 14 metalloles, dianionic plumboles,²⁴ to study heavy metal interactions.²⁵ To the best of our knowledge, dianionic plumboles have been coordinated to Li, Ru and Rh only.^21b,d,24 In general, there is only one contribution, which was published while this work was in progress, that is dealing with yttrium complexes ligated by a group 14 metallole dianion. Here, germole complexes were reported, but only half-sandwich or dimeric compounds and no classical sandwich complexes were obtained.²⁶ Therefore, we endeavoured to synthesize the first plumbole complexes of the f-elements.

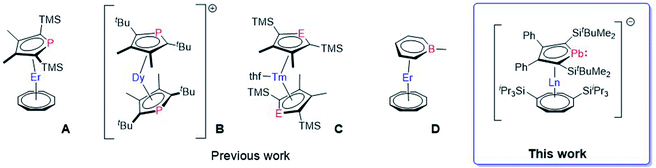Fig. 1 Molecular structures of [Er^III(η⁵-Dsp)(η⁸-COT)] A,¹³ [Dy^III(η⁵-Dtp)₂]⁺B,¹⁴ [Tm^II(thf)(η⁵-Dsp/Dsa)₂] (E = P, As) C,¹⁵ and [Er^III(η⁶-C₅H₅BMe)(η⁸-COT)] D.¹⁶ The anion of B is omitted for clarity. (Dsp = 3,4-dimethyl-2,5-bis(trimethylsilyl)phospholyl, Dsa = 3,4-dimethyl-2,5-bis(trimethylsilyl)arsolyl, Dtp = 3,4-dimethyl-2,5-bis(tert-butyl)phospholyl).

Results and discussion

Synthesis and structural characterization

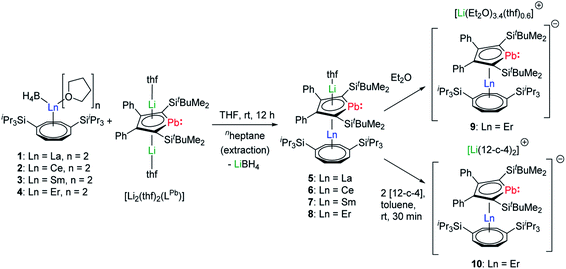
During our first attempts to introduce an intact L^Pb into the coordination sphere of a trivalent lanthanide ion, we reacted a variety of lanthanide precursors with [Li₂(thf)₂(η⁵-L^Pb)] to create different coordination environments. We initially aimed at synthesizing anionic homoleptic [Ln(η⁵-L^Pb)₂]⁻ complexes by treatment of different trivalent (pseudo)halide precursors with two equivalents of [Li₂(thf)₂(L^Pb)]. We moreover reacted equimolar amounts of [Ln(η⁵-Cp*)(BH₄)₂] species with [Li₂(thf)₂(η⁵-L^Pb)] to obtain neutral heteroleptic [(η⁵-L^Pb)Ln(η⁵-Cp*)] complexes. However, all these attempts resulted in intractable reaction mixtures. As Ln–COT frameworks are known to facilitate uncommon coordination environments in lanthanide compounds, we designed [Ln(η⁸-COT^TIPS)BH₄] (COT^TIPS = 1,4-bis-triisopropylsilyl-cyclooctatetraenyl) precursors. By introducing the bulky COT^TIPS moiety, we aimed to kinetically stabilize the desired compounds, by providing pronounced steric shielding through the bulky TIPS groups and stabilization of the Ln–COT^TIPS fragment through the high hapticity of the ring system. Additionally, the ligands system should provide sufficient solubility in common organic solvents.

The [Ln(η⁸-COT^TIPS)BH₄] (Ln = La (1), Ce (2), Sm (3), Er (4)) precursors were synthesized by salt metathesis of the corresponding [Ln(BH₄)₃(thf)_3–3.5]²⁷ starting materials with [K₂COT^TIPS]²⁸ in THF. Subsequent treatment of 1–4 with [Li₂(thf)₂(L^Pb)] in THF gave the desired heteroleptic [Li(Sol)(η⁵-L^Pb)Ln(η⁸-COT^TIPS)] (Ln = La (5), Ce (6), Sm(7), Er (8–10); Sol = thf (5–8), (Et₂O)_3.4(thf)_0.6 (9)) sandwich complexes 5–9 (Scheme 1). The addition of two equivalents of 12-crown-4 to a freshly prepared toluene solution of 8 led to the formation of the charge separated sandwich-complex 10 (Ln = Er, Sol = (12-crown-4)₂).

Scheme 1 Synthesis of compounds 5–10.

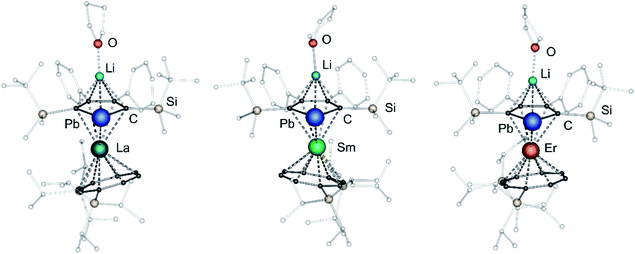
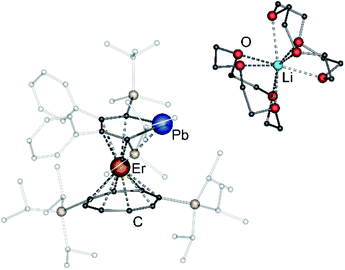
After extraction of the reaction mixture with ⁿheptane (Scheme 1), the crude products were isolated as brown, sticky solids, which were crystallized from hot ⁿheptane (5, 6, 8), hot toluene (7, 10) or by slow evaporation of diethyl ether (9) to yield the pure compounds as orange to red crystalline materials (crystalline yield: 5-La: 54%, 6-Ce: 49%, 7-Sm: 45%, 8-Er: 39%, 9-Er: 41%, 10-Er: 41%). The molecular solid-state structures of compounds 1–10 were determined by SCXRD. Herein only compounds 5–10 will be discussed. For compounds 1–4 see ESI‡ pages S35 and S39–S42. To the best of our knowledge, 5–10 are the first monomeric f-element sandwich complexes containing a dianionic group-14 metallole ligand. Compounds 5–8 are essentially isostructural, exhibiting a slightly bent s–p–f-element sandwich motif (Fig. 2). Compounds 9 and 10 on the other hand are charge separated species in the solid state, consisting of a solvated lithium cation and an anionic [(η⁵-L^Pb)Er(η⁸-COT^TIPS)]-fragment (Fig. 3 and S46‡). As expected, the lanthanide ions in 5–10 are η⁸-coordinated by the COT^TIPS–ligand with Ln–Ct_COTTIPS (Ct = centroid of the corresponding ring) distances ranging from 1.9804(4) Å for 5 to 1.7385(3) Å for 8, nicely correlated to the decreasing ionic radii along the lanthanide series (Table 1). As anticipated, the central lanthanide ions are η⁵-coordinated by the plumbole moiety, with Ln–Ct_LPb distances between 2.5464(4) Å in 5 and 2.3041(3) Å in 8 and Ln–Pb distances ranging from 3.3530(6) Å to 3.1492(4) Å for 5 and 8, respectively (Table 1). To date only one other publication is dealing with Ln–Pb bonds. Here, lanthanide κ¹-plumbylene complexes are discussed. However, a direct comparison of bond metrics appears futile due to the deviating coordination modes and chemical identities of the ligands (κ¹-plumbylene vs. η⁵-plumbole).²⁹ For all compounds discussed here, the C–C bond lengths within the five-membered PbC₄ ring are nearly identical and the sum of internal bond angles is close to 540°, indicating that the aromaticity of the plumbole ligand is retained. Interestingly the Ct_COTTIPS–Ln–Ct_LPb angle increases smoothly with decreasing ionic radius from 158.87(2)° to 168.77(2)° in the series of s–p–f-sandwich compounds 5–8 (Table 1). Comparing the Ln–Ct_COTTIPS distances in compounds 8 and the charge separated analogue 9, unveils a direct influence of the location of the counter ion on the bond metrics of the central [(η⁵-L^Pb)Er(η⁸-COT^TIPS)]⁻ fragment. The coordination of the Li ion in 8 significantly shortens the Er–Ct_COTTIPS distance from 1.7737(4) Å in 9 to 1.7385(3) Å in 8. This is most likely caused by formal removal of electron density from the plumbole moiety upon coordination towards the electron-deficient lithium cation. Consequently, the Er–Ct_LPb distance is elongated from 2.2777(4) Å in 9 to 2.3041(3) Å in 8 due to the weaker electrostatic interaction between the Er ion and L^Pb caused by the lowered local charge density in the plumbole system. As a result, the COT^TIPS moiety can approach the Er ion owing to the lowered inter ligand repulsion at shorter Er–Ct_COTTIPS distances. This effect might enhance the anisotropic properties of the erbium ion in 8, as we anticipate the COT^TIPS ligand to exert a more equatorial ligand field, compared to the plumbole ligand. On the other hand, the Ct_COTTIPS–Er–Ct_LPb angle in 9 accounts for 173.20° revealing a significant widening compared to 8. However, it should be noted here that the crystals of compound 9 were dried in vacuo at room temperature for 30 min whereupon combustion analysis of the sample indicates partial removal of the Li-coordinated solvent molecules, which is likely to be accompanied by coordination of lithium to the plumbole ligand, resulting in a compound similar to 8. To further confirm this hypothesis, magnetic measurements of the isolated crystals of 9 were performed and the out-of-phase component exhibits two maxima (see Fig. S80‡), which is most likely due to the presence of both the solvated and unsolvated species. We consequently synthesized the irreversibly ion separated 12-c-4 adduct 10. As expected, the Er–Ct_COTTIPS distance of 1.7800(3) Å in 10 is again elongated compared to 8. This effect is more pronounced than what we observed in 9, which is also accompanied by a smaller Ct_COTTIPS–Er–Ct_LPb angle of 168.26° compared to 173.20° in 9. The former one is almost identical to the angle observed in the neutral species 8. As a result, compounds 8 and 10 allow us to directly measure the influence of varying the Er–Ct_COTTIPS distances in an otherwise identical inner coordination sphere, which is rarely possible for lanthanidocene systems.^12a,13,16

Fig. 2 Molecular structures of [Li(thf)(η⁵-L^Pb)Ln(η⁸-COT^TIPS)] compounds 5 (left), 6 (middle) and 8 (right) in the solid state. For better clarity: hydrogen atoms are omitted, silyl- and phenyl-groups are transparent.

Fig. 3 Molecular structure of [Li(12-c-4)₂(η⁵-L^Pb)Er(η⁸-COT^TIPS)] (10) in the solid state. For better clarity: hydrogen atoms are omitted, silyl- and phenyl-groups are transparent. Only one of the half-occupied [Li(12-c-4)₂]⁺ moieties of 10 is depicted. Simultaneously, only one part of the disordered 12-c-4 ligands is shown.

Table 1 Comparison of selected bond-metrics for compounds 5–10 and calculated values (PBE0/def2-TZVP) for compounds 5, 7, 8 and 10

Compound	Ln–CtCOTTIPS [Å]		Ln–CtLPb [Å]		CtCOTTIPS–Ln–CtLPb [°]
	Exp.	Calc.	Exp.	Calc.	Exp.	Calc.
a The [Li(12-c-4)]^+ cation was omitted in the calculation.
5	1.9804(4)	2.016	2.5464(4)	2.616	158.87(2)	163.0
6	1.9540(4)		2.5186(4)		161.28(2)
7	1.8614(3)	1.901	2.4344(3)	2.517	163.60(2)	162.8
8	1.7385(3)	1.770	2.3041(3)	2.362	168.77(2)	167.2
9	1.7737(4)		2.2777(4)		173.20(2)
10	1.7800(3)	1.825^a	2.2807(4)	2.321^a	168.26(2)	168.4^a

---

As a result, magnetometric studies of 8 and 10 provide direct access to fundamental magneto-structural correlations in SMMs based on the Er–COT framework. In case of dysprosocenium cations, a detailed study also revealed the influence of Dy–ligand bond metrics on the SMM behaviour, by modulating the ligand substitution pattern and therefore also influencing the inner coordination sphere.¹⁷ To further understand the origin of these subtle changes in the solid-state structures upon coordination/decoordination of the Li cation, detailed quantum chemical calculations were performed.

Quantum chemical study of lanthanide plumbole bonding

Density functional theory (DFT) calculations at level PBE0/def2-TZVP³⁰ were carried out with the program system TURBOMOLE³¹ in order to investigate the lanthanide plumbole bonding situation. Effective core potentials were employed for the inner electrons of the heavy metal atoms. For Pb the effective core potential covered the inner 60 electrons (ECP-60),³² for La the inner 46 electrons (ECP-46)³³ and for Sm and Er the inner 28 electrons (ECP-28).³² Additionally, the RI-J-approximation was applied.³⁴ Magnetically induced current densities were calculated with the GIMIC program,³⁵ using the (perturbed) densities from TURBOMOLE as input, which are available also for open-shell systems in a local version at present.

For the optimized structures, the distances shown in Table 1 are consistently overestimated by ∼5 pm, thus the tendencies regarding changes (vide supra) are very well reproduced. Coordinates of the optimized structures are provided in the ESI (Table S24‡). To shed light on the origin of bonding in the lanthanide–plumbole complexes, energy decomposition analyses (EDA)³⁶ were performed for the free anions [(η⁵-L^Pb)La(η⁸-COT^TIPS)]⁻ and [(η⁵-L^Pb)Er(η⁸-COT^TIPS)]⁻. For that, the compounds were decomposed in the two fragments (L^Pb)²⁻ and [Ln(η⁸-COT^TIPS)]⁺. For the La/Er compound, a total interaction energy of 1007/1076 kJ mol⁻¹ was found, to the larger part caused by electrostatic interactions (812/931 kJ mol⁻¹) which is about half of the attractive interactions for both compounds. This is accompanied by donation of electron density from the plumbole ligand to the central lanthanide ion, which is evident from Mulliken population analyses.³⁷ The charge of the plumbole moiety in [(η⁵-L^Pb)Ln(η⁸-COT^TIPS)]⁻ is calculated to be −1.01/−0.69 for La/Er. As expected, the absolute value of the negative charge is somewhat lower in [Li(thf)(η⁵-L^Pb)Er(η⁸-COT^TIPS)] (−0.56), indicating removal of electron density from the plumbole moiety upon coordination of [Li(thf)]⁺.

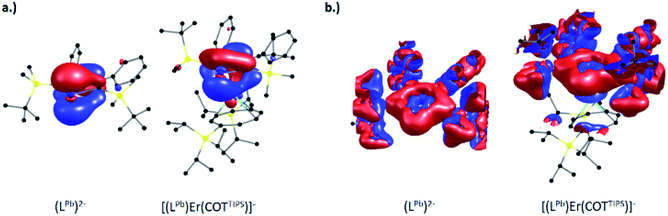
Detailed comparison of the molecular orbitals of the isolated plumbole ligand with those of [(η⁵-L^Pb)Er(η⁸-COT^TIPS)]⁻ shows that the electron transfer to [Ln(η⁸-COT^TIPS)]⁺ is mainly due to the change of the shape of the HOMO of the plumbole which is shown on the left hand side of Fig. 4 (for images of the corresponding orbitals in 5, 7 and 8 see Fig. S81–S83 in the ESI‡). Electron delocalization occurs from the plumbole HOMO to an orbital of mainly d-character at the lanthanide ion.

Fig. 4 (a) Molecular orbitals relevant for lanthanide plumbole bonding in [(η⁵-L^Pb)Er(η⁸-COT^TIPS)]⁻. HOMO of the free plumbole (left) and highest occupied α-orbital of [(η⁵-L^Pb)Er(η⁸-COT^TIPS)]⁻ (right) (b) Signed modulus of the current density in (L^Pb)²⁻ (left) and [(η⁵-L^Pb)Er(η⁸-COT^TIPS)]⁻ (right). Diatropic contributions are shown in red, paratropic contributions in blue. Hydrogen atoms were omitted for clarity.

Despite this partial depopulation of the π-electron system, the plumbole ligand is expected to retain its aromaticity in the complexes reported herein, as already indicated by the metric parameters (see above). This indeed is evident from calculations of the magnetically induced current density, which probe the aromaticity based on the magnetic criterion.³⁸

The signed modulus of the current density for the free dianionic plumbole ligand and [(η⁵-L^Pb)Er(η⁸-COT^TIPS)]⁻ is shown at the right hand side of Fig. 4 (for the former, the conductor-like screening model³⁹ with default parameters was employed to compensate the negative charge). For the free plumbole, a diatropic ring current is observed outside the ring, whereas a weaker paratropic ring current flows inside the ring, which goes in line with the expected aromaticity. The situation remains the same upon coordination of the plumbole ligand to the lanthanide ion in the complex, thereby indicating that aromaticity is indeed retained. The same holds for the remaining compounds reported herein. For comparison, the corresponding images for the Cp anion and the hypothetical compound [(η⁵-Cp)La(η⁸-COT^TIPS)] are available within the ESI‡ (Fig. S84 and S85).

Magnetic properties of 8 and 10

It is well described by Rinehart and Long that equatorial ligand fields are beneficial for stabilizing the prolate m_J states of trivalent lanthanide ions like erbium.¹¹ The COT ligand is known to exert an equatorial field which has been shown in multiple SMM compounds based on the {Er(η⁸-COT)⁺} moiety alongside other ligands.^8c,12g,13,16 With this in mind, we performed detailed magnetic studies on the erbium complexes 8 and 10.

The temperature dependent behaviour of the samples was tested upon cooling from room temperature to 2 K in an external magnetic field of 1000 Oe (0.1 T). Both compounds show almost identical temperature independent behaviour above 150 K with molar χ_MT values at room temperature of 10.07 and 10.42 cm³ K mol⁻¹, respectively (Fig. S48 and S60‡). The observed values in both cases are about 10% below the expected value of a single isolated Er(III) ion of 11.48 cm³ K mol⁻¹. We attribute these lowered signal values to the sample preparation, where, after flame sealing the sample in an NMR tube, we were not able to prevent small amounts of the sample being smeared across the glass walls. Upon cooling, χ_MT starts to slowly decrease below 150 K to about 8.5 cm³ K mol⁻¹. Both compounds reveal an abrupt drop of the susceptibility at very low temperatures, indicating magnetic blocking. Note, that antiferromagnetic coupling between Er-ions of neighbouring molecules might also play a role in the sudden drop of susceptibility. However, the effect of interactions should be very small, if not negligible, as the shortest intermolecular Er–Er distances found are very large with 12.7 Å and 10.9 Å for 8 and 10, respectively. The drop is observed at about 6 K for 8 with a final χ_MT value of 6.66 cm³ K mol⁻¹ at 2 K and at approximately 4 K for 10 with χ_MT = 7.84 cm³ K mol⁻¹ at 2 K.

Besides temperature dependent studies, we performed measurements of the molar magnetization versus the applied magnetic field. Both 8 and 10 show common behaviour, of a rapid increase in magnetization, which strongly flattens upon reaching higher fields. With values around 4 μ_B mol⁻¹ at 7 T, the values are again about 10% below the expected value for a single Er^III of 4.5 μ_B mol⁻¹, therefore, being in line with the susceptibilities we observed. Magnetic blocking and bistable behaviour, as suggested by the low temperature drop of the susceptibility, can ultimately be proven by magnetic hysteresis. We performed hysteresis measurements in a window of −2.5 T to 2.5 T at different temperatures with field sweep rates of 50 Oe s⁻¹ and 200 Oe s⁻¹. At 2 K we observed a butterfly-like hysteresis between −1.0 T and 1.0 T for 8, open at zero field only for the faster sweep rate (Fig. 5, top right). The butterfly-like shape of the hysteresis loop and the closing at zero field is typical for lanthanide ions where the abrupt increase and decrease is caused by efficient quantum tunnelling of the magnetization (QTM) at fields close to zero. With increasing temperature, the hysteresis loops are closing until they are no longer observable from 5 K (Fig. S50 and S51‡). We also observed hysteresis of 10, however, with a much less pronounced butterfly shape. The highest temperatures at which hysteresis is observed for 10 is 4 K (Fig. S62 and S63‡). Therefore, the observed hysteresis is in good agreement with the above-described drop in susceptibility for both compounds.

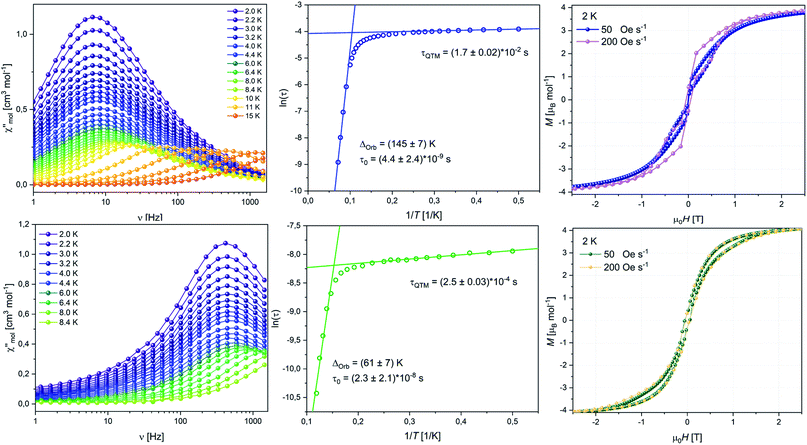Fig. 5 Frequency dependent out-of-phase susceptibility χ′′(ν) (left), Arrhenius plot (middle), hysteresis loop at 2 K (right) for 8 (top row) and 10 (bottom row).

To quantify our observations, we studied the dynamic behaviour of the samples through AC susceptibility measurements. Both compounds show a single maximum in the frequency-dependent out-of-phase component of the magnetic susceptibility χ′′(ν), in zero applied DC field, which starts shifting to higher frequencies upon increasing the temperature (Fig. 5, left). Upon application of an additional external field (tested at 1, 2, 3 and 4 kOe) a signal in the out-of-phase susceptibility is no longer observable for 8 and for 10 (Fig. S53 and S65‡). The temperature dependent shift of the signal at zero field is typically ascribed to the Orbach relaxation of SMMs. Between 2–8 K the maximum for 8 is observed at about 7 Hz without any visible shift. This region describes the temperature-independent regime where relaxation of the magnetic moment solely occurs through quantum tunnelling events. Above 8 K the maximum is shifting towards higher frequencies until it is no longer observable within our frequency window at about 15 K.

By fitting the in-phase and out-of-phase signals using a generalized Debeye model (Table S13‡), we obtained an α-parameter between 0.31 at low temperatures and 0.11 at higher temperatures. This indicates that at low T other processes as for example Raman processes could be involved in the relaxation mechanism, while Orbach relaxation is dominant at higher T. Arrhenius analysis of the low temperature QTM region gave τ_QTM = 1.7 × 10⁻² s, while analysis of the high temperature Orbach region gave an energy barrier U_eff = 145 K and τ₀ = 4.4 × 10⁻⁹ s (Fig. 5, top middle). Note, that despite mentioning Raman processes, we were not able to perform fits of the full Arrhenius plot using Orbach, QTM and Raman processes simultaneously without over parameterization, due to the relatively small Raman regions.

For compound 10 the maximum at low T is observed at about 300 Hz from where it starts shifting to higher frequencies above 5 K. Similar data treatment as described above gives us almost identical α-values at low T of 0.31 indicating that the relaxation happens via a similar distribution of processes, which is expected given the close structural relationship of 8 and 10 (Table S16‡). As suggested by the higher frequency of the maximum and the earlier shift with temperature, Arrhenius treatment gave a lower energy barrier U_eff = 61 K, τ₀ = 2.3 × 10⁻⁸ s and τ_QTM = 2.5 × 10⁻⁴ s (Fig. 5, bottom middle). Extrapolation of the Arrhenius data allows us to estimate at which T hysteresis might be observable. The calculated temperatures where τ = 100 s are 2.8 K and 6.1 K for 10 and 8, respectively. This estimation is in decent agreement with the hysteresis loops observed. As discussed previously the different magnetic behaviour of the two compounds can be explained by the variation of the Er–CtC_OTTIPS and Er–Ct_LPb distances. Although the coordination spheres of the Er^III ion in 8 and 10 are very similar to one another, in 8 the COT^TIPS ligand is closer to the ion than in 10, while the plumbole ligand is moved further away. Therefore, the ligand field exerted in 8 is more equatorial and with that, more beneficial for the prolate m_J states. Interestingly, and despite showing the same Er(η⁸-COT) motif as other compounds, the SMM performance of 8 and 10 falls short in comparison to reported ErCOT-SMMs. The parent compound [(η⁵-Cp*)Er(η⁸-COT)] is shown to feature two distinct relaxations based on different conformers of the molecule.^8c The relaxation barriers for the two conformers are reported at 197 and 323 K. Exchange of [Cp*]⁻ with [Dsp]⁻ resulted in a compound structurally very similar to 10 reported by Gao et al.¹³ Here the [(Dsp)Er(η⁸-COT)] shows a relaxation barrier of 358 K, higher than that of [(η⁵-Cp*)Er(η⁸-COT)] and much higher than that of 10. In the authors' comparison between [(Dsp)Er(η⁸-COT)] and [(η⁵-Cp*)Er(η⁸-COT)], [Cp*]⁻ and [Dsp]⁻ were essentially considered as the same ligand and the authors derived the differences in performance from the different bonding metrics. This is very much in line with what we observed with compounds 8 and 10 where the coordinating plumbole ligand remains the exact same and, therefore, only the change of distances and angles can have an influence on the SMM properties. However, drawing the line between 10 and either [(Dsp)Er(η⁸-COT)] or [(η⁵-Cp*)Er(η⁸-COT)], makes it seem unreasonable that the Er–Ct distances are the sole reason for the observed behaviour.

In fact, the Er–Ct_LPb distances of both 8 and 10 (Table 1) are in between the reported Er–Ct_Dsp and Er–Ct_Cp distances, while the Er–Ct_COT distances for 8 and 10 are longer in comparison, with the largest difference being about 0.1 Å between 10 and [(Dsp)Er(η⁸-COT)]. It is clear, that 0.1 Å cannot explain the difference in barrier height of almost 300 K. Instead, we assume that the introduction of the big and electron rich Pb-atom into the ring generated a significantly stronger axial ligand than the parent Cp*. The idea of introducing softer heteroatoms into the five-membered ring, was to lower the affinity of Er(III) towards the axial ligand. While this worked in case of the phospholyl ligand, for the plumbole the increased axiality of the ligand seems to outweigh the lowered bonding affinity. Thus, the plumbole ligand might be an interesting candidate for future synthesis employing other lanthanides like Dy or Tb.

To fully validate our assumptions on the different behaviours of 8 and 10, we performed ab initio CASSCF calculations using the MOLCAS package. The simulated χT(T) behaviour of 8 is in good agreement with the experimental data (Fig. S48‡) after applying a scaling factor of 0.9, as mentioned above. The M(H) data is well reproduced by the calculation at small fields while it exceeds the simulation towards higher fields. This behavior is commonly observed in compounds with strong anisotropy.^12g,40 Only small differences are observed for χT(T) in the region between 50 K and 100 K for 10 (Fig. S60‡), which might be caused by pinning of the freely rotating crown-ether at very low T and with that small structural changes that are not accounted for in the calculation.⁴¹ The calculation of the low-lying Kramer's doublets predicts rather pure m_J = ±|15/2> states to be the ground states characterized by g_x < g_y < 0.004, g_z = 17.783 for 8 and g_x < g_y < 0.07, g_z = 17.051 for 10. In both cases the highly axial ground state indicates that QTM is not efficient enough to quench SMM behaviour at zero DC field. The anisotropy axis of 8 is close to perpendicular to the COT plane, whereas, for 10 it is slightly tilted towards the Pb atom (Fig. 6). This tilting of the main magnetic axes in 10 is, alongside the above mentioned more axial ligand field, very likely a main reason for the lowered energy barrier compared to 8. The first excited doublet state of 8 is found at 137.6 K. Opposite to the ground doublet this state is strongly mixed (Table S14‡) with the anisotropy axis being tilted by 66°, allowing efficient relaxation via this state.

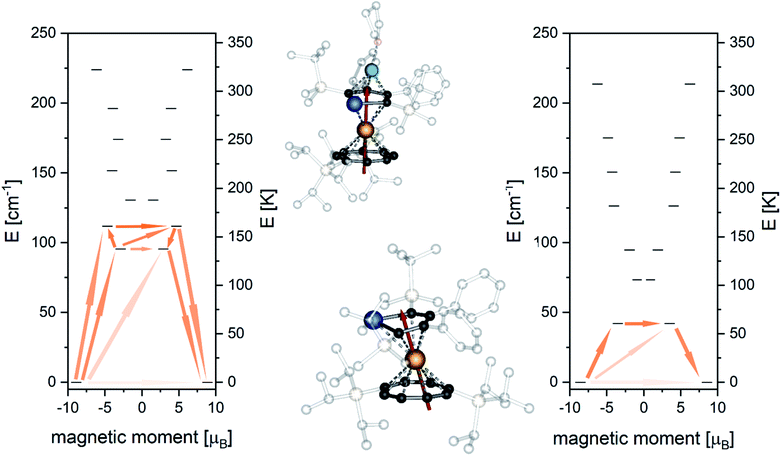Fig. 6 Ab initio doublet states and proposed relaxation pathway for 8 (left) and 10 (right). Orientation of the anisotropy axes of the ground state doublet for 8 (top middle) and 10 (bottom middle).

Similarly, for 10 the anisotropy axis of first excited doublet at 60.4 K is also strongly tilted by 79° and the state is a mixture of different m_J-states (Table S17‡). Relaxation through the first excited doublet state is likely the most efficient relaxation pathway for both compounds. The separations of 137.6 K and 60.4 K towards the excited states are in good agreement with the experimentally found relaxation barriers of 145 K and 61 K, respectively. Investigation of the transition probabilities between the states (Fig. 6 and Tables S15 and S18‡) suggests that relaxation via the second and third excited state could also play a role in the relaxation behaviour of the molecules. A second excited state of 8 is found at 160.7 K, which might cause the slight increase of the experimental energy barrier compared to the separation of the first excited state. The performed ab initio calculations confirmed our idea that the ligand field is enhanced towards stabilizing the magnetic moment when the plumbole ligand is moved further away and the COT ligand is moved closer to the Er-centre.

Magnetic measurements and ab initio calculations have also been performed on 6 and 7, the Ce and Sm analogues of 8. No slow relaxation is observed in 7, while 6 shows field-induced SMM behaviour with U_eff = 26 K at optimal field of 750 Oe (compare Fig. S72–S79 and Tables S19–S23‡).

Conclusions

In summary, we introduced a dianionic plumbole ligand for the first time into the coordination chemistry of the f-elements. As a result, a series of anionic plumbole-ligated sandwich complexes was obtained. In dependence of the crystallization conditions, the counterion Li⁺ is either separated by forming an ionic species or coordinated to the plumbole ligand opposite to the lanthanide ion. In any case, the aromaticity in the plumbole ring is retained, as confirmed by quantum chemical calculations. Due to the selective coordination or decoordination of the Li⁺ cation, the distance of the rings to the lanthanide atom and the magnetic properties of the resulting complexes can be manipulated. This can be studied in case of the Er complexes 8 and 10, which show SMM behaviour including magnetic hysteresis up to 5 K (8, 200 Oe s⁻¹). Here we obtained some direct insight into this fundamental magneto-structural correlation. Although, we did not obtain a new record in terms of SMM performance, the results of the magnetic measurements indicate that heavy metal containing heteroatomic ring systems are worth to be explored further, considering their unique electronic structure and coordination capabilities. Besides the magnetic properties we also observed a rare Ln–Pb heavy metal interaction, whereas electron delocalization from the plumbole HOMO to an orbital of mainly d-character at the lanthanide ion characterizes the bonding situation.

Funding sources

Deutsche Forschungsgemeinschaft (DFG) is acknowledged for financial support within the Reinhart Koselleck-Projekt 440644676, RO 2008/19-1.

Data availability

All computational data, synthetic protocols, data from magnetic measurements, spectroscopic data, supplementary figures and tables, and detailed crystallographic information can be found in the ESI.‡ Crystallographic data are available via the Cambridge Crystallographic Data Centre (CCDC): 2067569–2067577.

Author contributions

All authors have given approval to the final version of the manuscript. LM and XS synthesized and analyzed all compounds with support from AH. LM and CS conducted X-ray experiments. SS and MR conducted and interpreted magnetic measurements and carried out the ab initio CASSCF calculations and interpreted the results. SG and FW performed the quantum chemical analysis of the bonding situation. PWR originated the idea, supervised the work, and interpreted the results. All authors contributed to the preparation of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Prof. Dr Dieter Fenske for measuring single crystals of compound 6 and KMNF for the measuring time. Helga Berberich is acknowledged for support of NMR experiments. KIT is acknowledged for financial support.

Notes and references

1. T. J. Kealy and P. L. Pauson, Nature, 1951, 168, 1039–1040.
2. (a) G. Wilkinson, M. Rosenblum, M. C. Whiting and R. B. Woodward, J. Am. Chem. Soc., 1952, 74, 2125–2126; (b) E. O. Fischer and W. Pfab, Z. Naturforsch., B: Chem. Sci., 1952, 7, 377–379.
3. P. Štěpnička, Ferrocenes: Ligands, Materials and Biomolecules, John Wiley & Sons, Ltd, Chichester, 2008.
4. (a) C. Elschenbroich, Organometallchemie, Vieweg+Teubner Verlag, Springer, Wiesbaden, 2008; (b) R. N. Grimes, J. Organomet. Chem., 1999, 581, 1–12; (c) K. E. Stockman, E. A. Boring, M. Sabat, M. G. Finn and R. N. Grimes, Organometallics, 2000, 19, 2200–2207; (d) H. Yao and R. N. Grimes, Organometallics, 2003, 22, 4539–4546.
5. (a) G. Wilkinson and J. M. Birmingham, J. Am. Chem. Soc., 1954, 76, 6210; (b) J. M. Birmingham and G. Wilkinson, J. Am. Chem. Soc., 1956, 78, 42–44; (c) G. B. Deacon, C. M. Forsyth, B. M. Gatehouse, A. Philosof, B. W. Skelton, A. H. White and P. A. White, Aust. J. Chem., 1997, 50, 959–970.
6. K. Mashima, Y. Nakayama, A. Nakamura, N. Kanehisa, Y. Kai and H. Takaya, J. Organomet. Chem., 1994, 473, 85–91.
7. J. J. Le Roy, L. Ungur, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2014, 136, 8003–8010.
8. (a) F. Mares, K. Hodgson and A. Streitwieser, J. Organomet. Chem., 1970, 24, C68–C70; (b) H. Schumann, R. D. Koehn, F. W. Reier, A. Dietrich and J. Pickardt, Organometallics, 1989, 8, 1388–1392; (c) S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733; (d) L. Münzfeld, A. Hauser, P. Hädinger, F. Weigend and P. W. Roesky, Angew. Chem., Int. Ed., 2021, 60, 24493–24499.
9. (a) W. J. Evans, L. A. Hughes and T. P. Hanusa, J. Am. Chem. Soc., 1984, 106, 4270–4272; (b) W. J. Evans, L. A. Hughes and T. P. Hanusa, Organometallics, 1986, 5, 1285–1291.
10. (a) W. J. Evans, J. L. Shreeve and J. W. Ziller, Polyhedron, 1995, 14, 2945–2951; (b) J. Moutet, J. Schleinitz, L. La Droitte, M. Tricoire, F. Pointillart, F. Gendron, T. Simler, C. Clavaguéra, B. Le Guennic, O. Cador and G. Nocton, Angew. Chem., Int. Ed., 2021, 60, 6042–6046.
11. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085.
12. (a) K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952–17957; (b) L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., Int. Ed., 2014, 53, 4413–4417; (c) F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449; (d) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442; (e) C. A. Gould, K. R. McClain, J. M. Yu, T. J. Groshens, F. Furche, B. G. Harvey and J. R. Long, J. Am. Chem. Soc., 2019, 141, 12967–12973; (f) F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400; (g) L. Münzfeld, C. Schoo, S. Bestgen, E. Moreno-Pineda, R. Köppe, M. Ruben and P. W. Roesky, Nat. Commun., 2019, 10, 3135; (h) J. P. Durrant, J. Tang, A. Mansikkamäki and R. A. Layfield, Chem. Commun., 2020, 56, 4708–4711.
13. S.-M. Chen, J. Xiong, Y.-Q. Zhang, Q. Yuan, B.-W. Wang and S. Gao, Chem. Sci., 2018, 9, 7540–7545.
14. P. Evans, D. Reta, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2019, 141, 19935–19940.
15. F. Nief, D. Turcitu and L. Ricard, Chem. Commun., 2002, 1646–1647.
16. Y.-S. Meng, C.-H. Wang, Y.-Q. Zhang, X.-B. Leng, B.-W. Wang, Y.-F. Chen and S. Gao, Inorg. Chem. Front., 2016, 3, 828–835.
17. R. K. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503.
18. F.-S. Guo, A. K. Bar and R. A. Layfield, Chem. Rev., 2019, 119, 8479–8505.
19. D. P. Mills and P. Evans, Chem.–Eur. J., 2021, 27, 6645–6665.
20. (a) M. Saito and M. Yoshioka, Coord. Chem. Rev., 2005, 249, 765–780; (b) J. Wei, W.-X. Zhang and Z. Xi, Chem. Sci., 2018, 9, 560–568; (c) P. J. Fagan, W. A. Nugent and J. C. Calabrese, J. Am. Chem. Soc., 1994, 116, 1880–1889.
21. (a) T. Kuwabara, M. Nakada, J. Hamada, J. D. Guo, S. Nagase and M. Saito, J. Am. Chem. Soc., 2016, 138, 11378–11382; (b) M. Nakada, T. Kuwabara, S. Furukawa, M. Hada, M. Minoura and M. Saito, Chem. Sci., 2017, 8, 3092–3097; (c) M. Saito, Acc. Chem. Res., 2018, 51, 160–169; (d) M. Saito, M. Nakada, T. Kuwabara, R. Owada, S. Furukawa, R. Narayanan, M. Abe, M. Hada, K. Tanaka and Y. Yamamoto, Organometallics, 2019, 38, 3099–3103; (e) P. Tholen, Z. Dong, M. Schmidtmann, L. Albers and T. Müller, Angew. Chem., Int. Ed., 2018, 57, 13319–13324; (f) Z. Dong, K. Bedbur, M. Schmidtmann and T. Müller, J. Am. Chem. Soc., 2018, 140, 3052–3060; (g) Z. Dong, L. Albers and T. Müller, Acc. Chem. Res., 2020, 53, 532–543; (h) Z. Dong, J. M. Winkler, M. Schmidtmann and T. Müller, Chem. Sci., 2021, 12, 6287–6292.
22. (a) T. Kuwabara, J.-D. Guo, S. Nagase, T. Sasamori, N. Tokitoh and M. Saito, J. Am. Chem. Soc., 2014, 136, 13059–13064; (b) M. Saito, N. Matsunaga, J. Hamada, S. Furukawa, M. Minoura, S. Wegner, J. Barthel and C. Janiak, Dalton Trans., 2018, 47, 8892–8896.
23. (a) C. A. P. Goodwin, Dalton Trans., 2020, 49, 14320–14337; (b) K. L. M. Harriman and M. Murugesu, Acc. Chem. Res., 2016, 49, 1158–1167; (c) O. T. Summerscales, S. C. Jones, F. G. N. Cloke and P. B. Hitchcock, Organometallics, 2009, 28, 5896–5908.
24. (a) M. Saito, M. Sakaguchi, T. Tajima, K. Ishimura, S. Nagase and M. Hada, Science, 2010, 328, 339–342; (b) M. Saito, M. Nakada, T. Kuwabara and M. Minoura, Chem. Commun., 2015, 51, 4674–4676.
25. A. R. Eulenstein, Y. J. Franzke, N. Lichtenberger, R. J. Wilson, H. L. Deubner, F. Kraus, R. Clérac, F. Weigend and S. Dehnen, Nat. Chem., 2021, 13, 149–155.
26. J. Liu, K. Singh, S. Dutta, Z. Feng, D. Koley, G. Tan and X. Wang, Dalton Trans., 2021, 50, 5552–5556.
27. S. M. Cendrowski-Guillaume, G. Le Gland, M. Nierlich and M. Ephritikhine, Organometallics, 2000, 19, 5654–5660.
28. O. T. Summerscales, F. G. N. Cloke, P. B. Hitchcock, J. C. Green and N. Hazari, Science, 2006, 311, 829–831.
29. K. Zeckert, J. Griebel, R. Kirmse, M. Weiß and R. Denecke, Chem.–Eur. J., 2013, 19, 7718–7722.
30. (a) J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985; (b) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
31. (a) TURBOMOLE V7.4 2020, a development of University of Karlsruheand Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com; (b) S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. M. Khah, S. K. Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. v. Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
32. B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563–2569.
33. M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1989, 75, 173–194.
34. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
35. (a) J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963; (b) H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518; (c) S. Taubert, D. Sundholm and J. Jusélius, J. Chem. Phys., 2011, 134, 054123; (d) GIMIC version 2.1.4, a current density program, December 2020, can be freely downloaded from https://github.com/qmcurrents/gimic.
36. (a) T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10; (b) K. Morokuma, J. Chem. Phys., 1971, 55, 1236–1244; (c) P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102.
37. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840.
38. R. Gershoni-Poranne and A. Stanger, Chem. Soc. Rev., 2015, 44, 6597–6615.
39. A. Schäfer, A. Klamt, D. Sattel, J. C. W. Lohrenz and F. Eckert, Phys. Chem. Chem. Phys., 2000, 2, 2187–2193.
40. (a) I. Oyarzabal, J. Ruiz, J. M. Seco, M. Evangelisti, A. Camón, E. Ruiz, D. Aravena and E. Colacio, Chem.–Eur. J., 2014, 20, 14262–14269; (b) R. Marx, F. Moro, M. Dörfel, L. Ungur, M. Waters, S. D. Jiang, M. Orlita, J. Taylor, W. Frey, L. F. Chibotaru and J. van Slageren, Chem. Sci., 2014, 5, 3287–3293; (c) E. Lucaccini, J. J. Baldoví, L. Chelazzi, A.-L. Barra, F. Grepioni, J.-P. Costes and L. Sorace, Inorg. Chem., 2017, 56, 4728–4738.
41. (a) K. Sambe, N. Hoshino, T. Takeda, T. Nakamura and T. Akutagawa, Cryst. Growth Des., 2021, 21, 5928–5942; (b) K. Sambe, N. Hoshino, T. Takeda, T. Nakamura and T. Akutagawa, J. Phys. Chem. C, 2020, 124, 13560–13571.

---

Footnotes

† Dedicated to Professor Holger Braunschweig on the occasion of his 60th birthday.

‡ Electronic supplementary information (ESI) available: Analytical data, crystallographic data, details on quantum chemical calculations and details on SQUID experiments. CCDC 2067569–2067577. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc03805b

§ Both authors contributed equally.

---