Free-standing 2D non-van der Waals antiferromagnetic hexagonal FeSe semiconductor: halide-assisted chemical synthesis and Fe²⁺ related magnetic transitions

Abstract

The scarcity of two-dimensional (2D) magnetic nanostructures has hindered their applications in spintronics, which is attributed to that most magnetic materials exhibit non-van der Waals (nvdWs) structures and it is hard to reduce their thickness to 2D nanostructures. Thus it is necessary to develop a promising strategy for free-standing 2D magnetic nvdWs nanostructures. We have achieved free-standing 2D nvdWs hexagonal FeSe with a thickness of 2.9 nm by the reaction between the oleylamine–Se complex and Fe²⁺ with the assistance of Cl⁻, where the synergetic effects of Cl⁻ and –NH₂ lead to anisotropic growth. Inspiringly, the 2D hexagonal FeSe exhibits intrinsic antiferromagnetic order rooted in Fe²⁺ and semiconducting nature. In addition, the temperature variation would result in the chemical environment changes of Fe²⁺, responsible for the temperature-dependent magnetic transitions. This work promotes the potential applications of 2D hexagonal FeSe and the preparation of other 2D nvdWs materials.

---

Introduction

Two-dimensional (2D) magnetic nanostructures are promising candidates for integrated circuits and next-generation spintronic devices.^1–3 It is worth noting that antiferromagnetic materials could represent the future of spintronics, which could be attributed to that antiferromagnetic materials produce no stray fields, display ultrafast dynamics, and are capable of generating large magnetotransport effects.^4,5 Unfortunately, the magnetic order in 2D nanostructures is scarce which could be ascribed to that most magnetic materials exhibit non-van der Waals (nvdWs) structures and it is hard to reduce their thickness to 2D nanostructures where magnetic anisotropy could suppress thermal fluctuation.^4–7 The intrinsically nonmagnetic 2D vdWs nanostructures could be endowed with magnetism by doping,⁶ fluorination,⁸ and some other strategies,¹ but the induced magnetism is not always stable.

The 2D nvdWs magnetic nanostructures could be obtained on a substrate by the chemical vapor deposition method or molecular beam epitaxy method and the Cr₂Te₃ (ref. 9) and NbN¹⁰ thin films have been obtained by such methods, although the substrate may affect the magnetic and electrical properties, hindering the wide applications of such 2D nanostructures.^8–10 Therefore, it is urgent and significant to prepare free-standing 2D magnetic nvdWs nanostructures. Regardless of the considerable interest, it is really difficult to obtain free-standing 2D nvdWs structures, which meant that the covalent bonds should be broken.

Because the top-down method requires a quantity of energy to break the covalent bonds, to the best of our knowledge, 2D hematite is the only 2D magnetic nvdWs nanostructure obtained from the top-down strategy.¹¹ The bottom-up method is usually used for 2D magnetic nvdWs nanostructures, such as CoO, Co₉Se₈, FeF₂, and Fe₃Se₄ nanosheets.^12–16 It is worth noting that the Fe₃Se₄ nanosheets exhibited a large coercivity rooted in the huge magnetocrystalline anisotropy.^15,16 Among the various bottom-up methods, the wet-chemical method for 2D nvdWs nanostructures is low-cost and high-yield.^15–19 Unfortunately, the growth mechanism of 2D nvdWs nanostructures has not yet been fully addressed, especially the role of Cl⁻, though transition metal chlorides have usually been chosen as the precursors.^20–24

Hexagonal FeSe with nvdWs structures exhibits magnetic order and is a promising candidate for next-generation spintronic devices.^25,26 Unfortunately, all the reported 2D hexagonal FeSe compounds were grown on a substrate, which resulted in the controversial magnetic and electric nature.^16,17 The 2D hexagonal FeSe grown on Al₂O₃ and GaAs substrates exhibits ferromagnetism whereas it displays antiferromagnetism with SrTiO₃ as the substrate.^26–29 The first-principles calculations identify hexagonal FeSe as a semiconductor but it exhibits metallic behavior on the GaAs substrate.^27,29 Up to now, there have been no reports on the preparation of free-standing 2D nvdWs hexagonal FeSe, which is significant for the identification and investigation of the intrinsic magnetic and electrical nature of 2D hexagonal FeSe.

Herein, we report the preparation of free-standing 2D nvdWs hexagonal FeSe with a thickness of 2.90–2.95 nm and a lateral dimension of 1.0–2.2 μm by a high-temperature organic phase method. Both experiments and first-principles calculations uncover the growth mechanism, which is the synergetic effect of Cl⁻ and –NH₂. The free-standing 2D hexagonal FeSe exhibits an intrinsic antiferromagnetic and semiconducting nature. The Néel temperature is 553 K, which is suitable for high-temperature spintronics. Moreover, the origin of magnetic order and temperature-dependent magnetic transitions of the 2D hexagonal FeSe is explored, which is related to Fe²⁺. This work should hereby contribute greatly to the growth mechanism of free-standing 2D nvdWs hexagonal FeSe and investigation of the antiferromagnetic (AFM) semiconductor behaviors.

Results and discussion

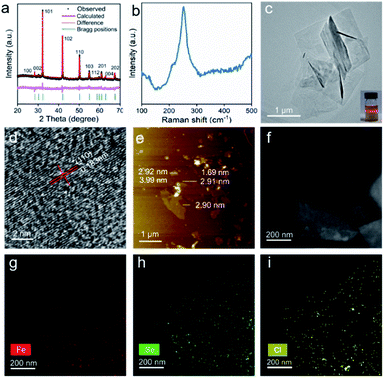
To achieve 2D hexagonal FeSe, the oleylamine (OAm)–Se complex was chosen as the Se precursor instead of Se or H₂Se because residual Se would cause damage to the magnetic properties of the products, and H₂Se is dangerous. The reaction between the OAm–Se complex and FeCl₂·4H₂O was carried out at 345 °C to guarantee a good crystallinity. Rietveld X-ray diffraction (XRD) analysis assigned the products to the hexagonal FeSe phase (space group P6₃/mmc) without impurities (Fig. 1a). It should be noted that the XRD refinement was carried out with the assistance of the powder XRD card of hexagonal FeSe (JCPDS: 26-0795, a = 0.3626 and c = 0.594 nm). And the obtained lattice parameters (a = 0.3635 nm and c = 0.5918 nm) were almost the same as those of the standard card. The inductively coupled plasma analysis of the as-synthesized hexagonal FeSe revealed that the molar ratio of Fe/Se was 0.98/1. Therefore, there were Fe vacancies in the as-synthesized hexagonal FeSe and the vacancy-ordered superstructure was common in hexagonal FeSe.^30,31 The first-principles Raman investigation of hexagonal FeSe with five-unit-cell thickness exhibited a Raman excitation at 140 cm⁻¹ (Fig. S1†), which was indexed as the (007) mode. The Raman spectra of the as-synthesized hexagonal FeSe showed an obvious Raman excitation at 250 cm⁻¹ (Fig. 1b). Despite the difference of Raman excitation frequency, the observed excitation at 250 cm⁻¹ could be assigned to the (007) mode. A typical transmission electron microscope (TEM) image (Fig. 1c) revealed that the as-synthesized hexagonal FeSe exhibited 2D morphology with a lateral dimension of 1.0–2.2 μm. The selected area electron diffraction (SAED) pattern of the FeSe nanosheets is shown in Fig. S2† and due to the stacking of FeSe nanosheets and the large size of the selected area aperture, the SAED patterns suggested polycrystalline diffraction rings. The emergence of the Tyndall effect in the diluted solution of n-hexane proved the colloidal nature of the 2D hexagonal FeSe. The high-resolution TEM (HRTEM) image of the 2D hexagonal FeSe (Fig. 1d) showed a lattice spacing of 0.183 nm, which was consistent with that of the (110) facet of hexagonal FeSe (0.182 nm), further confirming such nanosheets as hexagonal FeSe. The HRTEM image of the rolled-up edge exhibited a lattice fringe of 0.58 nm and an average thickness of approximately 2.91 nm (Fig. S3†), which meant that the exposed facet of the 2D hexagonal FeSe was (001). The atomic force microscopy detection (Fig. 1e) was applied to study the lateral size and thickness of hexagonal FeSe nanosheets. The lateral size and thickness distribution (Fig. S4†) were obtained from the atomic force microscopy image. The 2D nvdWs hexagonal FeSe nanosheets exhibited a varying thickness and showed five-unit-cell thickness. And the line profile scan for Fig. 1e is also shown in Fig S5,† which revealed the stacking of the nanosheets. The 2D nvdWs hexagonal FeSe was quite stable, and it could remain without phase transformation after exposure to air for a month or being heat-treated at 600 K for 1 h under a N₂ atmosphere (Fig. S6†).

Fig. 1 (a) Rietveld XRD pattern, (b) Raman spectra, (c) TEM image (inset: Tyndall effect), (d) HRTEM image, (e) atomic force microscopy image, and (f) HAADF-STEM image of the 2D hexagonal FeSe. Elemental mapping of (g) Fe, (h) Se, and (i) Cl for the 2D hexagonal FeSe.

A high-angle annular dark-field (HAADF) image and elemental mapping of Fe (red), Se (green), and Cl (yellow) (Fig. 1f–i) showed the uniform distribution of Fe, Se, and Cl, which implied that Cl⁻ may act as capping ligands. The presence of Cl⁻ was also supported by the energy dispersive X-ray (EDX) spectra (Fig. S7†).

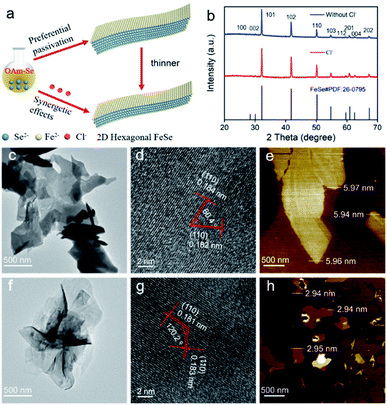
The Fourier transform infrared (FT-IR) spectra indicated that the 2D hexagonal FeSe was coordinated with amine groups (Fig. S8†). To confirm this, we carried out the synthetic experiments using the octadecene (ODE)–Se complex and Fe(acetylacetonate)₂ (Fe(acac)₂) in which FeCl₂·4H₂O did not react with ODE to form a complex. The obtained hexagonal FeSe was almost isotropic nanoparticles (Fig. S9†), which could identify OAm molecules as capping ligands. Considering that Cl⁻ may also act as capping ligands, NH₄Cl, the Cl⁻ precursor, was introduced into the system of the ODE–Se complex and Fe(acac)₂ to verify the role of Cl⁻. The products were still isotropic nanoparticles (Fig. S10†), which implied that –NH₂ induced the anisotropic growth instead of Cl⁻. The hexagonal FeSe nanoparticles could also be obtained by using FeCl₃ and ODE–Se as precursors.³² Based on the experimental results, density functional theory (DFT) calculations were performed to uncover the role of Cl⁻ and –NH₂ during the synthetic process. The crystal structure of hexagonal FeSe is shown in Fig. S11a.† Considering that OAm and Cl⁻ bound to the nanosheets during growth, we simplified the calculation by replacing OAm with NH₃ because OAm reacted with 2D hexagonal FeSe only through –NH₂ and it would not affect the calculated adsorption energy significantly.^14,33 DFT calculations were used to estimate the adsorption energy of only –NH₂ and the equal amount of –NH₂ and Cl⁻ on the (001) facet (Fig. S11b and c†). Half of the Fe atoms were bound to capping ligands to minimize the energy.¹⁴ The adsorption energy of only –NH₂ was −1.35 eV per unit and the synergism of –NH₂ and Cl⁻ made the adsorption energy decrease to −3.16 eV per unit. Therefore, the formation of ultrathin 2D hexagonal FeSe could be ascribed to the preferential passivation of –NH₂ and strong passivation of Cl⁻ (Fig. 2a).

Fig. 2 (a) Schematic illustration of the growth mechanism. (b) XRD patterns of the products of the reaction between the OAm–Se complex and Fe(acac)₂. (c) TEM image, (d) HRTEM image, and (e) atomic force microscopy image of the products without Cl⁻. (f) TEM image, (g) HRTEM image, and (h) atomic force microscopy image of the products with the adsorption of Cl⁻.

To demonstrate the DFT results, OAm–Se and Fe(acac)₂ were applied as precursors and the products were hexagonal FeSe (Fig. 2b) with 2D morphology (Fig. 2c and f) regardless of the presence or absence of NH₄Cl. The angle between the two (110) facets was about 60°/120° (Fig. 2d and g), which meant that the exposed facet was (001). Hence, it was proved that –NH₂ would prefer to passivate the (001) facet, responsible for the anisotropic growth. The nanosheets without Cl⁻ showed a thickness of ∼5.95 nm (Fig. 2e) and the presence of Cl⁻ during the synthetic process resulted in the nanosheets with a thickness of ∼2.93 nm (Fig. 2h), which proved the strong passivation ability of Cl⁻. Hence, the formation of ultrathin 2D nvdWs hexagonal FeSe was ascribed to the synergetic effect of Cl⁻ and –NH₂, where Cl⁻ acted as a strong capping ligand with the assistance of preferential passivation of –NH₂.

X-ray photoelectron spectroscopy (XPS) was carried out to investigate the valence state of ultrathin 2D nvdWs hexagonal FeSe. As shown in Fig. 3a, the binding energy peaks situated at 711.1 eV and 725 eV were assigned to Fe²⁺. The minor satellite peaks indicated that some Fe ions were in the trivalent state, which could be ascribed to the Fe vacancy in hexagonal FeSe.³⁰ The binding energy peaks of Se 3d were located at 53.4 and 54.2 eV (Fig. 3b), which were associated with Se²⁻ and ruled out the presence of selenium or selenium oxides. The Fe 3p peaks located at 54.9 and 57.9 eV (Fig. 3b) corresponded to Fe²⁺ and Fe³⁺,³⁴ respectively, which revealed that Fe²⁺ is dominant.

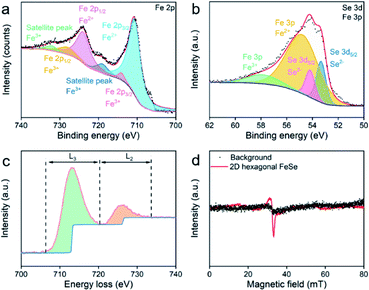Fig. 3 (a) Fe 2p core-level and (b) Se 3d and Fe 3p core-level XPS spectra of ultrathin 2D nvdWs hexagonal FeSe, (c) Fe L_2,3-edge EELS and (d) EPR spectra (5 K) of ultrathin 2D nvdWs hexagonal FeSe.

Fe L_2,3-edge electron energy loss spectroscopy (EELS) measurements were also performed to acquire the chemical and bonding information. The transition-metal 3d states can be revealed by measuring the integrated intensity of the white lines directly.³⁵ As shown in Fig. 3c, the ratio of L₃/L₂ was 4.6, suggesting the presence of some Fe³⁺. Se L-edge EELS of the 2D ultrathin hexagonal FeSe nanosheets indicated the presence of Se²⁻ (Fig. S12†).

We have applied EPR to study Fe²⁺ and Fe³⁺ in 2D hexagonal FeSe nanosheets. As shown in Fig. 3d, there were no signals in the EPR spectra. Hence, the Fe²⁺ in hexagonal FeSe nanosheets had low crystalline symmetry³⁶ and there was magnetic interaction between the minor Fe³⁺.

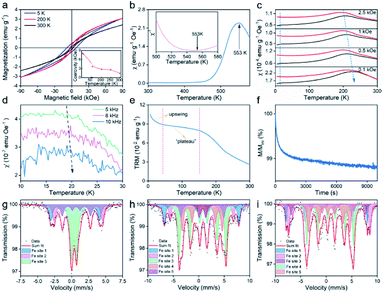
Hysteresis loops of 2D ultrathin nvdWs hexagonal FeSe were measured between 5 and 300 K (Fig. 4a and S13†). At 300 K, they exhibited hysteresis behavior with a coercivity of 0.6 kOe, which meant that magnetic anisotropy could suppress thermal fluctuation. The coercivity increased with the decrease of temperature and reached up to 8.4 kOe at 5 K. It should be mentioned that there was a slope at the high field on the hysteresis loops and initial magnetization curve (Fig. S14†). To identify the basic type of magnetism, the temperature dependence of susceptibility was measured. As shown in Fig. 4b, both χ–T and χ⁻¹–T showed a typical AFM behavior with the Néel temperature (T_N) up to 553 K. Compared with FeF₂ nanosheets, the T_N of hexagonal FeSe nanosheets was far higher, which was essential to the room-temperature applications.¹³ The large coercivity of AFM nanomaterials was not rare. For example, AFM NiO nanoparticles exhibited a huge coercivity at low temperature.³⁷ Different from the large coercivity of Fe₃Se₄ nanosheets rooted in magnetocrystalline anisotropy,^15,16 the large coercivity of the as-synthesized 2D hexagonal FeSe nanosheets could be ascribed to the relatively weak coupling between the multi-sublattices.³⁷ It was worth noting that the hexagonal FeSe exhibited A-type AFM order.³⁸

Fig. 4 (a) Hysteresis loops at 5–300 K (inset: temperature dependence of coercivity) (b) χ–T between 300 and 580 K, (inset: χ⁻¹–T between 500 and 580 K), (c) FC-ZFC curves with an applied field of 0.1, 0.5, 1, and 2.5 kOe, respectively, and (d) temperature dependence of the in-plane component χ′ between 10 and 30 K with frequencies of 5, 8, and 10 kHz, respectively, of the ultrathin 2D nvdWs hexagonal FeSe. (e) Temperature-dependence and (f) time relaxation of the TRM of the 2D nvdWs hexagonal FeSe with a cooling field of 2.5 kOe. ⁵⁷Fe Mössbauer spectrum of the ultrathin 2D nvdWs hexagonal FeSe at (g) 300, (h) 30, and (i) 10 K.

When AFM nanomaterials were exposed to a magnetic field, the resulting magnetization was composed of the surface with uncompensated spins and the core with bulk AFM spin configurations.³⁹ The uncompensated spins arose primarily from the surface atoms with lower coordination and loosely coupled spins. To investigate the magnetic behaviors of ultrathin 2D nvdWs hexagonal FeSe, we studied field-cooling (FC) and zero-field-cooling (ZFC) magnetization, the temperature dependence of ac susceptibility, and temperature decay and time relaxation of the thermoremanent moment (TRM).

As shown in Fig. 4c, there was a clear and broad peak on the four ZFC curves located at about 210 K. It should be noted that the position of the peak shifted to a lower temperature when the applied field increased. Such peaks were associated with the superparamagnetic transition and the position of the peaks was called the blocking temperature. In addition to the clear and broad peak, there was a cusp located at 20 K on the four ZFC curves and the position of the cusp was independent of the applied magnetic field which was like spin-glass behavior. Accordingly, the ac susceptibility of ultrathin 2D hexagonal FeSe between 10 and 30 K was studied as a function of frequency to investigate the phenomenon. During the measurements, no dc magnetic field was applied. The amplitude of the ac magnetic field was 10 Oe and the frequency of the ac magnetic field was 5, 8, and 10 kHz, respectively. Fig. 4d shows the temperature-dependent in-plane component of ac susceptibility, χ′ (the temperature-dependent ac susceptibility and the out-of-plane component of ac susceptibility, χ′′, are shown in Fig. S15†). With the increase of frequency, the freezing temperature shifted to a higher temperature which was unambiguously indicative of spin-glass behavior. The spin-glass behavior could be attributed to uncompensated surface spins. Regarding the FC curves in Fig. 4c, there was a strong upswing at low temperature, ascribed to spins weakly coupled to the AFM core.³⁹

The temperature decay of TRM (Fig. 4e) was used to study the magnetic interactions in ultrathin 2D nvdWs hexagonal FeSe. There was an upswing at low temperature on the curve, similar to that of the upswing on FC curves. And the upswing was also due to the spins weakly coupled to the AFM core. In addition to the strong upswing, there was another characteristic feature. A “plateau” was located between the temperature range of 40 and 150 K on the curve where the temperature relaxation moment was roughly independent of temperature. And the “plateau” could be ascribed to interfacial uncompensated spins strongly coupled to the AFM cores. The strongly coupled spins could also be proved by the time relaxation of TRM (Fig. 4f). The TRM moment decreased slowly with time, indicating the presence of strongly coupled spins.

To study the origin of magnetism and temperature-dependent magnetic transitions of ultrathin 2D nvdWs hexagonal FeSe, ⁵⁷Fe Mössbauer spectra were measured at 300 K, 30 K, and 10 K, respectively, which could probe the chemical environment changes of Fe.⁴⁰ The spectra excluded the presence of the impurity phase (Fig. 4g–i). The isomer shift, quadrupolar splitting, and magnetic field (Table S1†) also ruled out the presence of Fe in such nanosheets. At 300 K, there were three different Fe sites in the 2D hexagonal FeSe, with Fe sites 1 and 2 of sextets and the Fe 3 site of the doublet (Fig. 4g). The isomer shifts indicated Fe²⁺ for almost all Fe sites, correspondingly, Fe sites 1 and 2 displayed antiferromagnetism and Fe site 3 exhibited paramagnetism. Hence, the antiferromagnetism of the 2D hexagonal FeSe was intrinsic and rooted in Fe²⁺. It is worth noting that the co-existence of paramagnetism and magnetic order has also been observed in other materials.⁴¹ As the temperature decreased to 30 K, there were five different Fe sites, with Fe sites 1, 2, 3, and 4 of antiferromagnetism and Fe site 5 of paramagnetism (Fig. 4h). It should be mentioned that the room-temperature paramagnetic Fe site displayed antiferromagnetism, which should result from the superparamagnetic transition mentioned above. The difference of Fe sites between 300 and 30 K may be due to the vacancy-order superstructures. Upon decreasing the temperature to 10 K, there remained five Fe sites with sextets, which could be assigned to magnetically nonequivalent sites of the crystal (Fig. 4i). The paramagnetic Fe site at 30 K exhibited long-range magnetic order at 10 K which may be interpreted to be the spin-glass transition. Hence, the temperature-dependent magnetic transitions of the 2D hexagonal FeSe could be attributed to the chemical environment changes of Fe²⁺.

The electrical properties of the pressed ultrathin 2D nvdWs hexagonal FeSe were measured through the van der Pauw method.⁴² The measured pellet was pressed at ∼1.25 GPa and the thickness of the pellet was about 0.82 mm (Fig. S16†). The temperature-dependent electrical conductivity of the heating and cooling process was almost the same (Fig. 5a). And the positive temperature coefficient of electrical conductivity demonstrated the semiconductor nature of ultrathin 2D nvdWs hexagonal FeSe. The I–V curves were measured between 5 and 300 K (Fig. 5b and S17†). They exhibited an ohmic response between −2 and +2 V. And the 2D hexagonal FeSe displayed an electrical conductivity of 2.55 S m⁻¹ at 300 K.

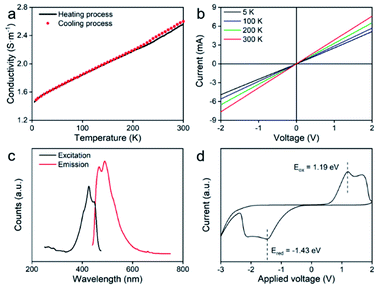Fig. 5 (a) Temperature-dependent conductivity, (b) I–V curves at different temperatures, (c) PL spectra, and (d) cyclic voltammetry of ultrathin 2D nvdWs hexagonal FeSe.

In addition, we have applied the generalized gradient approximation (GGA)+U and strongly constrained and appropriately normed semilocal density functional (SCAN) to study the bandgap of five-layer FeSe with the exposed (001) facet. The U value of Fe atoms for the GGA+U method was chosen as 7.0 eV. The GGA+U and SCAN approach confirmed the bandgaps of five-layer FeSe as 1.410 and 0.212 eV, respectively, indicating the semiconductor nature of hexagonal FeSe.

Photoluminescence spectra (PL) of ultrathin 2D nvdWs hexagonal FeSe were recorded to understand the optical-bandgap properties. As can be seen from Fig. 5c, two excitation bands appeared in the photoluminescence excitation spectra at around 425 and 447 nm, respectively. Correspondingly, there were two emission bands in the emission spectra and the intensity of the 461 nm peak was lower than that of the 489 nm peak, which suggested the semiconductor nature of 2D hexagonal FeSe. And the PL spectrum of 2D hexagonal FeSe was similar to that of hexagonal FeSe quantum dots.³² The PL spectra revealed that the bandgap of the 2D hexagonal FeSe was about 2.68 eV. Furthermore, cyclic voltammetry (CV) analysis was performed with an Ag/AgCl electrode to study the bandgap,⁴³ which confirmed the bandgap as 2.62 eV. The bandgaps obtained from the PL spectra and CV analysis were almost the same. It was evident that the experimental bandgap was smaller than the bandgap estimated by DFT. Because there was no consensus on the actual bandgap, it was common that the bandgap estimated by DFT was smaller than the experimental bandgap.⁴⁴ For example, the bandgap of ZnO calculated from the GGA+U method was 1.4 eV (about half of the experimental bandgap, 3.4 eV).⁴⁵

Ultraviolet photoelectron spectroscopy (UPS) spectra determined the Fermi edge and cutoff edge of the 2D hexagonal FeSe as 1.27 eV and 16.92 eV, respectively (Fig. S18†).

Conclusions

In conclusion, we have successfully achieved free-standing 2D nvdWs hexagonal FeSe with a thickness of 2.90–2.95 nm and a lateral dimension of 1.0–2.2 μm. The growth mechanism has been clarified as the synergetic effects of Cl⁻ and –NH₂, where Cl⁻ acted as capping ligands with strong passivation ability and –NH₂ preferred to adsorb on the (001) facet. Excitingly, such nanosheets have been identified as intrinsic AFM semiconductors with the Néel temperature up to 553 K. It was unambiguously confirmed that the intrinsic magnetic order was rooted in Fe²⁺. And the temperature variation would induce the chemical environment changes of Fe²⁺, which resulted in the temperature-dependent magnetic transitions. Regarding the semiconductor nature, such nanosheets showed a room-temperature conductivity of 2.55 S m⁻¹. It is expected that the insight into the growth mechanism, and magnetic and electrical properties of free-standing 2D ultrathin hexagonal FeSe will speed up the applications of 2D hexagonal FeSe and preparation of other 2D nvdWs materials.

Experimental section

Preparation of the OAm–Se complex

118.59 mg of diphenyl diselenide (98.5%, J&K) was dissolved in 17 ml of OAm (70%, J&K) at room temperature and then the solution was heated to 200 °C with a heating rate of 2 °C min⁻¹ under an Ar/H₂ atmosphere and maintained for 1 h.

Preparation of the ODE–Se complex

118.59 mg of diphenyl diselenide (98.5%, J&K) was dissolved in 17 ml of ODE (90%, Alfa Aesar) at room temperature and then the solution was heated to 200 °C with a heating rate of 2 °C min⁻¹ under an Ar/H₂ atmosphere and maintained for 1 h.

Preparation of 2D hexagonal FeSe nanosheets from the OAm–Se complex and FeCl₂·4H₂O

Under a gentle Ar/H₂ flow and magnetic stirring, 140 mg of FeCl₂·4H₂O (99.9%, Sigma Aldrich) was dissolved in 17 ml of the OAm–Se complex by heating the suspension to 80 °C. The solution was further heated to 345 °C with a heating rate of 3–4 °C min⁻¹ and kept at this temperature for 2 h. The solution was cooled to room temperature by removing the heat source. Ethanol (40 ml) and n-hexane (40 ml) were added to precipitate the product. The product was separated by centrifugation at 3000 rpm for 3 min.

Preparation of isotropic hexagonal FeSe nanoparticles from the ODE-complex and Fe(acac)₂

Under a gentle Ar/H₂ flow and magnetic stirring, 178 mg of Fe(acac)₂ (99.95%, Sigma Aldrich) was dissolved in 17 ml of the ODE–Se complex. The solution was maintained at 120 °C to remove moisture and then heated to 310 °C with a heating rate of 3–4 °C min⁻¹ and kept at this temperature for 2 h. The solution was cooled to room temperature by removing the heat source. Ethanol (40 ml) and n-hexane (40 ml) were added to precipitate the product. The product was separated by centrifugation at 9500 rpm for 5 min.

Preparation of isotropic hexagonal FeSe nanoparticles from the ODE-complex, Fe(acac)₂ and NH₄Cl

The synthetic process is similar to that of hexagonal FeSe nanoparticles using the ODE–Se complex and Fe(acac)₂, except for the introduction of 10 mg NH₄Cl.

Preparation of hexagonal FeSe nanosheets from the OAm-complex and Fe(acac)₂

The synthetic process is similar to that of hexagonal FeSe nanosheets using the OAm–Se complex and FeCl₂·4H₂O, except that 140 mg of FeCl₂·4H₂O was replaced with 178 mg of Fe(acac)₂.

Preparation of hexagonal FeSe nanosheets from the OAm-complex, Fe(acac)_2, and NH₄Cl

The synthetic process is similar to that of hexagonal FeSe nanosheets using the OAm–Se complex and Fe(acac)₂ except for the introduction of 10 mg NH₄Cl.

DFT calculations

First principles calculations were carried out, employing the Vienna ab initio simulation package (VASP) with the projector-augmented-wave (PAW) method. The thickness of the vacuum was larger than 20 Å for 2D FeSe to minimize interactions between periodic images. The criterion of convergence required that the residual force should be less than 0.01 eV Å⁻¹ and the total energy change should be less than 10⁻⁶ eV. The spin of Fe was also taken into consideration.

For structure optimizations of the five-layer FeSe (001) slab, a (3 × 3 × 1) k-mesh of the Monkhorst–Pack sampling scheme was employed to perform the Brillouin-zone integrations. To obtain more accurate bandgaps of the relaxed FeSe (001) slabs, both the GGA+U (U_eff = 7.0 eV for Fe atoms) and the SCAN methods were employed to calculate their band structures.

For the calculation of adsorption energy, the calculations applied periodic boundary conditions and the corresponding Brillouin-zone integrations were carried out using a 7 × 7 × 1 Monkhorst–Pack grid. In addition, a 2  ×  2  ×  1 supercell was used to calculate the adsorption energy of one species on 2D FeSe and a 2  ×  1  ×  1 supercell was used to calculate the adsorption energy of species adsorbed on half of surface Fe. The adsorption energy of X (X = NH₃, Cl, Fe, or Se) species on the surfaces of 2D FeSe is defined as E_a(FeSe–nX) = (E(FeSe–nX) − E(FeSe) − E(nX))/n, where n represents the number of adsorption species.

Fundamental property characterization

XRD (PANalytical X'Pert³ Powder X-ray diffractometer equipped with Cu-Kα radiation), Raman spectroscopy (XploRA PLUS), spherical aberration-corrected transmission electron microscopy (FEI Titan Themis), AFM (Bruker INNOVA), XPS (Axis Ultra DLD, Kratos Analytical Ltd), and EPR (X-band ELEXSYS E580 spectrometer) were all used to characterize the sample.

Magnetic property measurements

The magnetic properties of hexagonal FeSe nanosheets were measured using a physical property measurement system (DynaCool, Quantum Design).

Electrical property measurements

The solid sample was pressed under a pressure of ∼1.25 GPa. The gold wires were contacted on the pellet surface to define a square. All the measurements were performed in van der Pauw geometry under vacuum using a physical property measurement system (DynaCool, Quantum Design).

Data availability

The data that support the findings of this study are available in the ESI.†

Author contributions

Y. Hou supervised and developed the project. J. Xu performed the experiments. B. Zhang, W. Hao, and S. Li performed the DFT calculations. J. Xu and S. Hu performed the magnetic measurements. All authors analyzed the data and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the National Key R&D Program of China (2017YFA0206301), the National Natural Science Foundation of China (52027801 and 51631001), Natural Science Foundation of Beijing Municipality (2191001) and the China-German Collaboration Project (M-0199).

Notes and references

1. J. Xu, W. Li and Y. Hou, Trends Chem., 2019, 2, 163–173.
2. F. Cui, X. Zhao, J. Xu, B. Tang, Q. Shang, J. Shi, Y. Huan, J. Liao, Q. Chen and Y. Hou, Adv. Mater., 2019, 132, 1905896.
3. H. Yang, F. Wang, H. Zhang, L. Guo, L. Hu, L. Wang, D.-J. Xue and X. Xu, J. Am. Chem. Soc., 2020, 142, 4438–4444.
4. T. Jungwirth, X. Marti, P. Wadley and J. Wunderlich, Nat. Nanotechnol., 2016, 11, 231–241.
5. N. Sethulakshmi, A. Mishra, P. M. Ajayan, Y. Kawazoe, A. K. Roy, A. K. Singh and C. S. Tiwary, Mater. Today, 2019, 27, 107–122.
6. V. Kochat, A. Apte, J. A. H. Hiroyuki Kumazoe, A. Krishnamoorthy, S. Susarla, J. C. Idrobo, F. Shimojo, P. Vashishta, R. Kalia, A. Nakano, C. S. Tiwary and P. M. Ajayan, Adv. Mater., 2017, 29, 1703754.
7. P. Chen, K. Xu, X. Li, Y. Guo, D. Zhou, J. Zhao, X. Wu, C. Wu and Y. Xie, Chem. Sci., 2014, 5, 2251.
8. S. Radhakrishnan, D. Das, A. Samanta, C. A. Reyes, L. Deng, L. B. Alemany, T. K. Weldeghiorghis, V. N. Khabashesku, V. Kochat, Z. Jin, P. M. Sudeep, A. A. Martí, C. Chu, A. Roy, C. S. Tiwary, A. K. Singh and P. M. Ajayan, Sci. Adv., 2017, 3, e1700842.
9. D. M. Burn, L. B. Duffy, R. Fujita, S. L. Zhang, A. I. Figueroa, J. H. Martin, G. Laan and T. Hesjedal, Sci. Rep., 2019, 9, 10793.
10. X. Wei, P. Roy, Z. Yang, D. Zhang, Z. He, P. Lu, O. Licata, H. Wang, B. Mazumder, N. Patibandla, Y. Cao, H. Zeng, M. Zhu and Q. Jia, Mater. Res. Lett., 2021, 9, 336–342.
11. A. P. Balan, S. Radhakrishnan, C. F. Woellner, S. K. Sinha, L. Deng, C. de los Reyes, B. M. Rao, M. Paulose, R. Neupane and A. Apte, Nat. Nanotechnol., 2018, 13, 602–609.
12. X. Zhang, J. Zhang, J. Zhao, B. Pan, M. Kong, J. Chen and Y. Xie, J. Am. Chem. Soc., 2012, 134, 11908–11911.
13. Z. Yang, H. Zhang, J. Xu, R. Ma, T. Sasaki, Y.-J. Zeng, S. Ruan and Y. Hou, Natl. Sci. Rev., 2020, 7, 841–848.
14. J. Yang, Z. Zeng, J. Kang, S. Betzler, C. Czarnik, X. Zhang, C. Ophus, C. Yu, K. Bustillo and M. Pan, Nat. Mater., 2019, 18, 970–976.
15. H. Zhang, G. Long, D. Li, R. Sabirianov and H. Zeng, Chem. Mater., 2011, 23, 3769–3774.
16. G. Long, H. Zhang, D. Li, R. Sabirianov, Z. Zhang and H. Zeng, Appl. Phys. Lett., 2011, 99, 202103.
17. C. Tan and H. Zhang, Nat. Commun., 2015, 6, 7873.
18. X. Zhang and Y. Xie, Chem. Soc. Rev., 2013, 42, 8187–8199.
19. K. Zhu, Y. Ju, J. Xu, Z. Yang, S. Gao and Y. Hou, Acc. Chem. Res., 2018, 51, 404–413.
20. Z. Yang, T. Zhao, X. Huang, X. Chu, T. Tang, Y. Ju, Q. Wang, Y. Hou and S. Gao, Chem. Sci., 2017, 8, 473–481.
21. W. Lei, J. Xu, Y. Yu, W. Yang, Y. Hou and D. Chen, Nano Lett., 2018, 18, 7839–7844.
22. S. Ghosh and L. Manna, Chem. Rev., 2018, 118, 7804–7864.
23. M. H. Oh, M. G. Cho, D. Y. Chung, I. Park, Y. P. Kwon, C. Ophus, D. Kim, M. G. Kim, B. Jeong and X. W. Gu, Nature, 2020, 577, 359–363.
24. X. Liu, Y. Li, B. Zhou, X. Wang, A. N. Cartwright and M. T. Swihart, Chem. Mater., 2014, 26, 3515–3521.
25. C. E. M. Campos, J. C. d. Lima, T. A. Grandi, K. D. Machado and P. S. Pizani, Solid State Commun., 2002, 123, 179–184.
26. S. Tan, C. Wen, M. Xia, J. Jiang, Q. Song, B. Xie, X. Lai and D. Feng, Phys. Rev. B, 2017, 96, 155124.
27. K. Zhang, X. Zhang, F. Yang, Y. Song, X. Chen, C. Liu, D. Qian, W. Luo, C. Gao and J.-F. Jia, Appl. Phys. Lett., 2016, 108, 061601.
28. X. Wu, Z. Zhang, J. Zhang, B. Li, Z. Ju, Y. Lu, B. Li and D. Shen, J. Appl. Phys., 2008, 103, 113501.
29. Q. Feng, D. Shen, J. Zhang, B. Li, B. Li, Y. Lu, X. Fan and H. Liang, Appl. Phys. Lett., 2006, 88, 012505.
30. Ö. Amcoff and Z. ZKri, Kristallogr, 1994, 209, 197–205.
31. Z. Qin, C. Zhang, S. O'Malley, K. Lo and S. W. Cheong, Solid State Commun., 2010, 150, 768–771.
32. P. Mulpur, T. M. Rattan and V. Kamisetti, J. Nanosci., 2013, 2013, 1–5.
33. J. S. Son, J. H. Yu, S. G. Kwon, J. Lee, J. Joo and T. Hyeon, Adv. Mater., 2011, 23, 3214–3219.
34. A. Mekki, D. Holland, C. McConville and M. Salim, J. Non-Cryst. Solids, 1996, 208, 267–276.
35. W. Qiu, Q. Ma, Z. Ma, J. Tang, L. Sang, C. Cai, M. S. Al Hossain, Z. Cheng, X. Wang and Y. Liu, Phys. Rev. B, 2019, 99, 064502.
36. U. Kaufmann, Phys. Rev. B, 1976, 14, 1848–1857.
37. R. H. Kodama, S. A. Makhlouf and A. E. Berkowitz, Phys. Rev. Lett., 1997, 79, 1393–1396.
38. P. Terzieff, H. Schicketanz and K. L. Komarek, Monatsh. Chem., 1982, 113, 519–527.
39. C. Westman, S. Jang, C. Kim, S. He, G. Harmon, N. Miller, B. Graves, N. Poudyal, R. Sabirianov, H. Zeng, M. DeMarco and J. P. Liu, J. Phys. D: Appl. Phys., 2008, 41, 225003.
40. M. D. Dyar, D. G. Agresti, M. W. Schaefer, C. A. Grant and E. C. Sklute, Annu. Rev. Earth Planet. Sci., 2006, 34, 83–125.
41. P. Adler, S. A. Medvedev, P. G. Naumov, S. Mohitkar, R. Rüffer, M. Jansen and C. Felser, Phys. Rev. B, 2019, 99, 134443.
42. J. de Boor and V. Schmidt, Adv. Mater., 2010, 22, 4303–4307.
43. Z. Li, A. L. K. Lui, K. H. Lam, L. Xi and Y. M. Lam, Inorg. Chem., 2014, 53, 10874–10880.
44. P. Ágoston, P. Erhart, A. Klein and K. Albe, J. Phys.: Condens. Matter, 2009, 21, 455801.
45. G. Huang, C. Wang and J. Wang, Comput. Phys. Commun., 2012, 183, 1749–1752.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc04122c

---