 Open Access Article
Open Access ArticleElectrostatic vs. inductive effects in phosphine ligand donor properties and reactivity†
Margaret L.
Kelty
,
Andrew J.
McNeece
,
Josh W.
Kurutz
 ,
Alexander S.
Filatov
,
Alexander S.
Filatov
 and
John S.
Anderson
and
John S.
Anderson
 *
*
Department of Chemistry, University of Chicago, 929 E 57th St, Chicago, IL 60637, USA. E-mail: jsanderson@uchicago.edu
First published on 16th March 2022
Abstract
Enhanced rates and selectivity in enzymes are enabled in part by precisely tuned electric fields within active sites. Analogously, the use of charged groups to leverage electrostatics in molecular systems is a promising strategy to tune reactivity. However, separation of the through space and through bond effects of charged functional groups is a long standing challenge that limits the rational application of electric fields in molecular systems. To address this challenge we developed a method using the phosphorus selenium coupling value (JP–Se) of anionic phosphine selenides to quantify the electrostatic contribution of the borate moiety to donor strength. In this analysis we report the synthesis of a novel anionic phosphine, PPh2CH2BF3K, the corresponding tetraphenyl phosphonium and tetraethyl ammonium selenides [PPh4][SePPh2CH2BF3] and [TEA][SePPh2CH2BF3], and the Rh carbonyl complex [PPh4][Rh(acac)(CO)(PPh2(CH2BF3))]. Solvent-dependent changes in JP–Se were fit using Coulomb's law and support up to an 80% electrostatic contribution to the increase in donor strength of [PPh4][SePPh2CH2BF3] relative to SePPh2Et, while controls with [TEA][SePPh2CH2BF3] exclude convoluting ion pairing effects. Calculations using explicit solvation or point charges effectively replicate the experimental data. This JP–Se method was extended to [PPh4][SePPh2(2-BF3Ph)] and likewise estimates up to a 70% electrostatic contribution to the increase in donor strength relative to SePPh3. The use of PPh2CH2BF3K also accelerates C–F oxidative addition reactivity with Ni(COD)2 by an order of magnitude in comparison to the comparatively donating neutral phosphines PEt3 and PCy3. This enhanced reactivity prompted the investigation of catalytic fluoroarene C–F borylation, with improved yields observed for less fluorinated arenes. These results demonstrate that covalently bound charged functionalities can exert a significant electrostatic influence under common solution phase reaction conditions and experimentally validate theoretical predictions regarding electrostatic effects in reactivity.
Introduction
Spectroscopic and computational studies have cited oriented electric fields in active sites as key contributors to enzymatic reactivity.1–7 Enzymes maintain and orient electric fields using polar and charged functional groups in the protein scaffold around the active site, a strategy that is appealing for synthetic molecular systems but difficult to mimic.8–12 Multiple approaches have been proposed for incorporating similar electric fields into systems that lack an enzymatic superstructure. Electric fields can be directly applied to synthetic compounds through attachment to electrode surfaces or STM tips and these approaches have been shown to increase catalytic rates.13–23 Another approach is to rationally append charged functional groups onto molecular scaffolds to offer control over the orientation and magnitude of electrostatic effects. Indeed, there has been enormous interest in modeling or leveraging electrostatic interactions in organic and inorganic molecules.24–46 Computations predict that electrostatic effects can have a large impact on reactivity and catalysis.47–61A detailed understanding of the relative magnitudes of inductive and electrostatic charged substituent effects would be valuable in rationally tuning molecular reactivity. In this context, inductive represents through bond polarization of the molecule, similar to effects observed with electron donating or withdrawing groups, while electrostatic indicates through space polarization of a bond consistent with Coulomb's law. Experimentally parsing out the relative inductive and electrostatic contributions to reactivity and electronic structure from charged functional groups is challenging even in simple systems. A prime example of this is in classic Hammett literature where inductive through-bond and electrostatic through-space influences from substituents were predominantly treated as one lump effect, sometimes referred to as σi.62 However, in a subset of this literature, there has been considerable debate on whether electrostatics or through-bond electron density factors are dominant in σi. Hammett originally considered the influence of substituents to be entirely electrostatic in nature, a view supported by Ri, Eyring, and Westheimer.63,64 Conversely, Jaffe considered substituent effects primarily through electron density, foreshadowing modern computational analyses.65,66 The efficacy of both methods in rationalizing reactivity trends supports that both electrostatic and inductive interactions are active, and methods to distinguish between them are still being pursued to this day.67–69 A more thorough understanding of the inductive and electrostatic factors influencing the electronic structure and reactivity of distally charged ligands and complexes would be instructive, particularly as leveraging through-space interactions can serve as a strategy to break free-energy relationships.70–76
Phosphines are ideal scaffolds for quantifying the influence of electrostatics as these ligands feature prominently in catalysis and have well defined parameters for rationalizing reactivity trends, such as the Tolman Electronic Parameter (TEP) and cone angle.77 Indeed, cationic and anionic moieties have previously been incorporated into phosphines, frequently leading to distinct properties or reactivity in comparison to neutral analogues.78–83 Phosphine borate ligands specifically have been prepared through the incorporation of triaryl- and trifluoroborate and carborane functional groups, and have shown enhanced reactivity in polymerization,84–93 cross coupling,94–96 and hydrofunctionalization97,98 reactions. These anionic phosphines are uniformly considered to be stronger donors than their neutral isostructural analogues. However, the origin of this increase (electrostatic or inductive) has remained elusive, and has largely been considered inductive by default.68,69,94–96,98–101 The ambiguity regarding through space effects of covalently bound distal anions limits the rational design of ligand scaffolds that leverage electric fields to enhance reactivity. For instance, a recent computational study predicts accelerated oxidative addition (OA) reactivity at a PMe3 supported Pd complex in the presence of either an externally applied electric field or a correctly positioned chloride ion.53 This study suggests that similar effects may be replicated using distally charged anionic phosphines if a suitably thorough understanding of electrostatic effects in covalently bound anions can be obtained.
Herein we report a method to assign the electrostatic and inductive contributions of anionic functional groups to phosphine donor strength using the solvent dependence of phosphorus selenium coupling values (JP–Se). This method is initially developed using the novel phosphine PPh2CH2BF3− (1) (Scheme 1). The R–BF3− functional group is ideal for this analysis as it provides a more compact charge in comparison to commonly used aryl borates.96 Additionally, trifluoroborate groups are reatively inert in comparison to aryl borates, which can engage in aryl-group transfer decomposition pathways87 and intramolecular C–H oxidative addition reactivity.99 The methylene linker to the phosphine precludes convoluting resonance influences that may be present in aryl linkers. We report the synthesis of the potassium salt of this phosphine, K1, and assess the electrostatic impact of the R–BF3− moiety via both the solvent dependent NMR coupling constants of its phosphine selenide SePPh2CH2BF3− (1Se) and its complexation to Rh carbonyls to give [PPh4][Rh(acac)(CO)(PPh2(CH2BF3))] (2). The possibility of competing contributions to JP–Se from ion pairing is excluded through controls with two different countercations, [PPh4][1Se] and [TEA][1Se]. The solvent dependence of [PPh4][1Se] shows a 1/4πε dependence, consistent with Coulomb's law, and fits suggest that up to 80% of the increase in donor strength relative to SePPh2Et is attributable to electrostatic effects, a conclusion which we replicate using calculations. This study is then extended to an additional anionic phosphine selenide with a longer and more rigid aryl linker, SePPh2(2-BF3Ph)− (3Se),90,91 and the 1/4πε fit similarly suggests that up to 70% of the increase in donor strength relative to PPh3 results from electrostatic contributions.
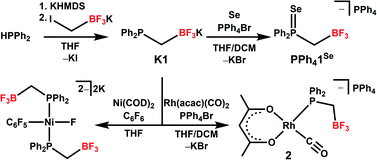 | ||
| Scheme 1 Synthesis of K1 and reactions to form [PPh4][1Se], 2, and the proposed product of C–F oxidative addition by a Ni complex featuring 1. | ||
Finally, an order of magnitude acceleration in the OA of aryl fluorides mediated by K1 and Ni(COD)2 is observed relative to neutral phosphines of comparable donor strengths, PEt3 and PCy3. This finding suggests a unique impact of electrostatic effects beyond that expected from increased donor strength. This accelerated reactivity is applied to the catalytic defluoroborylation of fluoroarenes, with improved reactivity observed with comparatively unactivated substrates. In summary, this work illustrates how electrostatic interactions from charged functional groups are a substantial contributor to phosphine donor strength in common organic solvents and that these electrostatic effects can be leveraged for increased reactivity and catalysis.
Results and discussion
Synthesis and characterization of PPh2CH2BF3K (K1)
Synthesis of the phosphine proceeds readily via deprotonation of Ph2PH with KHMDS (KHMDS = potassium hexamethyldisilazide), followed by dropwise addition to a stirring THF solution of potassium iodomethyltrifluoroborate, and yields K1 as a white powder following workup (Scheme 1). We note that a related zwitterionic triphenyl phosphonium methyl trifluoroborate has been previously synthesized.102–104 The 1H NMR of K1 shows the expected aromatic signals for the phenyl groups, and a doublet of quartets at 0.8 ppm from coupling of the CH2 linker to phosphorus, boron, and fluorine (Fig. S1†). The 31P{1H} NMR spectrum shows a quartet at −15 ppm due to fluorine coupling with an identical chemical shift to that observed for PPh2Et (Fig. S2†). This observation is consistent with previous reports that charged phosphines have similar shifts as their neutral analogues.90,91,101 Analysis by 19F{1H} and 11B{1H} NMR indicates the expected shifts and coupling for a R–BF3− group, supporting the presence of this anionic unit (Fig. S3 and S5†).105 Compound K1 was structurally characterized via single-crystal X-ray diffraction (SXRD, Fig. 1). The SXRD structure shows the expected connectivity with an average B⋯P distance of 2.858(3) Å and a close association between K and B (∼3 Å, Fig. S89†). While it is unclear if this association is preserved in solution, larger cations were chosen to limit ion pairing in further analyses (see below).Tolman electronic parameter and JP–Se determination
To assay the donor strength of phosphine 1, its Tolman Electronic Parameter (TEP) was determined using a Rh carbonyl complex of the form Rh(acac)(CO)L (L = phosphine). While the limitations of TEP in reflecting M–L bond strengths has been noted previously,106 it remains a standard in the literature for the comparison of phosphine donor strength.107 The TEP is a measure of the donation of electron density from a phosphine to a metal complex through the combined effects of σ donation (P → M) and π back-bonding (M → P) interactions.83,107 TEP is traditionally determined from the A1-symmetrical νCO stretching frequency in Ni(CO)3L complexes, where a higher νCO indicates a less electron rich metal center resulting from weaker phosphine donors. However, the toxicity of the Ni(CO)4 starting material has motivated the development of other model complexes to determine TEP. One such complex which displays a robust linear correlation between νCO and TEP is Rh(acac)(CO)L (see Fig. S67† for equation), and accordingly the complex with L = K1 was synthesized.108Addition of K1 to Rh(acac)(CO)2 with PPh4Br affords [PPh4][Rh(acac)(CO)(PPh2(CH2BF3))] (2) as a yellow solid. The SXRD structure of 2 shows a square planar geometry at Rh (Fig. 1). The BF3− unit is located significantly above the Rh square plane and close contacts (∼2.3 Å) are observed between the BF3− and protons on PPh4+, consistent with H-bonding interactions (Fig. S90†). No secondary interactions between PPh4+ and CO are observed. The B⋯C and B⋯O distances are 3.719(5) and 3.955(4) Å, notably shorter than the B⋯Rh distance of 4.150(4) Å, although the difference diminishes upon normalizing to van der Waals radii (see ESI†). Compound 2 is readily identified in solution by the appearance of a doublet of quartets in the 31P{1H} NMR spectrum arising from coupling of the phosphorus nucleus to 103Rh (JP-Rh = 166 Hz) and 19F (JP-F = 10 Hz), consistent with the solid-state structure (Fig. S7†). The solution IR spectrum of 2 in CH2Cl2 shows a νCO of 1965 cm−1, which correlates to a TEP of 2061.7 cm−1 (Fig. S67†). This TEP is identical to that of PEt3 (2061.7 cm−1), and is significantly more donating than the related alkyldiaryl phosphine PPh2Et (2066.7 cm−1) (Fig. 2).77 This result is consistent with the enhanced donation previously observed for phosphines with anionic borates.68,83,86,90–92,95,96,100,101,109–112
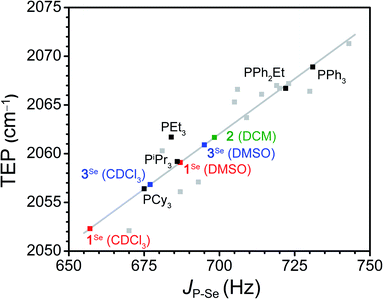 | ||
| Fig. 2 Correlation between the TEP of selected phosphine ligands and the JP–Se in CDCl3 of their respective phosphine selenides (black and grey squares, grey line is the linear fit).77,108,121 The green square is the experimental TEP for 1 determined using compound 2 and the calculated JP–Se. The squares in red and blue are the experimental JP–Se for [PPh4][1Se] and [PPh4][3Se] in DMSO-d6 and CDCl3 and the calculated TEP. The linear fit was used to determine calculated values (See SI for the fit parameters and a comprehensive list of phosphines included). | ||
In addition to metal carbonyl adducts, phosphine selenide compounds have also been used to quantify the donor strength and basicity of phosphines via their P–Se coupling constants (JP–Se).113,114 The use of NMR coupling constants is advantageous due to greater instrumental resolution and sensitivity in the coupling value as compared to vibrational spectroscopy.115 Changes in JP–Se report on changes in the s character of the P–Se bond.116,117 The electron donating/withdrawing character of the substituents on P influences this s character through hybridization changes as predicted by Bent's rule.118,119 Electron withdrawing R groups on PR3 increase the s character in the P–Se bond and thereby JP–Se, while electron donating R groups effect the opposite.113
The phosphine selenide, [PPh4][SePPh2CH2BF3] ([PPh4][1Se]), was prepared by stirring K1 overnight in THF with an excess of elemental Se and PPh4Br. The facile oxidation is consistent with the increased donor strength of 1, as most preparations require heating of elemental Se or the use of soluble red selenium.118,120 The SXRD structure confirms the geometry of [PPh4][1Se] and shows close contacts (≤2.7 Å) between the protons on PPh4+ and the BF3− (Fig. 1 and S91†). The 31P{1H} NMR spectrum of [PPh4][1Se] shows full conversion to the selenide with a quartet peak at ∼33 ppm and satellite quartets at ∼31 and ∼35 ppm from coupling to the 77Se nucleus (Fig. S12†). In DMSO-d6 the JP–Se of 687 Hz is nearly identical to the JP–Se of SePiPr3 (686 Hz, CDCl3) and indicates an increase in donor strength relative to the neutral congener SePPh2Et (722 Hz, CDCl3) (Fig. S27 and S28†).121
We then sought to compare our two experimental assays of phosphine donor strength. While the use of JP–Se to measure phosphine donor strength is well established, specific correlations between JP–Se and TEP have not been clearly defined.118,122 Fitting of the reported JP–Se and TEP values for a series of 18 alkyl and aryl phosphines resulted in a reasonable linear correlation (R2 = 0.84, Fig. 2, S88 and Table S11†).77,108,121 Using this analysis to extrapolate a value of JP–Se from the experimentally determined TEP of 2 provides JP–Se = 698 Hz, which is significantly larger than the experimentally determined value of 687 Hz for [PPh4][1Se] in DMSO-d6 (Table S10†). Surprisingly, measuring the JP–Se of [PPh4][1Se] in CDCl3 results in a significant decrease in JP–Se to 657 Hz (Δ30 Hz), suggesting that phosphine 1 is a stronger donor in CDCl3 than DMSO. Overall, the TEP and JP–Se values clearly indicate that the anionic charge promotes a large increase in the donor strength of phosphine 1. However, we wanted to further understand the origin of the large solvent dependence of this donor strength.
Analysis of donor strength solvent dependence
The presence of the charged borate in phosphine 1 and the discrepancy between TEP values determined via different methods prompted us to investigate how electrostatic effects contribute to these measurements. “Through-space” interactions have been suggested previously to explain anamolous JP–Se behavior in phosphines with 2-furyl and o-methoxyphenyl substituents, but a thorough analysis of this effect has not been undertaken.123 A dependence on solvent ionic strength was proposed as a means of separating electrostatic and inductive contributions of a R-NMe3+ substituent on the rate of acetate binding in iron porphyrins.34 We reasoned that a similar solvent variation approach would be useful for separating inductive and electrostatic contributions to the donor strength of 1. Specifically, the through-space electrostatic influence of the charged group should be modified by the solvent dielectric (ε), a measure of a medium's ability to shield a charge,124 while the through-bond interactions should remain constant.IR spectra of 2 and the parent Rh(CO)2(acac) were initially acquired in MeCN, THF, and DCM. However, no variation of νCO outside of instrumental error is observed (Fig. S72 and S73†). This is perhaps not surprising as the expected change in stretching frequency of ∼10 cm−1 is not large compared to the instrumental resolution (4 cm−1). Resolving dielectric induced shifts is further limited by spectral convolution or broadening, likely from Rh–P rotational isomers of 2 with different stretching frequencies as has been observed in other carbonyl systems.125 This manifests as substantially broader spectra for 2 than for Rh(CO)2(acac). These competing factors complicate the interpretation of donor strength in 2 and suggest that the higher sesitivity and resolution of JP–Se may make it a more conducive method for examining electrostatic effects.
While the inductive donor effects in [PPh4][1Se] should be insensitive to ε, the electrostatic stabilization of the formally cationic phosphonium in the dominant resonance structure Se−–P+R3 by the adjacent BF3− anion should increase as ε decreases.101,126 Lower ε solvents will less effectively screen the anion, resulting in greater stabilization of the positive formal charge and a lower JP–Se.136 Although it is difficult to predict solution structures, SXRD and DFT analysis (see below) of all phosphine selenides considered in this report show shorter distances between P and B than Se and B, supporting the feasibility of the anion stabilizing a formal positive charge on P (Table S15†). We note that previous literature studies demonstrate some solvent dependence to JP–Se, with one report suggesting variation between 2-3%.127,128 In our analysis, comparison of JP–Se in the anionic phosphine to a neutral analogue and restricting solvent choice to aprotic solvents serve as controls for any incidental trends.
As mentioned, an overall decrease of 30 Hz in the JP–Se of [PPh4][1Se] is observed upon moving from CDCl3 (ε = 4.8) to DMSO (ε = 46.7). Expanding the solvent selection to include CD3CN, acetone-d6, CD2Cl2, and mixtures thereof shows a consistent decrease in JP–Se as ε decreases (Fig. 3, S27–S30 and S12†). In comparison, only a slight change of 7 Hz is observed across the same ε range for the neutral congener SePPh2Et (Fig. 3, S37 and S12†). Coulomb's law suggests that a linear dependence on 1/4πε should be expected for a primarily electrostatic effect. Indeed, the observed solvent dependence of JP–Se for [PPh4][1Se] follows this trend. The variable solvent coupling data for [PPh4][1Se] was fit to the linear relationship JP–Se = 693(1) − 2.12(12) × 103 × (1/4πε) (R2 = 0.98). The neutral congener was also fit and shows a shallower slope of −5(6) × 102 and a worse R2 = 0.06 value (Table S13†).
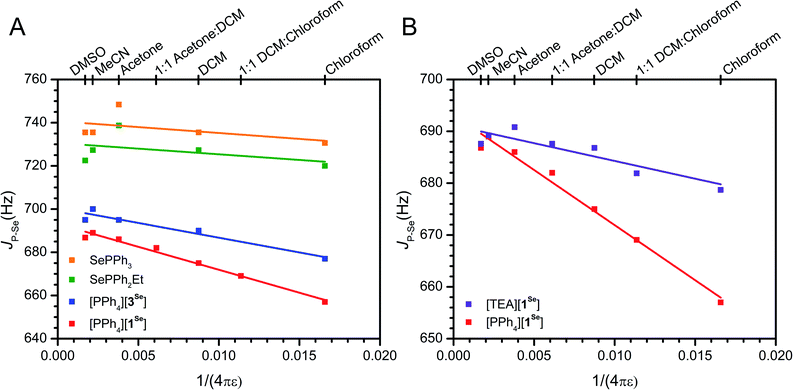 | ||
| Fig. 3 (A) Solvent dependence of JP–Se for anionic and neutral phosphines. The fit data for [PPh4][1Se] is provided in the text, and the fit data for [PPh4][3Se] is R2 = 0.92, JP–Se = 700(2) − 1.4(2) × 103 × (1/4πε). (B) Solvent dependence of [TEA][1Se] in comparison to [PPh4][1Se] (repeated from A for comparison), the fit data for [TEA][1Se] is R2 = 0.77, JP–Se = 691(2) − 7(2) × 102 × (1/4πε). Linear fits are shown as lines. Further discussion of the fits is provided in the ESI.† Different dielectrics (ε) were generated with CDCl3 (ε = 4.8), CD2Cl2 (ε = 9.1), acetone-d6 (ε = 21), CD3CN (ε = 36.6), DMSO-d6 (ε = 46.7), or mixtures thereof (Fig. S12†). | ||
While this solvent trend for [PPh4][1Se] is well modeled by an electrostatic effect, we also wanted to account for any ion pairing interactions. Ion pairing can range from separated free ions to close contact ion pairs, with varying degrees of ion solvation and association in between. These solvent separated ion pairs may also exist in an equilibrium, and generally it is difficult to precisely characterize the speciation of an ion pair in solution.129 Increased ion pairing in low ε solvents may influence the observed solvent dependence in the JP–Se of [PPh4][1Se]. To exclude this possibility, [TEA][1Se] (TEA+ = NEt4+) was prepared as a control with comparatively stronger ion pairing due to the higher charge density of the TEA+ cation. As H-bonding interactions between the cation and the BF3− are observed in the crystal structures of [TEA][1Se] and [PPh4][1Se], the CH2 and BF31H and 19F resonances are used as reporters on ion pairing in solution (Fig. S91 and S93†). In DMSO-d6, the methylene and fluorine resonances in [TEA][1Se] and [PPh4][1Se] are superimposable, consistent with identical 1Se environments. In CD2Cl2 (ε = 9.1), the methylene resonance in [TEA][1Se] is shifted downfield by 0.4 ppm relative to [PPh4][1Se] and the F resonance is shifted downfield by 1.0 ppm (Fig. S39–S42†). The downfield shift is consistent with stronger H-bonding interactions in solution deshielding the methylene protons and fluorines of [TEA][1Se] to a greater extent than in [PPh4][1Se]. Some degree of ion pairing in [PPh4][1Se] is likely present, as DOSY of [PPh4][1Se] in CDCl3 shows that the cation and anion diffuse at the same speed (Fig. S16†). However, the NMR experiments demonstrate that the extent of contact-ion pairing in solution appears to be greater in [TEA][1Se] than in [PPh4][1Se], as is expected based on the differing size of the cations.
Once it was established that TEA+ ion pairs more strongly than PPh4+, the impact of cation identity on JP–Se was investigated. The JP–Se of [TEA][1Se] in high ε solvents shows nearly identical JP–Se values to that of [PPh4][1Se], consistent with isolated free ions. However, moving to lower ε solvents only results in a decrease of 9 Hz in the JP–Se for [TEA][1Se] (Fig. 2, S34, S35 and S12†). The magnitude of this change and the slope of the linear fit (−7(2) × 102, R2 = 0.77) resembles those of the neutral analogues (Table S13†). Intuitively, these results suggest that the enhanced ion pairing between TEA+ and 1Se results in shielding of the BF3− charge, thus limiting the detection of electrostatic effects on JP–Se in low ε solvents. In contrast, the large size and diffuse charge of PPh4+ less effectively shields the BF3− and allows for the observation of solvent dependent through space effects. Similar effects have been observed in ion-pair catalysis, where a small compact SbF6− anion stabilizes polar transition states and affords greater product selectivity in lower ε solvents, while a larger and more diffuse B(3,5-CF3Ph)4− anion shows no improvement.27 The effect of alternative cations on the JP–Se of [PPh4][1Se] in CDCl3 was also explored. The addition of 20 equivalents of PPh4Br or PPNCl (PPN+ = bis(triphenylphosphine)iminium+) results in minimal deviation (<4 Hz), while 20 equivalents of NBu4Cl or TEABr result in significant increases in the coupling, as expected for the formation of tighter ion pairs and enhanced anion shielding (Table S14†). Overall, these controls with [TEA][1Se] support the assignment of electrostatic effects instead of ion pairing in rationalizing the observed solvent dependence.
Electrostatic contributions to donor strength
Assigning the solvent dependence of JP–Se as electrostatic in origin enables the separation of electrostatic and inductive contributions to donor strength (Table 1). The difference in JP–Se between [PPh4][1Se] and the SePPh2Et in high ε solvents, where the charge is effectively shielded, provides an estimate of the inductive contributions of the BF3− group. The change in JP–Se for [PPh4][1Se] upon moving to less shielding environments represents the introduction of electrostatic contributions, with the maximum contribution at the hypothetical vacuum limit. The high ε and vacuum limits of JP–Se obtained from the linear fits to [PPh4][1Se] and SePPh2Et therefore provide the relative electrostatic and inductive contributions to donor strength. Simply shifting from the high ε limit (693 Hz) to the vacuum limit (524 Hz) of [PPh4][1Se] yields an overall change in JP–Se of 169 Hz. Comparison of this electrostatic shift with the 207 Hz difference in coupling between the vacuum limit of [PPh4][1Se] (524 Hz) and the high ε limit of SePPh2Et (731 Hz) provides an estimated electrostatic contribution of 82% to the total increase in donor strength (Table 1). While this analysis uses the extrapolated limits, the experimental data from the accessible range of ε suggest that the electrostatic contribution is ∼50% (Table S12†). These analyses show that electrostatic factors have a major, and even dominant, impact on the donor properties in these systems.| Experimental | R = Et; X = 1 | R = Ph; X = 3 | DFT | |
|---|---|---|---|---|
| SePPh2R (ε = ∞, Jneutral) | 731 Hz | 741 Hz | SePPh2Et (ε = 1, Jneutral) | 872 Hz |
| [PPh4][XSe] (ε = ∞, J∞) | 693 Hz | 700 Hz | SePPh2Et (point charge, ε = 1, Jpoint) | 809 Hz |
| [PPh4][XSe] (ε = 1, Jvac) | 524 Hz | 591 Hz | [PPh4][1Se] (ε = 1, Janion) | 792 Hz |
| ΔJcovalent = J∞ − Jneutral | −38 Hz | −41 Hz | ΔJcovalent = Janion∞ − Jpoint | −17 Hz |
| ΔJelectrostatic = Jvac − J∞ | −169 Hz | −109 Hz | ΔJelectrostatic = Jpoint − Jneutral | −63 Hz |
| ΔJtot = Jvac − Jneutral | −207 Hz | −150 Hz | ΔJtot = Janion − Jneutral | −80 Hz |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Relative contributions to ΔJ | ||||
| ΔJelectrostatic/ΔJtot | 0.82 | 0.73 | ΔJelectrostatic/ΔJtot | 0.79 |
| ΔJcovalent/ΔJtot | 0.18 | 0.27 | ΔJcovalent/ΔJtot | 0.21 |
To further investigate the relative contribution of through-space and through-bond effects, Density Functional Theory (DFT) calculations were performed to estimate JP–Se and compare with experimentally determined values (Table 1). For simplicity, two local geometries of the phosphine 1Se were considered to capture limiting rotamers that may be present in solution: one transoid rotamer with a Se–P–C–B dihedral of 158° and one cis rotamer with a Se–P–C–B dihedral of 74° (Fig. S80 and S81†). A Boltzmann weighted average of these two extremes predicts a nearly 100% population of the transoid isomer at room temperature, with a calculated gas phase JP–Se of 792 Hz. We then performed optimizations of the transoid rotamer with explicit solvation to see if the observed experimental trends were reproduced computationally. Optimizations in CHCl3, DCM, and MeCN predict |JP–Se| values of 648, 675, and 684 Hz respectively (Fig. S84–S86 and S12†). These values are in remarkably good agreement with both the experimentally determined JP–Se as well as the observed trend with solvent dielectric.
To computationally deconvolute electrostatic contributions to JP–Se, we analyzed the effect of including point charges in the gas phase. Coulomb's law was used to estimate the electric field at P generated by a negative point charge located at B in the transoid rotamer of 1Se. This analysis gives an electric field parallel to the P–Se bond (defined as the z-axis) of ∼ −1.07 V Å−1 (Table S4†). The electrostatic contribution to JP–Se was then determined by calculating the JP–Se for SePPh2Et with a negative point charge at ∼3.7 Å from P in the z direction, resulting in an applied field of comparable magnitude. The inclusion of this point charge lowers JP–Se to 809 Hz from 872 Hz in the neutral analogue, suggesting that the purely electrostatic contribution to JP–Se is 63 Hz. This electrostatic contribution is 79% of the total computed difference in JP–Se between 1Se and SePPh2Et (80 Hz, Table 1), which is identical within error to that determined experimentally. Thus, DFT calculations support the experimental data demonstrating that electrostatic effects play a significant role in the donor properties of 1.
Extension and comparison to other phosphines
The selenide of an anionic phosphine previously investigated for Pd catalyzed olefin polymerization/oligomerization, [PPh4][SePPh2(2-BF3Ph)] ([PPh4][3Se]), was synthesized analogously to [PPh4][1Se]. This phosphine was targeted to test the generality of this solvent-dependence analysis of electrostatic contributions to donor properties, particularly in the presence of increased rigidity and possible convoluting resonance effects from an aryl linker.90,91 The SXRD structure of [PPh4][3Se] confirms the expected connectivity and also shows that the B of the BF3− group is farther from the phosphine than in [PPh4][1Se] (Fig. 1, 3.562(2) and 3.029(6) Å respectively). The P of the PPh4+ cation is located at 5.895(2) Å from the B, however H-bonding interactions between the PPh4+ aryl protons and the BF3− fluorines are observed (Fig. S95†).The solvent dependence of JP–Se for [PPh4][3Se] was measured with the related assumption that inductive and resonance contributions along the covalent linkage would be predominantly independent of solvent ε screening. The JP–Se of [PPh4][3Se] decreases by 18 Hz upon moving from DMSO-d6 to CDCl3, a smaller change than the 30 Hz shift observed for [PPh4][1Se] (Fig. 3, S36 and S12†). Furthermore, the magnitude of the slope of the linear fit to the solvent dependence for [PPh4][3Se] is ∼70% of that for [PPh4][1Se]. This is consistent with the ratio predicted from a 1/(r2) dependence from Coulomb's law based on the relative B⋯P distances in the anionic fragments of [PPh4][3Se] and [PPh4][1Se] from SXRD (3.562(2) and 3.029(6) Å respectively, 72%, see ESI†).
The neutral congener of [PPh4][3Se], SePPh3, was also prepared and the JP–Se changes by 5 Hz upon switching from CDCl3 to DMSO-d6 (Fig. 3, S38 and S12†). Using the JP–Se values from the high ε and vacuum limits determined from the linear fit of [PPh4][3Se] and an identical comparison method to that described above suggests an electrostatic contribution to the overall shift of 73%, which is slightly smaller than that for [PPh4][1Se] (82%). In sum, all the experimental data acquired on both [PPh4][1Se] and [PPh4][3Se] support a significant and potentially major role that through-space electrostatic interactions have in the donor properties of these phosphines, and furthermore illustrate that JP–Se is a useful probe for deconvoluting electrostatic from inductive or resonance effects.
Comparing the overall shifts in JP–Se from [PPh4][1Se] and [PPh4][3Se] from their respective neutral congeners to other anionic phosphine systems is instructive, even in the absence of comparable solvent dependence studies. In one example a triptycene borate phosphine with a P⋯B distance of 3.03 Å was compared to a silicon based neutral analogue.96,111 The shift in JP–Se observed in CDCl3 upon switching from the neutral to anionic version approached 90 Hz. The magnitude of this shift is larger than the 63 Hz shift between [PPh4][1Se] and SePPh2Et and the 54 Hz difference between [PPh4][3Se] and SePPh3 in CDCl3. The greater magnitude of the shift can be rationalized by the orientation of the anionic functional group, which is constrained to align with the P–Se bond in the triptycene case. The significant change in JP–Se coupling observed in the triptycene case contrasts with another example featuring an anionic BPh3− group, SePPh2(p-BPh3Ph)−.101 The difference in coupling between this compound and the neutral congener SePPh3 is only 30 Hz in CDCl3, likely due to the larger distance between the charged group and the phosphine (6.49 Å from DFT) and delocalization of the anionic charge into the aryl rings on boron.96,99,101 These examples illustrate that the distance, orientation, and anion structure influence the magnitude of the impact on phosphine donor properties.
C–F oxidative addition reactivity
The comparatively strong donor properties of phosphine 1 prompted up to consider its application in challenging oxidative addition (OA) reactions. Indeed, anionic phosphines have previously shown enhanced coupling reactivity with aryl chlorides in comparison to neutral isostructural congeners.94–96 Uniquely, the JP–Se analysis carried out above with [PPh4][1Se] allows for comparison between the reactivity of K1 and phosphines of quantitatively similar donor strengths. Comparison with PEt3 is instructive as the JP–Se (684 Hz) closely matches that of [PPh4][1Se] in DMSO (687 Hz) and the cone angles are similar (132° and 140° for PEt3 and PPh2Et).77 The reactivity of PCy3 was also investigated as the JP–Se (675 Hz) closely matches that predicted for [PPh4][1Se] in THF using the 1/4πε linear fit (ε = 7.6, 671 Hz). While these comparisons do not perfectly account for enhanced ion pairing from K+ or imperfect matching of cone angles, they are nonetheless useful to reveal trends in reactivity as a function of electrostatic contributions to donor strength.The OA of aryl fluoride bonds was chosen for this comparison due to a recent computational report suggesting that this reaction is accelerated in the presence of an electric field.53 Additionally, the OA of C6F6 by Ni(COD)2 (COD = 1,5-cyclooctadiene) with PEt3 has been previously reported to proceed very slowly, taking ∼4 weeks in hexane for completion.130 Therefore, the rates of C6F6 OA by Ni(COD)2 with K1, PEt3 and PCy3 in THF were determined along with the overall conversion.
The combination of Ni(COD)2 and 2 equivalents of K1 in THF generates a red solution with an absorbance in the UV-vis spectrum at 464 nm (Fig. S79†). The 31P{1H} NMR spectrum of the reaction shows the appearance of three new resonances with some unreacted K1, indicating a mixture of differentially ligated species (Fig. S43†). Addition of 10 equivalents of C6F6, as well as CF3Ph and OPPh3 as internal standards, results in the disappearance of these resonances and the formation of a new doublet at 9.6 ppm consistent with coupling to a Ni–F (Fig. S48†). Similarly, the 19F NMR spectrum shows the appearance of resonances consistent with Ni–C6F5 (−117.5, −166.4, and −167.1 ppm) and Ni–F (−383.6 ppm) moieties (Fig. S44 and S45†). The product resonances grow in with an average observed rate of 1.6(2) × 10−4 s−1, and level off after ∼7 hours with an average yield of 25(3)% (Fig. S47, S49 and Table S1†). The reaction between Ni(COD)2, 2 equivalents of K1 and 21 equivalents of C6F6 was also examined by monitoring the decay of the absorbance at 464 nm using UV-vis spectroscopy (Fig. S75†). The observed rate of decay is on the same order of magnitude as the rate of formation determined by NMR methods (5.6(4) × 10−4 s−1). Reducing the amount of added K1 to 1 equivalent decreases the observed rate (2.8 × 10−4 s−1), which is inconsistent with a mechanism involving the dissociation of a ligand prior to OA (Fig. S74†). The rate is also reduced with the addition of 3, 4, or 8 equivalents of K1, with the appearance of a new absorbance at 375 nm suggesting additional coordination of K1 to Ni may be possible (Fig. S76–S78†). As a control, the absorbance at 464 nm was monitored in the absence of substrate and indicated minimal decay over the same time frame (Fig. S79†).
Carrying out the same reaction with PEt3 and PCy3 results in the growth of similar NMR signals as those observed with K1, but with significantly slower rates of product formation (3.7(7) × 10−6 s−1 and 2.0(1) × 10−5 s−1, respectively) (Fig. S50–S58 and Table S1†). In contrast to K1, the OA product growth continues throughout the time the reaction was monitored, reaching 24(2)% at 114 h for PEt3 and 66(15)% at 53 h for PCy3. The enhanced rate observed with K1 not only supports previous observations that anionic groups enhance rates of OA reactions,94–96 but also demonstrates that the rate enhancement is greater than would be predicted on the basis of donor strength. This is perhaps most clearly illustrated by the one order of magnitude rate acceleration with K1 over PCy3, despite the nearly identical donor strengths predicted by our analysis. A distinct mechanism for electrostatic rate enhancement beyond an increase in donor strength has been suggested previously with an anionic carborane phosphine, wherein accelerated OA reactivity was attributed to ligand dissociation and transition state (TS) stabilization.95 The exact nature of the rate acceleration with K1 is not yet clear. It is possible that the TS is lowered by the presence of an electric field generated by the BF3−, as is predicted computationally,53 but other factors, such as ion pairing with K+, may also be determinative. Regardless, these results emphasize that anionic charges enhance reactivity through mechanisms beyond simply increasing donor strength.
Catalytic defluoroborylation reactivity
The significant rate acceleration observed in stoichiometric reactivity led us to investigate catalytic C–F borylation with K1 and Ni(COD)2. Defluoroborylation of fluorinated arenes with Ni has been reported previously with N-heterocyclic carbene (NHC) and PCy3 ligands.131–133 The use of strongly donating ligands is consistent with the difficulty of the OA step, as C–F bonds have the highest BDE among carbon–halogen bonds.131 Likewise, high catalyst loadings (10%), reaction temperatures (110 °C), and long reaction times (≥12 h) highlight the difficulty of these transformations.Optimization reactions were carried out using K1 and Ni(COD)2 for the defluoroborylation of 1,3-difluorobenzene using B2pin2 (bis(pinacolato)diboron) as the test substrate. Ultimately, a 50% yield of 1-Bpin-3-C6FH4 was realized with the following conditions: 9% catalyst loading with 1.8 equivalents of B2pin2, 0.72–0.75 equivalents of CsOH·xH2O (15–20% H2O), and 1.9 equivalents of methanol in THF heated at 50 °C for 4 hours (Tables S17–S24† contain information on optimization trials). Notably, substituting K1 with PEt3, PCy3, or PPh2Et under identical reaction conditions results in no conversion to the borylated product (Table S21†). NMR monitoring over time indicates that the reaction is complete after 2 hours (Table S21†). Increasing the temperature to 100 °C for 2 hours or stirring at room temperature for 22 hours only slightly affects the yield (48% and 44%, respectively, Table S22†). Switching B2pin2 for B2nep2 (bis(neopentyl gylcolato)diboron) or B2cat2 (bis(chatecolato)diboron) to test alternative transmetallating agents significantly reduces the yield (32% and 0%, Table S22†), in contrast to previous studies with PCy3.134 Both MeOH and CsOH are required for catalysis, with alternative alcohols or metal salts reducing the yield. Exchanging the K+ counterion on 1 for more solubilizing counterions does not improve the yield (Table S23†), and no trend is observed with solvent ε across a limited series of ethereal solvents (Table S24†).
This method was extended to other fluoroarenes to examine the scope of reactivity (Fig. 4). The highest yield observed is for 1,3 difluorobenzene (50%), followed by fluorobenzene (42%), with lower yields for more highly fluorinated substrates. The trend of decreasing yields with higher levels of fluorination contrasts with the trend observed with an NHC, where more highly fluorinated substrates are more easily defluoroborylated.133 Additionally, homocoupling is competitive in substrates with adjacent fluorine atoms in our system. The fluorobenzene borylation with K1 is higher than that with an NHC ligand (20%),133 but in general other systems perform defluoroborylation of more diverse fluoroarenes with higher yields than the current system.131,132
 | ||
| Fig. 4 Substrate scope defluoroborylation catalysis. Unless otherwise specified, all reactions were carried out in 1 mL of THF with Ni(COD)2 (10 mg, 0.036 mmol), K1 (22 mg, 0.072 mmol), B2pin2 (184 mg, 0.72 mmol), CsOH·xH2O (15–20%) (54 mg, 0.29–0.31 mmol), MeOH (30 μL, 0.72 mmol), CF3Ph (20 μL, 0.16 mmol) and substrate (0.4 mmol) and were heated with stirring for 4 hours at 50 °C. All yields unless otherwise specified were determined in triplicate by comparison to an internal CF3Ph integral standard. (a) Yield determined using GCMS, no CF3Ph added to the reaction. For more details see ESI†. | ||
Based on the observed formation of a C–F OA product with C6F6, it is likely that defluoroborylation proceeds through a traditional OA, transmetalation, and reductive elimination mechanism. The differing reactivity trend with arene fluorination implies that the enhanced OA rate in the present system makes transmetalation the turnover limiting step. This hypothesis is consistent with increased yields with an excess of B2pin2 as well as the need for more nucleophilic hydroxide or alkoxide additives over fluoride sources. We speculate that in situ generated methoxide may facilitate transmetalation of B2pin2 by exchanging with Ni–F intermediates, as a similar σ-bond metathesis of B2pin2 with Ni alkoxide complexes has been reported.135 However, the specific role played by Cs+ and MeOH remains unclear. Faster rates and unique reaction conditions for this system (i.e. lower temperature, base, water and alcohol) suggest that it may offer complementary reactivity to the established neutral phosphine systems and motivates further investigation. Regardless of specific methodological applications, the fact that the inclusion of a BF3− group enables a diarylalkyl phosphine to perform comparably with an NHC in C–F borylation highlights how electrostatic effects can both dramatically enhance stroichiometric OA reactivity as well as catalytic processes.
Conclusions
In conclusion, a new anionic phosphine ligand has been synthesized and demonstrates that the inclusion of an anionic trifluoroborate group dramatically increases the donor properties relative to neutral analogues. Furthermore, a series of experiments and calculations have demonstrated that a significant portion of the increase in donor strength arises from electrostatic as opposed to inductive effects. The electrostatic interactions in this ligand accelerate OA rates by an order of magnitude compared to ligands of similar donor strength, consistent with theoretical predictions. This enhanced OA reactivity can be leveraged for the catalytic defluoroborylation of C–F bonds with reactivity trends that differ from previously reported examples. While there are several reports on the influence of appended anionic groups on mono- or polydentate phosphine ligands, this work is the first case where the relative contributions from inductive versus electrostatic donation have been disentangled. The ability of charged groups to stabilize specific resonance structures, such as the zwitterionic Se−–P+R3 structure, offers tremendous potential in tuning catalytic systems as we demonstrate here. The fact that a major portion of the increase in donor strength arises from electrostatic effects in common organic solvents with charge-diffuse counterions has important implications for ligand design as the directionality of electric fields provides a unique variable for influencing reactivity and breaking classic free–energy relationships.Data availability
Detailed experimental and computational data can be found in the ESI.†Author contributions
The project was planned out and the manuscript was written by M. L. K., A. J. M., and J. S. A. The experiments were carried out by M. L. K. and A. J. M. The crystallographic characterization was carried out by A. J. M. and A. S. F. The optimization of NMR parameters for reaction kinetics was carried out my M. L. K. and J. W. K.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Institutes of Health (R35 GM133470). M. L. K. was supported by the NSF Graduate Student Fellowship Grant No. DGE-1144082 and DGE-1746045. We thank the University of Chicago for funding as well as 3M corporation for a NTFA and the Sloan Foundation for a Research Fellowship to J. S. A. (FG-2019-11497). We also thank the Research Computing Center at the University of Chicago for providing computing resources. We thank Joseph Schneider for helpful discussions and Sophie Whitmeyer for crystallography assistance.References
- A. Warshel, J. Biol. Chem., 1998, 273, 27035–27038 CrossRef CAS PubMed.
- A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. Liu and M. H. M. Olsson, Chem. Rev., 2006, 106, 3210–3235 CrossRef CAS PubMed.
- P. Schyman, W. Lai, H. Chen, Y. Wang and S. Shaik, J. Am. Chem. Soc., 2011, 133, 7977–7984 CrossRef CAS PubMed.
- S. D. Fried and S. G. Boxer, Acc. Chem. Res., 2015, 48, 998–1006 CrossRef CAS PubMed.
- S. D. Fried and S. G. Boxer, Annu. Rev. Biochem., 2017, 86, 387–415 CrossRef CAS PubMed.
- A. Morgenstern, M. Jaszai, M. E. Eberhart and A. N. Alexandrova, Chem. Sci., 2017, 8, 5010–5018 RSC.
- D. Bím and A. N. Alexandrova, ACS Catal., 2021, 11, 6534–6546 CrossRef PubMed.
- S. Shaik, D. Mandal and R. Ramanan, Nat. Chem., 2016, 8, 1091–1098 CrossRef CAS PubMed.
- S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Chem. Soc. Rev., 2018, 47, 5125–5145 RSC.
- S. Ciampi, N. Darwish, H. M. Aitken, I. Díez-Pérez and M. L. Coote, Chem. Soc. Rev., 2018, 47, 5146–5164 RSC.
- F. Che, J. T. Gray, S. Ha, N. Kruse, S. L. Scott and J.-S. McEwen, ACS Catal., 2018, 8, 5153–5174 CrossRef CAS.
- S. Ye, C. Riplinger, A. Hansen, C. Krebs, J. M. Bollinger and F. Neese, Chem.–Eur. J., 2012, 18, 6555–6567 CrossRef CAS PubMed.
- M. Alemani, M. V Peters, S. Hecht, K. H. Rieder, F. Moresco and L. Grill, J. Am. Chem. Soc., 2006, 128, 14446–14447 CrossRef CAS PubMed.
- C. F. Gorin, E. S. Beh and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 186–189 CrossRef CAS PubMed.
- Y. Zang, Q. Zou, T. Fu, F. Ng, B. Fowler, J. Yang, H. Li, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nat. Commun., 2019, 10, 1–7 CrossRef PubMed.
- C. F. Gorin, E. S. Beh, Q. M. Bui, G. R. Dick and M. W. Kanan, J. Am. Chem. Soc., 2013, 135, 11257–11265 CrossRef CAS PubMed.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91 CrossRef PubMed.
- M. Liu, Y. Pang, B. Zhang, P. De Luna, O. Voznyy, J. Xu, X. Zheng, C. T. Dinh, F. Fan, C. Cao, F. P. G. De Arquer, T. S. Safaei, A. Mepham, A. Klinkova, E. Kumacheva, T. Filleter, D. Sinton, S. O. Kelley and E. H. Sargent, Nature, 2016, 537, 382–386 CrossRef CAS PubMed.
- L. Zhang, E. Laborda, N. Darwish, B. B. Noble, J. H. Tyrell, S. Pluczyk, A. P. Le Brun, G. G. Wallace, J. Gonzalez, M. L. Coote and S. Ciampi, J. Am. Chem. Soc., 2018, 140, 766–774 CrossRef CAS PubMed.
- J. Ryu and Y. Surendranath, J. Am. Chem. Soc., 2019, 141, 15524–15531 CrossRef CAS PubMed.
- J. Heo, H. Ahn, J. Won, J. G. Son, H. K. Shon, T. G. Lee, S. W. Han and M.-H. Baik, Science, 2020, 370, 214–219 CrossRef CAS PubMed.
- M. Shetty, M. A. Ardagh, Y. Pang, O. A. Abdelrahman and P. J. Dauenhauer, ACS Catal., 2020, 10, 12867–12880 CrossRef CAS.
- R. E. Warburton, P. Hutchison, M. N. Jackson, M. L. Pegis, Y. Surendranath and S. Hammes-Schiffer, J. Am. Chem. Soc., 2020, 142, 20855–20864 CrossRef CAS PubMed.
- D. A. DiRocco, E. L. Noey, K. N. Houk and T. Rovis, Angew. Chem., Int. Ed., 2012, 51, 2391–2394 CrossRef CAS PubMed.
- M. C. Holland, S. Paul, W. B. Schweizer, K. Bergander, C. Mück-Lichtenfeld, S. Lakhdar, H. Mayr and R. Gilmour, Angew. Chem., Int. Ed., 2013, 52, 7967–7971 CrossRef CAS PubMed.
- B. Chattopadhyay, J. E. Dannatt, I. L. Andujar-De Sanctis, K. A. Gore, R. E. Maleczka, D. A. Singleton and M. R. Smith III, J. Am. Chem. Soc., 2017, 139, 7864–7871 CrossRef CAS PubMed.
- V. M. Lau, W. C. Pfalzgraff, T. E. Markland and M. W. Kanan, J. Am. Chem. Soc., 2017, 139, 4035–4041 CrossRef CAS PubMed.
- T. Chantarojsiri, J. W. Ziller and J. Y. Yang, Chem. Sci., 2018, 9, 2567–2574 RSC.
- D. Dhar, G. M. Yee and W. B. Tolman, Inorg. Chem., 2018, 57, 9794–9806 CrossRef CAS PubMed.
- K. Kang, J. Fuller, A. H. Reath, J. W. Ziller, A. N. Alexandrova and J. Y. Yang, Chem. Sci., 2019, 10, 10135–10142 RSC.
- J. D. Erickson, A. Z. Preston, J. C. Linehan and E. S. Wiedner, ACS Catal., 2020, 10, 7419–7423 CrossRef CAS.
- A. C. Deacy, E. Moreby, A. Phanopoulos and C. K. Williams, J. Am. Chem. Soc., 2020, 142, 19150–19160 CrossRef CAS PubMed.
- V. F. Oswald, J. L. Lee, S. Biswas, A. C. Weitz, K. Mittra, R. Fan, J. Li, J. Zhao, M. Y. Hu, E. E. Alp, E. L. Bominaar, Y. Guo, M. T. Green, M. P. Hendrich and A. S. Borovik, J. Am. Chem. Soc., 2020, 142, 11804–11817 CrossRef CAS PubMed.
- D. J. Martin, S. I. Johnson, B. Q. Mercado, S. Raugei and J. M. Mayer, Inorg. Chem., 2020, 59, 17402–17414 CrossRef CAS PubMed.
- A. B. Weberg, S. P. McCollom, L. M. Thierer, M. R. Gau, P. J. Carroll and N. C. Tomson, Chem. Sci., 2021, 12, 4395–4404 RSC.
- M. Klinska, L. M. Smith, G. Gryn’ova, M. G. Banwell and M. L. Coote, Chem. Sci., 2015, 6, 5623–5627 RSC.
- D. J. Martin, B. Q. Mercado and J. M. Mayer, Inorg. Chem., 2021, 60, 5240–5251 CrossRef CAS PubMed.
- D. J. Martin and J. M. Mayer, J. Am. Chem. Soc., 2021, 143, 11423–11434 CrossRef CAS PubMed.
- N. G. Léonard, T. Chantarojsiri, J. W. Ziller and J. Y. Yang, J. Am. Chem. Soc., 2022, 144, 1503–1508 CrossRef PubMed.
- K. Lee, D. L. Silverio, S. Torker, D. W. Robbins, F. Haeffner, F. W. van der Mei and A. H. Hoveyda, Nat. Chem., 2016, 8, 768–777 CrossRef CAS PubMed.
- C. R. Kennedy, J. A. Guidera and E. N. Jacobsen, ACS Cent. Sci., 2016, 2, 416–423 CrossRef CAS PubMed.
- G. Xiao, G. A. Cintron-Rosado, D. A. Glazier, B.-M. Xi, C. Liu, P. Liu and W. Tang, J. Am. Chem. Soc., 2017, 139, 4346–4349 CrossRef CAS PubMed.
- S. Yamada, Chem. Rev., 2018, 118, 11353–11432 CrossRef CAS PubMed.
- V. Dhayalan, S. C. Gadekar, Z. Alassad and A. Milo, Nat. Chem., 2019, 11, 543–551 CrossRef CAS PubMed.
- J. Grajeda, M. R. Kita, L. C. Gregor, P. S. White and A. J. M. M. Miller, Organometallics, 2016, 35, 306–316 CrossRef CAS.
- A. H. Reath, J. W. Ziller, C. Tsay, A. J. Ryan and J. Y. Yang, Inorg. Chem., 2017, 56, 3713–3718 CrossRef CAS PubMed.
- J. M. Um, D. A. Dirocco, E. L. Noey, T. Rovis and K. N. Houk, J. Am. Chem. Soc., 2011, 133, 11249–11254 CrossRef CAS PubMed.
- E. Lyngvi, J. W. Bode and F. Schoenebeck, Chem. Sci., 2012, 3, 2346–2350 RSC.
- T. Stuyver, R. Ramanan, D. Mallick and S. Shaik, Angew. Chem., Int. Ed., 2020, 59, 7915–7920 CrossRef CAS PubMed.
- L. Xu, E. I. Izgorodina and M. L. Coote, J. Am. Chem. Soc., 2020, 142, 12826–12833 CrossRef CAS PubMed.
- V. Doan, B. B. Noble and M. L. Coote, J. Org. Chem., 2020, 85, 10091–10097 CrossRef CAS PubMed.
- V. V. Welborn, L. Ruiz Pestana and T. Head-Gordon, Nat. Catal., 2018, 1, 649–655 CrossRef.
- J. Joy, T. Stuyver and S. Shaik, J. Am. Chem. Soc., 2020, 142, 3836–3850 CrossRef CAS PubMed.
- H. Yang and M. W. Wong, J. Am. Chem. Soc., 2013, 135, 5808–5818 CrossRef CAS PubMed.
- Q. N. N. Nguyen, M. W. Lodewyk, S. Bezer, M. R. Gagné, M. L. Waters and D. J. Tantillo, ACS Catal., 2015, 5, 1617–1622 CrossRef CAS.
- T. J. Seguin and S. E. Wheeler, ACS Catal., 2016, 6, 2681–2688 CrossRef CAS.
- T. J. Seguin and S. E. Wheeler, Angew. Chem., Int. Ed., 2016, 55, 15889–15893 CrossRef CAS PubMed.
- R. Maji and S. E. Wheeler, J. Am. Chem. Soc., 2017, 139, 12441–12449 CrossRef CAS PubMed.
- N. S. Hill and M. L. Coote, Aust. J. Chem., 2019, 72, 627–632 CrossRef CAS.
- M. T. Blyth and M. L. Coote, J. Org. Chem., 2019, 84, 1517–1522 CrossRef PubMed.
- M. T. Blyth, B. B. Noble, I. C. Russell and M. L. Coote, J. Am. Chem. Soc., 2020, 142, 606–613 CrossRef CAS PubMed.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- T. Ri and H. Eyring, J. Chem. Phys., 1940, 8, 433–443 CrossRef CAS.
- F. H. Westheimer, J. Am. Chem. Soc., 1939, 61, 1977–1980 CrossRef CAS.
- H. H. Jaffé, J. Chem. Phys., 1952, 20, 279–284 CrossRef.
- H. H. Jaffé, Chem. Rev., 1953, 53, 191–261 CrossRef.
- R. J. Burns, I. K. Mati, K. B. Muchowska, C. Adam and S. L. Cockroft, Angew. Chem., Int. Ed., 2020, 59, 2–10 CrossRef.
- P. J. Fischer, S. Senthil, J. T. Stephan, M. L. Swift, M. D. Storlie, E. T. Chan, M. V Vollmer and V. G. Young, Dalton Trans., 2018, 47, 6166–6176 RSC.
- J. Estrada, C. A. Lugo, S. G. McArthur and V. Lavallo, Chem. Commun., 2016, 52, 1824–1826 RSC.
- I. Azcarate, C. Costentin, M. Robert and J.-M. Savéant, J. Am. Chem. Soc., 2016, 138, 16639–16644 CrossRef CAS PubMed.
- M. L. Pegis, C. F. Wise, B. Koronkiewicz and J. M. Mayer, J. Am. Chem. Soc., 2017, 139, 11000–11003 CrossRef CAS PubMed.
- S. Sung, D. Kumar, M. Gil-Sepulcre and M. Nippe, J. Am. Chem. Soc., 2017, 139, 13993–13996 CrossRef CAS PubMed.
- Z. Yuan, H. Yang, N. Malik, M. Čolović, D. S. Weber, D. Wilson, F. Bénard, R. E. Martin, J. J. Warren, P. Schaffer and R. Britton, ACS Catal., 2019, 9, 8276–8284 CrossRef CAS.
- S. Sung, X. Li, L. M. Wolf, J. R. Meeder, N. S. Bhuvanesh, K. A. Grice, J. A. Panetier and M. Nippe, J. Am. Chem. Soc., 2019, 141, 6569–6582 CrossRef CAS PubMed.
- R. Zhang and J. J. Warren, J. Am. Chem. Soc., 2020, 142, 13426–13434 CrossRef CAS PubMed.
- C. G. Margarit, N. G. Asimow, M. I. Gonzalez and D. G. Nocera, J. Phys. Chem. Lett., 2020, 11, 1890–1895 CrossRef CAS PubMed.
- C. A. Tolman, Chem. Rev., 1977, 77, 313–348 CrossRef CAS.
- M. Stradiotto, K. D. Hesp and R. J. Lundgren, Angew. Chem., Int. Ed., 2010, 49, 494–512 CrossRef CAS PubMed.
- R. Puerta-Oteo, A. I. Ojeda-Amador, M. V. Jiménez and J. J. Pérez-Torrente, Dalton Trans., 2022, 51, 817–830 RSC.
- A. J. M. Miller, J. A. Labinger and J. E. Bercaw, J. Am. Chem. Soc., 2010, 132, 3301–3303 CrossRef CAS PubMed.
- B. R. Nichols, N. G. Akhmedov, J. L. Petersen and B. V Popp, Dalton Trans., 2018, 47, 8456–8465 RSC.
- A. J. M. Miller, J. A. Labinger and J. E. Bercaw, Organometallics, 2011, 30, 4308–4314 CrossRef CAS PubMed.
- M. Alcarazo, Acc. Chem. Res., 2016, 49, 1797–1805 CrossRef CAS PubMed.
- X. Jia, M. Zhang, F. Pan, I. Babahan, K. Ding, L. Jia, L. A. Crandall and C. J. Ziegler, Organometallics, 2015, 34, 4798–4801 CrossRef CAS.
- L. Zhu, Y. Dai, B. R. Schrage, C. J. Ziegler and L. Jia, J. Organomet. Chem., 2021, 952, 122045 CrossRef CAS.
- C. C. Lu and J. C. Peters, J. Am. Chem. Soc., 2002, 124, 5272–5273 CrossRef CAS PubMed.
- X. Jia, M. Zhang, M. Li, F. Pan, K. Ding, L. Jia, L. A. Crandall, J. T. Engle and C. J. Ziegler, Organometallics, 2017, 36, 1122–1132 CrossRef CAS.
- B. M. Schmidt, J. T. Engle, M. Zhang, I. Babahan, C. J. Ziegler and L. Jia, J. Organomet. Chem., 2016, 805, 94–99 CrossRef CAS.
- D. V Gutsulyak, A. L. Gott, W. E. Piers and M. Parvez, Organometallics, 2013, 32, 3363–3370 CrossRef.
- A. L. Gott, W. E. Piers, J. L. Dutton, R. McDonald and M. Parvez, Organometallics, 2011, 30, 4236–4249 CrossRef CAS.
- Y. Kim and R. F. Jordan, Organometallics, 2011, 30, 4250–4256 CrossRef CAS.
- Y. Dai, S. He, B. Peng, L. A. Crandall, B. R. Schrage, C. J. Ziegler and L. Jia, Angew. Chem., Int. Ed., 2018, 57, 14111–14115 CrossRef CAS PubMed.
- J. Estrada, D. H. Woen, F. S. Tham, G. M. Miyake and V. Lavallo, Inorg. Chem., 2015, 54, 5142–5144 CrossRef CAS PubMed.
- C. M. Thomas and J. C. Peters, Inorg. Chem., 2004, 43, 8–10 CrossRef CAS PubMed.
- A. L. Chan, J. Estrada, C. E. Kefalidis and V. Lavallo, Organometallics, 2016, 35, 3257–3260 CrossRef CAS.
- S. Konishi, T. Iwai and M. Sawamura, Organometallics, 2018, 37, 1876–1883 CrossRef CAS.
- V. Lavallo, J. H. Wright, F. S. Tham and S. Quinlivan, Angew. Chem., Int. Ed., 2013, 52, 3172–3176 CrossRef CAS PubMed.
- T. A. Betley and J. C. Peters, Angew. Chem., Int. Ed., 2003, 42, 2385–2389 CrossRef CAS PubMed.
- J. C. Thomas and J. C. Peters, J. Am. Chem. Soc., 2003, 125, 8870–8888 CrossRef CAS PubMed.
- J. C. Thomas and J. C. Peters, Inorg. Chem., 2003, 42, 5055–5073 CrossRef CAS PubMed.
- J. P. Tassone, R. C. Mawhinney and G. J. Spivak, J. Organomet. Chem., 2015, 776, 153–156 CrossRef CAS.
- D. Seyferth and S. O. Grim, J. Am. Chem. Soc., 1961, 83, 1610–1613 CrossRef CAS.
- D. Seyferth and S. O. Grim, J. Am. Chem. Soc., 1961, 83, 1613–1616 CrossRef CAS.
- C. M. Bateman, L. N. Zakharov and E. R. Abbey, Acta Crystallogr., 2017, 73, 1140–1142 CrossRef CAS PubMed.
- R. A. Oliveira, R. O. Silva, G. A. Molander and P. H. Menezes, Magn. Reson. Chem., 2009, 47, 873–878 CrossRef CAS PubMed.
- D. Setiawan, R. Kalescky, E. Kraka and D. Cremer, Inorg. Chem., 2016, 55, 2332–2344 CrossRef CAS PubMed.
- J. A. Gillespie, E. Zuidema, P. W. N. M. van Leeuwen and P. C. J. Kamer, Phosphorus Ligand Effects in Homogeneous Catalysis and Rational Catalyst Design, in Phosphorus(III) Ligands in Homogeneous Catalysis: Design and Synthesis, ed. P. C. J. Kamer and P. W. N. M. van Leeuwen, John Wiley & Sons, Ltd, Chichester, UK, 1st edn, 2012, pp. 1–26 Search PubMed.
- L. Chen, P. Ren and B. P. Carrow, J. Am. Chem. Soc., 2016, 138, 6392–6395 CrossRef CAS PubMed.
- J. C. Thomas and J. C. Peters, J. Am. Chem. Soc., 2001, 123, 5100–5101 CrossRef CAS PubMed.
- S. L. Granville, G. C. Welch and D. W. Stephan, Inorg. Chem., 2012, 51, 4711–4721 CrossRef CAS PubMed.
- M. W. Drover, K. Nagata and J. C. Peters, Chem. Commun., 2018, 54, 7916–7919 RSC.
- S. Qiao, D. A. Hoic and G. C. Fu, J. Am. Chem. Soc., 1996, 118, 6329–6330 CrossRef CAS.
- D. W. Allen and B. F. Taylor, J. Chem. Soc., Dalton Trans., 1982, 51–54 RSC.
- U. Beckmann, D. Süslüyan and P. C. Kunz, Phosphorus, Sulfur Silicon Relat. Elem., 2011, 186, 2061–2070 CrossRef CAS.
- H. V. Huynh, Chem. Rev., 2018, 118, 9457–9492 CrossRef CAS PubMed.
- K. Verlinden, H. Buhl, W. Frank and C. Ganter, Eur. J. Inorg. Chem., 2015, 2015, 2416–2425 CrossRef CAS.
- J. Autschbach and B. Le Guennic, J. Chem. Educ., 2007, 84, 156–171 CrossRef CAS.
- A. Muller, S. Otto and A. Roodt, Dalton Trans., 2008, 650–657 RSC.
- C. C. Levin, J. Am. Chem. Soc., 1975, 97, 5649–5655 CrossRef CAS.
- F. Wossidlo, D. S. Frost, J. Lin, N. T. Coles, K. Klimov, M. Weber, T. Böttcher and C. Müller, Chem.–Eur. J., 2021, 27, 12788–12795 CrossRef CAS PubMed.
- Z. L. Niemeyer, A. Milo, D. P. Hickey and M. S. Sigman, Nat. Chem., 2016, 8, 610–617 CrossRef CAS PubMed.
- A. M. Ejgandi, Measuring the electronic and steric effect of some phosphine ligands, University of Manchester, 2010 Search PubMed.
- D. W. Allen, I. W. Nowell and B. F. Taylor, J. Chem. Soc., Dalton Trans., 1985, 834, 2505–2508 RSC.
- E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science, Herndon, VA, 5th edn, 2005 Search PubMed.
- F. Grevels, J. Jacke, W. E. Klotzbücher, C. Krüger, K. Seevogel and Y. Tsay, Angew. Chem., Int. Ed., 1987, 26, 885–887 CrossRef.
- W. McFarlane and D. S. Rycroft, J. Chem. Soc., Dalton Trans., 1973, 2162–2166 RSC.
- S. W. Carr and R. Colton, Aust. J. Chem., 1981, 34, 35–44 CrossRef CAS.
- C. G. Hrib, F. Ruthe, E. Seppälä, M. Bätcher, C. Druckenbrodt, C. Wismach, P. G. Jones, W. W. du Mont, V. Lippolis, F. A. Devillanova and M. Bühl, Eur. J. Inorg. Chem., 2006, 2006, 88–100 CrossRef.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed.
- L. Cronin, C. L. Higgitt, R. Karch and R. N. Perutz, Organometallics, 1997, 16, 4920–4928 CrossRef CAS.
- X. W. Liu, J. Echavarren, C. Zarate and R. Martin, J. Am. Chem. Soc., 2015, 137, 12470–12473 CrossRef CAS PubMed.
- T. Niwa, H. Ochiai, Y. Watanabe and T. Hosoya, J. Am. Chem. Soc., 2015, 137, 14313–14318 CrossRef CAS PubMed.
- J. Zhou, M. W. Kuntze-Fechner, R. Bertermann, U. S. D. Paul, J. H. J. Berthel, A. Friedrich, Z. Du, T. B. Marder and U. Radius, J. Am. Chem. Soc., 2016, 138, 5250–5253 CrossRef CAS PubMed.
- C. A. Malapit, J. R. Bour, S. R. Laursen and M. S. Sanford, J. Am. Chem. Soc., 2019, 141, 17322–17330 CrossRef CAS PubMed.
- B. L. Tran, D. Adhikari, H. Fan, M. Pink and D. J. Mindiola, Dalton Trans., 2010, 39, 358–360 RSC.
- S. O. Grim and E. D. Walton, Inorg. Chem., 1980, 19, 1982–1987 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2090438–2090441. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc04277g |
| This journal is © The Royal Society of Chemistry 2022 |

