Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A generalized kinetic model for compartmentalization of organometallic catalysis†
Brandon J.
Jolly
 a,
Nathalie H.
Co
a,
Nathalie H.
Co
 a,
Ashton R.
Davis
a,
Ashton R.
Davis
 a,
Paula L.
Diaconescu
a,
Paula L.
Diaconescu
 *a and
Chong
Liu
*a and
Chong
Liu
 *ab
*ab
aDepartment of Chemistry and Biochemistry, University of California, Los Angeles, California 90095, USA. E-mail: pld@chem.ucla.edu; chongliu@chem.ucla.edu
bCalifornia NanoSystems Institute (CNSI), University of California, Los Angeles, CA 90095, USA
First published on 5th January 2022
Abstract
Compartmentalization is an attractive approach to enhance catalytic activity by retaining reactive intermediates and mitigating deactivating pathways. Such a concept has been well explored in biochemical and more recently, organometallic catalysis to ensure high reaction turnovers with minimal side reactions. However, the scarcity of theoretical frameworks towards confined organometallic chemistry impedes broader utility for the implementation of compartmentalization. Herein, we report a general kinetic model and offer design guidance for a compartmentalized organometallic catalytic cycle. In comparison to a non-compartmentalized catalysis, compartmentalization is quantitatively shown to prevent the unwanted intermediate deactivation, boost the corresponding reaction efficiency (γ), and subsequently increase catalytic turnover frequency (TOF). The key parameter in the model is the volumetric diffusive conductance (FV) that describes catalysts' diffusion propensity across a compartment's boundary. Optimal values of FV for a specific organometallic chemistry are needed to achieve maximal values of γ and TOF. As illustrated in specific reaction examples, our model suggests that a tailored compartment design, including the use of nanomaterials, is needed to suit a specific organometallic catalytic cycle. This work provides justification and design principles for further exploration into compartmentalizing organometallics to enhance catalytic performance. The conclusions from this work are generally applicable to other catalytic systems that need proper design guidance in confinement and compartmentalization.
Introduction
Compartmentalization has been well documented in biochemical literature as one method for achieving efficient in vivo tandem catalysis by encapsulating enzymes in well-defined micro- and nano-structures.1–7 By controlling the diffusion of species in and out of compartment boundaries, nature is able to retain reactive or toxic intermediates, increase local substrate concentration, and mitigate deactivating or competing pathways.1–7 For example, carboxysome microcompartments enhance the rate of CO2 fixation by encapsulating the cascade of carbonic anhydrase and ribose 1,5-bisphosphate carboxylase/oxygenase to generate high local concentration of CO2 and exclude deactivating O2 within their polyhedral structures.8,9 Also, the last two steps of tryptophan biosynthesis – the conversion of indole-3-glycerol-phosphate to indole and then to tryptophan – take advantage of the substrate-channeling effect bestowed by compartmentalized subunits of tryptophan synthase.10,11 Here, a hydrophobic tunnel between the two subunits retains the indole intermediate, which prevents its free diffusion and participation in deactivating side reactions.10 With billions of years of evolution, compartmentalization appears to be the mainstay of biology to manage the complex network of biochemical reactions that are frequently competing and incompatible with each other in a homogenous solution.The success of natural compartmentalized enzyme cascades inspires the development of bio-mimetic synthetic catalysis with organometallic chemistry being the latest frontier. Multiple groups have employed well-defined spatial organization at the nano- and microscopic levels to construct in vitro biocatalytic and organometallic cascades with enhanced catalytic performance.2,3,12–16 Encapsulating NiFe hydrogenase in virus capsids improves its proteolytic and thermal stability as well as enhances the rate of H2 production.12 Confining a biochemical cascade of β-galactose, glucose oxidase, and horse radish peroxidase in metal–organic frameworks led to an enhancement of reaction yield in comparison to a freely diffusing analogue.13,14 The extent to which reaction yields are enhanced in confined enzyme cascades is reported to correlate with the distance between active sites, suggesting that spatial organization or localization of catalysts is beneficial in tandem or cascade reactions.15 In addition to biocatalysis, recently compartmentalization of organometallic catalysts has been experimentally demonstrated.17–23 For example, our group employed a nanowire-array electrode to pair seemingly incompatible CH4 activation based on O2-sensitive rhodium(II) metalloradical (Rh(II)) with O2-based oxidation for CH3OH formation.17,24 The application of a reducing potential to the nanowire array electrode created a steep O2 gradient within the wire array electrode, such that an anoxic compartment was established at the bottom of the wires. As a result that was not observable for planar electrode without an anoxic region, a catalytic cycle was formed in which the air-sensitive Rh(II) activated CH4 in the O2-free region of the wire array electrode, while CH3OH synthesis proceeded in the aerobic domain with O2 as the terminal electron acceptor. The retainment of the ephemeral Rh(II) intermediate by the nanowire electrode for catalytic CH4-to-CH3OH conversion17,24 encourages us to further explore the design principles of compartmentalizing cascades for higher turnovers with mitigated deactivation pathways.
We envision that a theoretical framework for organometallic catalysis will expand the use of compartmentalization for organometallic chemistry and beyond. In biochemistry, mathematical modeling of confined enzyme cascades has been well developed and offers the design principles in natural systems11,25 and for engineered bio-compartments.11,16,25,26 The models pinpoint a key parameter, volumetric diffusive conductance (FV), which describes the diffusion propensity across a compartment's boundary. FV is determined by a compartment's surface-to-volume ratio and its boundary's permeability.26,27 An optimal value of FV tailored to the specific biochemical reactions are needed in order to achieve better reactivity in comparison to the non-compartmentalized alternative. Similarly, we contend that further development of compartmentalized organometallic chemistry demands a similar quantitative design principle. In a model organometallic cycle that includes oxidative addition (OA), isomerization/migratory insertion (Iso/MI), and reductive elimination (RE) along with undesirable deactivation pathways,28 what are the suitable values of the compartment's physical parameters for minimal deactivation and maximal turnover frequency (TOF) (Fig. 1)? Unfortunately, there has been a paucity of theoretical treatment for this question despite the exciting progresses in experimental demonstration.17–23 Such a lack of theoretical treatment motivates us to establish a general kinetic model and quantitatively investigate how compartmentalization will affect the competing reaction pathways and the corresponding turnover of the desired organometallic catalysis. The successful analysis of compartmentalization in organometallic catalysis, which bears the common features of catalysis in general, will pave the venue to analyze any catalytic cycle with synthetic compartments and confinement.
Here we report a general kinetic model and offer design guidance for a compartmentalized organometallic catalytic cycle. We took advantage of the established theoretical frameworks in biochemistry16,25,26 and applied such kinetic frameworks to a model compartmentalized cycle with competing deactivation pathways (Fig. 1A),28 and a non-compartmentalized counterpart as a control scenario (Fig. 1B). Under assumptions and simplifications applicable to organometallic catalysis, as a proof-of-concept we examined three important metrics of this catalytic cycle in both compartmentalized and non-compartmentalized scenarios: (1) reaction efficiency (γ) that gauges the percentage of intermediates funneled towards desirable catalytic turnover over deactivation pathways; (2) the deactivating rate of intermediate Cat − A(RI); and (3) the turnover frequency (TOF) that measures the steady-state catalytic rate despite intermediate deactivation. When compartments' FV values are smaller than the intrinsic kinetics of the organometallic cycle in question, a compartmentalized system can significantly outperform a homogeneous counterpart with respect to γ and TOF with a lower value of RI. We illustrated the general relationship for specific organometallic catalysis to achieve maximal γ and TOF. We additionally employed the developed model to exemplarily analyze the experimental results and offer guidance of compartmentalization in nanowire-based CH4 activation,17,29 the Fujiwara–Mirotani reaction,30,31 and the Negishi coupling reaction.32,33 The established kinetic model can be adapted to suit a plethora of catalytic cycles with synthetic compartments, offering a framework to be expanded on for advanced compartmentalization of general chemical catalysis.
Results and discussion
Establishing a general kinetic framework of compartmentalization for an organometallic catalytic cycle
Our investigation starts with a hypothetical three-step organometallic cycle confined within a compartment in conjunction with multiple deactivation pathways in the exterior bulk solution (Fig. 1A and ESI Section 1A†).28 Catalytic species Cat of a presumed constant concentration in the bulk ([Cat]b![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CCat) diffuses into the compartment of volume V and bind substrate molecule A through oxidative addition to form intermediate species Cat − A, either pseudo-first-order (m = 1)34–37 or pseudo-second-order (m = 2)24,38,39 with respect to Cat (rate constant k1). After a step of isomerization or migratory insertion (rate constant k2) converts Cat − A species to the product adduct Cat − B, the catalytic cycle is completed by the reductive elimination that transforms Cat − B back to Cat with the release of product B (rate constant k3). Here we presume that Cat, Cat − A and Cat − B intermediates all can diffuse across the compartment boundary and there are two possible competing deactivation pathways in the homogenous solution outside the compartment. The deactivations of Cat − A and Cat − B are presumed pseudo-first-order with respect to the intermediates with rate constants ke2 and ke3, respectively. Similarly, a non-compartmentalized system was constructed for the sake of comparison with the same set of kinetic reaction parameters (Fig. 1B and ESI Section 1B†). The established compartmentalized and non-compartmentalized catalytic cycles are generally applicable to a broad range of organometallic catalysis with concurrent deactivation processes,28,40–42 for which various deactivations have been well reviewed and comprehensively discussed in literature.41
CCat) diffuses into the compartment of volume V and bind substrate molecule A through oxidative addition to form intermediate species Cat − A, either pseudo-first-order (m = 1)34–37 or pseudo-second-order (m = 2)24,38,39 with respect to Cat (rate constant k1). After a step of isomerization or migratory insertion (rate constant k2) converts Cat − A species to the product adduct Cat − B, the catalytic cycle is completed by the reductive elimination that transforms Cat − B back to Cat with the release of product B (rate constant k3). Here we presume that Cat, Cat − A and Cat − B intermediates all can diffuse across the compartment boundary and there are two possible competing deactivation pathways in the homogenous solution outside the compartment. The deactivations of Cat − A and Cat − B are presumed pseudo-first-order with respect to the intermediates with rate constants ke2 and ke3, respectively. Similarly, a non-compartmentalized system was constructed for the sake of comparison with the same set of kinetic reaction parameters (Fig. 1B and ESI Section 1B†). The established compartmentalized and non-compartmentalized catalytic cycles are generally applicable to a broad range of organometallic catalysis with concurrent deactivation processes,28,40–42 for which various deactivations have been well reviewed and comprehensively discussed in literature.41
For the compartmentalized scenario (Fig. 1A), we additionally assign volumetric diffusive conductance (FV) to quantitatively describe the extent of mass transport, predominantly diffusion-based, between the compartment and the surrounding bulk solution (ESI Section 2†). As a measure of molecules' propensities to diffusively cross the compartment's boundary under a given concentration gradient, FV is defined as the product of compartment boundary's permeability (ρ) and its total surface area (SA) while divided by Avogadro's constant (NA) and the volume (V) of the corresponding compartment (Fig. 1A).26 In particular, p is proportional to the species' diffusion coefficients (D) and inversely proportional to the distance of diffusion path across the boundary.43 In our analysis, we assume p remains constant for Cat, Cat − A and Cat − B, given the fact that the catalytic center are frequently more bulky in comparison to the substrate/product, and the catalytic intermediates typically have similar diffusion coefficients despite the reaction-related adducts. We also assume that substrate A and product B are small enough that faster diffusion of A and B leads to minimal concentration gradients for A and B. Such assumption is also applicable to the practical applications when the substrates are used as the solvent in the catalysis that are pertinent to many organic/organometallic reactions. Under such assumptions, a single value of FV for the catalytic intermediates is sufficient to describe the effect of compartmentalization on a catalytic cycle. Because the value of ρ depends on the compartment's physical properties, the design of compartment's surface-to-volume ratio (SA/V) and materials' properties at the compartment's boundary has significant impacts on the value of FV, and subsequently the overall catalytic turnover as will be discussed in this study.
In this work we aim to study the steady-state phenomena of compartmentalized catalysis. We assume constant, time-independent concentrations of Cat, Cat − A and Cat − B in both the compartment ([Cat], [Cat − A], and [Cat − B], respectively) as well as the surrounding bulk solution ([Cat]b![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CCat (vide supra), [Cat − A]b and [Cat − B]b, respectively). Similarly, in the bulk solution substrate A is maintained at a constant concentration (CA) and fast removal of product B is ensured ([B] → 0). Such assumptions including [Cat]b
CCat (vide supra), [Cat − A]b and [Cat − B]b, respectively). Similarly, in the bulk solution substrate A is maintained at a constant concentration (CA) and fast removal of product B is ensured ([B] → 0). Such assumptions including [Cat]b![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CCat pertain to a flow reactor with sufficient amount of catalysts or a batch reaction under high catalyst loading and low conversion (ESI Section 1†). Alternatively, a constant total catalyst concentration including all catalytic species in the bulk can be presumed (CCat,total
CCat pertain to a flow reactor with sufficient amount of catalysts or a batch reaction under high catalyst loading and low conversion (ESI Section 1†). Alternatively, a constant total catalyst concentration including all catalytic species in the bulk can be presumed (CCat,total![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) [Cat]b + [Cat − A]b + [Cat − B]b = constant), ESI Section 3†). We have analyzed the catalysis under both sets of assumptions. We note that the latter set of assumptions with a constant total catalyst concentration, more complicated to solve mathematically and labeled as “model CCat,total” in ESI Section 3,† leads to similar conclusions and reinforces the general applicability of the following results solved when we assume [Cat]b
[Cat]b + [Cat − A]b + [Cat − B]b = constant), ESI Section 3†). We have analyzed the catalysis under both sets of assumptions. We note that the latter set of assumptions with a constant total catalyst concentration, more complicated to solve mathematically and labeled as “model CCat,total” in ESI Section 3,† leads to similar conclusions and reinforces the general applicability of the following results solved when we assume [Cat]b![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Ccat. Unless noted specifically, the results discussed below will be based on the former set of assumptions (ESI Section 1†).
Ccat. Unless noted specifically, the results discussed below will be based on the former set of assumptions (ESI Section 1†).
A set of steady-state kinetic equations are constructed to reflect both the compartmentalized and non-compartmentalized scenarios (eqn (S1)–(S5) and (S67)–(S69)†) for an organometallic catalytic cycle following the analysis protocols established in biochemistry.26 Comparing to the non-compartmentalized case that only includes reactions in the homogenous solution (eqn (S67)–(S69)†), the equations for the compartmentalized case (eqn (S1)–(S5)†) additionally consider the reactions in the compartment as well as the mass transport across the boundary, whose magnitudes are governed by both the value of FV and the concentration gradients across the compartment's boundary. Detailed mathematical treatment of the established equations can be found in ESI Section 1† and a few key outputs of the model are evaluated here. As one of the proposed benefits of compartmentalization is the capability of retaining reactive intermediates within the compartment without significant catalyst deactivation in the bulk,2,3,14,16 we are interested in evaluating the steady-state consumption rate of substrate A (RS), the generation rate of product B (RP), and the deactivation rate of intermediates Cat − A (RI) (Fig. 1A). Moreover, in both compartmentalized and non-compartmentalized scenarios, we aim to analyze the rate of reaction, numerically represented as turnover frequency TOF, and the efficacy of transforming the substrate A into targeted product B, numerically represented as reaction efficiency γ that is defined as the percentage of intermediates funneled towards desirable catalytic turnover.16,26 In both cases, γ is calculated as the ratio between the formation rate of product B and the consumption rate of substrate A. In the case of pseudo-first-order kinetics towards Cat in oxidative addition (m = 1), γ, RI,m=1, and TOFm=1 in a compartmentalized system can be expressed as,
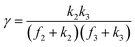 | (1) |
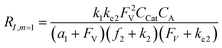 | (2) |
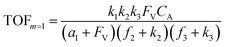 | (3) |
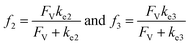 | (4) |
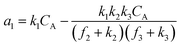 | (5) |
In comparison under a non-compartmentalized scenario, the corresponding γ′, 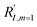 , and
, and 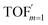 are expressed as,
are expressed as,
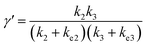 | (6) |
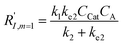 | (7) |
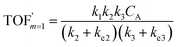 | (8) |
The mathematical expressions for γ, RI, and TOF results, derived from ESI Sections 1 and 3† for the assumptions outlined in the main text and for model CCat,total respectively, are summarized in Tables S1 and S2† as a reference. The successful construction and mathematical derivation of a general kinetic model in organometallic catalysis warrants quantitative evaluation about the efficacy of compartmentalization under different reaction kinetics and compartment properties.
Exemplary numerical comparisons between compartmentalized and non-compartmentalized catalysis
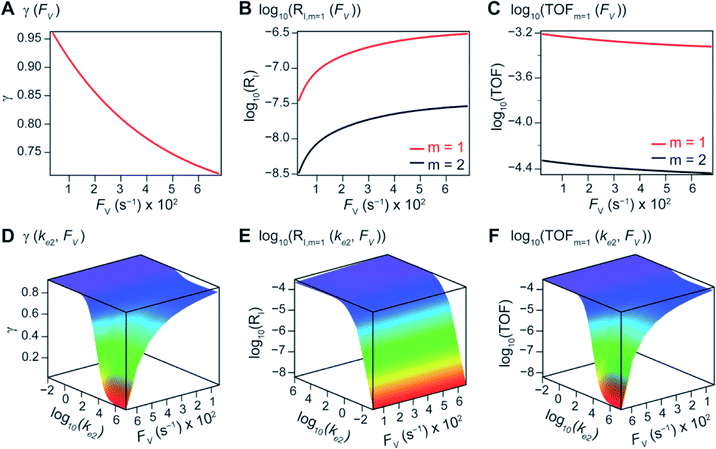
The derived analytical solutions to the established kinetic model allow us to numerically calculate the values of γ, RI, and TOF in both compartmentalized and non-compartmentalized scenarios. Specifically, we set out to evaluate under what conditions compartmentalization is beneficial with a given set of parameters pertaining to the compartment's properties and kinetics of organometallic reactions. As an introductory example representative to a typical organometallic catalytic cycle, we assume that CCat = 1 mM and CA = 10 mM, as organometallic catalytic systems often operate near 10 mol% catalyst loading.40 Values of kinetic parameters are k1 ∈ [10−5, 104] M−1 s−1 (m = 1) (ref. 34, 35, 36 and 37) or k1 ∈ [10−3, 106] M−2 s−1 (m = 2);17,24,38,39k2 ∈ [10−3, 106] s−1(ref. 44 and 45) and k3 = 106 s−1.46,47 When either k1 or k2 is not a variable of interest, they are set as k1 = 0.1 M−1 s−1 (m = 1) or 10 M−2 s−1 (m = 2) and k2 = 1 × 103 s−1.34–37 The selection of those kinetic parameters is based on reviews of oxidative addition and migratory insertion, as well as reported kinetic studies using techniques such as time resolved infrared spectroscopy for transient species on the intermediates during carbonylation and O2 reduction and transfer, among others.17,24,34–39,44,45 The selection of k3 parameter value implicitly assumes fast reductive elimination from Cat − B, which is supported by the observation that reductive eliminations are often not the rate-determining step in a catalytic cycle.46,47 The values of deactivation kinetics ke2 for Cat − A and ke3 for Cat − B are selected with additional assumptions, given the dearth of reported kinetic values for the less exciting deactivation steps. As the reductive elimination from Cat − B is sufficiently fast, our primary focus is to examine the deactivation from Cat − A hence how the comparison between k2 and ke2 will affect the overall catalysis. Subsequently we assign ke3 = k3 = 1 × 106 s−1 so that the rate of competing deactivation from Cat − B is no lower than rate of reductive elimination. Similarly, when ke2 is not a variable of interest, we set ke2 = k2 = 1 × 103 s−1 to match the kinetics of isomerization/migratory insertion. Last, we set FV ∈ [30, 600] s−1, whose range is estimated based on the diffusion coefficient of 9 × 10−10 m2 s−1 from tabulated organometallic catalysts,48,49 as well as the geometry and properties of reported microscopic compartments in porous materials, supramolecular assemblies, nanoscopic micelles, and the use of nanowire array electrode in our previous work (see ESI Section 2†).17–20,29,50,51 Overall, our selection of kinetic values here represents an organometallic catalytic cycle whose oxidative addition step is turnover-limiting and the deactivation of yielded Cat − A intermediate is the most critical issue, while the fast reductive elimination leaves the deactivation of Cat − B species secondary in terms of γ and TOF. With varying values of FV and changing ratios between the values of k2 and ke2, the trend of compartmentalization's efficacy can be unveiled.The numerically calculated values of γ, RI, and TOF as a function of k2 and FV illustrate that compartmentalization generally outperforms the non-compartmentalized scenarios with a higher tolerance towards undesirable deactivation reactions (Fig. 2). Under a fixed rate constant of deactivation (ke2 = 1 × 103 s−1) and pseudo-first-order oxidative addition (k1 = 0.1 M−1 s−1 for m = 1), values of γ, RI, and TOF in a compartmentalized system are plotted as a function of both k2 and FV in Fig. 2A–C. The rate of isomerization/migratory insertion (k2) is understandably a predominant factor in all three plots. When k2 is much smaller than the rate of deactivation (ke2), γ approaches zero (Fig. 2A) when the deactivation of Cat − A outcompetes the step of isomerization/migratory insertion, which is concurrent with a higher rate of deactivation (RI in Fig. 2B) and lower TOF value (Fig. 2C). Alternatively, when k2 is much larger than ke2 and the deactivation step is less relevant, γ plateaus towards unity with concomitant increase in TOF (Fig. 2A and C). Despite the dominant role of k2, whether or not the system is compartmentalized strongly affects the values of γ, RI, and TOF (Fig. 2D–F). While the trend is generally applicable for all values of FV, a specific case (FV = 320 s−1) that corresponds to the nanowire array electrode for CH4-to-CH3OH conversion in our previous work,17 illustrates under which situation the advantages of compartmentalization will be observed. As the value of k2 increases, the compartmentalized scenario observes an increase of reaction efficiency γ in a sigmoidal fashion when k2 approaches the value of FV (red trace in Fig. 2D); in contrast, γ in a non-compartmentalized case (black trace in Fig. 2D) won't increase until k2 approaches the value of ke2. Similarly, with FV ≪ ke2 and under a reasonably large value of k2, compartmentalization suppresses the rate of deactivation RI (Fig. 2E) and increases the TOF by roughly no less than one order of magnitude (Fig. 2F). Evaluations assuming pseudo-second-order kinetics towards Cat in the step of oxidative addition (m = 2) lead to the same conclusion (Fig. S3A and S4A†). Those observations suggest that the strategy of compartmentalization allows a catalytic cycle to be much more tolerant towards undesirable side reactions, as long as FV is much smaller than ke2 (FV ≪ ke2) with a judicious compartment design.
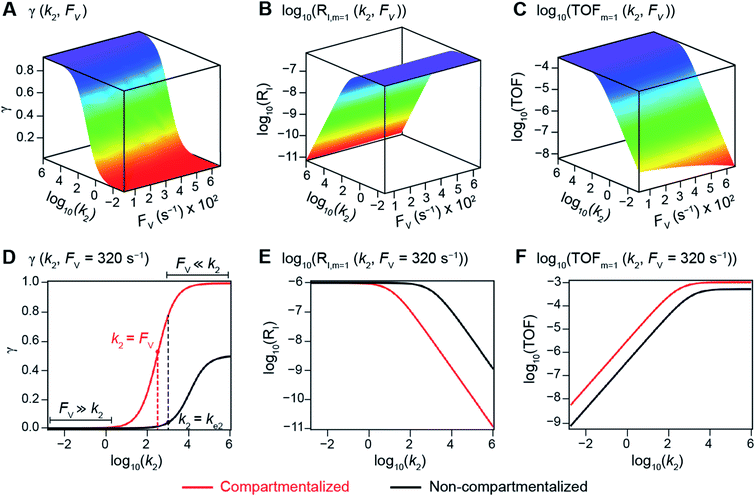 | ||
| Fig. 2 Reaction efficiency (γ, A and D), logarithmic of intermediate outflux rate (log10(RI), B and E), and logarithmic of turnover frequency (log10(TOF), C and F) as a function of volumetric diffusive conductance (FV) and logarithmic of the rate constant for isomerization or migratory insertion (Iso/MI) (log10(k2)). A to C, compartmentalized scenario depicted in Fig. 1A. D to F, comparisons between compartmentalized (red trace, when FV = 320 s−1) and non-compartmentalized (black trace) scenarios. m = 1, k1 = 0.1 M−1 s−1 notwithstanding A and D, ke2 = 1 × 103 s−1), k3 = ke3 = 1 × 106 s−1. The selection of those exemplary values is based on literature reports on the kinetics of relevant organometallic systems (vide supra). | ||
Additional examination suggests that a less “leaky” compartment, or one less prone to diffusive loss of intermediate, with smaller FV value should be more effective than one with a relatively larger FV. Here the extent of leakiness is relevant to the reactions of interests and a “leaky” compartment is defined as one whose FV is much larger than the one of k2 (FV ≫ k2), with about one or two orders of magnitude of difference (a factor of 10 to 100) as shown in Fig. 2D, because the difference of γ values between compartmentalization and non-compartmentalization is the biggest when FV < k2 ≪ ke2. Such a trend is more apparent when γ, RI, and TOF were plotted as a function of FV under fixed values of k2 and ke2 (Fig. 3A–C). In both situations when m = 1 and m = 2, a larger value of FV leads to smaller values of γ and TOF and large value of RI. This suggests that a more “leaky” compartment is not sufficient to conserve the yielded intermediates and is more prone to deactivation than one with a small FV. A similar conclusion can be obtained when investigating the dependence of γ, RI, and TOF as a function of FV and ke2 (Fig. 3D–F, S3B and S4B†). Significant decrease of γ and increase of RI was observed at high FV values, particularly when the values of ke2 are so large that the deactivation is much faster than the isomerization/migratory insertion step and intermediate Cat − A has a much shorter life time once it diffuses out of the compartment.
The above noted observations can be mathematically rationalized from our derived equations. When the value of FV is similar to or even larger than ke2 or ke3 (FV ≳ ke2 or ke3),
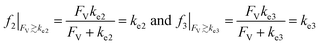 | (9) |
This will lead to γ ≈ γ′, i.e. the reaction efficiency is not significantly altered with compartmentalization in comparison to the non-compartmentalized case.
Alternatively, when FV ≪ ke2 or ke3, we have
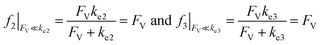 | (10) |
This leads to
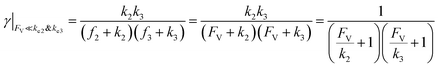 | (11) |
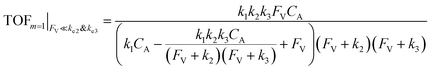 | (12) |
The equations noted above suggest that optimal, near-unity reaction efficiency γ, high TOF, and low RI values would be obtained when FV ≪ k2 and k3, which is consistent with our observations in Fig. 2. Under our above-stated assumption that isomerization/migratory insertion is the turnover-limiting step (k2 ≪ k3), γ = 0.9 and 0.99 when FV/k2 = 0.11 and 0.01, respectively. The corresponding expression of TOF can be simplified as,
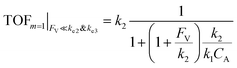 | (13) |
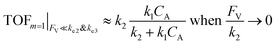 | (14) |
The monotonic yet asymptotic increase of TOF values suggests that maximal TOF will be achieved when FV/k2 → 0.
Lastly, when a constant total catalyst concentration including all catalytic species in the bulk is presumed (“modelCCat,total”, CCat,total![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) [Cat]b + [Cat − A]b + [Cat − B]b = constant, ESI Section 3†), the calculated values of RI and TOF as functions of FV and k2 displayed little difference to the above-mentioned observations (Fig. S5–S7†), while the derived expressions of γ are identical under both assumptions (Tables S1 and S2†). Such observations suggest that slight variation in the assumptions of the developed model does not significantly alter how the compartment's FV impacts the kinetics of overall catalysis.
[Cat]b + [Cat − A]b + [Cat − B]b = constant, ESI Section 3†), the calculated values of RI and TOF as functions of FV and k2 displayed little difference to the above-mentioned observations (Fig. S5–S7†), while the derived expressions of γ are identical under both assumptions (Tables S1 and S2†). Such observations suggest that slight variation in the assumptions of the developed model does not significantly alter how the compartment's FV impacts the kinetics of overall catalysis.
Implication on the design of compartmentalized catalysis
The established kinetic model and the numerical evaluation offers an affirmative answer to the efficacy of compartmentalized organometallic catalysis and, if needed, what is the desired properties of the established compartment. When the rate constants of the steps in the catalytic cycle (k2 and k3) are commensurate with or greater than the rate constants of deactivation steps (ke2 and ke3), i.e. k2 ≳ ke2 and k3 ≳ ke3, compartmentalization is not necessary since the intrinsic reactivity of catalysis is sufficiently fast with respect to undesirable side reactions. Compartmentalization should be considered under k2 < ke2 and k3 < ke3, when the intrinsic reactivities of the catalytic cycle cannot outcompete the deactivation pathways. The efficacy of compartmentalization will be observable, as long as the compartment's volumetric diffusive conductance FV is much smaller than ke2 or ke3 (FV ≪ ke2 or ke3). Nonetheless, one interesting conclusion from our analysis is that maximal efficacy of compartmentalization (reaction efficiency γ → 1) demands FV to be smaller not only than the rate constants of deactivation steps (ke2 and ke3) but also than the rate constants of steps in the catalytic cycle (k2 and k3). This requirement for maximal γ stems from the fact that a “leaky” compartment with large FV is not sufficient to conserve the yielded intermediates and is prone to deactivation. Practically, such a requirement is indeed a blessing for organometallic chemistry. As typical organometallic studies do not commonly characterize the deactivating side reactions, there lacks detailed kinetic information the values of ke2 or ke3 in comparison to the knowledge about catalytic kinetics (k2 and k3). Because we posit that criteria of FV < k2 and FV < k3 are sufficient for a compartment to “revive” a catalytic cycle unfunctional in a homogenous solution, kinetic information of the in-cycle steps (k2 and k3) is sufficient for future design of functional compartmentalization.The feasibility of obtaining the range of FV from the kinetics of the proposed catalytic cycle offers more guidance for the materials design for the compartment. As FV is proportional to the compartment boundary's permeability (ρ) and its surface-to-volume ratio (SA/V),26 multiple synthetic handles could be applied to achieve a desirable FV value. A less permeable interface at the boundary of compartment as well as smaller surface-to-volume ratio will help to reduce the mass transport hence the value of FV. Characterization techniques that help determine encapsulation geometry and assess permeability, such as electron microscopies and chromatographic methods, should be welcomed for more detailed mechanistic investigations in experimental demonstration.52–55 One interesting result from this argument is that a compartment of extremely small dimension, for example of nanoscopic scale, may not be necessarily beneficial, because nanoscopic dimensions with their large surface-to-volume ratio may create a “leaky” compartment. Here we set FV ≫ k2 as the criterion for a “leaky” compartment that poorly retains intermediates (vide supra), when there is minimal difference in reaction efficiency γ between a compartmentalized and non-compartmentalized system (Fig. 2D). As FV is calculated by a compartment's surface-to-volume ratio (SA/V), its boundary's permeability (ρ), and the Avogadro's constant (NA),26 a “leaky” compartment for a specific catalysis satisfies the following equations,
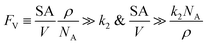 | (15) |
Provided a compartment's surface-to-volume ratio (SA/V) or chemicals' permeability across the compartment's boundary (ρ) is sufficiently large, our model predicts that compartmentalization will not be beneficial. In addition, the opposite inequality may be used to design optimal compartmentalized catalysis (FV ≪ k2). Careful compartment design tailored to the specific kinetics of the catalytic cycle is recommended before experimental implementation.
The developed model remains generally applicable in the presence of mass transport heterogeneity in the compartment. As a first-order approximation, a mean-field average diffusion coefficient D is sufficient to describe the permeation of molecules through a compartment at ensemble level as long as the compartment's porosity is isotropic, based on single-molecule studies of molecular diffusion in mesoporous silica and polymer films.56,57 In the presence of anisotropicity such as highly aligned pores or in our previous work's nanowire arrays,17,29 a mean-field averaged diffusion coefficient D is still good enough to account for the diffusion phenomena in the specific direction.58,59 In cases where anisotropic diffusion exists, the values of anisotropic ρ normal to the compartment's boundary should be used when calculating FV. Moreover, in scenarios in where drastically heterogenous D values are apparent inside a single compartment, an effective value of ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) V will be derived base on the volume-weighted average of FV across the whole compartment, similar to the studies in metabolic microcompartments.25 The order of magnitudes of the derived
V will be derived base on the volume-weighted average of FV across the whole compartment, similar to the studies in metabolic microcompartments.25 The order of magnitudes of the derived ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) V will be sufficient for the initial design of the compartmentalized catalysis, before further optimizations and detailed analysis proceed. Despite such additional mathematical treatment, how the FV values are determined does not affect the validity and applicability of our development model in designing compartments.
V will be sufficient for the initial design of the compartmentalized catalysis, before further optimizations and detailed analysis proceed. Despite such additional mathematical treatment, how the FV values are determined does not affect the validity and applicability of our development model in designing compartments.
We caution that our established model only considers the mass transport of catalysts and assumes an unconditionally fast supply of substrate A and quick removal of product B. While such assumptions have their real-life correspondence under certain circumstances (vide supra), the currently established model is incapable of accounting for the possible mass-transport limitation for the substrate and product, which could be induced by a small FV value recommended by the model presented here. Given that, we cautioned that a lower bound of FV exists for optimal performance in practical applications, and an unnecessarily small value of FV could be detrimental to the compartment design. This argument is corroborated by our prior work that utilizes nanowire array electrode to pair CH4 activation from O2-sensitive metalloporphyrin with CH3OH generation with O2 as the terminal oxidant.17,29 An increase of the nanowire array's length, corresponding to a smaller value of FV (ESI Section 2†), was experimentally observed to yield an increased rate of CH4 activation until the reaction rate plateaued for nanowire arrays of 27 μm length.17,29 Such experimental results illustrate the presence of a lower bound of FV for optimal performance, when the mass transport of substrate CH4 is probably limited due to the increased length of the nanowire array.
Examples to illustrate the utility of the developed model
We employed our model and analyzed the benefits of compartmentalizing the Fujiwara–Moritani reaction, which is a Pd-catalyzed oxidative C–C coupling reactions.30,31 In such a catalysis, stoichiometric oxidant is needed to regenerate the catalytically active Pd(II) species,30,31 yet the presence of spent oxidant can inhibit the reaction and result in mediocre yields.31,60 Therefore, one possible strategy of reconciling such an incompatibility is to compartmentalize the Pd-based catalysts. Based on the available kinetic data reported in literature,60 we translated our generally applicable model into the Fujiwara–Moritani reaction (Fig. S8†) and established the mathematical relationship that correlates volumetric diffusive conductance (FV) with reaction efficiency (γ), the rate of catalyst deactivation (RI), and turnover frequency (TOF) (ESI Section 4†). We compared the values of γ, RI, and TOF between the compartmentalized and non-compartmentalized cases. While the homogenous non-compartmentalized scenario yields γ ∼ 10−2 and RI ∼ 10−5 s−1, our model predicts that at FV ∼ 10−5 s−1, about 100 times smaller than the kinetic constant k2 for the turnover-limiting step,60 compartmentalization significantly decreases the rate of deactivation (RI = 2 × 10−11 s−1) and increase the reaction efficiency (γ = 0.99). Indeed, a recent experimental demonstration of compartmentalized Fujiwara–Moritani reaction with a “tube-in-tube” design is consistent with our model's prediction.61 As the minimally permeable tube-in-tube reactor is estimated to possess FV ∼ 10−28 s−1 that well surpasses the criterion FV ≪ k2 (vide supra), our model predicts little catalyst deactivation and high reaction efficiency (γ ∼ 1 and RI ∼ 1031 s−1). Indeed, our predictions are consistent with the experimental observations61 and illustrate the utility of our model.In another example, we analyzed the Negishi coupling reaction32 and concluded that compartmentalization of this reaction may have marginal benefits in the context of mitigating side reactions. In such a reaction, Ni or Pd catalysts enable the cross-coupling reactions between organic halides and organozinc, organoaluminum, or organozirconium compounds.32,33 Detailed kinetic information is available for the coupling between an aryl iodide compound with an aliphatic zinc chloride33 and we similarly established the kinetic model (Fig. S9 and ESI Section 5†). We found that in the non-compartmentalized scenario, γ is close to unity already (γ ∼ 1) because the deactivation steps (ke2 and ke3 ∼ 2 × 10−3 s−1) are slow in comparison to the steps in the catalytic cycle (k1 and k2 ∼ 1–10 M−1 s−1; k3 ∼ 0.5 s−1). This suggests that the benefits of compartmentalizing the Negishi coupling reaction will not be significant in the context of mitigating side reactions and boost reaction efficiency. Indeed, the model predicts that compartmentalization may even lower the TOF in comparison to the non-compartmentalized case, since the benefits of preventing already negligible side reactions is outweighed by the mass transport of catalyst. Overall, the developed model represents a viable tool to pick the catalytic reactions that are suitable for the study of compartmentalization.
Conclusion
In this study, we developed a general kinetic framework for compartmentalizing organometallic catalysis with competing deactivation reactions in the bulk solution. Compartmentalization is only necessary under k2 < ke2 and k3 < ke3, when the intrinsic reactivities of the catalytic cycle cannot outcompete the deactivation pathways. Under such situations, the kinetic model predicts that careful compartment design with suitable values of volumetric diffusive conductance (FV ≪ k2 and FV ≪ k3 of at least one or two orders of magnitude difference) is capable of achieving maximal reaction efficiency (γ) and turnover frequency (TOF). Under our stated assumption that isomerization/migratory insertion is the turnover-limiting step (k2 ≪ k3), the criterion of minimal deactivation and maximal TOF is equivalent to FV/k2 = 0.11 and 0.01 for γ = 0.9 and 0.99, respectively, in order for the established compartment to minimize intermediate elimination and maximize catalysis. It is intriguing that the kinetics of deactivation steps are not needed for the design of compartment, as long as it is known that k2 < ke2 and k3 < ke3. As discussed with the examples of nanowire-based CH4 activation,17,29 Fujiwara–Mirotani reaction,30,31 and the Negishi coupling reaction,32,33 a tailored compartment design, including the use of nanomaterials, is needed to suit a specific organometallic catalysis. Such insights will assist in future a priori design of compartmentalized organometallics for enhanced catalytic performance. Moreover, the developed quantitative model is applicable to any general catalytic cycle particularly in the liquid phase, because the model includes the general features of any catalysis: multiple reaction steps connected in a cyclic fashion: the existence of turnover-limiting step, the interference from deactivation/competing reactions, and the issue of mass transport in the proximity of active sites. The conclusions and design principles obtained from the reported model is adaptable to suit most if not any catalytic cycles with synthetic compartments and confinements, offering a framework to be expanded on for advanced compartmentalization of general chemical catalysis.Author contributions
C. L. supervised the project. B. J. J. performed the mathematical derivations for the theoretical framework. N. H. C., A. R. D., and P. L. D. contributed to discussion about the Fujiwara–Mirotani and Negishi reactions. All authors discussed the results and assisted during the manuscript preparation.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We thank support by NSF as part of the Center for Integrated Catalysis (CHE-2023955). C. L. acknowledges the startup fund from the University of California, Los Angeles, and the financial support of the Jeffery and Helo Zink Endowed Professional Development Term Chair.References
- S. Hurtley, Science, 2009, 326, 1205 CrossRef CAS PubMed.
- A. H. Chen and P. A. Silver, Trends Cell Biol., 2012, 22, 662–670 CrossRef CAS.
- U. Jandt, C. You, Y. H. P. Zhang and A. P. Zeng, Adv. Biochem. Eng./Biotechnol., 2013, 137, 41–65 CrossRef CAS.
- A. Zecchin, P. C. Stapor, J. Goveia and P. Carmeliet, Curr. Opin. Biotechnol., 2015, 34, 73–81 CrossRef CAS PubMed.
- J. L. Avalos, G. R. Fink and G. Stephanopoulos, Nat. Biotechnol., 2013, 31, 335–341 CrossRef CAS PubMed.
- B. P. Tu, Science, 2005, 310, 1152–1158 CrossRef CAS PubMed.
- M. T. Alam, V. Olin-Sandoval, A. Stincone, M. A. Keller, A. Zelezniak, B. F. Luisi and M. Ralser, Nat. Commun., 2017, 8, 16018 CrossRef CAS PubMed.
- G. C. Cannon, C. E. Bradburne, H. C. Aldrich, S. H. Baker, S. Heinhorst and J. M. Shively, Appl. Environ. Microbiol., 2001, 67, 5351–5361 CrossRef CAS PubMed.
- B. D. Rae, B. M. Long, L. F. Whitehead, B. Förster, M. R. Badger and G. D. Price, J. Mol. Microbiol. Biotechnol., 2013, 23, 300–307 CrossRef CAS PubMed.
- K. S. Anderson, E. W. Miles and K. A. Johnson, J. Biol. Chem., 1991, 266, 8020–8033 CrossRef CAS.
- K. S. Chavan and S. Calabrese Barton, J. Phys. Chem. C, 2018, 122, 14474–14480 CrossRef CAS.
- P. C. Jordan, D. P. Patterson, K. N. Saboda, E. J. Edwards, H. M. Miettinen, G. Basu, M. C. Thielges and T. Douglas, Nat. Chem., 2016, 8, 179–185 CrossRef CAS PubMed.
- W.-H. Chen, M. Vázquez-González, A. Zoabi, R. Abu-Reziq and I. Willner, Nat. Catal., 2018, 1, 689–695 CrossRef CAS.
- M. Vázquez-González, C. Wang and I. Willner, Nat. Catal., 2020, 3, 256–273 CrossRef.
- O. Idan and H. Hess, ACS Nano, 2013, 7, 8658–8665 CrossRef CAS PubMed.
- Y. Zhang and H. Hess, ACS Catal., 2017, 7, 6018–6027 CrossRef CAS.
- B. S. Natinsky, S. Lu, E. D. Copeland, J. C. Quintana and C. Liu, ACS Cent. Sci., 2019, 5, 1584–1590 CrossRef CAS.
- S. H. A. M. Leenders, R. Gramage-Doria, B. De Bruin and J. N. H. Reek, Chem. Soc. Rev., 2015, 44, 433–448 RSC.
- J. Lu, J. Dimroth and M. Weck, J. Am. Chem. Soc., 2015, 137, 12984–12989 CrossRef CAS.
- T. M. Rayder, A. T. Bensalah, B. Li, J. A. Byers and C.-K. Tsung, J. Am. Chem. Soc., 2021, 143, 1630–1640 CrossRef CAS PubMed.
- R. W. Simms and M. F. Cunningham, Macromolecules, 2008, 41, 5148–5155 CrossRef CAS.
- N. M. B. Smeets, J. P. A. Heuts, J. Meuldijk, M. F. Cunningham and A. M. Van Herk, Macromolecules, 2009, 42, 7332–7341 CrossRef CAS.
- K. Wang, J. H. Jordan, X. Y. Hu and L. Wang, Angew. Chem., Int. Ed., 2020, 59, 13712–13721 CrossRef CAS PubMed.
- B. B. Wayland, S. Ba and A. E. Sherry, J. Am. Chem. Soc., 1991, 113, 5305–5311 CrossRef CAS.
- F. Hinzpeter, U. Gerland and F. Tostevin, Biophys. J., 2017, 112, 767–779 CrossRef CAS PubMed.
- S. Tsitkov and H. Hess, ACS Catal., 2019, 9, 2432–2439 CrossRef CAS.
- H. C. Berg, Random Walks in Biology, Princeton University Press, 1993 Search PubMed.
- G. Miessler and D. Tarr, Inorganic Chemistry, Upper Saddle River, NJ, Pearson Education Inc., 2004 Search PubMed.
- B. S. Natinsky, B. J. Jolly, D. M. Dumas and C. Liu, Chem. Sci., 2021, 12, 1818–1825 RSC.
- I. Moritani and Y. Fujiwara, Tetrahedron Lett., 1967, 8, 1119–1122 CrossRef.
- Y. Fujiwara, I. Moritani, S. Danno, R. Asano and S. Teranishi, J. Am. Chem. Soc., 1969, 91, 7166–7169 CrossRef CAS PubMed.
- E. Negishi, A. O. King and N. Okukado, J. Org. Chem., 1977, 42, 1821–1823 CrossRef CAS.
- H. Zhang, X. Luo, K. Wongkhan, H. Duan, Q. Li, L. Zhu, J. Wang, A. S. Batsanov, J. A. Howard and T. B. Marder, Chem.–Eur. J., 2009, 15, 3823–3829 CrossRef CAS.
- J. A. Labinger, Organometallics, 2015, 34, 4784–4795 CrossRef CAS.
- K. L. Breno, M. D. Pluth, C. W. Landorf and D. R. Tyler, Organometallics, 2004, 23, 1738–1746 CrossRef CAS.
- P. R. Ellis, J. M. Pearson, A. Haynes, H. Adams, N. A. Bailey and P. M. Maitlis, Organometallics, 1994, 13, 3215–3226 CrossRef CAS.
- J. H. Espenson, O. Pestovsky, P. Huston and S. Staudt, J. Am. Chem. Soc., 1994, 116, 2869–2877 CrossRef CAS.
- T. D. Ju, R. F. Lang, G. C. Roper and C. D. Hoff, J. Am. Chem. Soc., 1996, 118, 5328–5329 CrossRef CAS.
- Z. M. Heiden and T. B. Rauchfuss, J. Am. Chem. Soc., 2007, 129, 14303–14310 CrossRef CAS.
- D. Astruc, Organometallic chemistry and catalysis, Springer, 2007 Search PubMed.
- R. H. Crabtree, Chem. Rev., 2015, 115, 127–150 CrossRef CAS.
- A. Meißner, E. Alberico, H.-J. Drexler, W. Baumann and D. Heller, Catal. Sci. Technol., 2014, 4, 3409–3425 RSC.
- W. Stein, Transport and diffusion across cell membranes, Elsevier Inc., 1986 Search PubMed.
- P. C. Ford and S. Massick, Coord. Chem. Rev., 2002, 226, 39–49 CrossRef CAS.
- S. M. Massick and P. C. Ford, Organometallics, 1999, 18, 4362–4366 CrossRef CAS.
- P. Nilsson and O. F. Wendt, J. Organomet. Chem., 2005, 690, 4197–4202 CrossRef CAS.
- L. Jin, H. Zhang, P. Li, J. R. Sowa Jr and A. Lei, J. Am. Chem. Soc., 2009, 131, 9892–9893 CrossRef CAS PubMed.
- P. S. Pregosin, P. G. A. Kumar and I. Fernández, Chem. Rev., 2005, 105, 2977–2998 CrossRef CAS PubMed.
- D. Drago, P. S. Pregosin and A. Pfaltz, Chem. Commun., 2002, 286–287 RSC.
- T. A. Bender, M. Morimoto, R. G. Bergman, K. N. Raymond and F. D. Toste, J. Am. Chem. Soc., 2019, 141, 1701–1706 CrossRef CAS.
- P. Qu, M. Kuepfert, M. Hashmi and M. Weck, J. Am. Chem. Soc., 2021, 143, 4705–4713 CrossRef CAS PubMed.
- C. Huang, C. Liu, X. Chen, Z. Xue, K. Liu, X. Qiao, X. Li, Z. Lu, L. Zhang, Z. Lin and T. Wang, Adv. Sci., 2020, 7, 1903180 CrossRef CAS PubMed.
- W. Li, Y. Zhang, Z. Xu, Q. Meng, Z. Fan, S. Ye and G. Zhang, Angew. Chem., Int. Ed., 2016, 55, 955–959 CrossRef CAS PubMed.
- L. Lei, Q. Zhang, S. Shi and S. Zhu, Langmuir, 2017, 33, 6108–6115 CrossRef CAS PubMed.
- E. Haldoupis, T. Watanabe, S. Nair and D. S. Sholl, ChemPhysChem, 2012, 13, 3449–3452 CrossRef CAS PubMed.
- B. Dong, N. Mansour, T. X. Huang, W. Huang and N. Fang, Chem. Soc. Rev., 2021, 50, 6483–6506 RSC.
- B. Dong, Y. Pei, F. Zhao, T. W. Goh, Z. Qi, C. Xiao, K. Chen, W. Huang and N. Fang, Nat. Catal., 2018, 1, 135–150 CrossRef.
- C. Jung, J. Kirstein, B. Platschek, T. Bein, M. Budde, I. Frank, K. Müllen, J. Michaelis and C. Bräuchle, J. Am. Chem. Soc., 2008, 130, 1638–1648 CrossRef CAS PubMed.
- F. Feil, V. Cauda, T. Bein and C. Bräuchle, Nano Lett., 2012, 12, 1354–1361 CrossRef CAS PubMed.
- C. J. Mulligan, J. S. Parker and K. K. Hii, React. Chem. Eng., 2020, 5, 1104–1111 RSC.
- F. Ferlin, I. Anastasiou, L. Carpisassi and L. Vaccaro, Green Chem., 2021, 23, 6576–6582 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Mathematical derivation of general compartmentalized, general non-compartmentalized Fujiwara–Mirotani reaction, and Negishi reaction kinetic models, tables of solutions to key reaction metrics, and additional figures. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc04983f |
| This journal is © The Royal Society of Chemistry 2022 |