Open Access Article
Open Access ArticleLow-entropy lattices engineered through bridged DNA origami frames†
Di
Gao
a,
Ningning
Ma
a,
Xuehui
Yan
a,
Min
Ji
a,
Jun-Jie
Zhu
 *a,
Qianhao
Min
*a,
Qianhao
Min
 *a and
Ye
Tian
*a and
Ye
Tian
 *ab
*ab
aState Key Laboratory of Analytical Chemistry for Life Science, School of Chemistry and Chemical Engineering, College of Engineering and Applied Sciences, Nanjing University, Nanjing 210023, China. E-mail: ytian@nju.edu.cn; minqianhao@nju.edu.cn; jjzhu@nju.edu.cn
bShenzhen Research Institute of Nanjing University, Shenzhen 518000, China
First published on 8th December 2021
Abstract
The transformation from disorder to order in self-assembly is an autonomous entropy-decreasing process. The spatial organization of nanoscale anisotropic building blocks involves the intrinsic heterogeneity in three dimensions and requires sufficiently precise control to coordinate intricate interactions. Only a few approaches have been shown to achieve the anisotropic extension from components to assemblies. Here, we demonstrate the ability to engineer three-dimensional low-entropy lattices at the nucleotide level from modular DNA origami frames. Through the programmable DNA bridging strategy, DNA domains of the same composition are periodically arranged in the crystal growth directions. We combine the site-specific positioning of guest nanoparticles to reflect the anisotropy control, which is validated by small-angle X-ray scattering and electron microscopy. We expect that our DNA origami-mediated crystallization method will facilitate both the exploration of refined self-assembly platforms and the creation of anisotropic metamaterials.
Introduction
Self-assembly is a holistic synergy where individual components associate and congregate spontaneously with the aim of forming a cohesive and ordered entirety.1 The interactions between individual components allow the structural information and surface chemistry to be encoded with spatial accuracy, inaccessible to top-down processing methods.2,3 Basic structural units act as building blocks, whose characteristics (including shape, charge, ligand shell, etc.) actually govern their interaction behaviors.4–6 Thus, the ability to design and regulate constituent units is directly correlated with the final state of the assemblies.In the last few decades, major advances in the customization and functionalization of nanomaterials have provided diversified research objects to comprehend and build relationships between nanoscopic and macroscopic systems.7–11 The DNA origami technique,12 as an emerging representative, can be used to construct the desired two-dimensional (2D) and three-dimensional (3D) nanostructures based on Watson–Crick base-pairing and internal periodic DNA crossovers.13–18 These spatially resolved DNA nanostructures at the nucleotide level can be manufactured with high throughput. Moreover, their excellent anisotropic positioning and composition uniformity guarantee ideal assembly capabilities in the nanometer scale, which are recognized as the outstanding advantages of DNA origami structures. Nevertheless, it is challenging to establish a precision-comparable interaction mechanism for these ingenious units. A common DNA guided self-assembly strategy is the hybridization of the outstretched single-stranded DNA (ssDNA) from nanomaterials with the complementary sequence to form a double strand as the connector.19–21 Due to the homology of DNA, this strategy is well suited for DNA origami systems.22 However, a critical issue is that the regions at the junctions differ markedly from those inside the DNA origami building blocks. For example, the exposed single/double-stranded DNA with dozens of nucleotides in length brings more flexibility than the parallel double helices tightly bound together by crossovers.23 Uncontrolled bending, skew or even rotation would isolate the assembly units without a definite orientation and position.24 The ambiguity created by weakened associations limits the maximum retention and utilization of fine-grained structural information.
Another key difficulty is to achieve an orderly expansion from the unit to the organization. Although DNA origami structures can be regarded as programmable atomic equivalents capable of producing crystal-like assemblies,25–27 the periodic arrangement of internal DNA modules remains challenging. The ordered assembly of subdivided DNA domains presents a low-entropy state, requiring highly specific connections and matching topology. So far, a successful method has been reported where tensegrity triangle motifs are used to form visible 3D DNA crystals with sticky ends propagating in three non-coplanar directions.28,29 These crystals can further couple with molecular devices and nanoparticles.30–33 However, they are limited by the small accommodating space and the low diversity of lattice types.
Here, we refine the association between assembly units for the integration between component structural domains. Specifically, polyhedral DNA origami frames, as DNA domain sets, are constructed into a series of 3D crystalline lattices accurate to the level of single DNA hybridization by a bridging strategy. Through the site-specific positioning of guest particles, we demonstrate that the inherent anisotropy of the DNA origami building blocks can be extended to the entire crystal structure while ensuring the minimized unit spacing. Thus, a well-ordered DNA origami crystal could be deconstructed into periodically arranged DNA domains, depending on the frame geometry and lattice topology.
Results and discussion
Polyhedral DNA frames as assembly units
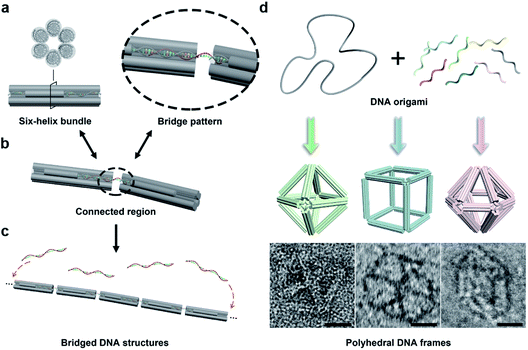
In this work, we begin with a reported rod-shape model, a six-helix bundle,34,35 to seek for potential connectivity. This rod consists of six DNA double helices packed in parallel with a honeycombed cross-section (Fig. 1a). To avoid the excessive flexibility incurred by the exposed sticky ends for connection, the connected regions are brought inside the structure of the six-helix bundles. To elaborate, a certain length of unhybridized single-stranded segments is reserved at both ends of a selected DNA double helix by shortening the internal staple strands in advance. Then a predetermined ssDNA termed “bridging DNA strand” is introduced, whose sequences at both ends are designed to be complementary to the single-stranded segments at the two reserved sites. Thus, the bridging strand can hybridize with two separate rods to form a DNA bridge (Fig. 1b and S1†). Under the action of multiple bridging strands, adjacent rod units will replicate the plug-in bridging behavior end to end to obtain a compact linear structure (Fig. 1c). It is worth noting that the bridging strands are highly specific to the reserved sites, which relies on the rational design of the complementary sequences.In order to extend the bridging principle to 3D high-order structures, assembly units should possess spatial directional polymerizability and large accommodating volumes. Thus, we designed three shapes of polyhedral frames, octahedron, cube and hexagonal bipyramid (HB), as shown in Fig. 1d. The edges of these shapes are composed of six-helix bundles with lengths of around 16–37 nm (Fig. S2†). According to the design, the octahedron and cube are highly symmetrical with Oh symmetry, while the HB belongs to the D6h point group. The octahedron with a high proportion of triangular faces has excellent rigidity, while the cube tends to deform into an irregular hexahedron due to the inability to maintain square faces. The hexagonal cross-section in the HB also brings potential flexibility to a large extent. Despite significant differences in structural stiffness, we focus on the topological properties of frames without overly considering possible deformations, and attempt to improve the natural characteristics of assembly units by bridging them into large-scale assemblies.
With reference to the above-mentioned bridging strategy for six-helix rods, all reserved sites are designed at both ends of the edges and converge at the vertices of the frames. By shortening the staple strands at the designated sites, the scaffold DNA provides unhybridized single-stranded segments for subsequent bridging. In addition, the internal space of the polyhedral frame structures was used to embed 10 nm gold nanoparticles (AuNPs) to realize the organizational manipulation for nano-objects. Guest AuNPs are positioned at the body center by hybridization with capture strands extending from the inside of frames. Efficient assembly and positioning were confirmed by negative-staining transmission electron microscopy (TEM) as shown in Fig. S3–S5.†
Bridge patterns for DNA origami building blocks
Next, we discussed the bridge patterns available for these different polyhedral frames, focusing on the formation of a 3D ordered crystal structure via vertex-to-vertex connection. The specific sequence design of bridging strands depends entirely on the selection and pairing of reserved sites. However, any two vertices involve multiple reserved sites, and randomly generated bridging combinations will lead to uncertain assembly results. Hence, the frame geometric symmetry and the arrangement rationality need to be carefully considered.For the octahedron, an obvious simple cubic (SC) structure is generated by translating along its 3 four-fold rotation axes (C4) as shown in Fig. 2a. The combination of two reserved sites with mirror symmetry on a diagonal plane determines eight bridging strands through opposite vertices in each C4 direction (Fig. S6†). The three crystallographic axes of crystal growth are equivalent and orthogonal. Thus, the angle between every two bridged edges is 90°, which is achieved by introducing a 4 nt single-stranded segment in the middle of the bridging strand for moderate angle flexibility and stress relief. All subsequent bridging strand designs followed this principle. The HB adopts a combination strategy similar to the octahedron's, that is, bridging along its four crystallographic axes (Fig. S7†). Theoretically, a 120° angle between three horizontal axes on the σh mirror plane results in a simple hexagonal (SH) lattice structure (Fig. 2c).
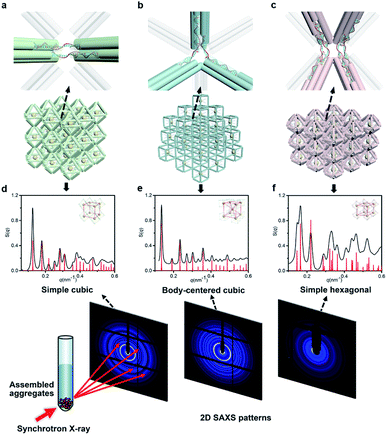 | ||
| Fig. 2 NP lattices assembled from polyhedral DNA frames through bridge patterns. (a–c) Magnified schematics of corresponding bridge patterns for the proposed lattice structures as discussed in the text. Representative bridged edges are highlighted at vertex junctions. (d–f) X-ray scattering structure factors, S(q), of 3D AuNP lattices extracted from 2D SAXS patterns (Fig. S9–S11†). For each type of lattice, the experimental data are in black and the standard peaks of the models are in red. | ||
For the cubic frame, things are different. We noticed that merely performing translation operations along its four body diagonals (three-fold rotation axis, C3) is not enough to satisfy the one-to-one correspondence between the bridged edges unless a rotation operation is introduced. However, such compound operations will cause alignment conflicts and hinder the generation of ordered structures. To solve this problem, we proposed a crossed bridge pattern that is still based on translation operations (Fig. 2b). Taking a set of opposite vertices as an example, two reserved sites on a vertical edge are paired with those on the neighboring horizontal edges, respectively (Fig. S8†). Six interlaced bridging strands together form three rectangular trihedral angles to realize a stringent orthogonal configuration, presenting a body-centered cubic (BCC) structure.
In a conventional lattice preparation method, the mixed solution of polyhedral frames, bridging strands and functionalized AuNPs was annealed from 50 °C to 20 °C circularly. Dark red sand-like aggregates appeared at the bottom of the reaction tube after the annealing process, suggesting the compact AuNP–DNA organization.
NP lattices under DNA origami crystals
The internal structures of these aggregates were first detected through in situ small angle X-ray scattering (SAXS) to confirm the formation of lattices and evaluate the degree of long-range order (see the ESI†). The integrated data extracted from the 2D SAXS pattern and corresponding structure factors, S(q), where q is the scattering vector, are shown in Fig. 2d–f and S9–S14.† The lattice formed by octahedral frames has more than 15 orders of identifiable Bragg peaks (Fig. 2d, black curve) and the ratio of peak positions (relative to the first peak)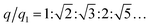 corresponds to a typical SC lattice. For the cubic frame, nearly 20 legible scattering peaks are shown in Fig. 2e, indicating that the assembled structure is highly ordered. Well-matched peaks show a narrow broadening and the peak intensity of the S(q) is in excellent agreement with the model of the BCC structure (Fig. 2e, red curve). The HB system also exhibits around 10 resolution-limited SAXS peaks with the positions markedly different from the S(q) of cubic lattices, corresponding to an expected SH lattice (Fig. 2f). For the above three shapes of polyhedral frames, the results deduced from the bridge patterns are well consistent with the SAXS experimental data, which shows that our strategy for constructing 3D superstructures is logical and goal-oriented.
corresponds to a typical SC lattice. For the cubic frame, nearly 20 legible scattering peaks are shown in Fig. 2e, indicating that the assembled structure is highly ordered. Well-matched peaks show a narrow broadening and the peak intensity of the S(q) is in excellent agreement with the model of the BCC structure (Fig. 2e, red curve). The HB system also exhibits around 10 resolution-limited SAXS peaks with the positions markedly different from the S(q) of cubic lattices, corresponding to an expected SH lattice (Fig. 2f). For the above three shapes of polyhedral frames, the results deduced from the bridge patterns are well consistent with the SAXS experimental data, which shows that our strategy for constructing 3D superstructures is logical and goal-oriented.
We calculated the lattice parameters based on the SAXS result, and compared them with the simulated close-packed models (Fig. S15–S17 and ESI†). As shown in Table 1, the spacing deviation of all lattice parameters is less than 1.0 nm. According to our knowledge, such close unit spacing has not been achieved in previous studies for DNA origami frameworks, which is always a challenging issue since a closer distance means more repulsion forces between nearby DNA units. The bridging strategy achieved in this report permits the minimized spacing of nearby building blocks to ∼4 ssDNA bases, compared with 44 ssDNA bases and 8 dsDNA base pairs as the linker part for the sticky-end hybridization strategy,26 providing a way to fabricate 3D nanomaterials with more sensitive collective effects.
| Frame shape | Lattice type | Lattice parameters, experimental and (designed) values |
|---|---|---|
| Octahedron | Simple cubic | a = b = c = 50.0 (50.1) nm |
| α = β = γ = 90° | ||
| Cube | Body-centered cubic | a = b = c = 65.9 (65.8) nm |
| α = β = γ = 90° | ||
| Hexagonal bipyramid | Simple hexagonal | a = b = 43.0 (42.4) nm; c = 42.1 (41.6) nm |
| α = β = 90°; γ = 120° | ||
| Regular and elongated octahedron | Simple tetragonal | a = b = 50.0 (50.1) nm; c = 58.4 (59.4) nm |
| α = β = γ = 90° |
Then, these lattices were observed by electron microscopy to directly visualize the arrangement of NPs and the local morphology (Fig. 3). Generally, DNA samples leaving the aqueous environment collapse and deform during the deposition process under dry conditions. The situation is particularly serious for 3D large-scale structures, resulting in distortion or even loss of the ordered information originally carried. Therefore, we performed in situ silicidation on the DNA origami to reinforce the nucleic acid backbones.36 Close-up views of TEM images display the multi-layered assemblies and well-defined streaks arranged with AuNPs (Fig. 3d–f and S18–S20†). Scanning electron microscope (SEM) images show the stereo vision of the entire lattices with a greater depth of field, and the ordered areas are conservatively estimated to be 0.8–1 μm in size (Fig. S21–S23†). Besides, 2D planar assemblies were prepared as indirect evidence to eliminate the adverse effects of overlap and stacking. By selecting only two (for the octahedron and cube) or three (for the HB) crystallographic axes for crystal growth, the regularly arranged AuNP arrays were clearly resolved (Fig. 3a–c and S24–S27†). We found that the polyhedral frames in these assemblies swelled significantly compared to the free states, especially for cube and HB frames with relatively weak stiffness (Fig. S4 and S5†). The trend of reduced deformations indicates that bridged domains could exert a certain tension at the vertex junctions to increase the frame rigidity. We emphasize that the bridge pattern provides a robust DNA crystal construction concept insensitive to structural stiffness, which is beneficial for the soft structures that tend to have larger accommodating space and adjustability.37,38
Anisotropy control in the assembled lattices
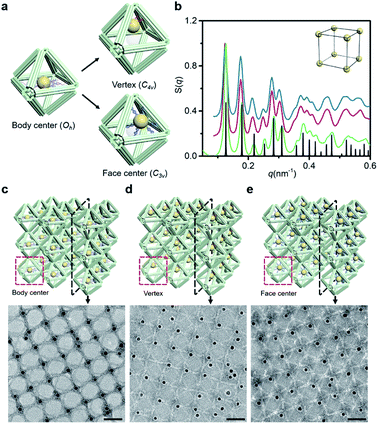
Since the DNA origami is composed of a scaffold DNA and hundreds of non-repetitive short staple DNAs, it means that different domains have disparate sequence compositions. From the perspective of oligonucleotides, the seemingly regular geometric frames are actually anisotropic in space. In our bridging strategy, the connections between polyhedral frames are eventually refined to designated bridged double helix pairs. Specific bridge patterns combined with the minimized unit spacing make it possible to maintain the anisotropy of building blocks when extended to the entire crystal.To verify this proposal, we chose the highly symmetrical SC lattice as a template, and broke the symmetry of conjugated monomers intentionally by changing the position of marker AuNPs relative to the octahedral DNA frames. The AuNP, originally located at the body center, was then positioned near the vertex (still inside the frame) or in the center of one selected triangular face by altering the protruding position of capture DNAs (Fig. 4a). In a simplified geometric model of the conjugated monomer, when the AuNP shifts from the body center to the vicinity of a vertex, the point group transforms from Oh to C4v, while it will belong to C3v when shifting to the triangular face center. It is conceivable that if the directions and vertices for crystal growth are treated indiscriminately (for example, isotropic connection26), the DNA domains used to locate guest nanoparticles in altered frameworks would become chaotic and unpredictable under the influence of symmetry breaking.
SAXS of altered 3D lattices shows that AuNPs are all arranged into an SC lattice, and there is barely any noticeable difference in peak position and broadening for the three preset positions (Fig. 4b). TEM images of the 2D planar assemblies confirm the site-specific positioning of AuNPs (Fig. 4c–e, S28 and S29†). Thus, the bridged DNA origami crystals successfully guide guest nanoparticles to appear in the consistent positions relative to frames. We can deduce that when propagating in the directions parallel to C4, the internal domains of the DNA origami building blocks, whose inter-frame spacing is the lattice parameter, are the same. In other words, they repeat periodically in space. As long as the orientation and composition of one frame unit is defined, the configuration of the entire lattice can be accurately predicted. The assembly units act like ‘clones’ with the same behavior, which is conducive to maximizing the positioning advantages of DNA origami technology in storing and using spatial structure information when forming large-scale anisotropic structures with a collective effect.
Bridging assembly in the binary system
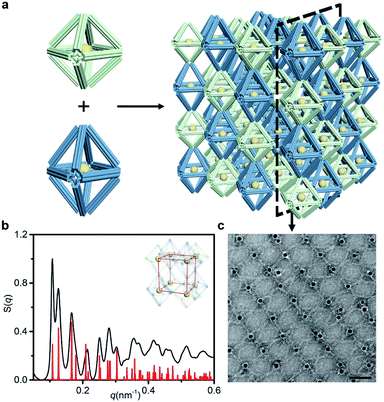
We further increased the assembly complexity to demonstrate the superior expandability of our approach. In this process, more than one frame component was introduced into the crystal structure. A new type of frame, termed the elongated octahedron, was designed to couple with the regular octahedron in the establishment of the binary system (Fig. 5a). The side edges of the elongated octahedron are 1.25 times the length of the regular octahedron's edges, resulting in a D4h point group (Fig. S2 and S30†). Owing to the uniform crystallographic axes of coupled frames, we mainly refer to the SC lattice to design the bridge pattern (Fig. S6 and S31†). In comparison, the two ends of the bridging strands in the binary system need to hybridize with two types of frame, respectively. Under the premise of the ordered organization, the resulting lattice will be a simple tetragonal structure because of the difference in the length of side edges.The binary system exhibits nearly 15 recognizable S(q) peaks, as illustrated in Fig. 5b. Compared with the peak shape of the SC lattice model, the appearance of several split peaks is caused by the lattice parameters (a = b ≠ c). We calculated the lattice parameters (shown in Table 1) and calibrated the scattering profile with the model fitting (Fig. S32–S34 and ESI†), confirming that the resulting structure corresponds to a simple tetragonal lattice. Representative TEM images of selected 2D planar assemblies show a rectangular array, and the alternant bridging can be observed clearly (Fig. 5c and S35†). Thus, we encode the structural information of the lattice by shaping polyhedral frames. While enriching the lattice types, the same kind of component in the assembly could be manipulated uniformly to achieve complex interactions. The specificity of bridge patterns prevents crosstalk between components and coordinates the orderly progress of the overall assembly process.
Conclusions
We have proposed a general approach to create 3D low-entropy lattices using a variety of polyhedral DNA origami frames. Importantly, the periodically arranged DNA domains in these crystal structures permit the anisotropy extension in units of frames, which is guaranteed by the minimized spacing and high specificity. The modular bridging principle can be further applied to diverse crystallographic types and multi-component systems through the ingenious designs of assembly unit geometry and lattice topology. By combining orientation-related functional nanomaterials, such as anisotropic nanoparticles,4 carbon nanotubes and proteins,39 the extra-fine integrated development platforms become feasible for potential application as chiral devices,40 nanoelectronics41 and biological reaction amplifiers.42Data availability
The experimental data associated with this work is available in the ESI.†Author contributions
D. G., J. Z., Q. M. and Y. T. conceived the project, analyzed the data and discussed the paper writing. D. G. and N. M. contributed to the design and synthesis of DNA origami frames. D. G. and X. Y. contributed to the silicification experiment of 3D lattices. D. G., N. M., and M. J. contributed to the SAXS model fitting. D. G., Q. M. and Y. T. wrote the manuscript. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the National Natural Science Foundation of China (No. 21834004) and the Fundamental Research Funds for the Central Universities (020514380255). This work is also supported by National Natural Science Foundation of China (No. 92056114, and No. 21971109), the Program for Innovative Talents and Entrepreneurs in Jiangsu and the Shenzhen International Cooperation Research Project, China (No. GJHZ20180930090602235). We thank the staff from the BL16B1 beamline at Shanghai Synchrotron Radiation Facility for assistance during the data collection. We thank the staff from the BL19U2 beamline of the National Facility for Protein Science in Shanghai (NFPS) at Shanghai Synchrotron Radiation Facility for assistance during the data collection.Notes and references
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- L. L. Ong, N. Hanikel, O. K. Yaghi, C. Grun, M. T. Strauss, P. Bron, J. Lai-Kee-Him, F. Schueder, B. Wang, P. Wang, J. Y. Kishi, C. Myhrvold, A. Zhu, R. Jungmann, G. Bellot, Y. Ke and P. Yin, Nature, 2017, 552, 72–77 CrossRef CAS PubMed.
- G. Tikhomirov, P. Petersen and L. Qian, Nature, 2017, 552, 67–71 CrossRef CAS PubMed.
- M. R. Jones, R. J. Macfarlane, B. Lee, J. Zhang, K. L. Young, A. J. Senesi and C. A. Mirkin, Nat. Mater., 2010, 9, 913–917 CrossRef CAS.
- C. Zhang, R. J. Macfarlane, K. L. Young, C. H. Choi, L. Hao, E. Auyeung, G. Liu, X. Zhou and C. A. Mirkin, Nat. Mater., 2013, 12, 741–746 CrossRef CAS PubMed.
- D. Nykypanchuk, M. M. Maye, D. van der Lelie and O. Gang, Nature, 2008, 451, 549–552 CrossRef CAS PubMed.
- Y. Ke, L. L. Ong, W. Sun, J. Song, M. Dong, W. M. Shih and P. Yin, Nat. Chem., 2014, 6, 994–1002 CrossRef CAS.
- Y. Tian, T. Wang, W. Liu, H. L. Xin, H. Li, Y. Ke, W. M. Shih and O. Gang, Nat. Nanotechnol., 2015, 10, 637–644 CrossRef CAS PubMed.
- M. M. Maye, D. Nykypanchuk, M. Cuisinier, D. van der Lelie and O. Gang, Nat. Mater., 2009, 8, 388–391 CrossRef CAS.
- J. I. Cutler, E. Auyeung and C. A. Mirkin, J. Am. Chem. Soc., 2012, 134, 1376–1391 CrossRef CAS.
- B. Liu and J. Liu, J. Am. Chem. Soc., 2017, 139, 9471–9474 CrossRef CAS.
- P. W. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS.
- H. Dietz, S. M. Douglas and W. M. Shih, Science, 2009, 325, 725–730 CrossRef CAS PubMed.
- S. M. Douglas, H. Dietz, T. Liedl, B. Hogberg, F. Graf and W. M. Shih, Nature, 2009, 459, 414–418 CrossRef CAS PubMed.
- S. Woo and P. W. Rothemund, Nat. Chem., 2011, 3, 620–627 CrossRef CAS PubMed.
- T. Gerling, K. F. Wagenbauer, A. M. Neuner and H. Dietz, Science, 2015, 347, 1446–1452 CrossRef CAS PubMed.
- P. Wang, S. Gaitanaros, S. Lee, M. Bathe, W. M. Shih and Y. Ke, J. Am. Chem. Soc., 2016, 138, 7733–7740 CrossRef CAS PubMed.
- F. Hong, F. Zhang, Y. Liu and H. Yan, Chem. Rev., 2017, 117, 12584–12640 CrossRef CAS.
- E. Auyeung, J. I. Cutler, R. J. Macfarlane, M. R. Jones, J. Wu, G. Liu, K. Zhang, K. D. Osberg and C. A. Mirkin, Nat. Nanotechnol., 2011, 7, 24–28 CrossRef PubMed.
- R. J. Macfarlane, B. Lee, M. R. Jones, N. Harris, G. C. Schatz and C. A. Mirkin, Science, 2011, 334, 204–208 CrossRef CAS PubMed.
- M. R. Jones, N. C. Seeman and C. A. Mirkin, Science, 2015, 347, 1260901 CrossRef.
- H. Ramezani and H. Dietz, Nat. Rev. Genet., 2020, 21, 5–26 CrossRef CAS.
- M. Wang, L. Dai, J. Duan, Z. Ding, P. Wang, Z. Li, H. Xing and Y. Tian, Angew. Chem., Int. Ed., 2020, 59, 6389–6396 CrossRef CAS PubMed.
- K. Huang, D. Yang, Z. Tan, S. Chen, Y. Xiang, Y. Mi, C. Mao and B. Wei, Angew. Chem., Int. Ed., 2019, 58, 12123–12127 CrossRef CAS PubMed.
- W. Liu, M. Tagawa, H. L. Xin, T. Wang, H. Emamy, H. Li, K. G. Yager, F. W. Starr, A. V. Tkachenko and O. Gang, Science, 2016, 351, 582–586 CrossRef CAS PubMed.
- Y. Tian, Y. Zhang, T. Wang, H. L. Xin, H. Li and O. Gang, Nat. Mater., 2016, 15, 654–661 CrossRef CAS PubMed.
- Y. Tian, J. R. Lhermitte, L. Bai, T. Vo, H. L. Xin, H. Li, R. Li, M. Fukuto, K. G. Yager, J. S. Kahn, Y. Xiong, B. Minevich, S. K. Kumar and O. Gang, Nat. Mater., 2020, 19, 789–796 CrossRef CAS PubMed.
- J. Zheng, J. J. Birktoft, Y. Chen, T. Wang, R. Sha, P. E. Constantinou, S. L. Ginell, C. Mao and N. C. Seeman, Nature, 2009, 461, 74–77 CrossRef CAS PubMed.
- E. Stahl, F. Praetorius, C. C. de Oliveira Mann, K. P. Hopfner and H. Dietz, ACS Nano, 2016, 10, 9156–9164 CrossRef CAS PubMed.
- Y. Hao, M. Kristiansen, R. Sha, J. J. Birktoft, C. Hernandez, C. Mao and N. C. Seeman, Nat. Chem., 2017, 9, 824–827 CrossRef CAS.
- X. Wang, R. Sha, M. Kristiansen, C. Hernandez, Y. Hao, C. Mao, J. W. Canary and N. C. Seeman, Angew. Chem., Int. Ed., 2017, 56, 6445–6448 CrossRef CAS PubMed.
- J. Zheng, P. E. Constantinou, C. Micheel, A. P. Alivisatos, R. A. Kiehl and N. C. Seeman, Nano Lett., 2006, 6, 1502–1504 CrossRef CAS PubMed.
- T. Zhang, C. Hartl, K. Frank, A. Heuer-Jungemann, S. Fischer, P. C. Nickels, B. Nickel and T. Liedl, Adv. Mater., 2018, 30, e1800273 CrossRef PubMed.
- A. Kuzuya, R. Wang, R. Sha and N. C. Seeman, Nano Lett., 2007, 7, 1757–1763 CrossRef CAS PubMed.
- W. Liu, N. A. Mahynski, O. Gang, A. Z. Panagiotopoulos and S. K. Kumar, ACS Nano, 2017, 11, 4950–4959 CrossRef CAS.
- L. Nguyen, M. Doblinger, T. Liedl and A. Heuer-Jungemann, Angew. Chem., Int. Ed., 2019, 58, 912–916 CrossRef CAS PubMed.
- F. Zhang, S. Jiang, S. Wu, Y. Li, C. Mao, Y. Liu and H. Yan, Nat. Nanotechnol., 2015, 10, 779–784 CrossRef CAS PubMed.
- R. Veneziano, S. Ratanalert, K. Zhang, F. Zhang, H. Yan, W. Chiu and M. Bathe, Science, 2016, 352, 1534 CrossRef CAS.
- J. Fu, M. Liu, Y. Liu, N. W. Woodbury and H. Yan, J. Am. Chem. Soc., 2012, 134, 5516–5519 CrossRef CAS PubMed.
- J. Dong, M. Wang, Y. Zhou, C. Zhou and Q. Wang, Angew. Chem., Int. Ed., 2020, 59, 15038–15042 CrossRef CAS PubMed.
- Y. Zhang, X. Mao, F. Li, M. Li, X. Jing, Z. Ge, L. Wang, K. Liu, H. Zhang, C. Fan and X. Zuo, Angew. Chem., Int. Ed., 2020, 59, 4892–4896 CrossRef CAS PubMed.
- Z. Zhao, J. Fu, S. Dhakal, A. Johnson-Buck, M. Liu, T. Zhang, N. W. Woodbury, Y. Liu, N. G. Walter and H. Yan, Nat. Commun., 2016, 7, 10619 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc05060e |
| This journal is © The Royal Society of Chemistry 2022 |