The inversion of tetrahedral p-block element compounds: general trends and the relation to the second-order Jahn–Teller effect

Abstract

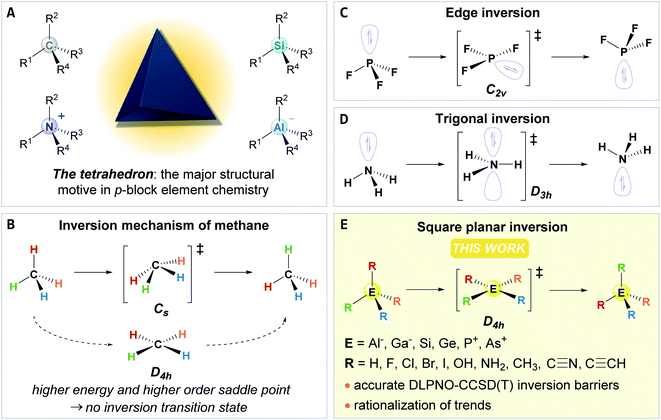
The tetrahedron is the primary structural motif among the p-block elements and determines the architecture of our bio- and geosphere. However, a broad understanding of the configurational inversion of tetrahedral compounds is missing. Here, we report over 250 energies (DLPNO-CCSD(T)) for square planar inversion of third- and fourth-period element species of groups 13, 14, and 15. Surprisingly low inversion barriers are identified for compounds of industrial relevance (e.g., ≈100 kJ mol⁻¹ for Al(OH)₄⁻). More fundamentally, the second-order Jahn–Teller theorem is disclosed as suitable to rationalize substituent and central element effects. Bond analysis tools give further insights into the preference of eight valence electron systems with four substituents to be tetrahedral. Hence, this study develops a model to understand, memorize, and predict the angular flexibility of tetrahedral species. Perceiving the tetrahedron not as forcingly rigid but as a dynamic structural entity might leverage new approaches and visions for adaptive matter.

---

Introduction

The tetrahedron dominates the structural chemistry of the p-block, e.g., that of carbon, aluminates, silanes, or ammonium ions. It thereby constitutes the fundamental building block for the molecular architecture of our bio- and geosphere (Fig. 1A). For species with eight valence electrons and four substituents (ER₄), the tetrahedral preference is well-founded by molecular orbital theory or by the VSEPR model.^1,2 But what do we know about the tetrahedron's structural deformation, its fluxionality, or its configurational inversion? Surprisingly little!

Fig. 1 (A) Examples of eight valence electron p-block element species with a tetrahedral ground state. (B) The C_s symmetric inversion transition state for CH₄ and its higher energy square planar state of D_4h symmetry. (C) Edge inversion process for group 15 element fluorides. (D) Trigonal inversion of ammonia and other group 15 element compounds. (E) The inversion process of p-block tetrahedrons analyzed within this work.

The potential energy surface for the structural deformation of the tetrahedron is by far the most developed for methane.^3–5 The minimum energy inversion path was found to traverse a C_s symmetric transition state, whereas the square planar D_4h symmetric state is significantly higher in energy with a higher-order saddle point on the potential energy surface (Fig. 1B).^6–9 Accordingly, tremendous progress has been made in the field of planar tetra-, penta- and hexacoordinate carbon during the past decades.^10–14 For the remaining p-block tetrahedrons, the inversion process is much less understood. For hydrides of less electronegative central elements (AlH₄⁻, SiH₄, PH₄⁺), inversion transition states of D_4h symmetry were suggested.¹⁵ For SiF₄ and PF₄⁺, analogies with the edge inversion of trigonal group 15 compounds with electronegative substituents were found (e.g., PF₃, Fig. 1C).^16,17 Strategies to stabilize square planar configurations for some other elements were probed computationally,^18–24 and substantial progress was made for compounds featuring planar silicon.^25–40 However, a systematic fundament of the inversion process in ER₄ compounds or more general statements on their tetrahedral preference are elusive. This lack appears surprising compared with the extensive knowledge on the inversion process of trigonal group 15 compounds ER₃ (Fig. 1D), which occupied generations of theoreticians and experimentalists.^41–43 Different approaches to explain the inversion of ER₃, like perturbational molecular orbital theory,^1,44–46 the second-order Jahn–Teller effect (SOJTE),^47–50 or recoupled pair bonding,⁵¹ afforded a profound base and thereby challenged our understanding of the chemical bonding.^52,53 Likely, this diverging interest stems from the absent or potentially overlooked experimental observation of structural dynamics of the tetrahedron, which are classically considered configurationally stable.⁵⁴ However, in recent years, several “anti-van't-Hoff–Le-Bel” species (i.e., stabilized inversion transition states), such as planar aluminates, silicon, or phosphonium ions, were isolated, offering unique reactivities.^55–70 Hence, knowledge on the tetrahedral inversion transforms from fundamental to applied interest.

In the present study, we first recapture and develop a framework for the second-order Jahn–Teller effect (SOJTE) on square-planar inversion. Second, we provide a systematic discussion of inversion energies of p-block tetrahedrons of groups 13, 14, and 15 with homo- and heteroleptic substitution patterns (Fig. 1E). Surprisingly low barriers are identified, including compounds of industrial relevance, e.g. Al(OH)₄⁻, but which have never been considered in light of configurational inversion. Finally, and most fundamentally, we prove that the SOJTE can rationalize and explain those trends. Additional bond analysis tools round off our understanding of the origin of the tetrahedral preference for ER₄ compounds.

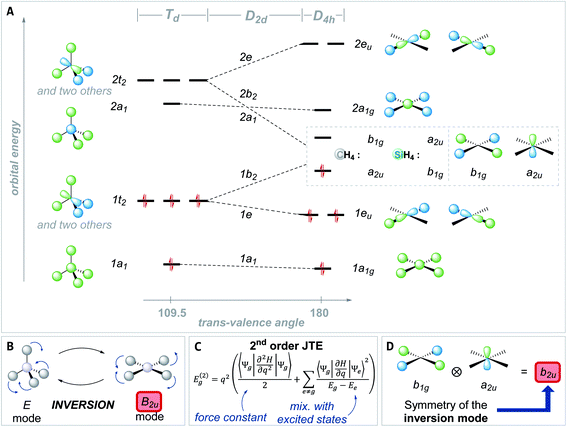
Qualitative remarks on the molecular orbitals during square planar inversion and the connection with the second-order Jahn–Teller effect (SOJTE).

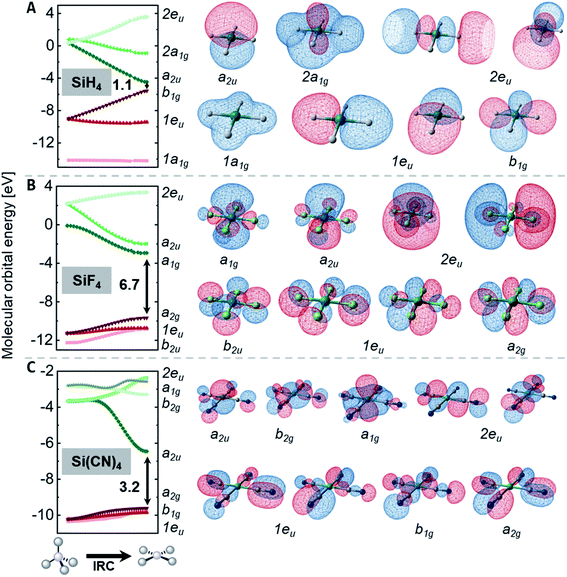
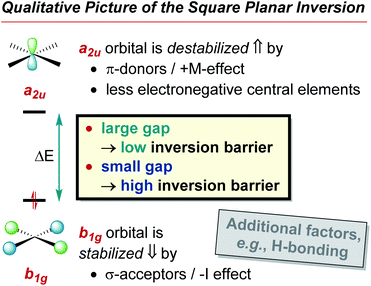
The preference of ER₄ molecules to adopt tetrahedral structures and the orbital variations upon distortion into the planar state are well-described by Walsh diagrams, as schematically shown for SiH₄ and CH₄ in Fig. 2A.^1,54,71 In T_d symmetry, four bonding (1a₁ and 1t₂) and four anti-bonding (2a₁ and 2t₂) molecular orbitals are built by combining the central elements' valence s- and p-orbitals with the symmetry-adapted linear combinations (SALCs) of the substituent fragment orbitals. The deformation into the planar D_4h symmetric state occurs along the E harmonic vibration via intermediate D_2d symmetry (Fig. 2B).¹⁶ Along this distortion coordinate, the 1a₁ orbital experiences slight stabilization due to the increased overlap of the substituent-centered in-phase lobes. The 1t₂ set of the T_d state splits up into 1e and 1b₂ molecular orbitals. The 1e set becomes slightly stabilized due to the increased overlap of substituent and central element orbitals. However, the 1b₂ orbital turns from bonding to non-bonding and becomes significantly destabilized in the a_2u molecular orbital of the final D_4h symmetric state. The character of the highest occupied (HOMO) and lowest unoccupied molecular orbital (LUMO) in the square planar state depends on the electronegativity of the central element relative to the substituents.¹⁵ The a_2u orbital is of π-character and is localized at the central atom, whereas the b_1g orbital is of δ-type and resides at the substituents. The latter molecular orbital emanates from the 2t₂ representation of the tetrahedral state and is energetically considerably lowered along the D_2d symmetric distortion. Hence, for central elements which are less electronegative than hydrogen (e.g., SiH₄, Fig. 2A), the substituent-centered b_1g orbital is the HOMO, and the LUMO is of a_2u symmetry (π-type orbital). For the inverse situation (e.g., CH₄, Fig. 2A), the a_2u orbital is the HOMO (primarily located at carbon), whereas the LUMO is the substituent-centered b_1g molecular orbital. In total, this MO theoretical perspective assigns the primary cause for the inversion barrier to the significant energy increase of one of the orbitals of the occupied 1t₂ set of molecular orbitals, which is not compensated by the stabilization of the other occupied orbitals.

Fig. 2 (A) Schematic Walsh diagram for the distortion from the tetrahedral to the square planar state of CH₄ and SiH₄. (B) Deformation vibrations that transform the tetrahedral ground state into the square planar inversion transition state and vice versa. (C) Second-order contributions for the deformation coordinate q to the energy of a given system. (D) Direct product of the b_1g and a_2uirrep within the D_4h point group. It transforms under b_2u, which is also the symmetry of the inversion vibration.

Although the MO interpretation draws a qualitative picture, it cannot easily rationalize differences in inversion barriers for different molecules. Vibronic coupling theory provides an alternative approach through the second-order Jahn–Teller theorem (SOJTE).^72–79 This model is more complex, but it allows to parametrize reaction pathways by considering the instability of transition states.⁸⁰ Some crucial arguments on the SOJTE are revised first, in order to prepare for their application in a later section of this article.

The curvature of the adiabatic potential energy surface (PES) at a stationary state under consideration, such as a transition state, is inspected with respect to a structural deformation along the coordinate q. The second-order terms of the Jahn–Teller theorem relate the energy change for this structural deformation with the electronic ground state (Ψ_g) and contributions of higher excited states (Ψ_e) (Fig. 2C).^74,81

The individual terms are interpreted as: (1) the force constant of the deformation (resistance toward deformation without electronic relaxation, first summand in Fig. 2C), (2) the symmetry and overlap of the electronic ground state coupling with excited states (“vibronic coupling constants”, the numerator of the second summand in Fig. 2C), and (3) their energy difference (denominator of the second term in Fig. 2C). Energy lowering upon distortion along q only happens, if the direct products of the irrep of the ground (Γ(Ψ_g)) and the excited state (Γ(Ψ_e)) contain the irrep under which the distortion coordinate q, i.e., its vibrational mode, transforms (Γ(Ψ_g) ⊗ Γ(Ψ_e) ∈ Γ(q)). The theory is only valid for small nuclear displacements from the reference structure, but the curvature may extrapolate the energy release upon structural relaxation.

For a quantitative analysis, all SOJTE-parameters of the equation given in Fig. 2C need to be evaluated along the entire adiabatic PES for all the states that fulfill the symmetry argument – a very tedious task.⁸² Several approximations offer simplification: (1) instead of using the full state wavefunctions, the coupling can be inspected at the level of one-electron molecular orbitals. The vibronic coupling constants become orbital vibronic coupling constants. (2) Instead of using the entire set of symmetry-allowed excited orbitals, only the two frontier molecular orbitals (FMO) can be considered. (3) If compounds with similar bonds are compared, it can be assumed that the vibronic coupling constants and the force constant, respectively, are not too different. Hence, the second-order contribution to the total energy gain (E_g⁽²⁾, see Fig. 2C) turns out to be inversely proportional to the HOMO–LUMO gap in the initial structure.

In this FMO approximation, the SOJTE was used for several phenomena, advocated by Pearson and got popularized among chemists while sharing many characteristics with perturbational molecular orbital theory.^79,83–86 Interpreted with precaution and bearing in mind its simplifications, it can be a valuable tool to obtain relations inaccessible by other approaches.⁸⁷ For example, it has been used to rationalize the inversion barrier of group 15 and 16 elements or to discuss the structure of (SiO)₄.^{1,44,45,47,88} In the context of tetra-coordinated species, the SOJTE has been mentioned, but was not further developed.^89,90

Applied to the square planar inversion of ER₄, the following relation can be formulated (Fig. 2D): In the D_4h symmetric state, the HOMO and LUMO are of a_2u and b_1g symmetry, therefore orthogonal and cannot mix. The direct product of the symmetry species of both orbitals transforms under the b_2u representation (a_2u ⊗ b_1g = b_2u). Consequently, the vibronic interaction becomes allowed upon coupling with the b_2u vibrational coordinate, which is just the deformation of the planar into the tetrahedral state (Fig. 2B). Thus, the qualitative hypothesis developed and to be probed in this manuscript reads as: the closer the FMOs are in the inversion transition state, the larger is the transition state instability, the larger is the inversion barrier. A small FMO gap in the inversion transition state results in a large contribution of the second summand in Fig. 2C's equation. Therefore, the relaxation into the tetrahedral structure promises the system significant energetic stabilization. Consequently, the energy span between ground and transition state must be large – a high inversion barrier is encountered. Complementarily, a large FMO gap diminishes the influence of the second summand (Fig. 2C), reduces the energetic stabilization due to structural deformation from the planar toward the tetrahedral state, and thus indicates a low inversion barrier.

Computational methods

The following set of molecules was included in the study: EH_4−yR_yⁿ for Eⁿ = Al⁻, Si, P⁺, and Ga⁻, Ge, As⁺ with R = F, Cl, Br, I, OH, NH₂, CH₃, CN, CCH and y = 0, 1, 2, 3, 4 (a total of 276 inversion barriers). The meta-GGA functional B97M, including Grimme's D3 correction, was combined with the cc-pVTZ basis set for structural optimization and frequency analysis.⁹¹ In six of the 276 cases, the optimization toward the desired transition structure remained unsuccessful (see the ESI† for details). In all other cases, proper transition structures for the inversion process were obtained by the applied DFT method as confirmed by numerical Hessian evaluations and IRC computations. For the final energies, the performance of several density functionals and approximated wave function methods were evaluated on a representative subset of molecules against CCSD(T)/CBS reference data. The DLPNO-CCSD(T)/cc-pVQZ method (tightPNO settings) showed a MAD of only 1.3 kJ mol⁻¹ and was used to calculate all final single point energies. The influence of diffuse basis functions was also investigated with the aug-cc-pVQZ basis set but was found minor.

The inversion transition states of D_4h symmetry of PH₄⁺ and AsH₄⁺ have an open-shell singlet electronic configuration (¹B_2u state). This was found by ab initio calculations on the NEVPT2/cc-pVQZ//CASSCF(8,8)/cc-pVTZ theoretical level. The barriers amount to 500 (PH₄⁺) and 498 kJ mol⁻¹ (AsH₄⁺). These numbers were used throughout the here presented work. The largest barriers (>480 kJ mol⁻¹, group 15 cations) need to be taken with some caution due to a potential multiconfigurational character of the transition states (see the ESI† for further details). The possibility of a tunneling contribution during inversion, in particular for the hydrides, was not considered.⁹ For the SOJTE-analysis, the B97M-cc-pVTZ derived Kohn–Sham molecular orbital energies were used.^92,93 For a selected number of compounds, the HOMO–LUMO gap of the inversion transition state was compared to the respective vertical excitation energy to the lowest energy excited singlet state obtained by TDDFT. Good correlations were obtained, and therefore the HOMO–LUMO gaps were used for the entire set of the investigated molecules. For any further details and specifics on natural bond orbital analysis (NBO), energy decomposition analysis (EDA), and the quantum theory of atoms in molecules (QTAIM) treatment, see the ESI.†

Results and discussion

Effects of substituent R and central element E in monosubstituted compounds EH3Rn

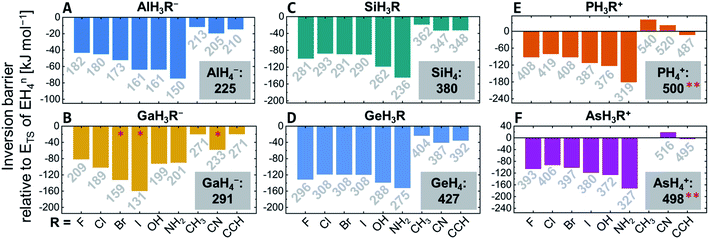
Comparing the inversion barriers for species EH₃Rⁿ with that of EH₄ⁿ allowed to assess the influence of the respective substituent R (Fig. 3). For GaH₃R⁻ (R = Br, I, CN), the transition structure optimizations converged to a dissociated species and should not be considered (red stars in Fig. 3B). Stabilization energies range from ≈10 (CH₃) to 180 kJ mol⁻¹ (NH₂) with respect to the barriers of the unsubstituted EH₄ⁿ. For the group 13 halide anions EH₃R⁻ (R = F, Cl, Br, I), the transition state lowering effect increases for the heavier halides, whereas for the neutral group 14 compounds and the group 15 cations, fluoride, and iodide stabilize more efficiently than chloride and bromide. In groups 14 and 15, the stabilizing effect of the hydroxy group is larger than that of the halides. The amino group generally has the most powerful impact of all considered substituents (up to 180 kJ mol⁻¹ in PH₃(NH₂)⁺versus PH₄⁺). Substituents without the ability for π-donation (methyl, nitrile, and ethynyl) stabilize less effectively but still substantially (up to 40 kJ mol⁻¹).

Fig. 3 Relative inversion barriers of EH₃Rⁿ with respect to EH₄ⁿ (grey panels), for E = Al (A), Ga (B), = Si (C), Ge (D), P (E), As (F). The label on each bar states the respective absolute inversion barrier of EH₃Rⁿ. No inversion transition state was found for AsH₃(CH₃)⁺.* The transition structure optimization converged to a dissociative structure (GaH₃ and R⁻). ** The inversion barriers were obtained with NEVPT2/cc-pVQZ//CASSCF(8,8)/cc-pVTZ.

The substituent effect is more pronounced for groups 14 and 15 versus group 13 and for the third period compared to the fourth period (Fig. 3). Concerning the central element, the inversion barriers increase significantly when going from left to right in the periodic table (Al < Si < P/Ga < Ge < As), with the group 15 element cations showing the largest inversion barriers (Fig. 3). Comparing the third- and fourth-period elements within one group, the trend of the inversion barrier is Al < Ga, Si < Ge but P > As. However, the difference between the periods is less pronounced than between the groups and is often outmatched by additive substitution effects.

Additive substitution effects along the series EH_4−yR_yⁿ

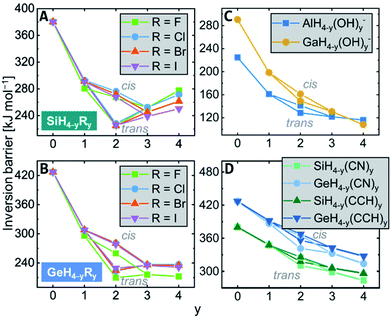
Consecutive replacement of the hydrogen substituents against R groups revealed additive and counter-additive substituent effects on the inversion barrier heights.

For the halido and amino series EH_4−yR_yⁿ (R = F, Cl, Br, I, NH₂), a maximum stabilization is reached with two substituents in trans-arrangement, i.e., the trans-EH₂R₂ⁿ transition states are lowest in energy as exemplarily shown for the silicon halides in Fig. 4A (for the plots of the other elements see the ESI†). The isomeric cis-EH₂R₂ⁿ transitions states are roughly 50 kJ mol⁻¹ higher in energy than the trans-isomers and range in the region of monosubstituted derivatives. The trend along EH₂R₂ⁿ → EHR₃ⁿ → ER₄ⁿ depends on the central element. For the third-period elements (E = Al, Si, P), the barriers rise again, reaching energies like in the monosubstituted EH₃Rⁿ. Thus, counter-stabilizing effects occur upon substitution with more than two R groups. This trend is different for the fourth-period atoms: the barriers remain invariant along three and four substituents, i.e., the stabilizing effect and the counter-stabilizing effect cancel (Fig. 4B). Accordingly, for EH₃Rⁿ, the fourth-period species have the larger inversion barriers than the third-period compounds but lower inversion barriers for ER₄.

Fig. 4 Additive substituent effects for the inversion barrier of (A) SiH_4−yR_y, (B) GeH_4−yR_y, with R = F, Cl, Br, I, of (C) AlH_4−y(OH)_y⁻ and GaH_4−y(OH)_y⁻, and of (D) EH_4−yR_y, with E = Si, Ge and R = CN, CCH.

Interestingly, the molecules with hydroxy groups show almost no saturation effect. In most cases, the four-fold substituted E(OH)₄ⁿ have the lowest energy transition states (E = Al, Ga, Ge, As, Fig. 4C), and only for Si and P, a minimum for the trans-transition states of EH₂(OH)₂ⁿ is slightly developed. This deviation is explained by hydrogen bonding, which is more efficient in the transition than in the ground states (see Chapter S11 in the ESI† for a detailed discussion). A comparison of different transition state conformers of the EH(OH)₃ⁿ class of compounds allowed to estimate the transition state stabilization for the individual elements to approximately 5 (E = Al), 10 (E = Ga), 12 (E = Si), 15 (E = Ge), and 21 (E = P, As) kJ mol⁻¹ per hydrogen bond on top of the direct electronic effects. A similar trend is found for the nitrile and ethynyl substituents, which are σ-acceptors (Fig. 4D) – no saturation occurs. The inversion barriers steadily drop with each substitution, finding a minimum for the four-fold substituted derivatives ER₄ⁿ (R = CN, CCH).

In all cases, the E–R bonds elongate upon going from the tetrahedral to square planar state (see Chapter S4 in the ESI†). Despite the larger s-orbital character at the central element in the transition states (Table S11 in the ESI†), this elongation agrees with the diminished formal bond order.

Excitingly, some compounds show inversion barriers that are easily surpassed at ambient conditions. For example, the di-substituted group 13 anions (EH₂R₂⁻) show barriers corresponding to configurational stability half-lives of several minutes at 25 °C. Most remarkably, Al(OH)₄⁻ has an inversion barrier of 116 kJ mol⁻¹. This well-known anion occurs during the Bayer process in worldwide aluminum production.⁹⁴ Process temperatures of 200 °C correspond to a tetrahedron inversion half-life for Al(OH)₄⁻ of ≈0.5 s. Thought-provokingly, a tetrahedral inversion process is, and was, happening for more than 130 years at a gigatonne scale but went unnoticed due to the degeneracy of products and educts.

Molecular orbitals during the deformation toward and in the transition state

For the rationalization of the inversion barrier energies, the discussion is narrowed to the homoleptic compounds, ER₄ⁿ, as their inversion transition states are of D_4h symmetry, facilitating MO theoretical considerations. In the following section, the intrinsic reaction coordinate (IRC) connecting the T_d symmetric ground state with the inversion transition state is analyzed for SiH_4, SiF₄, and Si(CN)₄. This is done with respect to the changes occurring in molecular orbital energies along the IRC (Walsh-type diagrams, Fig. 5). Comparisons among those three compounds illustrate the effects of π-donor or σ-acceptor substituents on the orbital energies. The generality of these findings was supported by sampling analysis throughout the data of other species.

Fig. 5 Kohn–Sham frontier molecular orbital energies along the inversion reaction coordinate and the corresponding molecular orbital isodensity plots (contour value 0.03 a.u.) of the D_4h symmetric inversion transition state of (A) SiH₄, (B) SiF₄, and (C) Si(CN)₄.

For the D_4h symmetric states of the element hydrides EH₄ⁿ (E = Al⁻, Si, Ga⁻, Ge), the Kohn–Sham molecular orbitals are in line with the qualitative perturbational MO-picture given in Fig. 2A: a HOMO of b_1g and LUMO a_2u symmetry. This is quantitatively illustrated for SiH₄ in Fig. 5A. SiH₄ possesses a relatively small FMO gap of 1.1 eV in its inversion transition state. The LUMO+1 is the anti-bonding 2a_1g molecular orbital which remains high in energy along the inversion reaction coordinate. In contrast, for systems with σ-acceptor/π-donor substituents, e.g. SiF₄ (Fig. 5B), the energetic spacing between the FMOs (6.7 eV) is much wider in the D_4h state than for the hydride. This difference is the consequence of the following:

(1) The a_2u orbital in D_4h symmetric SiH₄ is non-bonding, whereas its counterpart (2t₂) is fully anti-bonding in the tetrahedral ground state. Hence, it drops substantially by 5.3 eV upon planarization. For SiF₄, this drop is mitigated to 4.1 eV, as the a_2u orbital remains slightly anti-bonding in the D_4h state due to the π-donor interaction with the fluorides (→ π-donor effect).

(2) All the highest occupied molecular orbitals of the square planar transition states are constituted from the substituents. Hence, they are substantially lower in energy for fluorides in SiF₄ than for the hydrides in SiH₄ (→ σ-acceptor effect).

These effects increase the FMO gap in the transition state and also influence the energetic ordering of the orbitals. The diminished energy drop of the empty a_2u orbital in SiF₄ causes the LUMO to be of a_1g symmetry. The a_2u molecular orbital turns out as LUMO+1 (Fig. 5B).

The MO-situation for Si(CN)₄ settles between the hydrides and fluorides (Fig. 5C). As in the case of SiH₄, the a_2u orbital drops substantially, but the occupied orbitals remain little affected, resembling the situation of SiF₄. This signature reflects the σ-acceptor character of the nitrile group but the inability for π-donation, which would prevent the a_2u orbital from lowering in energy (as is the case for SiF₄).

The inversion transition state and the associated barrier evaluated by the SOJTE–FMO approximation

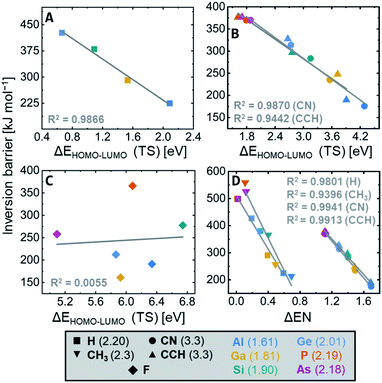
The general SOJTE–FMO hypothesis developed in the introduction claims that the barrier should increase with a decreasing FMO gap in the inversion transition state. Indeed, for the element hydrides, EH₄, a good correlation is obtained by plotting the FMO gap of the transition states against the inversion barrier heights (Fig. 6A). The smaller the FMO gap becomes, the larger is the inversion activation barrier. As shown in Fig. 6B, also σ-acceptor (nitrile and ethynyl) substituted systems show this correlation, indicating that these systems indeed obey the SOJTE-model sufficiently. It even holds reasonably for the entire set of EH_4−yR_yⁿ (R = CN, CCH, see Fig. S26 in the ESI†). Plotting the hydride and the CN/CCH correlations in the same chart gives an offset between the two groups (see Fig. S27 in the ESI†). This is due to differences in vibrational coupling constants and the primary force constant, which are not included in the SOJTE–FMO model (cf.Fig. 2C). Interestingly, CCH and CN correlate rather well (Fig. S24 and S25 in the ESI†), as both groups bind through sp-hybridized carbon atoms.

Fig. 6 Correlation plots of the inversion barrier height versus the Kohn–Sham HOMO–LUMO gap in the inversion transition state for (A) EH₄ⁿ, (B) E(CN)₄ⁿ and E(CCH)₄ⁿ, and (C) EF₄ⁿ, for which the correlation vanishes. (D) Correlation plot of the inversion barrier height versus the difference in electronegativity between the central element and substituents for ER₄ⁿ, R = H, CH₃, CN, CCH. Pauling (group) electronegativities are given in parenthesis in the legend.

Overall, these are unprecedented findings that allow explaining the influence of the central element and σ-acceptors on tetrahedral inversion barriers along the following arguments:

• The a_2u LUMO is localized at the central element whose electronegativity (EN) determines its orbital energy.¹ A larger EN causes a lower a_2u energy which leads to a smaller FMO gap. Consequently, the inversion barrier increases with the EN of the central element.

• The b_1g HOMO is located at the substituents. Thus, its energy is determined by the substituents' EN. An increasing EN lowers the HOMO energy and, therefore, the FMO gap. Consequently, the inversion barrier decreases with the EN of the substituents.

Indeed, the EN increases from left to right in the periodic table, as does the inversion barrier (Al < Si < P/Ga < Ge < As). The EN also increases from period three to period four (d-block effect), in line with the observed trend of inversion barriers between the periods (Al < Ga/Si < Ge/P ≈ As). If the FMO gap becomes too small, as for the most electronegative central elements P and As, multiconfigurational approaches are needed for an accurate description. Of course, one should consider that the absence of inner shell p-electrons leads to additional differences between the second and higher period elements, which are not considered here.^95,96

Having found these correlations, it was tempting to probe the difference of electronegativities of central elements and substituents as a parameter for the inversion barrier. Indeed, for the non-π-donor substituents (H, CH₃, CN, CCH), a proper correlation can be found (Fig. 6D). The observed offset again occurs due to differences in vibrational coupling constants and the primary force constant between E–H and E–C bonds. Interestingly, the group electronegativities of nitrile (3.3) and ethynyl (3.3) are identical.⁹⁷ Accordingly, their effect on the inversion barriers is almost the same.

Coming back to the SOJTE-approximation, the correlation was probed for π-donor cases next. For the fluoride substituted derivatives, EF₄ⁿ, the SOJTE-correlation breaks down (Fig. 6C). The same is observed for the hydroxy- and amido-substituted systems, which do not provide any apparent correlations between inversion barriers and FMO gaps in the D_4h state. Although the model recaptures validity along Cl < Br < I with a steady increase in the correlation coefficient (Fig. S18–S20 in the ESI†), it is far from ideal. Hence, for π-donor substituted systems, additional factors cause deviations from the SOJTE–FMO model. Similar observations have been made for the trigonal inversion of group 15 halido pyramids.⁴⁸ After all, one must not forget the participation of higher excited states that become particularly important for substituents with lone pairs but which are not considered in this approximation. However, the stabilizing effect of π-donor substituent can be understood qualitatively through the framework of the SOJTE.

• The lone pairs at the substituents interact with the a_2u orbital at the central atom. Hereby, the a_2u orbital becomes anti-bonding and increases in energy. The FMO gap in the transition state becomes larger for π-donors, and the inversion barrier decreases.

Summing up the ligand effects: if the electronegativity of the substituents increases, the b_1g molecular orbital becomes stabilized, the FMO gap increases and the barrier becomes lower (σ-acceptor effect). For π-donor substituents, the donation leads to an FMO gap increase by raising the energy of the a_2u molecular orbital. Gauged by the absolute values, π-donation appears more effective than σ-acceptance. For the hydride species and those substituted with less electronegative and non-π-donor groups, the SOJTE is a quantitatively fitting model. Here, the tetrahedral preference and the inversion barrier are dominated by orbital overlap effects. For π-donor substituents, the situation is more complex, and additional factors come into play that are elucidated next.

Analysis of differences in atom and bond properties by NBO, QTAIM, and EDA

To corroborate and extend the interpretations from the SOJTE analysis, the ground and inversion transition states for selected compounds were investigated by natural population analysis (see Chapter S14 of the ESI† for all data of the ER₄ⁿ compounds).⁹⁸ For SiH₄ and Si(CN)₄, the natural charge at Si gets more positive in the transition state. In contrast, for SiF_4, the transition state has a less positively polarized silicon center (Table 1). These characteristics, namely, stronger positive polarization of the central element for hydride and σ-acceptor-substituted systems (H, CH₃, CN, CCH) in the transition state and significantly less positive polarization for molecules with π-donor groups (F, OH, Cl, Br, NH₂) are indicated throughout the entire set, substantiating a clear difference between both types.

Table 1 NBO and QTAIM analysis (both obtained from densities calculated with PBE0/def2-TZVPP) of the tetrahedral ground state (GS) and square planar inversion transition state (TS) of SiH₄, SiF₄, and Si(CN)₄. Notations, ρ_BCP: electron density at the bond critical point, ∇²ρ_BCP: its Laplacian, K: Kraka's energy density descriptor, DI: bond delocalization index, BE: bond ellipticity. All values are given in atomic units

Compound		NBO charges		QTAIM analysis
		Si	R = H, F, CN	ρ BCP	∇^2ρBCP	K	DI	BE
SiH4	GS	0.560	−0.140	0.122	0.173	−0.0747	0.545	0.0008
	TS	1.137	−0.284	0.115	0.069	−0.0742	0.503	0.0192
	Diff.	0.578		−0.007	−0.104	0.0005	−0.042	0.0184
SiF4	GS	2.531	−0.633	0.154	1.135	−0.0492	0.351	0.0004
	TS	2.522	−0.631	0.142	0.959	−0.0495	0.359	0.0788
	Diff.	−0.009		−0.012	−0.176	−0.0003	0.008	0.0784
Si(CN)4	GS	1.362	−0.173	0.124	0.299	−0.0696	0.408	0.0003
	TS	1.580	−0.219	0.119	0.266	−0.0668	0.394	0.0596
	Diff.	0.218		−0.006	−0.033	0.0028	−0.014	0.0593

---

Changes in bond characteristics that occur during the inversion process were further inspected by QTAIM.⁹⁹ For molecules with hydride or σ-acceptor substituents, the electron density at the bond critical points (ρ_BCP) diminishes upon planarization (Table 1). The same trend is observed for the Laplacian of the electron density (∇²ρ_BCP), mirroring the generally diminished bonding strength. As an indicator of the amount of covalency, Kraka's energy density descriptor (K) and the delocalization index between Si and R (DI) were considered.^100,101 These parameters are indicating a diminished amount of covalency in the transition state (DI ↓, K ↑), in line with molecular orbital theory. Strikingly, for the π-donor systems, the situation is different. In SiF₄, the electron density and its Laplacian decrease, but the DI increases, and K decreases upon transformation to the transition state. These features indicate a diminished strength of bonding in the transition states with π-donors, but an increase in bond covalency! The bond ellipticity (BE) increases stronger for SiF₄ as for SiH₄ and Si(CN)₄, supporting a π-back bonding effect already noticed by the analysis of natural atomic charges and assumed qualitatively by the perturbational MO/SOJTE-arguments. Again, those characteristics were supported by control sampling throughout the entire set of ER₄ⁿ molecules.

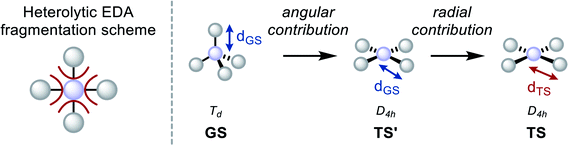
To verify and extend these hypotheses, the interaction between substituents and central elements was inspected by Ziegler and Rauk's version of the energy decomposition analysis (EDA).^102–105 Specifically, it was considered how Pauli repulsion (ΔE_Pauli), electrostatic (ΔE_Coul), and orbital interactions (ΔE_Orb) between substituent fragments and the central element change during planarization. Moreover, the process was dissected in a radial (change of bond lengths) and angular deformation (change in bond angle, Table 2), as recently demonstrated elsewhere.^106,107 Heterolytic fragmentation was chosen due to, on average, less sizeable orbital relaxation energy, as frequently suggested (Table 2).^108–110 Further, it was verified that the general conclusions are neither depending on the type (heterolytic vs. homolytic) or the number (four bonds vs. one bond) of fragmentation(s), nor on the order of deformation (i.e. radial/angular yields practically identical numbers as angular/radial, see Chapter S15 in the ESI†). The most significant points are illustrated here for SiH₄ and SiF₄.

Table 2 Energy decomposition analysis (BP86-D3(BJ)/QZ4P) of the ground state (GS) and the inversion transition state (TS) of SiH₄ and SiF₄. Individual angular and radial contributions were derived with the help of a D_4h symmetric structure with the bond lengths of the ground state (TS′). All numbers are given in kJ mol⁻¹. The values in parenthesis specify the contribution of the interaction and the preparation energy to the inversion barrier (Δ(ΔE_Int + ΔE_Prep), see Chapter S15 in the ESI for details). The values in brackets state the relative electrostatic and orbital contribution to the difference in interaction energy

		GS	TS′	TS	Angular contribution (GS → TS′, ΔΔEA)	Radial contribution (TS' → TS, ΔΔER)	Total (GS → TS, ΔΔE)
SiH4	ΔEPauli	692.0	709.5	582.4	17.5	−127.1	−109.6
	ΔECoul	−7847.3	−7807.0	−7795.3	40.3	11.7	52.0 [12%]
	ΔEOrb	−6241.3	−6018.8	−5872.7	222.6	146.0	368.6 [88%]
	ΔΔEInt				280.4	30.6	311.0 (85%)
	ΔΔEPrep				97.4	−43.3	54.1 (15%)
	Δ(ΔEInt + ΔEPrep)				377.8	−12.6	365.2
SiF4	ΔEPauli	957.8	961.9	831.5	4.1	−130.4	−126.3
	ΔECoul	−10558.3	−10406.3	−10370.2	152.0	36.1	188.2 [66%]
	ΔEOrb	−4277.9	−4317.1	−4182.5	−39.2	134.7	95.5 [34%]
	ΔΔEInt				117.0	40.4	157.3 (62%)
	ΔΔEPrep				154.8	−59.5	95.3 (38%)
	Δ(ΔEInt + ΔEPrep)				271.7	−19.1	252.6

---

The energy differences upon planarization for SiH₄ reveal that the barrier is dominated by a loss of ΔE_Orb, whereas ΔΔE_Coul is less decisive (Table 2). The relief of ΔE_Pauli is a consequence of the bond elongation in the square planar state. This becomes evident by inspecting the results of angular and radial deformation contributions. Upon distorting the ground state to square planarity, while conserving the bond lengths (“angular contribution”), the major portion of ΔE_Orb is lost, but ΔE_Pauli increases. Subsequent bond length relaxation (“radial contribution”) leads to a substantial reduction in ΔE_Pauli and a further reduction of ΔE_Orb. Thus, the bond elongation in the TS is a result of ΔE_Pauli-lowering, similar to the recently described effects for CH-bond lengths in the series of spⁿ (n = 1–3) hybridized carbon atoms.¹¹¹ The differences in preparation energy (ΔΔE_Prep) need to be added to reproduce the final inversion barrier energies. ΔΔE_Prep can be understood as the part of the inversion barrier caused by substituent–substituent repulsion. For SiH₄, ΔΔE_Prep is relatively small.

The situation is different for SiF₄. Here, the primary cause for the inversion barrier is the loss in ΔE_Coul (Table 2) and a larger relative amount of ΔΔE_Prep. As can be seen from the angular/radial analysis, both energies are mainly the consequence of the bending deformation. Remarkably, ΔE_Orb even increases when going from the ground state to the D_4h state with GS-bond lengths. This means that the covalent bonding of the fluorides to silicon is more effective in a compressed D_4h state. As for SiH₄, relaxation of the bond lengths to the optimized distance leads to an overall diminished ΔE_Orb and ΔE_Pauli. The larger value of ΔΔE_Prep can be understood as a consequence of electrostatic repulsion of the more negatively polarized fluorides and actual intersubstituent steric Pauli repulsion.

Comparing the contributions in bond energy changes and the percental contribution of the preparation energy on the overall barrier (values in parentheses in the Table 2) emphasizes the statements. The inversion barrier in SiH₄ is dominated by an energy loss in ΔE_Orb, but the barrier in SiF₄ is due to a loss in ΔE_Coul and a larger substituent–substituent repulsion (ΔΔE_Prep). Indeed, the loss of ΔE_Orb in the square planar state is not decisive at all. This picture is in line with the interpretation from real-space bonding analyses, which do not rely on artificially chosen reference states (cf. increased covalent bonding in the D_4h state of SiF₄, see Table 1).

Conclusions

The trigonal inversion of ER₃ species is well understood and this knowledge has been used in various contexts (e.g., phosphines can serve as chiral ligands whereas amines cannot). In contrast, the inversion of ER₄ species and their configurational stability has been virtually unexplored. The present study gives accurate barrier heights for p-block tetrahedron inversions through planar transition states. Barriers increase from group 13 to group 15 and decrease with π-donor/σ-acceptor substituents. Fundamentally, the second-order Jahn–Teller effect (SOJTE) is identified as a solid model to explain these general trends qualitatively. The core argument is: the closer the energies of the HOMO (b_1g) and the LUMO (a_2u) are in the D_4h symmetric inversion transition state, the stronger they mix, and the more energy is released upon relaxation into the tetrahedral ground state (see step-by-step explanation in the introduction). In turn, a larger energy release for D_4h → T_d corresponds to a larger inversion barrier T_d → D_4h → T_d (Fig. 7). The inverse correlation of HOMO–LUMO gap and energy also agrees with Pearson's principle of maximum hardness – the larger the gap, the more stable (the lower) the inversion transition state.¹¹² Electronegative central elements lower the LUMO (a_2u) energy; the inversion barrier increases. With more electronegative substituents, the HOMO (b_1g) energy is lowered; the inversion barrier decreases (σ-acceptor effect). π-Donor substituents increase the LUMO energy; the inversion barrier decreases (π-donor effect). Interestingly, these substituent effects are inverse to that found for carbon-based tetrahedra, owing to the inverted FMO symmetries (cf.Fig. 2A).⁴

Fig. 7 Simplified presentation of the factors that determine the height of the planar inversion barrier of tetrahedral p-block element-based species, for which the substituents are more electronegative than the central elements.

Correlations between FMO gap and inversion barrier are obtained for hydrides, sustain for sole σ-acceptor substituents, but almost vanish for π-donor groups. NBO, EDA, and QTAIM calculations shed light on these deviations. For less electronegative substituents, the tetrahedral preference is determined by optimal orbital overlap, thus conforming to the SOJTE-model. For σ-acceptor/π-donor substituents, the tetrahedral preference is dominated by favorable electrostatics and diminished ligand–ligand repulsion. Strikingly, the covalency in T_d and D_4h configurations is almost equal in compounds such as SiF₄ due to the favorable π-back bonding in the planar state.

There might be more than only fundamental interest in “molecular fluctionality”.¹¹³ One-third of the compounds studied in this contribution show transition state energies corresponding to configurational instability at ambient to elevated temperatures. One prominent example is Al(OH)₄⁻, which is right now exhibiting tetrahedral inversion at tonne scale (Baeyer process) without being recognized.

What are the consequences of low inversion barrier heights in our geosphere (aluminates) or materials properties (silicones)? Are there features that can be achieved by exploiting tetrahedral “hinges” for three-dimensional connectivity with shape “adaptive” behavior?¹¹⁴ Another aspect is the connection of molecular flexibility with the phenomenon of Lewis acidity. It has been noticed that the energy required to deform a Lewis acid into the structure of the Lewis adduct effectively quenches Lewis acidity.^115,116 In other words, compounds with a low deformation energy yield potentially strong Lewis acids. Of course, the deformation energy of tetrahedral compounds is entangled with the inversion barrier. Hence, the knowledge of tetrahedral inversion offers strategies to design Lewis acids that garner strengths not only from electron withdrawal but also from a low structural deformation penalty. Indeed, this has been proven most recently.^117,118

The herein-developed perspective of the process of tetrahedral inversion might be in parts too simplified (neglected effects of vibronic coupling constants and higher excited states). Still, it bolsters our fundamental understanding of molecular flexibility and might propel further realizations of anti-van't-Hoff–Le-Bel configurations by guided choice.

Data availability

The datasets supporting this article have been uploaded as part of the ESI† material.

Author contributions

All authors produced and interpreted the data. L. M. S. and L. G. wrote the manuscript. L. G. supervised the project.

Conflicts of interest

No conflict of interest is declared by the authors.

Acknowledgements

Prof. H.-J. Himmel is thanked for his constant support. Financial support was provided by the DFG (GR5007/2-1) and the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 948708). L. M. S. is grateful to the Studienstiftung des deutschen Volkes for a scholarship. The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster).

Notes and references

1. T. A. Albright, J. K. Burdett and M.-H. Whangbo, Orbital Interactions in Chemistry, Wiley, Hoboken, NJ, 2013.
2. R. J. Gillespie, Coord. Chem. Rev., 2008, 252, 1315–1327.
3. H. J. Monkhorst, Chem. Commun., 1968, 1111–1112,  10.1039/C19680001111.
4. R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4992–4993.
5. V. I. Minkin, R. M. Minyaev and R. Hoffmann, Russ. Chem. Rev., 2002, 71, 869–892.
6. S. Durmaz, J. N. Murrell and J. B. Pedley, J. Chem. Soc., Chem. Commun., 1972, 933–934,  10.1039/C39720000933.
7. D. C. Crans and J. P. Snyder, J. Am. Chem. Soc., 1980, 102, 7152–7154.
8. M. S. Gordon and M. W. Schmidt, J. Am. Chem. Soc., 1993, 115, 7486–7492.
9. M. J. M. Pepper, I. Shavitt, P. V. R. Schleyer, M. N. Glukhovtsev, R. Janoschek and M. Quack, J. Comput. Chem., 1995, 16, 207–225.
10. D. Röttger and G. Erker, Angew. Chem., Int. Ed., 1997, 36, 812–827.
11. R. Keese, Chem. Rev., 2006, 106, 4787–4808.
12. G. Merino, M. A. Méndez-Rojas, A. Vela and T. Heine, J. Comput. Chem., 2007, 28, 362–372.
13. V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Nat. Rev. Chem., 2018, 2, 0114.
14. L. Leyva-Parra, L. Diego, O. Yañez, D. Inostroza, J. Barroso, A. Vásquez-Espinal, G. Merino and W. Tiznado, Angew. Chem., Int. Ed., 2021, 60, 8700–8704.
15. M. B. Krogh-Jespersen, J. Chandrasekhar, E. U. Wuerthwein, J. B. Collins and P. von Ragué Schleyer, J. Am. Chem. Soc., 1980, 102, 2263–2268.
16. D. A. Dixon and A. J. Arduengo, J. Phys. Chem., 1987, 91, 3195–3200.
17. D. A. Dixon and A. J. Arduengo, J. Chem. Soc., Chem. Commun., 1987, 498–500,  10.1039/C39870000498.
18. E.-U. Würthwein and P. von Ragué Schleyer, Angew. Chem., Int. Ed., 1979, 18, 553–554.
19. A. I. Boldyrev, P. von Ragué Schleyer and R. Keese, Mendeleev Commun., 1992, 2, 93–95.
20. P. Belanzoni, G. Giorgi, G. F. Cerofolini and A. Sgamellotti, J. Phys. Chem. A, 2006, 110, 4582–4591.
21. P. Belanzoni, G. Giorgi, G. F. Cerofolini and A. Sgamellotti, Theor. Chem. Acc., 2006, 115, 448–459.
22. L. Fang, C. Zhang, X. Cao and Z. Cao, J. Phys. Chem. C, 2020, 124, 18660–18669.
23. Y. Zhang, C. Zhang, Y. Mo and Z. Cao, Chem.–Eur. J., 2021, 27, 1402–1409.
24. D. Szieberth, M. Takahashi and Y. Kawazoe, J. Phys. Chem. A, 2009, 113, 707–712.
25. P. v. R. Schleyer and A. E. Reed, J. Am. Chem. Soc., 1988, 110, 4453–4454.
26. S.-D. Li, C.-Q. Miao, J.-C. Guo and G.-M. Ren, J. Am. Chem. Soc., 2004, 126, 16227–16231.
27. S.-D. Li, G.-M. Ren and C.-Q. Miao, Inorg. Chem., 2004, 43, 6331–6333.
28. T. N. Gribanova, R. M. Minyaev and V. I. Minkin, Russ. J. Gen. Chem., 2005, 75, 1651–1658.
29. S.-D. Li, J.-C. Guo, C.-Q. Miao and G.-M. Ren, J. Phys. Chem. A, 2005, 109, 4133–4136.
30. S.-D. Li and C.-Q. Miao, J. Phys. Chem. A, 2005, 109, 7594–7597.
31. J.-C. Guo and S.-D. Li, J. Mol. Struct.: THEOCHEM, 2007, 816, 59–65.
32. W. Tiznado, N. Perez-Peralta, R. Islas, A. Toro-Labbe, J. M. Ugalde and G. Merino, J. Am. Chem. Soc., 2009, 131, 9426–9431.
33. Y. Li, F. Li, Z. Zhou and Z. Chen, J. Am. Chem. Soc., 2011, 133, 900–908.
34. J.-C. Guo, C.-Q. Miao and G.-M. Ren, Comput. Theor. Chem., 2014, 1032, 7–11.
35. J. Xu and Y.-h. Ding, J. Comput. Chem., 2015, 36, 355–360.
36. M.-J. Sun, X. Cao and Z. Cao, Nanoscale, 2018, 10, 10450–10458.
37. V. S. Thimmakondu and K. Thirumoorthy, Comput. Theor. Chem., 2019, 1157, 40–46.
38. M.-h. Wang, X. Dong, Z.-h. Cui, M. Orozco-Ic, Y.-h. Ding, J. Barroso and G. Merino, Chem. Commun., 2020, 56, 13772–13775.
39. Y. Wang, Y. Li and Z. Chen, Acc. Chem. Res., 2020, 53, 887–895.
40. C. Zhang, Z. Tian and W. Jia, J. Phys. Chem. A, 2021, 125, 843–847.
41. J. M. Lehn, in Top. Curr. Chem., Springer Berlin Heidelberg, 1970, vol. 15/3, ch. 2, pp. 311–377.
42. A. Rauk, L. C. Allen and K. Mislow, Angew. Chem., Int. Ed., 1970, 9, 400–414.
43. A. I. Boldyrev and O. P. Charkin, J. Struct. Chem., 1985, 26, 451–475.
44. C. C. Levin, J. Am. Chem. Soc., 1975, 97, 5649–5655.
45. W. Cherry and N. Epiotis, J. Am. Chem. Soc., 1976, 98, 1135–1140.
46. R. F. See, A. D. Dutoi, K. W. McConnell and R. M. Naylor, J. Am. Chem. Soc., 2001, 123, 2839–2848.
47. P. Schwerdtfeger, L. J. Laakkonen and P. Pyykkö, J. Chem. Phys., 1992, 96, 6807–6819.
48. P. Schwerdtfeger, P. D. W. Boyd, T. Fischer, P. Hunt and M. Liddell, J. Am. Chem. Soc., 1994, 116, 9620–9633.
49. M. Atanasov and D. Reinen, J. Phys. Chem. A, 2001, 105, 5450–5467.
50. M. Atanasov and D. Reinen, J. Am. Chem. Soc., 2002, 124, 6693–6705.
51. L. T. Xu, T. Y. Takeshita and T. H. Dunning, Theor. Chem. Acc., 2014, 133, 1493.
52. S. Pelzer, K. Wichmann, R. Wesendrup and P. Schwerdtfeger, J. Phys. Chem. A, 2002, 106, 6387–6394.
53. Z. Varga, P. Verma and D. G. Truhlar, J. Phys. Chem. A, 2019, 123, 301–312.
54. B. M. Gimarc, Acc. Chem. Res., 1974, 7, 384–392.
55. A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1998, 120, 7967–7972.
56. M. Driess, J. Aust, K. Merz and C. van Wullen, Angew. Chem., Int. Ed., 1999, 38, 3677–3680.
57. X. Li, L.-S. Wang, A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1999, 121, 6033–6038.
58. L.-S. Wang, A. I. Boldyrev, X. Li and J. Simons, J. Am. Chem. Soc., 2000, 122, 7681–7687.
59. D. W. Stephan, Angew. Chem., Int. Ed., 2000, 39, 501–502.
60. A. I. Boldyrev, X. Li and L.-S. Wang, Angew. Chem., Int. Ed., 2000, 39, 3307–3310.
61. N. L. Dunn, M. Ha and A. T. Radosevich, J. Am. Chem. Soc., 2012, 134, 11330–11333.
62. E. J. Thompson, T. W. Myers and L. A. Berben, Angew. Chem., Int. Ed., 2014, 53, 14132–14134.
63. T. P. Robinson, D. M. De Rosa, S. Aldridge and J. M. Goicoechea, Angew. Chem., Int. Ed. Engl., 2015, 54, 13758–13763.
64. K. Lee, A. V. Blake, A. Tanushi, S. M. McCarthy, D. Kim, S. M. Loria, C. M. Donahue, K. D. Spielvogel, J. M. Keith, S. R. Daly and A. T. Radosevich, Angew. Chem., Int. Ed., 2019, 58, 6993–6998.
65. F. Ebner, H. Wadepohl and L. Greb, J. Am. Chem. Soc., 2019, 141, 18009–18012.
66. T. M. Bass, C. R. Carr, T. J. Sherbow, J. C. Fettinger and L. A. Berben, Inorg. Chem., 2020, 59, 13517–13523.
67. F. Ebner, L. M. Sigmund and L. Greb, Angew. Chem., Int. Ed., 2020, 59, 17118–17124.
68. L. M. Sigmund and L. Greb, Chem. Sci., 2020, 11, 9611–9616.
69. P. Ghana, J. Rump, G. Schnakenburg, M. I. Arz and A. C. Filippou, J. Am. Chem. Soc., 2021, 143, 420–432.
70. J. M. Lipshultz, G. Li and A. T. Radosevich, J. Am. Chem. Soc., 2021, 143, 1699–1721.
71. K. Yoshizawa and A. Suzuki, Chem. Phys., 2001, 271, 41–54.
72. H. C. Longuet-Higgins and C. A. Coulson, Proc. R. Soc. London, Ser. A, 1956, 235, 537–543.
73. U. Öpik and M. H. L. Pryce, Proc. R. Soc. London, Ser. A, 1957, 238, 425–447.
74. R. F. W. Bader, Can. J. Chem., 1962, 40, 1164–1175.
75. I. B. Bersuker, Chem. Rev., 2001, 101, 1067–1114.
76. I. B. Bersuker, Chem. Rev., 2013, 113, 1351–1390.
77. I. B. Bersuker, Chem. Rev., 2021, 121, 1463–1512.
78. R. G. Pearson, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 2104–2106.
79. R. G. Pearson, J. Mol. Struct.: THEOCHEM, 1983, 103, 25–34.
80. R. G. Pearson, Symmetry Rules for Chemical Reactions: Orbital Topology and Elementary Processes, J. Wiley & Sons, New York, 1976.
81. H. A. Jahn and E. Teller, Proc. R. Soc. London, Ser. A, 1937, 161, 220–235.
82. W. Hermoso, A. R. Ilkhani and I. B. Bersuker, Comput. Theor. Chem., 2014, 1049, 109–114.
83. L. S. Bartell, J. Chem. Educ., 1968, 45, 754.
84. R. G. Pearson, J. Am. Chem. Soc., 1969, 91, 4947–4955.
85. W. Cherry, N. Epiotis and W. T. Borden, Acc. Chem. Res., 1977, 10, 167–173.
86. J. K. Burdett, Chem. Soc. Rev., 1978, 7, 507–526.
87. F. Cimpoesu and K. Hirao, in Adv. Quantum Chem., Academic Press, 2003, vol. 44, pp. 369–387.
88. S. Kozuch, D. A. Hrovat and W. T. Borden, J. Am. Chem. Soc., 2013, 135, 19282–19291.
89. I. B. Bersuker, N. N. Gorinchoi and V. Z. Polinger, J. Mol. Struct., 1992, 270, 369–380.
90. A. F. Saturno, Theor. Chim. Acta, 1967, 8, 273–276.
91. A. Najibi and L. Goerigk, J. Comput. Chem., 2020, 41, 2562–2572.
92. E. J. Baerends, O. V. Gritsenko and R. van Meer, Phys. Chem. Chem. Phys., 2013, 15, 16408–16425.
93. R. van Meer, O. V. Gritsenko and E. J. Baerends, J. Chem. Theory Comput., 2014, 10, 4432–4441.
94. J. C. Southern, in Materials & Equipment/Whitewares: Ceramic Engineering and Science Proceedings, ed. W. M. Carty, The American Ceramic Society, Westerville, OH, 2nd edn, 2001, vol. 22, ch. 12, p. 59.
95. W. Kutzelnigg, Angew. Chem., Int. Ed., 1984, 23, 272–295.
96. Z.-L. Wang, H.-S. Hu, L. von Szentpály, H. Stoll, S. Fritzsche, P. Pyykkö, W. H. E. Schwarz and J. Li, Chem.–Eur. J., 2020, 26, 15558–15564.
97. P. R. Wells, in Progress in Physical Organic Chemistry, ed. A. J. Streitwieser and R. W. Taft, John Wiley and Sons, Inc., New York, 1968, vol. 6, ch. 3, pp. 111–145.
98. E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42.
99. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
100. C. Outeiral, M. A. Vincent, Á. M. Pendás and P. L. A. Popelier, Chem. Sci., 2018, 9, 5517–5529.
101. D. Cremer and E. Kraka, Angew. Chem., Int. Ed., 1984, 23, 627–628.
102. L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345.
103. M. v. Hopffgarten and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43–62.
104. T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10.
105. M. v. Hopffgarten and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43–62.
106. D. Rodrigues Silva, L. de Azevedo Santos, M. P. Freitas, C. F. Guerra and T. A. Hamlin, Chem.–Asian J., 2020, 15, 4043–4054.
107. P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649–667.
108. A. Krapp, K. K. Pandey and G. Frenking, J. Am. Chem. Soc., 2007, 129, 7596–7610.
109. R. Tonner and G. Frenking, Chem.–Eur. J., 2008, 14, 3260–3272.
110. C. Mohapatra, S. Kundu, A. N. Paesch, R. Herbst-Irmer, D. Stalke, D. M. Andrada, G. Frenking and H. W. Roesky, J. Am. Chem. Soc., 2016, 138, 10429–10432.
111. P. Vermeeren, W.-J. van Zeist, T. A. Hamlin, C. Fonseca Guerra and F. M. Bickelhaupt, Chem.–Eur. J., 2021, 27, 7074–7079.
112. R. G. Pearson, Acc. Chem. Res., 1993, 26, 250–255.
113. M. L. McKee, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 943–951.
114. J.-M. Lehn, Angew. Chem., Int. Ed., 2015, 54, 3276–3289.
115. R. M. Guidry and R. S. Drago, J. Am. Chem. Soc., 1973, 95, 759–763.
116. H. Fleischer, Eur. J. Inorg. Chem., 2001, 2001, 393–404.
117. D. Roth, J. Stirn, D. W. Stephan and L. Greb, J. Am. Chem. Soc., 2021, 143, 15845–15851.
118. A. Ben Saida, A. Chardon, A. Osi, N. Tumanov, J. Wouters, A. I. Adjieufack, B. Champagne and G. Berionni, Angew. Chem., Int. Ed., 2019, 58, 16889–16893.

---

Footnote

† Electronic supplementary information (ESI) available: Full computational details, all calculated data, additional plots, further discussions. All xyz coordinates and molecular energies are given in a separate file. See DOI: 10.1039/d1sc05395g

---