Open Access Article
Open Access ArticleSynergetic stability enhancement with magnesium and calcium ion substitution for Ni/Mn-based P2-type sodium-ion battery cathodes†
Hongwei
Fu‡
a,
Yun-Peng
Wang‡
b,
Guozheng
Fan
c,
Shan
Guo
a,
Xuesong
Xie
a,
Xinxin
Cao
 a,
Bingan
Lu
a,
Bingan
Lu
 d,
Mengqiu
Long
d,
Mengqiu
Long
 e,
Jiang
Zhou
e,
Jiang
Zhou
 *af and
Shuquan
Liang
*af and
Shuquan
Liang
 *a
*a
aSchool of Materials Science and Engineering, Key Laboratory of Electronic Packaging and Advanced Functional Materials of Hunan Province, Central South University, Changsha 410083, China. E-mail: zhou_jiang@csu.edu.cn; lsq@csu.edu.cn
bSchool of Physics and Electronics, Hunan Key Laboratory for Super-micro Structure and Ultrafast Process, Central South University, 932 South Lushan Road, Changsha, China
cBremen Center for Computational Materials Science, University of Bremen, Bremen 28359, Germany
dSchool of Physics and Electronics, State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China
eSchool of Physics and Electronics, Central South University, Changsha 410083, Hunan, P. R. China
fCollege of Chemistry and Chemical Engineering, Jishou University, Jishou, Hunan 416000, P. R. China
First published on 21st December 2021
Abstract
The conventional P2-type cathode material Na0.67Ni0.33Mn0.67O2 suffers from an irreversible P2–O2 phase transition and serious capacity fading during cycling. Here, we successfully carry out magnesium and calcium ion doping into the transition-metal layers (TM layers) and the alkali-metal layers (AM layers), respectively, of Na0.67Ni0.33Mn0.67O2. Both Mg and Ca doping can reduce O-type stacking in the high-voltage region, leading to enhanced cycling endurance, however, this is associated with a decrease in capacity. The results of density functional theory (DFT) studies reveal that the introduction of Mg2+ and Ca2+ make high-voltage reactions (oxygen redox and Ni4+/Ni3+ redox reactions) less accessible. Thanks to the synergetic effect of co-doping with Mg2+ and Ca2+ ions, the adverse effects on high-voltage reactions involving Ni–O bonding are limited, and the structural stability is further enhanced. The finally obtained P2-type Na0.62Ca0.025Ni0.28Mg0.05Mn0.67O2 exhibits a satisfactory initial energy density of 468.2 W h kg−1 and good capacity retention of 83% after 100 cycles at 50 mA g−1 within the voltage range of 2.2–4.35 V. This work deepens our understanding of the specific effects of Mg2+ and Ca2+ dopants and provides a stability-enhancing strategy utilizing abundant alkaline earth elements.
Introduction
Large-scale energy storage systems are urgently required to meet the needs relating to electric power distribution and renewable energy utilization.1–4 Owing to the low cost and the abundant resources, sodium-ion batteries (SIBs) are promising candidates for large-scale applications.5–9 Although the mass production of commercial SIBs has already started, the insufficient cycling durability remains a challenge that needs to be overcome.Layered-structured oxides have attractive traits, such as their two-dimensional ion diffusion channels, relatively high capacities, convenient preparation methods, etc. However, irreversible phase transitions, volume changes, surface side reactions, and other drawbacks hinder their electrochemical performance.10–13 Targeted strategies have been proposed, however, these cathode materials are still far from achieving their theoretical limits.14–21
Early in 2001, Lu et al. reported the capacity and phase evolution process of P2-type Na2/3Ni1/3Mn2/3O2.22 Doping with both electrochemically active and inactive elements has been proved to be an effective method for improving the electrochemical performance of this material.23 Partially replacing Ni2+ with Mg2+ or Li+ can reduce the Na+ extraction levels during charging, altering the harmful P2–O2 phase transition to an acceptable P2–OP4 phase transition or even completely suppressing the phase transition.24–27 It is worth mentioning that Mg2+ ions can act as pillars in the AM layers to stabilize the structure under conditions of heavy use or deliberately-high-voltage charging. However, this can decrease the rate performance or the capacity above 4.0 V, and the number of Mg2+ pillars cannot be controlled directly. In addition, a stable electrolyte is required for long-term cycling at high voltages. By contrast, Ca2+ pillars have been adopted in P2-type NaxCoO2 and some O3-type cathode materials, resulting in significant enhancements in cycling and rate performance with the use of a simple preparation method.28–32
In this work, we dope two kinds of alkaline earth elements, i.e., Mg2+ and Ca2+, into P2-type Na0.67Ni0.33Mn0.67O2. Considering the ionic radii of the involved cations (Na+: 1.02 Å, Ca2+: 1.00 Å, Ni2+: 0.69 Å, Mn4+: 0.53 Å and Mg2+: 0.72 Å), Mg2+ and Ca2+ ions are likely to occupy the TM sites and the AM sites, respectively. A small number of Ca2+ pillars can effectively boost the stability during Ni3+/Ni2+ redox reactions in the layered cathode. Using Mg2+ to replace Ni2+ can enhance the cycling durability and, in particular, the stability of high-voltage reactions is markedly enhanced. However, capacity loss is unavoidable when the dopants are heavily used. As revealed via DFT calculations, this is mainly caused by the alteration of high-voltage reactions upon Mg- and Ca-doping. In the meantime, this reminds us that the usage of Ca2+ dopants requires close attention when oxygen redox reactions are involved. The instability at high levels of desodiation is also briefly studied. In addition, a significant synergetic effect has been found through which high-voltage reactions involving Ni–O bonding could be largely preserved when Ca2+ ions are trapped near Mg2+ ions. The obtained P2-type Na0.62Ca0.025Ni0.28Mg0.05Mn0.67O2 material possesses better all-round performance compared with the other discussed counterparts.
Experimental
Synthesis
The materials were prepared through a simple ball-milling-assisted solid-state reaction. Na2CO3 (99.8%), CaCO3 (99%), NiO (99%), MgO (98%), and Mn2O3 (98%) are the raw materials. After ball-milling for 12 h at 350 rpm, stoichiometric amounts of raw materials (5 mol% excess Na2CO3 was added) were pressed into pellets under a pressure of 15 MPa. Then the pellets were annealed at 1173 K for 12 h and naturally cooled to room temperature.Characterization
X-ray diffraction patterns were collected using a Rigaku mini flex 600 diffractometer (Cu Kα radiation, λ1 = 1.54060 Å, λ2 = 1.54439 Å). The morphologies, selected area electron diffraction patterns, and elemental mapping images were obtained using a transmission electron microscope (TEM, JEOL JEM-2100F).Electrochemical measurements
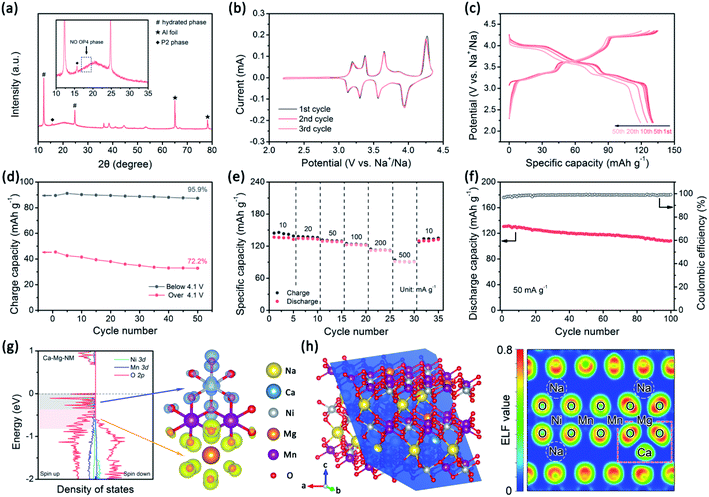
Cathodes were prepared via casting a slurry of active material (70 wt%), super P (20 wt%), and poly(vinylidene fluoride) (PVDF, 10 wt%) on Al foil and drying at 90 °C for 12 h under vacuum. The loaded mass of active material is about 2 mg cm−2. The above-mentioned cathode, a glass fiber separator (Whatman), a pure sodium foil counter electrode, and 1 M NaClO4 electrolyte (dissolved in propylene carbonate with 5% fluoroethylene carbonate) were used to assemble coin-type cells (CR2025) in an Ar-filled glovebox. The galvanostatic charge–discharge performance and galvanostatic intermittent titration technique (GITT) data were measured using a LANHE CT2001A battery test system. For GITT testing, the half cells were charged or discharged at 10 mA g−1 for 10 min, followed by relaxation for 60 min. If linear behavior of E vs. τ1/2 is observed during the pulse time, DNa+ can be calculated via the following equation:33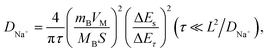 | (1) |
Computational methods
First-principles calculations were carried out using density functional theory with the projector augmented-wave method as implemented using Vienna Ab initio Simulation Package (VASP) code.34–37 Hubbard corrections to intra-atomic coulombic repulsion were considered via setting the effective Hubbard U parameters to 4.0 eV for Mn and 6.0 eV for Ni. The wave functions were expanded based on plane-waves with the energy cutoff set to 400 eV. The minimum spacing between k-points was set to 0.2 Å−1. A supercell containing 36 Mn and 18 Ni ions was considered for exploring the energies of different configurations of Na ions. More than 10 different configurations of Na ions were generated for each Na concentration and these were fully relaxed. The energy of the most stable Na configuration was selected to evaluate the relative stabilities of the P2 and O2 phases. Bader analysis was conducted using code developed by Henkelman's group.38 Crystal structures were visualized using the Visualization for Electronic and Structure Analysis (VESTA) program.39
supercell containing 36 Mn and 18 Ni ions was considered for exploring the energies of different configurations of Na ions. More than 10 different configurations of Na ions were generated for each Na concentration and these were fully relaxed. The energy of the most stable Na configuration was selected to evaluate the relative stabilities of the P2 and O2 phases. Bader analysis was conducted using code developed by Henkelman's group.38 Crystal structures were visualized using the Visualization for Electronic and Structure Analysis (VESTA) program.39
Results and discussion
Ca2+ substitution
Stabilizing structures with Ca2+ pillars has been reported in both P2 and O3 cathode materials. Given that the Na+ crystallographic sites are different between P2, O2, O3, and P3 structures (Fig. 1),11,40,41 we believe that pillars are more appropriate to be applied to P2-type cathodes rather than O3-type ones, and the detailed reasons are given below. Except for structural stabilization effects, the pillars also have the ability to hinder the phase transition, owing to stronger electrostatic interactions with nearby oxygen ions. The O3–P3 phase transition is inevitable and necessary for O3-type cathodes in order to acquire better Na+ conductivity, while the P2–O2 phase transition is commonly harmful and needs to be suppressed.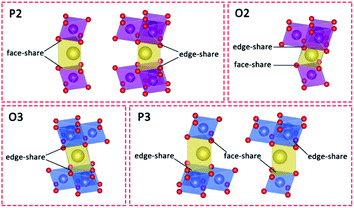 | ||
| Fig. 1 Schematic illustrations of the different prismatic and octahedral sites in AM layers in P2-, O2-, O3- and P3-type layered structures. | ||
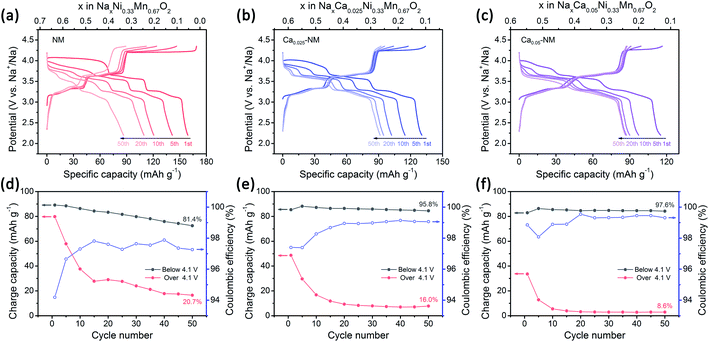
Here, Na0.67Ni0.33Mn0.67O2 (NM), Na0.62Ca0.025Ni0.33Mn0.67O2 (Ca0.025–NM), and Na0.57Ca0.05Ni0.33Mn0.67O2 (Ca0.05–NM) were synthesized through a solid-state method. The main phase of these three samples is the P2 phase with the P63/mmc space group (Fig. S1†). No obvious calcium-related impurities are observed, and the (002)P2 peak shifts to a high degree for the Ca-doped samples, inferring that Ca2+ ions are successfully doped into the AM layers. The shrinkage of the lattice parameter “c” here is consistent with reports relating to Ca-doped P2-type cathodes.29,30 For reports relating to O3-type cathodes, the outcomes are a bit more complicated. O3–Na0.98Ca0.01Ni0.5Mn0.5O2 shows a reduced “c” value, while O3–Na0.95Ca0.025Ni1/3Fe1/3Mn1/3O2 and O3–Na0.9Ca0.05Ni1/3Fe1/3Mn1/3O2 show expanded “c” values.31,32 However, no clear explanation for the expansion of “c” in O3-type cathodes has been provided.
The electrochemical performances were measured at a current density of 50 mA g−1 and in the voltage range of 2.2–4.35 V, and the results are displayed in Fig. 2. The charge–discharge profiles are composed of three plateau regions. The two plateaus in the lower voltage range (below 4.1 V) are mainly attributed to Ni3+/Ni2+ redox reactions (with a small number of oxygen redox reactions), and the plateau at 4.2 V is mainly attributed to oxygen redox reactions, while Ni4+/Ni3+ redox reactions are also involved.42 The results show that the amount of Ca2+ ions is positively associated with the cycling stability and negatively correlated with the initial capacity. Unlike NM, whose Na+ ions can be almost completely extracted when charged to 4.35 V, the Na+ deintercalation levels in the initial charging processes of Ca0.025–NM and Ca0.05–NM are about 0.52 and 0.45 mol, respectively, which are obviously lower than their initial Na content levels of 0.62 and 0.57. In particular, capacity differences occur above 4.1 V for these three samples, while their capacities below 4.1 V show negligible disparity (Fig. 2). This phenomenon indicates that Ca doping suppresses the reactivity of high-voltage reactions. To discern the variations related to Ni3+/Ni2+ and high-voltage reactions during cycling more intuitively, the capacities below and above 4.1 V are presented for the three samples in Fig. 2d–f. Rapid capacity decay above 4.1 V is observed for all three samples, inferring that merely adopting Ca2+ pillars is insufficient for maintaining the capacity based on high-voltage reactions. This may be caused by the enrichment of Ca2+ ions at the surface, leading to the deactivation of high-voltage reactions. Nonetheless, Ca doping is extremely useful for maintaining the Ni3+/Ni2+ redox capacity and boosting the coulombic efficiency (CE), as capacity retention below 4.1 V is promoted to above 95% and the CE is increased to about 99% at the 50th cycle with Ca doping.
The structural stabilization of Ca2+ pillars
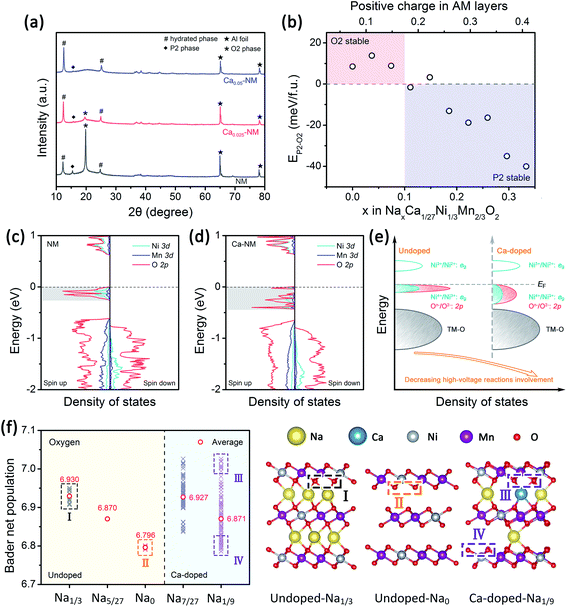
To examine the effects of Ca2+ doping on phase transitions, the XRD patterns of the three samples charged to 4.35 V were recorded and they are presented in Fig. 3a. The intensity of the (002)O2 peak is reduced as the amount of the Ca2+ is increased, and this peak vanished when the Ca-doping level reached 0.05, suggesting that the P2–O2 phase transition is weakened in the presence of Ca2+ pillars. This also indicates that Ca and Mg doping have different effects on phase transitions, as Mg doping leads to the P2–OP4 transition. To investigate the effects of Ca doping rationally, we need the help of first-principles calculations to evaluate the structural stabilization effect difference between Ca2+ and Na+ ions. The energy differences between the P2 and O2 structures of NaxCa1/27Ni1/3Mn2/3O2 (abbreviated to Ca–NM) are shown in Fig. 3b. The bottom axis shows the amount of Na+ and the top axis shows the amount of positive charge remaining in the AM layer. For NM, the O2 phase is more stable than the P2 phase when more than 1/3 mol Na+ has been extracted, and the P2–O2 phase transition will start, according to in situ XRD results obtained by Lu and co-workers22 and the calculation results obtained by Meng and co-workers.43 From our theoretical calculation results, the O2 structure is more stable than the P2 structure when x is below 0.1 for Ca–NM. We can more intuitively notice that less positive charge is required to maintain the P2 structure for Ca–NM than for NM. The critical values for these materials are 0.17 and 0.33, respectively, showing that Ca2+ ions are superior to Na+ ions with equal charge in stabilizing the structure. Since the Ca content in Ca–NM is 1/27, lying between 0.025 and 0.05, the existence of the O2 phase in Ca0.025–NM charged to 4.35 V is reasonable (0.1 mol Na+ remaining), while no O2 phase is detected in Ca0.05–NM.Adverse effects of Ca2+ ions
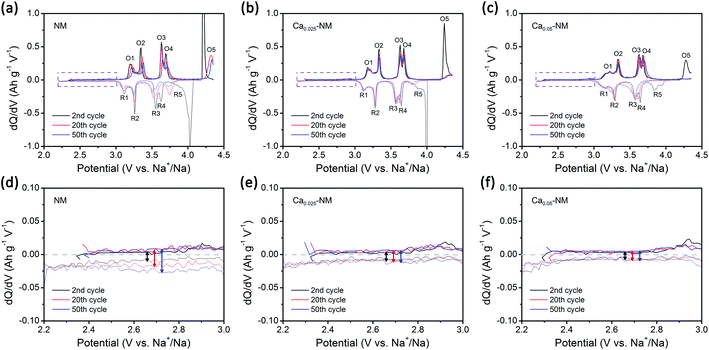
The GITT results from NM, Ca0.025–NM, and Ca0.05–NM conform with the analysis above. It is clearly shown in Fig. S2a–c† that the Ca-doped samples have higher Na+ diffusion coefficients (DNa+) than that of NM at the 4.2 V plateau, corresponding to different DNa+ values between the P2 and O2 phases. Furthermore, the Ca-doped samples exhibit higher voltage polarization in the high-voltage region than NM (Fig. S2g–i†). Since the high-voltage reactions of NM stem from Ni–O bonding with high ionicity,12,42 the lowering of the capacity caused by Ca-doping probably lies in the alteration of Ni–O bonding hybridization. Given that the high-voltage reactions mainly occur in the 4.2 V plateau region, corresponding to the removal of more than 1/3 mol Na+, we calculated the density of states (DOS) of NM and Ca–NM with 1/3 mol positive charge remaining in the AM layers and focused on the orbital differences below the Fermi level. In Fig. 3c and d, in the regions highlighted in gray, the ionicity of Ni–O bonding is obvious, as the contributions from the O 2p orbitals are much higher than those of the Ni 3d orbitals. This result tallies with the experimental results, suggesting that the high-voltage reactions mainly involve oxygen redox reactions with some Ni4+/Ni3+ redox reactions.12,42 It is worth noting that the distributions of the O 2p and the Ni 3d orbitals of Ca–NM in the gray region are expanded significantly to deeper energy levels, making the high-voltage reactions less accessible in the case of Ca–NM. In other words, the electronic states of the O atoms bonded to Ca2+ ions are stabilized. Even at the end of charging (Na1/9Ca1/27–NM), these O atoms remain unoxidized (Fig. 3f). In addition, some nickel remains in the form of Ni2+ and Ni3+ due to the limited deintercalation of the Na+ ions and the stabilization effects of Ca2+ ions (Fig. S3a†). These results conform to the electrochemical performance data, in which Ca0.025–NM and Ca0.05–NM have lower high-voltage reaction capacities than NM in the voltage range of 4.1–4.35 V. To provide a more direct comparison, we present the calculated redox potentials of NM and Ca–NM with positive charge lower than 1/3 in the AM layers in Fig. S3b.† The results reveals that the redox voltage of NM from Na = 1/3 to 0 is 4.20 V. In the meantime, the voltage of Ca–NM is increased to 4.54 V if all the Na+ ions are extracted from the lattice. Apparently, this is unachievable experimentally. According to the above analysis, the shortcomings of Ca doping demonstrated here imply that the use of Ca2+ pillars should be carried out with extreme caution, particularly when oxygen redox is involved. Other modifications are required to alleviate the impact on high-voltage reactions. This will be discussed below.When returning to the charge–discharge profiles during cycling, we notice a change that might be associated with the P2–O2 phase transition. The three samples possess three plateau regions (Fig. 2a–c), and the two plateaus below 4 V can be further divided into four peak-pairs, as presented in Fig. 4a–c (O1/R1, O2/R2, O3/R3, and O4/R4). Upon an increase in the cycle number, the dQ/dV plot of NM exhibits the greatest change. Ignoring the O5/R5 peak pair, which is mainly contributed to by high-voltage reactions, significant asymmetry is observed among the O3/R3 and the O4/R4 pairs from the 20th and 50th cycle for NM. Interestingly, the O1/R1 and O2/R2 peak pairs present relatively good symmetry. We can see in Fig. 4d that some of the discharge capacity that ought to belong to the R3 and R4 peaks shifts to the lower voltage region (2.2–3 V). This indicates that some redox reactions corresponding to the O3 and O4 peaks show abnormal high overpotentials compared with other redox reactions relating to NM during long-term cycling. We also highlight the variations in the charge–discharge profiles in Fig. S4† for an intuitive view. When Ca2+ ions are introduced into the AM layers in the cases of Ca0.025–NM and Ca0.05–NM, this phenomenon is restrained effectively, and no significant changes are observed in these two regions (Fig. 4b, c, e, f, and S4†).
We suspect that this is caused by the migration of nickel ions from the TM layers to the AM layers. The migration of TM ions can alter the Na environment in Na2/3Ni1/3Mn2/3O2,44 and TM ions have been directly detected in the AM layers of charged P2–Na0.78Al0.05Ni0.33Mn0.60O2,45 which is a derivative of Na2/3Ni1/3Mn2/3O2. Here, we prefer to only consider the migration of nickel rather than manganese, since the migration of iron and nickel ions to the AM layers has been observed.46–50 Meanwhile, our DFT calculation outcomes show that O2 structures with Ni migration are more stable than with Mn migration (Fig. S5†). It should be noted that the superstructure might be lost upon TM-ion migration, resulting in voltage hysteresis relating to oxygen redox reactions in the low-voltage range.42,51,52 Most TM migration happens in O-type stacking arrangements, since the TM ions tend to migrate to the tetrahedral and octahedral sites in the AM layers (which only exist in O-type stacking) when a large number of Na+ vacancies exist (Fig. S6†).47,53–55 Therefore, it is reasonable that the suppression of the P2–O2 phase transition in the presence of Ca2+ pillars weakens nickel migration.
In addition, if we adjust the voltage range to 2.2–4 V, NM exhibits great cycling performance without the phenomenon of the discharge capacity shifting towards a lower voltage (Fig. S7†), as the P2–O2 phase transition is prevented.
Mg2+ substitution
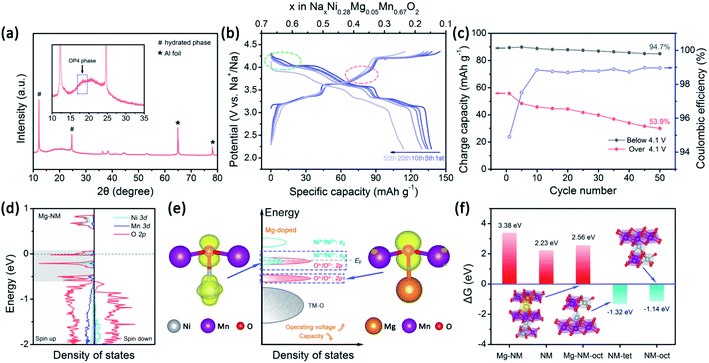
The strategy of replacing Ni2+ with Mg2+ in NM has already been recognized by several research groups.25–27,56,57 The P2–O2 phase transition is successfully altered to a more reversible P2–OP4 phase transition upon using Mg2+, however, some of the capacity is sacrificed. Komaba et al. concluded that MgO6 octahedra can strongly attract Na+ ions to realize a pillar effect at the end of charging.11 In addition, it has been proved that Mg2+ ions can also act as pillars under certain circumstances.26,27 Besides structural stabilization, Mg2+ substitution enables highly reversible oxygen redox reactions in Mn-based layered oxide cathodes.10,58,59 NM also has oxygen reactivity above 4.2 V.12,42 It is well-known that oxygen release is a serious issue for both lithium and sodium layered cathode materials.10,60,61 Unfortunately, irreversible oxygen release has been observed in NM through in situ differential electrochemical mass spectrometry analysis.12 Besides structural stabilization effects, we are also interested in how the doping of a small number of Mg2+ ions into NM can improve the reversibility of high-voltage reactions.Here, we choose 5% Mg-doped Na0.67Ni0.28Mg0.05Mn0.67O2 (NMM) since it has better overall performance, according to Guo's research.25 The cycling performance of NMM is better than that of NM (Fig. S8a†), in accordance with previous results.25–27,57 Although Mg doping promotes the stabilization of Ni3+/Ni2+ redox reactions to a lower extent compared with the Ca-doped samples, a dramatic enhancement of the reversibility of high-voltage reactions is observed (Fig. 5c). Meanwhile, a small amount of the OP4 phase is observed when the NMM electrode is charged to 4.35 V (Fig. 5a). Upon comparing the CV curves of NM and NMM, the difference is also obvious (Fig. S9†). It is clearly noticed that the high-voltage reaction peaks of NM change dramatically upon cycling, as the peaks broaden and shift to lower voltages. This indicates the existence of TM-ion migration and the loss of superstructure.51,52,62 However, for NMM, smaller changes are seen in the oxygen redox peaks. Moreover, the symmetry of the capacities of the O3/R3 and O4/R4 peak pairs and the 2.2–3 V region of NMM is higher than NM (Fig. S10 and S11†). These results all suggest the suppression of TM-ion migration, as less O-type stacking in the OP4 phase than that in the O2 phase might restrain TM-ion migration (Fig. S6†), leading to more reversible redox reactions and structure evolution in NMM.
Alteration of the properties with Mg2+
To understand the effects of Mg doping on high-voltage reactions, we calculated the DOS of NaxNi5/18Mg1/18Mn2/3O2 (Mg–NM) at x = 1/3. As shown in Fig. 5d, the orbitals of Mg–NM near the Fermi level split into three parts (labeled in gray). The two parts with higher energy levels are principally composed of O 2p and Ni 3d orbitals, similar to NM. However, the contribution from Ni 3d orbitals to the lowest part can almost be ignored, indicating that this part is attributed to Mg–O bonding, as verified based on the spatial charge density (Fig. 5e; a wider view is shown in Fig. S12†). When looking into the energy distributions of these three parts, we notice that the Fermi level penetrates the highest part. Given that the presence of 5/18 mol of Ni2+ in Mg–NM is not enough for the deintercalation of 1/3 mol of Na+ merely through Ni3+/Ni2+ redox, some Ni4+/Ni3+ redox and oxygen redox reactions are needed to participate in charge compensation, and an outward expression of this is shown in the changes in the charge–discharge profiles (red dotted circle in Fig. 5b). The other two parts of Mg–NM are lower in energy than the corresponding part of NM. This result shows that the remaining ∼1/9 mol of Na+ in NMM at 4.35 V comes from the less accessible high-voltage reactions upon Mg doping, and the corresponding calculated redox voltage is presented in Fig. S13.† In addition, the gap between the lowest two parts, coinciding with the charge profiles (Fig. 5b) and the CV (Fig. S9†) curves of NMM, is observed as a sloping region and a plateau region above 4.1 V (highlighted with green dotted circle in Fig. 5b).The DOS results discussed above only reveal the changes in high-voltage reactions upon Mg doping, however, they are not enough to explain the stabilization of the high-voltage reactions. For obtaining an intuitive view of the structural stability, we also calculated the Gibbs free energy change (ΔG) of oxygen evolution based on the following reaction:48
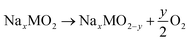 | (2) |
The corresponding enthalpy can be calculated as follows:
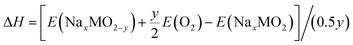 | (3) |
The case of Ni migration in OP4–Mg–NM at Na = 1/9 is also considered. The structural optimization results show that the migration of Ni to an octahedral site in O-type stacking is more preferable in energy than migrating to a tetrahedral site (Fig. S14a†). Thanks to Na+ ions remaining in the lattice of Mg–NM–oct, oxygen that ought to be under-bonded upon Ni migration is stabilized by Na+ ions, and no significant redistribution of charge density is observed among the oxygen atoms (Fig. S14b†). As a consequence, oxygen evolution is thermodynamically unfavorable for this example of Mg–NM–oct (Fig. 5f). Therefore, the higher retention of the high-voltage reaction capacity of NMM should come from the suppression (not the elimination) of Ni ion migration, with less O-type stacking and the stabilization of under-bonded oxygen with remaining Na+ ions.
Mg2+ and Ca2+ co-substitution
The oxidation of Ni2+ ions to higher valence will increase the electrostatic repulsion toward Ca2+ ions. Therefore, we speculate that under co-doping circumstances Ca2+ ions might be trapped near MgO6 octahedrons, and the calculation results show that the Ca2+ ions in the optimized structure occupy prismatic sites adjacent to the MgO6 octahedrons (Fig. S15†). On this basis, the reactivity of Ni–O bonding might be largely retained, since less active Mg–O bonding will suffer the effects of the Ca2+ ions. Considering that one Ca2+ pillar will affect two neighboring TM layers, the amount of Mg2+ should be twice that of Ca2+. In addition, the usage of 0.05 mol of Ca2+ will lead to unacceptably low capacity. Therefore, we synthesized Na0.62-Ca0.025Ni0.28Mg0.05Mn0.67O2 (Ca0.025–NMM) and examined its properties. The main phase of the Ca0.025–NMM is the P2 structure, as shown in Fig. S16a,† and the Rietveld refinement results are presented in Table S7 (ESI†). Some peaks with weak intensities are present in the range of 20–30°, suggesting the existence of Na+ ordering and Ni–Mn honeycomb ordering.43,65 In the HRTEM image, lattice spacing of 0.58 nm is noticed (Fig. S16c†). This is consistent with our Rietveld refinement results from Ca0.025–NMM, in which the lattice parameter “c” is calculated to be 1.166 nm.Synergetic effect of Mg2+ and Ca2+ ions
The electrochemical performance and XRD pattern in a fully charged state are exhibited in Fig. 6. Ca0.025–NMM possesses better stability compared with the previously mentioned examples. In particular, the high-voltage reaction peaks of Ca0.025–NMM remain almost unchanged over three CV cycles (Fig. 6b), and the highest capacity retention is seen after the 50th cycle over 4.1 V (Fig. 6d), suggesting that a synergetic effect from Mg and Ca doping is beneficial for maintaining the reactivity of Ni–O bonding. As seen in Fig. 6g, the DOS of Na7/27Ca1/27Ni7/27Mg2/27/Mn2/3O2 (Ca–Mg–NM) reveals that the reactivity suppression effect is mainly seen with respect to Mg–O bonding, as the corresponding orbitals expand to a deeper energy level compared with the DOS of Mg–NM. Meanwhile, we can find that the capacity associated with Mg–O (the slope region above 4.1 V) of Ca0.025–NMM is slightly lower than that in the case of NMM. Furthermore, the electron distribution around Mg–O bonding is changed upon Ca2+ doping according to the electron localization function (ELF) map shown in Fig. 6h. The ELF maps of the other structures are provided in Fig. S18,† and the effects of Ca2+ ions on bonding can be observed intuitively.Several works on Ca doping have shown that the introduction of Ca2+ is beneficial for the rate performance.29–32 Here in our study, similar results are also obtained. The capacity retention levels at 500 mA g−1 are 66.7% for Ca0.025–NMM (Fig. 6e), 42.2% for NM and 57.9% for NMM (Fig. S19a and S19b†). Moreover, Ca0.025–NMM possesses the highest energy efficiency at 500 mA g−1 among all the samples (Fig. S19i†). Considering that the phase transition occurs at the 4.2 V plateau, the rate performances above and below 4.1 V must be diverse. In Fig. S19g–i,† we present the capacities at different current densities separately. For the three samples, the capacity decay below 4.1 V is much lower than that above 4.1 V owing to the phase transition. It is widely accepted that the P-type structure has a better Na+ diffusion rate than the O-type structure. Apparently, NMM and Ca0.025–NMM have better rate performances above 4.1 V as the P2–O2 phase transition is prevented and prismatic Na+ sites still exist in the high voltage region. The GITT results in Fig. S20† support the same case. In addition, the overpotentials of these three samples are clearly different during the charge–discharge process, as shown in Fig. S20g–i.† NM shows a much larger overpotential than Ca0.025–NMM and NMM, demonstrating that the electrochemical reaction resistance is lower in the presence of Mg2+. In the meantime, a higher overpotential is observed for Ca0.025–NMM than NMM in the region related to Mg–O bonding reactions, while the overpotential for Ni–O bonding reactions is almost unchanged (Fig. S20g–i†). This also confirms the presence of neighboring Mg2+ and Ca2+ in the lattice. Thanks to structural stabilization due to Mg and Ca doping, Ca0.025–NMM shows the best capacity retention of 83% at 50 mA g−1 after 100 cycles (Fig. 6f). A more intuitive comparison can be seen in Fig. S8a.† Although NMM has a higher initial capacity and average voltage due to the absence of Ca2+ pillars, it is surpassed after 40 cycles by Ca0.025–NMM, which presents a slower deterioration in capacity. The XRD patterns of all samples after 100 cycles are shown in Fig. S21,† also verifying the superior stability of Ca0.025–NMM.
To achieve a cathode material with higher energy density, boosting either the capacity or the average voltage can be successful. Taking the anode material into account, enhancing the average voltage is more efficient if the energy density of the cathode is unchanged. Commonly, the potential of TM-ion redox reactions is in the range of 1.5–4 V vs. Na+/Na, while the potential of oxygen redox reactions can exceed 4 V if small voltage hysteresis is obtained. This is one of the reasons why several efforts have been made to unveil the mechanism relating to oxygen redox reactions in layered oxide cathodes. Although co-doping with Mg2+ and Ca2+ enhances the cycling stability, the capacity and voltage decays relating to high-voltage reactions are still much more serious than those relating to Ni3+/Ni2+ redox reactions, and the coulombic efficiency is not high enough (only 99%). This suggests that more modifications are needed to restrain TM-ion migration and reduce irreversible reactions, while better high-voltage electrolytes should be developed. Hopefully, our strategy can suppress the notorious P2–O2 phase transition effectively and economically, and this will help in maintaining the integrity of surface coatings if they are applied to P2-type materials.
Conclusions
In summary, we have investigated the stabilization effects of Mg and Ca doping on a P2-type Ni/Mn-based cathode material. The results show that when these two alkaline earth elements are doped individually, both can stabilize the structure, making the phase evolution process more reversible. In particular, the pillar effects of Ca2+ ions are better than those of Na+ ions with the same electric charge. However, side effects toward high-voltage reactions are observed, especially in the case of Ca doping alone. The DOS results reveal that Mg and Ca doping will make high-voltage reactions less accessible than in the undoped material, leading to a reduction in capacity. Furthermore, a synergetic effect involving Mg2+ and Ca2+ ions is discovered in co-doped Ca0.025–NMM, and better structural stability is obtained with a less adverse impact exerted on Ni–O bonding. A satisfying initial energy density of 468.2 W h kg−1 and the greater retention of both capacity and average voltage were observed. This work provides insight into structural stabilization based on Mg2+ and Ca2+ in P2-type cathodes, and it also warns that the adoption of Ca2+ ions requires particular attention when oxygen redox reactions are involved.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
J. Zhou and H. Fu designed the research. H. Fu carried out the experiments. Y.-P. Wang, G. Fan, H. Fu, and M. Long carried out the calculations. Y.-P. Wang, G. Fan, S. Guo, X. Xie, X. Cao, B. Lu, and H. Fu carried out the analysis. S. Liang and J. Zhou supervised the project. J. Zhou and H. Fu co-wrote the paper. S. Liang and J. Zhou guided and revised the paper. All authors read and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 51932011, 51972346), the Hunan Natural Science Fund for Distinguished Young Scholar (2021JJ10064), the Program of Youth Talent Support for Hunan Province (2020RC3011), and the Innovation-Driven Project of Central South University (No. 2020CX024). We are grateful for technical support from the High-performance Computing Centre of Central South University.References
- H. Chen, T. N. Cong, W. Yang, C. Tan, Y. Li and Y. Ding, Prog. Nat. Sci., 2009, 19, 291–312 CrossRef CAS
.
- Y. Li, X. Wu, S. Wang, W. Wang, Y. Xiang, C. Dai, Z. Liu, Z. He and X. Wu, RSC Adv., 2017, 7, 36909–36916 RSC
.
- L. Shan, Y. Wang, S. Liang, B. Tang, Y. Yang, Z. Wang, B. Lu and J. Zhou, InfoMat, 2021, 3, 1028–1036 CrossRef CAS
.
- Y. Shen, X. Wang, H. Hu, M. Jiang, Y. Bai, X. Yang and H. Shu, RSC Adv., 2015, 5, 38277–38282 RSC
.
- M. Chen, Q. Liu, S. W. Wang, E. Wang, X. Guo and S. L. Chou, Adv. Energy Mater., 2019, 9, 1803609 CrossRef
.
- J. Y. Hwang, S. T. Myung and Y. K. Sun, Chem. Soc. Rev., 2017, 46, 3529–3614 RSC
.
- Y. Sun, S. Guo and H. Zhou, Energy Environ. Sci., 2019, 12, 825–840 RSC
.
- F. Li and Z. Zhou, Small, 2018, 14, 1702961 CrossRef PubMed
.
- X. Li and J. Wang, InfoMat, 2019, 2, 3–32 CrossRef
.
- R. A. House, U. Maitra, L. Jin, J. G. Lozano, J. W. Somerville, N. H. Rees, A. J. Naylor, L. C. Duda, F. Massel, A. V. Chadwick, S. Ramos, D. M. Pickup, D. E. McNally, X. Lu, T. Schmitt, M. R. Roberts and P. G. Bruce, Chem. Mater., 2019, 31, 3293–3300 CrossRef
.
- K. Kubota, S. Kumakura, Y. Yoda, K. Kuroki and S. Komaba, Adv. Energy Mater., 2018, 8, 1703415 CrossRef
.
- Y. Zhang, M. Wu, J. Ma, G. Wei, Y. Ling, R. Zhang and Y. Huang, ACS Cent. Sci., 2020, 6, 232–240 CrossRef CAS PubMed
.
- Y. Wang, L. Wang, H. Zhu, J. Chu, Y. Fang, L. Wu, L. Huang, Y. Ren, C. J. Sun, Q. Liu, X. Ai, H. Yang and Y. Cao, Adv. Funct. Mater., 2020, 30, 1910327 CrossRef CAS
.
- X. Cao, X. Li, Y. Qiao, M. Jia, F. Qiu, Y. He, P. He and H. Zhou, ACS Energy Lett., 2019, 4, 2409–2417 CrossRef CAS
.
- Q. Wang, S. Mariyappan, G. Rousse, A. V. Morozov, B. Porcheron, R. Dedryvere, J. Wu, W. Yang, L. Zhang, M. Chakir, M. Avdeev, M. Deschamps, Y. S. Yu, J. Cabana, M. L. Doublet, A. M. Abakumov and J. M. Tarascon, Nat. Mater., 2021, 20, 353–361 CrossRef CAS PubMed
.
- X. Ma, X. Cao, Y. Zhou, S. Guo, X. Shi, G. Fang, A. Pan, B. Lu, J. Zhou and S. Liang, Nano Res., 2020, 13, 3330–3337 CrossRef CAS
.
- X. Cao, A. Pan, B. Yin, G. Fang, Y. Wang, X. Kong, T. Zhu, J. Zhou, G. Cao and S. Liang, Nano Energy, 2019, 60, 312–323 CrossRef CAS
.
- Y. Xiao, P.-F. Wang, Y.-X. Yin, Y.-F. Zhu, Y.-B. Niu, X.-D. Zhang, J. Zhang, X. Yu, X.-D. Guo, B.-H. Zhong and Y.-G. Guo, Adv. Mater., 2018, 30, 1803765 CrossRef PubMed
.
- T. Jin, P.-F. Wang, Q.-C. Wang, K. Zhu, T. Deng, J. Zhang, W. Zhang, X.-Q. Yang, L. Jiao and C. Wang, Angew. Chem., Int. Ed., 2020, 59, 14511–14516 CrossRef CAS PubMed
.
- Y.-E. Zhu, X. Qi, X. Chen, X. Zhou, X. Zhang, J. Wei, Y. Hu and Z. Zhou, J. Mater. Chem. A, 2016, 4, 11103–11109 RSC
.
- J. Zhang, H. Yuan, Y. Huang, S. Kan, Y. Wu, M. Bu, Y. Liu, P. He and H. Liu, Chem. Eng. J., 2021, 417, 128097 CrossRef CAS
.
- Z. Lu and J. R. Dahn, J. Electrochem. Soc., 2001, 148, A1224–A1229 Search PubMed
.
- Y. Li, M. Chen, B. Liu, Y. Zhang, X. Liang and X. Xia, Adv. Energy Mater., 2020, 10, 2000927 CrossRef CAS
.
- J. Xu, D. H. Lee, R. J. Clément, X. Yu, M. Leskes, A. J. Pell, G. Pintacuda, X.-Q. Yang, C. P. Grey and Y. S. Meng, Chem. Mater., 2014, 26, 1260–1269 CrossRef CAS
.
- P.-F. Wang, Y. You, Y.-X. Yin, Y. S. Wang, L.-J. Wan, L. Gu and Y.-G. Guo, Angew. Chem., Int. Ed., 2016, 55, 7445–7449 CrossRef CAS PubMed
.
- K. Wang, H. Wan, P. Yan, X. Chen, J. Fu, Z. Liu, H. Deng, F. Gao and M. Sui, Adv. Mater., 2019, 31, 1904816 CrossRef CAS PubMed
.
- Q. C. Wang, J. K. Meng, X. Y. Yue, Q. Q. Qiu, Y. Song, X. J. Wu, Z. W. Fu, Y. Y. Xia, Z. Shadike, J. Wu, X. Q. Yang and Y. N. Zhou, J. Am. Chem. Soc., 2019, 141, 840–848 CrossRef CAS PubMed
.
- L. Zheng, J. C. Bennett and M. N. Obrovac, J. Electrochem. Soc., 2019, 166, A2058–A2064 CrossRef CAS
.
- S. C. Han, H. Lim, J. Jeong, D. Ahn, W. B. Park, K.-S. Sohn and M. Pyo, J. Power Sources, 2015, 277, 9–16 CrossRef CAS
.
- M. Matsui, F. Mizukoshi and N. Imanishi, J. Power Sources, 2015, 280, 205–209 CrossRef CAS
.
- L. Sun, Y. Xie, X. Z. Liao, H. Wang, G. Tan, Z. Chen, Y. Ren, J. Gim, W. Tang, Y. S. He, K. Amine and Z. F. Ma, Small, 2018, 14, 1704523 CrossRef PubMed
.
- T.-Y. Yu, J. Kim, J.-Y. Hwang, H. Kim, G. Han, H.-G. Jung and Y.-K. Sun, J. Mater. Chem. A, 2020, 8, 13776–13786 RSC
.
- W. Weppner, J. Electrochem. Soc., 1977, 124, 1569–1578 CrossRef CAS
.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef
.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS
.
- C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81–85 CrossRef CAS
.
- J. M. Paulsen, J. R. Mueller-Neuhaus and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 508–516 CrossRef CAS
.
- K. Dai, J. Mao, Z. Zhuo, Y. Feng, W. Mao, G. Ai, F. Pan, Y.-d. Chuang, G. Liu and W. Yang, Nano Energy, 2020, 74, 104831 CrossRef CAS
.
- D. H. Lee, J. Xu and Y. S. Meng, Phys. Chem. Chem. Phys., 2013, 15, 3304–3312 RSC
.
- X. Wu, G. L. Xu, G. Zhong, Z. Gong, M. J. McDonald, S. Zheng, R. Fu, Z. Chen, K. Amine and Y. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 22227–22237 CrossRef CAS PubMed
.
- Y. Shi, S. Li, A. Gao, J. Zheng, Q. Zhang, X. Lu, L. Gu and D. Cao, ACS Appl. Mater. Interfaces, 2019, 11, 24122–24131 CrossRef CAS PubMed
.
- S. Chu, C. Zhang, H. Xu, S. Guo, P. Wang and H. Zhou, Angew. Chem., Int. Ed., 2021, 60, 13366–13371 CrossRef CAS PubMed
.
- E. Talaie, V. Duffort, H. L. Smith, B. Fultz and L. F. Nazar, Energy Environ. Sci., 2015, 8, 2512–2523 RSC
.
- Y. Li, Y. Gao, X. Wang, X. Shen, Q. Kong, R. Yu, G. Lu, Z. Wang and L. Chen, Nano Energy, 2018, 47, 519–526 CrossRef CAS
.
- S. Guo, Y. Sun, P. Liu, J. Yi, P. He, X. Zhang, Y. Zhu, R. Senga, K. Suenaga, M. Chen and H. Zhou, Sci. Bull., 2018, 63, 376–384 CrossRef CAS
.
- C. Chen, Z. Ding, Z. Han, C. Liang, X. Lan, P. Wang, P. Gao and W. Wei, J. Phys. Chem. Lett., 2020, 11, 5464–5470 CrossRef CAS PubMed
.
- R. A. House, U. Maitra, M. A. Perez-Osorio, J. G. Lozano, L. Jin, J. W. Somerville, L. C. Duda, A. Nag, A. Walters, K. J. Zhou, M. R. Roberts and P. G. Bruce, Nature, 2020, 577, 502–508 CrossRef CAS PubMed
.
- R. A. House, G. J. Rees, M. A. Pérez-Osorio, J.-J. Marie, E. Boivin, A. W. Robertson, A. Nag, M. Garcia-Fernandez, K.-J. Zhou and P. G. Bruce, Nat. Energy, 2020, 5, 777–785 CrossRef CAS
.
- S. Xu, J. Wu, E. Hu, Q. Li, J. Zhang, Y. Wang, E. Stavitski, L. Jiang, X. Rong, X. Yu, W. Yang, X.-Q. Yang, L. Chen and Y.-S. Hu, J. Mater. Chem. A, 2018, 6, 20795–20803 RSC
.
- Y. Zhang, S. Kim, G. Feng, Y. Wang, L. Liu, G. Ceder and X. Li, J. Electrochem. Soc., 2018, 165, A1184–A1192 CrossRef CAS
.
- X. Li, Y. Wang, D. Wu, L. Liu, S.-H. Bo and G. Ceder, Chem. Mater., 2016, 28, 6575–6583 CrossRef CAS
.
- H. Hou, B. Gan, Y. Gong, N. Chen and C. Sun, Inorg. Chem., 2016, 55, 9033–9037 CrossRef CAS PubMed
.
- G. Singh, N. Tapia-Ruiz, J. M. Lopez del Amo, U. Maitra, J. W. Somerville, A. R. Armstrong, J. Martinez de Ilarduya, T. Rojo and P. G. Bruce, Chem. Mater., 2016, 28, 5087–5094 CrossRef
.
- U. Maitra, R. A. House, J. W. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Jin, M. A. Perez-Osorio, F. Massel, D. M. Pickup, S. Ramos, X. Lu, D. E. McNally, A. V. Chadwick, F. Giustino, T. Schmitt, L. C. Duda, M. R. Roberts and P. G. Bruce, Nat. Chem., 2018, 10, 288–295 CrossRef CAS PubMed
.
- N. Yabuuchi, R. Hara, K. Kubota, J. Paulsen, S. Kumakura and S. Komaba, J. Mater. Chem. A, 2014, 2, 16851–16855 RSC
.
- J. Wandt, A. T. S. Freiberg, A. Ogrodnik and H. A. Gasteiger, Mater. Today, 2018, 21, 825–833 CrossRef CAS
.
- X. Yu, Nat. Energy, 2021, 6, 572–573 CrossRef CAS
.
- W. E. Gent, I. I. Abate, W. Yang, L. F. Nazar and W. C. Chueh, Joule, 2020, 4, 1369–1397 CrossRef CAS
.
- J. S. Hummelshoj, J. Blomqvist, S. Datta, T. Vegge, J. Rossmeisl, K. S. Thygesen, A. C. Luntz, K. W. Jacobsen and J. K. Norskov, J. Chem. Phys., 2010, 132, 071101 CrossRef CAS PubMed
.
- J. Vergnet, M. Saubanère, M.-L. Doublet and J.-M. Tarascon, Joule, 2020, 4, 420–434 CrossRef CAS
.
- P.-F. Wang, M. Weng, Y. Xiao, Z. Hu, Q. Li, M. Li, Y.-D. Wang, X. Chen, X. Yang, Y. Wen, Y.-X. Yin, X. Yu, Y. Xiao, J. Zheng, L.-J. Wan, F. Pan and Y.-G. Guo, Adv. Mater., 2019, 31, 1903483 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc05715d |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |