Internal conversion of the anionic GFP chromophore: in and out of the I-twisted S₁/S₀ conical intersection seam

Abstract

The functional diversity of the green fluorescent protein (GFP) family is intimately connected to the interplay between competing photo-induced transformations of the chromophore motif, anionic p-hydroxybenzylidene-2,3-dimethylimidazolinone (HBDI⁻). Its ability to undergo Z/E-isomerization is of particular importance for super-resolution microscopy and emerging opportunities in optogenetics. Yet, key dynamical features of the underlying internal conversion process in the native HBDI⁻ chromophore remain largely elusive. We investigate the intrinsic excited-state behavior of isolated HBDI⁻ to resolve competing decay pathways and map out the factors governing efficiency and the stereochemical outcome of photoisomerization. Based on non-adiabatic dynamics simulations, we demonstrate that non-selective progress along the two bridge-torsional (i.e., phenolate, P, or imidazolinone, I) pathways accounts for the three decay constants reported experimentally, leading to competing ultrafast relaxation primarily along the I-twisted pathway and S₁ trapping along the P-torsion. The majority of the population (∼70%) is transferred to S₀ in the vicinity of two approximately enantiomeric minima on the I-twisted intersection seam (MECI-Is). Despite their sloped, reactant-biased topographies (suggesting low photoproduct yields), we find that decay through these intersections leads to products with a surprisingly high quantum yield of ∼30%. This demonstrates that E-isomer generation results at least in part from direct isomerization on the excited state. A photoisomerization committor analysis reveals a difference in intrinsic photoreactivity of the two MECI-Is and that the observed photoisomerization is the combined result of two effects: early, non-statistical dynamics around the less reactive intersection followed by later, near-statistical behavior around the more reactive MECI-I. Our work offers new insight into internal conversion of HBDI⁻ that both establishes the intrinsic properties of the chromophore and enlightens principles for the design of chromophore derivatives and protein variants with improved photoswitching properties.

---

Introduction

The green fluorescent protein (GFP^1–4) and its relatives have established themselves as key tools in bioimaging and cell biology by enabling visualization of protein transport/localization in realistic environments.^5–8 The family of GFP proteins displays a remarkable variety in their photophysical properties, including spectral range, fluorescence quantum yield, photostability and photoswitchability.^9–12 Intriguingly, this functional diversity is enabled by relatively minor variations in the chromophore motif and/or the protein scaffold.^13–17 The function of these proteins is inextricably linked to the properties of the 4-hydroxybenzylidene-2,3-dimethylimidazolinone (HBDI⁻) chromophore core¹⁸ (Fig. 1a).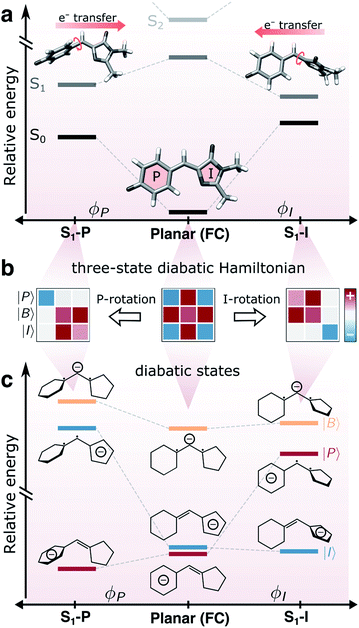

Fig. 1 Coupling between bridge-torsional motion and intramolecular charge-transfer character in gaseous HBDI⁻. (a) Torsional dependence of the S₀ and S₁ energies and the direction of intramolecular charge-transfer on S₁, computed at the α(0.64)-SA3-CASSCF(4,3)/6-31G* level. Adiabatic state energies and Mulliken charges are reported in Tables S1 and S2.† Note the broken y-axis, indicating that S₂ is located >1 eV above S₁ (Table S1†). (b) Schematic representation of the three-state diabatic Hamiltonian which upon diagonalization gives the adiabatic states in (a). Displacement along the torsional coordinates leads to a block-diagonal form. The colored shadings indicate the relative sign and magnitude of the matrix elements (diagonal: diabatic-state energies, off-diagonal: diabatic-state couplings). (c) Diabatic state energies (i.e., the diagonal elements of the effective Hamiltonians in (b)), their charge distribution and bonding character across the bridge.

Outside the protein environment (i.e., in vacuum and solution), the HBDI⁻ chromophore is essentially non-fluorescent at room temperature, quenched by ultrafast radiationless decay.¹⁹ In solution, fluorescence can be recovered by suppressing large amplitude molecular motion with lowered temperatures and/or increased viscosity.^20,21 Recently, Andersen and coworkers demonstrated using a femtosecond pump-probe scheme combined with a time-resolved action technique (detection of neutral fragments) that fluorescence is an intrinsic property of the HBDI⁻ chromophore.²² Specifically, upon cooling to 100 K, the existence of tiny barriers on S₁(ππ*) was demonstrated by trapping the isolated chromophore on the excited state for 1.2 ns, long enough to establish fluorescence conditions.

In the gas phase, the main deactivation pathways following photoexcitation to S₁ include internal conversion to the electronic ground state and electron autodetachment from the S₁ state to give the neutral HBDI radical in the D₀ state. With a vertical excitation energy of 2.57 eV,²³ the S₁ state of the isolated chromophore is bound with respect to vertical (2.68–2.85 eV (ref. ^24–27)) and adiabatic electron detachment (2.73 eV (ref. ²⁵)). Within the linear excitation regime, internal conversion is the dominant deactivation channel across the S₀–S₁ absorption band (415–500 nm),²⁸ with autodetachment playing a minor role (occurring on a ∼30 ps time scale), as measured by direct electron detection.²⁹ According to time-resolved photoelectron (TRPES)³⁰ and action spectroscopy,²² the excited-state population decay at room temperature is characterized by three time scales; a fast (∼330 fs), an intermediate (1.3–1.4 ps) and a longer-lived (>10 ps) component. However, the explicit nature of dominant decay mechanisms remains unresolved experimentally because of the difficulties associated with characterizing and controlling initial stereoisomer constitution and differentiating transient species.

Theoretical studies suggest that the excited-state decay proceeds along two alternative pathways, corresponding to rotation around one of the methine bridge bonds (i.e., either the imidazolinone, I, or phenolate, P), and is accompanied by twisted intramolecular charge-transfer (TICT) across the bridge (Fig. 1a). The coupling between torsion and charge-transfer is a common feature of monomethine dyes, with HBDI⁻ representing an asymmetric example near the so-called cyanine limit (i.e., characterized by the electronic charge being fully delocalized over the π-conjugated skeleton in the electronic ground state).^31–33 Importantly, the two torsional pathways in the anionic form feature oppositely directed intramolecular charge transfer.^34,35 Only internal conversion mediated by the I-twisted conical intersection (CI) seam may lead to direct E-stereoisomer formation whereas rotation around the P-bond recovers the original ground state (possibly the indistinguishable P-flipped configuration). This naturally raises two questions: (i) what is the relative dynamical importance of the competing I- and P-twisted excited-state pathways, and (ii) what is the intrinsic propensity of HBDI⁻ to undergo internal conversion with significant photoisomerization quantum yield? Addressing these questions could significantly refine our understanding of the photoswitching tunability of the chromophore, leading to proposed chemical substitutions or environmental modifications to accomplish a desired change. Recently, Carrascosa et al. employed a combination of tandem ion mobility mass spectrometry and laser spectroscopy to provide the first experimental evidence that successful isomerization, (i.e., leading to the E-isomer photoproduct) does occur in isolated HBDI⁻ upon photoexcitation.²⁸ However, the experiments were not able to determine whether isomerization is mediated directly by internal conversion or indirectly by subsequent torsional barrier crossing on the hot ground state, and the photoproduct quantum yield was not reported.

So far, electronic structure methods capable of describing the energetic ordering of the I- and P-twisted configurations of isolated HBDI⁻ have been limited to static calculations. Although these provide valuable insight into the potential energy landscape,^34,36 detailed dynamics remain unexplored with methods that can accurately describe the partitioning between I- and P-twisting. Early calculations suggested that torsional motion around both the I- and P-bonds was barrierless³⁵ or barrierless along the P-twisting coordinate.³⁴ However, the most recent high-level calculations confirm the existence of a shallow planar minimum on S₁ (∼0.1 eV below the Franck–Condon (FC) point), characterized by elongated bridge bonds and similar bridge torsional barriers of ∼0.05 eV.³⁶ However, due to the non-equilibrium conditions induced by photoexcitation, account of inertial effects is essential to address the dynamical relevance of competing pathways as well as the intrinsic photoreactivity of their associated CI seams.

In this work, we address the two unresolved questions of pathway bifurcation and photoproduct quantum yield of HBDI⁻ internal conversion dynamics. We investigate the competition between the I- and P-deactivation pathways by performing non-adiabatic dynamics simulations using ab initio multiple spawning^42,43 (AIMS) and monitor the ensuing ground-state dynamics following decay near the I-twisted CI seam to determine the photoisomerization quantum yield. We further present a photoisomerization committor analysis^45,46 which together with the dynamical behavior enables a mapping of potential and inertial effects governing the photoreactivity of the dynamically accessed regions of the I-twisted CI seam. Such detailed insight of the zeroth-order behavior (i.e., isolated chromophore) is a foundational step towards controlling the photodynamical features of the chromophore in a protein environment.

Computational details

The non-adiabatic dynamics following photoexcitation to S₁(ππ*) were modeled using AIMS with adiabatic energies, nuclear gradients and non-adiabatic couplings computed using the complete active space self-consistent field (CASSCF) implementation^47–49 in a development version of the graphical-processing-unit-accelerated TeraChem program.^50–53 Specifically, we use the empirically-corrected α-CASSCF method that was recently demonstrated to be an efficient way of modeling dynamical correlation effects in HBDI⁻ across relevant geometries.⁴⁷ We used an active space consisting of four electrons in three orbitals (the bonding, non-bonding and anti-bonding methine bridge orbitals, see Fig. S2a of the ESI†) with averaging over the three lowest singlet states and the 6-31G* basis set, i.e., α-SA3-CASSCF(4e,3o)/6-31G*. The three-state averaging provides a balanced description of the photoisomerization in the anionic HBDI⁻ chromophore, permitting deactivation through both bridge torsional modes.⁴⁴ The procedure used for fitting the α-parameter and its validation against extended multistate multireference second-order perturbation theory⁵⁴ (XMS-CASPT2) are described in section S1.†

The initial conditions (ICs) for the AIMS simulations were sampled from a ground-state harmonic Wigner distribution at 300 K, with normal modes and harmonic frequencies computed using MP2/cc-pVDZ.⁵⁵ To avoid artificially long C–H bonds, caused by the linearization of the methyl torsions in the harmonic approximation, three normal modes, dominated by these rotations, were excluded from the sampling. Absorption spectra were generated on the basis of 500 samples using the excitation energies and oscillator strengths computed with α(0.64)-SA3-CASSCF(4,3)/6-31G*. The stick spectra were convolved with a Gaussian line shape (FWHM = 0.07 eV) and uniformly blue-shifted by +0.16 eV to match the experimental absorption maximum for HBDI⁻ (Fig. S3†). To mimic the pump energy used in a previous TRPES experiment on anionic HBDI⁻ in the gas-phase,³⁰ 30 ICs were randomly sampled with the constraint of having a vertical excitation energy (shifted by +0.16 eV) within 2.48 ± 0.05 eV, i.e., slightly red-detuned with respect to the linear absorption maximum. Only the two lowest singlet electronic states relevant for the photodynamics (S₀ and S₁) were considered in the AIMS dynamics. Each IC was initiated on S₁ under the independent first-generation approximation,⁵⁶i.e., they are uncoupled and run independently from the beginning, and propagated using AIMS for ∼10 ps (4 × 10⁵ a.u.) or until the S₁ population dropped below 0.01. The equations of motion were integrated with an adaptive time step of 20 a.u. (∼0.48 fs), which was reduced upon encounter of regions with non-adiabatic coupling. A spawning threshold of 0.005 E_h/ℏ (scalar product between derivative coupling and nuclear velocity vectors at a given time step) was applied and the minimum population of a trajectory basis function (TBF) to spawn was 0.01. Errors of decay time constants were estimated with the bootstrap method,^57,58 using 1500 bootstrapping samples. TBFs on S₀ which did not couple with other TBFs for at least 5 fs were decoupled and continued independently on S₀. The stereoisomer distribution on S₀ was followed for a further 1 ps period and classified as described in section S2.†

To rationalize the effects of geometrical deformations, we use the three-state diabatic model proposed by Olsen and McKenzie⁴⁴ (summarized in Fig. 1b and c and section S3†). While earlier work has focused on the coupling between charge-transfer behavior and the bridge-torsional degrees of freedom,^31,44 we focus on the additional geometrical deformations required to reach the intersection seam. In this model, approximate diabatic states are constructed from the effective covalent Hamiltonian obtained by block-diagonalization^59,60 of the full Hamiltonian in the basis of singlet configuration-state functions (CSFs) into covalent and ionic blocks. The energy levels and electronic characters of the resulting covalent-dominated diabatic states (|I〉, |P〉 and |B〉) are shown in Fig. 1c. The six singlet CSFs are generated by distributing four electrons in the three fragment-localized active-space orbitals (labeled p, b and i according to their location) obtained from Boys localization⁶¹ (Fig. S2b†). Further details are provided in section S3.†

Results and discussion

We first validate the chosen method with respect to its ability to capture the relative energetics along the key I- and P-torsional modes. As shown in section S1,† α(0.64)-SA3-CASSCF(4,3) correctly reproduces the energetic ordering predicted by XMS-SA3-CASPT2(4,3) for the S₁ twisted configurations with respect to the FC point. In particular, only the I-twisted MECI is energetically accessible from the FC point, consistent with previous high-level calculations.³⁶ As noted earlier, progress along either of the torsional modes is almost barrierless and fluorescence from the shallow planar S₁ minimum is recoverable only at low temperatures.²² Although we find a small barrier along ϕ_P (∼0.01 eV), the S₁ planar structure does not represent a minimum with α-CASSCF due to the absence of a barrier along ϕ_I (Fig. S5†). Nevertheless, because of the substantial total initial kinetic energy (2.79 eV, half the energy of the zero-point vibrational energy on the ground state as obtained from the Harmonic Wigner sampling) and the negligible torsional barriers, we do not expect this discrepancy to be critical for determining the branching ratio of the competing twisting pathways at non-cryogenic temperatures. We conclude that α-CASSCF offers a sufficiently accurate and efficient route to explore dynamical effects in the excited-state deactivation of HBDI⁻. Geometric parameters of key critical points and their relative ground- and excited-state energies at both levels of theory are reported in Fig. S4 and Tables S1, S3 and S4.†

Fig. 2 presents the S₁ population decay profile for gas-phase HBDI⁻ obtained from the α-CASSCF AIMS simulations. The relaxation is characterized by three different time scales: an ultrafast femtosecond component, an intermediate and a longer-lived picosecond component. Initially after photoexcitation, there is a definite lag period before any population transfer to S₀ is observed. Fitting of the S₁ population profile (based on the ∼10 ps simulation) to a delayed biexponential decay yields a lag time of 177 ± 35 fs and decay time constants of 909 ± 169 fs and 9.0 ± 5.1 ps with amplitudes of 83 and 17%, respectively. This indicates that most of the wavepacket undergoes fast (∼1 ps) internal conversion to the ground state while a fraction remains trapped on S₁ for longer times. These time scales agree reasonably well with the experimental time constants reported for gaseous HBDI⁻ at ambient temperature (300–330 fs, 1.3–1.4 ps and >10 ps).^22,30 Although a rigorous experiment–theory comparison requires calculation of the relevant experimental observable (e.g., TRPES) and remains a task for future work, this overall good agreement lends credence to the following analysis of the simulations.

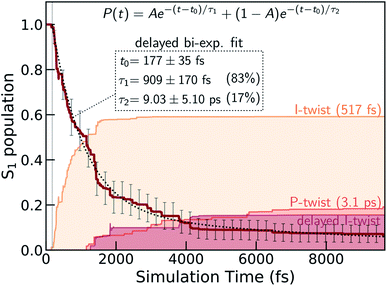Fig. 2 S₁ population decay obtained from the α(0.64)-SA3-CASSCF(4,3) AIMS dynamics together with a delayed bi-exponential fit (black dashed line). The labels give the lag time as well as the two decay time constants and their amplitudes (in parentheses). Associated error bars are standard errors estimated by bootstrapping with 1500 bootstrap samples. Less than 10% of the population remains trapped on S₁ by the end of the simulation time (∼10 ps). The colored shadings indicate the decomposition of the S₀ re-population into direct I- and P-twisting pathways as well as an indirect I-pathway which twists about the I bond only after first twisting and then untwisting about the P bond (see Fig. 5). These were computed as incoherent sums over TBF populations associated with S₀.

Origin of delayed bi-exponential decay

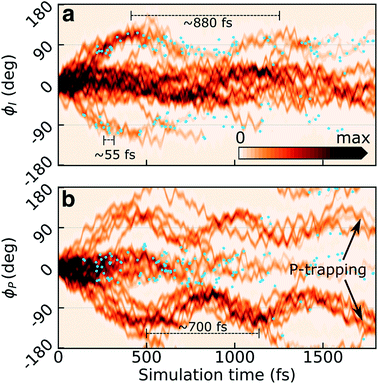
Previous static^34,36,62 (and in two cases dynamic^35,63) calculations suggested bridge torsions and pyramidalization as key deactivation coordinates. To investigate their dynamical importance and elucidate the mechanistic details underlying the experimentally reported time scales, we analyze the progress of the excited-state wavepacket and characterize the geometries which mediate population transfer.

Fig. 3a and b display the initial ∼2 ps time evolution of the one-dimensional reduced S₁ densities along the ϕ_I and ϕ_P dihedrals, respectively. These were computed using a previously-described Monte Carlo procedure.⁶⁴ The blue filled circles indicate spawning geometries (i.e., the centroid positions of the spawned TBFs) associated with non-adiabatic population transfer events. Departure from the FC region involves weakening of the both bridge bonds which facilitates subsequent redistribution of vibrational energy into the two bridge torsional coordinates. Owing to the asymmetry of the I-ring, oppositely directed I-twisted geometries are enantiomers, while the corresponding P-twisted structures are identical. Consistent with the essentially barrierless potential energy curves along both torsional modes, roughly half of the population (∼40%) initially undergoes ϕ_P twisting while the remaining proceeds along ϕ_I. That is, the torsional motion is dominated by one-bond-flip pathways (early temporal evolution of the S₁ density in the (ϕ_P,ϕ_I) plane is shown in Fig. S6†). The onset of the population decay (non-adiabatic transition events indicated as blue circles) coincides with nearly perpendicular I-twisted configurations but the emergence of oscillations with period of ∼880 fs (frequency of 38 ± 11 cm⁻¹, as obtained from a Fourier-component analysis of individual TBFs) is indicative of a sloped access to the CI seam (only ∼34% of the population is transferred during the first seam crossing). Displacement along the ϕ_P mode exhibits more pronounced oscillations (frequency of 48 ± 18 cm⁻¹, period of ∼700 fs), and the P-twisted fraction of the excited-state wavepacket largely remains trapped on S₁ beyond ∼2 ps. The coupling to the faster bridging methine hydrogen out-of-plane (HOOP) motion appears as a high-frequency component (582 ± 54 and 611 ± 100 cm⁻¹ along P- and I-twisted pathways, respectively, corresponding to a period of ∼55 fs) along both torsional modes.

Fig. 3 Time evolution of the S₁ wavepacket density along the bridge torsional modes within the first 1.8 ps after photoexcitation. The S₁ reduced density is projected onto the (a) ϕ_I and (b) ϕ_P dihedral angles. The fast-oscillating component (∼55 fs) originates from bridge HOOP motion. While motion along the ϕ_I dihedral mediates significant population transfer, the ϕ_P torsional mode leads to population trapping on S₁ for longer time scales. Blue filled circles indicate the location of non-adiabatic transition events. Slightly asymmetric density distributions with respect to the rotational sense of torsion are an indicator of sampling errors, since the underlying potential energy profiles are exactly symmetric.

The (ϕ_P,ϕ_I)-distribution of spawning geometries is shown in Fig. 4c. They cluster into two distinct pathways, dominated by torsional motion along either one of the bridge dihedrals. These geometries largely resemble the two types of MECIs reported previously,^34,62,63,65 here labeled MECI-I^+/− and MECI-P^+/− (Fig. 4a, b and S7†). The superscript +/− labels the sense of rotation and indicates enantiomeric structures. However, the sloped access to the intersection seam combined with the significant nuclear kinetic energy gained upon twisting means that higher-energy regions of the seam become increasingly relevant in the dynamics. This is seen from the distribution of S₁/S₀ energy gaps and the energetic locations of the spawning geometries relative to the geometrically nearest MECI (Fig. 4d and e). As shown by decomposing the re-population of S₀ according to its torsional mechanism (filled curves in Fig. 2), the I-twisting pathway accounts for the majority of the population transfer (∼60% via direct decay, see below) while only ∼20% transfers at P-twisted geometries. The remaining population (∼20%) is split between P-trapping on S₁ and delayed I-twist internal conversion following temporary trapping along ϕ_P. In the latter case, the initially P-twisted subpopulation is reflected back via a near-planar configuration to reverse the charge-transfer direction rather than following a higher-energy hula-twist like motion (i.e., concerted rotation around both bridge bonds).⁶⁶

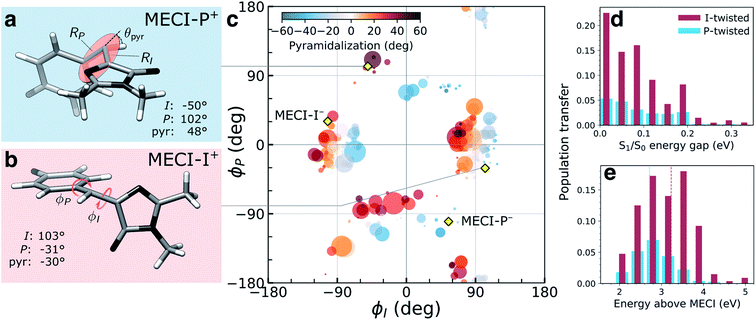Fig. 4 Geometric characterization of non-adiabatic transition events. Structures of (a) MECI-I⁺ and (b) MECI-P⁺ highlighting key geometric parameters (definitions are given in Fig. S1†). The arrows define positive direction of rotation for the bridge dihedrals with zero angles corresponding to the Z-isomer. (c) Distribution of (ϕ_I, ϕ_P)-dihedrals at the spawning geometries. The radius and color of each circle represent absolute population transfer and extent of bridge pyramidalization, respectively. The absolute population transfer is defined as the total population gained by the child TBF from the beginning of the coupled propagation until the gain drops below a threshold value of 10⁻⁴. Efficient population transfer is associated with significant pyramidalization of the methine bridge. Yellow diamonds indicate the location of MECIs. (d) Absolute population transfer versus S₁/S₀ energy gap at the non-adiabatic transition events divided according to the decay pathway. (e) Distribution of the S₁ energies at the I- and P-twisted spawning events relative to the geometrically closest MECI. The vertical dashed red (blue) line corresponds to the sum of the zero-point kinetic energy in the ground-state (within a harmonic approximation) and the energy gap between the FC point and MECI-I⁺ (MECI-P⁺) geometry.

The delayed onset and less efficient decay through the P-twist pathway is consistent with MECI-P^+/− being energetically inaccessible from the FC point (see Fig. S4†). In addition to the diabatic state-selective destabilization mediated by an asymmetric bond stretching across the bridge, access to the minima on the intersection seams requires pyramidalization of the methine C atom. The gradient difference vectors (g-vector) at both types of MECIs are dominated by this collective pyramidalization and bond-stretch motion whereas the derivative coupling vectors (h-vector) mainly represent torsional motion around the respective bridge bond (Fig. S7†). For later reference, note that the +h-direction corresponds to torsional motion toward E-isomer generation for the MECI-Is and P-flipping for the MECI-Ps. Consistent with the dynamical behavior discussed above, both types of MECIs are sloped and single path.^39,62 Following the paths of steepest descent on S₀ starting from points sampled around the MECIs leads exclusively to recovery of the original Z-isomer (data not shown). The pyramidalization on S₁ is governed by the fast methine HOOP motion, which primarily gains amplitude upon torsion, and its direction is initially dictated by that of the activated torsional mode (Fig. S8†). The stronger electron affinity of the P-ring (vertical electron affinities of 1.23 and 0.63 eV for the P- and I-ring, section S4†) leads to a larger S₁/S₀ energy gap at P-twisted geometries (Fig. 1a and Table S1†).³⁶ Similar to the asymmetric bond stretch, pyramidalization acts as a diabatic-state biasing potential that preferentially destabilizes the torsionally-decoupled diabatic state dominating S₀ (see section S3†). Due to the larger energy gap, a higher degree of pyramidalization is needed to reach the P-twisted intersection seam.

The hot ground state will eventually undergo chemical transformations (such as thermal isomerization, fragmentation and electron emission^28,29) due to absence of intermolecular energy dissipation channels in the gas phase. However, whether the preceding internal conversion directly produces E-isomer via photoisomerization remains an open question. Although one may provide a simple estimate based on the limiting regimes of ballistic and statistical behavior (see section S5 and Fig. S10†), account of dynamical features of the system is needed to predict its photoreactivity. To investigate this, we therefore followed the ensuing S₀ dynamics and classified the stereoisomer distribution over a 1 ps time period (section S2 and Fig. S11†). While ∼55% of the total excited-state population recovers the ground-state photoreactant (∼37% of this subpopulation also undergoes indistinguishable P-flip), a notable ∼35% generates photoproduct. An additional ∼5% falls into the non-determined region and the remaining fraction is trapped on S₁ till the end of the simulation. Considering only the population that undergoes decay via the I-twisted channel, the quantum yield increases to ∼50%. As seen in Fig. S11b,† excess energy in the torsional modes leads to large-amplitude oscillations (spanning ±55° relative to the respective minimum and with a period of ∼400 fs) but without any substantial additional isomerization on the ground state. Accordingly, the average Z- and E-isomer occupancies (51 ± 3% and 32 ± 3%, respectively) remain stable over the 150 fs to 1 ps time window.

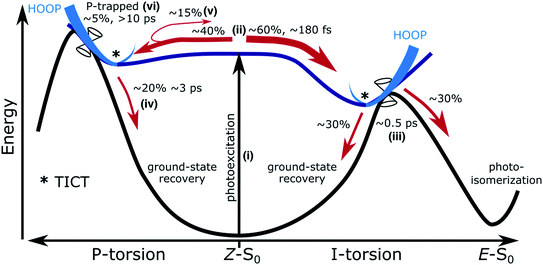
The main features of the excited-state decay mechanisms in isolated HBDI⁻ appearing from our simulations are summarized in Fig. 5. Photoexcitation is followed by bifurcation of the wavepacket in near-equal proportions along the two alternative bridge torsional coordinates. The ∼180 fs lag time corresponds to the time associated with vibrational energy redistribution from FC-active vibrations (low-frequency bridge-bending and high-frequency bridge-stretching modes^36,67) into the torsional modes required to reach the intersection seams. Not surprisingly, based on the shorter plateau and steeper torsional gradient with α-CASSCF compared to XMS-CASPT2 (Fig. S5 and S12†), this delay time is shorter than the fastest reported experimental decay constant of ∼300 fs. The ∼1 ps component of the biexponential decay is dominated by the faster excited-state relaxation through the I-twist pathway (∼0.5 ps) with a smaller but slower contribution from P-twist mediated decay (∼3 ps). The longer time-scale component is a consequence of a fraction being trapped on S₁ along the P-torsional mode. We note that the lifetime of the trapped P state may be somewhat underestimated given the energetic closer proximity of MECI-P^+/− to the FC point at the present level of theory compared to the XMS-CASPT2 prediction (Fig. S4†). Nevertheless, the mechanistic insight predicted by our simulations largely supports the models previously proposed on the basis of experimental data and high-level static calculations.^22,36 In addition, our dynamics results demonstrate that internal conversion through the I-twisted CI seam mediates photoproduct generation. This is in contrast to the unreactive behavior predicted by S₀ minimum energy pathways starting near the MECIs. Clearly, a dynamical mapping of the I-twisted intersection seam is necessary to understand the origin of the non-zero photoproduct quantum yield.

Fig. 5 Schematic of the excited-state dynamics of HBDI⁻, showing (i) photoexcitation, (ii) departure from the FC point along the torsional modes, internal conversion via the (iii) I-twist, (iv) P-twist and (v) delayed I-twist pathways and (vi) trapping along the P-channel. Branching ratios and time scales from the AIMS dynamics indicated. Ratios are determined relative to the total population. Twisted intramolecular charge-transfer (TICT) configurations are indicated by asterisks.

Mapping the sloped I-twisted intersection seam

To this end, we consider the dynamically accessed regions of the I-twisted intersection seam, focusing on the positive I-twist direction (MECI-I⁺). Fig. 6a shows the distribution and outcome of the non-adiabatic transition events along the I-torsion and HOOP coordinates, roughly approximating the branching space in a first-order analysis, together with contour plots of the S₀ and S₁ potential energy surfaces (PESs) (details in section S6†). The corresponding three-dimensional representations of the PESs are shown in Fig. 6b.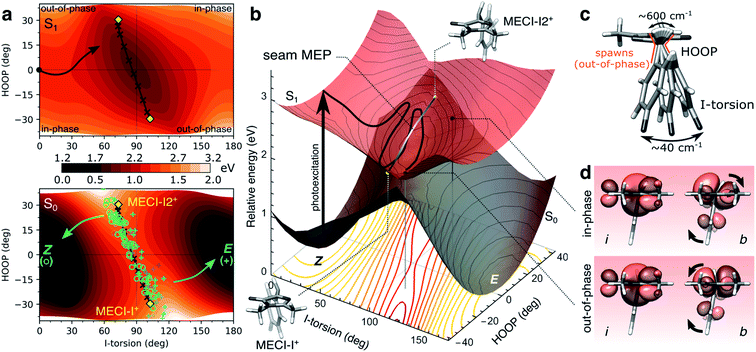

Fig. 6 The implications of HOOP on photoproduct generation along the positive I-twist mediated decay pathway. (a) Contour plots of the S₁ (top) and S₀ (bottom) PESs along the I-torsion and HOOP modes. These have been obtained by an unrelaxed HOOP scan along geometries derived from an I-torsional scan (keeping the P-torsion fixed at zero, while all remaining coordinates were allowed to relax). The black arrow in the top panel indicates the S₁ MEP from the Z-isomer towards the I-twisted geometry. Each quadrant is labeled according to the in-phase and out-of-phase definitions of configurations. MECIs are highlighted by the yellow diamonds while non-adiabatic transitions leading to ground-state recovery (Z-isomer) are indicated by open green circles and those producing photoproduct (E-isomer) by blue plus signs. These roughly correspond to each peak in the approximate bimodal distribution (see Fig. S8†). The black line connecting MECI-I⁺ and MECI-I2⁺ shows the seam MEP (see gray line in (b) and Fig. S13†). The MECIs are reached by tuning the bond distances (in particular, the P-bond and C₅–C₆ are extended by ∼3 and 4 pm, respectively) and contraction of the bridge angle by ∼6.8°. The main effect of this is a destabilization of S₀ (not shown) and a rotation of the S₀ ridge. (b) Three-dimensional representation of the PESs in (a). The contour plot below shows the energy gap between the S₁ and S₀ states, indicating a smaller gap (red) at out-of-phase geometries. The MECIs are shown as yellow points, and the seam MEP as the connecting gray line. The two black points on the S₁ surface correspond to out-of-phase and in-phase configurations at the same I-torsion angle, see (d). (c) Schematic representation of the HOOP and I-torsional modes with estimates of their frequencies as obtained from the dynamics. As indicated in (a), population transfer occurs when the two coordinates are at out-of-phase configurations. (d) Boys-localized orbitals on the I-ring and the methine bridge (labeled i and b, respectively) for the in-phase and out-of-phase configurations indicated in (b). Isovalue: 0.03 a.u. The HOOP direction at out-of-phase configurations counteracts the rotation of the b-orbital relative to the i-orbital induced by the I-torsion, thereby maintaining an effectively orthogonal arrangement of these orbitals similar to the situation at the 90° I-twisted minimum (S₁-I, Fig. 1a and b).

The non-adiabatic population transfer events (shown as markers) tend to follow a bimodal distribution with maxima centered around “out-of-phase” configurations (see also Fig. S8†). These are defined as geometries where the pyramidalization direction of the methine C atom is opposite of the sign of the torsional displacement relative to a 90° I-twist (Fig. 6c). In other words, this notation refers to a static phase relationship between the HOOP and torsional coordinates at the non-adiabatic transition events. At these geometries, simultaneous pyramidalization and a near-orthogonal arrangement of the localized i and b orbitals are achieved (Fig. 6d). This preserves the approximate block-diagonal structure of the Hamiltonian, as required to reach the S₁/S₀ intersection seam (see Fig. S9 and Table S6†). Furthermore, since the electronic coupling of the bridge and P-ring with the asymmetric I-ring is weak at I-twisted configurations, we may expect two MECIs related by a mirror plane perpendicular to the I-ring and passing through the I-bond (i.e., approximate enantiomers, in contrast to MECI-I^+/− and MECI-P^+/− that are exact enantiomers). Indeed, in addition to the previously reported MECI-I⁺, we located an essentially isoenergetic MECI, labeled MECI-I2⁺. While the population transfer efficiency is similar for both MECIs, the region around MECI-I2⁺ is reached earlier in the dynamics due to its closer proximity to the FC point. Consequently, the majority of the I-twisted population transfer (64%) occurs in the vicinity of MECI-I2⁺. The seam MEP connecting the two MECIs (gray line connecting the yellow markers in Fig. 6b) is characterized by a small barrier of ∼0.1 eV, associated with planarization of the methine C-atom and a ∼0.03 Å lengthening of the C₅–C₆ bond (Fig. S13a†). The topography along the seam MEP remains sloped towards the photoreactant (Fig. S13b and Table S5†). We note that the direction and degree of the P-torsion at both MECIs are governed by the pyramidalization so as to maximize the alignment of the p orbital and the now increasingly sp³-hybridized b orbital. However, motion along ϕ_P is associated with only a small energy-gap penalty (i.e., it is outside the branching space within the first-order approximation) easily compensated by small bond and angle adjustments. Therefore, population transfer occurs over an extended region of the seam where the P-ring can be misaligned with respect to the bridge pyramidalization. In particular, in the (ϕ_I, ϕ_P) = (+90°,>0°) quadrant (see Fig. 4c), the topography becomes sloped towards the photoproduct (Fig. S14 and Table S5†). In the following, we ignore the displacement along ϕ_P in the geometric classification of the non-adiabatic events.

Our dynamics simulations suggest a correlation between the location of the non-adiabatic population transfer events and the outcome of the internal conversion: the ratios between reactive and unreactive outcome of the internal conversion at the MECI-I⁺ and MECI-I2⁺ (combining data for both positive and negative ϕ_I-values) are ∼3 : 1 and ∼1 : 2, respectively. This is at variance with the seam MEP analysis (steepest descent paths from each of the MECIs), which found both of these MECIs to be unreactive. Since MECI-I2⁺ is encountered first in the dynamics (as it is closer to the FC point), one might expect that it would be especially reactive (as the molecule has been accelerated along the reactive torsional mode and there has been little time for energy dissipation). In the following, we explore the origin of this difference in photoreactivity around the two MECI-Is.

Origin of different dynamical behaviors

To uncover the origin of the difference in photoreactivity between the two I-twisted MECIs, we investigated the implications of inertial effects, i.e., the velocity and direction of the approach to and exit out of different regions of the I-twisted intersection seam. While inertial effects through the interplay of effective coupling strength and interaction time dictate the efficiency of population transfer,^37,41 we here focus on how they affect the outcome (i.e., successful or aborted isomerization). Previous theoretical and experimental work on rhodopsin, rhodopsin derivatives and retinal models has provided evidence that the stereochemical route taken on the ground state is controlled by the dynamic phase relationship of the C11=C12 torsion and H–C11=C12–H HOOP modes of the retinal protonated Schiff-base chromophore upon encounter of the intersection seam.^{38,40,68–73} Inspired by this, we initially examined the influence of the bridge HOOP motion on the photoproduct distribution in HBDI⁻ but found no clear trend. In hindsight, this may not be surprising given that the non-adiabatic events occur at large displacements along the HOOP mode and hence at low HOOP velocities (see Fig. 6c and S15†).

Next, we considered the inertial effects within the branching plane. Two limiting regimes can be envisioned. In the first limit, the non-adiabatic transitions occur at classical turning points within the branching space, i.e., at velocities with comparatively small components along the g- and h-vectors, such that the outcome is dictated by the momentum gained on the ground state. In the second regime, the population transfer occurs with substantial kinetic energy in the branching space. To explore these limits, we considered the photoproduct distributions obtained from 300 fs S₀ dynamics starting from geometries around each of the two MECI-Is (referred to as cone sampling) and two constructed sets of initial velocities: (i) zero initial velocities, where the only source of kinetic energy comes from the acceleration induced by the ground-state PES, and (ii) starting with all kinetic energy (∼0.44 eV, corresponding to the energy difference between the FC point and the MECI-I⁺) initially distributed entirely within the branching space. While 300 fs is too short to conclude whether the system has been arrested in the photoproduct valley or not, the analysis indicates the intrinsic photoreactivity following the passage through the intersection seam. To investigate the dynamical photoreactivity, we further estimate the committor distribution^45,46 around each of the two MECI-Is. Our procedure is similar to previous work by Sellner et al.⁷⁴ but also accounts for configurational sampling around MECIs. The photoisomerization committor surface gives an estimate of the probability of generating photoproduct under the assumption of a thermalized state. Although thermalization is not expected during ultrafast internal conversion, this analysis nevertheless provides insight into the influence of having non-zero kinetic energy within the intersection space. Further details are provided in section S7.†

Fig. 7a and b summarize the results for the zero- and random-initial-velocity sampling schemes applied to the two MECI-Is (middle and bottom rows) whereas those obtained from non-zero velocities restricted to the branching space are shown in Fig. S16.† The location of each point in the polar plots represents the geometric displacement within the branching plane while its color indicates the outcome of the ground-state dynamics or the probability of photoproduct formation for the zero- and random-initial-velocity sampling schemes, respectively. For low velocities in the branching plane, the location of the non-adiabatic population transfer on the I-twisted intersection seam determines the outcome, and photoproduct formation is confined to regions corresponding to displacements in the +h-direction and only around MECI-I⁺. At higher velocities with all kinetic energy restricted to the branching space, the dissimilarity between the two MECI-Is largely disappears (Fig. S16†), and the exit direction within the branching space now decides which product will be formed. In particular, the h-vector represents the isomerization-driving coordinate (+h-direction represents I-torsion towards the E-isomer, see Fig. S7b†), and velocity along this direction promotes photoproduct generation irrespective of the location of the non-adiabatic transition (MECI-I⁺ or MECI-I2⁺). A similar imprint of the +h-direction (in terms of both displacement and exit direction) is obtained upon introducing initial kinetic energy in the remaining degrees of freedom. The dashed black line in Fig. 7b represents the equicommittor (i.e., geometries at which initialization of S₀ dynamics will lead to ground-state recovery and photoproduct generation with equal probability). Consistent with the dynamics, we recover the picture of MECI-I⁺ being more photoreactive than MECI-I2⁺, and the comparison between the three different sets of initial conditions suggests that this intrinsic difference originates from the asymmetry of the I-ring as will be discussed below.

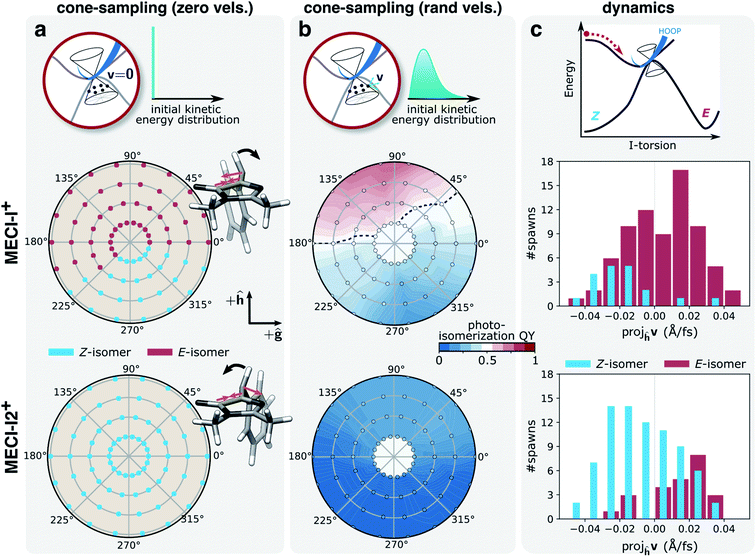Fig. 7 Implications of inertial effects on photoproduct generation from the I-twisted intersection seam. Top row: schematic of the three sampling schemes; middle row: MECI-I⁺; bottom row: MECI-I2⁺. Photoproduct distribution at each displacement within the branching plane, as given by the polar coordinates (radii: 0.005–0.02 a.u. in steps of 0.005 a.u.), based on the outcome of dynamics starting from (a) zero initial velocities. The asymmetric contraction of the I-ring and methine planarization on S₀ (orange arrows) lead to oppositely directed acceleration of the HOOP motion (black arrows) for the two MECI-Is. This promotes photoproduct formation at MECI-I⁺ while inhibiting it at MECI-I2⁺; (b) 50 initial conditions with randomized velocities. The black line represents the isocommittor line corresponding to 50% photoproduct generation. (c) Distributions of the velocity components for the parent TBF along the h-direction (dominated by I-torsional motion, see Fig. S7†) at the non-adiabatic transition events close to the two types MECI-Is and categorized based on the outcome of the ensuing S₀ dynamics. Events for both positive and negative ϕ_I directions have been combined. In line with the photoproduct distributions in (b), photoisomerization near MECI-I2⁺ correlates with a positive component along the h-direction, and ground-state recovery from MECI-I⁺ with a negative component.

The different dynamical behaviors around the MECI-Is at zero initial velocities can be explained by the directional bias of the momentum gained along the lighter HOOP coordinate upon reaching the ground state. Without initial kinetic energy, the early dynamics on S₀ will be governed by the direction of steepest descent on S₀ which involves a shortening of the C₅–C₆ bond and de-pyramidalization at the methine C atom (see Fig. 7a, gradient difference vector in Fig. S7 and section S3†). This results in a rapid, asymmetric contraction of the I-ring and methine bridge planarization. In turn, this induces oppositely-directed HOOP motion for the two MECI-Is before any substantial deformation of the slower I-torsional mode takes place. For MECI-I⁺, this promotes crossing of the S₀ ridge thereby enabling photoproduct generation, while impeding it for MECI-I2⁺ (see Fig. 7a). We tested this interpretation by artificially increasing the mass of the methine H-atom to that of a methyl group (∼15 amu). This confirmed that at zero initial velocities the now heavier HOOP mode is no longer fast enough to mediate barrier crossing prior to activation of the torsional mode, thereby preventing photoproduct generation around MECI-I⁺ (Fig. S17†).

Having explored various limiting behaviors at the I-twisted seam, the central question then becomes what characterizes the dynamical behavior of the system? In other words, what is the actual velocity distribution upon reaching the intersection seam? As expected from the oscillatory behavior along ϕ_I, the overall distribution of velocity components along the h-vector at the non-adiabatic transition events is symmetric and similar for both MECI-Is (Fig. S16a†). About 70% of the I-twisted population transfer occurs with a kinetic energy contribution along the h-direction that is larger than the kinetic energy per degree of freedom assuming equipartitioning among all vibrational degrees of freedom. Moreover, as indicated in Fig. 7c, a separation based on the outcome of the internal conversion process reveals a correlation between the direction of the component along the h-vector and the photoproduct: ground-state recovery close to MECI-I⁺ is associated with a negative velocity component whereas photoproduct formation in proximity to MECI-I2⁺ is mostly associated with a positive velocity component. An opposite but much weaker trend is observed for the reverse cases (i.e., photoproduct formation near MECI-I⁺ and ground-state recovery around MECI-I2⁺). The corresponding picture weighted by the absolute population transfer is provided in Fig. S18b.† Together, these results show that the ∼50% photoisomerization quantum yield for the I-twisted population is a consequence of two effects: (i) initial approach to the intrinsically unreactive MECI-I2⁺ region of the seam which is nevertheless more reactive than expected because non-statistical conditions prevail and there is significant velocity along the isomerization-driving +h-direction (i.e., driven by inertial effects on S₁), and (ii) the intrinsic higher photoreactivity of MECI-I⁺ compared to MECI-I2⁺ (i.e., mostly governed by the photoproduct-favoring inertial effects gained on the ground state caused by the planarization direction of the bridge and the asymmetry of the I-ring).

Our analysis suggests a possible strategy for optimizing the rate and quantum yield of photoisomerization of HBDI⁻. We recall that the appearance of the out-of-phase MECI-I configurations is a consequence of the non-vanishing S₁/S₀ energy gap at I-twisted structures: vibrational redistribution from the isomerization-driving I-torsion into the HOOP coordinate is required to reach the intersection seam. Applying a diabatic biasing potential, such as through a chemical modification or mutations of the protein scaffold, to selectively destabilize the torsionally-decoupled |I〉 state, could potentially remove the need for pyramidal motion, thereby changing the shallow double well on the seam to a single well with its minimum near or even coinciding with the I-twisted minimum. This could lead to a more direct approach to the intersection seam along the isomerizing-driving I-torsional coordinate with a consequent increase in rate and yield of photoisomerization. The extent to which such a strategy would be transferable to the chromophore inside a protein remains to be investigated given that particular movements may be arrested in the protein. Most apparently, conformational restrictions may direct the wavepacket towards alternative regions of the intersection seams, dynamically inaccessible in the gas phase, and not considered in this work. For example, the volume-conserving high-energy hula-twist motion in the isolated chromophore has been suggested as deactivation pathway in several GFP relatives.^75–77

Conclusions

In summary, we have simulated the excited-state dynamics of the isolated HBDI⁻ chromophore following photoexcitation to S₁(ππ*). Our simulations are in good agreement with experimental time scales enabling us to provide mechanistic insight into internal conversion dynamics of the chromophore. Our findings can be summarized as follows. The excited-state population predominantly undergoes ultrafast internal conversion through the I-twist pathway with only a minor fraction (∼5%) decaying through the competing P-twist pathway. However, the combination of equitable initial branching along the two pathways and existence of a P-twisted minimum on S₁ leads to P-trapping on longer timescales. The near mirror symmetry of the bridge-pyramidalized and I-twisted geometries introduces two minima on the I-twisted intersection seam (MECI-I⁺ and MECI-I2⁺) that dynamically display opposite trends in terms of photoproduct formation. By mapping the photoreactivity of each of the MECI-Is via a committor analysis and studying the influence of the exit direction on the outcome of the internal conversion process, we identified the origin of this difference: the asymmetry of the I-ring and bridge planarization direction leads, upon reaching the ground state, to differently directed HOOP motion, promoting selectively either photoproduct generation (MECI-I⁺) or ground-state recovery (MECI-I2⁺). Despite its lower photoreactivity, the earlier encounter of MECI-I2⁺ during the dynamics combined with the initial vibrational energy redistribution into the isomerization-driving I-torsional mode implies that internal conversion near both minima on the seam contribute about equally to photoproduct formation. Accordingly, HBDI⁻ represents an example where a combination of ballistic motion and statistical behavior involving an inherently more reactive part of the seam governs the product yield of the non-adiabatic decay. In other words, our work suggests that the experimentally evidenced photo-induced production of E-isomer²⁸ indeed originates from direct passage through the I-twisted intersection seam although thermal isomerization on the vibrationally hot ground state can also contribute at longer time scales.

The present explanatory study lays the foundation for future work focused on manipulation: specifically, addressing the extent to which perturbative effects, either inertial or potential (steric/electronic), induced by substituents or environmental modifications can be introduced to tailor the outcome of photoexcitation of HBDI⁻. Tuning the photoisomerization quantum yield is important not only in the traditional imaging role through super-resolution microscopy^8,9,78 but also for emerging opportunities within optogenetics. For example, light-activated strand-dissociation of split-GFP constructs could be used as an optogenetic tool for protein control but their utility is currently limited by the low yield of the strand-exchange-inducing photoisomerization.^79,80 Two key approaches are envisioned for such photoswitching applications. First, the competitive P-twisted excited-state paths leading to a distinct intersection seam could be eliminated by biasing the early dynamics towards the reactive I-twist channel. The non-selectivity of the torsional pathways upon departure of the FC point, inherent to the isolated chromophore, leads to almost equal bifurcation of the wavepacket into the I- and P-channels. Since P-torsion exclusively leads back to photoreactant, diminishing the importance of this channel should increase the yield of E photoproduct. Secondly, the rate and efficiency of photoisomerization along the reactive I-twist pathway could be improved by impeding the competitive aborted isomerization on the ground state. Although a strict distinction between effects of the surrounding protein and direct chromophore modifications cannot be made, the recent time-resolved fluorescence study on Dronpa2 variants by Romei et al.⁸¹ indicates the potential of using chemical substitution on the P-ring to selectively modify the excited-state torsional barrier by tuning the electronegativity of the substituent and hence the route taken by the excited-state wavepacket. In line with the second point, the fact that internal conversion in HBDI⁻ is gated by bridge pyramidalization suggests modifying the wavepacket approach to the intersection seam by shifting the location of the MECI closer to the S₁ minimum. Ideally, this could translate into higher kinetic energy in the isomerization-driving I-torsional coordinate with a consequent accelerated internal conversion and increased photoisomerization quantum yield. Work is currently underway to explore these possibilities.

Data availability

Coordinates for critical structures and data supporting this article have been uploaded as part of the ESI.†

Author contributions

N. H. L. contributed to the data curation, formal analysis, investigation, methodology, project administration, funding acquisition, visualization and writing (original draft) of the presented work. C. M. J. contributed to data curation, investigation and methodology. T. J. M. contributed to methodology, project administration, funding acquisition, resources, and supervision. All authors contributed to conceptualization of the project and review and editing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the AMOS program of the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Chemical Sciences, and Biosciences Division. N. H. L. acknowledges financial support from the Villum Foundation (Grant No. VKR023371), and C. M. J. from the NSF graduate research fellowship program. The authors thank Dr Matthew Romei, Dr Chi-Yun Lin and Prof. Steven Boxer for valuable discussions.

References

1. M. Ormö, A. B. Cubitt, K. Kallio, L. A. Gross, R. Y. Tsien and S. J. Remington, Science, 1996, 273, 1392–1395.
2. O. Shimomura, F. H. Johnson and Y. Saiga, J. Cell. Comp. Physiol., 1962, 59, 223–239.
3. O. Shimomura, FEBS Lett., 1979, 104, 220–222.
4. D. C. Prasher, V. K. Eckenrode, W. W. Ward, F. G. Prendergast and M. J. Cormier, Gene, 1992, 111, 229–233.
5. B. N. G. Giepmans, S. R. Adams, M. H. Ellisman and R. Y. Tsien, Science, 2006, 312, 217–224.
6. E. A. Rodriguez, R. E. Campbell, J. Y. Lin, M. Z. Lin, A. Miyawaki, A. E. Palmer, X. Shu, J. Zhang and R. Y. Tsien, Trends Biochem. Sci., 2017, 42, 111–129.
7. R. Y. Tsien, Annu. Rev. Biochem., 1998, 67, 509–544.
8. M. Hofmann, C. Eggeling, S. Jakobs and S. W. Hell, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17565–17569.
9. R. M. Dickson, A. B. Cubitt, R. Y. Tsien and W. E. Moerner, Nature, 1997, 388, 355–358.
10. M. Andresen, A. C. Stiel, J. Fölling, D. Wenzel, A. Schönle, A. Egner, C. Eggeling, S. W. Hell and S. Jakobs, Nat. Biotechnol., 2008, 26, 1035–1040.
11. T. Grotjohann, I. Testa, M. Leutenegger, H. Bock, N. T. Urban, F. Lavoie-Cardinal, K. I. Willig, C. Eggeling, S. Jakobs and S. W. Hell, Nature, 2011, 478, 204–208.
12. A. Acharya, A. M. Bogdanov, B. L. Grigorenko, K. B. Bravaya, A. V. Nemukhin, K. A. Lukyanov and A. I. Krylov, Chem. Rev., 2017, 117, 758–795.
13. V. Sample, R. H. Newman and J. Zhang, Chem. Soc. Rev., 2009, 38, 2852–2864.
14. A. A. Pakhomov and V. I. Martynov, Chem. Biol., 2008, 15, 755–764.
15. R. N. Day and M. W. Davidson, Chem. Soc. Rev., 2009, 38, 2887–2921.
16. C.-Y. Lin, M. G. Romei, L. M. Oltrogge, I. I. Mathews and S. G. Boxer, JACS, 2019, 141, 15250–15265.
17. K. S. Sarkisyan, D. A. Bolotin, M. V. Meer, D. R. Usmanova, A. S. Mishin, G. V. Sharonov, D. N. Ivankov, N. G. Bozhanova, M. S. Baranov, O. Soylemez, N. S. Bogatyreva, P. K. Vlasov, E. S. Egorov, M. D. Logacheva, A. S. Kondrashov, D. M. Chudakov, E. V. Putintseva, I. Z. Mamedov, D. S. Tawfik, K. A. Lukyanov and F. A. Kondrashov, Nature, 2016, 533, 397–401.
18. S. Kojima, T. Hirano, H. Niwa, M. Ohashi, S. Inouye and F. I. Tsuji, Tetrahedron Lett., 1997, 38, 2875–2878.
19. H. Niwa, S. Inouye, T. Hirano, T. Matsuno, S. Kojima, M. Kubota, M. Ohashi and F. I. Tsuji, Proc. Natl. Acad. Sci., 1996, 93, 13617.
20. K. L. Litvinenko, N. M. Webber and S. R. Meech, J. Phys. Chem. A, 2003, 107, 2616–2623.
21. A. D. Kummer, C. Kompa, H. Niwa, T. Hirano, S. Kojima and M. E. Michel-Beyerle, J. Phys. Chem. B, 2002, 106, 7554–7559.
22. A. Svendsen, H. V. Kiefer, H. B. Pedersen, A. V. Bochenkova and L. H. Andersen, J. Am. Chem. Soc., 2017, 139, 8766–8771.
23. M. W. Forbes and R. A. Jockusch, JACS, 2009, 131, 17038–17039.
24. Y. Toker, D. B. Rahbek, B. Klærke, A. Bochenkova and L. H. Andersen, Phys. Rev. Lett., 2012, 109, 128101.
25. S. Deng, X.-Y. Kong, G. Zhang, Y. Yang, W.-J. Zheng, Z.-R. Sun, D.-Q. Zhang and X.-B. Wang, J. Phys. Chem. Lett., 2014, 5, 2155–2159.
26. D. A. Horke and J. R. Verlet, Phys. Chem. Chem. Phys., 2012, 14, 8511–8515.
27. C. R. S. Mooney, M. E. Sanz, A. R. McKay, R. J. Fitzmaurice, A. E. Aliev, S. Caddick and H. H. Fielding, J. Phys. Chem. A, 2012, 116, 7943–7949.
28. E. Carrascosa, J. N. Bull, M. S. Scholz, N. J. A. Coughlan, S. Olsen, U. Wille and E. J. Bieske, J. Phys. Chem. Lett., 2018, 9, 2647–2651.
29. C. W. West, A. S. Hudson, S. L. Cobb and J. R. Verlet, J. Chem. Phys., 2013, 139, 071104.
30. C. R. S. Mooney, D. A. Horke, A. S. Chatterley, A. Simperler, H. H. Fielding and J. R. R. Verlet, Chem. Sci., 2013, 4, 921–927.
31. S. Olsen and R. H. McKenzie, J. Chem. Phys., 2009, 131, 234306.
32. M. Dekhtyar, W. Rettig and V. Rozenbaum, J. Photochem. Photobiol., A, 1999, 120, 75–83.
33. S. Olsen and R. H. McKenzie, J. Chem. Phys., 2012, 137, 164319.
34. M. E. Martin, F. Negri and M. Olivucci, J. Am. Chem. Soc., 2004, 126, 5452–5464.
35. S. Olsen, K. Lamothe and T. J. Martinez, J. Am. Chem. Soc., 2010, 132, 1192–1193.
36. A. V. Bochenkova and L. H. Andersen, Faraday Discuss., 2013, 163, 297–319.
37. J. P. Malhado and J. T. Hynes, J. Chem. Phys., 2016, 145, 194104.
38. I. Schapiro, M. N. Ryazantsev, L. M. Frutos, N. Ferré, R. Lindh and M. Olivucci, JACS, 2011, 133, 3354–3364.
39. I. F. Galván, M. l. G. Delcey, T. B. Pedersen, F. Aquilante and R. Lindh, J. Chem. Theory Comput., 2016, 12, 3636–3653.
40. C. Schnedermann, X. Yang, M. Liebel, K. M. Spillane, J. Lugtenburg, I. Fernández, A. Valentini, I. Schapiro, M. Olivucci, P. Kukura and R. A. Mathies, Nat. Chem., 2018, 10, 449–455.
41. C. A. Farfan and D. B. Turner, Phys. Chem. Chem. Phys., 2020, 22, 20265–20283.
42. M. Ben-Nun, J. Quenneville and T. J. Martinez, J. Phys. Chem. A, 2000, 104, 5161–5175.
43. B. F. Curchod and T. J. Martínez, Chem. Rev., 2018, 118, 3305–3336.
44. S. Olsen and R. H. McKenzie, J. Chem. Phys., 2009, 130, 184302.
45. P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Annu. Rev. Phys. Chem., 2002, 53, 291–318.
46. C. Dellago, P. Bolhuis and P. L. Geissler, Adv. Chem. Phys., 2002, 123, 1–78.
47. J. W. Snyder Jr, B. S. Fales, E. G. Hohenstein, B. G. Levine and T. J. Martinez, J. Chem. Phys., 2017, 146, 174113.
48. J. W. Snyder Jr, B. F. Curchod and T. J. Martinez, J. Phys. Chem. Lett., 2016, 7, 2444–2449.
49. J. W. Snyder Jr, E. G. Hohenstein, N. Luehr and T. J. Martinez, J. Chem. Phys., 2015, 143, 154107.
50. I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2008, 4, 222–231.
51. I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 1004–1015.
52. I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 2619–2628.
53. S. Seritan, C. Bannwarth, B. S. Fales, E. G. Hohenstein, S. I. L. Kokkila-Schumacher, N. Luehr, J. W. Snyder Jr, C. Song, A. V. Titov, I. S. Ufimtsev and T. J. Martinez, J. Chem. Phys., 2020, 152, 224110.
54. T. Shiozaki, W. Gyorffy, P. Celani and H. J. Werner, J. Chem. Phys., 2011, 135, 081106.
55. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
56. M. D. Hack, A. M. Wensmann, D. G. Truhlar, M. Ben-Nun and T. J. Martínez, J. Chem. Phys., 2001, 115, 1172–1186.
57. B. Efron and R. J. Tibshirani, An introduction to the bootstrap, Chapman & Hall, New York, 1993.
58. B. Efron, Bootstrap methods: Another look at the jackknife, Breakthroughs in Statistics, ed. S. Kotz and N. L. Johnson, Springer, 1992, pp. 569–593,  DOI:10.1007/978-1-4612-4380-9_41.
59. T. Pacher, L. S. Cederbaum and H. Köppel, J. Chem. Phys., 1988, 89, 7367–7381.
60. L. S. Cederbaum, J. Schirmer and H. D. Meyer, J. Phys. A: Math. Gen., 1989, 22, 2427–2439.
61. S. F. Boys, Rev. Mod. Phys., 1960, 32, 296–299.
62. J. W. Park and T. Shiozaki, J. Chem. Theory Comput., 2017, 13, 3676–3683.
63. L. Zhao, P.-W. Zhou, B. Li, A.-H. Gao and K.-L. Han, J. Chem. Phys., 2014, 141, 235101.
64. J. D. Coe, B. G. Levine and T. J. Martínez, J. Phys. Chem. A, 2007, 111, 11302–11310.
65. J. W. Park and T. Shiozaki, J. Chem. Theory Comput., 2017, 13, 2561–2570.
66. T. Mori and T. J. Martínez, J. Chem. Theory Comput., 2013, 9, 1155–1163.
67. M. D. Davari, F. J. Ferrer, D. Morozov, F. Santoro and G. Groenhof, ChemPhysChem, 2014, 15, 3236–3245.
68. O. Weingart, Chem. Phys., 2008, 349, 348–355.
69. O. Weingart, I. Schapiro and V. Buss, J. Mol. Model., 2006, 12, 713–721.
70. O. Weingart, A. Migani, M. Olivucci, M. A. Robb, V. Buss and P. Hunt, J. Phys. Chem. A, 2004, 108, 4685–4693.
71. O. Weingart and M. Garavelli, J. Chem. Phys., 2012, 137, 22A523.
72. O. Weingart, P. Altoè, M. Stenta, A. Bottoni, G. Orlandi and M. Garavelli, Phys. Chem. Chem. Phys., 2011, 13, 3645–3648.
73. R. A. Mathies and J. Lugtenburg, in Handbook of Biological Physics, ed. D. G. Stavenga, W. J. DeGrip and E. N. Pugh, North-Holland, 2000, vol. 3, pp. 55–90.
74. B. Sellner, M. Barbatti and H. Lischka, J. Chem. Phys., 2009, 131, 024312.
75. D. Morozov and G. Groenhof, Angew. Chem., Int. Ed., 2016, 55, 576–578.
76. M. Andresen, M. C. Wahl, A. C. Stiel, F. Gräter, L. V. Schäfer, S. Trowitzsch, G. Weber, C. Eggeling, H. Grubmüller, S. W. Hell and S. Jakobs, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13070.
77. N. Coquelle, M. Sliwa, J. Woodhouse, G. Schirò, V. Adam, A. Aquila, T. R. M. Barends, S. Boutet, M. Byrdin, S. Carbajo, E. De la Mora, R. B. Doak, M. Feliks, F. Fieschi, L. Foucar, V. Guillon, M. Hilpert, M. S. Hunter, S. Jakobs, J. E. Koglin, G. Kovacsova, T. J. Lane, B. Lévy, M. Liang, K. Nass, J. Ridard, J. S. Robinson, C. M. Roome, C. Ruckebusch, M. Seaberg, M. Thepaut, M. Cammarata, I. Demachy, M. Field, R. L. Shoeman, D. Bourgeois, J.-P. Colletier, I. Schlichting and M. Weik, Nat. Chem., 2018, 10, 31–37.
78. E. Betzig, G. H. Patterson, R. Sougrat, O. W. Lindwasser, S. Olenych, J. S. Bonifacino, M. W. Davidson, J. Lippincott-Schwartz and H. F. Hess, Science, 2006, 313, 1642.
79. C. Y. Lin, J. Both, K. Do and S. G. Boxer, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E2146–E2155.
80. M. G. Romei and S. G. Boxer, Annu. Rev. Biophys., 2019, 48, 19–44.
81. M. G. Romei, C.-Y. Lin, I. I. Mathews and S. G. Boxer, Science, 2020, 367, 76–79.

---

Footnotes

† Electronic supplementary information (ESI) available: Validation of α-CASSCF against XMS-CASPT2, relative energies at critical point geometries, analysis of the intersection parameters for the I- and P-twisted MECIs, three-state diabatic-state analysis and critical point geometries. See DOI: 10.1039/d1sc05849e

‡ Present address: School of Engineering Sciences in Chemistry, Biotechnology and Health (CBH), Department of Theoretical Chemistry and Biology, KTH Royal Institute of Technology, Stockholm, Sweden.

---