Molecular rotational conformation controls the rate of singlet fission and triplet decay in pentacene dimers

Abstract

Three pentacene dimers have been synthesized to investigate the effect of molecular rotation and rotational conformations on singlet fission (SF). In all three dimers, the pentacene units are linked by a 1,4-diethynylphenylene spacer that provides almost unimpeded rotational freedom between the pentacene- and phenylene-subunits in the parent dimer. Substituents on the phenylene spacer add varying degrees of steric hindrance that restricts both the rotation and the equilibrium distribution of different conformers; the less restricted conformers exhibit faster SF and more rapid subsequent triplet-pair recombination. Furthermore, the rotational conformers have small shifts in their absorption spectra and this feature has been used to selectively excite different conformers and study the resulting SF. Femtosecond transient absorption studies at 100 K reveal that the same dimer can have orders of magnitude faster SF in a strongly coupled conformer compared to a more weakly coupled one. Measurements in polystyrene further show that the SF rate is nearly independent of viscosity whereas the triplet pair lifetime is considerably longer in a high viscosity medium. The results provide insight into design criteria for maintaining high initial SF rate while suppressing triplet recombination in intramolecular singlet fission.

---

Introduction

Singlet fission (SF) is the process of splitting one exciton of high energy into two excitons of lower energy. One excited molecule or chromophore of singlet multiplicity, generated by absorption of one photon, can by SF create two excited molecules of triplet multiplicity. Implemented in photovoltaics, for example, the excess energy of high energy photons typically lost could be used to generate an extra charge carrier. By that, SF has the potential to increase the solar energy harvesting efficiency of photovoltaics beyond the Shockley–Queisser limit.^1,2 Being a fast and spin allowed process, the rate of SF can outcompete other decay channels from the singlet excited state, leading to high efficiency and high SF quantum yield, where the maximum quantum yield is 200%. The details of the mechanism of SF are not fully understood, but the overall process can be described as an electronic interaction between a molecule in its singlet excited state with a molecule in its singlet ground state resulting in a spin-correlated pair of molecules, both in the triplet excited state but with overall singlet multiplicity,¹ (T₁T₁). Dissociation of the triplet pair by molecular diffusion in solution,³ by exciton migration in oligomers/polymers⁴ and crystals,⁵ together with spin decorrelation,⁶ can subsequently result in two independent triplet excitons (T₁ + T₁). One of the most important requirements for a molecule to undergo SF is that the energy of the triplet excited state should be equal to or less than half of energy of the singlet excited state, although endothermic SF has been reported.^7,8

In the limited range of molecules that fulfil the requirements for SF, pentacene and its derivatives are one of the most studied. Due to the short lifetime of the singlet excited state (nanoseconds), SF is only observed in systems where the chromophores are in close contact, such as in dimers or polymers of covalently connected chromophores, in crystals, or in highly concentrated solutions. One factor that has been predicted to be highly important for the rate and efficiency of SF is the relative orientation of the two chromophores undergoing SF because the molecular orientation decides the strength and nature of the electronic coupling between the chromophores.^9–14 Compared to intermolecular SF of monomeric systems in solution, where SF can occur in a broad range of collision-complex conformers, intramolecular SF between covalently-linked chromophores in a more well-defined molecular structure provides the possibility to analyze how SF depends on molecular orientation. The simplest model system for studying intramolecular SF is the molecular dimer. Several studies of pentacene dimers, connected in different positions and with various linking groups, have been published.^15–17 Although the published studies have contributed with understanding and mechanistic insight into the SF process in the respective systems, there is no unified model about the detailed mechanism of SF. For example, SF in pentacene dimers have been described both as a direct process¹⁸ or as a sequential process where a charge transfer state^19,20 (virtual^21,22 or populated²³) and/or various triplet pair states of overall singlet or quintet multiplicity and of various degrees of spin correlation, act as intermediates.^22,24 Based on the conclusions from several studies of SF in monomers and dimers of acenes, the exact mechanism of SF is best described as system dependent. A consensus has been reached, however, that the correlated triplet pair (T₁T₁) resulting from the initial SF event must be regarded as a real intermediate state distinct from the final pair of individual triplets, (T₁ + T₁).^24–27 For the sake of clarity, SF will in this article from now on refer to the initial step of formation of a correlated triplet pair (T₁T₁) from the initially photoexcited singlet excited state localized on one of the chromophores. The rate of SF in a dimer can be ultrafast (femtoseconds) due to the close proximity and strong electronic coupling between the chromophores. However, the spin decorrelation and dissociation of the triplet pair to individual triplets may be the rate limiting step in the overall process of triplet generation by SF. Further, decay to the ground state by recombination of the triplet pair can be the limiting factor for the efficiency of the overall process. Both the rate of SF and the rate of triplet recombination depend on the electronic coupling between the chromophores, but not necessarily in the same way. Optimizing the electronic coupling in a SF dimer is thus about finding the optimum of efficient SF and slow triplet recombination to enable highly efficient free triplet generation. Molecular dimers used for the investigation of SF are usually regarded as well-defined static systems in which the molecular structure defines the electronic coupling between the chromophores. However, even though the dimer is defined by its structure, it can possess a range of conformers with varying degree of electronic coupling.^28,29 Rotational and conformational relaxation in the excited state, and its influence on the decay channels from the triplet pair state, has garnered attention in the SF field. A recent study investigated the SF kinetics in a set of pentacene dimers where the relative orientation of the pentacene moieties was controlled by changing the connection position.³⁰ Other studies have described effects on SF from intramolecular rotation and rotational conformers. A detailed description of structure–function relationship for pentacene dimers has not, however, been described.^18,23,31,32

Herein, we present an experimental investigation on the rates of SF and triplet recombination in a set of three pentacene dimers in which the angle of the linker relative to the pentacene units is controlled by functionalization of the bridging unit, while the connection position of the three dimers remains identical. This design allows us to carefully study the effects of rotational conformers and rotational freedom in the excited state. The molecular structure of the three pentacene dimers PD1–3 is illustrated in Scheme 1. The pentacene units are linked by a 1,4-diethynylphenylene spacer in which the two triple bonds provide, in principle, nearly unrestricted rotational freedom between the pentacene- and phenylene-subunits. For PD2–3, the phenylene spacer has been modified with 2,5-substituents that result in a more twisted configuration and restricted rotational freedom due to steric hindrance. Herein, we show that the rate of SF is strongly dependent on the dihedral angle of the conjugated components of the dimer-bridge system. Furthermore, small differences in excitation energy between rotational conformations have been used to selectively populate different excited conformers and examine SF as well as the subsequent triplet recombination. We have discovered that excitation of the lowest energy conformation results in ultrafast SF due to the large coupling between the pentacene moieties whereas excitation of less coupled conformers yields much slower SF and slower recombination. The triplet pair decay has been investigated in high viscosity media, and we demonstrate that the rate of triplet recombination is highly dependent on the rotational freedom of the dimers.

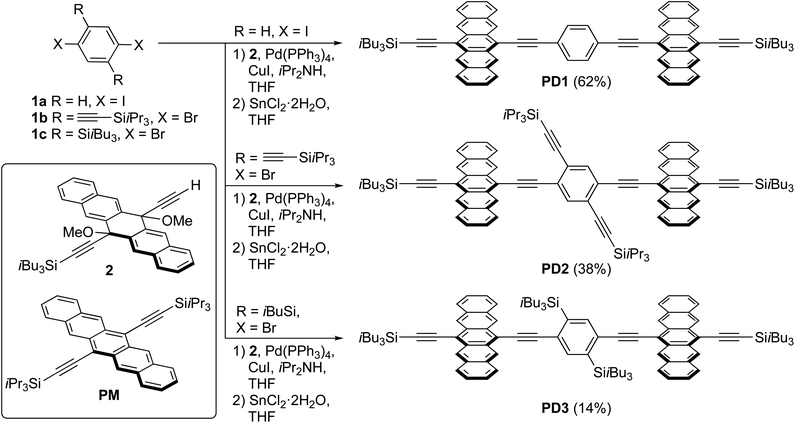Scheme 1 Synthesis of pentacene dimers PD1–3 and structure of the monomer PM (yields of PD1–3 are over two synthetic steps from 1a–c, respectively).

Experimental

Synthesis

A series of pentacene dimers was synthesized via a general, two-step procedure (Scheme 1).³³ A two-fold Sonogashira coupling reaction based on the appropriate dihaloarene 1a–c and pentacene precursor 2 was used to construct the dimeric framework. The resulting product (not shown) was then subjected to SnCl₂-mediated reductive aromatization³⁴ (see Section 1 in the ESI† for full details). The products were purified by crystallization (PD1) or column chromatography (PD2, PD3) and were isolated in acceptable yield as blue solids. While PD1–3 are sensitive to light when in solution, resulting in partial decomposition over a period of days, they are stable indefinitely as pure solids.

Spectroscopy

Steady state absorption measurements were recorded with Varian-Cary 50 Bio and 4000 spectrophotometers. The emission spectra were obtained with a Spex Fluorolog 3 spectrofluorometer from JY Horiba. Cryogenic temperature measurements were performed by using a temperature controlled liquid nitrogen cryostat (Optistat-Oxford Instrument). Nanosecond transient absorption spectra were recorded using an Edinburgh Instrument LP 980 spectrometer and femtosecond transient absorption were carried out with an amplified Ti:sapphire laser system with an output of 800 nm, 1 kHz and ∼200 fs pulse width. A more detailed description of the setups used for the photophysical characterization as well as the kinetic analysis is provided in Section 2 in the ESI.†

Computational details

Full details on the computational part can be found in Section 2 in the ESI.† Briefly, the computational analysis was performed using the Gaussian 16 program package.³⁵ Density functional theory (DFT) with the B3LYP functional and the 6-31G(dp) basis set was used to calculate the lowest energy conformations. Time dependent DFT (TD-DFT) was subsequently used with the CAM-B3LYP functional and the 6-31G(dp) basis set to calculate the electronic transition of various rotational conformers of the molecules in vacuum.

Results and discussion

In the following subsections, a thorough characterization of the pentacene dimers is presented. Theoretical calculations of the rotational freedom and lowest energy conformations of the dimers are followed by experimental investigation of the SF rate and its dependence on these parameters. Then, we show that it is possible to selectively excite different rotational conformers at cryogenic temperatures, which display varying electronic coupling strength between the pentacene units. Finally, the triplet-pair decay and its dependence on dihedral relaxation are discussed.

Steric hindrance restricts rotational freedom

To support the hypothesis that the different substituents on the phenylene bridge result in various rotational conformers of the dimer-bridge system, theoretical calculations using density functional theory (DFT) were performed (see Section 2 in the ESI† for details). The rotational freedom about the acetylenic groups in the bridge was investigated by calculating the potential energy of the conformer at different angles of the pentacene units relative to the phenylene bridge, Fig. 1a. To save computational time, the potential energy of rotation was calculated by scanning over the dihedral angle between one of the pentacene units and the phenylene spacer in a relaxed scan, i.e., by freezing the dihedral angle between one of the pentacene units and the phenylene spacer and letting all other coordinates relax to find the energy minimum. The scan was performed with a step size of 10° and was initiated from the lowest energy structure of each compound (found from an unrestricted optimization) corresponding to the global minimum of the respective potential energy curve in Fig. 1a. The calculated potential energy is a result of steric hindrance and π-conjugation, acting as repulsive and attractive forces between the pentacene- and phenylene-units, respectively. This results in one or more energy minima in the potential energy curve, separated by a rotational energy barrier. The structure of the conformer(s) corresponding to each minimum found in the dihedral scan is shown in Fig. 1b. In this dihedral scan, PD1 only shows one energy minimum corresponding to a planar structure that includes both pentacene units and the phenylene linker. For PD2 and PD3, which have bulky substituents on the phenylene bridge, two energy minima are found in this scan – one global and one local. In the optimized structure of PD2 (the global minimum), the pentacene units are close to being orthogonal and show a pentacene–phenylene angle of 42°. The local minimum of PD2 is at only slightly higher energy (ca. 5 meV), and in this conformer the pentacene units are nearly coplanar and with a pentacene–phenylene angle of 132°, i.e., the same angle as for the global minimum (90° + 42° = 132°). For PD3, having the bulkiest substituents on the phenylene spacer, the pentacene units in the global minimum structure are almost coplanar and the phenylene spacer is twisted approximately 100° with respect to the pentacene units. Due to the large and bulky substituents, the local minimum conformer has a bent pentacene–phenylene bridge. Space filling models which are presented in Fig. S3.1–4† provide a clearer picture of the degree of steric hindrance in the different dimers. The structures of PD1–3 in the solid state have been analyzed by X-ray crystallography, which support the validity of the calculated lowest energy conformations (see Fig. S3.5–7 and Section 3 in the ESI† for full details). The energy barrier of rotation seen in Fig. 1a is on the order of 2–3 times the thermal energy at room temperature for PD1 and PD2, and approximately 10 times thermal energy for PD3. The relatively low energy barriers implies that there exists a broad distribution of rotational conformers for all three dimers at room temperature, although it must be slightly narrower for PD3. It should be highlighted that the potential energy curves presented in Fig. 1a cannot possibly describe all possible conformers of PD1–3, because it is only a scan over one out of the two dihedral angles defining the relative orientation of the pentacene moieties and the phenylene bridge. To map the full conformation space, a multi-dimensional scan must be performed, creating a multi-dimensional potential energy surface, where other local energy minimum conformers might exist. This is particularly true for the more sterically crowded dimer and an example of such local minimum conformer found for PD3 is shown in Fig. S3.8.† This conformer has the pentacene units arranged in a nearly coplanar geometry with the phenylene bridge at only approximately 22–38° relative the pentacene units. Even though it is much closer to a totally coplanar geometry compared to the global minimum of PD3 shown in Fig. 1b, this conformer is only at ∼8 meV higher energy than the global minimum. Thus, this conformer, and potentially many other low energy local minima conformers that were not found in the simplified dihedral scan, will be present in sample at thermal equilibrium at room temperature.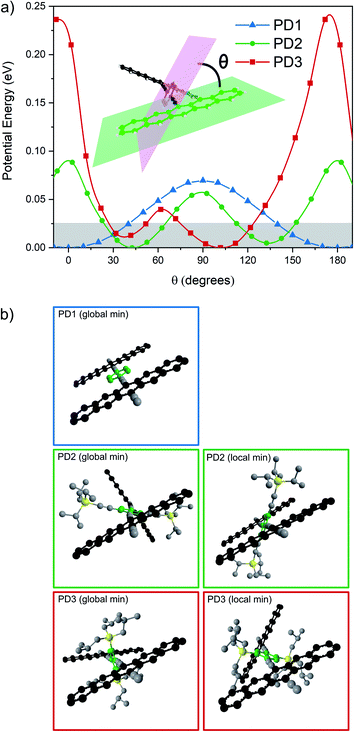

Fig. 1 (a) Potential energy landscape scanning over rotation of one pentacene–phenylene dihedral angle. Thermal energy at 295 K is highlighted by the shaded area. (b) Optimized structures of PD1–3 corresponding to the global and local minima in (a). PD1 has one global minimum in which it adopts a totally coplanar structure. PD2 and PD3 have at least one local minimum in addition to their respective global minima as shown in the right column in (b). An additional local minimum of PD3 is presented in Fig. S3.8.†

The broad distribution of rotational conformers can qualitatively explain the significant broadening of the absorption bands for PD1–3 compared to the monomer, as seen in the spectra presented in Fig. 2. In addition to the broadening, some additional absorption bands seem to appear in the red end of the absorption spectrum of PD3. This could be interpreted as an indication of formation of aggregates. However, all three pentacene dimers show virtually the same spectral shape independent of solvent polarity when measured in toluene, 2-methyltetrahydrofuran (MTHF), and benzonitrile (see Fig. S8.3†), which is a clear indication that the additional bands are not due to aggregates (further evidence regarding lack of aggregation is presented below). Relative to the pentacene monomer, PM, the absorption maxima and absorption onset are red-shifted for PD1–3, indicating a substantial and varying electronic interaction between the pentacene units.^36,37 The electronic coupling between chromophores linked by phenylenes has previously been shown to be highly dependent on the dihedral angle with a more coplanar geometry displaying the strongest coupling.³⁸ In the next section, we investigate the influence of the different phenylene-bridge substituents for the three dimers on the SF dynamics.

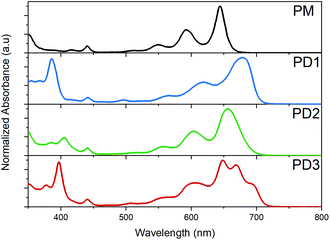Fig. 2 Ground state absorption spectra of the monomer, PM, and dimers PD1–3 in toluene at room temperature.

Rotational conformations and rotational freedom control the rate of singlet fission

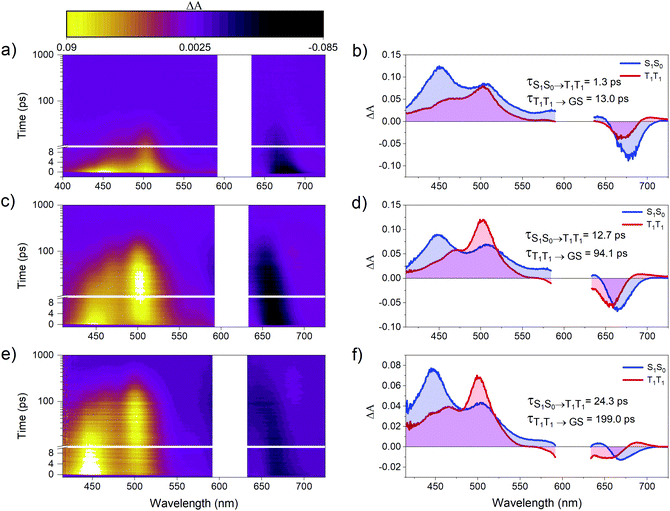
Femtosecond transient absorption (fsTA) spectroscopy was used to characterize the excited-state dynamics of PD1–3. Fig. 3 shows the room-temperature fsTA spectra and the corresponding evolution associated spectra (EAS) of PD1–3 in toluene at room temperature following excitation into the singlet excited state at 612 nm. The absorption of the singlet excited state at 445 and 510 nm is discernible immediately following excitation for all dimers.³ The early spectra also exhibit overlapping ground state bleach and stimulated emission centered around 675 nm. The blue shift of this negative feature at longer time delays will be explained in the next section. At later time delays, the spectra evolve as the initial excited state absorption bands decay and a new signal grows in with a characteristic excited state absorption band at around 500 nm. Global analysis using a two-component sequential model (see Section 2 in the ESI† for more details) fits the data satisfactorily and results in the EAS in Fig. 3 with time constants included in the figure of each dimer. The first component is assigned to the singlet excited state, S₁S₀, where one of the pentacene units is in the singlet excited state and the other is in the ground state. The second component is very similar for all three dimers and is assigned to the correlated triplet pair (T₁T₁). The assignment of this signal is based on its similarity to other reported pentacene-dimer systems³⁹ and is also confirmed by triplet sensitization measurements shown in Fig. S4.1.† The overall spin multiplicity of the triplet pair is likely of singlet character, at least in the early stages, as previously reported for other dimeric pentacene systems.²² The multiplicity term is omitted in the discussion herein since we lack access to techniques such as electron paramagnetic resonance (EPR) used to accurately distinguish different spin multiplicities.⁴⁰ The conversion of S₁S₀ to T₁T₁ occurs on time scales too fast to be a result of intersystem crossing in the absence of heavy atoms. Consequently, it follows that the triplet formation is a result of rapid intramolecular SF. The observed triplet lifetime is shorter by more than four orders of magnitude in comparison to the triplet excited state lifetime of the monomer (24 μs).³⁹ This difference indicates that triplet-pair decorrelation is inefficient and outcompeted by triplet recombination and decay to the ground state, which is similar to what has been seen for other strongly coupled dimer systems.^19,41 Notably, the rate of the formation and decay of the triplet pair is the largest for PD1, followed by PD2, and finally PD3, and hence it follows a trend of slower rates for the rotationally restricted dimers, akin to observations made for pentacene dimers with connection at the 2,2′-position.^18,29 The observed variation in rate of SF and triplet decay could potentially be an effect of the trialkylsilyl substituents altering the energetics of the phenylene linker. However, from a comparison of experimental results with calculated excited state energies of the phenylene linkers, this effect can be disregarded (see ESI† Section 5 for details). Measurements in the more polar solvent benzonitrile (ϵ = 26) are shown in Fig. S6.1† and yield comparable transient absorption spectra to those in toluene (ϵ = 2.4). From the calculated rate constants in benzonitrile and toluene, summarized in Table S6.1,† it is evident that the rate of SF is slightly increased in the more polar environment suggesting that the fission is mediated by a charge transfer state.^20,42 Since there is neither a charge transfer species observed in the fsTA spectra nor any major differences between the spectra in toluene and benzonitrile, we conclude that the charge-transfer state is likely a virtual intermediate.^21,43 In the following sections we will demonstrate that the SF dynamics depend not only on the substituents attached to the phenylene-bridge unit, but also on the excitation wavelength.

Fig. 3 Room temperature transient absorption spectra and corresponding evolution associated spectra (EAS) of dimers (a and b) PD1, (c and d) PD2, and (e and f) PD3. All three dimers were successfully fit to a two-component sequential model (S₀S₁ → T₁T₁ → ground state (GS)) using global analysis with components and lifetimes indicated in the figure. The measurements were performed in toluene with a pump pulse at 612 nm and the pump scatter near the excitation wavelength has been removed for clarity.

The dimer absorption spectra are composed of contributions from different rotational conformations

As mentioned earlier, closer inspection of the absorption spectra of the dimers PD1–3 in Fig. 2 reveals that not only are the bands red-shifted compared to the monomer, but they are also significantly broadened. The broadened absorption bands can be explained by the presence of different rotational conformers with slightly different excitation energies.^44,45 This hypothesis is supported by the dihedral scan in Fig. 1a, which can be directly related to the distribution of rotational conformations that are present at different temperatures. At room temperature, a large range of conformers are available to PD1, PD2, and PD3. However, the probability distribution is significantly narrower at cryogenic temperatures (Fig. S7.1†). Lowering the temperature should therefore allow for more selective excitation of different rotamers. Upon cooling samples of the dimers PD1, PD2, and PD3 from 295 K to 100 K dissolved in MTHF, the absorption spectra undergo drastic changes as seen in Fig. 4. For all three pentacene dimers, the absorption bands become narrower and additional bands that were under-resolved at room temperature are revealed. Notably, the red edge of the lowest energy absorption band grows significantly for all dimers upon cooling. From Fig. 4 we can see that for PD1 at 100 K, the lowest energy absorption band is split into one intense peak at 697 nm with a smaller shoulder at 676 nm. Because the lowest energy conformation of PD1 is the totally planar structure shown in Fig. 1, it is reasonable to assign the most redshifted and intense absorption peak to a more coplanar structure with high electronic coupling between the pentacene units. The lower energy absorption shoulder can, with the same argument, be assigned to conformers with more twisted structure with lower electronic coupling. Similar arguments can also be used for PD2 and PD3 in assigning the red-shifted absorption bands to the conformers with higher electronic coupling, which likely are the more coplanar conformers. Specifically, the local energy minima of PD3 discussed previously and shown in Fig. S3.8† is expected to have relatively high pentacene–pentacene electronic coupling due to the small dihedral angles between the pentacene moieties and the phenylene bridge. This conformer is thus likely to show a more red-shifted absorption onset compared to the more twisted global energy minimum conformer shown in Fig. 1b. Noticing again that this conformer has a ground state energy only ∼8 meV above the global minimum conformer, it is likely to be present in a sample at thermal equilibrium also at 100 K (k_BT = 8.6 meV at T = 100 K). Even though we can speculate that this conformer is likely to contribute to the most red-shifted bands in the low temperature absorption spectrum of PD3, it is not possible to assign an absorption band to any specific conformer based on this data due to the complexity of the conformation potential energy surfaces of the pentacene dimers (vide supra).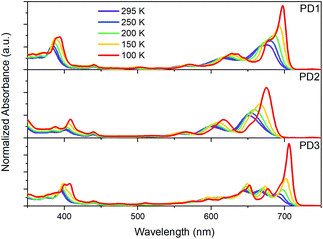

Fig. 4 Ground-state absorption spectra of dimers PD1–3 in MTHF at temperatures ranging from 295 to 100 K.

Considering that the monomer, PM, is known to exhibit aggregation induced absorption in this wavelength region,^5,46,47 we carefully investigated the concentration dependence of the absorption spectra and concluded that the growth of the red edge band is independent of concentration in the range that the transient absorption measurements were conducted in (Fig. S8.1,† 30 μM). Furthermore, flash-freezing very dilute dimer solutions in MTHF by submerging the cuvette in liquid nitrogen results in an absorption spectrum that is identical to the 100 K spectra where equilibrium has been allowed to be reached stepwise at intervals of 50 K from room temperature, see Fig. S8.2.† The low temperature absorption spectra of PM further shows that the red-shift and growth of the lowest energy band also occurs for the monomer (see Fig. S9.1†). These observations taken together indicate that the red edge absorption growth does not stem from aggregation, and we therefore conclude that all measurements in solution are of isolated molecules. Furthermore, the discussion regarding the different absorption bands corresponding to different rotational conformations of the dimers is supported by a comparison of the room temperature absorption and fluorescence excitation spectra, Fig. S10.1.† The quantum yield of fluorescence is very low for all three dimers, and additionally, from the excitation spectra, it is evident that the species responsible for the lowest energy absorption bands are essentially non-emissive. This suggests that the non-emissive bands correspond to a subpopulation of the pentacene dimers in which the singlet excited state is heavily quenched by a non-radiative decay mechanism. As discussed in the next section, this subpopulation could be a rotational conformer for which the fluorescence is quenched by ultrafast SF. This hypothesis is supported by the fsTA measurements in Fig. 3 where the ground-state bleach signal at 675 nm blue shift at longer time delays. The blue shift is likely a result of red-shifted conformers undergoing SF much faster than the less coupled, blue-shifted conformers which are still in the singlet excited state.

Selective excitation of rotational conformations results in different rates of SF

A pump pulse at 612 nm, which was used in the room-temperature fsTA measurements shown in Fig. 3, likely results in excitation of multiple conformers since the different rotational conformations have vibronic progressions that overlaps at shorter wavelengths. To elucidate whether selective excitation of different rotamers is possible, we investigated the SF rate and subsequent triplet-pair decay with different excitation energies at 100 K using fsTA. The upper panel in Fig. 5 shows the 100 K fsTA decay traces of the PD1 triplet excited state at 505 nm with three different excitation wavelengths starting at the lowest energy vibronic peak of the absorption spectra at 697 nm followed by the shoulder of the growing band at 676 nm and finally the second band at 628 nm. The full details and spectra of the excitation energy dependent fsTA measurements are presented in Section 11 in the ESI.† The fits presented in Fig. 5 are based on single wavelength kinetics which is deemed sufficient for a qualitative assessment of the triplet kinetics. However, Section 11 in the ESI† also contains global analysis of the cryogenic data for a more complete picture of the kinetics. With an excitation energy of 697 nm, the formation of the triplet state occurs within the instrument response time (∼300 fs). The excited state absorption band at 445 nm corresponding to the initial singlet excited state is barely resolved, and the remaining signal is very similar to the spectrum previously assigned to the T₁T₁ state, see Fig. S11.1.† Triplet pair decay is also very fast with a lifetime of only 3.1 ps. In contrast, when shifting the excitation wavelength to 676 nm (a shift of only 450 cm⁻¹) both the characteristic absorption of the singlet and the triplet are observed and, notably, they both persist much longer (triplet pair lifetime ∼350 ps) than in the case of excitation at 697 nm. This suggests that excitation at 676 nm results in population of a more weakly coupled excited conformer. Excitation at 628 nm accesses another conformer, or possibly set of conformers, that also displays slower SF rate and longer recombination time than the conformer excited at 697 nm. The SF of PD2 at 100 K presented in Fig. 5 also exhibits clear dependence on excitation energy. However, when PD2 is excited at its lowest energy band at 677 nm, there is no evidence of fast and efficient SF as observed for PD1. Instead, the growth of the triplet excited state absorption is observed with a rise time of 4.2 ps and decay with an average lifetime of 800 ps. A possible explanation for this result could be that PD2 does not adopt a strongly coupled structure as found for PD1 due to the steric hindrance of bulky substituents on the phenylene-bridged unit of PD2. This rationale would also explain why the absorption spectra of PD2 (Fig. 4) show a weaker red shift and less substantial growth of the lowest energy band upon cooling. Weaker growth of the lowest energy band can also be rationalized by the fact that PD2 has two conformational minima close in energy (Fig. 1a), which would result in a broader distribution of conformers. Similar to the behaviour of dimers PD1 and PD2, SF for PD3 exhibits a clear dependence on excitation energy as evident from the kinetics at 100 K (Fig. 5). Considering that the triplet-pair of PD2 does not display the extremely fast formation and decay that was seen for PD1 when excited at the lowest energy band, it is somewhat surprising that we observe it for PD3 when exciting its lowest energy transition (707 nm). This observation, combined with the fact that PD3 shows the most substantial growth and red shift of the lowest energy absorption band in Fig. 4, implies that PD3 can adopt a very strongly coupled conformation, despite being the apparently most rotationally restricted dimer according to calculations (Fig. 1). This could be due to the presence of other local energy minimum conformers that were not identified in the simplified dihedral scan in Fig. 1a, but whose existence have been verified from further calculations (Fig. S3.8,†vide supra). We further hypothesize that enhanced electronic coupling between the pentacene units can be mediated through the silyl substituents on the phenylene spacer in this highly sterically encumbered dimer (see space filling models in Fig. S3.3 and S3.4†), similar to previously reported observations²² and in line with the effect of hyperconjugation between a silyl substituent and an unsaturated carbon in β-position.^48,49 Additionally, from the decay trace obtained with excitation at 651 nm (Fig. 5), it becomes apparent that this excitation wavelength populates the excited state of at least two distinct conformations of PD3. One of the conformations appear to display kinetics similar to the strongly coupled conformer observed with excitation at the red-most band at 707 nm, while the other conformer results in SF and subsequent triplet pair decay on much longer time scales (>7 ns). It is likely that the excitation of the strongly coupled conformer for PD3 is caused by excitation of a higher energy vibronic transition of the band at 707 nm with the pump at 651 nm. The strong and rapidly decaying ground state bleach signal at around 707 nm lends credence to this assignment, see Fig. S11.10.† The triplet excited state behaviour when exciting at 651 nm is similar to that observed when exciting at 677 nm, but with substantially different rate constants for the different processes, as evident from the lifetimes in Table S11.1.†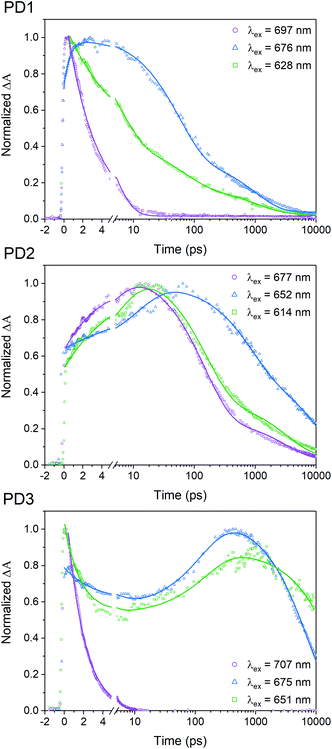

Fig. 5 Transient absorption single wavelength kinetics of the triplet-pair peak at 505 nm for different excitation wavelengths given by the legend. The measurements were performed at 100 K in MTHF. Full details and obtained fitting parameters are presented in Section 11 in the ESI.†

Theoretical calculations provide insight regarding the possibility of selective excitation of conformers

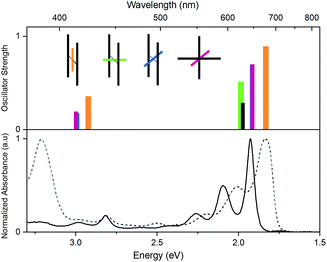
In Fig. 6, time dependent density functional theory (TD-DFT) calculations are presented, in which the lowest energy electronic transitions of specific conformers are calculated. The transition energies are plotted together with the absorption spectrum of PD1 and PM for comparison. For these calculations, the molecular structure of PD1 was used, but the silyl-substituents on the pentacene units were omitted and replaced with hydrogens to save computational time. The pentacene and phenylene subunits were locked in different orientations resembling the optimized structures of PD1-3 (Fig. 1b) as shown in the graph legend. The energy and oscillator strength of electronic transitions were calculated under symmetry restrictions, see Section 2 in the ESI† for details. From Fig. 6 it is evident that the level of theory used here gives a good agreement with experimental results, as the calculated transitions matches well with the lowest energy absorption band of both PD1 and PM. It should be noted that the calculations do not take vibrations into account. Therefore, the calculated transitions only show discrete energies without the vibrational progression that is seen in the experimental absorption spectra. From Fig. 6 we can see that the fully coplanar conformer (orange) has the lowest energy transition. This is reasonable because this conformer is expected to have the largest electronic coupling between the pentacene units, both through bond and space. In comparison, the conformer with coplanar pentacene units and orthogonal phenylene spacer (green) shows its lowest energy transition at an energy similar to what is calculated for the monomer (PM, black), indicating that the through space electronic coupling between pentacene units is low in the dimers. Further, the lowest energy transitions of the intermediately twisted conformers (blue and red) are very close in energy and in-between the energy of the lowest energy transition of the above-mentioned conformers. By comparing the calculated transition energy of the various conformers in Fig. 6 it can be concluded that the electronic coupling between the pentacene units is dominated by through bond coupling, mediated by the phenylene spacer. We encourage other researchers in the field to perform further computational studies investigating the role of rotational conformation and electronic coupling for SF. In total, the computational results shown in Fig. 6 support the hypothesis that the electronic transitions of different rotational conformers of the studied pentacene dimers occurs at different excitation energies. This further confirms that the varying rates of SF and triplet decay depending on excitation wavelength observed in Fig. 5 is indeed a result of selective excitation of various rotational conformers.

Fig. 6 Top: lowest energy transitions in different conformations of an unsubstituted pentacene dimer (PD1, orange, red, blue and green bars) and the monomer (PM, black bar), calculated using TD-DFT, functional CAM-B3LYP, basis set 6-31G(dp). The inset illustrates the pentacene–phenylene–pentacene geometry of the respective conformer. The shorter colored bars represent the phenylene-bridge unit at different dihedral angles and the longer grey bars represent the pentacene moieties. Note that the blue and red conformations (θ = 45°) have very similar transition energies and oscillator strengths causing their bars to overlap. Bottom: steady state absorption spectra of PD1 (dashed) and PM (solid) in toluene.

Restricted rotation and its effect on triplet-pair decay kinetics

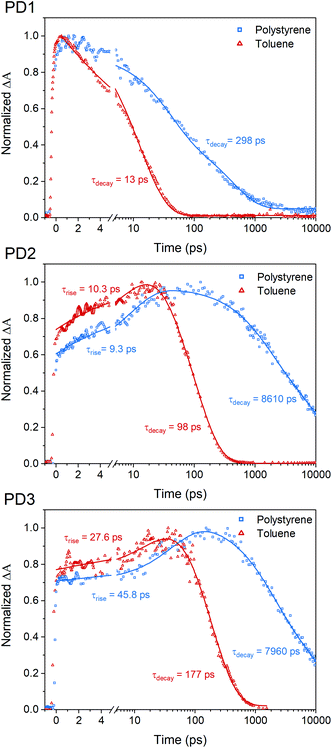
The fsTA measurements at 100 K in Fig. 5 show that the more weakly coupled rotational conformers of PD1–3 appear to have significantly longer lived triplet-pairs relative to the measurements at room-temperature (Fig. 3). This indicates that the triplet-pair recombination is either a thermally activated process or that the highly viscous environment at 100 K, near the glass transition temperature of MTHF,⁵⁰ prevents geometric relaxation to a more planar geometry, which in turn slows down the triplet recombination. A more planar chromophore–phenylene–chromophore, and thus a more strongly coupled conformer, has been previously reported to increase the rate of triplet recombination.⁷ A comparison of the triplet-pair decay kinetics of PD1 at 100, 150, and 200 K (Fig. S12.1†) reveals that the lifetime of the triplet-pair is significantly reduced as the temperature is increased. Increasing the temperature will also reduce the viscosity, and, consequently, this data suggest that the dihedral relaxation could have a more substantial impact on the triplet lifetime than the temperature considering that the thermal energy is still quite low at 150 K. To gain more insight regarding the importance of environment rigidity on the triplet-pair lifetime, we investigated the SF dynamics of the dimers in polystyrene films at room temperature. Fig. 7 presents the room temperature triplet-pair kinetics at 505 nm for PD1–3 in toluene and in polystyrene films following excitation at 612 nm. All three dimers show similar spectral features in both toluene and when embedded in polystyrene matrices (full details and spectra are presented in Section 13 in the ESI†). Due to the presence of multiple rotational conformers, it is not possible to fit the kinetics of the polystyrene matrix measurements to a simple two component model as in the case of the solution measurements in Fig. 3. A two-component fitting is further complicated by the possibility of formation of T₁T₁-states with different multiplicities with unique decay rates, which is known to occur on longer timescales.⁴⁰ Instead, tail-fits of the triplet decays are used to compare the recombination rates of the solution and polymer samples. The triplet-pair of PD1 in polystyrene decays with an average lifetime of 298 ps. The lifetime in toluene solution is comparatively short at only 13 ps. For PD2 and PD3 in polystyrene, the triplet-pair decays with average lifetimes of 8610 and 7960 ps, respectively. This can, in turn, be compared to their triplet-pair lifetime in toluene of 98 and 177 ps, respectively. The rate constants for PD1–3 are summarized in Table S13.1.† It is noteworthy that the recombination kinetics of the formed triplet pair appear to be more affected by the restricted molecular motion in polystyrene than the triplet formation. For instance, the triplet-pair lifetime of PD2 is increased by a factor of 88, whereas the rise time is approximately the same in polystyrene as in toluene (9.3 vs. 10.3 ps). The same trend is seen for PD3, although to a lesser degree. For PD1, the formation of the triplet-pair is under-resolved in both polystyrene and toluene, and we still see a clear increase of the triplet-pair lifetime in polystyrene relative to toluene. The results here suggest that the triplet-pair deactivation is more dependent on the dihedral relaxation to a more strongly coupled conformation than the actual SF event. This design parameter could thus be of importance in future technological applications where it might be crucial to extend the triplet lifetime while maintaining efficient and fast SF.

Fig. 7 Room temperature single wavelength kinetics of the triplet-pair peak for PD1–3 at 505 nm in toluene (red triangles) and in polystyrene (blue squares). The measurements were performed with a pump pulse at 612 nm. Tail-fits of the triplet-pair kinetics reveal significantly longer triplet-pair lifetime in polystyrene compared to toluene.

Conclusion

In this work, we have experimentally investigated the effect of pentacene dimer rotational conformers in SF. A set of three pentacene dimers with varying degree of rotational steric hindrance have been used to study both the triplet formation by SF as well as the triplet recombination. The interpretation of the experimental results was supported by DFT calculations. By selective photoexcitation of different rotational conformers, we have shown that the relative orientation of the SF chromophores is a critical parameter determining the intramolecular electronic coupling and hence the rate of SF. This effect is most clearly seen for the dimer with most steric hindrance (PD3) where the rate of SF varies by three orders of magnitude and the rate of triplet recombination varies by four orders of magnitude, only depending on which rotational conformer that initially is photoexcited. Further, we have shown that triplet formation by SF is nearly independent of viscosity while the triplet pair lifetime is substantially longer in a viscous medium. This indicates that the triplet pair decay is mediated by conformational relaxation in the excited state. The results presented in this work highlights the importance of controlling both the static lowest energy molecular geometry as well as the dynamic molecular reorganization processes when designing molecules for SF. Finally, we encourage future research investigating conformational flexibility and relaxation in the excited state as an additional design parameter in the development of intramolecular SF molecules realizing both efficient SF and extended triplet pair lifetimes.

Data availability

Data is available upon request from the corresponding author.

Author contributions

B. A. and R. R. T. secured funding for, designed, and oversaw the project. L. C., Z. W. S., and R. R. T. designed the molecules. L. C. and Z. W. S. synthesized and characterized the molecules. R. R. and F. E. performed all photophysical characterization. The computational part was done by F. E., and the kinetic analysis was carried out by R. R. M. F. conducted X-ray crystallographic characterization, refinement, and analysis. R. R. and F. E. wrote the majority of the paper with contributions from all authors. All authors analyzed the results and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

B. A. acknowledges support from the Swedish research council and the Swedish Energy Agency (contract: 46526-1). R. R. T. acknowledges support from NSERC (the Natural Sciences and Engineering Research Council of Canada). Z. W. S. acknowledges graduate scholarship support from NSERC and Alberta Innovates. The authors wish to express gratitude to Jens Uhlig for providing access to his kinetic analysis fitting software.

References

1. W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519.
2. M. C. Hanna and A. J. Nozik, J. Appl. Phys., 2006, 100, 074510.
3. B. J. Walker, A. J. Musser, D. Beljonne and R. H. Friend, Nat. Chem., 2013, 5, 1019–1024.
4. A. B. Pun, A. Asadpoordarvish, E. Kumarasamy, M. J. Y. Tayebjee, D. Niesner, D. R. McCamey, S. N. Sanders, L. M. Campos and M. Y. Sfeir, Nat. Chem., 2019, 11, 821–828.
5. R. D. Pensack, C. Grieco, G. E. Purdum, S. M. Mazza, A. J. Tilley, E. E. Ostroumov, D. S. Seferos, Y.-L. Loo, J. B. Asbury, J. E. Anthony and G. D. Scholes, Mater. Horiz., 2017, 4, 915–923.
6. G. D. Scholes, J. Phys. Chem. A, 2015, 119, 12699–12705.
7. N. V. Korovina, C. H. Chang and J. C. Johnson, Nat. Chem., 2020, 12, 391–398.
8. A. Thampi, H. L. Stern, A. Cheminal, M. J. Y. Tayebjee, A. J. Petty, J. E. Anthony and A. Rao, J. Am. Chem. Soc., 2018, 140, 4613–4622.
9. K. Bhattacharyya and A. Datta, J. Phys. Chem. C, 2017, 121, 1412–1420.
10. M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936.
11. E. A. Buchanan and J. Michl, J. Am. Chem. Soc., 2017, 139, 15572–15575.
12. A. M. Müller, Y. S. Avlasevich, W. W. Schoeller, K. Müllen and C. J. Bardeen, J. Am. Chem. Soc., 2007, 129, 14240–14250.
13. J. D. Cook, T. J. Carey and N. H. Damrauer, J. Phys. Chem. A, 2016, 120, 4473–4481.
14. J. N. Schrauben, A. Akdag, J. Wen, Z. Havlas, J. L. Ryerson, M. B. Smith, J. Michl and J. C. Johnson, J. Phys. Chem. A, 2016, 120, 3473–3483.
15. N. V. Korovina, N. F. Pompetti and J. C. Johnson, J. Chem. Phys., 2020, 152, 040904.
16. C. Hetzer, D. M. Guldi and R. R. Tykwinski, Chem. - Eur. J., 2018, 24, 8245–8257.
17. E. Kumarasamy, S. N. Sanders, M. J. Y. Tayebjee, A. Asadpoordarvish, T. J. H. Hele, E. G. Fuemmeler, A. B. Pun, L. M. Yablon, J. Z. Low, D. W. Paley, J. C. Dean, B. Choi, G. D. Scholes, M. L. Steigerwald, N. Ananth, D. R. McCamey, M. Y. Sfeir and L. M. Campos, J. Am. Chem. Soc., 2017, 139, 12488–12494.
18. E. G. Fuemmeler, S. N. Sanders, A. B. Pun, E. Kumarasamy, T. Zeng, K. Miyata, M. L. Steigerwald, X. Y. Zhu, M. Y. Sfeir, L. M. Campos and N. Ananth, ACS Cent. Sci., 2016, 2, 316–324.
19. J. Zirzlmeier, R. Casillas, S. R. Reddy, P. B. Coto, D. Lehnherr, E. T. Chernick, I. Papadopoulos, M. Thoss, R. R. Tykwinski and D. M. Guldi, Nanoscale, 2016, 8, 10113–10123.
20. B. S. Basel, J. Zirzlmeier, C. Hetzer, S. R. Reddy, B. T. Phelan, M. D. Krzyaniak, M. K. Volland, P. B. Coto, R. M. Young, T. Clark, M. Thoss, R. R. Tykwinski, M. R. Wasielewski and D. M. Guldi, Chem, 2018, 4, 1092–1111.
21. T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, J. Chem. Phys., 2013, 138, 114103.
22. I. Papadopoulos, J. Zirzlmeier, C. Hetzer, Y. J. Bae, M. D. Krzyaniak, M. R. Wasielewski, T. Clark, R. R. Tykwinski and D. M. Guldi, J. Am. Chem. Soc., 2019, 141(15), 6191–6203.
23. S. Lukman, K. Chen, J. M. Hodgkiss, D. H. P. Turban, N. D. M. Hine, S. Dong, J. Wu, N. C. Greenham and A. J. Musser, Nat. Commun., 2016, 7, 13622.
24. K. Miyata, F. S. Conrad-Burton, F. L. Geyer and X. Y. Zhu, Chem. Rev., 2019, 119, 4261–4292.
25. C. Grieco, E. R. Kennehan, H. Kim, R. D. Pensack, A. N. Brigeman, A. Rimshaw, M. M. Payne, J. E. Anthony, N. C. Giebink, G. D. Scholes and J. B. Asbury, J. Phys. Chem. C, 2018, 122, 2012–2022.
26. R. D. Pensack, A. J. Tilley, C. Grieco, G. E. Purdum, E. E. Ostroumov, D. B. Granger, D. G. Oblinsky, J. C. Dean, G. S. Doucette, J. B. Asbury, Y.-L. Loo, D. S. Seferos, J. E. Anthony and G. D. Scholes, Chem. Sci., 2018, 9, 6240–6259.
27. S. Khan and S. Mazumdar, J. Phys. Chem. C, 2020, 124, 1171–1177.
28. A. Aster, F. Zinna, C. Rumble, J. Lacour and E. Vauthey, J. Am. Chem. Soc., 2021, 143, 2361–2371.
29. T. Yamakado, S. Takahashi, K. Watanabe, Y. Matsumoto, A. Osuka and S. Saito, Angew. Chem., Int. Ed., 2018, 57, 5438–5443.
30. L. M. Yablon, S. N. Sanders, K. Miyazaki, E. Kumarasamy, G. He, B. Choi, N. Ananth, M. Y. Sfeir and L. M. Campos, Mater. Horiz., 2022, 9(1), 462–470.
31. S. Paul, C. Govind and V. Karunakaran, J. Phys. Chem. B, 2021, 125, 231–239.
32. S. Nakamura, H. Sakai, H. Nagashima, M. Fuki, K. Onishi, R. Khan, Y. Kobori, N. V. Tkachenko and T. Hasobe, J. Phys. Chem. C, 2021, 125(33), 18287–18296.
33. R. R. Tykwinski, Acc. Chem. Res., 2019, 52, 2056–2069.
34. J. L. Marshall, D. Lehnherr, B. D. Lindner and R. R. Tykwinski, ChemPlusChem, 2017, 82, 967–1001.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
36. S. Lukman, A. J. Musser, K. Chen, S. Athanasopoulos, C. K. Yong, Z. Zeng, Q. Ye, C. Chi, J. M. Hodgkiss, J. Wu, R. H. Friend and N. C. Greenham, Adv. Funct. Mater., 2015, 25, 5452–5461.
37. B. S. Basel, C. Hetzer, J. Zirzlmeier, D. Thiel, R. Guldi, F. Hampel, A. Kahnt, T. Clark, D. M. Guldi and R. R. Tykwinski, Chem. Sci., 2019, 10, 3854–3863.
38. N. V. Korovina, J. Joy, X. Feng, C. Feltenberger, A. I. Krylov, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2018, 140, 10179–10190.
39. J. Zirzlmeier, D. Lehnherr, P. B. Coto, E. T. Chernick, R. Casillas, B. S. Basel, M. Thoss, R. R. Tykwinski and D. M. Guldi, Proc. Natl. Acad. Sci., 2015, 112, 5325–5330.
40. B. S. Basel, J. Zirzlmeier, C. Hetzer, B. T. Phelan, M. D. Krzyaniak, S. R. Reddy, P. B. Coto, N. E. Horwitz, R. M. Young, F. J. White, F. Hampel, T. Clark, M. Thoss, R. R. Tykwinski, M. R. Wasielewski and D. M. Guldi, Nat. Commun., 2017, 8, 15171.
41. S. N. Sanders, E. Kumarasamy, A. B. Pun, M. T. Trinh, B. Choi, J. Xia, E. J. Taffet, J. Z. Low, J. R. Miller, X. Roy, X. Y. Zhu, M. L. Steigerwald, M. Y. Sfeir and L. M. Campos, J. Am. Chem. Soc., 2015, 137, 8965–8972.
42. I. Papadopoulos, M. J. Álvaro-Martins, D. Molina, P. M. McCosker, P. A. Keller, T. Clark, Á. Sastre-Santos and D. M. Guldi, Adv. Energy Mater., 2020, 2001496,  DOI:10.1002/aenm.202001496.
43. E. A. Margulies, C. E. Miller, Y. Wu, L. Ma, G. C. Schatz, R. M. Young and M. R. Wasielewski, Nat. Chem., 2016, 8, 1120–1125.
44. K. Schmieder, M. Levitus, H. Dang and M. A. Garcia-Garibay, J. Phys. Chem. A, 2002, 106, 1551–1556.
45. M. U. Winters, J. Kärnbratt, M. Eng, C. J. Wilson, H. L. Anderson and B. Albinsson, J. Phys. Chem. C, 2007, 111, 7192–7199.
46. M. J. Y. Tayebjee, K. N. Schwarz, R. W. Macqueen, M. Dvořák, A. W. C. Lam, K. P. Ghiggino, D. R. McCamey, T. W. Schmidt and G. J. Conibeer, J. Phys. Chem. C, 2016, 120, 157–165.
47. Z. Zhou, L. Ma, D. Guo, X. Zhao, C. Wang, D. Lin, F. Zhang, J. Zhang and Z. Nie, J. Phys. Chem. C, 2020, 124, 14503–14509.
48. J. C. Giordan, J. Am. Chem. Soc., 1983, 105, 6544–6546.
49. K. K. Laali, G. Rasul, G. K. Surya Prakash and G. A. Olah, J. Org. Chem., 2002, 67, 2913–2918.
50. M. Mizukami, H. Fujimori and M. Oguni, Prog. Theor. Phys. Suppl., 2013, 126, 79–82.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 2099715–2099717. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d1sc06285a

‡ These authors contributed equally.

---