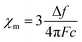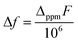Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic structure studies reveal 4f/5d mixing and its effect on bonding characteristics in Ce-imido and -oxo complexes†
Liane M.
Moreau‡
 a,
Ekaterina
Lapsheva
b,
Jorge I.
Amaro-Estrada
a,
Ekaterina
Lapsheva
b,
Jorge I.
Amaro-Estrada
 c,
Michael R.
Gau
c,
Michael R.
Gau
 b,
Patrick J.
Carroll
b,
Brian C.
Manor
b,
Yusen
Qiao
b,
Patrick J.
Carroll
b,
Brian C.
Manor
b,
Yusen
Qiao
 ab,
Qiaomu
Yang
ab,
Qiaomu
Yang
 b,
Wayne W.
Lukens
b,
Wayne W.
Lukens
 a,
Dimosthenis
Sokaras
d,
Eric J.
Schelter
a,
Dimosthenis
Sokaras
d,
Eric J.
Schelter
 *b,
Laurent
Maron
*b,
Laurent
Maron
 *c and
Corwin H.
Booth
*c and
Corwin H.
Booth
 *a
*a
aChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
bDepartment of Chemistry, University of Pennsylvania, Philadelphia, PA 19104, USA
cLPCNO, UMR 5215, CNRS, INSA, UPS, Université de Toulouse, 31000 Toulouse, France
dStanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA
First published on 24th January 2022
Abstract
This study presents the role of 5d orbitals in the bonding, and electronic and magnetic structure of Ce imido and oxo complexes synthesized with a tris(hydroxylaminato) [((2-tBuNO)C6H4CH2)3N]3− (TriNOx3−) ligand framework, including the reported synthesis and characterization of two new alkali metal-capped Ce oxo species. X-ray spectroscopy measurements reveal that the imido and oxo materials exhibit an intermediate valent ground state of the Ce, displaying hallmark features in the Ce LIII absorption of partial f-orbital occupancy that are relatively constant for all measured compounds. These spectra feature a double peak consistent with other formal Ce(IV) compounds. Magnetic susceptibility measurements reveal enhanced levels of temperature-independent paramagnetism (TIP). In contrast to systems with direct bonding to an aromatic ligand, no clear correlation between the level of TIP and f-orbital occupancy is observed. CASSCF calculations defy a conventional van Vleck explanation of the TIP, indicating a single-reference ground state with no low-lying triplet excited state, despite accurately predicting the measured values of f-orbital occupancy. The calculations do, however, predict strong 4f/5d hybridization. In fact, within these complexes, despite having similar f-orbital occupancies and therefore levels of 4f/5d hybridization, the d-state distributions vary depending on the bonding motif (Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vs. Ce
O vs. Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) of the complex, and can also be fine-tuned based on varying alkali metal cation capping species. This system therefore provides a platform for understanding the characteristic nature of Ce multiple bonds and potential impact that the associated d-state distribution may have on resulting reactivity.
N) of the complex, and can also be fine-tuned based on varying alkali metal cation capping species. This system therefore provides a platform for understanding the characteristic nature of Ce multiple bonds and potential impact that the associated d-state distribution may have on resulting reactivity.
Introduction
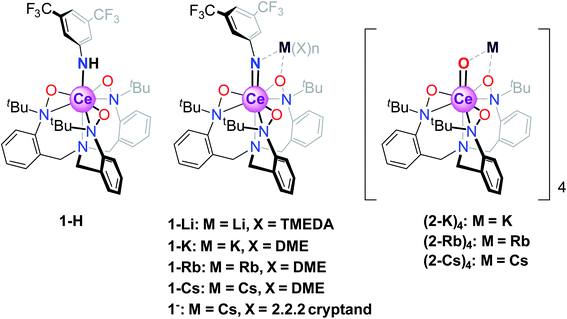
The canonical view of lanthanide 4f-orbitals is that they are localized enough that they don't participate in bonding, or, in metals, in conductivity. In addition, their localization imparts local moment magnetism, whereby the orbital angular momentum is not quenched in contrast to typical transition metal d-orbital systems. This view, however, has been shown to be incorrect in that within certain lanthanide intermetallic materials, mixed valence is implicated in low-temperature temperature-independent paramagnetism (TIP) and in heavy-fermion conductivity.1 In such materials, the many–body interactions between the f-orbital and the conduction band (for example, the 5d orbital in elemental Ce metal2 or the Cu 3d orbital in YbIn1−xAgxCu43) are an important feature in determining the lanthanide (Ln) 4f orbital occupancy and magnetic properties. More recently, various Ce and Yb organometallic molecules, including Ce(C8H8)2 (cerocene)4–10 and Cp*2Yb(bipy) (bispentamethylcyclopentadienyl ytterbium bipyridyl),8,11 among others,12–17 have been shown to exhibit similar f-orbital mixing, not with a fully metallic band, but rather with delocalized orbitals from aromatic rings proximal to the metal center. In these materials, single-electron theories such as DFT typically indicate no mixing of the 4f/ligand orbitals, while theories that account for configuration interactions between various magnetic singlets show a mixed ground state with non-integral occupancy of the 4f orbital, allowing for enhanced TIP behavior from a van Vleck mixing of an excited state triplet. In cerocene,4–10 for example, the ground state is primarily a quantum mechanical mixture of f0 and f1 configurations (closed- and open-shell singlet configurations, respectively), with a fractional f-occupancy of about 0.89 despite its formal oxidation state assignment as Ce(IV) based on a typical (C8H8)2−, and a van Vleck-induced TIP susceptibility of χ0 = 1.4 × 10−4 emu mol−1. Other formal Ce(IV) molecules have recently been shown to display similar behavior.12 More recent advances by Sergentu et al.18 have importantly confirmed that the doublet peak observed in Ce(III)/Ce(IV) systems is due to differences in the core hole interactions between f1 and f0 configurations. Additionally, they emphasized the f2 contribution to what had been assigned as a pure f1 spectral peak (although less than 10%), and therefore what has been traditionally referred to as the f1 configuration is more accurately described as f1,2.In the aforementioned systems, the Ln 5d orbital does not play a crucial role. This is in contrast to what is believed to be true for inorganic compounds such as CeO2 and Ce2O3, where magnetism has no clearly measurable contribution from the f-orbitals,12 likely due to the stronger delocalization of the f-electrons from hybridization with the ligand 2p and metal 5d orbitals. Unfortunately, CAS methods used to elucidate electronic characteristics in organometallic molecules are not currently applicable to extended solids, such as CeO2. It would therefore be of interest to consider the behavior of formal Ce(IV) organometallics where Ce forms metal–ligand multiple bonds, which could serve as molecular analogs to CeO2. In addition, the notable reactivity patterns observed for transition metal oxo and imido compounds, which stem from the iminyl/oxyl character,19–33 prompt the investigation of electronic structures and spectroscopic properties of lanthanide systems with metal–ligand multiple bonds. Towards this end, we consider a class of Ce imido and oxo complexes which are designed to enhance 5d participation while de-emphasizing ligand 2p orbital mixing. Recently, several alkali metal-capped Ce(IV) imido compounds [M(solv)n][Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NArF(TriNOx)] (solv = DME or TMEDA, M = Li+, K+, Rb+, Cs+, ArF = 3,5-(CF3)2–C6H3, TriNOx3− = (tBuN(O))C6H4CH2}3N]3−, 1-M) and the uncapped congener [Cs(2.2.2 cryptand)][Ce
NArF(TriNOx)] (solv = DME or TMEDA, M = Li+, K+, Rb+, Cs+, ArF = 3,5-(CF3)2–C6H3, TriNOx3− = (tBuN(O))C6H4CH2}3N]3−, 1-M) and the uncapped congener [Cs(2.2.2 cryptand)][Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NArF(TriNOx)] (1−), as well as the parent anilide compound Ce–NHArF(TriNOx) (1-H) have been reported (Scheme 1).34 These compounds feature the TriNOx3− ligand, which affords stabilization of the Ce(IV) oxidation state, protecting these compounds against reduction. Following isolation of the Ce(IV)–imidos and the uncapped congener, we isolated the cerium oxo complex Rb4 [Ce
NArF(TriNOx)] (1−), as well as the parent anilide compound Ce–NHArF(TriNOx) (1-H) have been reported (Scheme 1).34 These compounds feature the TriNOx3− ligand, which affords stabilization of the Ce(IV) oxidation state, protecting these compounds against reduction. Following isolation of the Ce(IV)–imidos and the uncapped congener, we isolated the cerium oxo complex Rb4 [Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (TriNOx)]4 (2-Rb)4 through an aza-Wittig reaction.34
O (TriNOx)]4 (2-Rb)4 through an aza-Wittig reaction.34
With this synthetic foothold established, in the current work, we present a detailed examination of the electronic structures of the cerium(IV)–anilide complex (1-H), select alkali metal-capped cerium imidos, 1-M, complexes and their uncapped congener, 1−, as well the alkali metal-capped oxo, (2-K)4, M = K, Rb, Cs, compounds outlined in Scheme 1. A chief challenge in the study of the cerium congeners is the participation of both the 4f- and 5d-orbitals in the valence electronic structure, and as will be shown below, considering both sets of orbitals is necessary to begin to understand these systems, and, in turn, to gain insight into Ce–ligand multiple bonding characteristics. Here, the 4f- and 5d-orbitals are probed through a union of synthesis, structural characterization, magnetometry, and Ce LIII-edge X-ray absorption spectroscopy (XAS) techniques, combined with complete active space self-consistent field (CASSCF) calculations. The results of this combined investigation into electronic structure reveal that fractional f-occupancy is less impacted by structural differences between the imido and oxo constructs than d-state distributions controlled by bonding characteristics and alkali metal capping cation species. In contrast to cerocene and previously studied systems that involve direct bonding to an aromatic ligand, these structures present a single-reference ground state with strong 4f/5d hybridization. Ultimately, the insight gained from this study can be applied towards understanding how bonding characteristics can affect the electronic properties of Ln organometallic complexes.
Results
Synthesis and X-ray
For our expanded electronic structure studies of Ce(IV)–oxo compounds, we report the synthesis of the tetramer oxo complexes K4[Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(TriNOx)]4(2-K)4 and Cs4[Ce
O(TriNOx)]4(2-K)4 and Cs4[Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(TriNOx)]4(2-Cs)4. These compounds were prepared through an aza-Wittig-type reaction by reacting the corresponding imido compounds 1-K and 1-Cs with benzophenone and isolated in 59% and 39% yield, respectively. The relatively low yield of (2-Cs)4 was attributed to its increased solubility compared to (2-K)4. Compounds (2-K)4 and (2-Cs)4 were crystallized from hot, concentrated THF solutions set undisturbed at RT. Complexes (2-K)4 and (2-Cs)4 are poorly soluble in most organic solvents and exhibit limited solubility in THF. In both cases, 1H NMR spectroscopy of THF-d8 solutions revealed the formation of a C3-symmetric, cerium-containing, product (Fig. S2 and S5†). Complex (2-K)4 indicated a solution magnetic susceptibility of χm = 3.3 × 10−3 emu mol−1 following measurement by Evans method, a value that was largely consistent with the solid state magnetic susceptibility, vide infra. Evans method measurement of (2-Cs)4 indicated a diamagnetic complex in solution. The characteristic doublets of diastereotopic protons of the CH2 groups originating from the TriNOx-ligand were observed in the 1H NMR spectra at 4.17 and 2.26 ppm for (2-Cs)4, and 4.16 and 2.25 ppm for (2-K)4. An X-ray structural study of (2-K)4 and (2-Cs)4 revealed the tetrameric structural motif that was essentially identical to the one reported for (2-Rb)4.34 In all cases, the alkali metal cations aggregated with [(TriNOx)Ce
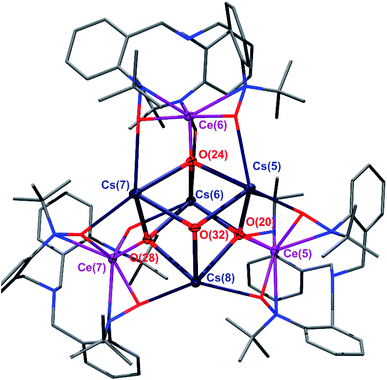
O(TriNOx)]4(2-Cs)4. These compounds were prepared through an aza-Wittig-type reaction by reacting the corresponding imido compounds 1-K and 1-Cs with benzophenone and isolated in 59% and 39% yield, respectively. The relatively low yield of (2-Cs)4 was attributed to its increased solubility compared to (2-K)4. Compounds (2-K)4 and (2-Cs)4 were crystallized from hot, concentrated THF solutions set undisturbed at RT. Complexes (2-K)4 and (2-Cs)4 are poorly soluble in most organic solvents and exhibit limited solubility in THF. In both cases, 1H NMR spectroscopy of THF-d8 solutions revealed the formation of a C3-symmetric, cerium-containing, product (Fig. S2 and S5†). Complex (2-K)4 indicated a solution magnetic susceptibility of χm = 3.3 × 10−3 emu mol−1 following measurement by Evans method, a value that was largely consistent with the solid state magnetic susceptibility, vide infra. Evans method measurement of (2-Cs)4 indicated a diamagnetic complex in solution. The characteristic doublets of diastereotopic protons of the CH2 groups originating from the TriNOx-ligand were observed in the 1H NMR spectra at 4.17 and 2.26 ppm for (2-Cs)4, and 4.16 and 2.25 ppm for (2-K)4. An X-ray structural study of (2-K)4 and (2-Cs)4 revealed the tetrameric structural motif that was essentially identical to the one reported for (2-Rb)4.34 In all cases, the alkali metal cations aggregated with [(TriNOx)Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]− units to form the tetramer. The TriNOx3− ligands provided steric protection for the M4Ce4O4 core, where M = K, Cs, Rb. The structural motif inside the core was a cube-like M4O4 arrangement, where each oxygen atom was located at four vertices of the cube, with three adjacent vertices occupied by alkali metal cations, resulting in the Ce
O]− units to form the tetramer. The TriNOx3− ligands provided steric protection for the M4Ce4O4 core, where M = K, Cs, Rb. The structural motif inside the core was a cube-like M4O4 arrangement, where each oxygen atom was located at four vertices of the cube, with three adjacent vertices occupied by alkali metal cations, resulting in the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety being capped by three alkali metal cations (Fig. 1 and S1†). The distances between the alkali metal cation and the oxygen atom of the Ce
O moiety being capped by three alkali metal cations (Fig. 1 and S1†). The distances between the alkali metal cation and the oxygen atom of the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moieties ranged from 2.638–2.671 Å for (2-K)4 and from 2.893–2.966 Å for (2-Cs)4. As with (2-Rb)4, the structural arrangement of (2-K)4 and (2-Cs)4 evidently stabilizes the Ce
O moieties ranged from 2.638–2.671 Å for (2-K)4 and from 2.893–2.966 Å for (2-Cs)4. As with (2-Rb)4, the structural arrangement of (2-K)4 and (2-Cs)4 evidently stabilizes the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety.34 The Ce
O moiety.34 The Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond lengths ranged from 1.878(4)–1.885(4) Å for (2-K)4 and from 1.876(4)–1.887(4) Å for (2-Cs)4, similarly to the Rb congener.34 This range of bond distances is somewhat longer than the 1.857(3) Å Ce
O bond lengths ranged from 1.878(4)–1.885(4) Å for (2-K)4 and from 1.876(4)–1.887(4) Å for (2-Cs)4, similarly to the Rb congener.34 This range of bond distances is somewhat longer than the 1.857(3) Å Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distance in acetamide-capped terminal oxo compound reported by the Leung group.35 However, the Ce
O distance in acetamide-capped terminal oxo compound reported by the Leung group.35 However, the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances in (2-K)4 and (2-Cs)4 were shorter than in the monomeric, previously reported cerium oxo complex capped with a [Li-12-crown-4]+ cation reported by Hayton, where this distance was 1.902(2) Å.36
O bond distances in (2-K)4 and (2-Cs)4 were shorter than in the monomeric, previously reported cerium oxo complex capped with a [Li-12-crown-4]+ cation reported by Hayton, where this distance was 1.902(2) Å.36
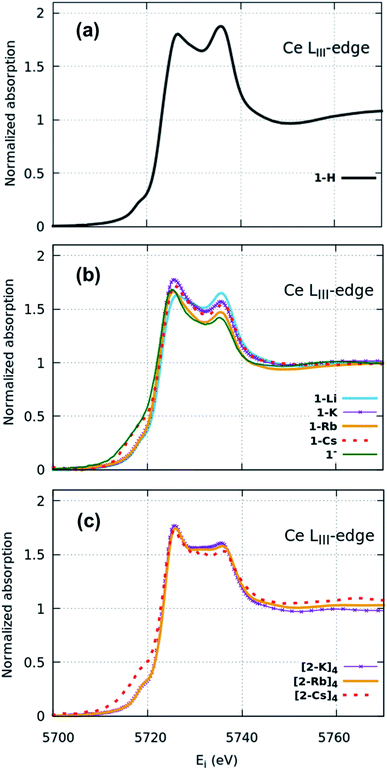
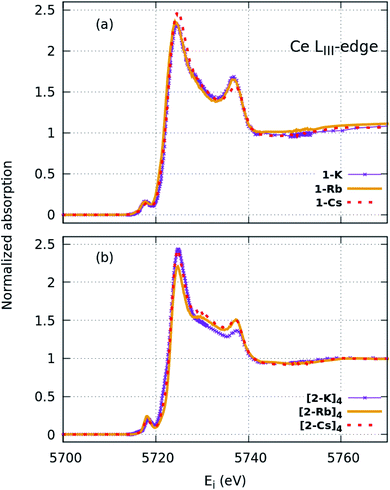
XANES spectra (Fig. 2) indicate that both the 1-H starting material as well as 1-M, 1− and (2-M)4 samples can all be considered as formal Ce(IV). Similar spectra have been widely used to determine the f-orbital occupancy, although the relationship between the ground state and the actual spectra, which represent a final state with a 2p3/2 core hole, has, until recently, not been well understood.18,40 In all measured samples here, the double peak characteristic to formal Ce(IV) is observed and confirmed by comparisons to a Ce(III) and a Ce(IV) standard (Fig. S12†). All data were collected at multiple temperatures (50 K and 300 K) and exhibit no temperature-dependent changes in the spectra (Fig. S13†). Note that in Ce(IV) XANES, the leading-edge peak near 5726 eV indicates primarily the degree of f1 character due to covalence with the ligand,18,40,41 since this fraction will screen the 2p3/2 core hole and shift the 2p3/2 → 5d5/2 transition to lower energy compared to the peak near 5736 eV that corresponds to the f0 part of the wavefunction. Since the lower energy peak should also include a small contribution from f2 character,11,18 hereafter, we refer to these peaks as the “f1,2” and “f0” peaks, respectively, recognizing that the predominant contribution to the f1,2 peak is due to the f1 configuration. We do, however, emphasize that these peaks are not due to transitions into f states, but rather are due primarily to dipole transitions into empty 5d5/2 states and this notation refers to energy shifts of these states depending on the f-orbital configuration. There is also a small peak at ∼5718 eV which has been attributed to arising either from a 2p–4f quadrupole excitation42 or from mixed d- and f-states.43 This peak is notably larger in the 1-Cs, 1− and [2-Cs]4 due to the additional contribution from the Cs LI absorption edge at 5714 eV in these samples, but otherwise appears similar between the other samples. The 1-H data appear to have the greatest ratio of peak intensities between the f0 peak at higher energy and the f1,2 peak at lower energy compared with the 1-M, 1− and (2-M)4 complexes. The imido spectra also have well-defined f1,2 and f0 peaks, but with visually higher peak intensities for the f1,2 feature compared with the anilide. The oxo spectra, in contrast, while featuring the double-peak characteristic to Ce(IV), also have a flat region in the middle of the two characteristic peaks indicative of other contributions. The origin of this feature was investigated using HERFD-XAS and is described below.
Surprisingly, no significant differences in the f1,2 and f0 peaks were observed in the imido or oxo spectra as a function of alkali metal capping species. The only exception to this trend is 1-Li, which appears to have a slightly lower f1,2 peak than the other imido counterparts. These trends were further explored through fitting the areas under the f1,2 and f0 peaks (see Methods) in order to extract the f0-configuration fraction, n(f0), within each complex (Table 1, Fig. S11 and Table S1†). Reporting n(f0) rather than the traditional use of the f-orbital occupation, nf, is necessary because we currently have no way of knowing the significance of any f2 configuration contribution to the f1,2 peak, which has been calculated18 to be separated by only about 5 eV and is therefore convolved with any 5d ligand field splitting. Previous estimates of nf took the fraction of the f1,2-peak area compared to the total area of the f0 and f1,2 peaks with effectively nf = 1 − n(f0), and are therefore in error insofar as the f2 configuration fraction exceeded ∼3% (the best estimate of the systematic error using this technique). We therefore follow ref. 18 and report the fraction of the well-resolved f0 peak to the total area of the f0 and f1,2 peaks, which corresponds to the f0 configuration fraction, n(f0).
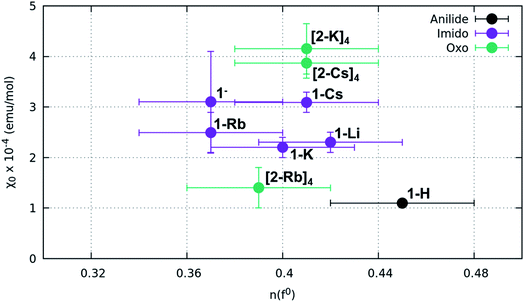
| Sample | n(f0)a | χ 0 (emu mol−1) | Calculated ground to excited state s–t gap (Δ eV) |
|---|---|---|---|
| a Error bars on n(f0) are estimated to be ±0.03 electrons based on variability in samples across multiple data sets. Values reported represent an average n(f0) where multiple data sets were measured. | |||
| 1-H | 0.45(3) | 1.10(6) × 10−4 | N/A |
| 1-Li | 0.42(3) | 2.3(2) × 10−4 | N/A |
| 1-K | 0.40(3) | 2.2(2) × 10−4 | 1.51 |
| 1-Rb | 0.37(3) | 2.5(4) × 10−4 | 0.84 |
| 1-Cs | 0.41(3) | 3.1(2) × 10−4 | 0.51 |
| 1− | 0.37(3) | 3(1) × 10−4 | N/A |
| (2-K)4 | 0.41 (3) | 4.2(5) × 10−4 | 2.60 |
| (2-Rb)4 | 0.39(3) | 1.4(4) × 10−4 | 2.22 |
| (2-Cs)4 | 0.41(3) | 3.9(3) × 10−4 | N/A |
Fitting results from a two-peak model suggest a narrow range for all samples. The anilide has a slightly higher n(f0) value (0.45) than the imidos and oxos, which matches the observable difference in relative peak intensity. All imido and oxo samples have an n(f0) value of ∼0.4, without any perceivable trend based on alkali metal capping species or imido versus oxo bonding character. This lack of a trend is particularly interesting given the clear differences observed in the spectral features between the imido and oxo samples.
 | ||
| Fig. 3 HERFD-XAS spectra collected at the Ce LIII edge for the (a) imido and (b) oxo complexes. Greater spectral detail can be resolved compared with XANES (Fig. 2). | ||
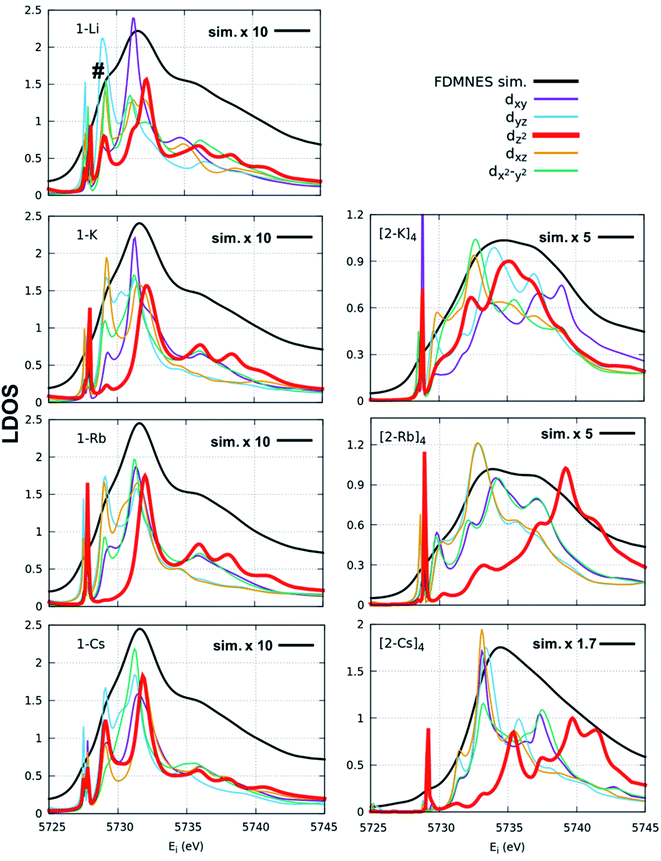
FDMNES simulations of the local density of states (LDOS) provide insight into d-state splitting observed from HERFD-XAS. While FDMNES is limited to features due to the f1 configuration as only one configuration can be simulated, the individual peak shapes are well-reproduced (Fig. 4, S16–S20†). Through simulation, the separate contributions from various d orbitals to the density of states can be observed. From HERFD-XAS, a trend is visible in d-state broadening from the imidos (narrowest) to anilide to oxos (broadest). In the imidos, differences in d-state distributions are observed between varying alkali metal capping cations. Specifically, a lower energy shoulder, marked with # in Fig. 4, is more pronounced in the 1-Li simulation than for the other imidos. In the oxos, the increased d-state splitting observed in the (2-Cs)4 measurement compared with those from (2-K)4 and (2-Rb)4 in the HERFD-XAS can then be attributed to the dz2 contribution splitting off to higher energy. While in (2-K)4, all d orbital distributions appear broad and at similar energy, the dz2 contribution to the density of states splits to higher energy for (2-Rb)4 and even higher for (2-Cs)4.
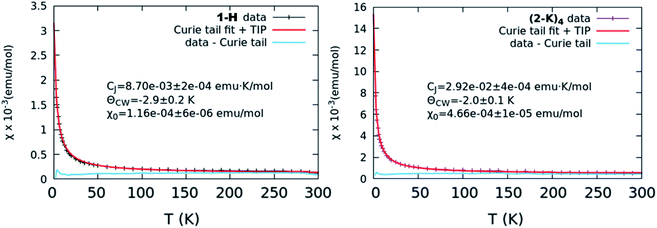 | ||
| Fig. 5 χ vs. T curves representative of the lowest level of TIP (left, 1-H) and greatest level of TIP (right, (2-K)4). In both cases, the collected curve is shown along with the results from a Curie–Weiss fit as well as the data with the Curie tail subtracted. Other collected curves and fits are shown in Fig. S17.† | ||
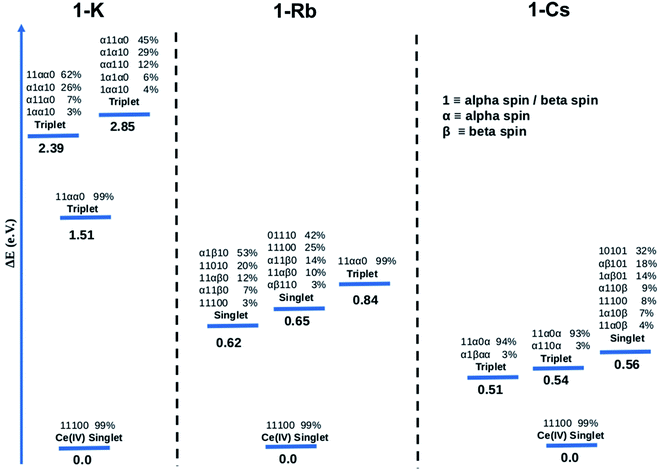
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 for the singlet ground state of 1-K. When the orbital is half-filled, the spin of the electron is given (alpha or beta). Since there are 5 active orbitals, this corresponds to 5 presented digits, where the lowest energy is on the far left and the highest on the far right. The ground electronic state of 1-K is predicted to be a closed-shell singlet despite the fact that the active orbitals were taken from the restricted open shell Hartree–Fock (ROHF) calculation of the spin triplet state (S = 1). Interestingly, the two f-type orbitals are empty (see ESI† for more information about the MOs used in these calculations) in line with a Ce(IV)-type complex. These CASSCF calculations predict that the first excited state is a single-reference triplet located 1.51 eV above the ground state. Two multiconfigurational triplet states are also found 2.39 and 2.85 eV above the ground state.
100 for the singlet ground state of 1-K. When the orbital is half-filled, the spin of the electron is given (alpha or beta). Since there are 5 active orbitals, this corresponds to 5 presented digits, where the lowest energy is on the far left and the highest on the far right. The ground electronic state of 1-K is predicted to be a closed-shell singlet despite the fact that the active orbitals were taken from the restricted open shell Hartree–Fock (ROHF) calculation of the spin triplet state (S = 1). Interestingly, the two f-type orbitals are empty (see ESI† for more information about the MOs used in these calculations) in line with a Ce(IV)-type complex. These CASSCF calculations predict that the first excited state is a single-reference triplet located 1.51 eV above the ground state. Two multiconfigurational triplet states are also found 2.39 and 2.85 eV above the ground state.
The computed ground state for the 1-Rb is also a single-reference closed-shell spin singlet. However, in this case three excited states, two multiconfigurational singlets and one single-reference triplet are closer in energy to the ground state (0.62, 0.65 and 0.84 eV, respectively) than in 1-K. In the case of the 1-Cs ground state, the CASSCF method predicts a closed-shell spin singlet with three excited states (two nearly single-reference triplets and one multireference singlet) 0.51, 0.54 and 0.56 eV above the ground state.
CASSCF results show single-reference closed-shell singlet ground states for the three alkali metal-capped Ce imido complexes. However, the lack of 4f orbital occupancy in the CAS calculations appears inconsistent with the n(f0) values determined from XANES (∼0.4). Therefore, the bonding characteristics of the capped imido complexes were further analyzed using Natural Bonding Analysis (NBO) and Wiberg Indexes (WBI), with nearly the same results for all three of these complexes: in each case, a double bond Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N was found. Both σ and π bonds are strongly polarized towards nitrogen (82% for σ and 85% for π) and involve a hybrid 5d/4f orbital on Ce. Directly consistent with the XANES-derived results, the 5d/4f mixtures in these bonding orbitals are 60% 5f – 40% 5d. The associated WBI is 1.76 (close to 2.0) indicating that the bonds are significantly covalent. Therefore, in a covalent picture, a large fraction of these bonding electrons could be attributed to the Ce (and mainly on the 4f orbital), explaining the n(f0) value obtained experimentally. For the sake of completeness, CASSCF calculations were carried out using the same methodology for the uncapped imido complexes. The ground state is found to be a closed-shell singlet, as for all alkali-capped complexes. The first excited states are found to be two open-shell singlets (0.45 and 0.54 eV) and a triplet (0.74 eV).
N was found. Both σ and π bonds are strongly polarized towards nitrogen (82% for σ and 85% for π) and involve a hybrid 5d/4f orbital on Ce. Directly consistent with the XANES-derived results, the 5d/4f mixtures in these bonding orbitals are 60% 5f – 40% 5d. The associated WBI is 1.76 (close to 2.0) indicating that the bonds are significantly covalent. Therefore, in a covalent picture, a large fraction of these bonding electrons could be attributed to the Ce (and mainly on the 4f orbital), explaining the n(f0) value obtained experimentally. For the sake of completeness, CASSCF calculations were carried out using the same methodology for the uncapped imido complexes. The ground state is found to be a closed-shell singlet, as for all alkali-capped complexes. The first excited states are found to be two open-shell singlets (0.45 and 0.54 eV) and a triplet (0.74 eV).
The CASSCF results for the alkali metal-capped Ce oxo complexes (Fig. 8) are quite similar to those determined for the imido case. For all complexes, we found single-reference ground states where the f-type orbitals included in the CAS are unoccupied. For both (2-K)4 and (2-Rb)4, the first excited state is a single-reference triplet, whereas for the (2-Cs)4 it is a multi-reference singlet. The energy of the second singlet and second triplet of (2-K)4 are 2.75 eV and 3.29 eV above the ground state respectively. On the other hand, the next calculated excited electronic states for (2-Rb)4 (Fig. 8) are single-reference triplets in which one electron with alpha spin occupies one of the f orbitals of the Ce atom. For (2-Cs)4, three singlet excited states located 1.52, 1.98 and 2.18 eV above the singlet ground state have been identified. Following a similar procedure as for the imido complexes, the bonding was analyzed further. At the NBO level, only purely donor–acceptor interactions were observed, where the oxygen acts as a donor and the cerium as an acceptor. The associated WBI for each of the oxos is 1.34, indicating that the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds are less covalent than for the imido cases, and therefore having a stronger ionic component. This is reminiscent of the study by Barros et al.47 regarding the nature of the bonding in uranium oxo and imido complexes. The acceptor orbitals on Ce are again hybrid 5d/4f orbitals that are based on 60% 4f and 40% 5d, just as with the imido complexes. These results are in line with the experimental observation of similar n(f0) values between the imido and oxo complexes. CASSCF calculations for an uncapped oxo complex also predict the ground state to be a closed-shell singlet with the first excited states being up to 4.0 eV higher in energy.
O bonds are less covalent than for the imido cases, and therefore having a stronger ionic component. This is reminiscent of the study by Barros et al.47 regarding the nature of the bonding in uranium oxo and imido complexes. The acceptor orbitals on Ce are again hybrid 5d/4f orbitals that are based on 60% 4f and 40% 5d, just as with the imido complexes. These results are in line with the experimental observation of similar n(f0) values between the imido and oxo complexes. CASSCF calculations for an uncapped oxo complex also predict the ground state to be a closed-shell singlet with the first excited states being up to 4.0 eV higher in energy.
Discussion
The overall results described above are surprising due to (1) the feature between the f1,2 peak and f0 peak in the L3-edge XANES which necessitated more detailed analysis using HERFD; (2) the similarity in n(f0) between the imido and oxo compounds, irrespective of Ce = N or Ce = O motif or alkali metal capping cation species; and (3) the same lack of variability despite large changes in the degree of temperature-independent paramagnetism. In fact, our initial hypothesis was that the capping cation species might enable tunability in n(f0) based on changing the degree of covalency; however, this was not observed.More specifically, the XAS results show that the anilide, imido and oxo samples can all be considered as formal Ce(IV), yet despite the similarities in n(f0) between the Ce imido and Ce oxo complexes, XANES and HERFD data both exhibit notable differences in the characteristics of the f1,2 and f0 peaks. HERFD results confirm that these dissimilarities are not attributable to differences in f-orbital occupancy, but rather to ligand-field splitting behavior of the 5d states. This result is interesting in that, while the electronic structure between the two classes of complexes is identical with respect to fractional f0 occupancy, the distribution of the d-states differs depending on the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N vs. Ce
N vs. Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonding species, with the splitting greater in the oxo complexes (Fig. 4). In addition, the dz2 state is notably shifted to higher energy in comparison to the imidos. The greater ligand-field splitting in the oxos is somewhat expected, based on bond length trends, as indicated in Table 1: Ce–L bond lengths (L = ligand) are shortest for the oxos (most splitting) and longer for the imidos (least splitting). Computationally, all alkali metal-capped imido and oxo complexes are determined to have closed-shell singlet ground states with hybrid 5d/4f orbitals that are based on a 60% 4f and 40% 5d mixture, consistent with the n(f0) values extracted from XANES fitting. As a general trend, however, the energy gap between the ground and lowest-lying excited state is smaller for the imidos than for the oxos. A different degree of covalent behavior is also observed between the classes of complexes. The WBI parameter corresponds to Ce
O bonding species, with the splitting greater in the oxo complexes (Fig. 4). In addition, the dz2 state is notably shifted to higher energy in comparison to the imidos. The greater ligand-field splitting in the oxos is somewhat expected, based on bond length trends, as indicated in Table 1: Ce–L bond lengths (L = ligand) are shortest for the oxos (most splitting) and longer for the imidos (least splitting). Computationally, all alkali metal-capped imido and oxo complexes are determined to have closed-shell singlet ground states with hybrid 5d/4f orbitals that are based on a 60% 4f and 40% 5d mixture, consistent with the n(f0) values extracted from XANES fitting. As a general trend, however, the energy gap between the ground and lowest-lying excited state is smaller for the imidos than for the oxos. A different degree of covalent behavior is also observed between the classes of complexes. The WBI parameter corresponds to Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double-bonded character for the imidos, suggesting that the bonding is significantly covalent. In contrast, the WBI parameter for the oxo case suggests closer to single-bond character with a greater ionic component. Despite the different covalent character, similar n(f0) values result from two different mechanisms. In the imidos, a fraction of the bonding electrons can be attributed to Ce on the 4f orbital, leading to a 5d/4f mixture in the bonding orbitals of 60% 4f and 40% 5d. In the oxos, only pure donor–acceptor behavior is observed, where Ce is the acceptor, with hybrid 5d/4f orbitals also with 60% 4f and 40% 5d. This observation provides an important example of how complexes with significantly different bonding characteristics can still result in similar n(f0) values.
N double-bonded character for the imidos, suggesting that the bonding is significantly covalent. In contrast, the WBI parameter for the oxo case suggests closer to single-bond character with a greater ionic component. Despite the different covalent character, similar n(f0) values result from two different mechanisms. In the imidos, a fraction of the bonding electrons can be attributed to Ce on the 4f orbital, leading to a 5d/4f mixture in the bonding orbitals of 60% 4f and 40% 5d. In the oxos, only pure donor–acceptor behavior is observed, where Ce is the acceptor, with hybrid 5d/4f orbitals also with 60% 4f and 40% 5d. This observation provides an important example of how complexes with significantly different bonding characteristics can still result in similar n(f0) values.
We consider also the effects of varying the alkali-metal capping cation species from harder (Li+, K+) to softer (Cs+) on the resulting electronic structure of the Ce imido and oxo complexes. Capping-cation-dependent trends observed for the Ce imido complexes are subtle, and best perceived through FDMNES simulations (Fig. 4). The d-state distribution narrows as noted from a lower-energy shoulder going from Li+ to Cs+. The opposite trend is observed in the oxo complexes, where d-state splitting is enhanced, resulting in distribution broadening going from K+ to Cs+. This trend is visible in experimental HERFD data (Fig. 3) and explained through FDMNES simulations (Fig. 4) as resulting from the out-of-plane d-states (dz2) shifting to higher energies. The uncapped imido 1− was synthesized and exhibits very similar spectroscopic behavior to 1-Cs. Computational results provide additional information regarding the excited states of the complexes, and how they are affected by the capping alkali metal cation. As a general trend, for both the imidos and oxos, the energy gap between the ground state and lowest-lying excited state is largest for K+ and lowest for Cs+ capping species. With the exception of (2-Rb)4, all complexes feature multireference excited states within the three lowest energy states, but the nature of these excited states varies from complex to complex in an apparently non-systematic manner. Together, the data suggest that the alkali metal capping species, while having no perceivable effect on n(f0), have the capability to fine-tune the d-state and excited state distributions within the complexes. Moving forward, it would be interesting to consider how this might be used as a tool to provide finer control over complex reactivity.
Results from our magnetism study as well as CASSCF calculations indicate that the electronic picture within the Ce imido/oxo systems is even more complex than the systematic trends observed from XANES and HERFD suggest. All complexes exhibit enhanced levels of TIP; however, a number of anomalies suggest that TIP is not driven by a simple van Vleck mixing of the ground state singlet and excited state triplet states involving localized f- and ligand orbitals as is believed to be the case for some other lanthanide organometallic systems.7–9,11–14 For one, in contrast to previous work on Ln coordination complexes where multiconfigurational, open-shell singlet ground states exist, all these closed-shell Ce imido and oxo complexes exhibit a large difference in χ0 despite having similar n(f0) values. In fact, it should be noted that the χ0 values represent a wider range than has been reported previously even for more structurally diverse formal Ce(IV) complexes,46 although the amount of available literature data remain limited. Additionally, no observed correlation exists between the ground state and the first excited state triplet determined from CASSCF results and χ0, as would be expected for a conventional van Vleck mechanism for TIP. Moreover, while the imidos exhibit generally lower levels of TIP than the oxos, (2-Rb)4 is a reproducible outlier in this trend. Lastly, within the imido and oxo species with varying alkali metal capping cation, there is no systematic trend from harder to softer cation species regarding the level of TIP observed. While some form of van Vleck mixing must occur to generate TIP behavior, some additional mechanism must be at play than those discussed here to result in the high χ0 values observed. Future work is needed to rationalize the TIP behavior and the lack of energetically close magnetic excited states from calculations.
An interesting factor that should affect the overall magnetic behavior is that the 5d mixing with the 4f states changes the degree of angular momentum quenching through a combination of the degree of d character and possible variations in the ensuing degree of delocalization of the f-orbital. Measuring the degree of delocalization of Ce 4f orbitals is very challenging. It has been previously noted that a small shift in the white line of the Ce LIII-edge between the f1,2 peak in CeO2 and Ce(III) compounds is due to a more delocalized configuration of the 4f orbital in CeO2.48 Recent calculations suggest this shift may instead be due to increased f2 character when intermediate valence increases, which has a similar effect to a delocalized configuration.18 In any case, similar shifts are observed in other formal Ce(IV) compounds,1 with cerocene having the closest correspondence to the leading f1,2 peak of a pure Ce(III) compound.2 In fact, the f1,2 peak energy is shifted from the position of pure Ce(III) (Table S2†), indicative of delocalized behavior. Notably, the f1,2 peak is not shifted as far as in CeO2, suggesting that the 4f orbital in either the imido and oxo samples presented in this study is not as delocalized. However, there are no notable differences between the imido and oxo samples regarding the f1,2 peak from XANES, the lack of which suggests that if this effect plays a role in the variations in χ0 for the present compounds, the ensuing edge shifts are within the resolution of the data.
CASSCF calculations provide some additional insight into the non-systematic differences observed in the magnetism data for the imido and oxo complexes. We find that the distribution and nature of these excited states varies from complex to complex. These variations could, in part, explain the lack of trends between the complexes in magnetism data. Although CASSCF results show trends in ground-to-excited state gaps that reflect periodic trends in the alkali metal cations, related trends are not apparent in the measured TIP values. It is also worth considering why (2-Rb)4 remains an outlier with respect to its low level of TIP in comparison to the other oxo complexes. While this exception does not mimic any of the trends observed from our spectroscopic measurements, there is precedence for magnetic behavior to follow non-systematic trends based on associated alkali metal species.3 We can also consider anomalies in the nature of the excited states of the complexes. In particular, what differs for (2-Rb)4 compared with the other complexes is both the lack of multireference excited states and the large energy differences between its excited states. Each of the three lowest-lying triplets is fairly discrete in energy (Fig. 8), rather than clustering around a similar energy range as is apparent especially for the imido samples (Fig. 7). Regardless of the exact reason for the anomaly in magnetism trends, it is apparent that the electronic structure of these complexes is complex, and beyond the predictability of periodic trends.
Conclusion
We performed electronic structure studies on previously reported Ce(IV) imido and oxo compounds, as well as two new Ce(IV) oxo species. The electronic behavior of the Ce imido and oxo complexes presented herein contrasts that of Ln organometallics in which delocalized electrons from aromatic groups are directly interacting with the Ln center, and as a result exhibit multiconfigurational ground states. Rather, by separating the Ln center from the aromatic groups and stabilizing Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N or Ce
N or Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moieties through use of an alkali metal capping cation, the ground states are not multiconfigurational, but rather closed-shell singlet single-reference ground states. We observe that these closed-shell singlet systems are fundamentally different than those with open-shell singlet ground states due to the involvement of the 5d orbital, which we track in detail using XANES and HERFD-XAS. The 4f/5d hybridization within these systems is strong and is what gives rise to the double-peak feature observed in the resulting XANES spectra. Our spectroscopy results confirm that despite having n(f0) values that are essentially the same across the complexes, the energy distribution of d-states within the complexes varies substantially. This distribution is also more subtly affected by the identity of the alkali metal capping cation. While previous studies have shown that small changes in molecular perturbation can result in large f-orbital occupancy changes in lanthanide organometallics, this study shows that small changes in molecular structure can result in relatively fixed f-orbital occupancy, with different distributions of underlying states, potentially driving large differences in their paramagnetic states. Moving forward, such complexes provide a platform to consider in future studies how fine-tuning d-state distributions within Ln organometallic complexes such as those reported herein can affect reactivity in a manner that is independent of lanthanide valence.
O moieties through use of an alkali metal capping cation, the ground states are not multiconfigurational, but rather closed-shell singlet single-reference ground states. We observe that these closed-shell singlet systems are fundamentally different than those with open-shell singlet ground states due to the involvement of the 5d orbital, which we track in detail using XANES and HERFD-XAS. The 4f/5d hybridization within these systems is strong and is what gives rise to the double-peak feature observed in the resulting XANES spectra. Our spectroscopy results confirm that despite having n(f0) values that are essentially the same across the complexes, the energy distribution of d-states within the complexes varies substantially. This distribution is also more subtly affected by the identity of the alkali metal capping cation. While previous studies have shown that small changes in molecular perturbation can result in large f-orbital occupancy changes in lanthanide organometallics, this study shows that small changes in molecular structure can result in relatively fixed f-orbital occupancy, with different distributions of underlying states, potentially driving large differences in their paramagnetic states. Moving forward, such complexes provide a platform to consider in future studies how fine-tuning d-state distributions within Ln organometallic complexes such as those reported herein can affect reactivity in a manner that is independent of lanthanide valence.
Experimental
General synthesis methods
All reactions and manipulations were performed under an inert atmosphere (N2) using standard Schlenk techniques or in a drybox equipped with a molecular sieves 13X/Q5 Cu-0226S catalyst purifier system. Glassware was oven-dried for at least 3 h at 150 °C prior to use. 1H NMR spectra were obtained on a Bruker DMX-300 Fourier transform NMR spectrometer operating at 300 MHz for 1H, 75.48 MHz for 13C and 282.2 MHz for 19F. Chemical shifts were recorded in units of parts per million and referenced against residual proteo solvent peaks. Infrared spectra were measured on a PerkinElmer 1600 series spectrometer. UV-vis spectra were recorded on PerkinElmer Lamba 950 spectrometer. Infrared spectra were recorded in the range from 4000 to 500 cm−1 on Bruker Invenio R spectrometer in KBr pellets. Elemental analyses were recorded on a Costech ECS 4010 analyzer. Cyclic Voltammetry (CV) experiments were performed using a CH-Instruments 620D Electrochemical Analyzer/Workstation. Data were processed using CHI software v9.24. All experiments were performed in an N2 atmosphere glove-box using electrochemical cells consisting of a 4 mL vial, glassy carbon working electrode, a platinum wire counter electrode, and a silver wire plated with AgCl as a quasi-reference electrode. The working electrode surfaces were polished prior to each set of experiments. THF solutions of the analyzed compound (∼1 mM) and supporting electrolyte [nPr4N][BArF24] (0.1 M) were used for electrochemical studies. Potentials were reported versus the ferrocene/ferrocenium (Fc/Fc+) couple. Ferrocene was added as an internal standard for calibration at the end of each run. All data were collected in a positive-feedback IR compensation mode. THF and pentane were sparged for 20 min with dry argon and dried using a commercial two-column solvent purification system comprising columns packed with Q5 reactant and neutral alumina respectively (for pentane and hexanes). Deuterated toluene and benzene (Cambridge Isotopes) were stored over molecular sieves (4 Å) overnight prior to use. THF-d8 (Cambridge Isotopes) was dried over sodium and distilled prior to use. Benzophenone (ACROS organics) was recrystallized from ethanol and vacuum-dried prior to use. Potassium bis(trimethylsilyl)amide (Sigma) was used as received. Cesium bis(trimethylsilyl)amide was prepared according to published reports.49Powder samples were prepared in an argon-filled drybox for measurement by mixing with dry boron nitride and packed into a slotted aluminum holder with aluminized mylar windows, sealed with crushed indium wire. Since the samples are air sensitive, the sealed holders were kept under argon until measurement, and exposed to air for less than one minute during transfer to vacuum. Samples were measured both at 50 K and 300 K using a liquid-helium cooled cryostat to test for temperature dependence of the resulting spectra. An easily-oxidizable sample, such as cerium tris(tetramethylcyclopentadienyl) (CeCptet3), was measured along with the samples to ensure that no O2 had leaked into the sample holder during measurement.
XANES data were fit in order to extract information about the f-orbital occupancy according to previously described methods,11,12,14 although we report the f0-configuration fraction, n(f0), rather than the f-orbital occupancy for reasons that are described in the Results section. Details are provided in ESI.† In particular, the major peaks at approximately 5726 eV and at 5736 eV, which are predominantly due to 2p3/2 → 5d5/2 transitions that have been split in the presence of the core hole due to the majority f1 (with minority f2) or the f0 configuration fraction, respectively, have been modeled with a single Gaussian function each, even when other contributions are visible. This methodology was chosen so that the data from all the samples could be fit with the same model. Consideration of using a more a complex model is provided in the ESI.† Reported errors include uncertainty from this issue.
HERFD spectra were simulated using the FDMNES code.45 A convolution over the density of states was calculated for a cluster with a 7 Å radius in multiple scattering mode using a Green's function method on a muffin-tin potential. The partial projection of the density of states, including specific d-state contributions, were extracted. The core level width was reduced to 1.2 eV in order to obtain simulations comparable to the experimental HERFD data. For meaningful orbital contributions, the z-axes of the structures were aligned to be along the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N or Ce
N or Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in the complex structure. Throughout, orbitals are listed according to FDMNES convention, where (l,m) = (2,−2) corresponds to dxy, (2,−1) to dyz, (2,0) to dz2, (2,1) to dxz and (2,2) to dx2−y2.
O bond in the complex structure. Throughout, orbitals are listed according to FDMNES convention, where (l,m) = (2,−2) corresponds to dxy, (2,−1) to dyz, (2,0) to dz2, (2,1) to dxz and (2,2) to dx2−y2.
TIP values were extracted by fitting the background-subtracted and two-field corrected data to a constant + Curie–Weiss model with χ = CJ/(T − ϴCW) + χ0, where CJ is the Curie constant, ϴCW is the Curie–Weiss temperature indicating the strength of magnetic interactions, and χ0 is the magnitude of the TIP component to the susceptibility. The Curie–Weiss part of the model is used primarily to subtract small paramagnetic impurity contributions which are generally present for low-susceptibility samples. Multiple measurements per sample were collected to ensure reproducibility. Error bars in the reported χ0 results were determined by averaging over multiple measurements and samples, and are typically larger than the systematic ∼10–15% error from the quartz-wool background subtraction combined with diamagnetic correction.
where c is the analyte concentration in mol ml−1, F is the measurement frequency in Hz, and Δf is the difference between the standard peak shifts in solution and in the capillary in Hz. Δf was calculated using the equation:
Data availability
All experimental data, procedures for data analysis and pertinent data sets are provided in the ESI.†Author contributions
Moreau, Lapsheva, Schelter and Booth conceived of the project and designed the experiments. The synthetic work and initial characterization by XRD was performed by Lapsheva, Gau, and Manor. Carroll also assisted with XRD data collection and analysis. Characterization using cyclic voltammetry and Evans method analysis was performed by Lapsheva and Yang. XANES data were collected by Moreau, Qiao, and Booth, with the addition of Sokaras for the HERFD data. Analysis of the XANES and HERFD data was performed by Moreau and Booth. Magnetic data were collected and analyzed by Moreau and Booth. Computational studies were performed by Amaro-Estrada and Maron. Lukens oversaw aspects of the overall interpretation. The manuscript was written by Moreau, Lapsheva, Lukens, Schelter, Maron, and Booth.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The presented work was supported by the Director, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, Quantum Information Systems Program of the U.S. Department of Energy (DOE) at LBNL under Contract No. DE-AC02-05CH11231. XANES and HERFD-XAS measurements were performed at beamlines 11-2 and 6-2, respectively, at the Stanford Synchrotron Radiation Lightsource, which is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under contract no. DE-AC02-76SF00515. We would like to thank Ryan Davis for his assistance with XANES measurements and Julian Rees for his assistance with HERFD-XAS data collection. Additionally, we thank Dr Peter Glatzel and the European Synchrotron Radiation Facility for the use of their Ge(331) analyzer crystals. E. J. S. thanks the National Science Foundation (CHE-1955724) for support of E. L. and the Office of Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division, Materials and Chemical Sciences Research for Quantum Information Science Program, of the U.S. Department of Energy under Award DE-SC0020169 for support of this work. E. J. S. also thanks the University of Pennsylvania for support. We thank Dr Lukman Solola for the initial experiments on the isolation of the Ce(IV) oxo compounds presented in this paper. Laurent Maron is a senior member of the Institut Universitaire de France. CalMip is also acknowledged for a generous grant of computing time.References
- G. R. Stewart, Rev. Mod. Phys., 1984, 56, 755–787 CrossRef CAS.
- J. W. Allen and R. M. Martin, Phys. Rev. Lett., 1982, 49, 1106–1110 CrossRef CAS.
- A. L. Cornelius, J. M. Lawrence, J. L. Sarrao, Z. Fisk, M. F. Hundley, G. H. Kwei, J. D. Thompson, C. H. Booth and F. Bridges, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 7993–8000 CrossRef CAS.
- M. Dolg, P. Fulde, W. Küchle, C. S. Neumann and H. Stoll, J. Chem. Phys., 1991, 94, 3011–3017 CrossRef CAS.
- M. Dolg, P. Fulde, H. Stoll, H. Preuss, A. Chang and R. M. Pitzer, Chem. Phys., 1995, 195, 71–82 CrossRef CAS.
- W. Liu, M. Dolg and P. Fulde, Inorg. Chem., 1998, 37, 1067–1072 CrossRef CAS.
- N. M. Edelstein, P. G. Allen, J. J. Bucher, D. K. Shuh, C. D. Sofield, N. Kaltsoyannis, G. H. Maunder, M. R. Russo and A. Sella, J. Am. Chem. Soc., 1996, 118, 13115–13116 CrossRef CAS.
- C. H. Booth, M. D. Walter, M. Daniel, W. W. Lukens and R. A. Andersen, Phys. Rev. Lett., 2005, 95, 267202 CrossRef CAS PubMed.
- M. D. Walter, C. H. Booth, W. W. Lukens and R. A. Andersen, Organometallics, 2009, 28, 698–707 CrossRef CAS.
- A. Kerridge, R. Coates and N. Kaltsoyannis, J. Phys. Chem. A, 2009, 113, 2896–2905 CrossRef CAS PubMed.
- C. H. Booth, M. D. Walter, D. Kazhdan, Y.-J. Hu, W. W. Lukens, E. D. Bauer, L. Maron, O. Eisenstein and R. A. Andersen, J. Am. Chem. Soc., 2009, 131, 6480–6491 CrossRef CAS PubMed.
- R. L. Halbach, G. Nocton, C. H. Booth, L. Maron and R. A. Andersen, Inorg. Chem., 2018, 57, 7290–7298 CrossRef CAS PubMed.
- A. Ashley, G. Balazs, A. Cowley, J. Green, C. H. Booth and D. O'Hare, Chem. Commun., 2007, 1515–1517, 10.1039/B700303J.
- C. H. Booth, D. Kazhdan, E. L. Werkema, M. D. Walter, W. W. Lukens, E. D. Bauer, Y.-J. Hu, L. Maron, O. Eisenstein, M. Head-Gordon and R. A. Andersen, J. Am. Chem. Soc., 2010, 132, 17537–17549 CrossRef CAS PubMed.
- C. S. Neumann and P. Fulde, Z. Phys. B: Condens. Matter, 1989, 74, 277–278 CrossRef.
- M. Dolg and P. Fulde, Chem. –Eur. J., 1998, 4, 200–204 CrossRef CAS.
- R. G. Denning, J. Harmer, J. C. Green and M. Irwin, J. Am. Chem. Soc., 2011, 133, 20644–20660 CrossRef CAS PubMed.
- D.-C. Sergentu, C. H. Booth and J. Autschbach, Chem. –Eur. J., 2021, 27, 7188 CrossRef CAS PubMed.
- M. Lundberg, M. R. A. Blomberg and P. E. M. Siegbahn, Inorg. Chem., 2004, 43, 264–274 CrossRef CAS PubMed.
- S. A. Venturinelli Jannuzzi, Q. M. Phung, A. Domingo, A. L. B. Formiga and K. Pierloot, Inorg. Chem., 2016, 55, 5168–5179 CrossRef CAS PubMed.
- B. K. Mai and Y. Kim, Inorg. Chem., 2016, 55, 3844–3852 CrossRef CAS PubMed.
- D. F. Leto, A. A. Massie, D. B. Rice and T. A. Jackson, J. Am. Chem. Soc., 2016, 138, 15413–15424 CrossRef CAS PubMed.
- M. Srnec, S. D. Wong and E. I. Solomon, Dalton Trans., 2014, 43, 17567–17577 RSC.
- J. Amtawong, D. Balcells, J. Wilcoxen, R. C. Handford, N. Biggins, A. I. Nguyen, R. D. Britt and T. D. Tilley, J. Am. Chem. Soc., 2019, 141, 19859–19869 CrossRef CAS PubMed.
- D. Delony, M. Kinauer, M. Diefenbach, S. Demeshko, C. Würtele, M. C. Holthausen and S. Schneider, Angew. Chem., Int. Ed., 2019, 58, 10971–10974 CrossRef CAS PubMed.
- Y. Dong, J. T. Lukens, R. M. Clarke, S.-L. Zheng, K. M. Lancaster and T. A. Betley, Chem. Sci., 2020, 11, 1260–1268 RSC.
- D. A. Iovan and T. A. Betley, J. Am. Chem. Soc., 2016, 138, 1983–1993 CrossRef CAS PubMed.
- K. M. Carsch, I. M. DiMucci, D. A. Iovan, A. Li, S.-L. Zheng, C. J. Titus, S. J. Lee, K. D. Irwin, D. Nordlund, K. M. Lancaster and T. A. Betley, Science, 2019, 365, 1138 CrossRef CAS PubMed.
- C. A. Laskowski, A. J. M. Miller, G. L. Hillhouse and T. R. Cundari, J. Am. Chem. Soc., 2011, 133, 771–773 CrossRef CAS PubMed.
- I. T. Alt, C. Guttroff and B. Plietker, Angew. Chem., Int. Ed., 2017, 56, 10582–10586 CrossRef CAS PubMed.
- D. Fujita, A. Kaga, H. Sugimoto, Y. Morimoto and S. Itoh, Bull. Chem. Soc. Jpn., 2019, 93, 279–286 CrossRef.
- M. Goswami, V. Lyaskovskyy, S. R. Domingos, W. J. Buma, S. Woutersen, O. Troeppner, I. Ivanović-Burmazović, H. Lu, X. Cui, X. P. Zhang, E. J. Reijerse, S. DeBeer, M. M. van Schooneveld, F. F. Pfaff, K. Ray and B. de Bruin, J. Am. Chem. Soc., 2015, 137, 5468–5479 CrossRef CAS PubMed.
- D.-Q. Wu, Z.-Y. Guan, Y. Peng, J. Sun, C. Zhong and Q.-H. Deng, Adv. Synth. Catal., 2018, 360, 4720–4725 CrossRef CAS.
- L. A. Solola, A. V. Zabula, W. L. Dorfner, B. C. Manor, P. J. Carroll and E. J. Schelter, J. Am. Chem. Soc., 2016, 138, 6928–6931 CrossRef CAS PubMed.
- Y.-M. So, Y. Li, K.-C. Au-Yeung, G.-C. Wang, K.-L. Wong, H. H. Y. Sung, P. L. Arnold, I. D. Williams, Z. Lin and W.-H. Leung, Inorg. Chem., 2016, 55, 10003–10012 CrossRef CAS PubMed.
- P. L. Damon, G. Wu, N. Kaltsoyannis and T. W. Hayton, J. Am. Chem. Soc., 2016, 138, 12743–12746 CrossRef CAS PubMed.
- O. Mooßen and M. Dolg, Chem. Phys. Lett., 2014, 594, 47–50 CrossRef.
- A. Kotani, T. Jo and J. C. Parlebas, Adv. Phys., 1988, 37, 37–85 CrossRef CAS.
- W. Kohn and T. K. Lee, Philos. Mag., 1982, 45, 313–322 CrossRef CAS.
- S. G. Minasian, E. R. Batista, C. H. Booth, D. L. Clark, J. M. Keith, S. A. Kozimor, W. W. Lukens, R. L. Martin, D. K. Shuh, S. C. E. Stieber, T. Tylisczcak and X.-d. Wen, J. Am. Chem. Soc., 2017, 139, 18052–18064 CrossRef CAS PubMed.
- W. W. Lukens, C. H. Booth and M. D. Walter, Dalton Trans., 2021, 50, 2530–2535 RSC.
- K. O. Kvashnina, S. M. Butorin and P. Glatzel, J. Anal. At. Spectrom., 2011, 26, 1265–1272 RSC.
- O. Hirsch, K. O. Kvashnina, L. Luo, M. J. Süess, P. Glatzel and D. Koziej, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 15803 CrossRef CAS PubMed.
- O. Keski-Rahkonen and M. O. Krause, At. Data Nucl. Data Tables, 1974, 14, 139–146 CrossRef CAS.
- O. Bunău and Y. Joly, J. Phys.: Condens. Matter, 2009, 21, 345501 CrossRef PubMed.
- K. J. McLean and A. W. Munro, Drug Metab. Rev., 2008, 40, 427–446 CrossRef CAS PubMed.
- N. Barros, D. Maynau, L. Maron, O. Eisenstein, G. Zi and R. A. Andersen, Organometallics, 2007, 26, 5059–5065 CrossRef CAS.
- H. Dexpert, R. C. Karnatak, J. M. Esteva, J. P. Connerade, M. Gasgnier, P. E. Caro and L. Albert, Phys. Rev. B, 1987, 36, 1750–1753 CrossRef CAS PubMed.
- F. T. Edelmann, F. Pauer, M. Wedler and D. Stalke, Inorg. Chem., 1992, 31, 4143–4146 CrossRef CAS.
- Bruker, SAINT, Bruker AXS Inc., Madison, Wisconsin, USA, 2009 Search PubMed.
- Bruker, SHELXTL, Bruker AXS Inc., Madison, Wisconsin, USA, 2009 Search PubMed.
- G. M. Sheldrick, SADABS, University of Gottingen, Germany, 2007 Search PubMed.
- G. M. Sheldrick, TWINABS, University of Gottingen, Germany, 2012, 2012 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- G. M. Sheldrick, SHELXL 2014/7, University of Gottingen, Germany, 2014 Search PubMed.
- D. Sokaras, T. C. Weng, D. Nordlund, R. Alonso-Mori, P. Velikov, D. Wenger, A. Garachtchenko, M. George, V. Borzenets, B. Johnson, T. Rabedeau and U. Bergmann, Rev. Sci. Instrum., 2013, 84, 053102 CrossRef CAS PubMed.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532 CrossRef CAS.
- G. Nocton, F. Burdet, J. Pecaut and M. Mazzanti, Angew. Chem., Int. Ed., 2007, 46, 7574–7578 CrossRef CAS PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- M. J. Frisch, G. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. Sonnenberg, M. Hada and D. Fox, 2009.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2071351 and 2071352. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc06623d |
| ‡ Current address: Department of Chemistry, Washington State University, Pullman, WA 99164, United States. |
| This journal is © The Royal Society of Chemistry 2022 |